Abstract
In the framework of risk assessment for flash floods, vulnerability is a key concept to assess the susceptibility of elements at risk. Vulnerability is defined as expected degree of loss for an element at risk due to a hazard impact of a defined magnitude and frequency. Besides the increasing number of studies on flash floods available, in-depth information on vulnerability was missing so far. In order to close this gap, a vulnerability model was created for micro-sized enterprises exposed to flash floods in Greece. This model was based on a nonlinear regression approach using data from four different events. By means of bootstrapping, different functions were fitted to the data, and a modified Weibull distribution was found to represent the relationship between process magnitude and degree of loss best. Moreover, there is no need to distinguish between different business sectors when computing vulnerability for buildings exposed. The model can be applied on a local scale and may serve as a basis for flash flood risk management.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A significant increase in losses due to flooding was repeatedly claimed by several scholars, including river flooding (Barredo 2007; Kreibich et al. 2014; Winsemius et al. 2014) and flash floods (Gaume et al. 2009; Calianno et al. 2013). Besides the ongoing discussion on climate change (Keiler 2013), this increase is triggered by exposure dynamics of elements at risk (Fuchs et al. 2015). Flash flood is usually understand as a high-intensity rainfall event [intensive rainfall up to 12 h (Gaume et al. 2009)] leading to high peak discharges (IAHS-UNESCO-WMO 1974), where the size of the catchment area is in most of the cases less than 1000 km2; with rather low runoff coefficients (Marchi et al. 2010). Additionally, the catchment shape includes a mean channel slope of less than 5–10 % (Rickenmann et al. 2008; Scheidl and Rickenmann 2010; Heiser et al. 2015). The timeliness of flood anticipation (relationship between catchment size and flood response time) is (depending on the catchment size) most of the time less than 6 h (Creutin et al. 2013). Nevertheless, the literature shows no clear definition of flash flood hazards. The National Weather Service Glossary (NWS 2016) defines flash floods as “rapid and extreme flow of high water into a normally dry area, or a rapid water level rise in a stream or creek above a predetermined flood level, beginning within 6 h of the causative event (e.g., intense rainfall, dam failure, ice jam). However, the actual time threshold may vary in different parts of the country. Ongoing flooding can intensify to flash flooding in cases where intense rainfall results in a rapid surge of rising flood waters”. On the other hand, Borga et al. (2014, p. 194) described flash floods as a result of “extreme rainstorms in headwater catchments [which] may trigger liquid floods, debris floods or debris flows. The type of process triggered depends on several characteristics, including the hydrologic, geomorphometric and geotechnical features of the slopes, the source materials and the availability of sediments, and the frequency-magnitude characteristics of the precipitation event”. Therefore, flash flood events strongly depend on the interconnection between rainfall distribution as well as geomorphological and hydrological factors of the area. Further important characteristics refer to the relationship between time and space of the rainfall distribution and the flash flood event; usually both aspects occur at the same place (Norbiato et al. 2008; Rozalis et al. 2010). The losses of such flood events highlight the increased importance of studies on flood hazard and risk, not only on a global scale but in particular on a national and sub-national level (Adhikari et al. 2010; Karagiorgos et al. 2016a). Apart from droughts, flash floods are reported to be among the most severe hazards in Mediterranean countries (Llasat et al. 2010). The Mediterranean region is especially vulnerable because of its propensity for high intense rainfalls in certain areas (Koutsoyiannis et al. 2012), its relatively high population density (Ganoulis 2003) and degree of development compared with some other semi-arid regions. Furthermore, the long history of settlement and land use (Papagiannaki et al. 2015) resulting in urban sprawl has produced major soil erosion and associated environmental impacts (Ganoulis 2003; Hooke 2016), which in turn support the generation of flash floods.
An analysis of flash flood events has shown a high amount of economic loss and fatalities resulting from the impact on the built environment (Gaume et al. 2009). Traditionally, besides the increasing amount of studies available on flash floods (e.g., Zorn et al. 2006; Comiti et al. 2008; Gaume et al. 2009; Llasat et al. 2010), most of the efforts are centred around physical process characteristics so far (e.g., Gaume et al. 2004; Delrieu et al. 2005; Zorn et al. 2006). Recently, some studies were explicitly focusing on the effects of flash floods, such as Gaume et al. (2009) taking a European perspective, Llasat et al. (2010) for Mediterranean countries, or Vinet (2008), Lasda et al. (2010) and Karagiorgos et al. (2016b) funnelling down to individual countries or regions exposed. In order to study the effects of flash floods, in addition to meteorological triggering and hydrological or hydraulic process propagation, information on elements at risk and their vulnerability is required. Consequently, a particular need for studies on vulnerability was repeatedly claimed in order to enhance risk management capabilities (De Marchi and Scolobig 2012; Borga et al. 2014). Following the axiom that risk is a function of hazard (i.e. events with a given magnitude and probability) times consequences (i.e. economic loss), the ability to quantitatively determine the vulnerability to flash floods is an essential need for reducing these consequences and planning for mitigation and adaptation (Fuchs 2009). While the understanding of hazard and exposure has significantly improved over the last decades, the analysis of vulnerability remains one of the challenges in the ongoing flood risk management discussion (Koks et al. 2015).
In overall, vulnerability to natural hazards refers to the potential losses (based on an impact event) and exposed elements, such as people or buildings (Cutter et al. 2003; Birkmann 2006; Thywissen 2006; Fuchs et al. 2015). Within the domain of natural sciences, vulnerability is usually considered as a function of a given process magnitude towards physical structures (Mazzorana et al. 2014), often referred as “technical” or “physical” vulnerability, and is defined as the expected degree of loss for an element at risk as a consequence of a design event (e.g. Fell et al. 2008; Fuchs et al. 2012a). The assessment includes in many cases the analysis of a complex system with the evaluation of several different parameters and factors such as building materials and techniques (Holub et al. 2012), damage analysis (Fuchs et al. 2007; 2011; 2012b) and process characteristics (Mazzorana et al. 2009; 2012). Consequently, vulnerability values range from 0 (no damages) to 1 (complete destruction) (Varnes 1984).
In recent years, several attempts have been made to address vulnerability to flooding focusing on tangible damages as outlined by Messner (2007) and Meyer et al. (2013) as well as on different empirical or synthetic approaches of model development for use on different scales (Papathoma-Köhle et al. 2011). The most common internationally accepted approach for the assessment of physical vulnerability for all hazards considered is the use of vulnerability functions. Governmental agencies, research institutions and insurance companies in many countries develop and use these functions to assess the potential damages and further apply these functions as a basis for prioritisation in flood risk management options (Penning-Rowsell et al. 2005). In almost all the models in use, flood depth is treated as the determining parameter for expected damages (Jongman et al. 2012) because there is a particular lack of other factors defining magnitude, such as e.g. flow velocity (Fuchs et al. 2007). Local-scale analyses are used to evaluate losses on an object level (individual buildings, e.g. Papathoma-Köhle et al. 2015) in contrast to regional analyses which are based on aggregated data, such as different land-use categories, using vulnerability indicators (e.g. Eidsvig et al. 2014). Different vulnerability models were developed in the past based on different approaches for the estimation of losses. These empirical models use observed data collected after an event by official authorities or insurance companies, or they are based on surveys, such as Fuchs et al. (2007), Totschnig et al. (2011) and Papathoma-Köhle et al. (2012) for torrential flooding in the European Alps, Thieken et al. (2008) and Kreibich et al. (2010) for river flooding in Central Europe and Luino et al. (2009) for flash floods in Southern Europe. Most of the studies performed were aiming in vulnerability assessment for either residential buildings (Totschnig et al. 2011; Papathoma-Köhle et al. 2012) or commercial buildings (Kreibich et al. 2010; Seifert et al. 2010), where some of the works were also targeted at hostels and hotels to mirror the importance of the tourism sector in individual case studies (Totschnig and Fuchs 2013).
Focusing on the commercial sector exposed to river flooding, Kreibich et al. (2010) presented an empirical model based on three different flood events in Germany. Losses were estimated using relative loss functions (expressed as a ratio between the loss and the total value of elements at risk) on local scale. Loss was separately computed for the building envelope, the building equipment, and the goods and products for different enterprise sizes (small and medium-sized businesses and larger companies). The data were gained through interviews, followed by the development of a vulnerability model, and a sensitivity analysis was performed using results of competitive models and information gained from reconstruction grants. Penning-Rowsell et al. (2005) presented flood damage losses on a local scale (expressed in absolute monetary terms) by combining flood duration and water depth. Information on vulnerability was provided for the building envelope, the building equipment, the mobile and immobile inventory as well as the stock of products and finally summed up in terms of cumulative vulnerability. Further, the US HAZUS-MH model (Scawthorn et al. 2006a, b) is based on an assessment of relative loss and provides vulnerability information for the building envelope, the building equipment, and the goods and products for different enterprise sizes (small and medium-sized businesses and larger companies). Similarly, the Australian RAM model is focusing on an assessment of vulnerability, taking absolute figures for larger enterprise sizes (NRE 2000).
It was repeatedly stated that an estimation of flood losses in the commercial sector is challenging because of the data generation and inhomogeneity due to the high range of loss for different types of companies and economic sectors affected (Seifert et al. 2010) or because of a general lack of information on losses (Gissing and Blong 2004; Kreibich et al. 2010). While for larger river floods in Europe, these challenges have been recognised and increasingly acknowledged in the different modelling approaches (see Kreibich et al. 2010 for a discussion), the gap still remains open for local-scale flash flood hazards. While it has been shown by Totschnig et al. (2011), Papathoma-Köhle et al. (2012) and Totschnig and Fuchs (2013) that fundamental differences between vulnerability functions for river flooding and torrential flooding exist, in-depth studies on flash flood vulnerability are still outstanding. However, such local-scale events repeatedly cause considerable damage in particular in Southern European countries, as shown for the example of Greece by Diakakis et al. (2012) and Karagiorgos et al. (2016a).
Hence, the objective of this study is to contribute to this gap and to assess the vulnerability of buildings occupied by micro-sized enterprises using data from well-documented flash flood events in Greece. Focusing on the commercial sector in Greece, 85 % of private employment is concentrated in small and medium-sized enterprises (SMEs) and more than 50 % in micro-sized enterprises. Micro-sized enterprises are defined as businesses with less than ten employees and an annual turnover and/or annual balance not exceeding €2 million (EU 2003), as such they often are family enterprises. In terms of total numbers, 96.7 % of businesses belong to the category of micro-sized enterprises (92.3 % for the EU27), employing 54.5 % of workforce (28.9 % for the EU27) and adding to the local economy a share of 34.6 % of the added value (21.1 % for the EU27) (EU 2013). These figures indicate the high dependence of the Greek economy on this type of enterprises compared to other European countries.
The presented model is based on object-specific empirical data, refers to the damage assessment of buildings and their content (equipment and goods) and supports the ongoing efforts in enhancing the capabilities in risk computation in the Mediterranean region (Karagiorgos et al. 2016a, b). For model validation, we used recent flood events from 2001, 2002, 2003 and 2007 which occurred in Greece. Further, the model results are compared with other loss models, such as those presented by Totschnig et al. (2011), Papathoma-Köhle et al. (2012, 2015) and Kreibich et al. (2010).
2 Study area
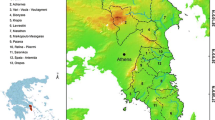
The study has been carried out in the region of East Attica, which is a part of the Attica administrative district located east of Athens in the Republic of Greece (Fig. 1). The study area extends from the municipality of Oropos in the north to the municipality of Lavreotiki in the south and is considerably influenced by counter urbanisation due to the adjacent capital of the country. The district covers an area of 1513 km2 between sea level and 1109 m a.s.l. with a plain hilly relief and a population amounting to 502,348 inhabitants (Hellenic Statistical Authority 2011). The geological structure of East Attica is dominated by two main units (Alexakis 2011): (a) the crystalline basement (Palaeozoic–Upper Cretaceous) which is composed of metamorphic rocks (marbles, schists and phyllites) and (b) Neogene–Quaternary deposits consisting of clays, marls, conglomerates, ophiolite fragments, sandstones and other coarse and unconsolidated erosion-prone sediments, the latter being responsible for the high number of flash floods in the region. The climate of the area is typical Mediterranean with hot, dry summers and cool, wet winters, including a long arid period between April and September (Petropoulos et al. 2012). The land surface is mainly covered by sparse sclerophyllous vegetation and some agricultural land at lower elevations. The higher altitudes are dominated by forest of different types as well as transitional woodland–scrubland vegetation.
The study area is characterised by extensive anthropogenic activities with settlements continuously growing. The economic development of this area is closely related to the construction of the international airport of Athens in 2001. In the period 1998–2010, the annual rate of increase in the building stock has been within a range of 5 to 30 % (Sapountzaki et al. 2011). As reported by Mantelas et al. (2010), the province of Mesogia has developed faster than any other area in Attica during the last 20 years. Specifically, the urban land cover increased from 60 km2 in 1994 to 75 km2 in 2000 and to 125 km2 in 2007. While the urban cover has grown by 25 % during the period 1994–2000, it increased by 66 % during the period 2000–2007 (Mantelas et al. 2010).
3 Method
The method is based on object-specific empirical data for micro-sized enterprises in order to derive vulnerability curves linking absolute loss data with flash flood magnitudes. The conceptual framework of the vulnerability model implies a quantitative valuation of the individual vulnerability components.
The study is based on the evaluation of loss assessment reports of the exposed micro-sized enterprises collected in the Prefecture of East Attica following the flood events of November 2001, 2002, January 2003 and May 2007. These loss assessment reports document the incurring losses shortly after each event and are regularly used by the public authority for possible compensation. These reports describe the characteristics of the affected building (building location and type, number of floors, building size, construction materials used and the year of construction), the process characteristics (flash flood magnitude using the water depth as proxy) and the incurring losses (description of the damages to the building envelope and/or damages regarding the content). A total of 61 reports with 41 belonging to the retail and 20 to the service sector was analysed. For the building envelope, damages had only been reported qualitatively in the loss assessment reports and the necessary quantitative values were calculated using data provided by the Earthquake Recovery Service of Greece (see also Appendix). Damages referring to the contents have been reported in quantitative values. The data were collected in a database, adjusted to inflation and checked for plausibility using available in situ and online information (Gordon and Janzen 2013).
A damage ratio was used to compute vulnerability, using an economic approach by establishing a ratio between the empirically collected loss and the value of every individual element at risk (Hausmann 1992). In a second set of calculations, this value obtained for every individual building was attributed to the respective process magnitude collected from the loss assessment reports. Scatter-plots were obtained linking these data on an object level. To analyse the differences between retail and service sectors, the Kruskal–Wallis test was used. In a subsequent step, a vulnerability function was fitted using non-linear regression approaches. This function represented the relationship between the degree of loss (DoL) and the process magnitude (I) for the businesses affected by flash floods in the study area (Eq. 1).
The targeted type of function had to fulfil three requirements. Firstly, the vulnerability values had to be between zero and one (\(f:I \mapsto [0,1]\)), the vulnerability function had to pass through the origin (\(f(I = 0) = 0\)) and the function had to be strictly increasing (\(I_{1} \le I_{2} \Rightarrow f(I_{1} ) \le f(I_{2} )\)).
Different functions meet these requirements and were tested within this study for their ability to best reflect the behaviour of vulnerability in the test site (Table 1). These functions were repeatedly used in similar studies, such as Totschnig et al. (2011) and Papathoma-Köhle et al. (2015), and were found to represent the loss behaviour adequately: as long as the process magnitude is relatively low, the DoL increases slowly; within the range of medium process magnitude, the DoL increases almost linear; and for high process magnitude, the DoL flattens out to one. Because of this behaviour, other functions such as linear functions were not used. The functions presented were modified from their original form in order to mirror the three requirements outlined above (Totschnig et al. 2011). The parameters \(\theta\) of all the presented models were calculated by minimising the root-mean-squared error (RMSE, Eq. 2).
In order to select the most appropriate model \(M^{*}\) based on the ability to predict the degree of loss from water depth, the data set was separated. The data were randomly split into a training data set (D train) which contained 51 data points and a test data set (D test) with ten data points. To avoid selecting a model which follows the training data set (D train) and therefore capturing a trend which is only apparent in the training data but not in the underlying population, the RMSE should be calculated on an independent data set. However, as the data set was relatively small, bootstrapping was used to calculate the RMSE for all models under consideration (Efron 1979). This was done by drawing a random sample with replacement of the same size than D train, named first bootstrap sample \(x^{*1}\). The model was then fitted on \(x^{*1}\), and the RMSE was calculated on the left-out sample. This sampling–training–validation cycle was repeated in total for 2000 times. The model with the lowest RMSE was chosen for the final vulnerability model.
The selection of the best-fitting model \((M^{*} )\) was done by comparing the mean of the 2000 RMSEs for all models where \(M^{*}\) is the one with the lowest error. In a next step, in order to estimate the predictive error, M* was applied on the D test. Finally, \(M^{*}\) was fitted to the entire data set (61 data points) to determine the parameters for the final vulnerability model \((\theta^{\varvec{*}} )\). Confidence intervals for the \(\theta^{*}\) were estimated using the bias-corrected and accelerated \({\text{BC}}_{a}\) bootstrap percentiles.
4 Results
As presented in Table 2 for the 61 elements at risk, the average process magnitude causing losses was 0.75 m and ranged between 0.30 and 1.40 m with a median of 0.7. The mean damage amounted to € 16,909 per business ranging from € 200 to € 181,256 with a median of € 5850. Comparing the relatively low median to the relatively high mean, it becomes obvious that the data are positively skewed and that only a few incidents caused high losses, while the overall average loss was considerable lower. The mean degree of loss was 0.08 ranging from 0.001 to 0.43 with a median of 0.03.
In Fig. 2, the results are shown as box plots separating the data set into the two categories of retail and service sector. The median and the lower quartile is 0.034 and 0.013 for the retail sector and 0.028 and 0.016 for the service sector. The third quartile is slightly higher for the retail sector (0.104) in comparison with the service sector (0.089). Independently from the data distribution, there is no significant influence of the business category on the degree of loss (p = 0.485).
In Fig. 3, the results of the bootstrapping are presented for D train. The grey lines show the respective series of curves drawing from a random sample with replacements, while every grey line represents one bootstrap sample \(x^{*i}\).The exponential model (M 2) shows a systematic underestimation in the degree of loss for water depths >1 m. In contrast, the other models (M 1, M 3 and M 4) do not show a systematic bias. As shown in Fig. 4 in terms of box plots, the models M 1, M 3 and M 4 exhibit similar behaviour with regard to the mean and the position of the quartiles of the RMSE. The systematic underestimation of M 2 results in a RMSE distribution shifted to higher values and higher variance.
Box-plots of the RMSE for the models M 1–M 4 with the mean (solid line) and the standard deviations (dashed lines). M 1, M 3 and M 4 show similar behaviour with regard to the mean and the position of the quartiles of the RMSE. The systematic underestimation of M 2 results in a RMSE distribution shifted to higher values and higher variance
The mean RMSEs resulting from the 2000 repetitions during bootstrapping are provided in Table 3, and it is shown that the Weibull function has the lowest RMSE (0.0478) followed by the Frechet No. 1 (0.0480) and No. 2 (0.0481) and the Exponential function (0.0795). Therefore, the Weibull function was considered as M* and applied during subsequent analyses. The prediction error for D test was 0.0723.
Finally, the model was fitted to the entire data set (61 points) resulting in Eq. 3. The final model is presented in Fig. 5 (including the 5 and 95 % confidence intervals).
As defined by the Weibull function, vulnerability is strictly increasing. For process intensities from 0 to 0.2, the DoL is zero; and therefore, vulnerability equals zero. For process intensities >0.5 m, the DoL and therefore vulnerability is strictly increasing until a value of 0.468 for a water depth of 1.5 m. Similarly, the 5 and 95 % intervals are increasing until 0.1 and 0.7, respectively.
5 Discussion
The study resulted in a local-scale vulnerability model for micro-sized enterprises located in a Mediterranean environment prone to flash floods. The data were based on an assessment of 61 incidents which occurred during four flash flood events in the province of East Attica, Greece.
The data included 41 claims from the retail sector and 20 from the service sector. When comparing the degree of loss of these two sectors, it was found that the median and the mean in both subsets were quite low (0.03 and 0.08) compared to the overall data range. Even if the upper limits of the upper quartile were different, it has to be concluded that there was no statistically significant difference between the two business categories. As for the two subsets, the median of the population was also low compared to the spread. This value is considerably below the values reported from other studies. Totschnig et al. (2011) presented a study on the vulnerability of residential buildings prone to fluvial sediment transport and their data resulted in a mean degree of loss of 0.17, ranging from 0.02 to almost 0.4 in different test sites. Totschnig and Fuchs (2013) had shown a mean of 0.17 and a median of 0.08 for 471 documented losses in the Eastern Alps. Similarly, Papathoma-Köhle et al. (2015) reported a mean degree of loss of 0.16 and a median of 0.07. One reason for the lower degree of losses is the lack of considerable sediment transport during the studied flash flood events, compared to fluvial sediment transport and other types of torrential flooding and flash floods with higher sediment concentration. On the other hand, as reported by Karagiorgos et al. (2016a), the low vulnerability values in the area are also a result of local building construction techniques as well as construction materials used. This is in line with conclusions drawn in Fuchs et al. (2012c) and Highfield et al. (2014) showing that building codes and standards are an important factor to reduce physical vulnerability.
Studies presented by Totschnig et al. (2011), Totschnig and Fuchs (2013) and Papathoma-Köhle et al. (2015) were focusing on fluvial sediment transport and debris flow processes in mountain torrents with considerably higher impact pressure than the flash flood events analysed in East Attica. As reported by Merz et al. (2010), impact reflects the specific effects of a flood event on the element at risk and depends on the type and magnitude of the flood event. In contrast, available studies on the vulnerability to river flooding resulted in a mean degree of loss of 0.3 and a median of 0.14 for the building envelope of small and medium-sized enterprises, but a mean degree of loss of 0.6 and a median of 0.7 for the affected stock (Kreibich et al. 2010). One possible explanation for these higher values in comparison with the presented material is that Kreibich et al. (2010) computed a considerable part of the loss as result of the contamination apart from the water depth inside the exposed elements at risk. Based on the RMSE, a modified Weibull function was found to represent the data set best. This is in line with earlier studies in small catchments (Totschnig et al. 2011; Papathoma-Köhle et al. 2012; Totschnig and Fuchs 2013) but in contrast with studies using damage classes (Jakob et al. 2012) and studies in larger catchments using stepped vulnerability functions such as Kreibich et al. (2010), Seifert et al. (2010) or MURL (2000) based on a linear function and ICPR (2001) based on a quadratic equation.
Finally, the modified Weibull function had shown a clear relation between the process magnitude and the degree of loss. As given by the requirements of Weibull distributions, vulnerability increased strictly with increasing process intensities. Similarly, as indicated by the confidence intervals based on bootstrap re-sampling the range increased considerably with increasing process intensities. Because the analysed buildings suffered damage from water depths ≤1.4 m, it was not possible to fit the model to higher process intensities. This is a restriction compared to other studies which also included losses resulting from higher process intensities (e.g. Tsao et al. 2010; Totschnig et al. 2011; Lo et al. 2012; Papathoma-Köhle et al. 2012; Totschnig and Fuchs 2013; Papathoma-Köhle et al. 2015). However, since flash floods have considerably different process characteristics with respect to the sediment load, the range in the data has to be smaller (Gissing and Blong 2004; Fuchs et al. 2007). The resulting curve is in line with the results presented by Kreibich et al. (2010) for small and medium-sized enterprises exposed to river flooding as well as by Papathoma-Köhle et al. (2015) for residential buildings and tourist accommodations exposed to torrential flooding, but in the latter study, the overall range in the data was higher.
The vulnerability model presented here is an essential step for designing and implementing effective and efficient flood risk mitigation strategies (Holub et al. 2012; Thaler and Hartmann 2016; Thaler et al. 2016). The results as well as the comparisons with other models provide valuable information in the ongoing discussion on vulnerability and highlight the importance of relatively small study areas with local and heterogenic characteristics in order to provide valuable insights for the development of a sophisticated pan-European flood damage modelling approach (Jongman et al. 2012).
6 Conclusion
The high number of losses due to flash floods in Mediterranean countries highlighted a particular need for studies on exposure and risk. Even if an increasing amount of studies focusing on the physical process characteristics of flash floods is available, there is still a gap in the assessment of vulnerability to this hazards type. Consequently, a vulnerability model has been built focusing on flash flood-prone commercial buildings in a Greek test site. The method was based on object-specific empirical data for micro-sized enterprises linking absolute loss data with process magnitudes. The vulnerability model followed a modified Weibull distribution for properties suffering damages from process intensities ≤1.4 m. The accuracy of the model was estimated by the RMSE, and the bootstrap validation procedure has shown reliable results.
The validation of the vulnerability model based on data from the Greek test site suggested a wider applicability of the presented approach. Based on the limitations discussed, there is a need for further research in order to increase the amount of data and consequently to improve the significance of the vulnerability model. To achieve this goal, additional studies in other Mediterranean countries facing flash flood hazards are recommended, such as in Portugal, Spain and southern France. In these countries, small and medium-sized enterprises account for a high proportion of total employment compared to other countries of the European Union. Future research should also be focused on the improvement of the model by using data from events with higher process magnitudes. Moreover, since vulnerability is highly dependent on the characteristics of exposed elements at risk, different Mediterranean building types should also be assessed with respect to their susceptibility to flash floods.
Future needs concerning research may include the spatiotemporal dynamics in vulnerability to natural hazards. During the past decades, Mediterranean regions experienced major transformations in population size, economic conditions and social characteristics, leading to changing development patterns. As a result, vulnerability may have changed considerably. To improve natural hazard risk management, these changes should be quantified according to institutional, economic and social concerns. The assessment of flood risk is required by the EU Floods Directive in order to set up risk management plans. As such, the presented approach contributes to a deeper insight of vulnerability in Mediterranean countries and supports the ongoing efforts in minimising risk.
References
Adhikari P, Hong Y, Douglas KR, Kirschbaum DB, Gourley J, Adler R, Brakenridge GR (2010) A digitized global flood inventory (1998–2008): compilation and preliminary results. Nat Hazards 55(2):405–422
Alexakis D (2011) Diagnosis of stream sediment quality and assessment of toxic element contamination sources in East Attica, Greece. Environ Earth Sci 63(6):1369–1383
Barredo J (2007) Major flood disasters in Europe: 1950–2005. Nat Hazards 42(1):125–148
Birkmann J (2006) Measuring vulnerability to promote disaster resilient societies. Conceptual frameworks and definitions. In: Birkmann J (ed) Measuring vulnerability to natural hazards-towards disaster resilient societies. United Nations University Press, Tokyo, pp 9–54
Borga M, Stoffel M, Marchi L, Marra F, Jakob M (2014) Hydrogeomorphic response to extreme rainfall in headwater systems: flash floods and debris flows. J Hydrol 518:194–205
Calianno M, Ruin I, Gourley JJ (2013) Supplementing flash flood reports with impact classifications. J Hydrol 477:1–16
Comiti F, Mao L, Preciso E, Picco L, Marchi L, Borga M (2008) Large wood and flash floods: evidences from the 2007 event in the Davča basin (Slovenia). In: De Wrachien D, Brebbia CA, Lenzi MA (eds) Monitoring, simulation, prevention and remediation of dense and debris flow II. WIT Transactions on Information and Communication Technologies 39. WIT Press, Southampton, pp 173–182
Creutin JD, Borga M, Gruntfest E, Lutoff C, Zoccatelli D, Ruin I (2013) A space and time framework for analyzing human anticipation of flash floods. J Hydrol 482:14–24
Cutter SL, Boruff BJ, Shirley WL (2003) Social vulnerability to environmental hazards. Soc Sci Q 84(2):242–261
De Marchi B, Scolobig A (2012) The views of experts and residents on social vulnerability to flash floods in an Alpine region of Italy. Disasters 36(2):316–337
Delrieu G, Ducrocq V, Gaume E, Nicol J, Payrastre O, Yates E, Kirstetter PE, Andrieu H, Ayral PA, Bouvier C, Creutin JD, Livet M, Anquetin S, Lang M, Neppel L, Obled C, Parent-Du-Châtelet J, Saulnier GM, Walpersdorf A, Wobrock W (2005) The catastrophic flash-flood event of 8–9 September 2002 in the Gard Region, France: a first case study for the Cévennes-Vivarais Mediterranean Hydrometeorological Observatory. J Hydrometeorol 6:34–52
Diakakis M, Mavroulis S, Deligiannakis G (2012) Floods in Greece, a statistical and spatial approach. Nat Hazards 62(2):485–500
Efron B (1979) Bootstrap methods: another look at the jackknife. Ann Stat 7(1):1–26
Eidsvig UMK, McLean A, Vangelsten BV, Kalsnes B, Ciurean RL, Argyroudis S, Winter MG, Mavrouli OC, Fotopoulou S, Pitilakis K, Baills A, Malet J-P, Kaiser G (2014) Assessment of socioeconomic vulnerability to landslides using an indicator-based approach: methodology and case studies. Bull Eng Geol Environ 73(2):307–324
EU (2003) Commission recommendation 2003/361/EC of the Commission of the European Communities of 6 May 2003 concerning the definition of micro, small and medium-sized enterprises, Brussels
EU (2013) 2013 SBA fact sheet, Greece. Directorate general enterprise and industry. http://ec.europa.eu/enterprise/policies/sme/facts-figures-analysis/performance-review/files/countries-sheets/2013/greece_en.pdf.Accessed. 11 March 2015
Fell R, Corominas J, Bonnard C, Cascini L, Leroi E, Savage W (2008) Guidelines for landslide susceptibility, hazard and risk zoning for land-use planning. Eng Geol 102(3–4):85–98
Fuchs S (2009) Susceptibility versus resilience to mountain hazards in Austria—paradigms of vulnerability revisited. Nat Hazards Earth Syst Sci 9(2):337–352
Fuchs S, Heiss K, Huebl J (2007) Towards an empirical vulnerability function for use in debris flow risk assessment. Nat Hazards Earth Syst Sci 7(5):495–506
Fuchs S, Kuhlicke C, Meyer V (2011) Editorial for the special issue: vulnerability to natural hazards-the challenge of integration. Nat Hazards 58(2):609–619
Fuchs S, Birkmann J, Glade T (2012a) Vulnerability assessment in natural hazard and risk analysis–current approaches and future challenges. Nat Hazards 64(3):1969–1975
Fuchs S, Holub M, Suda J (2012b) Reducing physical vulnerability to mountain hazards by local structural protection. In: Koboltschng G, Hübl J, Braun J (eds) Internationales symposion interpraevent, vol 2. Internationale Forschungsgesellschaft Interpraevent, Genoble, pp 675–686
Fuchs S, Ornetsmüller C, Totschnig R (2012c) Spatial scan statistics in vulnerability assessment—an application to mountain hazards. Nat Hazards 64(3):2129–2151
Fuchs S, Keiler M, Zischg A (2015) A spatiotemporal multi-hazard exposure assessment based on property data. Nat Haz Earth Syst Sci 15(9):2127–2142
Ganoulis J (2003) Risk-based floodplain management: a case study from Greece. Intl J. River Basin Management 1(1):41–47
Gaume E, Livet M, Desbordes M, Villeneuve JP (2004) Hydrological analysis of the river Aude, France, flash flood on 12 and 13 November 1999. J Hydrol 286:135–154
Gaume E, Bain V, Bernardara P, Newinger O, Barbuc M, Bateman A, Blaskovicova L, Blöschl G, Borga M, Dumitrescu A, Daliakopoulos I, Garcia J, Irimescu A, Kohnova S, Koutroulis A, Marchi L, Matreata S, Medina V, Preciso E, Sempere-Torres D, Stancalie G, Szolgay J, Tsanis I, Velasco D, Viglione A (2009) A compilation of data on European flash floods. J Hydrol 367(1–2):70–78
Gissing A, Blong R (2004) Accounting for variability in commercial flood damage estimation. Aust Geogr 35(2):209–222
Gordon DLA, Janzen M (2013) Suburban nation? Estimating the size of Canada’s suburban population. J Archit Plan Res 30(3):197–220
Greek Ministry of Infrastructure, Transport and Networks (2011) Invoice for the calculation of necessary repair works in buildings affected by natural hazards (earthquake, forest fires, floods, landslides) and the respective housing assistance. Official Gazette 3201/B/30.12.2011. (In Greek)
Hausmann P (1992) Die Schadenempfindlichkeit, ein Teilaspekt bei der Abschätzung des Schadenpotentials von Überschwemmungen. In: Forschungsgesellschaft für vorbeugende Hochwasserbekämpfung (ed) Internationales Symposion Interpraevent, vol. 3. Internationale Forschungsgesellschaft Interpraevent, Klagenfurt, pp 147–158
Heiser M, Scheidl C, Eisl J, Spangl B, Hübl J (2015) Process type identification in torrential catchments in the eastern Alps. Geomorphology 232:239–247
Hellenic Statistical Authority (2011) Population Census 2011. http://www.statistics.gr/portal/page/portal/ESYE/PAGE-census2011. Accessed 02 March 2015
Highfield WE, Peacock WG, Van Zandt S (2014) Mitigation planning: why hazard exposure, structural vulnerability, and social vulnerability matter. J Plann Educ Res 34:287–300
Holub M, Suda J, Fuchs S (2012) Mountain hazards: reducing vulnerability by adapted building design. Environ Earth Sci 66(7):1853–1870
Hooke JM (2016) Morphological impacts of flow events of varying magnitude on ephemeral channels in a semiarid region. Geomorphology 252:128–143
IAHS-UNESCO-WMO (1974) (Ed.) Flash floods, proceedings of the Paris symposium, September 1974
ICPR (International Commission for the Protection of the River Rhine) (2001) Übersichtskarten der Überschwemmungsgefährdung und der möglichen Vermögensschäden am Rhein. ICPR, Koblenz
Jakob M, Stein D, Ulmi M (2012) Vulnerability of buildings to debris flow impact. Nat Hazards 60(2):241–261
Jongman B, Kreibich H, Appel H, Barredo JI, Bates PD, Feyen L, Gericke A, Neal J, Aerts JCJH, Ward PJ (2012) Comparative flood damage model assessment: towards a European approach. Nat Hazards Earth Syst Sci 12(12):3733–3752
Karagiorgos K, Thaler T, Heiser M, Hübl J, Fuchs S (2016a) Integrated flash flood vulnerability assessment: insights from East Attica. J Hydrol, Greece. doi:10.1016/j.jhydrol.2016.02.052
Karagiorgos K, Thaler T, Hübl J, Maris F, Fuchs S (2016b) Multi-vulnerability analysis for flash flood risk management. Nat Hazards 82(Suppl. 1):63–87
Keiler M (2013) World-wide trends in natural disasters. In: Bobrowski P (ed) Encyclopedia of natural hazards. Springer, Dordrecht, pp 1111–1114
Koks EE, Jongman B, Husby TG, Botzen WJW (2015) Combining hazard, exposure and social vulnerability to provide lessons for flood risk management. Environ Sci Policy 47:42–52
Koutsoyiannis D, Mamassis N, Efstratiadis A, Zarkadoulas N, Markonis I (2012) Floods in Greece. IAHS-AISH Publication: pp 238–256
Kreibich H, Seifert I, Merz B, Thieken AH (2010) Development of FLEMOcs—a new model for the estimation of flood losses in the commercial sector. Hydrolog Sci J 55(8):1302–1314
Kreibich H, van den Bergh JCJM, Bouwer LM, Bubeck P, Ciavola P, Green C, Hallegatte S, Logar I, Meyer V, Schwarze R, Thieken AH (2014) Costing natural hazards. Nat Clim Chang 4:303–306
Lasda O, Dikou A, Papapanagiotou E (2010) Flash flooding in Attica, Greece: climate change or urbanization? Ambio 39(8):608–611
Llasat M, Llasat-Botija M, Prat M, Porcú F, Price C, Mugnai A, Lagouvardos K, Kotroni V, Katsanos D, Michaelides S, Yair Y, Savvidou K, Nicolaides K (2010) High-impact floods and flash floods in Mediterranean countries: the FLASH preliminary database. Adv Geosci 23:47–55
Lo WC, Tsao TC, Hsu CH (2012) Building vulnerability to debris flows in Taiwan: a preliminary study. Nat Hazards 64(3):2107–2128
Luino F, Cirio CG, Biddoccu M, Agangi A, Giulietto W, Godone F, Nigrelli G (2009) Application of a model to the evaluation of flood damage. Geoinformatica 13:339–353
Mantelas L, Prastacos P, Hatzichristos T, Koutsopoulos K (2010) Using fuzzy cellular automata to access and simulate urban growth. GeoJournal 77:13–28
Marchi L, Borga M, Preciso E, Gaume E (2010) Characterisation of selected extreme flash floods in Europe and implications for flood risk management. J Hydrol 394:118–133
Mazzorana B, Hübl J, Fuchs S (2009) Improving risk assessment by defining consistent and reliable system scenarios. Nat Hazards Earth Syst Sci 9(1):145–159
Mazzorana B, Comiti F, Scherer C, Fuchs S (2012) Developing consistent scenarios to assess flood hazards in mountain streams. J Environ Manage 94(1):112–124
Mazzorana B, Simoni S, Scherer C, Gems B, Fuchs S, Keiler M (2014) A physical approach on flood risk vulnerability of buildings. Hydrol Earth Syst Sci 18(9):3817–3836
Merz B, Kreibich H, Schwarze R, Thieken A (2010) Review article “Assessment of economic flood damage”. Nat Hazards Earth Syst Sci 10(8):1697–1724
Messner F (2007) Evaluating flood vulnerability—scope of approaches and challenges to research. In: Schanze J (ed) Flood risk management research—from extreme events to citizens involvement. Proceedings of European symposium on flood risk management research (EFRM 2007), 6th–7th February 2007. IOER, Dresden, pp 75–82
Meyer V, Becker N, Markantonis V, Schwarze R, van den Bergh JCJM, Bouwer LM, Bubeck P, Ciavola P, Genovese E, Green C, Hallegatte S, Kreibich H, Lequeux Q, Logar I, Papyrakis E, Pfurtscheller C, Poussin J, Przyluski V, Thieken AH, Viavattene C (2013) Review article: assessing the costs of natural hazards –state of the art and knowledge gaps. Nat Hazards Earth Syst Sci 13(5):1351–1373
MURL (Ministerium für Umwelt, Raumordnung und Landwirtschaft des Landes Nordrhein-Westfalen) (2000) Potentielle Hochwasserschäden am Rhein in NRW. MURL, Düsseldorf
Norbiato D, Borga M, Degli Esposti S, Gaume E, Anquetin S (2008) Flash flood warning based on rainfall thresholds and soil moisture conditions: an assessment for gauged and ungauged basins. J Hydrol 362:274–290
NRE (Department of Natural Resources and Environments, Victoria) (2000) Appraisal method (RAM) for floodplain management report prepared by read sturgess and associates, Melbourne, Australia
NWS (2016) National Weather Service glossary. http://w1.weather.gov/glossary/index.php
Papagiannaki K, Lagouvardos K, Kotroni V, Bezes A (2015) Flash flood occurrence and relation to the rainfall hazard in a highly urbanized area. Nat Hazards Earth Syst Sci 15(8):1859–1871
Papathoma-Köhle M, Kappes M, Keiler M, Glade T (2011) Physical vulnerability assessment for alpine hazards: state of the art and future needs. Nat Hazards 58(2):645–680
Papathoma-Köhle M, Keiler M, Totschnig R, Glade T (2012) Improvement of vulnerability curves using data from extreme events: debris flow event in South Tyrol. Nat Hazards 64(3):2083–2105
Papathoma-Köhle M, Zischg A, Fuchs S, Glade T, Keiler M (2015) Loss estimation for landslides in mountain areas—anintegrated toolbox for vulnerability assessment and damage documentation. Environ Model Softw 63:156–169
Penning-Rowsell E, Johnson C, Tunstall S, Tapsell S, Morris J, Chatterton J, Green C (2005) The benefits of flood and coastal risk management: a manual of assessment techniques. Middlesex University Press, London
Petropoulos GP, Kontoes CC, Keramitsoglou I (2012) Land cover mapping with emphasis to burnt area delineation using co-orbital ALI and Landsat TM imagery. Int J Appl Earth Obs Geoinf 18:344–355
Rickenmann D, Hunzinger L, Koschni A (2008) Hochwasser und Sedimenttransport während des Unwetters vom August 2005 in der Schweiz. In: Mikoš M, Hübl J, Koboltschnig G (eds) Internationales symposion interpraevent, vol 1. Internationale Forschungsgesellschaft Interpraevent, Klagenfurt, pp 465–476
Rozalis S, Morin E, Yair Y, Price C (2010) Flash flood prediction using an uncalibrated hydrological model and radar rainfall data in a Mediterranean watershed under changing hydrological conditions. J Hydrol 394:245–255
Sapountzaki K, Wanczura S, Casertano G, Greiving S, Xanthopoulos G, Ferrara FF (2011) Disconnected policies and actors and the missing role of spatial planning throughout the risk management cycle. Nat Hazards 59(3):1445–1474
Scawthorn C, Blais N, Seligson H, Tate E, Mifflin E, Thomas W, Murphy J, Jones C (2006a) HAZUS-MH flood loss estimation methodology. I: overview and flood hazard characterization. Nat Haz Rev 7:60–71
Scawthorn C, Flores P, Blais N, Seligson H, Tate E, Chang S, Mifflin E, Thomas W, Murphy J, Jones C, Lawrence M (2006b) HAZUS-MH flood loss estimation methodology. II. Damage and loss assessment. Nat Haz Rev 7:72–81
Scheidl C, Rickenmann D (2010) Empirical prediction of debris-flow mobility and deposition on fans. Earth Surf Process Landf 35(2):157–173
Seifert I, Kreibich H, Merz B, Thieken AH (2010) Application and validation of FLEMOcs—a flood-loss estimation model for the commercial sector. Hydrolog Sci J 55(8):1315–1324
Thaler T, Hartmann T (2016) Justice and flood risk management: reflecting on different approaches to distribute and allocate flood risk management in Europe. Nat Hazards
Thaler T, Priest S, Fuchs S (2016) Evolving interregional co-operation in flood risk management: distances and types of partnership approaches in Austria. Reg Environ Change 16(3):841–853
Thieken AH, Olschewski A, Kreibich H, Kobsch S, Merz B (2008) Development and evaluation of FLEMOps—a new flood loss estimation model for the private sector. WIT Trans Ecol Environ 118:315–324
Thywissen K (2006) Components of risk: a comparative glossary. Institute of Environment and Human Security, Βonn
Totschnig R, Fuchs S (2013) Mountain torrents: quantifying vulnerability and assessing uncertainties. Eng Geol 155:31–44
Totschnig R, Sedlacek W, Fuchs S (2011) A quantitative vulnerability function for fluvial sediment transport. Nat Hazards 58(2):681–703
Tsao T-C, Hsu W-K, Cheng C-T, Lo W-C, Chen C-Y, Chang Y-L, Ju J-P (2010) A preliminary study of debris flow risk estimation and management in Taiwan. In: Chen S-C (ed) International symposium interpraevent in the Pacific Rim—Taipei, 26–30 April 2010. Internationale Forschungsgesellschaft Interpraevent, Klagenfurt, pp 930–939
Varnes D (1984) Landslide hazard zonation: a review of principles and practice. UNESCO, Paris
Vinet F (2008) Geographical analysis of damage due to flash floods in southern France: the cases of 12–13 November 1999 and 8–9 September 2002. Appl Geogr 28(4):323–336
Winsemius HC, Aerts JCJH, van Beek LPH, Bierkens MFP, Bouwman A, Jongman B, Kwadijk JCJ, Ligtvoet W, Lucas PL, van Vuuren DP, Ward PJ (2014) Global drivers of future river flood risk. Nat Clim Chang 6:381–385
Zorn M, Natek K, Komac B (2006) Mass movements and flash-floods in Slovene Alps and surrounding mountains. Studia Geomorphologica Carpatho-Balcanica XL:127–145
Acknowledgments
Open access funding provided by University of Natural Resources and Life Sciences Vienna (BOKU). Sven Fuchs received funding by the Austrian Science Fund (FWF: P 27400). The authors acknowledge the insightful comments by Viktor Roezer and another anonymous referee on an earlier version of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
See Table 4.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Karagiorgos, K., Heiser, M., Thaler, T. et al. Micro-sized enterprises: vulnerability to flash floods. Nat Hazards 84, 1091–1107 (2016). https://doi.org/10.1007/s11069-016-2476-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-016-2476-9