1 Introduction

A sufficiently thick low shear strength film of lubricant is usually desired to form in all contact conjunctions to carry the applied load and guard against the direct interaction of asperities on the opposing surfaces, thus reducing frictional losses. However, in practice this ideal situation is often not achieved, owing to many circumstances, such as stop–start or reciprocating motions, which affect the entrainment of the lubricant into the contact with relative motion of surfaces [1, 2]. There may also be a lack of lubricant availability at the inlet to a conjunction as well as reverse and swirl flows there [3, 4]. As the result, many contacts suffer from a lack of a coherent lubricant film where a proportion of applied load is carried by the ubiquitous asperities on the counterface surfaces. These interactions increase the generated friction, for example in the cases of piston-cylinder system at dead centre reversals [5–8] and cam-follower contact in the inlet reversal positions [9]. Various palliative actions are undertaken in order to mitigate these adverse effects within the mixed regime of lubrication, including the use of hard wear-resistant coatings. Another approach has been surface modifications such as cross-hatching of cylinder surfaces or texturing in order to entrap reservoirs of lubricant for instances of poor entraining motion. In order to opt for any method of palliation, it would be instructive to initially predict the extent of boundary interactions in an accurate manner.

Greenwood and Tripp [10] and Greenwood and Williamson [11] provided mathematical discourses for asperity interactions between pairs of rough surfaces for simplified asperity geometry and an assumed Gaussian distribution of peak heights. A further series of assumptions were made, most crucially an average asperity tip radius and an average indentation depth at given separations with the mutual approach of rough counterfaces. The method also accounted for the oblique interaction of any pair of opposing asperities. These are usually regarded as necessary assumptions to deal with the complex nature of rough surface topography. The Gaussian assumption made in Greenwood and Tripp [10] is not a prerequisite of the method. Consideration of typical rough surfaces suggests that a peak height distribution would have a mean value above the mid-line of the surface as the majority of the peaks would reside in the upper reaches of the surface. It is, therefore, advantageous to develop an asperity model which allows more representative peak height distributions to be utilised, particularly for lubricated contacts which were not discussed by Greenwood and Tripp [10].

Greenwood and Tripp [10] used a Gaussian distribution to approximate the probability of peak height interactions at a given surface separation; \( \lambda \) where this is inversely proportional to \( \sigma \) (root mean square; RMS) of the surface heights. As a result the mean of the peak height distribution is set to the same mean as the surface height distribution as a simplification for the proof of concept which, for engineering surfaces, tends to predict that the first surface interactions occur at a lower value of \( \lambda \) than is otherwise the case. This results in an estimate of asperity load carrying capacity significantly below a real case at the upper reaches of the surface and a lower separation limit at which the mixed regime of lubrication is expected to commence. One way to deal with this shortcoming is to measure the mean peak height relative to the surface centre-line and shift the mean of the Gaussian distribution to this location. This requires the analysis of the surface and identification of the peak height distribution. Therefore, “the surface specific distribution” might as well be used for the rest of the analysis, thus improving the accuracy of surface representation with little extra effort. Furthermore, the Gaussian distribution used to describe the peak height distribution must have the same standard deviation as the actual peak height distribution, not the RMS roughness, \( \sigma \), which is derived from the surface height distribution.

Greenwood and Williamson’s model [11] was further developed to account for non-uniform radii of curvature of asperity peaks by Hisakado [12], and for elliptic paraboloid asperities by Bush et al. [13], as well as for anisotropic surfaces by McCool [14]. The Greenwood and Tripp model [10] was extended by Pullen and Williamson [15] to account for the plastic deformation of asperities and further improved by Cheng et al. [16] for an elasto-plastic model. A recent extension of the model for combined elasto-plastic and adhesion of asperities for fairly smooth surfaces, using fractal geometry was reported by Chong et al. [17]. Nevertheless, the original Greenwood and Tripp model [10] has been widely used in many applications [18–21].

2 Background Theory

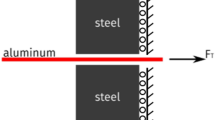
It is initially assumed that the surfaces are replaced by an equivalent surface comprising a collection of hemispherical asperities of an average tip radius, \( \beta \) (Fig. 1) and with the same peak height distribution as the original surfaces themselves.

Fig. 1
figure 1

Geometry of asperity pair interaction

Full size image

The asperity radii (\( \beta_1 \) and \( \beta_2 \)) and the radial separation \( r \) allow \( w_p \) (the peak height interference) to be related to \( w \) (the asperity compression) this results in the load carrying capacity of the surface. For the interference of two spheres the asperity compression can be shown to be:

$$ w = \left\langle {w_{p} - \frac{{r^{2} }}{{2\left(\beta_1+ \beta_2\right)}}} \right\rangle $$
(1)

where, 〈〉 is a “Macauley bracket”. Let:

$$ \beta = \frac{{\beta_{1} + \beta_{2} }}{2} $$
(2)

where:

$$ \beta_{1} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \beta_{1i} }}{n} $$
(3)

The average asperity density over both surfaces is \( \xi \) and the apparent area of contact is \( {\mathcal{A}} \). Therefore, the probable load supported by this representative equivalent surface at a given separation, \( \tilde{P}\left( d \right) \) becomes:

$$ \tilde{P}\left( d \right) = 2\pi \xi^{2} {\mathcal{A}}\mathop \int \nolimits_{r}^{ } \mathop \int \nolimits_{{z_{1} }}^{ } \mathop \int \nolimits_{{z_{2} }}^{ } P\left( {w,r} \right)\phi \left( {z_{1} } \right)\phi \left( {z_{2} } \right)r \cdot dz_{2} \cdot dz_{1} \cdot dr $$
(4)

where, \( P\left( {w,r} \right) \) is the load carried by an asperity pair with misalignment \( r \) and peak penetration of \( w \). Equation (4) states that the total carried load is as the result of the load supported at a given penetration between all pairs of opposing asperities at any given surface height.

The surface specific contributions are the peak height distributions, \( \phi \left( {z_{1} } \right) \) and \( \phi \left( {z_{2} } \right) \), and the asperity peak density, \( \xi \). Examples of measured surface height distributions can be seen in the work of Peklenik [22] who also discussed some of the key variations between measured and generated surface properties.

Combining the probabilities by taking the convolution of the asperity peak height distributions for counterface surfaces leads to:

$$ \phi^{ *} \left( z \right) = \phi \left( {z_{1} } \right) *\phi \left( {z_{2} } \right) $$
(5)

Using Hertzian theory to express the load carrying capacity as a function of the deformation (penetration) of two spheres in elastic contact with the effective composite elastic modulus, \( E^{\prime } \):

$$ P = \frac{4}{3}E^{\prime } {\Psi} ^{{\frac{1}{2}}} w^{{\frac{3}{2}}} $$
(6)

Where \( \Psi \) is the composite curvatures for two contacting spheres defined as:

$$ {\frac{1}{\Psi}} = {\frac{1}{\beta_1}} + {\frac{1}{\beta_2}}$$
(7)

Equation (4) now reduces to:

$$ \tilde{P}\left( d \right) = 2\pi \xi^{2} {\mathcal{A}}\mathop \int \nolimits_{r}^{ } \mathop \int \nolimits_{z}^{ } \left( {\frac{4}{3}} \right)E^{\prime } {\Psi^{\frac{1}{2}}}{w^{\frac{3}{2}}}\phi^*(Z)r.dz.dr$$
(8)

With the inclusion of Eqs. (1) and (2) the equation for the probable asperity carried load at a given separation simplifies to:

$$ \tilde{P}\left( d \right) = 2\pi \xi^{2} {\mathcal{A}}\mathop \int \nolimits_{r}^{ } \mathop \int \nolimits_{z}^{ } \left( {\frac{4}{3}} \right)E^{\prime } {\Psi^{\frac{1}{2}}}{{\left\langle {w_{p} - \frac{{r^{2} }}{{4\beta }}} \right\rangle}^{\frac{3}{2}}}\phi^*(Z)r.dz.dr$$
(9)

Extracting the constants and setting the limits of integration, yields:

$$ \tilde{P}\left( d \right) = \frac{8}{3}\pi \xi ^{2} E^{\prime } {\Psi^{\frac{1}{2}}} {\mathcal{A}}\int\nolimits_{d}^{\infty } {\phi ^{*} } \left( z \right) \cdot dz\int\nolimits_{0}^{\infty } {\left\langle {w_{p} - \frac{{r^{2} }}{{4\beta }} } \right\rangle }^{{\frac{3}{2}}} r \cdot dr $$
(10)
$$ \tilde{P}\left( d \right) = \frac{8}{3}\pi \xi ^{2} E^{\prime } {\Psi^{\frac{1}{2}}} {\mathcal{A}}\int\nolimits_{d}^{\infty } {\phi ^{*} } \left( z \right) \cdot dz\left[ { - \frac{4}{5}\beta \left\langle {w_{p} - \frac{{r^{2} }}{{4\beta }}} \right\rangle ^{{\frac{5}{2}}} } \right]_{0}^{\infty } $$
(11)
$$ \tilde{P}\left( d \right) = \frac{32}{15}\pi \xi ^{2} E^{\prime } {\Psi^{\frac{1}{2}}}{\beta} {\mathcal{A}}\int\nolimits_{d}^{\infty } {{\left\langle{z}-{d}\right\rangle}^{\frac{5}{2}}} {\phi ^{*} } \left( z \right) \cdot dz $$
(12)

Standardising the form of the probability distribution as \( s = \sigma z \):

$$ \tilde{P}\left( d \right) = \frac{32 }{15}\pi \xi^{2}{\Psi^{\frac{1}{2}}} \beta\sigma^{{\frac{5}{2}}} E^{\prime } {\mathcal{A}}\mathop \int \nolimits_{d/\sigma }^{\infty } \left( {s - \frac{d}{\sigma }} \right)^{{\frac{5}{2}}} \phi^{ *} \left( s \right) \cdot ds $$
(13)

Equation (13) can then be rearranged to:

$$ \tilde{P}\left( d \right) = \frac{32 }{15}\pi \xi^{2}{\Psi^{\frac{1}{2}}} \beta\sigma^{{\frac{5}{2}}} E^{\prime } {\mathcal{A}}{\text F_{\frac{5}{2}}}\left( {\frac{d}{\sigma }} \right)$$
(14)

In a similar manner, the mean asperity contact area within the apparent contact area is found as:

$$ \tilde{A}\left( d \right) = 2\pi^{2} \left( {\xi \sigma } \right)^{2} \Psi\beta{\mathcal{A}}F_{2} \left( \lambda \right) $$
(15)

Where the probability functions in Eqs. (14) and (15) are defined as:

$$ F_{n} \left( \lambda \right) = \mathop \int \nolimits_{\lambda }^{\infty } \left( {s - \lambda } \right)^{n} \phi^{ *} \left( s \right) \cdot ds $$
(16)

It is of note that in the original theory proposed by Greenwood and Tripp [10] the radii on each surface are assumed to be equal and therefore:

$$\Psi = {\frac{\beta}{2}}$$
(17)

If Eq. (17) is true then Eqs. (14) and (15) respectively reduce to those given in [10] as

$$ \tilde{P}\left( d \right) = \frac{16\sqrt 2 }{15}\pi \left( {\xi \beta \sigma } \right)^{2} E^{\prime } \sqrt {\frac{\sigma }{\beta }} {\mathcal{A}}{\text{F}}_{{\frac{5}{2}}} \left( {\frac{d}{\sigma }} \right) $$
(18)
$$ \tilde{A}\left( d \right) = \pi^{2} \left( {\xi \beta \sigma } \right)^{2} {\mathcal{A}}F_{2} \left( \lambda \right) $$
(19)

The function, \( F_{5/2} \left( \lambda \right) \), represents the statistical likelihood of interactions of deformed asperities at all separations as one surface is lowered onto the other. In order to improve the accuracy of the model for a specific pair of surfaces the specific parameter must be calculated. The parameters; \( \xi \), \( \beta \) and \( \sigma \) can be readily determined by many commercially available metrology systems. Determination of the function \( F_{5/2} \left( \lambda \right) \) from measured surface topography is more involved. As already noted, to correctly apply the assumption of a Gaussian distribution of peak heights, the standard deviation and mean of the peak heights are needed a priori. However, it is more representative to determine the peak height distributions of the surfaces through a simple extension of the approach highlighted above, using instead the surface specific data.

\( F_{5/2} \left( \lambda \right) \) and the roughness parameter determine the probable number of asperities which are penetrated at a given surface separation and the extent of their deformation.

3 Extension to measured surface data

Measuring surface topography using a variety of measurement techniques yields an array of surface height data at discrete measured nodes. The discrete surface data is then used in a probabilistic model, such as that described above, with the frequency distributions required in the form of a histogram of each surface. The distribution is dependent on the size and resolution of the sampled area, as well as the surface itself.

Identifying the asperity summits and their heights leads to a discrete peak height distribution for each surface. The convolution of these two peak height distributions is then found, \( \phi^{ *} \), must conform to:

$$ \mathop \int \nolimits_{ - \infty }^{\infty } \phi^{ *} \left( x \right) \cdot dx = 1 $$
(20)

Then, the calculation of functions such as \( {\text{F}}_{5/2} \left(\uplambda \right) \) is a routine matter for any desired surface height through integration of the histogram columns residing above the \( \uplambda \) value being considered with a weighting as shown in Eq. (16).

The remaining surface specific parameters considered in this model are: \( \xi \), \( \beta \), \( \Psi \) are and \( \sigma \). The determination of \( \beta \) and \( \Psi \) not considered satisfactory techniques for measured surfaces. \( \beta \) represents the mean radius of all the asperity pairs in contact at a given separation. For multi-scale surfaces, such as cross-hatched cylinder liners, the manufacturing process often comprises several stages. Honing creates a rough, isotropic surface with a negatively skewed surface height distribution by machining away the upper levels of the surface with successively smoother machining processes. This means that there is a variation in \( \beta \) at different heights of the surface. At the upper levels there are likely to be smoother and more rounded asperities, whilst any lower peaks formed by the initial machining process and untouched by any subsequent operation would have a lower asperity radius (i.e. sharper peaks). As a result a variable \( \beta \) value is encountered at different separations.

For the individual surfaces, \( \beta_{i} \left( h \right) \) should be determined as the mean of all the asperity radii above a given height, \( h \), from the centre-line of the topography as weighted by their heights since higher asperities have a greater probability of contacting the counter-surface. Taking a double integral, the variable asperity radius can be determined from:

$$ \beta_{1} (h) = {\int\nolimits_{h}^{h_{ini1}}} {\int\nolimits_{x}^{h_{ini1}}} \frac{{\mathop \sum \nolimits_{i = 1}^{n} \beta_{1i} (s)}}{n} ds\,dx$$
(21)

Subsequently, the mean of the same with any probability of contact at any given separation should be used. With the variation of the asperity radii of the individual counter surfaces determined, consideration of the combined effect from two surfaces in contact should then be considered. The two functions thus found for the individual surfaces cannot be convoluted in the same manner as the peak height distributions. It is necessary to know the height of the upper most asperity on each surface in order to determine the maximum separation at which a contact can be made. These peak asperity pairs represent the initial possible direct contact of the surfaces as the mean centre-lines are moved closer. They are designated as \( h_{ini1} \) and \( h_{ini2} \). A variable asperity radius distribution can then be found as:

$$ \beta \left( h \right) = \frac{{\beta_{1} \left( {h - h_{ini2} } \right) + \beta_{2} \left( {h - h_{ini1} } \right)}}{2} $$
(22)

Similarly, the variable asperity curvature \( {\Psi_i}{\left(h\right)}\) can be determined from:

$$ \Psi_1 (h) = {\int\nolimits_{h}^{h_{ini1}}} {\int\nolimits_{x}^{h_{ini1}}} \frac{{\mathop \sum \nolimits_{i = 1}^{n} {\frac{1}{\beta_{1i} (s)}}}}{n} ds\,dx$$
(23)
$$ \Psi \left( h \right) = \frac{2}{{\Psi_{1} \left( {h - h_{ini2} } \right) + \Psi_{2} \left( {h - h_{ini1} } \right)}} $$
(24)

4 Results for measured surfaces

Measured data from real surfaces is used in order to determine a more realistic \( F_{5/2} \left( \lambda \right) \) function. The surfaces considered in this study are those of a flat plate with a skewed surface height distribution and a surface finish similar to that of a plateau-honed cylinder liner (surface 1 as shown in Fig. 2a) and a corresponding flat surface with an approximately Gaussian surface height distribution and low RMS roughness similar to that of a piston ring (surface 2 as shown in Fig. 2b). The peak and surface height distributions for these surfaces are shown in Figs. 3 and 4.

Fig. 2
figure 2

Images of surface topography using an Alicona Infinite Focus Microscope at ×50 optical magnification applying the focus variation technique: 284 × 216 µm. a Surface 1. b Surface 2

Full size image
Fig. 3
figure 3

Characteristic distributions for surface 1 averaged from 10 measured areas. a Peak height distribution. b Surface height distribution

Full size image
Fig. 4
figure 4

Characteristic distributions for surface 2 averaged from 10 measured areas. a Peak height distribution. b Surface height distribution

Full size image

The convoluted distributions for the pairs of contacting surfaces 1 and 2 are shown in Fig. 5.

Fig. 5
figure 5

Convoluted characteristic distributions for contacting pairs averaged from 10 measured areas. a Peak height distribution. b Surface height distribution

Full size image

It can be seen from the convolution of the peak height distributions (Fig. 5a) that there are significantly more asperities above the centre-line than would be predicted by a Gaussian distribution with a mean of 0. Not only is there a non-Gaussian peak height distribution, but also the mean height is non-zero which can also be seen for surface 2 with approximately Gaussian peak height and surface height distributions. This was given in the curve fit process of Greenwood and Tripp [10] or subsequent studies which have used this distribution assumption.

A comparison between the surface specific \( F_{5/2} \left( \lambda \right) \) function and the same function provided by Greenwood and Tripp [10] for a Gaussian surface distribution, to which Arcoumanis et al. [23] fitted a 6th order curve fit, is shown in Fig. 6.

Fig. 6
figure 6

Comparison between \( F_{5/2} \) functions from surface specific data and from an assumed Gaussian distribution

Full size image

Figure 6 shows significant differences between the calculated functions. This is in part due to the increased proportion of asperities in the higher regions of the surface for the case of surface specific data. There is also a greater cumulative effect in these differences as the surfaces are moved together and the asperities continue to deform to a greater extent. For this case, the Gaussian assumption under predicts the \( F_{5/2} \) function for these surfaces by over 80 %.

Figure 7 shows the mean asperity radius, \( \beta_i \left( h \right) \), above a certain height as measured from the mean centre-line of the surface topography.

Fig. 7
figure 7

Asperity radius distributions for the counter surfaces 1 and 2, averaged from 10 measured areas. a Surface 1. b Surface 2

Full size image

It is clear from Fig. 7 that a mean value used for contacting asperity radii, \( \beta \), would not be a fair representation. Therefore, a more complex analysis of asperity radii is required. Determining \( \beta \left( h \right) \) as a variable for the combination of the two surfaces under consideration gives the curve shown in Fig. 8 as the convolution of the asperity radii distributions for the rough counter surfaces.

Fig. 8
figure 8

Convoluted asperity radius and curvature distributions averaged from 10 measured areas

Full size image

Figure 8 shows a significant variation in \( \beta \left( h \right) \) at the level of the upper asperities even though surface 2 has a minimal radius variation (Fig. 7b). The characteristic equations for asperity load share (Eq. 14) and contact area (Eq. 15) show that the variation in the asperity radius with mutually converging surfaces would significantly alter the load carrying capacity and thus any predicted generated friction. To apply the variables \( \beta \left( h \right) \) and \( \Psi \left( h \right), \) sixth order polynomial curve fits are used in the numerical model. The full range of the surface height distributions has bee shown in Figs. 7 and 8 to demonstrate the convergence to the mean. On the other hand, the Greenwood and Tripp model [10] is concerned only with the upper reaches of the topography.

5 Validation of methology

The methodology for representation of contact of a pair of rough surfaces (described above) using surface specific data is validated against experimental measurements of friction from a precision sliding tribometer.

5.1 Sliding tribometer

A reciprocating slider tribometer is used to measure the generated friction between the two measured rough surfaces. A ‘strip’ (surface 2 described above) comprising a 20 × 20 mm flat area with 45° chamfered inlet and outlets slides on a flat sample (surface 1 described above), the latter mounted onto a floating flat plate, supported by frictionless bearings and intervened from the solid base of the rig by piezo-resistive load cells (Fig. 9). The floating plate is dragged by the sliding contact conjunction, lubricated by 1 ml of base oil applied to the plate surface, furnishing a very thin lubricant film and significant asperity interactions. The drag force (generated contact friction, f) equates the inertial force measured by the load cells as:

$$ \sum F = f = ma $$
(25)
Fig. 9
figure 9

Detail view of the sliding tribometer

Full size image

The base oil used is a Grade 3 base stock (Highly paraffinic with ultra-low Sulphur content, Viscosity Index; VI > 125). By not introducing boundary active lubricant species, which can adsorb to the surfaces and form an ultra-thin low shear strength film, the repeatability of the experimental work is improved. The pertinent base oil rheological parameters are listed in Table 1.

Table 1 Lubricant data
Full size table

The rig is operated at low sliding velocity, representative of poor kinematic conditions of piston motion near the dead centre reversals and in this case under isothermal conditions and at relatively low load. The load is applied through the loading mechanism shown in the figure. Mixed or boundary regimes of lubrication would be expected under these conditions. Further details about the slider rig and its operation are provided in Morris et al. [24].

Relatively low load and large apparent contact area, \( {\mathcal{A}} \) (contacting face of the strip) yields insufficient lubricant pressures to cause any elasto-hydrodynamic deformation of the surfaces. Furthermore, any lubricant film thickness, h, above the mean surface height of topography, d, is expected to be quite thin, yielding a mixed regime of lubrication.

5.2 The numerical model

The generated friction under the anticipated mixed-hydrodynamic regime of lubrication is obtained as:

$$ f = f_{v} + f_{b} $$
(26)

where, the total friction, \( f \) is as the result of contributions due to the viscous shear of a thin lubricant film and boundary friction due to the interaction of asperities on the counterfaces of the contacting surfaces.

The viscous friction force is obtained as follow:

$$ f_{v} = \mathop \int \nolimits_{0}^{L} \mathop \int \nolimits_{ - b/2}^{b/2} \left| { \pm \frac{h}{2}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\nabla } p - U\frac{\eta }{h}} \right|dxdy $$
(27)

Boundary friction is due to the interaction of counterface asperities, as well as any pockets of lubricant entrapped between them, which are assumed to be subject to the limiting Eyring [25] shear stress as [9]:

$$ f_{b} =\uptau_{0} \tilde{A} + {\varsigma }\tilde{P} $$
(28)

where, \( \tilde{A} \) is given by Eq. (15). This value is clearly different for the measured surface specific topography and that based on the assumption of Gaussian distribution of Greenwood and Tripp [10] model. Therefore, the resultant friction predicted for an assumed Gaussian peak height distribution, using Greenwood and Tripp [10] model and that for peak height distribution determined using the measured surface data are compared with the directly measured friction using the experimental rig.

The first term on the right-hand side of Eq. (28) represents the non-Newtonian shear of thin pockets of lubricant. The second term corresponds to the direct interaction of asperities. \( {\varsigma } \) is the coefficient of shear strength of asperities, measured using an atomic force microscope in the lateral force mode [8]. The Eyring shear stress is given in Table 1, and \( {\varsigma } = 0.17 \) [26].

It is clear that the lubricant film thickness, h is required in order to predict the viscous friction contribution in Eq. (27). Therefore, a quasi-static load balance must be sought between the contact load carrying capacity, comprising asperity load share and any hydrodynamic lubricant reaction against the applied load, thus:

$$ W = W_{hy} + \tilde{P}\left( d \right) $$
(29)

The hydrodynamic lubricant film reaction is obtained as:

$$ W_{hy} = {\iint }pdxdy $$
(30)

The hydrodynamic generated pressure distribution is obtained through solution of Reynolds equation:

$$ \frac{\partial }{\partial x}\left( {\frac{{\rho h^{3} }}{6\eta }\frac{\partial p}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\frac{{\rho h^{3} }}{6\eta }\frac{\partial p}{\partial y}} \right) = U\frac{{\partial \left( {\rho h} \right)}}{\partial x} + 2\frac{{\partial \left( {\rho h} \right)}}{\partial t} $$
(31)

where, U is the sliding velocity of the strip in the x-direction. The strip is of finite length, thus the Poiseuille side-leakage flow due to pressure gradient in the lateral y-direction is also taken into account. The final term on the right-hand side of the equation takes the squeeze film effect into account due to the transient nature of the problem.

The lubricant film shape is given as:

$$ h\left( {x,y} \right) = h_{0} + \frac{{x^{2} }}{2R} + \delta \left( {x,y} \right) $$
(32)

where, \( h_{0} \) is the initial gap. As already noted there is no localised elastohydrodynamic deformation of the contacting surfaces for the relatively low generated pressures, thus: \( \delta \left( {x,y} \right) \cong 0 \).

The boundary conditions used for the solution of Reynolds equation are:

$$ p_{{\left( {x = - b/2} \right)}} = P_{atm} , p_{{\left( {x = c} \right)}} = P_{cav} \;and\; \left. {\frac{\partial p}{\partial x}} \right|_{{\left( {x = c} \right)}} = 0 $$
(33)

These correspond to atmospheric pressure at the inlet (\( x = - {\raise0.7ex\hbox{$b$} \!\mathord{\left/ {\vphantom {b 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}} \)), where b is the effective face-width of the sliding strip and Swift–Stieber boundary conditions at the film rupture point at the contact exit constriction (\( x = c \)), where the cavitation pressure is that of the lubricant at the environmental temperature of 20 °C. In this study the cavitation pressure is assumed to be equal to the atmospheric pressure.

In the lateral direction (side-leakage direction):

$$ p_{{\left( {y = 0} \right)}} = p_{{\left( {y = l} \right)}} = P_{atm} $$
(34)

The rheological properties of the lubricant vary with pressure in the current isothermal analysis. The relationships given by Dowson and Higginson [27] and Houpert [28] are utilised to take into account the variations of lubricant density and dynamic viscosity with pressure and temperature as:

$$ \rho = \rho_{0} \left[ {1 + \frac{{6 \times 10^{ - 10} \left( {p - p_{atm} } \right)}}{{1 + 1.7 \times 10^{ - 9} \left( {p - p_{atm} } \right)}}} \right] $$
(35)

and:

$$ \eta = \eta_{0} { \exp }\left\{ {\left( {\ln \eta_{0} + 9.67} \right)\left( {\left[ {1 + 5.1 \times 10^{ - 9} \left( {p - p_{atm} } \right)} \right]^{Z} - 1} \right)} \right\} $$
(36)

where:

$$ Z = \frac{\alpha }{{5.1 \times 10^{ - 9} \left( {\ln \eta_{0} + 9.67} \right)}} $$
(37)

A second order finite difference method is used to solve Reynolds equation by utilising Point-Successive Over-Relaxation scheme. During the iterations the lubricant properties are also updated. The procedure used, including for convergence criteria, are described in Rahmani et al. [29].

6 Results and discussion

Figure 10 shows a comparison of numerical predictions of friction with that measured using the sliding tribometer. In general, the numerical predictions show very good agreement with the measured data, with a maximum deviation from the measured friction of 3.98 % in the case of boundary friction contribution, based on the Greenwood and Tripp model with a constant average asperity tip radius. This difference is further reduced to 2.67 % when the boundary friction contribution is based on the surface-specific distribution data (\( F_{5/2} \) and \( F_{2} \), thus \( \tilde{P}\left( d \right) \) and \( \tilde{A} \)) with an assumed constant average asperity tip radius. An even further reduced difference (i.e. 2.47 %) from measured friction is obtained when surface-specific topographic distributions are used with a variable determined asperity tip radius \( \beta \left( h \right) \) for any given separation h. Therefore, the results illustrate the importance of considering the asperity radii as a variable with respect to separation (i.e. \( \beta \left( h \right) \)). The progressive improved predictions account for small gains in accuracy, but represent significant gains in practice.

Fig. 10
figure 10

Comparison of friction predicted by various asperity models with experimental data

Full size image

7 Conclusions

The current analysis highlights the potential mis-representation which may occur as a result of assuming a Gaussian surface roughness distribution in modelling asperity interactions. Considering real surface-specific roughness distributions and comparing with experimental data the potential difference is clearly demonstrated. The repercussions of this for asperity load carrying capacity and also the onset of mixed regime of lubrication is described.

It is also clear that the method of considering variation in asperity radii at different separations, developed here, offers additional improvements for surface analysis and modelling. The use of measured surface-specific distribution and separation-dependent variable asperity radii are the main contributions made to knowledge in this paper. The developed methodology also shows very good agreement with experimental measurements of friction.