1 Introduction

In archery, the compound bow is a bow in which a pulley system is used at the end of the limb tips in order to make the bow easier and more accurate to shoot. When a traditional bow is drawn, the force-draw relation is nearly linear: the more you draw the bow, the higher is the holding force. In full draw situation, the archer has to keep the maximum force and aim at the same time. With a compound bow the required force increases more rapidly, but after a certain point the force begins to reduce towards the local minimum value in the full draw. This not only helps aiming, but also makes it possible to shoot the arrow faster when compared to a traditional bow with the same maximum force.

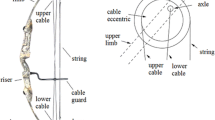
The compound bows can be classified in several types. The earlier compound bow models had sometimes even 6 pulleys and also levers [1], but nowadays the classification of compound bows is mostly based on the type of pulleys at the tips of the upper and lower limb. In modern compound bows in use, the pulleys (or cams) at the end of the limbs are either similar (twin and binary cam configuration) or different (single and hybrid cam configuration) [2]. The pulleys are used to create the unique force-draw relation for the compound bow. In this paper we shall restrict our considerations on one bow type only, the compound bow with similar round pulleys at the tip of the upper and the lower limb. We shall call this bow type a twin-round-wheel compound bow, and a typical bow of this type in the initial position is presented in Fig. 1.

Fig. 1
figure 1

A typical twin-round-wheel compound bow in the initial position and its upper wheel system

Full size image

The research concerning archery bow modelling is mostly done with the traditional long and recurve bows, the compound bow being quite an uncommon subject. The mechanics of the single-cam compound bow is investigated by Park [3]. Zanevskyy [4] has studied the asymmetrical positioning of the grip and the nock point of the bow with a special compound bow model, where the axle goes through the centre of the cable (inner) eccentric. Usually the axle is clearly aside from the centre of both eccentrics, as in Fig. 1, when the lever arms of both the cable and the string forces change in a complicated way when drawing the bow. A more advanced model for the twin-round-wheel compound bow is therefore needed, which is the motivation of this paper.

2 Mathematical model

Let us consider a compound bow with similar pulley wheels at the tips of the upper and the lower limb. The bow is supposed to be symmetric with respect to some horizontal line. This line is also the line in which the end of the arrow moves when the bow string is drawn or released from the midpoint of the string. In our considerations the bow is in a vertical position and the riser is on the left side with respect to the wheels as in Fig. 1.

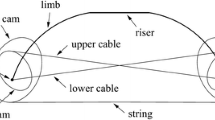
At first we shall examine the action of the upper wheel of the bow. The wheel consists of two concentric eccentric discs, which are firmly attached to each other, and the wheel can rotate only around the non-centred axle, from which the wheel is connected to the upper limb. Note that in our considerations the small portion of the upper limb above the axle point (Fig. 1) does not play any role, so on the following the tip of the limb always refers to the axle point of the wheel. The string is wrapped around the string (outer) eccentrics of both the upper and the lower limb. From one end, the upper cable is twisted around the cable (inner) eccentric of the upper wheel, but on the other side than the string, as seen from Fig. 1. The other end of this cable is connected to the axle of the lower wheel, as presented in Figs. 1 and 2. The lower cable is similar with respect to the lower wheel: it is connected to the axle of the upper wheel and to the cable eccentric of the lower wheel. In real bows the cable guard (Fig. 1) shifts both cables slightly aside to clear the way for the arrow. However, for the sake of simplicity and symmetry we shall ignore the cable guard and assume that the cables are straight and on the same plane with the string. Let us also suppose that the cables and the string are inextensible, and that they do not slide with respect to the wheels. The symbols used are:

\( \alpha \) :

the angle between the horizontal line and the line that connects the centre of the upper wheel and the upper axle point

\( \beta \) :

the angle between the vertical line and the line that connects the centre of the upper wheel to the axle point of the lower wheel

\( \gamma \) :

the angle in which the radius of the upper cable eccentric is seen from the lower axle point

\( \delta \) :

the angle between the horizontal line and the line that connects the centre of the upper wheel and the point where the straight cable contacts the upper cable eccentric

\( \theta \) :

the angle between the vertical line and the line that connects the upper axle point and the supposed hinge point of the limb

\( \theta _U \) :

the angle between the undeflected bow limb and the vertical line

\( \varphi \) :

the angle between the horizontal line and the line that connects the centre of the upper wheel and the point where the string touches the string eccentric

A :

the ratio between the length of the supposed elastic portion of the limb with respect to the total limb length

a :

the torque constant of the elastic portion of the limb

B :

the point of the bottom of the limb

c :

the length of the straight cable

D :

the draw; the distance from the midpoint of the string to the vertical line that connects the bottoms of the upper and the lower limb

d :

the distance between the axle and the centre of the wheel

\( d_c \) :

the lever arm of the cable tension

\( d_s \) :

the lever arm of the string tension

e :

the distance between the upper and the lower axle

F :

the absolute value of the force acting on the arrow

\( \overline{F}_{cu} \) :

the upper cable tension

\( \overline{F}_{cl} \) :

the lower cable tension

\( F_c \) :

the absolute value of the upper and the lower cable tension

\( \overline{F}_s \) :

the string tension

\( F_s \) :

the absolute value of the string tension

g :

the distance between the bottoms of the upper and the lower limb; the length of the riser

k :

the spring constant of the elastic portion of the limb

L :

the length of the limb (from the bottom to the axle point)

P :

the supposed hinge point of the limb

R :

the radius of the string (outer) eccentric

r :

the radius of the cable (inner) eccentric

s :

the length of the straight half-string

Moreover, the subscript “0” refers to the value of the respective variable in the initial position.

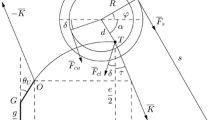
Let us suppose that the bow parameters \(e_0\), g, \(\theta _U\), \( \alpha _0 \), L, R, r and d are known. The upper cable eccentric with the axle point of the lower wheel in the initial and the drawn positions is presented in Fig. 2, from which we see that

$$ c_{0}\tan \gamma _{0} \,=\, r, \quad c\tan \gamma =r $$
(1)
$$\begin{aligned} \tan \beta _{0}= & {} \frac{d\cos \alpha _{0}}{e_{0}-d\sin \alpha _{0}}, \quad \tan \beta =\frac{d\cos \alpha }{e-d\sin \alpha } \end{aligned}$$
(2)
$$ \delta _{0}\,=\,\beta _{0}+\gamma _{0}, \quad \delta =\beta +\gamma $$
(3)
$$ {c_{0}}^{2}\,=\,{e_{0}}^{2}-2e_{0}d\sin \alpha _{0}+d^{2}-r^{2} $$
(4)
$$ {c}^{2}\,=\,{e}^{2}-2ed\sin \alpha +d^{2}-r^{2} $$
(5)

The values of \(\beta _{0}\), \(c_{0}\), \(\delta _{0}\) and \(\gamma _{0}\) can thus be calculated from the bow parameters \(\alpha _{0}\), \(e_{0}\), r and d. On the other hand, from Fig. 2 we also notice that

$$ c_{0}+r\delta _{0}=c+r\delta +r\left( \alpha _{0}-\alpha \right) $$
(6)
Fig. 2
figure 2

The upper cable eccentric in the initial (1) and drawn (2) position with the upper cable and the axle of the lower wheel

Full size image

By using Eqs. (4) and (5) and the right-side Eqs. (1)–(3) we may write Eq. (6) as

$$\begin{aligned}&\sqrt{e_{0}^{2}-2e_{0}d\sin \alpha _{0}+d^{2}-r^{2}} \nonumber \\&\quad -\,\sqrt{e^{2}-2ed\sin \alpha +d^{2}-r^{2}} \nonumber \\&\quad -\,r(\alpha _{0}-\alpha ) +r \left( \delta _{0}-\arctan \frac{d\cos \alpha }{e-d\sin \alpha }\right) \nonumber \\&\quad -\,r\arctan \frac{r}{\sqrt{e^{2}-2ed\sin \alpha +d^{2}-r^{2}}}=0 \end{aligned}$$
(7)

Here the unknowns are \(\alpha \) and e. We may choose \(\alpha \) as the prime variable, when with a fixed \(\alpha \) the variable e can be solved from Eq. (7). There is no analytical solution, so for iteration the Brent-Dekker root finding algorithm [5] is chosen. After iteration of e the variables c, \( \gamma \) ,\( \beta \) and \(\delta \) can be calculated using Eq. (5) and the right-side Eqs. (1)–(3).

Fig. 3
figure 3

The upper part of the compound bow in the initial (1) and drawn (2) positions. Note that in position 2 \( \alpha \) is negative. The cables and the cable eccentric are left out from the figure for clarity

Full size image

When the upper wheel has rotated the angle \(\alpha _{0}{-}\alpha \) clockwise, we see from Fig. 3 that the length of the straight half-string is

$$\begin{aligned} s & = s_{0}+R (\alpha _{0}-\alpha )+R\varphi \nonumber \\&= \frac{e_{0}}{2}-d\sin \alpha _{0}+R (\alpha _{0}-\alpha )+R\varphi \end{aligned}$$
(8)

We also notice from Fig. 3 that

$$ s\cos \varphi =\frac{e}{2}-d\sin \alpha +R\sin \varphi $$
(9)

when using Eq. (8) we get

$$\begin{aligned}&\left[ \frac{e_{0}}{2}-d\sin \alpha _{0}+R(\alpha _{0}-\alpha +\varphi ) \right] \cos \varphi -\frac{e}{2} \nonumber \\&\quad +\,d\sin \alpha -R\sin \varphi =0 \end{aligned}$$
(10)

In Eq. (10) the only unknown is \(\varphi \), for \(\alpha \) is the prime variable and e was solved before. Again, the unknown \(\varphi \) can be solved by iteration using for example the Brent-Dekker algorithm, which after s can be calculated from Eq. (8).

The perpendicular distances from the axle point to the string and the cable lines are according to Figs. 3 and 2,

$$\begin{aligned} d_{s}=R-d\cos (\alpha -\varphi ), \quad d_{c}=r+d\cos (\delta -\alpha ) \end{aligned}$$
(11)

Now let us consider the limb tip movement of the compound bow. For a traditional bow with a limb length L, Hickman noticed that the path made by the limb tip is almost a perfect arc of a circle whose radius is 3L/4 and whose centre is located at a distance of 3L/4 from the tip of the undeflected bow [6]. However, since the width of the compound bow limb does not taper to the tip, it is not clear whether we can use this kind of approximation. Let us still assume that the path made by a compound bow limb tip (or axle point) is analogous with the Hickman model, but the radius of the circle and the distance of its centre from the tip of the undeflected limb with length L is AL, where the value of A may differ from 3/4. The validity of this assumption and the value of A will be checked later on by measurement.

The following equivalences may also be seen from Fig. 3,

$$\begin{aligned} AL\cos \theta _{0}& = \frac{e_{0}}{2}-\frac{g}{2}-(1-A)L\cos \theta _{U} \nonumber \\& = AL\cos \theta +\frac{e_{0}}{2}-\frac{e}{2} \end{aligned}$$
(12)

The unknowns \( \theta _{0} \) and \( \theta \) can be calculated from Eq. (12). With a fixed \( \alpha \) the draw is, according to Fig. 3,

$$\begin{aligned} D& = (1-A)L\sin \theta _{U}+AL\sin \theta -d\cos \alpha \nonumber \\& \quad +\,R\cos \varphi +s\sin \varphi \end{aligned}$$
(13)
Fig. 4
figure 4

The force diagram of the upper limb of the compound bow. The tension of the string is \(\overline{F}_{s}\), and the upper and the lower cable tensions are \(\overline{F}_{cu}\) and \(\overline{F}_{cl}\). In balance, the supporting force \(\overline{T}\) of the riser prevents the limb from moving. Point B is the bottom of the limb, and point P the hinge point of the limb

Full size image

Let us suppose that the undeflected limb is straight and the deflection of the limb is elastic. Let us also assume the Hooke’s law valid for the bending, which is a good approximation in most cases [7]. Then from Fig. 4 the equation for the torque directed to the elastic portion of the upper limb is

$$\begin{aligned} a(\theta -\theta _{U})& = AL[F_{s}\sin (\theta +\varphi ) +F_{c}\sin (\theta +\delta ) \nonumber \\&\quad +\,F_{c}\sin (\theta -\delta )] \end{aligned}$$
(14)

In static situation the wheel does not move, so

$$ F_{c}d_{c}=F_{s}d_{s} $$
(15)

From Eqs. (14) and (15) we get the string tension,

$$\begin{aligned} F_{s}=\frac{a(\theta -\theta _{U})}{AL[\sin (\theta +\varphi )+\frac{2d_{s}}{d_{c}}\sin \theta \cos \delta ]} \end{aligned}$$
(16)

There is also a lower part of the bow, so on the grounds of symmetry, the total force acting on the arrow is

$$\begin{aligned} F=2F_{s}\sin \varphi =\frac{2d_{c}k(\theta -\theta _{U})\sin \varphi }{d_{c}\sin (\theta +\varphi )+2d_{s}\sin \theta \cos \delta } \end{aligned}$$
(17)

where \(k = \frac{a}{AL}\). This completes our model.

3 Results of model testing

The bow used in all measurements was “JahtiJakt 55 lbs” compound bow with the type of eccentrics discussed before. All the initial parameters of the bow are presented in Table 1.

Table 1 The initial parameters of the compound bow used in measurements
Full size table

The values \(e_{0}\), g and L were measured straightforwardly with a steel ruler. The values of R, r and d were measured from magnified pictures of the wheel with the ruler. Also the grooves for the cable and the string are taken into account on the values of R and r, assuming that the effective radius are the distances of the middle lines of the cables from the centre of the wheel. The value of \(\theta _U\) was measured from the actual bow with straight-line background using a marine navigation protractor triangle. The value of \( \alpha _0 \) was determined from the magnified picture with the help of the symmetric radial grooves of the eccentric using the same protractor.

The values of L, R, r, d, \( \theta _{U} \) and \( \alpha _{0} \) were measured from both the upper and the lower parts of the bow. There were no significant differences between the upper and the lower bow part parameters. The values of these parameters in Table 1 are the average values of the upper and the lower parts of the bow, for our model is symmetric.

Fig. 5
figure 5

The measured places of the axle points of the deflected limbs and the fitted arc of the circle

Full size image

The constant A was found by using several measured places of the axle points of the eccentrics on the tip of the deflected bow limbs and fitting the modified one-hinge model of Hickman as discussed before into the measured data. The model function is, according to previous Section,

$$ y_{L}=\sqrt{(AL)^{2}-(x_{L}-L+AL)^{2}} $$
(18)

where \(x_{L}\) is the distance of the axle point (or tip point) of the deflected limb from the bottom point B of the limb along the line BP parallel to the undeflected limb (see Fig. 4) and \(y_{L}\) the perpendicular distance of the axle point of the deflected limb from that line. The model is non-linear, so for curve fitting the common Levenberg–Marquardt algorithm [8] was chosen. Using the value of \( A=0.598 \) given by the algorithm the fitted arc of the circle is quite close to the measured axle points of the limbs, as can be seen from Fig. 5. The assumption for the path of the tip of the limb as presented in Sect. 2 is therefore valid.

The force-draw (FD) curve of the compound bow was measured by using the steel ruler mentioned before and Hanson 8910 Bow Scale. The accuracy of the ruler was checked by comparing it to two other steel rulers. The calibration of the Bow Scale was made by using disc weights of 2.5 kg, inserting them one by one on the Scale up to 27.5 kg. The masses of the disc weights were checked with two commercial scales of nominal accuracy of 1 g. The calibration of the Hanson Scale and the initial bow parameters \(e_{0}\), \( \theta _{U} \) and \( \alpha _{0} \) were checked before and after the measurements. The bow was set in a horizontal position on the top of the specific steel-made deflecting rack, and the steel ruler was attached on the rack in vertical position. The Hanson Bow Scale was connected to the midpoint of the string, and the other end of the Scale was connected via pulley to the manual winch. The arrangements of the FD curve measurement are presented in Fig. 6.

Fig. 6
figure 6

The arrangements of the measurement of the force-draw curve

Full size image

A small plastic indicator was attached on the top of the Scale to help read the draw. The bow was drawn slowly with the winch slightly over the full draw, which is the draw with local minimum force (the bottom of the force-draw valley). The bow was also relaxed slowly back to the initial position. The readings of the Bow Scale and the ruler were recorded with a video camera. In the measurements the sensitive end of the Hanson Scale is at the bottom, so the mass of the Scale with the plastic indicator and the hook was measured with a laboratory scale and added to the readings of the Hanson Scale.

Fig. 7
figure 7

The force-draw curve of the compound bow. The solid line is the prediction of the model with the bow parameter values of Table 1

Full size image

The constant k was determined indirectly with the help of the model. First, 1000 evenly distributed values of the prime variable \(\alpha \) were selected from the domain \(-200^{\circ } \le \alpha \le 52.5^{\circ }\). Using an initial guess value for k and the other initial parameter values of Table 1, the procedure described in Sect. 2 can be executed separately with every value of \(\alpha \), resulting also the respective values of D and F.

Finally, the value of k was chosen so that the model fits to the measurements as well as possible in the sense of least squares. For continuity reasons, a cubic spline was fitted to the (D, F) -values of the model, and the least squares method was applied on the values of this spline and the measured data. Both the drawing and relaxing FD data of the bow were included in the fitting.

From Fig. 7 we see that the model match on the FD data is good. We also notice that the measured values of the force are systematically bigger when drawing the bow compared to relaxing the bow. Apparently this is caused by the friction of the wheels and the elastic hysteresis of the limbs, string and cables. Also from Fig. 7 we can see that near the full draw the calculated FD curve is slightly aside the measured data. This is probable due to the elongation of the string and the cables, which are not taken into account in the model.

The area between the FD curve and the draw-axis defines also the energy stored to the bow limbs,

$$ V(D)=\int _{D_{0}}^D F(D) \, {\mathrm {d}}D $$
(19)

On the other hand, with the assumptions mentioned before, in our model we may write the potential energy stored to the limbs as

$$\begin{aligned} V(\theta )& = 2\int _{\theta _{0}}^\theta a(\theta -\theta _{U}) \, {\mathrm {d}}\theta \nonumber \\ & = ALk\left( \theta ^{2}-\theta _{0}^{2}+2\theta _{0}\theta _{U}- 2\theta \theta _{U}\right) \end{aligned}$$
(20)

which can be used for checking the computations. With the parameter values presented in Table 1 the cubic spline function which was fitted to the (D, F)-values of the model was integrated numerically. Using the draw from the initial position to the full draw \(D = 0.68\) m and 2000 knot points, the differences between the calculations based on Eqs. (19) and (20) were \({<}10^{-6}\) J.

4 Conclusion

A detailed mathematical model of the twin-round-wheel compound bow is introduced. The prediction of the model for the FD curve fits very well on measured data.

The assumption of the Hooke’s law on the bending portion of the deflecting limb is also adequate. While the profile of the compound bow limb differs from the traditional Hickman bow limb, a good approximation for the path of the limb tip of the compound bow can still be found by supposing that the limb is a rigid straight rod with length L and bends only on one point whose distance from the tip of the bow limb is AL. The dimensionless constant A depends on the limb profile and must be determined from the actual limb.

The model does not take into account the elongation of the string or cables. However, this lack has only a possible minor effect on the FD curve near the full draw.

The FD curve was measured while both drawing and relaxing the bow. There is a difference between these measurements. Apparently this difference is caused by the friction of the wheels and the elastic hysteresis of the bow limbs, string and cables.

The mathematical model of the compound bow presented here is quite accurate. Obviously it can be used when designing or adjusting this type of compound bows.