Plane strain transversely anisotropic analysis in sheet metal forming simulation using 6-component Barlat yield function

Abstract

In most FEM codes, the isotropic-elastic and transversely anisotropic-elastoplastic model using Hill’s yield function has been widely adopted in 3D shell elements (modified to meet the plane stress condition) and 3D solid elements. However, when the 4-node quadrilateral plane strain or axisymmetric element is used for 2D sheet metal forming simulation, the above transversely anisotropic Hill model is not available in some FEM code like Ls-Dyna. A novel approach for explicit analysis of transversely anisotropic 2D sheet metal forming using 6-component Barlat yield function is elaborated in detail in this paper, the related formula between the material anisotropic coefficients in Barlat yield function and the Lankford parameters are derived directly. Numerical 2D results obtained from the novel approach fit well with the 3D solution.

1 Introduction

In order to accurately simulate sheet metal forming processes, it is essential to describe correctly the material constitutive behaviors. Since most sheet metals exhibit anisotropic material behaviors, the use of appropriate anisotropic yield criterion is important to predict material behaviors accurately. Moreover, anisotropy has an important effect on the strain distribution in sheet metal forming process, and it is closely related to thinning and formability of sheet metal, so the anisotropy of the material should be properly considered to capture the realistic material behaviors.

The influence of plastic anisotropy on sheet metal forming has been studied with the help of FEM codes combined with appropriate anisotropic yield functions. Many such functions have been proposed. The quadratic yield function by Hill (1948) has long been one of the popular choices to represent planar anisotropy and has been widely used in FEM forming simulation. Several non-quadratic criteria were developed by Hill (1979, 1990), Hershey (1954), Hosford (1972), Bassani (1977), Gotoh (1977), Logan and Hosford (1980), Barlat and Lian (1989), Karafillis and Boyce (1993), Bron and Besson (2004), Banabic et al. (2005) and Barlat et al. (1991, 1997, 2003, 2005). In general, Hill (1948) has been useful for explaining phenomena associated to anisotropic plasticity particularly for steels, the others can be used to improve the yielding description of aluminum alloys. But in many circumstances Yld89 (Barlat and Lian 1989), Yld91 (Barlat et al. 1991) can be used for steels or aluminum alloys. In particular, the yield criteria Yld89 for planar anisotropy, and Hill (1990) have three stress components and are applicable to plane stress condition. The analytical forms of these criteria are relative simple. The criteria Yld91 account for six stress components and can be applied to general 3D elasto-plastic continuum codes. Barlat et al. (2007) have made detailed discussion about the relation between these yield criteria. In fact, Yld91 is a particular case of Yld2004-18p (Barlat et al. 2005), Yld89 is a particular case of Yld2000-2d (Barlat et al. 2003), the yield function proposed by Banabic et al. (2005) is identical to Yld2000-2d. In some special conditions, Yld91 can reduce to Hill (1948), Mises or Tresca yield function.

Section analysis provides a faster and more efficient alternative procedure for analyzing complex part shapes in some cases. In this procedure, a cross section is selected from the tooling along a direction of interest. The problem is then analyzed in 2D, assuming plane strain or axisymmetric conditions. Although most sections in sheet forming do not completely satisfy such assumptions, there are still many local sections in a complicated sheet forming process which can be successfully simulated by 2D section analysis. In general, this method can provide a quicker analysis and designers can modify local geometry of tools with experience at preliminary design stages.

The present study attempts to conduct an explicit section analysis of 2D sheet metal forming using the 4-node quadrilateral plane strain element. In most FEM codes, the isotropic-elastic, transversely anisotropic-elastoplastic model proposed by Hill (1948) has been widely used in 3D shell elements (modified to meet the plane-stress condition) and 3D solid elements. However, the above transversely anisotropic model is not available for simulating 2D sheet metal forming process using 4-node quadrilateral plane strain or axisymmetric element in some FEM code like Ls-Dyna (Hallquist 2007). In this paper, a novel approach for the explicit analysis of transversely anisotropic 2D sheet metal forming using 6-component Barlat yield function (Barlat et al. 1991) is proposed, the related formula and parameters are derived directly in detail, the numerical 2D results obtained from the novel approach fit well with the 3D solution.

2 Fundamental theory

2.1 Basic finite element equation

The sheet metal forming process can be treated as a dynamic contacting problem. In the forming process, the whole system should satisfy the following finite element equation:

$${\user2{M}}\ddot{\user2{U}} = {\user2{F}}^{ext} + {\user2{F}}^{c} - {\user2{F}}^{int} $$

(1)

where F ^ext is the vector of external force, F ^c the vector of contact force, F ^int the vector of internal force, and M the mass matrix. In the explicit algorithm, Eq. (1) can be solved as follows:

$$ {\ddot{\user2{U}}}_{n} = {\user2{M}}_{n}^{ - 1} \left( {{\user2{F}}_{n}^{ext} + {\user2{F}}_{n}^{c} - {\user2{F}}_{n}^{int} } \right) $$

(2)

$$ {\dot{\user2{U}}}_{n + 1/2} = {\dot{\user2{U}}}_{n - 1/2} + \Updelta t \cdot {\ddot{\user2{U}}}_{n} $$

(3)

$$ {\user2{U}}_{n + 1} = {\user2{U}}_{n} + \Updelta t \cdot {\dot{\user2{U}}}_{n + 1/2} $$

(4)

If a concentrated mass matrix is assumed, it is not necessary to solve the assembled equations since the mass matrix becomes diagonal. The acceleration vector ${\ddot{\user2{U}}}_{n}$ at t _n can be solved by Eq. (2) furthermore, the displacement vector U _n+1 at t _n+1 can be solved by Eqs. (3) and (4).

2.2 Transversely anisotropic model

2.2.1 The general Hill orthotropic anisotropic yield criteria

In 1948, Hill proposed a orthotropic anisotropic yield function (Hill 1948) according to Mises criteria:

$$ 2f = F\left( {\sigma_{22} - \sigma_{33} } \right)^{2} + Q\left( {\sigma_{33} - \sigma_{11} } \right)^{2} + H\left( {\sigma_{11} - \sigma_{22} } \right)^{2} + 2L\sigma_{23}^{2} + 2M\sigma_{31}^{2} + 2N\sigma_{12}^{2} = 1 $$

(5)

where F, Q, H, L, M and N are anisotropic constants relating with the material yield behaviors. When F = Q = H = L/3 = M/3 = N/3, (5) reduces to Mises criteria. For the general anisotropic material behaviors, they meets the follow condition:

$$ \begin{aligned} &F + H = 1/\sigma_{{s_{2} }}^{2} ,\quad Q + H = 1/\sigma_{{s_{1} }}^{2} ,\quad F + Q = 1/\sigma_{{s_{3} }}^{2} \hfill \\ &L = 1/2\sigma_{{s_{23} }}^{2} ,\quad M = 1/2\sigma_{{s_{31} }}^{2} ,\quad N = 1/2\sigma_{{s_{12} }}^{2} \hfill \\ \end{aligned} $$

(6)

where $\sigma_{{s_{1} }} ,\sigma_{{s_{2} }} ,\sigma_{{s_{3} }} ,\sigma_{{s_{23} }} ,\sigma_{{s_{31} }}$ and $\sigma_{{s_{12} }}$ are the tension or shear yield stresses in corresponding directions.

2.2.2 Transversely anisotropic criteria

For the plane strain problems, Hill’s orthotropic yield function can be simplified:

$$ 2f = F(\sigma_{22} - \sigma_{33} )^{2} + Q(\sigma_{33} - \sigma_{11} )^{2} + H(\sigma_{11} - \sigma_{22} )^{2} + 2M\sigma_{31}^{2} = 1 $$

(7)

For transversely anisotropic sheet material, $F = Q,\;\sigma_{{s_{1} }} = \sigma_{{s_{2} }}$. The following relation can be derived from (6).

$$ Q = 1/2\sigma_{{s_{3} }}^{2} ;\quad H = 1/\sigma_{{s_{1} }}^{2} - 1/2\sigma_{{s_{3} }}^{2} $$

(8)

The Lankford parameter is determined as follows:

$$ R = \dot{\varepsilon }_{11}^{p} /\dot{\varepsilon }_{33}^{p} = \dot{\varepsilon }_{22}^{p} /\dot{\varepsilon }_{33}^{p} = H/Q = 2\sigma_{{s_{3} }}^{2} /\sigma_{{s_{1} }}^{2} - 1 $$

(9)

2.3 6-Component Barlat model

A more elaborate yield model (Barlat et al. 1991, 1997) was proposed (Yld91) where the yield function is formulated in the following way:

$$ \Upphi \left( {S_{k} \left( {\sigma_{ij} ,a,b,c,f,g,h,m} \right)} \right) = \left| {S_{1} - S_{2} } \right|^{m} + \left| {S_{2} - S_{3} } \right|^{m} + \left| {S_{3} - S_{1} } \right|^{m} = 2\bar{\sigma }^{m} $$

(10)

In this equation S _k (k = 1–3) represents the three eigenvalues of the following matrix:

$$ {\mathbf{s}} = \left[ {\begin{array}{*{20}l} {s_{xx} } & {s_{xy} } & {s_{zx} } \\ {s_{xy} } & {s_{yy} } & {s_{yz} } \\ {s_{zx} } & {s_{yz} } & {s_{zz} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\frac{cC - bB}{3}} & {hH} & {gG} \\ {hH} & {\frac{aA - cC}{3}} & {fF} \\ {gG} & {fF} & {\frac{bB - aA}{3}} \\ \end{array} } \right] $$

(11)

where

$$ \begin{aligned} &A = \sigma_{yy} - \sigma_{zz} ,\quad B = \sigma_{zz} - \sigma_{xx} ,\quad C = \sigma_{xx} - \sigma_{yy} \hfill \\ &F = \sigma_{yz} ,\quad G = \sigma_{zx} ,\quad H = \sigma_{xy} \hfill \\ \end{aligned} $$

(12)

From (11) the characteristic equation for computing the three eigenvalues of the matrix can be expressed as:

$$ \begin{aligned} &P\left( {S_{k} } \right) = \det \left| {{\mathbf{s}} - S_{k} {\mathbf{I}}} \right| = 0 \hfill \\ &S_{k}^{3} - 3I_{1} S_{k}^{2} - 3I_{2} S_{k} - 2I_{3} = 0 \hfill \\ \end{aligned} $$

(13)

where I is the identity matrix, I ₁, I ₂ and I ₃ are the following tensor invariants:

$$ I_{1} = (s_{xx} + s_{yy} + s_{zz} )/3 = 0 $$

(14)

$$ I_{2} = (s_{yz}^{2} + s_{zx}^{2} + s_{xy}^{2} - s_{yy} s_{zz} - s_{zz} s_{xx} - s_{xx} s_{yy} )/3 = \frac{{(fF)^{2} + (gG)^{2} + (hH)^{2} }}{3} + \frac{{(aA - cC)^{2} + (cC - bB)^{2} + (bB - aA)^{2} }}{54} $$

(15)

$$ I_{3} = (2s_{yz} s_{zx} s_{xy} + s_{xx} s_{yy} s_{zz} - s_{xx} s_{yz}^{2} - s_{yy} s_{zx}^{2} - s_{zz} s_{xy}^{2} )/2 = \frac{(cC - bB)(aA - cC)(bB - aA)}{54} + fghFGH - \frac{{(cC - bB)(fF)^{2} }}{6} - \frac{{(aA - cC)(gG)^{2} + (bB - aA)(hH)^{2} }}{6} $$

(16)

$$ \theta = \arccos \left( {\frac{{I_{3} }}{{I_{2}^{3/2} }}} \right),\quad 0 \le \theta \le \pi $$

(17)

Therefore, the 6-component Barlat anisotropic yield function (Yld91) can also be expressed as:

$$ \Upphi = (3I_{2} )^{m/2} \left\{ {\left[ {2\cos \left( {\frac{2\theta + \pi }{6}} \right)} \right]^{m} + } \right.\left[ {2\cos \left( {\frac{2\theta - 3\pi }{6}} \right)} \right]^{m} \left. { + \left[ { - 2\cos \left( {\frac{2\theta + 5\pi }{6}} \right)} \right]^{m} } \right\} = 2\bar{\sigma }^{m} $$

(18)

In fact, if m = 2 or 4, Yld91 reduces to Hill (1948) model; it can further reduce to Mises model if a = b = c = f = g = h = 1. If m = 1 or ∞, and a = b = c = f = g = h = 1, Yld91 reduces to Tresca model.

$$ \Upphi = 2\bar{\sigma }^{m} = 2f^{m} ,\quad f = \left( {\frac{\Upphi }{2}} \right)^{1/m} $$

(19)

$$ \frac{\partial f}{{\partial \sigma_{ij} }} = \frac{1}{2m}\left( {\frac{\Upphi }{2}} \right)^{1/m - 1} \frac{\partial \Upphi }{{\partial \sigma_{ij} }} = \frac{1}{{2m\bar{\sigma }^{m - 1} }}\frac{\partial \Upphi }{{\partial \sigma_{ij} }} $$

(20)

After some manipulations, Eq. (20) can be described explicitly in details, given in Appendix.

2.4 The relation between material anisotropic coefficients

In general, the Lankford parameters R in three directions (i.e., 0°, 45° and 90°) should be available when sheet metals are provided. On the other hand, the six material anisotropic coefficients a, b, c, f, g and h are generally not available. In order to use the above derived model, it is necessary to obtain their quantitative values from the Lankford parameters.

The arbitrary Lankford parameters R _ϕ can be described as:

$$ R_{\phi } = \frac{{\dot{\varepsilon }_{t}^{p} }}{{\dot{\varepsilon }_{z}^{p} }} $$

(21)

where $\dot{\varepsilon }_{t}^{p}$ is the plastic strain rate which is perpendicular to tensile axis of the uniaxial tensile sheet metal specimen, $\dot{\varepsilon }_{z}^{p}$ the plastic strain rate which is along the thickness direction of sheet metal, and ϕ the angle between the tensile axis and the rolling direction.

The stress status of a body unit in the uniaxial tensile sheet metal specimen is shown in Fig. 1. From Fig. 1 it can be obtained that:

$$ \begin{aligned} &\sigma_{xy} = \sigma_{11} \sin \phi \cos \phi ,\quad \sigma_{xx} = \sigma_{11} \cos^{2} \phi ,\quad \sigma_{yy} = \sigma_{11} \sin^{2} \phi \hfill \\ &\dot{\varepsilon }_{11}^{p} = \cos^{2} \phi \dot{\varepsilon }_{xx}^{p} + \sin^{2} \phi \dot{\varepsilon }_{yy}^{p} + 2\sin \phi \cos \phi \dot{\varepsilon }_{xy}^{p} ,\quad \dot{\varepsilon }_{22}^{p} = \sin^{2} \phi \dot{\varepsilon }_{xx}^{p} + \cos^{2} \phi \dot{\varepsilon }_{yy}^{p} - 2\sin \phi \cos \phi \dot{\varepsilon }_{xy}^{p} \hfill \\ \end{aligned} $$

(22)

Assuming that the sheet metal material is incompressible, the Lankford parameter can be derived:

$$ R_{\phi } = \frac{{\dot{\varepsilon }_{t}^{p} }}{{\dot{\varepsilon }_{z}^{p} }} = - \frac{{\dot{\varepsilon }_{22}^{p} }}{{\dot{\varepsilon }_{11}^{p} + \dot{\varepsilon }_{22}^{p} }} $$

(23)

Substituting formula (22) into Eq. (23), it can be obtained:

$$ R_{\phi } = - \frac{{\sin^{2} \phi \dot{\varepsilon }_{xx}^{p} + \cos^{2} \phi \dot{\varepsilon }_{yy}^{p} - 2\sin \phi \cos \phi \dot{\varepsilon }_{xy}^{p} }}{{\dot{\varepsilon }_{xx}^{p} + \dot{\varepsilon }_{yy}^{p} }} $$

(24)

According to the related flow criteria, the relation between R _ϕ and the yield function can be derived:

$$ R_{\phi } = - \frac{{\sin^{2} \phi \frac{\partial f}{{\partial \sigma_{xx} }} - \sin 2\phi \frac{\partial f}{{\partial \sigma_{xy} }} + \cos^{2} \phi \frac{\partial f}{{\partial \sigma_{yy} }}}}{{\left( {\frac{\partial f}{{\partial \sigma_{xx} }} + \frac{\partial f}{{\partial \sigma_{yy} }}} \right)}} $$

(25)

Applying formula (20), Eq. (25) can be represented in detail as follows:

$$ R_{\phi } = \frac{{\left( {\frac{m}{2}\frac{W}{{I_{2} }}\frac{{\partial I_{2} }}{{\partial \sigma_{xy} }} + \frac{\partial W}{{\partial \sigma_{xy} }}} \right)\sin 2\phi }}{{\frac{m}{2}\frac{W}{{I_{2} }}\frac{{\partial I_{2} }}{{\partial \sigma_{xx} }} + \frac{\partial W}{{\partial \sigma_{xx} }} + \frac{m}{2}\frac{W}{{I_{2} }}\frac{{\partial I_{2} }}{{\partial \sigma_{yy} }} + \frac{\partial W}{{\partial \sigma_{yy} }}}} - \frac{{\left( {\frac{m}{2}\frac{W}{{I_{2} }}\frac{{\partial I_{2} }}{{\partial \sigma_{xx} }} + \frac{\partial W}{{\partial \sigma_{xx} }}} \right)\sin^{2} \phi }}{{\frac{m}{2}\frac{W}{{I_{2} }}\frac{{\partial I_{2} }}{{\partial \sigma_{xx} }} + \frac{\partial W}{{\partial \sigma_{xx} }} + \frac{m}{2}\frac{W}{{I_{2} }}\frac{{\partial I_{2} }}{{\partial \sigma_{yy} }} + \frac{\partial W}{{\partial \sigma_{yy} }}}} - \frac{{\left( {\frac{m}{2}\frac{W}{{I_{2} }}\frac{{\partial I_{2} }}{{\partial \sigma_{yy} }} + \frac{\partial W}{{\partial \sigma_{yy} }}} \right)\cos^{2} \phi }}{{\frac{m}{2}\frac{W}{{I_{2} }}\frac{{\partial I_{2} }}{{\partial \sigma_{xx} }} + \frac{\partial W}{{\partial \sigma_{xx} }} + \frac{m}{2}\frac{W}{{I_{2} }}\frac{{\partial I_{2} }}{{\partial \sigma_{yy} }} + \frac{\partial W}{{\partial \sigma_{yy} }}}} = \frac{{\frac{m}{2}\frac{W}{{I_{2} }}\left( {\frac{{\partial I_{2} }}{{\partial \sigma_{xy} }}\sin 2\phi - \frac{{\partial I_{2} }}{{\partial \sigma_{xx} }}\sin^{2} \phi - \frac{{\partial I_{2} }}{{\partial \sigma_{yy} }}\cos^{2} \phi } \right)}}{{\frac{m}{2}\frac{W}{{I_{2} }}\left( {\frac{{\partial I_{2} }}{{\partial \sigma_{xx} }} + \frac{{\partial I_{2} }}{{\partial \sigma_{yy} }}} \right) + \frac{\partial W}{{\partial \sigma_{xx} }} + \frac{\partial W}{{\partial \sigma_{yy} }}}} + \frac{{\left( {\frac{\partial W}{{\partial \sigma_{xy} }}\sin 2\phi - \frac{\partial W}{{\partial \sigma_{xx} }}\sin^{2} \phi - \frac{\partial W}{{\partial \sigma_{yy} }}\cos^{2} \phi } \right)}}{{\frac{m}{2}\frac{W}{{I_{2} }}\left( {\frac{{\partial I_{2} }}{{\partial \sigma_{xx} }} + \frac{{\partial I_{2} }}{{\partial \sigma_{yy} }}} \right) + \frac{\partial W}{{\partial \sigma_{xx} }} + \frac{\partial W}{{\partial \sigma_{yy} }}}} $$

(26)

In order to obtain the relation explicitly between R _ϕ and the six material anisotropic coefficients a, b, c, f, g and h, for simplicity and not losing generality, it can be obtained by assuming m = 2:

$$ W = 4\cos^{2} \frac{2\theta + \pi }{6} + 4\cos^{2} \frac{2\theta - 3\pi }{6} + 4\cos^{2} \frac{2\theta + 5\pi }{6} = 6 $$

$$ K\left( {\theta ,\pi } \right) = - \frac{8}{3}\left( {\cos \frac{2\theta + \pi }{6}\sin \frac{2\theta + \pi }{6} + \cos \frac{2\theta - 3\pi }{6}\sin \frac{2\theta - 3\pi }{6} + \cos \frac{2\theta + 5\pi }{6}\sin \frac{2\theta + 5\pi }{6}} \right) = 0 $$

$$ \frac{\partial W}{{\partial \sigma_{ij} }} = K\left( {\theta ,\pi } \right)\frac{\partial \theta }{{\partial \sigma_{ij} }} = 0 $$

$$ R_{\phi } = \frac{{\frac{{\partial I_{2} }}{{\partial \sigma_{xy} }}\sin 2\phi - \frac{{\partial I_{2} }}{{\partial \sigma_{xx} }}\sin^{2} \phi - \frac{{\partial I_{2} }}{{\partial \sigma_{yy} }}\cos^{2} \phi }}{{\frac{{\partial I_{2} }}{{\partial \sigma_{xx} }} + \frac{{\partial I_{2} }}{{\partial \sigma_{yy} }}}} = \frac{{18h^{2} H\sin 2\phi }}{{\left( {2a^{2} + ab} \right)A - \left( {2b^{2} + ab} \right)B + \left( {bc - ac} \right)C}} - \frac{{\sin^{2} \phi \left[ {\left( {ab - ac} \right)A - \left( {2b^{2} + bc} \right)B + \left( {2c^{2} + bc} \right)C} \right]}}{{\left( {2a^{2} + ab} \right)A - \left( {2b^{2} + ab} \right)B + \left( {bc - ac} \right)C}} - \frac{{\cos^{2} \phi \left[ {\left( {2a^{2} + ac} \right)A + \left( {bc - ab} \right)B - \left( {2c^{2} + ac} \right)C} \right]}}{{\left( {2a^{2} + ab} \right)A - \left( {2b^{2} + ab} \right)B + \left( {bc - ac} \right)C}} $$

(27)

Applying formula (12) and (22), it can be obtained:

$$ R_{\phi } = \frac{{2\sin^{2} \phi \cos^{2} \phi \left( {18h^{2} - a^{2} - b^{2} - 4c^{2} - 2bc - 2ac + ab} \right)}}{{2\left( {b^{2} + bc} \right)\cos^{2} \phi + 2\left( {a^{2} + ac} \right)\sin^{2} \phi + \left( {ab - ac - bc} \right)}} + \frac{{\left( {2c^{2} + ac + bc - ab} \right)}}{{2\left( {b^{2} + bc} \right)\cos^{2} \phi + 2\left( {a^{2} + ac} \right)\sin^{2} \phi + \left( {ab - ac - bc} \right)}} $$

(28)

Substituting three angles (ϕ = 0°, 45°, 90°) into Eq. (25), it can be obtained:

$$ R_{0} = \frac{{2c^{2} + ac + bc - ab}}{{2b^{2} + bc + ab - ac}} $$

(29)

$$ R_{45} = \frac{{18h^{2} - a^{2} - b^{2} - ab}}{{2a^{2} + 2b^{2} + 2ab}} $$

(30)

$$ R_{90} = \frac{{2c^{2} + ac + bc - ab}}{{2a^{2} + ab + ac - bc}} $$

(31)

The three Eqs. (29)–(31), contain four unknown coefficients a, b, c and h. They can’t be solved deterministically. However, it is noted that the coefficients f, g and h represent the influences of material anisotropy applying to the stress component (σ _yz , σ _zx , σ _xy ). For isotropy materials, the six coefficients a, b, c, f, g and h are all equal to 1. When the anisotropy of the sheet metal is described, it can approximately be made that f = g = h = 1. It is now possible to solve a, b and c in the assembled Eqs. (29)–(31).

Fig. 1

The stress status of a body unit in the uniaxial tensile sheet metal specimen

For transversely anisotropic sheet metal, it’s easy to see that:

$$ R_{0} = R_{45} = R_{90} = R = 2\sigma_{{s_{3} }}^{2} /\sigma_{{s_{1} }}^{2} - 1 $$

(32)

The three coefficients a, b and c can be solved in the Eq. (32).

3 Numerical example

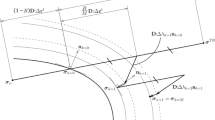
The tool geometry data of sheet metal drawing and bending is defined in Fig. 2, the plate is L × W × H = 210 × 40 × 0.65 mm, and the hoderforce is 32 kN. The material property of the sheet is the isotropic-elastic transversely anisotropic-elastoplastic, whose parameters are listed below:

Fig. 2

Initial sheet shape and tool data

$$ \begin{aligned} E = &2.1 \times 10^{5} \;{\text{MPa}},\quad \nu = 0.3,\quad \sigma_{{s_{1} }} = \sigma_{{s_{2} }} = 330\;{\text{MPa}},\quad \sigma_{{s_{3} }} = 495\;{\text{MPa}} \hfill \\ &E_{t1} = E_{t2} = 210\;{\text{MPa}},\quad \mu = 0.15 \hfill \\ \end{aligned} $$

where μ is Coulomb friction coefficient. For transversely anisotropic sheet metal, we assume f = g = h = 1 as discussed earlier. For BCC materials, when Yld91 is used, let m = 6, but the three coefficients a, b and c can still be solved from (32) for simplicity and almost not losing accuracy. For this example, they are a = b = 0.866, c = 1.688. A 320 × 4, mesh of 320 elements along the length direction and 4 elements across the thickness are used. The plane strain element in Ls-Dyna code is used. The deformed shapes and distributions of equivalent stress at punch depth 60 mm are shown in Fig. 3. It can be seen from Fig. 3 that the peak equivalent stress appears near the corner of the die.

Fig. 3

Deformed shapes and equivalent stress at punch depth 60 mm

In Fig. 4, the 3D solution using the same Barlat model and the 3D BT shell element model is provided by Ls-Dyna code. Figure 5 shows the punch force as a function of the time for the 2D and 3D results. From Figs. 3 and 4, it can be concluded that the peak equivalent stress and equivalent stress distribution of the 2D results are almost same as those of the 3D results. From Fig. 5, it shows that there is a good agreement of punch force between 2D and 3D results. Therefore, the novel approach for transversely anisotropic section analysis is successful and valid.

Fig. 4

Deformed shapes and equivalent stress at punch depth 60 mm

Fig. 5

Comparison of 2D and 3D results for punch force versus time

4 Conclusions

The explicit analysis of transversely anisotropic plane strain sheet metal forming is implemented in Ls-Dyna code using 6-component Barlat yield function. The related formula and parameters has been derived explicitly. The transversely anisotropic property of sheet metal can be described by the three parameters a, b, and c. Numerical results demonstrated the validity of this approach.

Appendix

It’s made that:

$$ W = \left\{ {\left[ {2\cos \left( {\frac{2\theta + \pi }{6}} \right)} \right]^{m} + } \right.\left. {\left[ {2\cos \left( {\frac{2\theta - 3\pi }{6}} \right)} \right]^{m} + \left[ { - 2\cos \left( {\frac{2\theta + 5\pi }{6}} \right)} \right]^{m} } \right\} $$

(33)

From formula (18), then:

$$ \frac{\partial \Upphi }{{\partial \sigma_{ij} }} = \frac{{\partial \left( {3I_{2} } \right)^{m/2} }}{{\partial \sigma_{ij} }}W + \left( {3I_{2} } \right)^{m/2} \frac{\partial W}{{\partial \sigma_{ij} }} = \left( {3I_{2} } \right)^{m/2} \left( {\frac{m}{2}\frac{W}{{I_{2} }}\frac{{\partial I_{2} }}{{\partial \sigma_{ij} }} + \frac{\partial W}{{\partial \sigma_{ij} }}} \right) $$

(34)

where:

$$ \frac{\partial W}{{\partial \sigma_{ij} }} = \left\{ { - \frac{m}{3}\left[ {2\cos \left( {\frac{2\theta + \pi }{6}} \right)} \right]^{m} tg\left( {\frac{2\theta + \pi }{6}} \right) - \frac{m}{3}\left[ {2\cos \frac{2\theta - 3\pi }{6}} \right] \cdot tg\left( {\frac{2\theta - 3\pi }{6}} \right)} \right.\left. { - \left( { - 1} \right)^{m} \frac{m}{3}\left[ {2\cos \frac{2\theta + 5\pi }{6}} \right]^{m} tg \left( {\frac{2\theta + 5\pi }{6}} \right)} \right\}\frac{\partial \theta}{\partial \sigma_{ij}}=-\frac{2^m}{3}m\frac{\partial \theta}{\partial \sigma_{ij}}\left\{ {\cos^{m - 1} \left( {\frac{2\theta + \pi }{6}} \right)\sin \left( {\frac{2\theta + \pi }{6}} \right) + \cos^{m - 1} \left( {\frac{2\theta - 3\pi }{6}} \right) \cdot \sin \left( {\frac{2\theta - 3\pi }{6}} \right) + \left( { - 1} \right)^{m} \cos^{m - 1} \left( {\frac{2\theta + 5\pi }{6}} \right)\sin \left( {\frac{2\theta + 5\pi }{6}} \right)} \right\} $$

(35)

$$ \frac{\partial \theta }{{\partial \sigma_{ij} }} = - \frac{1}{{\sqrt {1 - \left( {\frac{{I_{3} }}{{I_{2}^{3/2} }}} \right)^{2} } }}\frac{{\frac{{\partial I_{3} }}{{\partial \sigma_{ij} }}I_{2}^{3/2} - I_{3} \frac{3}{2}I_{2}^{3/2 - 1} \frac{{\partial I_{2} }}{{\partial \sigma_{ij} }} }}{{\left( {I_{2}^{3/2} } \right)^{2} }} = \frac{{3I_{3} \frac{{\partial I_{2} }}{{\partial \sigma_{ij} }} - 2I_{2} \frac{{\partial I_{3} }}{{\partial \sigma_{ij} }}}}{{2I_{2} \sqrt {I_{2}^{3} - I_{3}^{2} } }} $$

(36)

where:

$$ \frac{{\partial I_{2} }}{{\partial \sigma_{xx} }} = \frac{{c\left( {cC - aA} \right) + \left( {b + c} \right)\left( {cC - bB} \right) + b\left( {aA - bB} \right)}}{27} $$

(37)

$$ \frac{{\partial I_{2} }}{{\partial \sigma_{yy} }} = \frac{{\left( {a + c} \right)\left( {aA - cC} \right) + c\left( {bB - cC} \right) + a\left( {aA - bB} \right)}}{27} $$

(38)

$$ \frac{{\partial I_{2} }}{{\partial \sigma_{xy} }} = \frac{2}{3}h^{2} H $$

(39)

$$ \frac{{\partial I_{3} }}{\partial \sigma } = - \frac{{\left( {c\frac{\partial C}{\partial \sigma } - b\frac{\partial B}{\partial \sigma }} \right)\left( {fF} \right)^{2} + \left( {a\frac{\partial A}{\partial \sigma } - c\frac{\partial C}{\partial \sigma }} \right)\left( {gG} \right)^{2} }}{6} - \frac{{\left( {b\frac{\partial B}{\partial \sigma } - a\frac{\partial A}{\partial \sigma }} \right)\left( {hH} \right)^{2} }}{6} + \frac{{\left( {c\frac{\partial C}{\partial \sigma } - b\frac{\partial B}{\partial \sigma }} \right)\left( {aA - cC} \right)\left( {bB - aA} \right)}}{54} + \frac{{\left( {cC - bB} \right)\left( {a\frac{\partial A}{\partial \sigma } - c\frac{\partial C}{\partial \sigma }} \right)\left( {bB - aA} \right)}}{54} + \frac{{\left( {cC - bB} \right)\left( {aA - cC} \right)\left( {b\frac{\partial B}{\partial \sigma } - a\frac{\partial A}{\partial \sigma }} \right)}}{54} $$

(40)

(where: σ = σ _xx or σ _yy )

$$ \frac{{\partial I_{3} }}{{\partial \sigma_{xy} }} = fghFG - \frac{1}{3}\left( {bB - aA} \right)h^{2} H $$

(41)