The M-principal graph of a commutative ring

Abstract

Let $R$ be a commutative ring and $M$ be an $R$-module. In this paper, we introduce the $M$-principal graph of $R$, denoted by $M-PG(R)$. It is the graph whose vertex set is $R\backslash \{0\}$, and two distinct vertices $x$ and $y$ are adjacent if and only if $xM=yM$. In the special case that $M=R, M-PG(R)$ is denoted by $PG(R)$. The basic properties and possible structures of these two graphs are studied. Also, some relations between $PG(R)$ and $M-PG(R)$ are established.

1 Introduction

There are many papers on assigning a graph to a ring $R$, see [1–4, 9, 10]. In this paper, we introduce the M-principal graph of $R$, denoted by $M-PG(R)$, where $M$ is an $R$-module. Throughout the paper all rings are commutative with non-zero identity and all modules are non-zero unitary.

Let $R$ be a ring and $M$ be an $R$-module. The annihilator of $M$ is denoted by $ann(M)$. The module $M$ is called a faithful $R$-module if $ann(M)=0$. Also, $M$ is called an simple $R$-module if $M\ne 0$, and $M$ has no submodules other than $0$ and $M$. We denote the characteristic of $R$ by char $R$. Also, $J(R)$ denotes the Jacobson radical of $R$ and $U(R)$ denotes the group of units of $R$. A ring having just one maximal ideal is called a local ring and a ring having only finitely many maximal ideals is said to be a semilocal ring. The direct product of a family of rings $\{R_i \mid i\in I \}$ is denoted by $\prod _{i\in I}{R_i}$. As usual, $\mathbb {Z}$, $\mathbb {R}, \mathbb {C}$, and $\mathbb {Z}_n$ will denote the integers, real numbers, complex numbers and integers modulo $n$, respectively.

A graph in which each pair of distinct vertices is joined by an edge is called a complete graph. The complete graph on $n$ vertices is denoted by $K_n$. A graph $G$ is called regular if each vertex has the same number of neighbors. An empty graph is one whose edge set is empty. Let $G$ be a graph. The set of vertices and the set of edges of $G$ are denoted by $V(G)$ and $E(G)$, respectively. “A subgraph $H$ of $G$ is said to be an induced subgraph of $G$ if it is a subgraph i.e. $V(H)\subset V(G)$ and $E(H)\subset E(G)$ and it has exactly the same edges that appear in $G$ over the vertices $V(H)$ i.e. $\forall u,v\in V(H)$ an edge $e=uv\in E(H)$ if and only if $e\in E(G)$.”

Also a subgraph $H$ of $G$ is called a spanning subgraph if $V(H)=V(G)$. We say that $G$ is connected if there is a path between any two distinct vertices of $G$. A cycle of $G$ is a path such that the start and end vertices are the same. The girth of $G$, denoted by $gr(G)$, is the length of a shortest cycle in $G$ ($gr(G)=\infty$ if $G$ contains no cycles). A Hamiltonian cycle is a spanning cycle in a graph. A graph $G$ is called Hamiltonian if $G$ has a Hamiltonian cycle. A forest is a graph with no cycles. A clique in $G$ is a set of pairwise adjacent vertices and a set in $G$ whose no two vertices are adjacent is called an independent set. The clique number and the independence number of $G$, denoted by $\omega (G)$ and $\alpha (G)$, are the largest orders of a clique and an independent set of $G$, respectively. Also, the chromatic number of $G$, denoted by $\chi (G)$, is the smallest number of colors which can be assigned to the vertices of $G$ in such a way that every two adjacent vertices have different colors.

In this article, we introduce and investigate the $M$-principal graph of $R$, denoted by $M-PG(R)$, where $R$ is a commutative ring and $M$ is a non-zero $R$-module. If $R$ is regarded as a module over itself, that is, $M=R$, then the $M$-principal graph of $R$ is denoted by $PG(R)$. Also, we study some properties of $PG(R)$, in particular we consider the graph $PG(\mathbb {Z}_n)$ for each positive integer $n>1$. Finally, some relations between $PG(R)$ and $M-PG(R)$ are established.

2 The $M$-principal graph of $R$

In this section, we introduce the $M$-principal graph of $R$ and study its basic properties.

Definition 2.1

Let $R$ be a ring and $M$ be a non-zero $R$-module. The $M$ -principal graph of $R$, denoted by $M-PG(R)$, is the (undirected) graph whose vertex set is $R\backslash \{0\}$ and two distinct vertices $x$ and $y$ are adjacent if and only if $xM=yM$.

It is clear that if $M$ and $N$ are isomorphic modules over $R$, then $M-PG(R)$ is the same as $N-PG(R)$, but the converse is not true in general. For instance, consider $\mathbb {R}-PG(\mathbb {Z})$ and $\mathbb {C}-PG(\mathbb {Z})$.

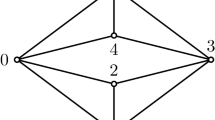
Example 2.2

Let $R=\mathbb {Z}_6$. So we have the following graphs.

Remark 2.3

Clearly, $M-PG(R)$ is a disjoint union of complete graphs. Hence $gr(M-PG(R))\in \{3,\infty \}$ and also $|U(R)|\le \omega (M-PG(R))=\chi (M-PG(R))$.

By the previous remark, we have the next immediate result.

Corollary 2.4

Let $R$ be a ring with $|R|>3$, and let $M$ be a non-zero $R$-module. Then the following conditions are equivalent:

• (1) $M-PG(R)$ is a complete graph.

• (2) $M-PG(R)$ is a Hamiltonian graph.

• (3) $M-PG(R)$ is a connected graph.

Remark 2.5

Let $x$ be a non-zero element of $R$. Then each coset $x+ann(M)$ is a clique in $M-PG(R)$ and so $|ann(M)|\le \omega (M-PG(R))$. Also, $\alpha (M-PG(R)) \le |R/ ann(M)|$. Moreover, if $ann(M)\ne 0$, then $M-PG(R)$ is disconnected.

Theorem 2.6

Let $R$ be a ring and $M$ be a non-zero $R$-module. Then $M$ is a faithful simple $R$-module if and only if $M-PG(R)$ is a complete graph and $M$ is a cyclic $R$-module.

Proof

Suppose that $M-PG(R)$ is a complete graph and there exists a non-zero element $m\in M$ such that $M=Rm$. If $0\ne x\in ann(M)$, then $x$ is not adjacent to $1$, a contradiction. So $ann(M)=0$. Let $m'$ be a non-zero element of $M$. We have $m'=xm$ for some $x\in R$. Since $M-PG(R)$ is a complete graph, $M=xM=xRm=Rm'$. Thus $M$ is simple. For the other direction, assume that $x\in R$ and $x\ne 0$. Since $xM$ is a non-zero submodule of $M$ and $M$ is simple, we have $xM=M$. The proof is complete. $\square$

Theorem 2.7

Let $R$ be a ring and $M$ be a (non-zero) finitely generated $R$-module. If $M-PG(R)$ is a complete graph, then $J(R)=0$.

Proof

By contradiction, assume that $x\in J(R)$ and $x\ne 0$. Since $M-PG(R)$ is a complete graph, $xM=M$. So $J(R)M=M$ and by Nakayama’s Lemma [7, Proposition 2.6], we have $M=0$, a contradiction. $\square$

Theorem 2.8

Let $R$ be a ring and $M$ be a non-zero $R$-module. If $M-PG(R)$ is empty, then $M$ is a faithful $R$-module and we have $|U(R)|=1$. Moreover, if $R$ is an Artinian ring, then $R\cong {(\mathbb {Z}_2)}^k$ for some positive integer $k$.

Proof

By Remark 2.5, $ann(M)=0$ and since $xM=M$ for every $x\in U(R)$, we have $|U(R)|=1$ (so char $R=2$ and $J(R)=0$). If $R$ is Artinian, then by [7, Theorem 8.7], $R\cong R_1\times \cdots \times R_k$, where $R_i$ is a local ring and $k$ is a positive integer. Suppose that $m_i$ is a maximal ideal of $R_i$, for each integer $i, 1\le i \le k$. Since $|R_i\backslash m_i|=|U(R_i)|=1$, we have $|m_i|=1$ and hence $R_i\cong \mathbb {Z}_2$. Thus $R\cong {(\mathbb {Z}_2)}^k$. $\square$

Theorem 2.9

Let $R$ be an integral domain and $M$ be an Artinian module. If $R$ contains a non-zero element $x$ such that $x^k\ne 1$ for each positive integer $k$, then $\omega (M-PG(R))=\infty$.

Proof

Since $M$ is Artinian, there exists a positive integer $n$, such that $x^kM=x^nM$ for each positive integer $k\ge n$. Now, $\{x^k \ | \ k\ge n$ } is a clique in $M-PG(R)$ and hence $\omega (M-PG(R))=\infty$. $\square$

Let $R$ be a commutative ring. An $R$-module $M$ is said to be secondary (see [8, p. 42]), if $M\ne 0$ and, for each $x\in R, xM =M$ or $x\in \sqrt{ann(M)}$. ($\sqrt{ann(M)}$ denotes the radical of $ann(M)$.)

Theorem 2.10

Let $R$ be a ring and $M$ be a secondary $R$-module. Then $|R\backslash P|\le \omega (M-PG(R))$, where $P=\sqrt{ann(M)}$.

Proof

Since $M$ is a secondary $R$-module, $xM=M$ for every $x\in R\backslash P$. So $R\backslash P$ is a clique in $M-PG(R)$ and hence $|R\backslash P|\le \omega (M-PG(R))$. $\square$

Theorem 2.11

Let $R$ be a ring and $M$ be a non-zero $R$-module. If $N$ is a proper submodule of $M$, then $M-PG(R)$ is a spanning subgraph of $M/N-PG(R)$.

Proof

Suppose that $x,y\in R$ and $xM=yM$. So $x(M/N)=(xM+N)/N=(yM+N)/N=y(M/N)$. Hence if $x$ and $y$ are adjacent vertices of $M-PG(R)$, then $x$ is adjacent to $y$ in $M/N-PG(R)$. Therefore $M-PG(R)$ is a spanning subgraph of $M/N-PG(R)$. $\square$

Suppose that $R$ is a commutative ring and $M$ is a module over $R$. It is well known (see [7, p. 19]) that if $I$ is an ideal of $R$ such that $IM=0, M$ can be regarded as an $R/I$-module, as follows: if $\overline{x}\in R/I$ is represented by $x\in R$, define $\overline{x}m$ to be $xm$ for every $m\in M$. So we can deduce the next theorem.

Theorem 2.12

Let $R$ be a ring and $M$ be a non-zero $R$-module, and let $I$ be an ideal of $R$ such that $IM=0$. Then $M-PG(R/I)$ is an induced subgraph of $M-PG(R)$. Moreover, if $I=ann(M)\ne 0$ and $M-PG(R/I)$ is a complete graph, then $M-PG(R)$ is a disjoint union of two complete graphs.

Proof

Suppose that $x,y\in R$. Clearly, $xM=yM$ if and only if $\overline{x}M=\overline{y}M$. So (by assigning $\overline{x}$ to $x$), $M-PG(R/I)$ is an induced subgraph of $M-PG(R)$. Now, assume that $M-PG(R/ann(M))$ is a complete graph and let $x,y\in R\backslash \{0\}$. If $x,y\in ann(M)$, then $xM=yM=0$. Suppose that $x,y\in R\backslash ann(M)$. If $\overline{x}=\overline{y}$, then $x-y\in ann(M)$ implies that $xM=yM$. Otherwise, $\overline{x}$ and $\overline{y}$ are two distinct vertices of $M-PG(R/ann(M))$ and hence $\overline{x}$ is adjacent to $\overline{y}$. So $x$ is adjacent to $y$. It is clear that if $x\in ann(M)$ and $y\in R\backslash ann(M)$, then $xM\ne yM$. Thus $M-PG(R)$ is a disjoint union of two complete graphs. $\square$

Let $S$ be a multiplicatively closed subset of a commutative ring $R$, and let $M$ be an $R$-module. We denote the ring of fractions of $R$ and the module of fractions of $M$ (with respect to $S$) by $R_S$ and $M_S$, respectively. Now, we have the following theorem.

Theorem 2.13

Let $R$ be a ring and $M$ be a non-zero $R$-module. If $S=Reg(R)$, then $M-PG(R)$ is a subgraph of $M_S-PG(R_S)$. Moreover, if $M-PG(R)$ is complete, then $M_S-PG(R_S)$ is also a complete graph.

Proof

Suppose that $x,y\in R$ and $xM=yM$. So $(x/1)M_S=(xM)_S=(yM)_S=(y/1)M_S$. Thus by assigning $x$ to $x/1$, $M-PG(R)$ is a subgraph of $M_S-PG(R_S)$. Note that if $x\ne 0$, then $x/1\ne 0$. Now, assume that $M-PG(R)$ is a complete graph and $x/r,y/t$ are two distinct vertices of $M_S-PG(R_S)$. Then $tx$ and $ry$ are two distinct vertices of $M-PG(R)$ and so $txM=ryM$. Thus $(x/r)M_S=(tx/tr)M_S=(txM)_S=(ryM)_S=(ry/tr)M_S=(y/t)M_S$ and hence $x/r$ is adjacent to $y/t$. $\square$

3 The principal graph of $R$

If $R$ is regarded as a module over itself, that is, $M=R$, then the $M$-principal graph of $R$ is denoted by $PG(R)$ (the principal graph of $R$). In this section we study some properties of $PG(R)$, in particular we consider the graph $PG(\mathbb {Z}_n)$ for each positive integer $n>1$.

Note that for two rings $R$ and $S$ if $R\cong S$, then $PG(R)\cong PG(S)$, but the converse is not true. For instance, consider $PG(\mathbb {Z}_4)$ and $PG(\mathbb {Z}_2[x]/(x^2))$.

Example 3.1

Corollary 3.2

Let $R$ be a ring with $|R|>3$. Then the following conditions are equivalent:

• (1) $R$ is a field.

• (2) $PG(R)$ is a complete graph.

• (3) $PG(R)$ is a Hamiltonian graph.

• (4) $PG(R)$ is a connected graph.

Notice that $\alpha (PG(R))$ is equal to the number of non-zero principal ideals of $R$. So we have the next theorem.

Theorem 3.3

Let $R$ be a ring. If $\alpha (PG(R))$ is finite, then $R$ is Artinian.

Proof

$R$ has only a finite number of distinct principal ideals, since $\alpha (PG(R))$ is finite. Now, suppose that $I$ is a non-zero ideal of $R$. We have $I=\sum _{x\in I} xR$, so $R$ contains only finitely many ideals and hence $R$ is Artinian. $\square$

Remark 3.4

Note that there exist some infinite rings which have only a finite number of ideals, for example the ring $F[x]/(x^2)$, where $F$ is an infinite field.

Theorem 3.5

Let $R$ be a semilocal ring. If $\omega (PG(R))$ is finite, then $R$ is finite.

Proof

Suppose that $m_1,\ldots ,m_k$ are all the maximal ideals of $R$. We have $U(R)=R\backslash \bigcup ^{k}_{i=1}m_i$. Since $\omega (PG(R))$ is finite, $U(R)$ is finite and so by [4, Theorem 2], $R$ is finite. $\square$

Corollary 3.6

Let $R$ be a semilocal ring. If $PG(R)$ is empty, then $R\cong {(\mathbb {Z}_2)}^k$ for some positive integer $k$.

Proof

By the previous theorem, $R$ is finite and so by Theorem 2.8, the result holds. $\square$

Theorem 3.7

Let $R$ be an Artinian ring. If $PG(R)$ is a forest, then $R$ is isomorphic to one of the rings:

$$\begin{aligned} \mathbb {Z}_3,\ \mathbb {Z}_4,\ \mathbb {Z}_2[x]/{(x^2)},\ {(\mathbb {Z}_2)}^k,\ {(\mathbb {Z}_2)}^k \times \mathbb {Z}_3,\ {(\mathbb {Z}_2)}^k\times \mathbb {Z}_4,\ {(\mathbb {Z}_2)}^k \times \mathbb {Z}_2[x]/{(x^2)}, \end{aligned}$$

for some positive integer $k$.

Proof

Since $gr(PG(R))=\infty$, so $|U(R)|\le 2$ and by [4, Lemma 1], $R$ is isomorphic to one of the rings:

$$\begin{aligned} \mathbb {Z}_3,\ \mathbb {Z}_4,\ \mathbb {Z}_2[x]/{(x^2)},\ {(\mathbb {Z}_2)}^k,\ {(\mathbb {Z}_2)}^k \times \mathbb {Z}_3,\ {(\mathbb {Z}_2)}^k\times \mathbb {Z}_4,\ {(\mathbb {Z}_2)}^k \times \mathbb {Z}_2[x]/{(x^2)}, \end{aligned}$$

for some positive integer $k$. $\square$

The strong product $G \boxtimes H$ of graphs $G$ and $H$ is a graph such that the vertex set of $G \boxtimes H$ is the Cartesian product $V(G) \times V(H)$; and any two distinct vertices $(u_1,u_2)$ and $(v_1,v_2)$ are adjacent in $G \boxtimes H$ if and only if ($u_1=v_1$ and $u_2$ adj $v_2$) or ($u_1$ adj $v_1$ and $u_2=v_2$) or ($u_1$ adj $v_1$ and $u_2$ adj $v_2$). Now, suppose that $R_1$ and $R_2$ are two rings. Let $x_1,y_1\in R_1$ and $x_2,y_2\in R_2$. We know that $(x_1,x_2)(R_1\times R_2)=(y_1,y_2)(R_1\times R_2)$ if and only if $x_1R_1=y_1R_1$ and $x_2R_2=y_2R_2$. So $PG(R_1\times R_2)=PG(R_1)\boxtimes PG(R_2)$ and also $\omega (PG(R_1\times R_2))=\omega (PG(R_1))\times \omega (PG(R_2))$.

Theorem 3.8

Let $R_1$ and $R_2$ be two rings, and let $\alpha (PG(R_1))=\alpha _1$ and $\alpha (PG(R_2))=\alpha _2$. Then $\alpha (PG(R_1\times R_2))=\alpha _1+\alpha _2+\alpha _1\alpha _2$.

Proof

It is obvious that $PG(R_1)$ is the union of $\alpha _1$ disjoint complete graphs and similarly, $PG(R_2)$ is the union of $\alpha _2$ disjoint complete graphs. Suppose that $A_1,\ldots ,A_{\alpha _1}$ are all the components of $PG(R_1)$ and $B_1,\ldots ,B_{\alpha _2}$ are all the components of $PG(R_2)$. Then $A_1\times 0,\ldots ,A_{\alpha _1}\times 0$ and $0\times B_1,\ldots ,0\times B_{\alpha _2}$ and $A_i\times B_j$, where $1\le i\le \alpha _1$ and $1\le j \le \alpha _2$ are all the components of $PG(R_1\times R_2)$, each of which is a complete graph. Hence $\alpha (PG(R_1\times R_2))=\alpha _1+\alpha _2+\alpha _1\alpha _2$. $\square$

Let $R_1,\ldots ,R_n$ be rings. By induction, one can easily prove that $PG(R_1\times \cdots \times R_n)=PG(R_1)\boxtimes \cdots \boxtimes PG(R_n)$.

Now, we consider the graph $PG(\mathbb {Z}_n)$ for each positive integer $n>1$. Let $d(n)$ denote the number of positive divisors of $n$. Clearly, $\alpha (PG(\mathbb {Z}_n))=d(n)-1$. Suppose that $\varphi$ is the Euler phi function. By [6, Theorem 2.5], if $d$ is a positive divisor of $n$, then $\varphi (d)\le \varphi (n)$. So $\chi (PG(\mathbb {Z}_n))=\omega (PG(\mathbb {Z}_n))=\varphi (n)$.

The chromatic index of $G$, denoted by $\chi '(G)$, is the smallest number of colors which can be assigned to the edges of $G$ such that no two edges incident on the same vertex have the same color. By Vizing’s Theorem, if $G$ is a graph whose maximum vertex degree is $\Delta$, then $\Delta \le \chi '(G) \le \Delta +1$. Vizing’s Theorem divides the graphs into two classes according to their chromatic index; graphs satisfying $\chi '(G)=\Delta$ are called class 1, those with $\chi '(G)=\Delta + 1$ are class 2.

We now state the following result which shows that the graph $PG(\mathbb {Z}_n)$ is class 1.

Theorem 3.9

The principal graph $PG(\mathbb {Z}_n)$ is class 1, for each positive integer $n>1$.

Proof

By [6, Theorem 2.5], $\varphi (d)$ is even for each positive integer $d\ge 3$. Thus each connected component of $PG(\mathbb {Z}_n)$ with two or more vertices is a complete graph which contains an even number of vertices. So by [5, Theorem 5.11], $PG(\mathbb {Z}_n)$ is class 1. $\square$

Remark 3.10

By [6, Theorem 2.5], $\varphi (d)\ge 2$ for each positive integer $d\ge 3$. So if $n$ is even, then $PG(\mathbb {Z}_n)$ contains exactly one isolated vertex and otherwise it contains no isolated vertex.

Theorem 3.11

If $G = PG(\mathbb {Z}_n)$, then the following conditions are equivalent:

• (1) $G$ is a regular graph.

• (2) $n$ is a prime number.

• (3) $G$ is a complete graph.

• (4) $G$ is a Hamiltonian graph or $G\cong PG(\mathbb {Z}_2)$ or $G\cong PG(\mathbb {Z}_3)$.

• (5) $G$ is a connected graph.

Proof

Suppose that $PG(\mathbb {Z}_n)$ is a regular graph. So if $d\ne 1$ is a positive divisor of $n$, then $\varphi (d)=\varphi (n)$. Assume that $p$ and $q$ are prime divisors of $n$. Then $\varphi (p)=\varphi (q)$ implies that $p=q$ and thus $n$ is a prime number (note that $\varphi (p^2)\ne \varphi (p)$). By Corollary 3.2, the proof is complete. $\square$

Let $m,n>1$ be positive integers. We know that $PG(\mathbb {Z}_m\times \mathbb {Z}_n)=PG(\mathbb {Z}_m)\boxtimes PG(\mathbb {Z}_n)$ and so $\omega (PG(\mathbb {Z}_m\times \mathbb {Z}_n))=\varphi (m)\varphi (n)$. Then $\omega (PG(\mathbb {Z}_m\times \mathbb {Z}_n))\le \omega (PG(\mathbb {Z}_{mn}))$.

We close this article by considering some relations between $PG(R)$ and $M-PG(R)$, where $R$ is a ring and $M$ is a non-zero $R$-module.

Theorem 3.12

Let $R$ be a ring and $M$ be a non-zero $R$-module. Then $PG(R/ann(M))$ is a subgraph of $M-PG(R)$. Moreover, $|ann(M)|\omega (PG(R/ann(M)))\le \omega ($M-PG(R)$)$.

Proof

Let $\overline{R}=R/ann(M)$ and suppose that $\overline{x}$ and $\overline{y}$ are two adjacent vertices of $PG(\overline{R})$. Now, assume that $m\in M$. Since $\overline{x}\overline{R}=\overline{y}\overline{R}$, there exists $r\in R$ such that $\overline{x}=\overline{yr}$. Hence $(x-yr)m=0$ which implies that $xM\subseteq yM$. Similarly, $yM\subseteq xM$. So $x$ and $y$ are two adjacent vertices of $M-PG(R)$. Thus by assigning $\overline{x}$ to $x, PG(\overline{R})$ is a subgraph of $M-PG(R)$. By Remark 2.5, the last part is clear. $\square$

Theorem 3.13

Let $R$ be a ring and $M$ be a non-zero $R$-module. Then $PG(R)$ is a spanning subgraph of $M-PG(R)$. Furthermore, if $M$ is a faithful cyclic $R$-module, then the graph $PG(R)$ is exactly the same as the graph $M-PG(R)$.

Proof

Suppose that $x$ and $y$ are two adjacent vertices of $PG(R)$. Clearly, $xR=yR$ implies that $xM=yM$. So $x$ and $y$ are two adjacent vertices of $M-PG(R)$. Thus $PG(R)$ is a spanning subgraph of $M-PG(R)$. Now, assume that $ann(M)=0$ and $M=Rm$ for some $m\in M$. If $x$ and $y$ are two adjacent vertices of $M-PG(R)$, then $xM=yM$ and so there exists $r\in R$ such that $xm=yrm$. Hence $x-yr\in ann(M)=0$ which implies that $xR\subseteq yR$. Similarly, $yR\subseteq xR$. Therefore $x$ and $y$ are two adjacent vertices of $PG(R)$. So $PG(R)$ is exactly the same as $M-PG(R)$. $\square$

Theorem 3.14

Let $R$ be a ring. If $M=\prod _{i\in I}{R_i}$, where $R_i\cong R$ for each $i\in I$, then $PG(R)$ is exactly the same as $M-PG(R)$.

Proof

Suppose that $x,y\in R\backslash \{0\}$. By the previous theorem, $xR=yR$ implies that $x\prod _{i\in I}{R_i}=y\prod _{i\in I}{R_i}$. Now, assume that $x\prod _{i\in I}{R_i}=y\prod _{i\in I}{R_i}$. Let $e=(e_i)$, where $e_1=1$ and $e_i=0$, for each $i\ne 1$. So there exists $r=(r_i)\in \prod _{i\in I}{R_i}$ such that $xe=y(r_i)$ and hence $x=yr_1$. Thus $xR\subseteq yR$. Similarly, $yR\subseteq xR$ and so $xR=yR$. $\square$

Corollary 3.15

Let $R$ be a ring and $F$ be a free $R$-module. Then $PG(R)$ is exactly the same as $F-PG(R)$.

Proof

Since $F$ is isomorphic to a direct sum of copies of $R$, the result holds by the previous theorem. $\square$