Ranking data with ordinal labels: optimality and pairwise aggregation

Abstract

The paper describes key insights in order to grasp the nature of K-partite ranking. From the theoretical side, the various characterizations of optimal elements are fully described, as well as the likelihood ratio monotonicity condition on the underlying distribution which guarantees that such elements do exist. Then, a pairwise aggregation procedure based on Kendall tau is introduced to relate learning rules dedicated to bipartite ranking and solutions of the K-partite ranking problem. Criteria reflecting ranking performance under these conditions such as the ROC surface and its natural summary, the volume under the ROC surface (VUS), are then considered as targets for empirical optimization. The consistency of pairwise aggregation strategies are studied under these criteria and shown to be efficient under reasonable assumptions. Eventually, numerical results illustrate the relevance of the methodology proposed.

1 Introduction

In many situations, a natural ordering can be considered over a set of observations. When observations are documents in information retrieval applications, the ordering reflects degree of relevance for a specific query. In order to predict future ordering on new data, the learning process uses past data for which some relevance feedback is some provided, such as ratings, say from 0 to 4, from the poorly relevant to the extremely relevant. For an example of such data, we refer to the LETOR benchmark data repository, see http://research.microsoft.com/en-us/um/people/letor/. A similar situation occurs in medical applications where decision-making support tools provide a scoring of the population of patients based on diagnostic test statistics in order to rank the individuals according to the advance state of a disease which are described as discrete grades, see Pepe (2003), Dreiseitl et al. (2000), Edwards et al. (2005), Mossman (1999) or Nakas and Yiannoutsos (2004) for instance.

A particular case which has received increasing attention both in machine learning the statistics literature is when only binary feedback is available (relevant vs. not relevant, ill vs. healthy) and this is known as the bipartite ranking problem (see Clémençon and Vayatis 2009b, 2010; Freund et al. 2003; Agarwal et al. 2005; Clémençon et al. 2008, etc.). In the presence of ordinal feedback (i.e. ordinal label taking a finite number of values, K≥3 say), the task consists in learning how to order temporarily unlabeled observations so as to reproduce as accurately as possible the ordering induced by the labels not observed yet. This problem is referred to as K-partite ranking and various approaches have been proposed in order to develop efficient algorithms in that case (see Rudin et al. 2005; Pahikkala et al. 2007). A closely related approach which points at both parametric and nonparametric statistical estimation is represented by ordinal regression modeling (see Waegeman et al. 2008b; Herbrich et al. 2000). To compare and assess the quality of these methods, a first concern is how to extend the typical performance measures such as the ROC curve and the AUC in this setup and this issue has been tackled in Scurfield (1996), Flach (2004). However, many interesting issues are still unexplored such as the theoretical optimality of learning rules, the statistical consistency of empirical performance maximization procedures, error bounds for K-partite ranking algorithms, ….

In the present paper, we tackle some of these open problems. In particular, we explore the connection between bipartite and K-partite ranking. Indeed, a natural approach is to transfer virtuous bipartite ranking methods to derive optimal and consistent rules for K-partite ranking. This idea is quite successful in the multiclass classification setup (see Hastie and Tibshirani 1998 or Fürnkranz 2002 for instance). We propose to build on the original proposition in Fürnkranz et al. (2009) to combine of bipartite ranking tasks in order to solve the K-partite case. A first intuition suggests that rules which are optimal for all bipartite ranking subproblems simultaneously should be optimal for the global problem. We offer examples in which this is not always the case and we state sufficient conditions for optimality which are called monotonicity likelihood ratio conditions. Based on this finding, we examine strategies which allow to combine rules dedicated for the pairwise subproblems for consecutive labels in order to derive interesting rules for the initial problem. We describe an efficient procedure for the pairwise aggregation of scoring rules which establishes a ranking consensus, called a median scoring rule, through an extension of the Kendall tau metric. It is also shown that such a median scoring rule always exists in the important situation where the scoring functions one seeks to summarize/aggregate are piecewise constant, and computation of this median rule is feasible. Next, we consider concepts such as the ROC surface and the Volume Under the ROC Surface (or VUS) which can be used to assess performance for scoring rules in K-partite ranking. Consistency can then be considered as convergence to optimal elements in terms of ROC surface or VUS. We then study conditions under which consistency of pairwise aggregation can be achieved. Indeed, it can be shown that under the monotone likelihood ratio condition together with a margin condition over the posterior distributions, the median scoring rule built out of pairwise AUC-consistent rules is VUS-consistent. We also consider specific strategies to derive scoring rules for this problem such as the empirical maximization of the VUS or the plug-in scoring rule. We also provide an analysis of the empirical performance of the Kendall-type pairwise aggregation method using the TreeRank algorithm developed by the authors (Clémençon and Vayatis 2009b). An extensive comparison with state-of-the-art ranking methods is presented both on artificial and real data sets and we exhibit performance in terms of VUS, as well as the form of the level sets of the estimated scoring rules. The latter visualization show interesting insights about the geometry of risk segments in the input space.

The rest of the paper is structured as follows. In Sect. 2, the probabilistic setting is introduced and optimal scoring rules for K-partite ranking are successively defined and characterized. A specific monotonicity likelihood ratio condition is stated, which is shown to guarantee the existence of a natural optimal ordering over the input space. A novel Kendall-type aggregation procedure is presented in Sect. 3 and performance metrics, such as the VUS, are the subject matter of Sect. 4. Consistency results and insights on the passage from bipartite subproblems to the full K-partite case are discussed in Sect. 5. Finally, Sect. 6 displays a series of numerical results and illustrations for the aggregation principle considered in this paper. Mathematical proofs are postponed to the Appendix A.

2 Optimal elements in ranking data with ordinal labels

2.1 Probabilistic setup and notations

We consider a black-box system with random input/output pair (X,Y). We assume that the input random vector X takes values over ℝ^d and the output Y over the ordered discrete set $\mathcal{Y}=\{1,\ldots , K\}$. Here it is assumed that the ordered values of the output Y can be reflected by an ordering over ℝ^d. The case where K=2 is known as the bipartite ranking setup. In this paper, we focus on the case where K>2. Though the objective pursued here is different, the probabilistic setup is exactly the same as that of ordinal regression, see Sect. 5.4 for a discussion of the connections between these two problems. We denote by f _k the density function of the class-conditional distributions of X given Y=k and by $\mathcal{X}_{k} \subseteq\mathbb{R}^{d}$ the support of f _k . We also set p _k =ℙ{Y=k}, k∈{1,…,K}, the mixture parameter for class Y=k, and η _k (x)=ℙ{Y=k∣X=x} the posterior probability. Set f=p ₁ f ₁+⋯+p _K f _K and recall that:

$$\forall k\in\{1, \ldots, K\}, \ \forall x\in\bigcup _{l=1}^K \mathcal{X}_l, \quad \eta_k(x) = p_k \cdot\frac{f_k}{f}(x). $$

The regression function $\eta(x) = \mathbb{E}[Y \mid X=x]$ can be expressed in the following way:

$$\forall x\in\bigcup_{l=1}^K \mathcal{X}_l, \quad\eta(x) = \sum_{k=1}^K k \cdot\eta_k (x), $$

as the expectation of a discrete random variable. We shall make use of the following notation for the likelihood ratio of the class-conditional distribution:

$$\forall k, l\in\{1, \ldots, K\}, \ l<k , \ \forall x\in \mathcal{X}_l, \quad\varPhi_{k,l}(x)=\frac{f_k}{f_l}(x) = \frac{p_k}{p_l } \cdot\frac{\eta_k}{\eta_l}(x). $$

Along the paper, we shall use the convention that u/0=∞ for any u∈ ]0,∞[ and 0/0=0.

2.2 Optimal scoring rules

The problem considered in this paper is to infer an order relationship over ℝ^d after observing vector data with ordinal labels. For this purpose, we consider real-valued decision rules of the form s : ℝ^d→ℝ called scoring rules. In the case of ordinal labels, the main idea is that good scoring rules s are those which assign a high score s(X) to the observations X with large values of the label Y. We now introduce the concept of optimal scoring rule for ranking data with ordinal labels.

Definition 1

(Optimal scoring rule)

An optimal scoring rule s ^∗ is a real-valued function such that:

$$\forall k, l\in\{1, \ldots, K\}, \ l<k , \ \forall x, x' \in\mathcal{X}_l, \ \varPhi_{k,l}(x)< \varPhi_{k,l} \bigl(x'\bigr) \Rightarrow s^*(x) < s^*\bigl(x'\bigr). $$

The rationale behind this definition can be understood by considering the case K=2. The class Y=2 should receive higher scores than the class Y=1. In this case, an optimal scoring rule s ^∗ should score observations x in the same order as the posterior probability η ₂ of the class Y=2 (or equivalently as the ratio η ₂/(1−η ₂)). Since η ₁(x)+η ₂(x)=1, for all x, it is easy to see that this is equivalent to the condition described in the previous definition (see Clémençon and Vayatis 2009b for details). In the general case (K>2), optimality of a scoring rule s ^∗ means that s ^∗ is optimal for all bipartite subproblems with classes Y=k and Y=l, with l<k.

An important remark is that, in the probabilistic setup introduced above, an optimal scoring rule may not exist as shown in the next example.

Example 1

Consider a discrete input space $\mathcal{X}=\{x_{1}, x_{2}, x_{3}\}$ and K=3. We assume the following joint probability distribution ℙ(X=x _i ,Y=j)=ω _i,j for the random pair (X,Y):

$$\begin{array}{l} \omega_{1,1}=\omega_{2,2}=\omega_{3,3}=1/2, \\ \omega_{1,2}=\omega_{2,3}=\omega_{3,1}=1/3, \\ \omega_{1,3}=\omega_{2,1}=\omega_{3,2}=1/6. \end{array} $$

Note that in the case of a discrete distribution for X, the density function coincides with mass function and we have f(x)=ℙ(X=x). It is then easy to check that, in this case, there is no optimal scoring rule for this distribution in the sense of Definition 1.

2.3 Existence and characterization of optimal scoring rules

The previous example shows that the existence of optimal scoring rules cannot be guaranteed under any joint distribution. Our first important result is the characterization of those distributions for which the family of optimal scoring rules is not an empty set. The next proposition offers a necessary and sufficient condition on the distribution which ensures the existence of optimal scoring rules.

Assumption 1

For any k,l∈{1,…,K} such that l<k, for all $x,x'\in \mathcal{X}$, we have:

$$\varPhi_{k+1,k}(x)< \varPhi_{k+1,k}\bigl(x'\bigr) \Rightarrow\varPhi_{l+1,l}(x)\leq\varPhi_{l+1,l}\bigl(x' \bigr). $$

Proposition 1

The following statements are equivalent:

• (1) Assumption 1 holds.

• (2) There exists an optimal scoring rule s ^∗.

• (3) The regression function $\eta(x) = \mathbb{E}(Y \mid X=x)$ is an optimal scoring rule.

• (4) For any k∈{1,…,K−1}, for all $x,x'\in\mathcal{X}_{k}$, we have:

  $$\varPhi_{k+1,k}(x)< \varPhi_{k+1,k}\bigl(x'\bigr) \Rightarrow s^*(x)< s^*\bigl(x'\bigr). $$

• (5) For any k,l∈{1,…,K} such that l<k, the ratio Φ _k,l (x) is a nondecreasing function of s ^∗(x).

Assumption 1 characterizes the class distributions for the random pair (X,Y) for which the very concept of an optimal scoring rules makes sense. The proposition says that if this condition is not satisfied then the ordinal nature of the labels, when seen through the observation X, is violated. We point out that a related condition, called ERA ranking representability, has been introduced in Waegeman and Baets (2011), see Definition 2.1 therein. Precisely, it can be easily checked that the condition in the previous proposition means that the collection of (bipartite) ranking functions {Φ _k+1,k :1≤k<K} is an ERA ranking representable set of ranking functions. Statement (3) suggests that plug-in rules based on the statistical estimation of the regression function η and multiple thresholding of the estimate will offer candidates for practical resolution of K-partite ranking. Such strategies are indeed reminiscent of ordinal logistic regression methods and will be discussed in Sect. 5.3.2. Statement (4) offers an alternative characterization to Definition 1 for optimal scoring rules. Statement (5) means that the family of densities of the class-conditional distributions f _k has a monotone likelihood ratio (we refer to standard textbooks of mathematical statistics which use this terminology, e.g. Lehmann and Romano 2005).

Proposition 2

Under Assumption 1 we necessarily have:

$$\mathcal{X}_{k'}\cap\mathcal{X}_{l'}\subseteq\mathcal{X}_{k}\cap \mathcal{X}_{l}\quad \mathrm{for\ any}\ k, k', l, l'\ \mathrm{such\ that}\ 1 \leq k'\leq k <l\leq l'\leq K. $$

2.4 Examples and counterexamples of monotone likelihood ratio families

It is easy to see that, in absence of Assumption 1, the notion of K-partite ranking hardly makes sense. However, it is a challenging statistical task to assess whether data arise from a mixture of distributions F _k with monotone likelihood ratio. We now provide examples and counterexamples of such cases.

Disjoint supports

Consider the separable case where: ∀k,l, $\mathcal{X}_{k} \cap\mathcal{X}_{l} = \emptyset$. Then Assumption 1 is clearly fulfilled as for k≠l, we have either Φ _k,l =0 or ∞. It is worth mentioning that in this case, the nature of the K-partite ranking problem does not differ from the multiclass classification setup where there is no order relation between classes.

Exponential families

We recall that $f = \sum_{k=1}^{K} p_{k} f_{k}$ is the marginal distribution function of X. We introduce the following choice for the class-conditional distributions f _k :

$$f_k(x) =\exp\bigl\{\kappa(k)T(x)-\psi(k)\bigr\} f(x), \quad \forall x \in\mathbb{R}^d, $$

where:

• κ:{1,…,K}→ℝ is strictly increasing,

• T:ℝ^d→ℝ such that $\psi(k)=\int_{x\in\mathbb{R}^{d}}\exp\{\kappa(k)T(x)\}f(x) dx<+\infty$, for 1≤k≤K.

It is easy to check that he family of density functions f _k has the property of monotone likelihood ratio.

1-D Gaussian distributions

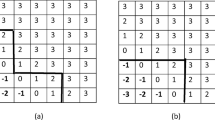
We consider here a toy example with K=3 and the f _k are Gaussian distributions $\mathcal {N}(m_{k}, \sigma^{2}_{k})$ over ℝ, where m _k is the expectation and $\sigma^{2}_{k}$ is the variance. Depending on the values of the parameters $m_{k}, \sigma^{2}_{k}$, the collection {f ₁,f ₂,f ₃} may or may not satisfy the property of having a monotone likelihood ratio. Assume first that the variances are equal, then the property of monotone likelihood ratio is satisfied if and only if either m ₁≤m ₂≤m ₃ or m ₃≤m ₂≤m ₁ (see Fig. 1(a)). Figure 1(b) depicts a situation where m ₁<m ₂<m ₃ and $\sigma^{2}_{3}>\sigma^{2}_{2}=\sigma^{2}_{1}$ for which the random observation X does not permit to recover the preorder induced by the output variable. The monotonicity condition is violated for instance at (x,x′)=(−2,1) and there is no optimal scoring rule in this case.

Fig. 1

Two examples of 1-D conditional Gaussian distributions in the case K=3—class 1 in green, class 2 in blue and class 3 in red

Uniform noise

Let t ₀=−∞<t ₁<⋯<t _K−1<+∞ and g:ℝ^d→ℝ a measurable function. We define the output random variable through:

$$Y=\sum_{k=1}^{K}\mathbb{I}\bigl \{g(X)+U>t_{k-1}\bigr\}, $$

where U is a uniform random variable on some interval of the real line, independent from X. Then it can be easily seen that the class-conditional distributions form a collection with monotone likelihood ratio, provided that t ₁ and t _K−1 both lie inside the interval defined by the essential infimum and supremum of the random variable g(X)+U. In this case, any strictly increasing transform of g is an optimal scoring rule.

3 Pairwise aggregation: from bipartite to K-partite ranking

In the present section, we propose a practical strategy for building scoring rules which approximate optimal scoring rules for K-partite ranking based on data. The principle of this strategy is the aggregation of scoring rules obtained for the pairwise subproblems. We emphasize the fact that the situation is very different from multiclass classification where aggregation boils down to linear combination, or majority voting, over binary classifiers (for “one against one” and “one versus all”, we refer to Allwein et al. 2001; Hastie and Tibshirani 1998; Venkatesan and Amit 1999; Debnath et al. 2004; Dietterich and Bakiri 1995; Beygelzimer et al. 2005a, 2005b and the references therein for instance). We propose here, in the K-partite ranking setup, a metric-based barycentric approach to build the aggregate scoring rule from the collection of scoring rules estimated for the bipartite subproblems. In order to avoid technical discussions dealing with special cases, we assume in the sequel that all class-conditional distributions have a continuous density f _k and share the same support $\mathcal{X}\subset\mathbb{R}^{d}$.

3.1 Median scoring rules and optimal aggregation

Every scoring rule induces an order relation over the input space ℝ^d and, for the ranking problem considered here, a measure of similarity between two scoring functions should only take into consideration the similarity in the ranking induced by each one of them. We propose here a measure of agreement between scoring rules which is based on the probabilistic Kendall τ for a pair of random variables.

Definition 2

(Probabilistic Kendall τ)

Consider X,X′ i.i.d. random vectors with density function f over ℝ^d. The measure of agreement between two real-valued scoring rules s ₁ and s ₂ is defined as the quantity:

This definition of agreement between scoring rules s ₁ and s ₂ coincides indeed with the Kendall τ between real-valued random variables s ₁(X) and s ₂(X). Note that the contribution of the two last terms in the definition of τ(s ₁,s ₂) vanishes when the distributions of the s _i (X)’s are continuous.

From there one can define the notion of median scoring rule which accounts for the consensus of many real-valued scoring rules over a given class of candidates.

Definition 3

(Median scoring rule)

Consider a given class $\mathcal{S}_{1}$ of real-valued scoring rules and Σ _K ={s ₁,…,s _K−1} a finite set of real-valued scoring rules. A median scoring rule $\overline{s}$ for $(\mathcal{S}_{1}, \varSigma_{K})$ satisfies:

$$ \sum_{k=1}^{K-1}\tau (\overline{s}, s_k )= \sup_{s\in\mathcal{S}_1} \sum_{k=1}^{K-1}\tau(s, s_k ). $$

(1)

In general, the supremum appearing on the right hand side of Eq. (1) is not attained. However, when the supremum over $\mathcal{S}_{1}$ can be replaced by a maximum over a finite set $\mathcal{S}'_{1}\subset \mathcal{S}_{1}$, a median scoring rule always exists (but it is not necessarily unique). In particular, this is the case when considering piecewise constant scoring functions such as those produced by the bipartite ranking algorithms proposed in Clémençon et al. (2011a), Clémençon and Vayatis (2009a, 2010) (we also refer to Clémençon and Vayatis 2009c for a discussion of consensus computation/approximation in this case). The idea underlying the measure of consensus through Kendall metric in order to aggregate scoring functions that are nearly optimal for bipartite ranking subproblems is clarified by the following result.

Definition 4

(Pairwise optimal scoring rule)

A pairwise optimal scoring rule $s_{l,k}^{*}$ is an optimal scoring rule for the bipartite ranking problem with classes Y=k and Y=l, where k>l in the sense that:

$$\forall x, x' \in\mathcal{X}, \ \varPhi_{k,l}(x)< \varPhi_{k,l}\bigl(x'\bigr) \Rightarrow s_{l,k}^*(x) < s_{l,k}^*\bigl(x'\bigr). $$

We denote by $\mathcal{S}^{*}_{l,k}$ the set of such optimal rules and, in particular, $\mathcal{S}^{*}_{k} = \mathcal{S}^{*}_{k, k+1}$.

Proposition 3

Denote by $\mathcal{S}$ the set of all possible real-valued scoring rules and consider pairwise optimal scoring rules $s_{k}^{*} \in\mathcal{S}^{*}_{k}$ for k=1,…,K−1, which form the set $\varSigma_{K}^{*} = \{s_{1}^{*}, \ldots, s_{K-1}^{*} \}$. Under Assumption 1, we have:

• 1. A median scoring rule $\overline{s}^{*}$ for $(\mathcal{S}, \varSigma ^{*}_{K})$ is an optimal scoring rule for the K-partite ranking problem.

• 2. Any optimal scoring rule s ^∗ for the K-partite ranking problem satisfies:

  $$\sum_{k=1}^{K-1} \tau\bigl(s^*,s^*_k\bigr) = K-1. $$

The proposition above reveals that “consensus scoring rules”, in the sense of Definition 3, based on K−1 optimal scoring rules are still optimal solutions for the global K-partite ranking problem and that, conversely, optimal elements necessarily achieve the equality in Statement (2) of the previous proposition. This naturally suggests to implement the following two-stage procedure, that consists in (1) solving the bipartite ranking subproblem related to the pairwise case (k,k+1) of consecutive class labels, yielding a scoring function s _k , for 1≤k<K, and (2) computing a median according to Definition 3, when feasible, based on the latter over a set $\mathcal{S}_{1}$ of scoring functions. Beyond the difficulty to solve each ranking subproblem separately (for instance refer to Clémençon and Vayatis 2009b for a discussion of the nature of the bipartite ranking issue), the performance/complexity of the method sketched above is ruled by the richness of the class $\mathcal{S}_{1}$ of scoring function candidates: too complex classes clearly make median computation unfeasible, while poor classes may not contain sufficiently accurate scoring rules.

3.2 A practical aggregation procedure

We now propose to convert the previous theoretical results which relate pairwise optimality to K-partite optimality in ranking into a practical aggregation procedure. Consider two independent samples:

• a sample $\mathcal{D}=\{(X_{i},Y_{i}){:}\; 1\leq i \leq n \}$ with i.i.d. labeled observations,

• a sample $\mathcal{D}'=\{X'_{i},{:}\; 1\leq i \leq n' \}$ a sample with unlabeled observations.

The first sample $\mathcal{D}$ is used for training bipartite ranking rules $\hat{s}_{k}$, while the second sample $\mathcal{D}'$ will be used for the computation of the median. In practice a proxy for the median is computed based on the empirical version of the Kendall τ, the following U-statistic of degree two, see Clémençon et al. (2008).

Definition 5

(Empirical Kendall τ)

Given a sample X ₁,…,X _n , the empirical Kendall τ is given by:

$$\widehat{\tau}_n (s_1, s_2)= \frac{2}{n(n-1)}\sum_{1\leq i<j \leq n} h \bigl( \bigl(s_1(X_i), s_1(X_j)\bigr),\bigl(s_2(X_i), s_2(X_j)\bigr)\bigr), $$

where

for (v,w) and (v′,w′) in ℝ².

Denote by $\mathcal{D}_{k} = \{ (X_{i}, Y_{i}) \in\mathcal{D}{:}\; Y_{i} = k\}$. The following aggregation method describes a two-steps procedure which takes as input the two data sets, a class $\mathcal{S}_{1}$ of candidate scoring rules, and a generic bipartite ranking algorithm $\mathcal {A}$.

Practical implementation issues

Motivated by practical problems such as the design of meta-search engines, collaborative filtering or combining results from multiple databases, consensus ranking, which the second stage of the procedure described above is a special case of, has recently enjoyed renewed popularity and received much attention in the machine-learning literature, see Meila et al. (2007), Fagin et al. (2004) or Lebanon and Lafferty (2002) for instance. As shown in Hudry (2008) or Wakabayashi (1998) in particular, median computations are NP-hard problems in general. Except in the case where $\mathcal {S}_{1}$ is of very low cardinality, the (approximate) computation of a supremum involves in practice the use of meta-heuristics such as simulated annealing, tabu search or genetic algorithms. The description of these computational approaches to consensus ranking is beyond the scope of this paper and we refer to Barthélemy et al. (1989), Charon and Hudry (1998), Laguna et al. (1999) or Mandhani and Meila (2009) and the references therein for further details on their implementation. We also underline that the implementation of the Kendall aggregation approach could be naturally based on K(K−1)/2 scoring functions, corresponding to solutions of the bipartite subproblems defined by all possible pairs of labels (the theoretical analysis carried out below can be straightforwardly extended so as to establish the validity of this variant), at the price of an additional computational cost for the median computation stage however.

Rank prediction vs. scoring rule learning

When the goal is to rank accurately new unlabeled datasets, rather than to learn a nearly optimal scoring rule explicitly, the following variant of the procedure described above can be considered. Given an unlabeled sample of i.i.d. copies of the input r.v. X $\mathcal{D}_{X}=\{ X_{1},\ldots,X_{m} \}$, instead of aggregating scoring functions s _k defined on the feature space $\mathcal{X}$ and use a consensus rule for ranking the elements of $\mathcal{D}_{X}$, one may aggregate their restrictions to the finite set $\mathcal{D}_{X}\subset\mathcal {X}$, or simply the ranks of the unlabeled data as defined by the s _k ’s.

4 Performance measures for K-partite ranking

We now turn to the main concepts for assessing performance in the K-partite ranking problem. We focus on the notion of ROC surface and Volume Under the ROC Surface (VUS) in the case where K=3 in order to keep the presentation simple. These concepts are generalizations of the well-known ROC curve and AUC criterion which are popular performance measures for bipartite ranking.

4.1 ROC surface

Given a scoring rule s:ℝ^d→ℝ, the ROC surface offers a visual display which reflects how the conditional distributions of s(X) given the class label Y=k are separated between each other as k=1,…,K. We introduce the notation F _s,k for the cumulative distribution function (cdf) over the real line ℝ of the random variable s(X) given the class label Y=k:

$$\forall t\in\mathbb{R}, \quad F_{s,k}(t) = \mathbb{P}\bigl\{ s(x) \le t \mid Y=k\bigr\} . $$

Definition 6

(ROC surface)

Let K≥2. The ROC surface of a real-valued scoring rule s is defined as the plot of the continuous extension of the parametric surface in the unit cube [0,1]^K:

where Δ={(t ₁,…,t _K−1)∈ℝ^K−1:t ₁<⋯<t _K−1}.

By “continuous extension”, it is meant that discontinuity points, due to jumps or flat parts in the cdfs F _s,k , are connected by linear segments (parts of hyperplanes). The same convention is considered in the definition of the ROC curve in the bipartite case given in Clémençon and Vayatis (2009b). In the case K=3, on which we restrict our attention from now for simplicity (all results stated in the sequel can be straightforwardly extended to the general situation), the ROC surface thus corresponds to a continuous manifold of dimension 2 in the unit cube of ℝ³. We also point out that the ROC surface contains the ROC curves of the pairwise problems (f ₁,f ₂), (f ₂,f ₃) and (f ₁,f ₃) which can be obtained as the intersections of the ROC surface with planes orthogonal to each of the axis of the unit cube.

In order to keep track of the relationship between the ROC surface and its sections, we introduce the following notation:

$$\forall\alpha\in[0,1], \quad\mathrm{ROC}_{f_k,f_{k+1}}(s,\alpha )=1-F_{s,k+1}\circ F_{s,k}^{-1}(1-\alpha), $$

where we have used the following definition of the generalized inverse of a cdf F: F ⁻¹(u)=inf{t∈ ]−∞,+∞]: F(t)≥u}, u∈[0,1].

Proposition 4

(Change of parameterization)

The ROC surface of the scoring rule s can be obtained as the plot of the continuous extension of the parametric surface:

where

(2)

(3)

with the notation u ₊=max(0,u), for any real number u.

We point out that, in the case where s has no capacity to discriminate between the three distributions, i.e. when F _s,1=F _s,2=F _s,3, the ROC surface boils down to the surface delimited by the triangle that connects the points (1,0,0), (0,1,0) and (0,0,1), we then have ROC(s,α,γ)=1−α−γ. By contrast, in the separable situation (see Sect. 2.4), the optimal ROC surface coincides with the surface of the unit cube [0,1]³.

The next lemma characterizes the support of the function whose plot corresponds to the ROC surface (see Fig. 2).

Fig. 2

Plot of the ROC surface of a scoring function

Lemma 1

For any (α,γ)∈[0,1]², the following statements are equivalent:

• 1. ROC(s,α,γ)>0

• 2. $\mathrm{ROC}_{f_{1},f_{3}}(s,1-\alpha) >\gamma$.

Other notions of ROC surface have been considered in the literature, depending on the learning problem considered and the goal pursued. In the context of multi-class pattern recognition, they provide a visual display of classification accuracy, as in Ferri et al. (2003) (see also Fieldsend and Everson 2005, 2006 and Hand and Till 2001) from a one-versus-one angle or in Flach (2004) when adopting the one-versus-all approach. The concept of ROC analysis described above is more adapted to the situation where a natural order on the set of labels exists, just like in ordinal regression, see Waegeman et al. (2008b).

4.2 ROC-optimality and optimal scoring rules

The ROC surface provides a visual tool for assessing ranking performance of a scoring rule. The next theorem provides a formal statement to justify this practice.

Theorem 1

The following statements are equivalent:

• 1. Assumption 1 is fulfilled and s ^∗ is an optimal scoring rule in the sense of Definition 1.

• 2. We have, for any scoring rule s and for all (α,γ)∈[0,1]²,

  $$\mathrm{ROC}(s,\alpha,\gamma)\leq\mathrm{ROC}\bigl(s^*,\alpha ,\gamma\bigr). $$

A nontrivial byproduct of the proof of the previous theorem is that optimizing the ROC surface amounts to simultaneously optimizing the ROC curves related to the two pairs of distributions (f ₁,f ₂) and (f ₂,f ₃).

The theorem indicates that optimality for scoring rules in the sense of Definition 1 is equivalent to optimality in the sense of the ROC surface. Therefore, the ROC surface provides a complete characterization of the ranking performance of a scoring rule in the K-partite problem.

We now introduce the following notations: for any α∈[0,1] and any scoring rule s,

• the quantile of order (1−α) of the conditional distribution of the random variable s(X) given Y=k:

  $$Q^{(k)}(s,\alpha) = F^{-1}_{s, k}(1-\alpha), $$

• the level set of the scoring rule s with the top elements of class Y=k:

  $$R^{(k)}_{s,\alpha}=\bigl\{x\in\mathcal{X}|s(x)>Q^{(k)}(s,\alpha) \bigr\} . $$

Proposition 5

Suppose that Assumption 1 is fulfilled and consider s ^∗ an optimal scoring rule in the sense of Definition 1. Also assume that η(X) is a continuous random variable, then we have: ∀(α,γ)∈[0,1]²:

$$\mathrm{ROC}^{*} \bigl(s^*, \alpha,\gamma\bigr)-\mathrm {ROC}(s,\alpha,\gamma )\leq \mathbb{I}\bigl\{ \gamma\leq\mathrm{ROC}_{F_1,F_3}\bigl (s^*,1-\alpha \bigr)\bigr\} \cdot\bigl( \varTheta_1(s,\alpha)+\varTheta_2(s,\gamma) \bigr), $$

where

We have used the notation AΔB=(A∖B)∪(B∖A) for the symmetric difference between sets A and B.

The previous proposition provides a key inequality for the statistical results developed in the sequel.

4.3 Volume Under the ROC Surface (VUS)

In the bipartite case, a standard summary of ranking performance is the Area Under an ROC Curve (or AUC). In a similar manner, one may consider the volume under the ROC surface (VUS in abbreviated form) in the three-class framework. We follow here Scurfield (1996) but we mention that other notions of ROC surface can be found in the literature, leading to other summary quantities, also referred to as VUS, such as those introduced in Hand and Till (2001).

Definition 7

(Volume Under the ROC Surface)

We define the VUS of a real-valued scoring rule s as:

$$\mathrm{VUS}(s) = \int_{0}^1\int_0^1 \mathrm{ROC}(s,\alpha,\gamma)\, \mathrm{d}\alpha\,\mathrm{d}\gamma. $$

An alternative expression of VUS can be derived with a change of parameters:

The next proposition describes two extreme cases.

Proposition 6

Consider a real-valued scoring rule s.

• 1. If F _s,1=F _s,2=F _s,3, then VUS(s)=1/6.

• 2. If the density functions of F _s,1, F _s,2, F _s,3 have disjoint supports, then VUS(s)=1.

Like the AUC criterion, the VUS can be interpreted in a probabilistic manner. For completeness, we recall the following result.

Proposition 7

(Scurfield 1996)

For any scoring function $s\in\mathcal{S}$, we have:

where (X ₁,Y ₁), (X ₂,Y ₂) and (X ₃,Y ₃) denote independent copies of the random pair (X,Y).

In the case where the distribution of s is continuous, the last three terms in the term on the right hand side vanish and the VUS boils down to the probability that, given three random instances X ₁, X ₂ and X ₃ with respective labels Y ₁=1, Y ₂=2 and Y ₃=3, the scoring rule s ranks them in the right order.

4.4 VUS-optimality

We now consider the notion of optimality with respect to the VUS criterion and provide expressions of the deficit of VUS for any scoring rule which highlight the connection with AUC maximizers for the bipartite subproblems.

Proposition 8

(VUS optimality)

Under Assumption 1, we have, for any real-valued scoring rule s and any optimal scoring rule s ^∗:

$$\mathrm{VUS}(s)\leq\mathrm{VUS}\bigl(s^*\bigr). $$

We denote the maximal value of the VUS by VUS^∗=VUS(s ^∗)

This result shows that optimal scoring rules in the sense of Definition 1 coincide with optimal elements in the sense of VUS. This simple statement grounds the use of empirical VUC maximization strategies for the K-partite ranking problem.

When the Assumption 1 is not fulfilled, the VUS can still be used as a performance criterion, both in the multiclass classification context (Landgrebe and Duin 2006; Ferri et al. 2003) and in the ordinal regression setup (Waegeman et al. 2008b). However, the interpretation of maximizers of VUS as optimal orderings is highly questionable. For instance, in the situation described in Example 1, one may easily check that, when ω _1,1=4/11, ω _1,2=6/11, ω _1,3=ω _3,1=1/11, ω _2,1=ω _2,2=3/11 and ω _2,3=ω _3,2=ω _3,3=5/11, the maximum VUS (equal to 0.2543) is reached by the scoring rule corresponding to strict orders ≺ and ≺′, such that x ₃≺x ₂≺x ₁ and x ₂≺′x ₃≺′x ₁ respectively, both at the same time.

We introduce the definition for the AUC of the bipartite ranking problem with the pair of distributions (f _k ,f _k+1):

Definition 8

(AUC)

Let X ₁ and X ₂ independent random variables with distribution f _k and f _k+1 respectively. We set:

$$\mathrm{AUC}_{f_{k},f_{k+1}}(s)=\mathbb{P} \bigl\{s(X_1)<s(X_2) \bigr\}+\frac {1}{2}\mathbb{P} \bigl\{s(X_1)=s(X_2) \bigr\} . $$

We now state the result which establishes the relevance of AUC as an optimality criterion for the bipartite ranking problem.

Proposition 9

Fix k∈{1,…,K−1} and consider $s^{*}_{k}$ a pairwise optimal scoring rule according to Definition 4. Then we have, for any scoring rule:

$$\mathrm{AUC}_{f_{k},f_{k+1}}(s) \le\mathrm{AUC}_{f_{k},f_{k+1}}\bigl (s^*_k\bigr) . $$

Moreover, we denote the maximal value of the AUC for the bipartite (f _k ,f _k+1) ranking problem by: $\mathrm{AUC}^{*}_{f_{k},f_{k+1}} = \mathrm{AUC} _{f_{k},f_{k+1}}(s^{*}_{k})$.

The next result makes clear that if a scoring rule s solves simultaneously all the bipartite ranking subproblems then it also solves the global K-partite ranking problem. For simplicity, we present the result in the case K=3.

Theorem 2

(Deficit of VUS)

Suppose that Assumption 1 is fulfilled. Then, for any scoring rule s and any optimal scoring rule s ^∗, we have

5 Consistency of pairwise aggregation and other strategies for K-partite ranking

5.1 Definition of VUS-consistency and main result

In this section, we assume a data sample $\mathcal{D}_{n}=\{(X_{1},Y_{1}), \ldots, (X_{n},Y_{n})\}$ is available and composed by n i.i.d. copies of the random pair (X,Y). Our goal here is to learn from the sample $\mathcal{D}_{n}$ how to build a real-valued scoring rule $\widehat{s}_{n}$ such that its ROC surface is as close as possible to the optimal ROC surface. We propose to consider a weak concept of consistency which relies on the VUS.

Definition 9

(VUS-consistency)

Suppose that Assumption 1 is fulfilled. Let (s _n ) _n≥1 be a sequence of random scoring rules on ℝ^d, then:

• the sequence {s _n } is called VUS-consistent if

  $$\mathrm{VUS}^*-\mathrm{VUS}(s_n)\rightarrow0 \quad\text{in probability}, $$

• the sequence {s _n } is called strongly VUS-consistent if

  $$\mathrm{VUS}^*-\mathrm{VUS}(s_n)\rightarrow0\quad\text{with probability one}. $$

Remark 1

We note that the deficit of VUS can be interpreted as an L ₁ distance between ROC surfaces of s _n and s ^∗:

$$\mathrm{VUS}^*-\mathrm{VUS}(s_n)=\int\int_{(\alpha,\gamma)\in [0,1]^2}\bigl\vert \mathrm{ROC} \bigl(s^*,\alpha,\gamma\bigr) -\mathrm{ROC}(s_n,\alpha,\gamma )\bigr \vert\, \mathrm{d}\alpha\,\mathrm{d}\gamma, $$

and in this sense the notion of consistency is weak. Indeed, a stronger sense of consistency could be given by considering the supremum norm between surfaces:

$$d_{\infty}\bigl(s^*,s_n\bigr)=\sup_{(\alpha,\gamma)\in [0,1]^2}\bigl\vert\mathrm{ROC} \bigl(s^*,\alpha,\gamma\bigr) -\mathrm{ROC}(s_n,\alpha,\gamma )\bigr \vert. $$

The study of accuracy of K-partite ranking methods in this sense is beyond the scope of the present paper (in contrast to the L ₁ norm, the quantity d _∞(s ^∗,s) cannot be decomposed in an additive manner). Extensions of bipartite ranking procedures such as the TreeRank and the RankOver algorithms (see Clémençon and Vayatis 2009b and 2010), for which consistency in supremum norm is guaranteed under some specific assumptions, will be considered in future work.

In order to state the main result, we need an additional assumption on the distribution of the random pair (X,Y). The reason why this assumption is needed will be explained in the next section.

Assumption 2

For all k∈{1,…,K−1}, the (pairwise) posterior probability given by η _k+1(X)/(η _k (X)+η _k+1(X)) is a continuous random variable and there exist c<∞ and a∈(0,1) such that

$$ \forall x\in\mathcal{X},\quad \mathbb{E} \biggl[\biggl\vert \frac{\eta_{k+1}(X)}{\eta_{k+1}(X)+\eta_k(X)}-\frac{\eta _{k+1}(x)}{\eta_{k+1}(x) +\eta_k(x)}\biggr\vert^{-a} \biggr]\leq c. $$

(4)

In the statistical learning literature, Assumption 2 is referred to as the noise condition and goes back to the work of Tsybakov (2004). It has been adapted to the framework of bipartite ranking in Clémençon et al. (2008). For completeness, we state a result from this latter paper (see Corollary 8 within) which offers a simple sufficient condition for the Assumption 2 to be fulfilled.

Proposition 10

If the distribution of the r.v. η _k+1(X)/(η _k (X)+η _k+1(X)) has a bounded density, then Assumption 2 is satisfied.

We will also need to use the notion of AUC consistency for the bipartite ranking subproblems.

Definition 10

(AUC consistency)

For k fixed in {1,…,K−1}, a sequence (s _n ) _n≥1 of scoring rules is said to be AUC-consistent (respectively, strongly AUC-consistent) for the bipartite problem (f _k ,f _k+1) if it satisfies:

$$\mathrm{AUC}_{f_k, f_{k+1}}(s_n) \rightarrow\mathrm{AUC}^*_{f_k, f_{k+1}}\ \text{in probability (resp., with probability one).} $$

We can now state the main consistency result of the paper which concerns the Kendall aggregation procedure described in Sect. 3.2. Indeed, the following theorem reveals that the notion of median scoring rule introduced in Definition 3 preserves AUC consistency for bipartite subproblems and thus yields a VUS consistent scoring rule for the K-partite problem. It is assumed that the solutions to the bipartite subproblems are AUC-consistent for each specific pair of class distributions (f _k ,f _k+1), 1≤k<K. For simplicity, we formulate the result in the case K=3.

Theorem 3

We consider a class of candidate scoring rules $\mathcal{S}_{1}$, $(s^{(1)}_{n})_{n\geq1}$, $(s^{(2)}_{n})_{n\geq1}$ two sequences of scoring rules in $\mathcal{S}_{1}$. We use the notation $\varSigma _{2,n} = \{ s^{(1)}_{n},s^{(2)}_{n}\}$. Assume the following:

• 1. Assumptions 1 and 2 hold true.

• 2. The class $\mathcal{S}_{1}$ contains an optimal scoring rule.

• 3. The sequences $(s^{(1)}_{n})_{n\geq1}$ and $(s^{(2)}_{n})_{n\geq1}$ are (strongly) AUC-consistent for the bipartite ranking subproblems related to the pairs of distributions (f ₁,f ₂) and (f ₂,f ₃) respectively.

• 4. Assume that, for all n, there exists a median scoring rule $\overline{s}_{n}$ in the sense of Definition 3 with respect to $(\mathcal{S}_{1}, \varSigma_{2,n})$.

Then the median scoring rule $\overline{s}_{n}$ is (strongly) VUS-consistent.

Discussion

The first assumption of Theorem 3 puts a restriction on the class of distributions for which such a consistency result holds. Assumption 1 actually guarantees that the very problem of K-partite makes sense and the existence of an optimal scoring rule. Assumption 2 can be seen as a “light” restriction since it still covers a large class of distributions commonly used in probabilistic modeling. The third and fourth assumptions are natural as we expect first to have efficient solutions to the bipartite subproblems before considering reasonable solutions to the K-partite problem. The most restrictive assumption is definitely the second one about the fact that the class of candidates contains an optimal element. Indeed, it is easy to weaken this assumption at the price of an additional bias term by assuming that the scoring rules $s^{(1)}_{n}$, $s^{(2)}_{n}$ and $\overline{s}_{n}$ belong to a set $\mathcal{S}_{1}^{(n)}$, such that there exists a sequence $(s_{n}^{*})_{n\geq1}$ with $s_{n}^{*}\in\mathcal{S}_{1}^{(n)}$ and $\mathrm{VUS} (s_{n}^{*})\rightarrow\mathrm{VUS}^{*}$ as n→∞. We decided not to include this refinement as this is merely a technical argument which does not offer additional insights on the nature of the problem.

5.2 From AUC consistency to VUS consistency

In this section, we introduce auxiliary results which contribute to the proof of the main theorem (details are provided in the Appendix). Key arguments rely on the relationship between the solutions of the bipartite ranking subproblems and those of the K-partite problem. In particular, a sequence of scoring rules that is simultaneously AUC-consistent for the bipartite ranking problems related to the two pairs of distributions (f ₁,f ₂) and (f ₂,f ₃) is VUS-consistent. Indeed, we have the following corollary.

Corollary 1

Suppose that Assumption 1 is satisfied. Let (s _n ) _n≥1 be a sequence of scoring rules. The following assertions are equivalent.

• (i) The sequence (s _n ) _n of scoring rules is (strongly) VUS-optimal.

• (ii) We have simultaneously when n→∞:

  

  (with probability one) in probability.

It follows from this result that the 3-partite ranking problem can be cast in terms of a double-criterion optimization task, consisting in finding a scoring rule s that simultaneously maximizes $\mathrm{AUC}_{f_{1},f_{2}}(s)$ and $\mathrm{AUC}_{f_{2},f_{3}}(s)$. This result provides a theoretical basis for the justification of our pairwise aggregation procedure. We mention that the idea of decomposing the K-partite ranking into several bipartite ranking subproblems has also been considered in Fürnkranz et al. (2009) but the aggregation stage is performed with a different strategy.

The other type of result which is needed concerns the connection between the aggregation principle based on a consensus approach (Kendall τ) and the performance metrics involved in the K-partite ranking problem. The next results establish inequalities which relate the AUC and the Kendall τ in a quantitative manner.

Proposition 11

Let p be a real number in (0,1). Consider two probability distributions f _k and f _k +1 on the set  $\mathcal{X}$. We assume that the distribution of X comes from the mixture with density function given by (1−p)f _k +pf _k+1. For any real-valued scoring rules s ₁ and s ₂ on ℝ^d, we have:

$$ \bigl\vert\mathrm{AUC}_{f_k,f_{k+1}}(s_1)-\mathrm{AUC}_{f_k,f_{k+1}}(s_2) \bigr\vert\leq\frac {1-\tau(s_1,s_2 )}{4p(1-p)}. $$

We point out that it is generally vain to look for a reverse control: indeed, scoring functions yielding different rankings may have exactly the same AUC. However, the following result guarantees that a scoring function with a nearly optimal AUC is close to optimal scoring functions in a certain sense, under the additional assumption that the noise condition introduced in Clémençon et al. (2008) is fulfilled.

Proposition 12

Under Assumption 2, we have, for any k∈{1,…,K−1}, for any scoring rule s and any pairwise optimal scoring rule  $s_{k}^{*}$:

$$ 1-\tau\bigl(s_k^*,s \bigr) \le C\cdot\bigl(\mathrm{AUC}_{f_k,f_{k+1}}^*- \mathrm{AUC}_{f_k,f_{k+1}}(s) \bigr)^{a/(1+a)}, $$

with C=3c ^1/(1+a)⋅(2p _k p _k+1)^a/(1+a).

5.3 Alternative approaches to K-partite ranking

In this section, we also mention, for completeness, two other approaches to K-partite ranking.

5.3.1 Empirical VUS maximization

The first approach extends the popular principle of empirical risk minimization, see Vapnik (1999). For K-partite ranking, this programme has been carried out in Rajaram and Agarwal (2005) with an accuracy measure based on the loss function $(Y-Y')^{\xi}_{+}({\mathbb{I}}\{ s(X)<s(X')\} + (1/2)\cdot{\mathbb {I}}\{ s(X)=s(X')\})$, with ξ≥0. In our setup, the idea would be to optimize a statistical counterpart of the unknown functional VUS(.) over a class $\mathcal{S}_{1}$ of candidate scoring rules. Based on the training dataset $\mathcal{D}_{n}$, a natural empirical counterpart of VUS(s) is the three-sample U-statistic

$$ \widehat{\mathrm{VUS}}_n(s)= \frac{1}{n_1n_2n_3}\sum_{1\leq i, j,k\leq n} h_s(X_i,X_j,X_k) \cdot\mathbb{I}\{Y_i=1, Y_j=2, Y_k=3\}, $$

(5)

with kernel given by

for any $(x_{1},x_{2},x_{3})\in\mathcal{X}^{3}$. The computational complexity of empirical VUS calculation is investigated in Waegeman et al. (2008a).

The theoretical analysis shall rely on concentration properties of U-processes in order to control the deviation between the empirical and theoretical versions of the VUS criterion uniformly over the class $\mathcal{S}_{1}$. Such an analysis was performed in the bipartite case in Clémençon et al. (2008) and we expect that it can be extended in the K-partite case. In contrast, algorithmic aspects of the issue of maximizing the empirical VUS criterion (or a concave surrogate) are much less straightforward and the question of extending optimization strategies such as those introduced in Clémençon and Vayatis (2009b) or Clémençon and Vayatis (2010) requires, for instance, significant methodological progress.

5.3.2 Plug-in scoring rule

As shown by Proposition 1, when Assumption 1 is fulfilled, the regression function η is an optimal scoring function. The plug-in approach consists of estimating the latter and use the resulting estimate as a scoring rule. For instance, one may estimate the posterior probabilities (η ₁(x),…,η _K (x)) by an empirical counterpart $(\widehat{\eta}_{1}(x),\ldots,\widehat{\eta}_{K}(x))$ based on the training data and consider the ordering on ℝ^d induced by the estimator $\widehat{\eta}(x)=\sum_{k=1}^{K} k \widehat{\eta}_{k}(x)$. We refer to Clémençon and Vayatis (2009a) and Clémençon and Robbiano (2011) for preliminary theoretical results based on this strategy in the bipartite context and Audibert and Tsybakov (2007) for an account of the plug-in approach in binary classification. It is expected that an accurate estimate of η(x) will define a ranking rule similar to the optimal one, with nearly maximal VUS. As an illustration of this approach, the next result relates the deficit of VUS of a scoring function $\widehat{\eta}$ to its L ₁(μ)-error as an estimate of η. We assume for simplicity that all class-conditional distributions have the same support.

Proposition 13

Suppose that Assumption 1 is fulfilled. Let $\widehat {\eta}$ be an approximant of η. Assume that both the random variables η(X) and $\widehat{\eta}(X)$ are continuous. We have:

$$\mathrm{VUS}^*-\mathrm{VUS}(\widehat{\eta})\leq\frac {p_{1}+p_{3}}{p_{1}p_{2}p_{3}}\cdot\mathbb{E}\bigl[\bigl\vert \eta(X)-\widehat{\eta}(X)\bigr\vert\bigr]. $$

This result reveals that a L ₁(μ)-consistent estimator, i.e. an estimator $\widehat{\eta}_{n}$ such that $\mathbb {E}[|\eta (X)-\widehat {\eta}_{n}(X)|]$ converges to zero in probability as n→∞, yields a VUS-consistent ranking procedure. However, from a practical perspective, such procedures should be avoided when dealing with high-dimensional data, since they are obviously confronted to the curse of dimensionality.

5.4 Connections with regression estimation and ordinal regression

Whereas standard multi-class classification ignores the possible ordinal structure of the output space, ordinal regression takes the latter into account by penalizing more and more the error of a classifier candidate C on an example (X,Y) as |C(X)−Y| increases. In general, the loss function chosen is of the form ψ(c,y)=Ψ(|c−y|), (c,y)∈{1,…,K}², where Ψ:{0,…,K−1}→ℝ₊ is some nondecreasing mapping. The most commonly used choice is Ψ(u)=u, corresponding to the risk $L(C)=\mathbb{E}[\vert C(X)-Y \vert]$, referred to as the expected ordinal regression error sometimes, cf. Agarwal (2008). In this case, it is shown that the optimal classifier can be built by thresholding the regression function at specific levels $t_{0}=0<t^{*}_{1}<\cdots<t^{*}_{K-1}<1=t_{K}$, that it so say it is of the form $C^{*}(x)=\sum_{k=1}^{K}k\cdot\mathbb{I}\{ t^{*}_{k-1}\leq\eta(x)<t^{*}_{k} \}$ when assuming that $\eta(X)=\mathbb {E}[Y\mid X]$ is a continuous r.v. for simplicity. Based on this observation, a popular approach to ordinal regression lies in estimating first the regression function η by an empirical counterpart $\widehat{\eta}$ (through minimization of an estimate of $R(f)=\mathbb{E}[( Y-f(X))^{2}]$ over a specific class $\mathcal{F}$ of function candidates f, in general) and choosing next a collection t of thresholds t ₀=0<t ₁<⋯<t _K−1<1=t _K in order to minimize a statistical version of L(C _t ) where $C_{\mathbf {t}}(x)=\sum_{k=1}^{K}k\cdot\mathbb{I}\{ t_{k-1}\leq\widehat{\eta }(x)<t_{k} \}$. Such procedures are sometimes termed regression-based algorithms, see Agarwal (2008). One may refer to Kramer et al. (2001) in the case of regression trees for instance.

6 Illustrative numerical experiments

It is the purpose of this section to illustrate the approach described above by numerical results and provide some empirical evidence for its efficacy. Since our goal is here to show that, beyond its theoretical validity, the Kendall aggregation approach to multi-class ranking actually works in practice, rather than to provide a detailed empirical study of its performance on benchmark artificial/real datasets compared to that of possible competitors (this will be the subject of a forthcoming paper), in the subsequent experimental analysis we have considered two simple data generative models, for which one may easily check Assumption 1 and compute the optimal ROC surface (as well as the optimum value VUS^∗), which the results obtained must be compared to. The first example involves mixtures of Gaussian distributions, while the second one is based on mixtures of uniform distributions, the target ROC surface being piecewise linear in the latter case (cf. assertion 4 in Proposition 14). Here, the artificial data simulated are split into a training sample and a test sample, used for plotting the “test ROC surfaces”.

The learning algorithm used for solving the bipartite ranking subproblems at the first stage of the procedure is the TreeRank procedure based on locally weighted versions of the CART method (with axis parallel splits), see Clémençon et al. (2011a) for a detailed description of the algorithm (as well as Clémençon and Vayatis 2009b for rigorous statistical foundations of this method). Precisely, we used a package for R statistical software (see http://www.r-project.org) implementing TreeRank (with the “default” parameters: minsplit = (size of training sample)/20, maxdepth = 10, mincrit = 0), available at http://treerank.sourceforge.net, see Baskiotis et al. (2010). The scoring rules produced at stage 1 are thus (tree-structured and) piecewise constant, making the aggregating procedure described in Sect. 3.2 quite feasible. Indeed, if s ₁,…,s _M are scoring functions that are all constant on the cells of a finite partition $\mathcal{P}$ of the input space $\mathcal{X}$, one easily see that the infimum $\inf_{s\in\mathcal{S}_{0}}\sum_{m=1}^{M}d_{\tau_{\mu }}(s,s_{m})$ reduces to a minimum over a finite collection of scoring functions that are also constant on $\mathcal{P}$’s cells and is thus attained. As underlined in Sect. 3.2, when the number of cells is large, median computation may become practically unfeasible and the use of a meta-heuristic can be then considered for approximation purpose (simulated annealing, tabu search, etc.), here the ranking obtained by taking the mean ranks over the K−1 rankings of the test data has been improved in the Kendall consensus sense by means of a standard simulated annealing technique.

For comparison purpose, we have also implemented two ranking algorithms, RankBoost (when aggregating 30 stumps, see Rudin et al. 2005) and SVMRank (with linear and Gaussian kernels with respective parameters C=20 and (C,γ)=(0.01), see Herbrich et al. 2000), using the SVM-light implementation available at http://svmlight.joachims.org/. We have also used the RankRLS method (http://www.tucs.fi/RLScore, see Pahikkala et al. 2007) that implements a regularized least square algorithm with linear kernel (“bias=1”) and with Gaussian kernel (γ=0.01), selection of the intercept on a grid being performed through a leave-one-out procedure. For completeness, the Kendall aggregation procedure has also been implemented with RankBoost for solving the bipartite subproblems.

First example (mixtures of Gaussian distributions)

Consider a q-dimensional Gaussian random vector Z, drawn as $\mathcal{N}(\mu ,\varGamma)$, and a Borelian set C⊂ℝ^q weighted by $\mathcal {N}(\mu ,\varGamma)$. We denote by $\mathcal{N}_{C}(\mu,\varGamma)$ the conditional distribution of Z given Z∈C. Equipped with this notation, we can write the class distributions used in this example as:

When p ₁=p ₂=p ₃=1/3, the regression function is then an increasing transform of (x ₁,x ₂)∈[0,1]²↦x ₁+x ₂, it is given by:

$$\eta(x) =\frac{2.79\cdot e^{-(x_{1}+x_{2})^{2}}+2\cdot1.37\cdot e^{-(x_{1}+x_{2}-1)^{2}}+3\cdot2.79\cdot e^{-(x_{1}+x_{2}-2)^{2}}}{2.79\cdot e^{-(x_{1}+x_{2})^{2}}+1.37\cdot \exp^{-(x_{1}+x_{2}-1)^{2}}+2.79\cdot e^{-(x_{1}+x_{2}-2)^{2}}}. $$

The simulated dataset is plotted in Fig. 3a, while some level sets of the regression function are represented in Fig. 3b. We have drawn 50 training samples of size n=3000 and a test sample of size 3000. Using TreeRank, we learn 3 bipartite ranking rules: s ⁽¹⁾(x) based on data with labels “1” and “2”, s ⁽²⁾(x) based on data with labels “2” and “3” and s ⁽³⁾(x) based on data with labels “1” and “3”. Finally, s ⁽¹⁾ and s ⁽²⁾ are aggregated through the procedure described in Sect. 3.2, yielding the score called “TreeRank Agg” in Table 1. We also used each scoring function separately to rank the test data and compute a test estimate of the VUS (“TreeRank 1v2”, “2v3”, “1v3”). The scoring function produced by RankBoost is referred to as “RankBoostVUS”, while that obtained by Kendall aggregation based on (a bipartite implementation of) RankBoost is called “RankBoost Agg”. The scoring rule computed through SVMrank (respectively, through RankRLS) based on a linear and a Gaussian kernels are respectively called “SVMrank lin” and “SVMrank gauss” (respectively, “RLScore lin” and “RLScore gauss”). Averages ($\overline{\mathrm{VUS}}$) over the 50 training samples have been next computed, as well as standard deviations $\widehat{\sigma}$, they are given in Table 1 with the results of the earlier described algorithms. For comparison purpose, some level sets of the TreeRank scoring functions learnt from the first training sample are displayed in Fig. 4.

Fig. 3

First example—mixture of Gaussian distributions

Fig. 4

Levels sets of the scoring functions “TreeRank 1v2”, “TreeRank 2v3”, “TreeRank 1v3” and “TreeRank Agg” in a top-down left-right manner

Table 1 Comparison of the VUS: “Gaussian” experiment—VUS^∗=0.4369

Second example (mixtures of uniform distributions)

The artificial data sample used in this second example is represented in Fig. 5a and has been generated as follows. The unit square $\mathcal{X}= [0,1]^{2}$ is split into 9 squares of equal size and we defined next the scoring function s ^∗ as the function constant on each of these squares depicted by Fig. 5b). We then chose the uniform distribution over the unit square as marginal distribution of X and took $\phi_{1,2}(x)= s_{1,2}^{*}(x)/1.3$ and $\phi_{2,3}=1.3\times s_{2,3}^{*}(x)$. As $s_{1,2}^{*}$ and $s_{2,3}^{*}$ are non-decreasing functions of s ^∗ (see Table 2): ϕ _2,1 and ϕ _3,2 are thus non-decreasing functions of s ^∗, by virtue of Theorem 1, the class distributions check the monotonicity assumption 1. Computation of the η _i ’s on each part of $\mathcal{X}$ is then straightforward, see Table 2.

Fig. 5

Second example—mixtures of uniform distributions

Table 2 Values of the η _k ’s on each of the nine subsquare of [0,1]², cf. Fig. 5b

Here 50 training samples of size n=9000 plus a test sample of size 9000 have been generated. The performance results are reported in Table 3. For comparison purpose, some level sets of the scoring functions learned on the first training sample for each method are represented in Fig. 6.

Fig. 6

Levels sets of the scoring functions “TreeRank Agg”, “SVMrank lin”, “RLScore lin”, “RLScore gauss”, “SVMrank gauss”, “RankBoostVUS”, “RankBoost Agg”

Table 3 Comparison of the VUS: “uniform” experiment—VUS^∗=0.3855

Cardiotocography data

We also illustrate the methodology promoted in this paper by implementing it on a real data set, the Cardiotocography Data Set considered in Frank and Asuncion (2010) namely. The data have been collected as follows: 2126 fetal cardiotocograms (CTG’s in abbreviated form) have been automatically processed and the respective diagnostic features measured. The CTG’s have been next analyzed by three expert obstetricians and a consensus ordinal label has been then assigned to each of them, depending on the degree of anomaly observed: 1 for “normal”, 2 for “suspect” and 3 for “pathologic”.

We have split the data set into a training sample $\mathcal{D}_{e}$ and a test sample $\mathcal{D}_{t}$ of same sizes: scoring functions have been built based on the sample $\mathcal{D}_{e}$ and next tested on the sample $\mathcal{D}_{t}$ (i.e. we have computed the empirical versions of the ROC and VUS criteria based on $\mathcal{D}_{t}$). In this experiment, parameters have been selected by cross-validation: the scoring rule RankBoostVUS is based on 300 stumps and the bipartite rules produced by RankBoost are based on 100 stumps, the intercept involved in SVM ranklin is C=(0.001), while SVMrank gauss, RLScore lin and RLScore gauss have been obtained with the respective parameters (C,γ)=(0.001,0.0001), bias=1 and (bias,γ)=(1,0.001). Performance results are reported in Table 4 and the ROC surfaces test are plotted in Fig. 7.

Fig. 7

ROC surfaces “test” of the scoring functions bipartite “TreeRank”, “TreeRank Agg”, “SVMrank lin”, “RLScore lin”, “RLScore gauss”, “SVMrank gauss”, “RankBoostVUS”, “RankBoost Agg”

Table 4 Comparison of the VUS test—“Cardiotocography” experiment

Discussion

We observe that, in each of these experiments, Kendall aggregation clearly improves ranking accuracy, when measured in terms of VUS. In addition, looking at the standard deviation, we see that the aggregated scoring function is more stable. In terms of level sets, Kendall aggregation yielded more complex subsets and thus sharper results. Notice additionally that, as in the “Gaussian” experiment the level sets are linear, it is not surprising that the kernel methods outperform the tree-based ones in this situation. In contrast, for the “uniform” experiment, the tree-based methods performed much better than the others, the performance of TreeRank Agg is nearly optimal. Looking at the level sets (see Fig. 6), they seem to recover well their geometric structure. Observe also that Kendall aggregation of (bipartite) scoring functions produced by RankBoost has always lead to (slightly) better results than those obtained by a direct use of RankBoost on the 3-class population, with a computation time smaller by a factor 10 however. Finally, notice that, on the Cardiotocography data set, the Kendall aggregation approach based on RankBoost is the method that produced the scoring function with largest VUS test among the algorithms candidates. In particular, it provides the best discrimination for the bipartite subproblem “1 vs 2”, the most difficult to solve apparently, in view of the ROC surfaces plotted in Fig. 7.

Psychometric data

For completeness, we also carried out experiments based on four datasets with ordinal labels (ERA, ESL, LEV and SWD namely), considered in David (2008) (due to the rarity of such data, regression datasets are sometimes transformed into ordinal datasets to serve as benchmarkk, see Fürnkranz et al. 2009 and Huhn and Hüllermeier 2008). Because of the wide disparity between certain class sizes, data with certain labels are ignored (in the ESL dataset for instance, the class “1” counts only two observations). On top of the ranking bipartite algorithms used previously, we also implemented the aggregation method based on the algorithm Ranking Forest with 50 trees and a linear SVM with constant C=50 as LeafRank procedure (see Clémençon et al. 2011b for more details), this is referred to as “TreeRankF Agg” in the tables. For each experiment, in addition to the VUS, we computed alternative ranking performance statistics over five replications of a five-fold cross validation: the C-index (see Fürnkranz et al. 2009; Herbrich et al. 2000) and the Jonckheere-Terpstra statistic (JPstat in abbreviated form, see Hand and Till 2001 and Higgins 2004). The results are reported in the Tables 5, 6, 7 and 8 (standard deviations are not indicated, their order of magnitude, 10⁻³ namely, being negligible).

Table 5 Comparison of the VUS test—“ERA” experiment

Table 6 Comparison of the VUS test—“ESL” experiment (class 3–7)

Table 7 Comparison of the VUS test—“LEV” experiment

Table 8 Comparison of the VUS test—“SWD” experiment

We highlight the fact that the results we obtained with the approach promoted in this paper are quite comparable to those in Fürnkranz et al. (2009), they find a C-index of 0.7418 and a JPstat of 0.7265 in the case of ERA with nine classes as well as a C-index of 0.8660 and a JPstat of 0.8757 in the case of LEV with five classes. Contrary to the C-index and the JPstat for which all the values obtained are very close to each other, the VUS seems to reveal more contrast in the ranking performance. For instance, the aggregation procedure based on the TreeRank algorithm clearly outperforms the other competitors when considering the SWD dataset with classes 2–5, assessing the relevance of this approach in a situation where the dimension of the input space is not small (10 namely) and the population very skewed (the size of class “2” is very small compared to that of the others). Observe also that, in the other cases, the aggregation technique implemented using Ranking Forest has performance very similar to the state-of-the-art: sometimes not considerably below (cf. ERA with 7 classes, ERA and LEV) sometimes slightly better (cf. ESL and SWD with 3 classes).

These empirical results only aim at illustrating the Kendall aggregation approach for K-partite ranking, the limited goal pursued here being to show how aggregation helps to improve results. Beyond the theoretical validity framework sketched in Sect. 3, since a variety of bipartite ranking algorithms have been proposed in the literature and dedicated libraries are readily available, one of the main advantages of the Kendall aggregation approach lies in the fact that it is very easy to implement, when applied to bipartite rules that are not too complex, so that the (approximate) median computation is feasible, see Sect. 3.2. A more complete and detailed empirical analysis of the merits and limitations of this procedure is currently the subject of ongoing work, where comparisons with competitors are carried out and computational issues are investigated at length, provided that more real datasets with ordinal labels can be obtained.

7 Conclusion

In this article, we have presented theoretical work on ranking data with ordinal labels. In the first part of the paper, the issue of optimality has been tackled. We have proposed a monotonicity likelihood ratio condition that guarantees the existence and unicity of an “optimal” preorder on the input space, in the sense that it is optimal for any bipartite ranking subproblem, considering all possible pairs of labels. In particular, the regression function is proved to define an optimal ranking rule in this setting, highlighting the connection between K-partite ranking and ordinal regression. The second part is dedicated to describe a specific method for decomposing the multi-class ranking problem into a series of bipartite ranking tasks, as proposed in Fürnkranz et al. (2009). We have introduced a specific notion of median scoring function based on the (probabilistic) Kendall τ distance. We have next shown that the notion of ROC manifold/surface and its summary, the volume under the ROC surface (VUS), then provide quantitative criteria for evaluating ranking accuracy in the ordinal setup: under the afore mentioned monotonicity likelihood ratio condition, scoring functions whose ROC surface is as high as possible everywhere exactly coincide with those forming the optimal set (i.e. the set of scoring functions that are optimal for all bipartite subproblems, defined with no reference to the notions of ROC surface and VUS). Conversely, we have proved that the existence of a scoring function with such a dominating ROC surface implies that the monotonicity likelihood ratio condition is fulfilled. It is shown that the aggregation procedure leads to a consistent ranking rule, when applied to scoring functions that are, each, consistent for the bipartite ranking subproblem related to a specific pair of consecutive class distributions. This approach allows for extending the use of ranking algorithms originally designed for the bipartite situation to the ordinal multi-class context. It is illustrated by three numerical examples. Further experiments, based on more real datasets in particular, will be carried out in the future in order to determine precisely the situations in which this method is competitive, compared to alternative ranking techniques in the ordinal multi-class setup. In this respect, we underline that, so far, very few practical algorithms tailored for ROC graph optimization have been proposed in the literature. Whereas, as shown at length in Clémençon and Vayatis (2009b) and Clémençon et al. (2011a), partitioning techniques for AUC maximization, in the spirit of the CART method for classification, can be implemented in a very simple manner, by solving recursively cost-sensitive classification problems (with a local cost, depending on the data lying in the cell to be split), recursive VUS maximization remains a challenging issue, for which no simple interpretation is currently available. Hence, the number of possible strategies for direct optimization of the ranking criterion in the K-partite situation contrasts with that in the bipartite context and strongly advocates, for the moment, for considering techniques that transform multi-class ranking into a series of bipartite tasks, such as the method analyzed in this article.

Appendices

Appendix A: Properties of the ROC surface

The next result summarizes several crucial properties of ROC surfaces. To the best of our knowledge, though expected, these properties have not been formulated in the literature. The technical proof straightforwardly relies on Proposition 17 in Clémençon and Vayatis (2009b) and the definition of the ROC surface given in Eq. (2), it is thus left to the reader.

Proposition 14

(Properties of the ROC surface)

For any distributions f ₁(x), f ₂(x) and f ₃(x) on $\mathcal{X}$ and any scoring function $s\in\mathcal{S}$, the following properties hold.

• 1. Intersections with the facets of the ROC space. The intersection of the ROC surface {(α,ROC(s,α),γ)} with the plane of Eq. “α=0” coincides with the curve $\{ (\beta ,\mathrm{ROC}_{f_{2},f_{3}}(s,\beta))\}$ up to the transform (β,γ)∈[0,1]²↦ψ(β,γ)=(1−β,γ), that with the plane of Eq. “β=0” corresponds to the image of the curve $\{(\alpha,\mathrm{ROC}_{f_{1},f_{3}}(s,\alpha))\}$ by the mapping ψ(α,γ) and that with the plane of Eq. “γ=0” to the image of $\{ (\alpha,\mathrm{ROC}_{f_{1},f_{2}}(s,\alpha))\}$ by the transform ψ(α,β).

• 2. Invariance. For any strictly increasing function T:ℝ∪{+∞}→ℝ∪{+∞}, we have, for all (α,γ)∈[0,1]²:

  $$\mathrm{ROC}(T \circ s, \alpha,\gamma) = \mathrm{ROC}( s, \alpha ,\gamma). $$

• 3. Concavity. If the likelihood ratios dF _s,2/dF _s,1(u) and dF _s,3/dF _s,2(u) are both (strictly) increasing transforms of a certain function T(u), then the ROC surface is (strictly) concave. In particular, if Assumption 1 is fulfilled, the surface $\mathrm{ROC}^{*}\overset{def}{=}\mathrm{ROC}(s^{*},.,.)$, with $s^{*}\in\mathcal{S}^{*}$, is concave.

• 4. Flat parts. If the likelihood ratios dF _s,2/dF _s,1(u) and dF _s,3/dF _s,2(u) are simultaneously constant on some interval in the range of the scoring function s(x), then the ROC surface will present a flat part (i.e. will be a part of a plane) on the corresponding domain. In addition, under the Assumption 1, (α,γ)↦ROC^∗(α,γ) is a linear function of (α,γ) on $[\alpha_{1},\alpha_{2}]\times [\gamma_{1},\gamma_{2}]\subset\mathcal{I}_{s}$ iff f ₂/f ₁(x) and f ₃/f ₂(x) are constant on the subsets

  $$\bigl\{x\in\mathcal{X}\mid Q\bigl(f_{2}/f_{1}(X), \alpha_2\bigr)\leq f_{2}/f_{1}(x) \leq Q \bigl(f_{2}/f_{1}(X), \alpha_1\bigr)\bigr\} $$

  and

  $$\bigl\{x\in\mathcal{X}\mid Q\bigl(f_{3}/f_{2}(X), \gamma_2\bigr)\leq f_{3}/f_{2}(x) \leq Q \bigl(f_{3}/f_{2}(X),\gamma_1\bigr)\bigr\} $$

  respectively, denoting by Q(Z,α) the quantile of order 1−α of any random variable Z.

• 5. Differentiability. Assume that the distributions f ₁(x), f ₂(x) and f ₃(x) are continuous. Then, the ROC surface of a scoring function s is differentiable if and only if the conditional distributions F _s,1(du), F _s,2(du) and F _s,3(du) are continuous. In such a case, denoting by f _s,1, f _s,2 and f _s,3 the corresponding densities, we have in particular: $\forall (\alpha,\gamma)\in\mathcal{I}_{s}$,

  

Preliminary results related to statistical estimation of the ROC surface of a fixed scoring function s(x) can be found in Li and Zhou (2009), additional results related to the building of confidence regions in the ROC space [0,1]³ are established in Robbiano (2010).

Alternative ROC graph

Another way of quantifying the ranking accuracy of a scoring function in the multi-class setting is to evaluate its ability to discriminate between X’s conditional distributions given Y≤k and Y>k respectively, which we denote h _k (x) and g _k (x), for k∈{1,…,K−1}. This boils down to plot the graph of the mapping $\alpha\in[0,1]\mapsto(\mathrm{ROC}_{h_{1},g_{1}}(s,\alpha),\ldots ,\mathrm{ROC} _{h_{K-1},g_{K-1}}(s,\alpha))$. It straightforwardly follows from the stipulated monotonicity hypothesis (cf. Assumption 1) that the curve related to $s^{*}\in\mathcal{S}^{*}$ dominates the curve of any other scoring function s in the coordinatewise sense: $\mathrm{ROC}_{h_{k},g_{k}}(s,\alpha)\leq \mathrm{ROC} _{h_{k},g_{k}}(s^{*},\alpha)$ for all α∈[0,1], 1≤k<K. The likelihood ratio g _k /h _k (X) is indeed a non decreasing function of s ^∗(X), see Theorem 3.4.1 in Lehmann and Romano (2005) for instance. However, with such a functional representation of ranking performance, one loses an attractive advantage, the insensitivity to the class probabilities p _k . Indeed, the distributions h _k (x) and g _k (x) depend on the latter, they can be expressed as ∑ _l≤k p _l f _l (x)/(∑ _l≤k p _l ) and ∑ _l>k p _l f _l (x)/(∑ _l>k p _l ) respectively.

On the ROC surface of a classification rule

We point out that, with the convention previously introduced, the ROC surface of a classifier $C:\mathcal{X}\rightarrow\{1,2,3\}$ is the polyhedron with vertices (0,0,1), (0,α _2,1,1−α _3,1), (0,1−α _2,3,α _3,3), (0,1,0), (α _1,1,0,1−α _3,1), (α _1,1,α _2,2,α _3,3), (α _1,1,1−α _2,1,0), (1−α _1,3,0,α _3,3), (1−α _1,3,α _2,3,0) and (1,0,0), where α _k,l =ℙ{C(X)=l∣Y=k}. We underline that the confusion matrix $\mathcal{M}(C)=\{\alpha _{k,l}\}$ can be fully recovered from this geometric solid, which is actually a decahedron when the matrix $\mathcal{M}(C)$ has no null entry. Observe finally that this graphic representation of $\mathcal {M}(C)$ differs from that which derives from the multi-class notion of ROC analysis proposed in Ferri et al. (2003). In the latter case, the ROC space is defined as [0,1]⁶ and $\mathcal{M}(C)$ is represented by the point with coordinates (α _1,2,α _1,3,α _2,1,α _2,3,α _3,1,α _3,2). Notice incidentally that the latter concept of ROC analysis is more general in the sense that it permits to visualize the performance of K(K−1)/2 classifiers involved in a one-versus-one classification method.

Appendix B: Technical proofs

2.1 B.1 Proof of Proposition 1

The assertions (3)⇒(2), (2)⇒(4) and (2)⇒(5) are straightforward.

(1)⇒(3) Recall that $\eta(x)=\sum^{K}_{k=1}k\cdot\eta_{k}(x)$. Our goal is to establish that: $\forall(x,x')\in\mathcal{X}^{2}$,

$$\varPhi_{k,l}(x)< \varPhi_{k,l}\bigl(x'\bigr) \Rightarrow\eta(x)< \eta\bigl(x'\bigr). $$

The proof is based on the next lemma.

Lemma 2

Suppose Assumption 1 is satisfied. Let $(x,x')\in \mathcal{X}^{2}$. If there exists 1≤l<k≤K such that 0<Φ _k,l (x)<Φ _k,l (x′), then for all j∈{1,…,K}, we have

$$ \sum^{K}_{i=j} \eta_{i}(x)\leq\sum^{K}_{i=j} \eta_{i}\bigl(x'\bigr). $$

(6)

Additionally, a strict version of inequality (6) holds true when j=l+1.

Proof

Let $(x,x')\in\mathcal{X}^{2}$ and 1≤l<k≤K be such that Φ _k,l (x)<Φ _k,l (x′)

Combining $\varPhi_{k,l}(x) = \frac{p_{l}\eta_{k}(x)}{p_{k}\eta_{l}(x)}$ and η _l (x)=1−∑ _i≠l η _i (x), we clearly have

$$\eta_{k}(x)-\eta_{k}(x)\sum_{i\neq l} \eta_{i}\bigl(x'\bigr)< \eta_{k} \bigl(x'\bigr)-\eta_{k}\bigl(x'\bigr)\sum _{i\neq l}\eta_{i}(x), $$

and, by virtue of Assumption 1, for 1≤j≤m≤K:

(7)

(8)

Summing up, term-by-term, inequalities (7) for m=j,…,K, one gets that

$$\sum_{m=j}^K\eta_m(x)\leq \sum_{m=j}^K\eta_m \bigl(x'\bigr)+\sum_{m=j}^K \sum_{i=j}^K \bigl\{\eta_m(x) \eta_i\bigl(x'\bigr)-\eta_{m} \bigl(x'\bigr)\eta_{i}(x) \bigr\}. $$

The proof is finished by noticing that the sum on the right hand side of the inequality above is equal to 0. □

The desired result is established by summing up the inequalities (6) stated in Lemma 2 for j=1,…,K.

(4)⇒(2) Using the fact that $\varPhi_{k,l}(x)=\prod^{k-1}_{j=l}\varPhi_{j+1,j}(x)$, immediatly gives the result.

(5)⇒(1) We call Ψ _k,l the nondecreasing function such that Φ _k,l (x)=Ψ _k,l (s ^∗(x)). Let (k,l)∈{1,…,K}² s.t. l<k and x, x′ in $\mathcal{X}_{k}\cap\mathcal {X}_{l}$. Suppose that Φ _k+1,k (x)<Φ _k+1,k (x′). The functions $\varPsi ^{-1}_{k,l}$ are nondecreasing, just like the Ψ _k,l ’s. The equality $\varPhi_{l+1,l}(x)=\varPsi_{l+1,l}(\varPsi ^{-1}_{k+1,k}\circ\varPhi_{k+1,k}(x))$ on $\mathcal{X}_{k}\cap\mathcal{X}_{l}$ leads to the result.

2.2 B.2 Proof of Proposition 2

Notice first that it is actually sufficient to prove that $\mathcal{X} _{k-1}\cap \mathcal{X}_{k+1}\subset\mathcal{X}_{k}$ for all k∈{2,…,K−1}. Let 1<k<K and suppose that $\mathcal{X}_{k-1}\cap\mathcal{X}_{k} \neq\emptyset$ (the inclusion is immediate otherwise). Consider $x\in\mathcal{X}_{k-1}\cap\bar {\mathcal{X}}_{k}\cap\mathcal{X}_{k+1}$, where $\bar{\mathcal{X}}_{k}=\mathcal{X}\setminus\mathcal{X}_{k}$. We thus have: Φ _k,k−1(x)=0 and Φ _k+1,k (x)=+∞. Hence, for any $x'\in\mathcal{X}_{k}$, we have: 0=Φ _k,k−1(x)≤Φ _k,k−1(x′) and Φ _k+1,k (x′)≤Φ _k+1,k (x)=+∞. Assumption 1 implies that both inequalities are actually equalities, which is in contradiction with the fact that $x'\in\mathcal{X}_{k}$.

2.3 B.3 Proof of Proposition 3

Under Assumption 1, the regression function η is an optimal scoring function (see Theorem 1(3)). Using the fact that $\phi_{k+1,k}\in\mathcal{S}^{*}_{k+1,k}$ combined with Theorem 1(4), we obtain $\tau(s^{*}_{k},\eta)=1$ for k=1,…,K−1. As $\eta\in\mathcal{S}_{1}$, it achieves the maximum over the class $\mathcal{S}_{1}$, yielding (2). Hence, for any median scoring rule $\bar{s}$, we have $\tau(s^{*}_{k},\bar{s})=1$ for k∈{1,…,K−1}, i.e. $\bar {s}\in\mathcal{S}^{*}_{k+1,k}$ for k∈{1,…,K−1}, and thus $\bar {s}\in\mathcal{S}^{*}$.

2.4 B.4 Proof of Proposition 4

This results from the change of parameters: α=F _s,1(t ₁) and γ=1−F _s,3(t ₂).

2.5 B.5 Proof of Lemma 1

(1)⇒(2) If ROC(s,α,γ)>0 using Proposition 4, we get t ₁<t ₂, α=F _s,1(t ₁) and γ=1−F _s,3(t ₂). Using the definition of the ROC curve and t ₁<t ₂, we have $\mathrm{ROC}_{f_{1},f_{3}}(s,1-\gamma) =1-F_{s,3}(t_{1})>1-F_{s,3}(t_{2})=\gamma$. (2)⇒(1) If $\mathrm{ROC}_{f_{1},f_{3}}(s,1-\gamma) >\gamma$ then 1−F _s,3(t ₁)>1−F _s,3(t ₂) so t ₁<t ₂, and F _s,2(t ₂)−F _s,2(t ₁)>0. This yields the desired result.

2.6 B.6 Proof of Theorem 1

Let $(s,s^{*})\in\mathcal{S}\times\mathcal{S}^{*}$. Since, in particular, the scoring function s ^∗ belongs to the set $\mathcal{S}^{*}_{1,3}$, we have $\mathrm{ROC}_{F_{1},F_{3}}(s^{*},1-\alpha)\geq\mathrm {ROC}_{F_{1},F_{3}}(s,1-\alpha)$ for all α∈[0,1]. Hence, as the desired bound obviously holds true on the set $\{(\alpha,\gamma){:}\; \gamma> \mathrm{ROC}_{F_{1},F_{3}}(s^{*},1-\alpha )\} \subset\{ (\alpha,\gamma){:}\; \gamma> \mathrm{ROC}_{F_{1},F_{3}}(s,1-\alpha)\}$, we place ourselves on the complementary set $\{(\alpha,\gamma){:}\; \gamma \leq \mathrm{ROC}_{F_{1},F_{3}}(s^{*},1-\alpha)\}$, on which we have

The terms on the right hand side of the equation are both nonnegative, since s ^∗ lies in $\mathcal{S}^{*}_{1,2}$ and $\mathcal{S}^{*}_{3,2}$ respectively (observing that, whatever the two distributions H and G on ℝ and for any $s\in\mathcal{S}$ and (α,β)∈[0,1]², we have: ROC _H,G (s,α)≤β⇔α≤ROC _G,H (s,β)). The first part of the result is thus established.

Suppose that there exists $s^{*}\in\mathcal{S}$ such that, for any $s\in\mathcal{S}$, we have: ∀(α,γ)∈[0,1]²,

$$ \mathrm{ROC}\bigl(s^*,\alpha,\gamma\bigr)\geq\mathrm{ROC}(s, \alpha,\gamma). $$

(9)

Observe that, if $\gamma>\mathrm{ROC}_{f_{1},f_{3}}(s^{*},1-\alpha)$, this implies that $\gamma>\mathrm{ROC}_{f_{1},f_{3}}(s,1-\alpha)$, whatever (α,γ). It then follows that $s^{*}\in\mathcal{S}^{*}_{1,3}$. Now the fact that s ^∗ belongs to $\mathcal{S}^{*}_{1,2}$ (respectively, to $\mathcal{S}^{*}_{1,3}$) straightforwardly result from Eq. (9) with β=0 (respectively, with α=1).

2.7 B.7 Proof of Proposition 5

We denote by $\bar{E}=\mathcal{X}\setminus E$ the complementary set of any subset $E\subset\mathcal{X}$ and set $m_{1}(x)={\mathbb{I}}\{x\in \bar {R}^{*(1)}_{\alpha }\}-{\mathbb{I}}\{x\in\bar{R}^{(1)}_{s,\alpha}\}$ and $m_{3}(x)={\mathbb{I}}\{x\in R^{*(3)}_{1-\gamma}\}-{\mathbb{I}}\{x\in R^{(3)}_{s,1-\gamma}\}$ for α∈[0,1]. On the set $\{(\alpha,\gamma){:}\; \gamma\leq\mathrm{ROC} _{f_{1},f_{3}}(s^{*},1-\alpha)\}$, we may then write:

$$\mathrm{ROC}\bigl(s^*,\alpha,\gamma\bigr)-\mathrm{ROC}(s,\alpha ,\gamma)\leq-\mathbb{E} \bigl[m_{1}(X)|Y=2\bigr]-\mathbb{E}\bigl[m_{3}(X)|Y=2\bigr]. $$

Considering the first ROC curve deficit, we have:

$$-\mathbb{E}\bigl[m_{1}(X)|Y=2\bigr]= -\frac{p_{1}}{p_{2}}\mathbb{E} \biggl[m_{1}(X)\frac{\eta_{2}(X)}{\eta_{1}(X)}\biggm|Y=1 \biggr]. $$

Then we add and subtract $\frac{\eta_{3}(x)}{\eta_{1}(x)} -\frac {1-Q^{(1)}(\eta_{1},\alpha)}{Q^{(1)}(\eta_{1},\alpha)}$, this leads to:

By definition of s ^∗, the second term on the right hand side of the equation above is equal to

$$\frac{p_{3}}{p_{2}}\mathbb{E}\bigl[ m_{1}(X)|Y=3\bigr]= \mathrm {ROC}_{f_1,f_3}(s,1- \alpha)-\mathrm{ROC}_{f_1,f_3}\bigl(s^*,1-\alpha\bigr), $$

while, for the first term, by removing the conditioning with respect to Y=1 and using then the definition of Q ⁽¹⁾(η ₁,α), we get:

$$\frac{1}{p_{2}Q^{(1)}(\eta_{1},\alpha)}\mathbb{E}\bigl[ m_{1}(X) \bigl (\eta_{1}(X)-Q^{(1)}( \eta_{1},\alpha) \bigr) \bigr]=\frac{1}{p_{2}} \mathbb{E}\bigl [\bigl \vert \eta_{1}(X)-Q^{(1)}(\eta_{1},\alpha)\bigr\vert m_{1}(X) \bigr]. $$

The first part of the desired bound follows from $A\varDelta B=\bar {A}\varDelta\bar{B}$. The other ROC curve difference can be handled the same way. This leads to the desired result.

2.8 B.8 Proof of Proposition 6

We have:

which establishes the first assertion, while the second one results from:

$$\mathrm{VUS}(s) =\int_{0}^1\int_0^{1} \mathrm{d}\alpha\, \mathrm{d}\gamma=1. $$

2.9 B.9 Proof of Proposition 8

The result simply follows from integration over (α,γ)∈[0,1]² of the inequality stated in Theorem 1.

2.10 B.10 Proof of Proposition 9 (sketch of)

This result simply derives from Proposition 4 in Clémençon and Vayatis (2009b), applied to the bipartite ranking subproblems related to the pairs (k, k+1), with 1≤k<K.

2.11 B.11 Proof of Theorem 2

Let $(s,s^{*})\in\mathcal{S}\times\mathcal{S}^{*}$. Notice that, as $s^{*}\in\mathcal{S}^{*}_{1,3}$, we have $\{(\alpha,\gamma){:}\; \gamma\leq\mathrm {ROC}_{f_{1},f_{3}}(s,1-\alpha )\} \subset\{(\alpha,\gamma){:}\; \gamma\leq\mathrm{ROC} _{f_{1},f_{3}}(s^{*},1-\alpha)\}$, so that

Integrating over (α,γ)∈[0,1]² then yields the desired bound, using the fact that, for any $s\in\mathcal{S}_{0}$, $\int_{\gamma=0}^{1}\mathrm{ROC}_{f_{3},f_{2}}(s,\gamma)\,\mathrm {d}\gamma =1-\mathrm{AUC}_{f_{2},f_{3}}(s)$.

2.12 B.12 Proof of Proposition 10 (sketch of)

Observe that this result corresponds to Corollary 8 in Clémençon et al. (2008), applied to the regression function obtained when conditioning upon the event Y∈{k,k+1}, 1≤k<K. We refer to the argument of the latter.

2.13 B.13 Proof of Proposition 11

Recall that τ(s ₁,s ₂)=1−2d _τ (s ₁,s ₂), where d _τ (s ₁,s ₂) is given by:

Observe first that, for all $s\in\mathcal{S}_{0}$, $\mathrm {AUC}_{f_{1},f_{2}}(s)$ may be written as:

Notice also that, using Jensen’s inequality, one easily obtain that the quantity $2p(1-p)\vert\mathrm{AUC}_{f_{1},f_{2}}(s_{1})-\mathrm {AUC}_{f_{1},f_{2}}(s_{2})\vert$ is bounded by the expectation of the random variable

which is equal to d _τ (s ₁,s ₂)=(1−τ(s ₁,s ₂))/2. This proves the assertion.

2.14 B.14 Proof of Proposition 12

Set $\varGamma_{s}=\{(x,x')\in\mathcal{X}^{2}{:}\; (\zeta(x)-\zeta (x'))(s(x)-s(x'))< 0\}$. We have, for all real valued scoring functions $(s,s^{*})\in\mathcal{S}\times\mathcal{S}_{1,2}^{*}$:

$$d_{\tau}\bigl(s,s^*\bigr)\leq\mathbb{P} \bigl\{\bigl(X,X' \bigr)\in\varGamma_{s} \bigr\}+\frac {1}{2}\mathbb{P}\bigl\{s(X)=s \bigl(X'\bigr)\bigr\}. $$

Recall also that

see Example 1 in Clémençon et al. (2008) for instance.

Observe that Hölder inequality combined with the noise condition shows that the quantity $\mathbb{E}\ [{\mathbb{I}}\{(X,X')\in \varGamma_{s}\}]$ is bounded by

$$\mathbb{E}\bigl[\bigl|\zeta(X)-\zeta\bigl(X'\bigr)\bigr|\cdot {\mathbb{I} }\bigl\{ \bigl(X,X'\bigr)\in\varGamma_s\bigr\} \bigr]^{a/(1+a)}c^{^{1/(1+a)}}. $$

In addition, we have

and the upper bound can be easily seen as larger than $\mathbb{E} [\mathbb{I}\{s(X)=s(X')\}\cdot\vert\zeta(X)-\zeta(X') ]/2$. Therefore, using the same Hölder argument as above, we obtain that

Combining the bounds above, the concavity of t↦t ^a/(1+a) permits to finish the proof.

2.15 B.15 Proof of Theorem 3

Let $(s^{(1)}_{n}, s^{(2)}_{n})$ be a sequence of real-valued scoring functions in $\mathcal{S}_{1}$ such that, as n→∞, $\mathrm{AUC}_{f_{1},f_{2}}(s^{(1)}_{n})\rightarrow\mathrm {AUC}^{*}_{f_{1},f_{2}}$ and $\mathrm{AUC}_{f_{2},f_{3}}(s^{(2)}_{n})\rightarrow\mathrm{AUC}^{*}_{f_{2},f_{3}}$. Here we consider the following consensus measure: $\forall s\in \mathcal{S}_{1}$,

$$\varDelta_n(s)=d_{\tau} \bigl(s,s_n^{(1)} \bigr)+d_{\tau} \bigl(s,s_n^{(2)} \bigr). $$

Let $s^{*}\in\mathcal{S}_{1}\cap\mathcal{S}^{*}$. Denote by $d_{\tau _{{1,2}}}$ the Kendall tau distance when X∼(p ₁/(1−p ₃))F ₁+(p ₂/(1−p ₃))F ₂. Proposition 11, combined with the triangular inequality applied to the pseudo-distance $d_{\tau_{1,2}}$, implies that

The desired result follows from Proposition 12 combined with the AUC-consistency assumptions.

2.16 B.16 Proof of Proposition 13

By virtue of Theorem 2, we have:

$$\mathrm{VUS}^*-\mathrm{VUS}(\widehat{\eta}) \leq\bigl( \mathrm {AUC}^*_{f_1,f_2}- \mathrm{AUC}_{f_1,f_2}(\widehat{\eta}) \bigr) + \bigl( \mathrm {AUC}^*_{f_2,f_3}- \mathrm{AUC}_{f_2,f_3}(\widehat{\eta}) \bigr). $$

Considering the first term on the right hand side of the equation above, we have:

$$\mathrm{AUC}^*_{f_1,f_2}- \mathrm{AUC}_{f_1,f_2}(\widehat{\eta })=\frac {1}{2p_{1}p_{2}}\mathbb{E} \bigl[\bigl|\eta_{1}(X)\eta_{2}\bigl(X'\bigr)- \eta_{1}\bigl(X'\bigr)\eta_{2}(X)\bigr|\cdot{\mathbb{I}}\bigl \{\bigl(X,X'\bigr)\in\varGamma\bigr\}\bigr], $$

where

$$\varGamma=\bigl\{\bigl(x,x'\bigr)\in\mathcal{X}^2{:}\; \bigl( \eta(x)-\eta\bigl(x'\bigr)\bigr) \bigl(\widehat{\eta }(x)-\widehat{ \eta}\bigl(x'\bigr)\bigr)<0\bigr\}. $$

By using the triangular inequality and Lemma 2, one may establish that: $\forall(x,x')\in\mathcal{X}^{2}$, ∀i∈{1,2,3},

$$\bigl|\eta_{i}(x)-\eta_{i}\bigl(x'\bigr)\bigr|<\bigl|\eta (x)-\eta\bigl(x'\bigr)\bigr|. $$

Then, we get:

$$\mathrm{AUC}^*_{f_1,f_2}- \mathrm{AUC}_{f_1,f_2}(\widehat{\eta })\leq\frac {1}{2p_{1}p_{2}} \mathbb{E}\bigl[\bigl|\eta(X)-\eta\bigl(X'\bigr)\bigr|{\mathbb {I}}\bigl\{ \bigl(X,X' \bigr)\in\varGamma\bigr\}\bigr]. $$

But, one may easily check that, if (x,x′)∈Γ, then

$$\bigl|\eta(x)-\eta\bigl(x'\bigr)\bigr|\leq\bigl|\eta (x)-\widehat{\eta}(x)\bigr|+ \bigl|\eta\bigl(x'\bigr)-\widehat{\eta}\bigl(x'\bigr)\bigr|. $$

As the same argument can be applied to the second AUC difference, this gives the desired result.