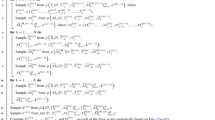Causal mediation analysis on failure time outcome without sequential ignorability

Abstract

Mediation analysis is an important topic as it helps researchers to understand why an intervention works. Most previous mediation analyses define effects in the mean scale and require a binary or continuous outcome. Recently, possible ways to define direct and indirect effects for causal mediation analysis with survival outcome were proposed. However, these methods mainly rely on the assumption of sequential ignorability, which implies no unmeasured confounding. To handle the potential confounding between the mediator and the outcome, in this article, we proposed a structural additive hazard model for mediation analysis with failure time outcome and derived estimators for controlled direct effects and controlled mediator effects. Our methods allow time-varying effects. Simulations showed that our proposed estimator is consistent in the presence of unmeasured confounding while the traditional additive hazard regression ignoring unmeasured confounding produces biased results. We applied our method to the Women’s Health Initiative data to study whether the dietary intervention affects breast cancer risk through changing body weight.

Appendices

Appendix A: Proof for Theorem 1

Here we first list the regularity conditions for the proof.

• $\varvec{\varTheta }(t)$ belong to a compact range of support and with the true value $\varvec{\varTheta }_0(t)$ in the interior.

• The joint density of observed variables has third order partial derivatives for $\varvec{\varTheta }$.

• Z, M and $\varvec{X}$ are bounded.

• $S_C(t|z,m,\varvec{x})$ and $S(t|z,m,\varvec{x})$ is bounded from 0.

Here, we will show the above conditions combined with Assumptions 1–9 is sufficient condition for locally (globally if stronger version of assumption 8 hold) identifiability of the parameter $\varvec{\varTheta }$ from the estimating equation (4) with $R(\varvec{X})=I_{n_i}$ and some $A(Z,\varvec{X},t)$. For simplicity, we simply denote the summand of the right hand side of Eq. (4) as $F_i(\varvec{\varTheta })$. Since the estimation of censoring survival distribution does not depend on $\varvec{\varTheta }$ and can be identified and consistently estimated. So for the proof below, we will treat $S_C(t|z,m,\varvec{x})$ as known. We will use the following steps to show the identifiability for each time point t and thus we will omit the notation t below. For any two parameters $\varvec{\varTheta }_1$ and $\varvec{\varTheta }_2$ that result in same distribution of observed variables, we will have

$$\begin{aligned} 0=E_{\varvec{\varTheta }_1}F_i(\varvec{\varTheta }_1)=E_{\varvec{\varTheta }_2}F_i(\varvec{\varTheta }_1). \end{aligned}$$

Also, we know that $E_{\varvec{\varTheta }}F_i(\varvec{\varTheta })=0$ for any $\varvec{\varTheta }$. So we have

$$\begin{aligned} 0=E_{\varvec{\varTheta }_2}F_i(\varvec{\varTheta }_1)=E_{\varvec{\varTheta }_2}F_i(\varvec{\varTheta }_2). \end{aligned}$$

So to prove that $\varvec{\varTheta }_1=\varvec{\varTheta }_2$, we will just need to show $0=E_{\varvec{\varTheta }_2}F_i(\varvec{\varTheta })$ have unique solution. It is suffice to show that the derivative of $E_{\varvec{\varTheta }_2}F_i(\varvec{\varTheta })$ is positive definite. For local identifiability, as we assume the derivative is positive definite at $\varvec{\varTheta }_0$ and the derivative is continuous with respect to $\varvec{\varTheta }$, so there exists a region contain $\varvec{\varTheta }_0$ such that the derivative above is positive definite at any value within the value, this is sufficient for the locally identifiability hold. For the global identifiability, the assumption 9 tells us that the derivative is positive definite at any $\varvec{\varTheta }$.

Appendix B: Proof for Theorem 2

Here we prove that our estimator is regular and asymptotically linear (RAL) for a fixed time point t and thus we simply denote $\varvec{\varTheta }(t)$ by $\varvec{\varTheta }$ and the true value as $\varvec{\varTheta }_0$. As the estimation of the survival distribution of C does not depend on $\varvec{\varTheta }$ and we assumed that a regular asymptotic linear (RAL) estimator is used. By definition of RAL, we have

$$\begin{aligned} \sqrt{n}(\hat{S}_C(t|z,m,\varvec{x})-S_C(t|z,m,\varvec{x}))=n^{-1/2} \sum _i\tilde{\phi }_{i}(t|z,m,\varvec{x})+o_p(1). \end{aligned}$$

By delta method and the assumption that $S_C(t)$ is bounded away from 0, we have

$$\begin{aligned} \sqrt{n}(\hat{S}_C^{-1}(t|z,m,\varvec{x})-S_C^{-1}(t|z,m,\varvec{x}))= & {} -n^{-1/2} \sum _iS_C^{-2}(t|z,m,\varvec{X})\phi _{i}(t|z,m,\varvec{x})\\&\quad +\,o_p(1)\\= & {} \,n^{-1/2}\sum _i\phi _{i}(t|z,m,\varvec{x})+o_p(1). \end{aligned}$$

For simplicity, we denote the estimating equation (4) for $\varvec{\varTheta }$ as below:

$$\begin{aligned} n^{-1}\sum _i\sum _j \hat{S}_C^{-1}(t|Z_{ij},M_{ij},\varvec{X}_{ij})F_{ij}(\varvec{\varTheta }) \end{aligned}$$

where $F_{ij}(\varvec{\varTheta })=F(T^{*}_{ij},Z_{ij},M_{ij},\varvec{X}_{ij},\varvec{\varTheta })$. Also, we denote $\hat{S}_C^{-1}(t|Z_{ij},M_{ij},\varvec{X}_{ij})$ as $\hat{S}_{Cij}$ and $S_C^{-1}(t|Z_{ij},M_{ij},\varvec{X}_{ij})$ as $S_{Cij}$ for notation simplicity.

We will first prove the consistency of $\hat{\varvec{\varTheta }}$.

$$\begin{aligned} 0= & {} n^{-1}\sum _i\sum _j \hat{S}_{Cij}^{-1}(t)F_{ij}(\hat{\varvec{\varTheta }})\\= & {} n^{-1}\sum _i\sum _j S_{Cij}^{-1}(t)F_{ij}(\hat{\varvec{\varTheta }})+n^{-1}\sum _i\sum _j [\hat{S}_{Cij}^{-1}(t)-S_{Cij}^{-1}(t)]F_{ij}(\hat{\varvec{\varTheta }})\\ \end{aligned}$$

Since $\hat{S}_{C}^{-1}(t|z,m,\varvec{x})-S_{C}^{-1}(t|z,m,\varvec{x})$ converge to 0 uniformly over t, z, m and $\varvec{x}$ and $F_{ij}(\hat{\varvec{\varTheta }})$ is bounded in probability, we know that the second term converge to 0 in probability. By regularity condition, we can take derivative over $F_{ij}(\hat{\varvec{\varTheta }})$ and thus the first term become

$$\begin{aligned} n^{-1}\sum _i\sum _j S_{Cij}^{-1}(t)F_{ij}(\hat{\varvec{\varTheta }})= & {} n^{-1}\sum _i\sum _j S_{Cij}^{-1}(t)F_{ij}(\varvec{\varTheta }_0)\\&+\,n^{-1}\sum _i\sum _j S_{Cij}^{-1}(t)\frac{\partial F_{ij}(\varvec{\varTheta }^{*})}{\partial \varvec{\varTheta }}(\hat{\varvec{\varTheta }}-\varvec{\varTheta }_0)\\= & {} o_p(1)+\frac{\partial E(\sum _j S_{Cij}^{-1}(t)F_{ij}(\varvec{\varTheta }^{*}))}{\partial \varvec{\varTheta }}(\hat{\varvec{\varTheta }}-\varvec{\varTheta }_0) \end{aligned}$$

where $\varvec{\varTheta }^{*}$ is between $\varvec{\varTheta }_0$ and $\hat{\varvec{\varTheta }}$. Under the locally identifiability assumption, we have $\frac{\partial E(\sum _j S_{Cij}^{-1}(t)F_{ij}(\varvec{\varTheta }^{*}))}{\partial \varvec{\varTheta }}$ is positive definite, Since the derivative is continuous respect to $\varvec{\varTheta }$, we have $\frac{\partial E(\sum _j S_{Cij}^{-1}(t)F_{ij}(\varvec{\varTheta }^{*}))}{\partial \varvec{\varTheta }}$ is positive definite when $\varvec{\varTheta }^{*}$ is within certain range of $\varvec{\varTheta }_0$. So we have there exist a sequence of root $\hat{\varvec{\varTheta }}$ such that $\hat{\varvec{\varTheta }}-\varvec{\varTheta }_0=o_p(1)$. Or if we use the assumption of global identifiability, the derivative is positive definite for all $\varvec{\varTheta }$ and thus we have $\hat{\varvec{\varTheta }}-\varvec{\varTheta }_0=o_p(1)$. So we obtain the consistency of $\hat{\varvec{\varTheta }}$. Note that $\hat{S}(t|z,m,\varvec{x})$ and $E_n(F_{ij}(\varvec{\varTheta }))$ are $\sqrt{n}-$ consistency, so $\forall d<1/2$, $n^d(\hat{\varvec{\varTheta }}-\varvec{\varTheta }_0)=o_p(1)$.

Now we find the asymptotic expansion of $\varvec{\varTheta }$.

$$\begin{aligned} 0= & {} n^{-1/2}\sum _i\sum _j \hat{S}_{Cij}^{-1}(t)F_{ij}(\hat{\varvec{\varTheta }})\\= & {} n^{-1/2}\sum _i\sum _j S_{Cij}^{-1}(t)F_{ij}(\varvec{\varTheta }_0)+n^{-1/2}\sum _i\sum _j S_{Cij}^{-1}(t)\frac{\partial F_{ij}}{\partial \varvec{\varTheta }}(\hat{\varvec{\varTheta }}-\varvec{\varTheta }_0)\\&+\,n^{-1/2}\sum _i\sum _j \big [\hat{S}_{Cij}^{-1}(t)-S_{Cij}^{-1}(t)\big ]F_{ij}(\hat{\varvec{\varTheta }}) +o\big (\sqrt{n}\Vert \hat{\varvec{\varTheta }}-\varvec{\varTheta }_0\Vert \big ) \end{aligned}$$

Here we just need to expand the third term as below

$$\begin{aligned} n^{-1/2}\sum _i\sum _j\big [\hat{S}_{Cij}^{-1}(t)-S_{Cij}^{-1}(t)\big ]F_{ij}(\hat{\varvec{\varTheta }})= & {} n^{-1/2}\sum _i\sum _j \big [\hat{S}_{Cij}^{-1}(t)-S_{Cij}^{-1}(t)\big ]\\&\quad \times \,F_{ij}(\varvec{\varTheta }_0)\,+\,o_p(1)\\= & {} n^{-3/2}\sum _i\sum _j \sum _{l}[\phi _{l}(t|Z_{ij},M_{ij},\varvec{X}_{ij})]\\&\quad \times \,F_{ij}(\varvec{\varTheta }_0)\,+\,o_p(1)\\= & {} n^{-1/2}\sum _{l} [n^{-1}\sum _i\sum _j\phi _{l}(t|Z_{ij},M_{ij},\varvec{X}_{ij})\\&\quad \times \,F_{ij}(\varvec{\varTheta }_0)]\,+\,o_p(1) \end{aligned}$$

Let $E[\sum _j\phi _{l}(t|Z_{ij},M_{ij},\varvec{X}_{ij})F_{ij}(\varvec{\varTheta }_0)]=\psi _l$, then we have the quantity above is

$$\begin{aligned} n^{-1/2}\sum _{l}\psi _l+o_p(1) \end{aligned}$$

With the identification assumption, we know that

$$\begin{aligned} E\left[ \sum _jS_{Cij}^{-1}(t)\frac{\partial F_{ij}}{\partial \varvec{\varTheta }}\right] =\left[ \frac{\partial E\sum _jS_{Cij}^{-1}(t)F_{ij}}{\partial \varvec{\varTheta }}\right] \equiv \mathcal {A} \end{aligned}$$

is positive definite, so we have

$$\begin{aligned} \sqrt{n}(\hat{\varvec{\varTheta }}-\varvec{\varTheta })= & {} \mathcal {A}^{-1}(n^{-1/2}\sum _i\left[ \sum _j S_{Cij}^{-1}(t)F_{ij}(\varvec{\varTheta })+\psi _i\right] +o_p(1)\\= & {} n^{-1/2}\sum _i \varPsi _i \end{aligned}$$

where $\varPsi _i=\sum _j S_{Cij}^{-1}(t)F_{ij}(\varvec{\varTheta })+\psi _i$. So we have proved that our estimator is asymptotic linear at each time point t. For any finite time points, the $o_p(1)$ term in the proof above will be uniform and thus we can have that for any finite dimension, the distribution is joint normal. Then it follows that we have $\varvec{\varTheta }(t),t\in [t_1,t_2]$ converge to a Gaussian Process.

Appendix C: Proof for Theorem 3

The proof is similar to that for Theorem 2 and we will just list the general steps here. For notation simplicity, we denote the estimating equations (6) and (7) as

$$\begin{aligned} 0= & {} \sum _{i=1}^n S_{1i}(\varvec{\varTheta },\varvec{\beta },\hat{S}(t|z))\\ 0= & {} \sum _{i=1}^n S_{2i}(\varvec{\varTheta },\varvec{\beta },\hat{S}(t|z))\\ \end{aligned}$$

Since we have shown the estimator in Theorem 2, denoted as $\hat{\varvec{\varTheta }}^{(0)}$ consistent to $\varvec{\varTheta }$, so we have

$$\begin{aligned} \sum _{i=1}^n S_{1i}(\hat{\varvec{\varTheta }}^{(0)},\varvec{\beta },\hat{S}(t|z))\longrightarrow _p 0 \end{aligned}$$

for any $\varvec{\beta }$. We also have

$$\begin{aligned} \sum _{i=1}^n S_{2i}(\varvec{\varTheta },\varvec{\beta },\hat{S}(t|z))\longrightarrow _p ES_{2i}(\varvec{\varTheta }_0,\varvec{\beta }, S(t|z)). \end{aligned}$$

Under following additional assumptions:

• For the A(z, x, t) and R(x) we choose, Eq. 4 is bounded in probability for all $\varvec{\varTheta }$;

• The joint density of observed variables have third order partial derivatives for both $\varvec{\varTheta }$ and $\varvec{\beta }$;

• The estimating equation for $\varvec{\beta }$ have unique solution under $\varvec{\varTheta }_0$;

we know that $\hat{\varvec{\beta }}^{(1)}\longrightarrow _p \varvec{\beta }^0$. Using same argument, we can show for k-th iteration, $\hat{\varvec{\varTheta }}^{(k)}$ and $\hat{\varvec{\beta }}^{(k)}$ consistent to their true values. So if the limiting exist, then the final estimator $\hat{\varvec{\varTheta }}$ and $\hat{\varvec{\beta }}$ is consistent estimator and jointly solve estimating equations (6) and (7). Then the asymptotic normality and linear expansion can be obtained using standard Taylor expansion as used for sandwich estimator.

Appendix D: Pseudo-Code for Implementation

1.1 Appendix D.1: Pseudo Code for Table 1

• 1. Fit traditional additive hazard model to obtain $\hat{\varvec{\varTheta }}(t)$.

• 2. Fit Cox model or additive hazard regression model to obtain $\hat{S}_C(t|Z,M,X)$.

• 3. Fit regression model to obtain $E(Z|\varvec{X})$, $E[M|Z=0,\varvec{X}]$ and $E[M|Z=1,\varvec{X}]$ and compute $A(Z,\varvec{X},t)=(Z-E(Z|\varvec{X}))(E[M|Z=1,\varvec{X}]-E[M|Z=0,\varvec{X}])$.

• 4. For a series of fixed t, solve the estimation equation in (3) via quasi-Newton method starting from $\hat{\varvec{\varTheta }}(t)$ to obtain $\hat{\varvec{\varTheta }}^{(0)}(t)$.

• 5. Fit weighted linear regression of $\frac{I(T^{*}_{i}>t)}{\hat{S}_C(t|Z_{i},M_{i},\varvec{X}_{i})}\exp (\varTheta _{z}^{(k)}(t) Z_{i}+\varTheta _m^{(k)}(t)M_{i})$ on X to obtain $\varvec{\beta }^{(k+1)}(t)$.

• 6. Solve estimation equation in (5), treating $\varvec{\beta }(t)=\varvec{\beta }^{(k+1)}(t)$ as fixed to obtain $\hat{\varvec{\varTheta }}^{(k+1)}(t)$.

• 7. Repeat 4 and 5 until converge to obtain estimation with linear adjusted covariates.

• 8. Compute $\hat{\theta }$ from $\hat{\varTheta }$ using formula $\hat{\theta }_z=\hat{\varTheta }_z(t)/(t-t_z)$ and $\hat{\theta }_m=\hat{\varTheta }_m(t)/(t-t_m)$

• 9. Use Bootstrap to obtain confidence interval

1.2 Appendix D.2: Pseudo Code for Table 2

• 1. Fix a sequence of t, denoted as $t_1$, $\ldots$, $t_K$. For each $t_i$, using the algorithm in Appendix D.1 to obtain corresponding $\hat{\theta }_z(i)$ and $\hat{\theta }_m(i)$ with or without linear adjustment.

• 2. Compute standard error $se_z(i)$ and $se_m(i)$ for $\hat{\theta }_z(i)$ and $\hat{\theta }_m(i)$.

• 3. For the “select method”, let $\hat{\theta }_z$ be the $\hat{\theta }_z(i)$ such that $se_z(i)$ attains minimum among all i’s, and $\hat{\theta }_m$ be the $\hat{\theta }_m(i)$ such that $se_m(i)$ attains minimum among all i’s.

• 4. For “combine method”, let $\hat{\theta }_z=\frac{\sum _{i=1}^K se^{-1}_z(i)\hat{\theta }_z(i)}{\sum _{i=1}^K se^{-1}_z(i)}$ and $\hat{\theta }_m=\frac{\sum _{i=1}^K se^{-1}_m(i)\hat{\theta }_m(i)}{\sum _{i=1}^K se^{-1}_m(i)}$.

• 5. Use Bootstrap to obtain the confidence interval.