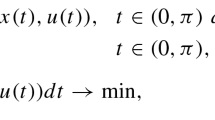Abstract
In the paper, a Lagrange optimal control problem governed by a fractional Dirichlet problem with the Riemann–Liouville derivative is considered. To begin with, based on some variational method, the existence and continuous dependence of solution to the aforementioned Dirichlet problem is investigated. Then, continuous dependence is applied to show the existence of optimal solution to the Lagrange problem. An important point is that the solution to Dirichlet problem does need to be unique; therefore, the above dependence should be understood as a continuity of some multifunction—the concept of the Kuratowski–Painlevé limit of the sequence of sets is used to formulate this property.
Similar content being viewed by others
1 Introduction
The main concepts of fractional calculus were introduced by Riemann, Abel, Dirichlet and Liouville in the nineteenth century. The rapid development of the fractional calculus, which took place at the beginning of the twenty-first century, is connected with a number of successful attempts to apply these notions in description of many real phenomena, among others in physics [1], electronics [2], mechanics [3, 4], viscoelasticity [5] and many others [6] (see also references therein). For an interesting overview of the methods and applications of fractional calculus and fractional differential equations, we refer the reader to [7].
In this paper, we investigate the problem of the existence of optimal solution to the Lagrange optimal control problem (1) governed by fractional Eq. (2) with a parameter and with a homogeneous condition. Equation (2) has a special form—a variational structure. In fact, the cost functional is minimized over the set of admissible pairs defined by minimizers of functional of action (3) for which the Euler–Lagrange equation is the mentioned in Eq. (2). However, under some convexity assumption the set of solutions to (2) coincides with the set of minimizers of functional of action (3). The motivation for such an approach is justified in Sect. 2. The main result, i.e. the existence of optimal solution, is presented in Sect. 5. However, to prove the main result we need some results on the existence and continuous dependence on parameter of the solution to fractional Eq. (2) with homogeneous Dirichlet condition. This is discussed in Sect. 4.
To be more specific, using some variational method we first prove that for a given parameter u there exists a critical point (minimum) for the functional of action (3) (see Theorem 4.1); next, that this critical point solves fractional Eq. (2) with homogeneous condition (see Theorem 4.2). Then, we investigate the problem of continuous dependence of solution on functional parameter u (see Theorem 4.4). The continuous dependence is the main tool in the proof of existence of minimum for the Lagrange optimal control problem (1), what is the last but not least result of this paper. It is worth emphasizing that to show the above dependence we use a very interesting approach. Namely, the solution to the investigated fractional Euler–Lagrange Eq. (2) does not need to be unique; therefore, we shall use an additional tool to describe such a dependence. We use here the notion of the upper limit of the sequence of sets in Kuratowski–Painlevé sense. The above approach was initiated by Walczak [8] and developed by his collaborators.
On the other hand, the continuous dependence of solutions on the parameter u is quite important from the practical point of view. Following Courant and Hilbert (see [9]), we say that: “A mathematical problem which is to correspond to physical reality should satisfy the following basic requirements: (1) The solution must exist. (2) The solution should be uniquely determined. (3) The solution should depend continuously on the data (requirement of stability). (...) The third requirement, particularly incisive, is necessary if the mathematical formulation is to describe observable natural phenomena. Data in nature cannot possibly be conceived as rigidly fixed; the mere process of measuring them involves small errors.”
Some results on the existence of solutions to the special case of fractional Euler–Lagrange equation with homogeneous Dirichlet conditions were published in [10]. However, the assumptions made by the author in [10] are more stronger. On the other hand, our paper can be considered as a continuation of the research initiated by Loïc Bourdin. In fact, in [11] Bourdin proved theorem on the existence of minimizers for the analogous functional of action which generates the same, up to a parameter u, Euler–Lagrange equations as we consider in the presented paper. Nevertheless, in contrast to [11], assumption (A4) on the coercivity of the integrand f made in our paper is a bit weaker, and we investigate the problem with Dirichlet conditions instead of the Cauchy problem. Furthermore, we study the problem which depends on some functional parameter u that can be viewed as a control. From this point of view, our results can be treated as a part of fractional optimal control theory. Recently, many papers have been published on the control theory for fractional systems. For instance, optimal control problems were investigated in [12–14]. In [15], the author proves fractional version of Pontryagin principle. Some interesting results concerning controllability, reachability and stability of fractional system can be also found in [16–19].
2 Motivations
As we mentioned, the main result of the paper is the existence of optimal solution to the following Lagrange optimal control problem
where \(f=f\left( t,x,y,u\right) , L=L\left( t,x,y,u\right) :\left[ a,b\right] \times {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\times {\mathbb {R}} ^{m}\rightarrow {\mathbb {R}}\); \(D_{a+}^{\alpha }x\) and \(D_{b-}^{\alpha }x\) stand, respectively, for the left and the right Riemann–Liouville fractional derivative of a function x. It should be emphasized that the equation
has a special variational structure—it is an Euler Lagrange equation for the following functional of action
In the classical theory of optimal control, most authors consider Lagrange optimal control problems governed by a differential equation of the first order. However, in physics there are many phenomena for which natural description is a second-order equation (note, for example, that Newton’s equation is of the second order). Most, but not all, of them can be transformed to the first-order equation. However, some times it is more convenient to use the second-order equation, and this is especially true for Dirichlet problems or periodic problems (i.e. pendulum equation) and, of course, for a variational description of the phenomena. In other words, our approach describes the situation where the argument \(\left( x,u\right) \) of the functional \({\mathcal {L}}\) is such that x is a critical point (minimizer) of a functional of action \({\mathcal {J}}_{u},\) for a given parameter u. The physical motivation for considering such a type of problem is the fact that the functional \({\mathcal {J}}_{u}\) can be interpreted as a fractional generalization of the total energy. Indeed, for \(\alpha =1\) one has \(D_{b-}^{\alpha } D_{a+}^{\alpha }x=-\ddot{x}\) and, for the special case of f, i.e. \(f(t,x,y,u)=\frac{1}{2}|y|^{2}+F(t,x),\)
The Euler–Lagrange equation for such a case has the form of the classical Newton’s equation
or
for a fractional counterpart. In this way, the approach proposed in the paper uses the application of variational methods to the optimization. The cost functional \({\mathcal {L}}\) is considered over the set of “states of lowest energy.” The function u in (1) can be viewed as a parameter, which can be used to control the physical system. Consequently, problem (1) describes the situation where the main goal is to control a given object in such a way that its state of lowest energy minimizes the cost functional \({\mathcal {L}}\).
The above approach was investigated among others in [8] where the author considers the classical case of problem (1) and in [20] where the interpretations connected with biological oscillators, systems with variable mass and Schrödinger equation are presented. Also in [21] the author proves maximum principle for the classical counterpart of (1).
Finally, let’s note that the fractional counterpart of the first-order equation with parameter is the equation
Equation (2) involves both the left and the right fractional derivatives and cannot be transformed to the equation of the type of (4). This is a consequence of the application of the fractional fundamental lemma see [22, Lemma 2]).
The problem of the existence of solutions to the equation
was investigated among others in [10], where the author interprets it as the equation of fractional forced pendulum. The linear case of (5), i.e.
describes so-called fractional oscillator (see [10, 23–25] ), and it can be applied to the problem of emptying a silo (see [26]). Also, some numerical results for (6) can be found in [27]. We believe that the next natural step is to consider optimal problem with cost functional (of a Lagrange or Bolza type) governed by Eq. (5).
3 Basic Notions and Problem Formulation
Many authors often use different symbols and definitions of fractional integrals and derivatives; therefore, for the convenience of the reader, we repeat some basic definitions and properties.
It is said that \(x\in L^{1}\left( \left[ a,b\right] ,{\mathbb {R}}^{n}\right) \) possesses the left Riemann–Liouville derivative \(D_{a+}^{\alpha }x\) of order \(\alpha \in ] 0,1 [ \) on the interval [a, b], iff the function
is absolutely continuous on [a, b]. In such a case, \(D_{a+}^{\alpha } x:=\frac{d}{dt}(I_{a+}^{1-\alpha }x)\).
Similarly, it is said that \(x\in L^{1}\left( \left[ a,b\right] ,{\mathbb {R}}^{n}\right) \) possesses the right Riemann–Liouville derivative \(D_{b-}^{\alpha }x\) of order \(\alpha \in ] 0,1[ \) on the interval [a, b] iff the function
is absolutely continuous on [a, b]. We put \(D_{b-}^{\alpha }x:=-\frac{d}{dt}(I_{b-}^{1-\alpha }x)\).
For \(\alpha >0 \) and \(x\in L^{1}\left( \left[ a,b\right] ,{\mathbb {R}} ^{n}\right) \) the functions \(I_{a+}^{\alpha }x\) and \(I_{b-}^{\alpha }x\) defined by (7) and (8) are called the left and the right Riemann–Liouville integral of order \(\alpha \) of x. If we additionally put \(I_{a+}^{0}x=x\) and \(I_{b-}^{0}x=x,\) for \(x\in L^{1}\left( \left[ a,b\right] ,{\mathbb {R}}^{n}\right) \) we may extend the notion of fractional derivatives to the order \(\alpha =1.\)
By \(AC_{a+}^{\alpha ,p}\), \(p\ge 1\) let us denote the set of all functions \(x:\left[ a,b\right] \rightarrow {\mathbb {R}}^{m}\) such that there exist a constant \(c\in {\mathbb {R}}^{m}\) and a function \(\varphi \in \) \(L^{p} ([a,b],{\mathbb {R}}^{m})\) such that
Similarly by \(AC_{b-}^{\alpha ,p}\), we denote the set of all functions \(x:\left[ a,b\right] \rightarrow {\mathbb {R}}^{m}\) such that there exist a constant \(d\in {\mathbb {R}}^{m}\) and a function \(\psi \in \) \(L^{p}([a,b],{\mathbb {R}} ^{m})\) such that
It can be proved (see [22]) that a function x possesses a left-sided Riemann–Liouville derivative \(D_{a+}^{\alpha }x\) on the interval \(\left[ a,b\right] \) if and only if \(x\in AC_{a+}^{\alpha ,1}.\) Moreover,
where x is of the form (9). Similarly a function x possesses a right-sided Riemann–Liouville derivative \(D_{b-}^{\alpha }x\) on the interval \(\left[ a,b\right] \) if and only if \(x\in AC_{b-}^{\alpha ,1} \), and we have that
where x is of the form (10).
Let for \(p>1\) and \(\alpha >\frac{1}{p}\)
Here, the symbol \(I_{a+}^{\alpha }\left( L^{p}\right) \) stands for the image of the space \(L^{p}\) of the operator \(I^{\alpha }_{a+}\). It is known (see [11]), that since \(\alpha >\frac{1}{p}\), it follows that any \(x\in I_{a+}^{\alpha }\left( L^{p}\right) \) is a continuous function (even Hölder continuous on ] a, b] with exponent \(\alpha -\frac{1}{p}\)); thus, it makes sense to consider the pointwise condition \(x\left( b\right) =0.\) Also, in [11] the author proved that \(\lim _{t\downarrow a}\left( I_{a+}^{\alpha } \varphi \right) (t) =0\) for any \(\varphi \in L^{p},\); consequently, any \(x\in I_{a+}^{\alpha }\left( L^{p}\right) \) (which belongs to \(L^{p}\) in general) can be treated as a continuous function such that \(x\left( a\right) =0.\) Moreover, the space \(I_{a+}^{\alpha }\left( L^{p}\right) \) with the norm
is a reflexive Banach space (see [11]).
Another interesting and useful property of the space \(I_{a+}^{\alpha }\left( L^{p}\right) \) describes
Lemma 3.1
(see [11]) Assume that \(\alpha \in {]} \frac{1}{p},1{[} \) then the embedding
is compact. Moreover, for every \(x\in I_{a+}^{\alpha }\left( L^{p}\right) \) we have
and
where \(\frac{1}{p}+\frac{1}{q}=1.\)
As a consequence of Lemma 3.1, we have, among others, that the space \(H_{0}^{\alpha ,p}\) with the norm \(\Vert \cdot \Vert \) is a reflexive Banach space as the closed subspace of \(I_{a+}^{\alpha }\left( L^{p}\right) \).
We now move to the main problem in this paper, namely consider the following Lagrange problem
where \(x\in H_{0}^{\alpha ,p}\) is the solution of the following Dirichlet problem
corresponding to the control u. Here \(f=f\left( t,x,y,u\right) :\left[ a,b\right] \times {\mathbb {R}}^{n}\times {\mathbb {R}}^{n}\times {\mathbb {R}} ^{m}\rightarrow {\mathbb {R}}\).
In what follows, we shall assume that the parameter \(u\in {\mathcal {U}}\), where
\(M\subset {\mathbb {R}}^{m}\) is a given bounded and convex set.
From now on, we shall assume that
-
(A1)
The functions \(f,f_{x},f_{y},f_{u}\) are of Carathéodory’s type, i.e. \(f\left( \cdot ,x,y,u\right) , f_{x}\left( \cdot ,x,y,u\right) ,f_{y}\left( \cdot ,x,y,u\right) ,f_{u}\left( \cdot ,x,y,u\right) \) are measurable for \(\left( x,y,u\right) \) and \(f\left( t,\cdot ,\cdot ,\cdot \right) \), \(f_{x}\left( t,\cdot ,\cdot ,\cdot \right) \), \(f_{y}\left( t,\cdot ,\cdot ,\cdot \right) \), \(f_{u}\left( t,\cdot ,\cdot ,\cdot \right) \) are continuous for a.e. \(t\in \left[ a,b\right] .\)
-
(A2)
The function \(f\left( t,x,\cdot ,u\right) \) is convex for a.e. \(t\in \left[ a,b\right] \) and every \(x\in {\mathbb {R}}^{n} ,u\in {\mathbb {R}}^{m}.\)
-
(A3)
There are functions \(a_{0}(\cdot )\in C\left( {\mathbb {R}}^{+},{\mathbb {R}}^{+}\right) ,\) \(b_{0}(\cdot )\in L^{1}\left( \left[ a,b\right] ,{\mathbb {R}}^{+}\right) ,\) \(c_{0}(\cdot )\in L^{q}\left( \left[ a,b\right] ,{\mathbb {R}}^{+}\right) \), where \(\frac{1}{p}+\frac{1}{q}=1\) such that
$$\begin{aligned} \left| f\left( t,x,y,u\right) \right|&\le a_{0}\left( \left| x\right| \right) \left( b_{0}\left( t\right) +\left| y\right| ^{p}\right) ,\\ \left| f_{x}\left( t,x,y,u\right) \right|&\le a_{0}\left( \left| x\right| \right) \left( b_{0}\left( t\right) +\left| y\right| ^{p}\right) ,\\ \left| f_{y}\left( t,x,y,u\right) \right|&\le a_{0}\left( \left| x\right| \right) ( c_{0}\left( t\right) +\left| y\right| ^{p-1}) ,\\ \left| f_{u}\left( t,x,y,u\right) \right|&\le a_{0}\left( \left| x\right| \right) \left( b_{0}\left( t\right) +\left| y\right| ^{p}\right) , \end{aligned}$$for a.e. \(t\in \left[ a,b\right] \) and every \(x,y\in {\mathbb {R}}^{n},\) \(u\in M\).
-
(A4)
There are constants \(a_{1}>0\), \(a_{2},b_{1},b_{2}\ge 0 \) and a function \(d_{0}(\cdot )\in L^{1}\left( [a,b],{\mathbb {R}}\right) \) such that
$$\begin{aligned} f\left( t,x,y,u\right) \ge a_{1}\left| y\right| ^{p}-b_{1}\vert y\vert - a_{2}\left| x\right| ^{p}- b_{2}\vert x\vert +d_{0}(t) \end{aligned}$$and \(a_{1}-a_{2}\frac{\left( b-a\right) ^{\alpha p}}{\left( \Gamma \left( \alpha +1\right) \right) ^{p}}>0\), for a.e. \(t\in \left[ a,b\right] \) and every \(x,y\in {\mathbb {R}}^{n},\) \(u\in M\).
Example 3.1
Let \(f:\left[ 0,1\right] \times {\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}} \rightarrow {\mathbb {R}}\) be of the form
Assume that \(\alpha =\frac{2}{3},\) \(p=2\) and \(M=\left[ -1,1\right] .\) We will show that f satisfies (A1)–(A4). It is obvious that f satisfies (A1) and (A2). Moreover,
for \(t\in \left[ 0,1\right] ,x,y\in {\mathbb {R}}\) and \(u\in \left[ -1,1\right] \). Thus, f satisfies (A3). Finally,
for \(t\in \left[ 0,1\right] ,x,y\in {\mathbb {R}}\) and \(u\in \left[ -1,1\right] \). Since
therefore \(3-\frac{9}{4\Gamma ^{2}\left( \frac{2}{3}\right) }2>0\) and f satisfies (A4).
4 Existence of Solutions and Continuous Dependence Via a Variational Method
We will prove that for any \(u\in {\mathcal {U}}\) there exists a solution \(x_{u}\in H_{0}^{\alpha ,p}\) to (11), which minimizes the functional
defined on \(H_{0}^{\alpha ,p}.\) In different words, we will prove that Eq. (11) is the Euler–Lagrange equation for \({\mathcal {J}}_{u}\), and it possesses a solution. From now on, we assume that \(p>1\) and \(\alpha \in {]} \frac{1}{p},1{[} \).
To begin with, we will show that the functional \({\mathcal {J}}_{u}\) possesses at least one minimum. We have
Proposition 4.1
For any \(u\in {\mathcal {U}}\), the functional \({\mathcal {J}}_{u}\) is sequentially weakly lower semicontinuous.
The above property is an easy consequence of the convexity assumption (A2), Lemma 3.1 and application of the Lebesgue-dominated convergence theorem.
Theorem 4.1
For any fixed \(u\in {\mathcal {U}}\), there exists at least one global minimizer \(x_{u}\in H_{0}^{\alpha ,p}\) for \({\mathcal {J}}_{u}\), i.e. \({\mathcal {J}}_{u}\left( x_{u}\right) =\inf _{x\in H_{0}^{\alpha ,p}} {\mathcal {J}}_{u}\left( x\right) \). Moreover, the set of all global minimizers
is bounded, i.e. there exists a ball \(B\left( 0,\rho \right) \subset H_{0}^{\alpha ,p},\) \(\rho >0\) such that \(V\subset B\left( 0,\rho \right) \).
Proof
Fix \(u\in {\mathcal {U}}\). By (A4), applying Lemma 3.1 and Hölder’s inequality we get
where \(b_{3},c_{3}\) are some constant which do not depend on u. Since \( a_{1}-a_{2}\frac{\left( b-a\right) ^{\alpha p}}{\left( \Gamma \left( \alpha +1\right) \right) ^{p}}>0\) (cf. (A4)), therefore the functional \({\mathcal {J}} _{u}\) is coercive and, consequently, any minimizing sequence \(\left( x_{u}^{k}\right) \) for \({\mathcal {J}}_{u}\) (i.e. such a sequence that \( {\mathcal {J}}_{u}\left( x_{u}^{k}\right) \rightarrow \inf _{x\in H_{0}^{\alpha ,p}}{\mathcal {J}}_{u}\left( x\right) \)) is bounded. By the reflexivity of \( H_{0}^{\alpha ,p}\), the sequence \(\left( x_{u}^{k}\right) \) possesses a cluster point \(x_{u}\in H_{0}^{\alpha ,p}\) (in the weak topology), and finally passing, if necessary to a subsequence, and applying Proposition 4.1, we get
This means that \(x_{u}\) is a global minimizer for \({\mathcal {J}}_{u}.\) For the proof of the second part, let us notice that the function w defined in (14) does not depend on u. Let \(\omega :=a_{0}\left( 0\right) \int _{a}^{b}b_{0}\left( t\right) dt\ge {\mathcal {J}}_{u}\left( 0\right) \) (cf. (A3)). Then, for any \(u\in {\mathcal {U}}\) and any minimizer \(x_{u}\in H_{0}^{\alpha ,p}\) for \({\mathcal {J}}_{u}\), we have by (14) that
From the fact that \(\lim _{\left\| x\right\| \rightarrow \infty }w\left( x\right) =\infty \) and w does not depend on u, we get that there is \(\rho >0\) such that \(V\subset B\left( 0,\rho \right) \). \(\square \)
Now, we are ready to prove theorem on the existence of solutions.
Theorem 4.2
For any fixed \(u\in {\mathcal {U}}\), there exists at least one solution \(x_{u}\in H^{\alpha ,p}_{0}\) to (11), (12).
Proof
From Theorem 4.1, we have that for any \(u\in {\mathcal {U}}\) there exists at least one minimizer \(x_{u}\in H_{0}^{\alpha ,p}\) for \({\mathcal {J}}_{u}.\) It is easy to notice that thanks to (A1) and (A3) functional \({{\mathcal {J}}}_{u}\) possesses a variation \(\delta \mathcal J_{u}\left( x,h\right) \) in the Lagrange sense for any \(x\in H_{0}^{\alpha ,p}\) in any direction \(h\in H_{0}^{\alpha ,p}\) and
Consequently,
for any \(h\in H_{0}^{\alpha ,p}.\) Applying fractional fundamental lemma ([22, Lemma 2]), we get that\(f_{y}\left( \cdot ,x_u\left( \cdot \right) ,\left( D_{a+}^{\alpha }x_u\right) \left( \cdot \right) ,u\left( \cdot \right) \right) \in AC_{b-}^{\alpha ,1}\) and
The fact that \(x_u\left( a\right) =x_u\left( b\right) =\left( I_{a+}^{1-\alpha }x_u\right) \left( a\right) =0\) follows immediately from the fact that \(x_{u}\in H_{0}^{\alpha ,p}.\) \(\square \)
We have proved that for any u there exists a solution to (11), (12), which is a minimizer for \({\mathcal {J}}_{u}.\) Observe that the solution does not have to be a minimizer unless the functional \({\mathcal {J}}_{u}\) is convex. Namely, we have
Theorem 4.3
Assume instead of (A2) that the following stronger assumption is satisfied
-
(A2’)
the function \(f\left( t,\cdot ,\cdot ,u\right) \) is convex for a.e. \(t\in \left[ a,b\right] \) and every \(u\in {\mathbb {R}}^{m}.\)
Then, any solution to (11), (12) is a minimizer for \({\mathcal {J}}_{u}.\) In other words, for any \(u\in {\mathcal {U}}\) the set of solutions to (11), (12) coincides with the set of minimizers for \({\mathcal {J}}_{u}\). In particular, the set of all solutions is bounded.
On the other hand, even the solution \(x_{u}\) that minimizes \({\mathcal {J}}_{u}\) does not need to be unique in general. Therefore, to consider dependence of solution on a parameter u we have to investigate a continuity of a multifunction. Here, we use the concept of the Kuratowski–Painlevé limit of the sequence of sets.
Definition 4.1
Let \(\left( X,\tau \right) \) be a topological space and \(\left( V_{k}\right) _{k\in {\mathbb {N}}}\) be a sequence of subsets of X. The upper limit of the sequence \(\left( V_{k}\right) _{k\in {\mathbb {N}}}\) is defined as the set of all cluster points of all sequences \(\left( v_{k}\right) _{k\in {\mathbb {N}}}\) such that \(v_{k}\in V_{k}\) for \(k\in {\mathbb {N}}.\) We denote the above set by \({\text {*}}{LimSup}V_{k}.\)
Let \(\left( u_{k}\right) \subset {\mathcal {U}}\) and \(u_{0}\in {\mathcal {U}}\). Next, let
and
We have
Theorem 4.4
If \(u_{k}\rightarrow u_{0}\) in \(L^{\infty }\) then \({\text {*}}{LimSup}V_{k}\subset V_{0}\)
Proof
To begin with, we will show that \({\mathcal {J}}_{k}\) tends uniformly to \({\mathcal {J}}_{0}\) on any closed ball \(B\left( 0,\rho \right) \subset H_{0}^{\alpha ,p}\). Let \(g_t\left( s\right) =f\left( t,x\left( t\right) ,D_{a+}^{\alpha }x\left( t\right) ,su_{k}\left( t\right) +\left( 1-s\right) u_{0}\left( t\right) \right) ,\) \(s\in \left[ 0,1\right] \). In virtue of the mean value theorem (note, that by (A1) \(f_u\) is continuous), there exists \(0\le \theta \left( t\right) \le 1\) such that
which means that
where \(\tilde{u}\left( t\right) =u_{0}\left( t\right) +\theta \left( t\right) \left( u_{k}\left( t\right) -u_{0}\left( t\right) \right) \). Consequently, thanks to (A3) we have that
and by Lemma 3.1 we get that
for any \(x\in B\left( 0,\rho \right) \) which means that \(\mathcal J_{k} \rightrightarrows {{\mathcal {J}}}_{0}\) on \(B\left( 0,\rho \right) .\) Let \(\left( x_{k}\right) \in V_{k}\) for \(k=1,2,\ldots \). Note that the space \(H_{0}^{\alpha ,p}\) is reflexive, and by Theorem 4.1, there exists a ball \(B\left( 0,\rho \right) \) such that \(\left( x_{k}\right) \subset B\left( 0,\rho \right) \). As a result, there exists at least one cluster point (in the sense of the weak topology of \(H_{0}^{\alpha ,p})\) \(\bar{x}\in B\left( 0,\rho \right) \) of the sequence \(\left( x_{k}\right) \). Consequently, \({\text {*}}{LimSup}\ne \emptyset .\) We can clearly assume that \(x_{k}\rightharpoonup \bar{x}\) weakly in \(H_{a+}^{\alpha ,p}.\) Suppose that \(\bar{x}\notin V_{0}.\) The set \(V_{0}\) is nonempty; thus, there exists \(x_{0}\in V_{0}.\) Let \(m_{k} ={{\mathcal {J}}}_{k}\left( x_{k}\right) \) for \(k=0,1,2\ldots ,\) since \(\mathcal J_{k}\rightrightarrows {{\mathcal {J}}}_{0}\) on \(B\left( 0,\rho \right) \) therefore
We have that
thus, by (15), thanks to the fact that \(\mathcal J_{k}\rightrightarrows {{\mathcal {J}}}_{0}\) and \({{\mathcal {J}}}_{0}\) is sequentially weakly lower semicontinuous we get that
This is a clear contradiction of the fact that \(\bar{x}\) is not a minimizer for \({{\mathcal {J}}}_{0}\) (\(\bar{x}\notin V_{0}\)). \(\square \)
Example 4.1
Consider the function
discussed in Example 3.1. Assume that \(\alpha =\frac{2}{3},\) \(p=2\) and \( M=\left[ -1,1\right] .\) Then, the functional of action is of the form
By Theorems 4.1 and 4.2 for any \(u\in {\mathcal {U}}\), there exists at least solution \(x_{u}\in H_{0}^{\frac{2}{3},2}\) which minimizes \({\mathcal {J}}_{u}\left( x\right) \). It is obvious that for \(u_{0}=0 \) \(x_{u_{0}}=0\) solves
Theorem 4.4 states that for any control u which is ”not too far” from 0 in the sense of norm of \(L^{\infty }\) the corresponding solution \(x_{u}\) is ”not too far” in the sense of the weak topology of \(H_{0}^{\frac{2}{ 3},2},\) and thanks to Lemma 3.1, ”not too far” in the pointwise sense.
Remark 4.1
If we assume that the function \(f\left( t,\cdot ,\cdot ,u\right) \) is convex for a.e. \(t\in \left[ a,b\right] \) and every \(u\in {\mathbb {R}}^{m}\) then the assertion of Theorems 4.4 remains true for the sequence \(W_{k}\) of solutions to (11), (12) corresponding to \(u_{k}.\)
5 Existence of Solutions to Optimal Control Problem
The existence of solutions to system (11), (12) and continuous dependence on parameter u can be applied in investigating the existence of optimal solutions to some Lagrange problem.
To be more specific, we minimize
subject to
i.e. x is any solution to (17) corresponding to \(u\in {\mathcal {U}} _{K},\) \(K>0\) is a given number.
We say that problem (16)–(19) has a solution iff there is at least one pair \(\left( u_{*}\,x_{*}\right) \) optimal for (16), i.e. \(x_{*}\in H_{0}^{\alpha ,p}\) solves (17) with \(u_{*}\in {\mathcal {U}}_{K}\) and for every control \(u\in {\mathcal {U}}_{K}\) and any solution x to (17) corresponding to u
We have
Theorem 5.1
Suppose that
-
(1)
\(L:\left[ a,b\right] \times {\mathbb {R}}^{n_{1}}\times {\mathbb {R}}^{n_{1}}\ni \left( t,x_{1},x_{2},u\right) \mapsto L\left( t,x_{1},x_{2},u\right) \in {\mathbb {R}}\) is measurable in t for every \(\left( x_{1},x_{2},u\right) ,\) continuous in \(\left( x_{1},x_{2},u\right) \) for almost all t and convex in \(\left( x_1,x_{2}\right) \) for almost all t and all u,
-
(2)
There exists a function \(\psi \in L^{1}\left( \left[ a,b\right] ,{\mathbb {R}}^{+}\right) \) and a constant \(C>0\) such that
$$\begin{aligned} L\left( t,x_{1},x_{2},u\right) \ge -\psi \left( t\right) -C\left( \left| x_{2}\right| +\left| u\right| \right) \end{aligned}$$
then problem (16)–(19) has a solution.
Proof
Let
be the set of admissible pairs. Let \(\left( u_{k},x_{k}\right) _{k} \subset {\mathcal {D}}\) be a minimizing sequence for (16)–(19), i.e.
From the definition of \({\mathcal {U}}_{K}\), it follows that \(\left( u_{k}\right) _{k}\) is bounded and equicontinuous; therefore, applying Ascoli–Arzelà theorem, we get that there exists a function \(u_{0} \in {\mathcal {U}}_{K}\) such that, passing to a subsequence if necessary, \(u_{k}\rightarrow u_{0}\) in \(L^{\infty }.\) Since \(\left( x_{k}\right) _{k}\) is bounded (cf. Theorem 4.3) and \(H_{0}^{\alpha ,p}\) is reflexive, it follows that there is a weak cluster point \(x_{0}\) of \(\left( x_{k}\right) _{k}.\) Consequently, applying Theorem 4.4 we have that \(x_{0}\) is a solution to (17), (18) corresponding to \(u_{0}.\) Finally, by Lemma 3.1 and applying lower closure theorem (see [28, 10.8.i]) we get that
which means that \(\left( u_{0},x_{0}\right) \) is an optimal pair. \(\square \)
6 Conclusions
We applied the classical variational method, which is to minimize functional of action and to generate solutions of Dirichlet problem as minimizers of this functional. The continuous dependence proved in the paper is a consequence of the continuity of the multifunction which assigns the parameter u to the set of minimizers. The practical meaning of the continuous dependence is that it shows that any small disturbance of the parameters of the model described by fractional system cannot significantly affect the answer of this system. As an application of the above continuous dependence, the proof of the existence of solution to Lagrange problem has been presented.
References
Hilfer, R.: Applications of Fractional Calculus in Physics. Wspc, Singapore (2000)
Ortigueira, M.D.: Fractional Calculus for Scientists and Engineers. Lecture Notes in Electrical Engineering, vol. 84. Springer, Dordrecht (2011)
Malinowska, A.B., Torres, D.F.M.: Introduction to the Fractional Calculus of Variations. Imperial College Press, London (2012)
Leszczynski, J.S.: An Introduction to Fractional Mechanics. Publishing Office of Czestochowa University of Technology, Czestochowa (2011)
Meral, F.C., Royston, T.J., Magin, R.: Fractional calculus in viscoelasticity: an experimental study. Commun. Nonlinear Sci. Numer Simul. 15(4), 939–945 (2010)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego, New York, London (1998)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier Science Inc, New York (2006)
Walczak, S.: On the continuous dependence on parameters of the Dirichlet problem. Académie Royal de Belgique, Bulletin de la Classe des Sciences 7–12, 247–273 (1995)
Courant, R., Hilbert, D.: Methods of Mathematical Physics. Volume 2: Partial Differential Equations. Wiley-VCH (1989)
Torres, C.: Existence of a solution for the fractional forced pendulum. J. Appl. Math. Comput. Mech. 13(1), 125–142 (2014)
Bourdin, L.: Existence of a weak solution for fractional Euler-Lagrange equations. J. Math. Anal. Appl. 399(1), 239–251 (2013)
Agrawal, O.P.: A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 38(1–4), 323–337 (2004)
Kamocki, R.: On the existence of optimal solutions to fractional optimal control problems. Appl. Math. Comput. 235, 94–104 (2014)
Guo, T.L.: The necessary conditions of fractional optimal control in the sense of Caputo. J. Optim. Theory Appl. 156(1), 115–126 (2013)
Kamocki, R.: Pontryagin maximum principle for fractional ordinary optimal control problems. Math. Methods Appl. Sci. 37(11), 1668–1686 (2014)
Fečkan, M., Wang, J., Zhou, Y.: Controllability of fractional functional evolution equations of Sobolev type via characteristic solution operators. J. Optim. Theory Appl. 156(1), 79–95 (2013)
Kaczorek, T.: Selected Problems of Fractional Systems Theory. Springer-Verlag Berlin Heidelberg (2011)
Wang, J., Feckan, M., Zhou, Y.: Relaxed controls for nonlinear fractional impulsive evolution equations. J. Optim. Theory Appl. 156(1), 13–32 (2013)
Wang, J., Feckan, M., Zhou, Y.: Controllability of Sobolev type fractional evolution systems. Dyn. Partial Differ. Equ. 11(1), 71–87 (2014)
Bors, D., Majewski, M., Walczak, S.: Optimal control systems with constrains defined on unbounded sets. In: Cakaj S. (ed.) Modeling Simulation and Optimization—Tolerance and Optimal Control. InTech (2010)
Idczak, D.: Optimal control of a coercive Dirichlet problem. SIAM J. Control Optim. 36(4), 1250–1267 (1998)
Bourdin, L., Idczak, D.: A fractional fundamental lemma and a fractional integration by parts formula—Applications to critical points of Bolza functionals and to linear boundary value problems. Adv. Differ. Equ. 20(3/4), 213–232 (2015)
Agrawal, O.: Formulation of Euler-Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 272(1), 368–379 (2002)
Baleanu, D., Trujillo, J.J.: On exact solutions of a class of fractional Euler-Lagrange equations. Nonlinear Dyn. 52(4), 331–335 (2008)
Klimek, M.: Existence-uniqueness result for a certain equation of motion in fractional mechanics. Bull. Pol. Acad. Sci. Tech. Sci. 58(4), 573–581 (2010)
Leszczynski, J.S., Blaszczyk, T.: Modeling the transition between stable and unstable operation while emptying a silo. Granul. Matt. 13(4), 429–438 (2011)
Blaszczyk, T., Ciesielski, M.: Fractional oscillator equation Transformation into integral equation and numerical solution. Appl. Math. Comput. 257, 428–435 (2015)
Cesari, L.: Optimization—Theory and Applications. Springer, New York (1983)
Acknowledgments
The authors would like to thank anonymous reviewers for their valuable comments and suggestions to improve the quality of the paper. The project was financed with funds of National Science Centre, granted on the basis of decision DEC-2011/01/B/ST7/03426.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kamocki, R., Majewski, M. On the Existence and Continuous Dependence on Parameter of Solutions to Some Fractional Dirichlet Problem with Application to Lagrange Optimal Control Problem. J Optim Theory Appl 174, 32–46 (2017). https://doi.org/10.1007/s10957-016-0954-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-016-0954-6
Keywords
- Fractional optimal control problem
- Fractional Dirichlet problem
- Fractional Lagrange problem
- Continuous dependence
- Kuratowski–Painlevé limit