Typicality of Thermal Equilibrium and Thermalization in Isolated Macroscopic Quantum Systems

Abstract

Based on the view that thermal equilibrium should be characterized through macroscopic observations, we develop a general theory about typicality of thermal equilibrium and the approach to thermal equilibrium in macroscopic quantum systems. We first formulate the notion that a pure state in an isolated quantum system represents thermal equilibrium. Then by assuming, or proving in certain classes of nontrivial models (including that of two bodies in thermal contact), large-deviation type bounds (which we call thermodynamic bounds) for the microcanonical ensemble, we prove that to represent thermal equilibrium is a typical property for pure states in the microcanonical energy shell. We believe that the typicality, along with the empirical success of statistical mechanics, provides a sound justification of equilibrium statistical mechanics. We also establish the approach to thermal equilibrium under two different assumptions; one is that the initial state has a moderate energy distribution, and the other is the energy eigenstate thermalization hypothesis.

Appendices

Appendix 1: Three Toy Models

We shall discuss three simple solvable examples in which the assumptions made in Sects. 6 and 7 can be easily verified. Although the results are in a sense trivial, we hope that these elementary examples shed light on the general scenario, and also provide insight to truly nontrivial many body systems. The material in this section is partly based on our unpublished work [7].

1.1 Independent Spins Under Random Magnetic Field

Let us start with a trivial example of independent spins under random magnetic field. In this model, independent precession of each spin causes the “approach to equilibrium” for certain observables. Although everything is trivial, it may be a good idea to look at the simple (but genuinely quantum) mechanism that realizes the relaxation-like behavior. Interestingly, the same model also offers a counterexample to the assumptions.

We use the same notation as in Sect. 3.3, but here regard $\Lambda$ simply as a set of V sites. We consider a system of $S=1/2$ spins on $\Lambda$, and take the Hamiltonian

$$\begin{aligned} \mathsf {H}_V=\sum _{x\in \Lambda }^Nh_x\,\mathsf {S}^{(1)}_x, \end{aligned}$$

(10.1)

where independent spins are under nonuniform magnetic field. The local magnetic field $h_x$ is independently drawn from the interval $[-h_0,h_0]$ according to the uniform probability measure, where $h_0>0$ is a fixed constant.

As in (3.17), we denote by $|\varphi ^\pm _x\rangle$ the basis states of the local Hilbert space $\mathcal{H}_x$. Then the eigenstates of $\mathsf {H}_V$ is written as

$$\begin{aligned} |\Psi _{\varvec{\tau }}\rangle =\bigotimes _{x\in \Lambda }\frac{1}{\sqrt{2}} \Bigl \{|\varphi ^+_x\rangle +\tau _x|\varphi ^-_x\rangle \Bigr \}, \end{aligned}$$

(10.2)

where we used the multi-index (or the spin configuration) $\varvec{\tau }:=(\tau _x)_{x\in \Lambda }$ with $\tau _x=\pm 1$. The corresponding energy eigenvalue is

$$\begin{aligned} E_{\varvec{\tau }}=\frac{1}{2}\sum _xh_x\,\tau _x. \end{aligned}$$

(10.3)

Since $h_x$ are drawn randomly, the energy eigenvalues are nondegenerate with probability one.

As in Sect. 3.3, we take the total magnetization (in the direction orthogonal to the magnetic filed) $\mathsf {M}_V=\sum _{x\in \Lambda }\mathsf {S}^{(3)}_x$ as the thermodynamic quantity of interest. From the symmetry, one has $\langle \mathsf {M}_V\rangle ^\mathrm {mc}_{V,u}=0$ for any V and u.

Since each spin independently points upward or downward (in the 3-direction) with probability 1 / 2 in the energy eigenstate (10.2), the probability distribution of $\mathsf {M}_V$ is given by the binomial distribution

$$\begin{aligned} \langle \Psi _{\varvec{\tau }}|\,\mathsf {P}[\mathsf {M}_V=M]\,|\Psi _{\varvec{\tau }}\rangle =\frac{1}{2^V}\frac{V!}{N_+!\,N_-!}. \end{aligned}$$

(10.4)

Here $N_+$ and $N_-$ are the numbers of up and down spins, respectively, which are determined by $N_++N_-=V$ and $(N_+-N_-)/2=M$. By recalling the standard large deviation property of the coin toss⁶¹ [54, 55], (10.4) implies

$$\begin{aligned} \langle \Psi _{\varvec{\tau }}|\,\mathsf {P}\bigl [|\mathsf {M}_V|\ge M\bigr ]\,|\Psi _{\varvec{\tau }}\rangle \le 2\,e^{-\kappa (\delta )\,V}, \end{aligned}$$

(10.5)

with $\kappa (\delta )=\log 2-S_2[(1/2)+\delta ]=2\delta ^2+O(\delta ^4)$, where $S_2(p)=-p\log p-(1-p)\log (1-p)$ is the binary entropy. We thus find that the energy eigenstate thermalization hypothesis (7.1) is valid in any range of energy.⁶²

We thus conclude that, as far as one looks at the total magnetization $\mathsf {M}_V=\sum _{x\in \Lambda }\mathsf {S}^{(3)}_x$, the model approaches (thermal) equilibrium from any initial state. As we have noted in the beginning, this “approach to equilibrium” is nothing but a trivial consequence of independent precession of each spin.

It is interesting to see what happens if we take $\mathsf {M}_V'=\sum _{x\in \Lambda }\mathsf {S}^{(1)}_x$, which is the total spin in the 1-direction, as the thermodynamic quantity of interest. In this case we have $\mathsf {M}_V'|\Psi _{\varvec{\tau }}\rangle =(\sum _{x\in \Lambda }\tau _x/2)|\Psi _{\varvec{\tau }}\rangle$, i.e., the energy eigenstate (10.2) is also the eigenstate of $\mathsf {M}_V'$. Since the energy eigenvalue (10.3) is the sum of the continuously distributed random quantities, it happens in general that two energy eigenvalues $E_{\varvec{\tau }}$ and $E_{\varvec{\tau }'}$ which are extremely close to each other have radically different configurations $\varvec{\tau }$ and $\varvec{\tau }'$. As a consequence, the eigenvalue $\sum _{x\in \Lambda }\tau _x/2$ shows an erratic behavior when viewed as a function of the energy eigenvalue $E_{\varvec{\tau }}$. See the discussion in [42]. This observation implies that, when one is interested in $\mathsf {M}_V'$, the model does not satisfy the energy eigenstate thermalization hypothesis.

This trivial example illustrates how the tendency of the approach to equilibrium can be lost in a system with a quenched disorder. Pal and Huse [42] numerically studied the $S=1/2$ model with the Hamiltonian

$$\begin{aligned} \mathsf {H}=J\sum _{j=1}^N{\varvec{\mathsf {S}}}_j\cdot {\varvec{\mathsf {S}}}_{j+1}+\sum _{j=1}^Nh_j\,\mathsf {S}^{(3)}_j, \end{aligned}$$

(10.6)

where J is a constant and $h_j$ is uniformly distributed in $[-h,h]$. A systematic analysis suggests that the “localization” observed above for $J=0$ persists in a model with sufficiently small |J|. In this case, the model lacks the ability to relax to equilibrium by itself. For large enough |J|, the system enters the delocalized phase where it can relax to equilibrium. See [42] and references therein for further discussions about the localization in many body quantum systems and its relation to the problem of the approach to equilibrium. See also [43] for a recent rigorous result.

1.2 Free Fermions on a Double Chain

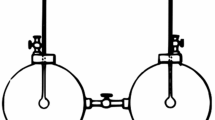
We next discuss a slightly less trivial (but still easily solvable) model of free fermions on a double chain. We shall confirm that all the assumptions made in Theorems 6.1 and 7.1 are valid in this model.

Fig. 5

The free fermion model defined on a pair of chains is a simple solvable model where we can prove all the assumptions in Theorems 6.1 and 7.1. Solid lines represent intra-chain hopping, and dotted lines represent (weak) inter-chain hopping (or coupling). The model is equivalent to a free fermion on a single chain with nearest and next-nearest neighbor hopping

The Model: We consider a free fermion model defined on a double chain as depicted in Fig. 5. The two chains are identified with sets of odd and even integers, respectively, as

$$\begin{aligned} \Lambda _1=\{1,3,\ldots ,2L-1\},\quad \Lambda _2=\{2,4,\ldots ,2L\}, \end{aligned}$$

(10.7)

where L is a fixed integer. We also denote the whole lattice as

$$\begin{aligned} \Lambda =\Lambda _1\cup \Lambda _2=\{1,2,3,\ldots ,2L\}, \end{aligned}$$

(10.8)

and identify the volume with $V=2L$.

For each $x \in \Lambda$, let $\mathsf {c}_{x}$ and $\mathsf {c}^\dagger _{x}$ be the annihilation and the creation operators, respectively, of a fermion at x. They satisfy the standard canonical anticommutation relations⁶³

$$\begin{aligned} \{\mathsf {c}^\dagger _{x},\mathsf {c}_{y}\}=\delta _{x,y},\quad \{\mathsf {c}_{x},\mathsf {c}_{y}\}=\{\mathsf {c}^\dagger _{x},\mathsf {c}^\dagger _{y}\}=0, \end{aligned}$$

(10.9)

for any $x,y\in \Lambda$. We consider states with N fermions on the lattice. (We fix $\rho =N/V$ when we make V large.) The whole Hilbert space is spanned by the states of the form $\mathsf {c}^\dagger _{x_1}\ldots \mathsf {c}^\dagger _{x_N}|\Phi _\mathrm {vac}\rangle$, where $x_j\in \Lambda$ with $x_j<x_{j+1}$, and $|\Phi _\mathrm {vac}\rangle$ is the normalized state with no fermions in the system. It satisfies $\mathsf {c}_x|\Phi _\mathrm {vac}\rangle =0$ for any x.

We consider the Hamiltonian

$$\begin{aligned} \mathsf {H}_V=\frac{1}{2}\sum _{x\in \Lambda }(e^{i\theta }\mathsf {c}^\dagger _{x}\mathsf {c}_{x+2}+e^{-i\theta }\mathsf {c}^\dagger _{x+2}\mathsf {c}_{x}) +\frac{\lambda }{2}\sum _{x\in \Lambda }(e^{i\theta }\mathsf {c}^\dagger _{x}\mathsf {c}_{x+1}+e^{-i\theta }\mathsf {c}^\dagger _{x+1}\mathsf {c}_{x}), \end{aligned}$$

(10.10)

where $\lambda \in (0,1]$ and $\theta \in [0,2\pi )$ are parameters. The phases $\theta$ is introduced (rather artificially) to avoid degeneracy.⁶⁴ See Proposition 10.1. We impose periodic boundary conditions, and make identifications $\mathsf {c}_{2L+1}=\mathsf {c}_1$ and $\mathsf {c}_{2L+2}=\mathsf {c}_1$.

The first term in (10.10) represents hopping within each chain, while the second term represents hopping between the two chains. The model is also interpreted as that on a single chain $\Lambda$ with nearest neighbor and next-nearest neighbor hopping.

Energy Eigenstates and Eigenvalues: Define the set of wave numbers as

$$\begin{aligned} \mathcal{K}:=\left\{ \frac{2\pi }{2L}j\,\Bigl |\,j=1,2,\ldots ,2L\right\} . \end{aligned}$$

(10.11)

We introduce fermion operators $\mathsf {a}^\dagger _k$ for $k\in \mathcal{K}$, which are related with $\mathsf {c}^\dagger _x$ by

$$\begin{aligned} \mathsf {a}^\dagger _k=\frac{1}{\sqrt{2L}}\sum _{x\in \Lambda }e^{ikx}\mathsf {c}^\dagger _x,\quad \mathsf {c}^\dagger _x=\frac{1}{\sqrt{2L}}\sum _{k\in \mathcal{K}}e^{-ikx}\mathsf {a}^\dagger _k, \end{aligned}$$

(10.12)

and satisfy the anticommutation relations

$$\begin{aligned} \{\mathsf {a}^\dagger _k,\mathsf {a}_{k'}\}=\delta _{k,k'},\quad \{\mathsf {a}^\dagger _k,\mathsf {a}^\dagger _{k'}\}=\{\mathsf {a}_k,\mathsf {a}_{k'}\}=0, \end{aligned}$$

(10.13)

for any $k,k'\in \mathcal{K}$.

A standard calculation shows that the Hamiltonian (10.10) is diagonalized by using the $\mathsf {a}$ operators as

$$\begin{aligned} \mathsf {H}_V=\sum _{k\in \mathcal{K}}\bigl \{\epsilon _0(k)+\lambda \epsilon _\mathrm{coup}(k)\bigr \}\mathsf {a}^\dagger _k\mathsf {a}_k, \end{aligned}$$

(10.14)

where

$$\begin{aligned} \epsilon _0(k)=\cos (2k+\theta ),\quad \epsilon _\mathrm{coup}(k)=\cos (k+\theta ). \end{aligned}$$

(10.15)

Take an arbitrary subset $K\subset \mathcal{K}$ such that $|K|=N$, and define

$$\begin{aligned} |\Psi _K\rangle :=\Bigl (\prod _{k\in K}\mathsf {a}^\dagger _{k}\Bigr )|\Phi _\mathrm {vac}\rangle . \end{aligned}$$

(10.16)

From (10.14) one finds that $|\Psi _K\rangle$ is an eigenstate of $\mathsf {H}_V$, i.e.,

$$\begin{aligned} \mathsf {H}_V|\Psi _K\rangle =E_K\,|\Psi _K\rangle , \end{aligned}$$

(10.17)

with the energy eigenvalue

$$\begin{aligned} E_K=\sum _{k\in K}\bigl \{\epsilon _0(k)+\lambda \epsilon _\mathrm{coup}(k)\bigr \}. \end{aligned}$$

(10.18)

It can be also shown that the corresponding number of states exhibits the standard behavior (2.1) when U / V is sufficiently small. The energy shell $\mathcal {H}_{V,u}$ is spanned by $|\Psi _K\rangle$ with

$$\begin{aligned} u- \Delta u<\frac{E_K}{V}\le u. \end{aligned}$$

(10.19)

In Sects. 6 and 7, we have assumed that the energy eigenvalues are nondegenerate. Although nondegeneracy is always achieved by adding a small (random) perturbation to any given Hamiltonian, it is nice to know that nondegeneracy is guaranteed under certain conditions. By making use of standard results in number theory [66, 67], we can prove that the present model generically has no degeneracy. See the end of the section for the proof.

Proposition 10.1

Let $L>2$ be a prime number with $N<L/2$. Fix an arbitrary constant $\lambda _0>0$. For any $\lambda \in (0,\lambda _0]$ except for (at most) a finite number of points, and for any $\theta \in [0,2\pi )$ except for a finite number of points⁶⁵, the energy eigenvalues are nondegenerate, i.e., $E_K=E_{K'}$ implies $K=K'$.

From a physical point of view, it is absurd to assume that the chain length is equal to a prime number. We of course do not believe that this is really crucial. When some of the conditions of the proposition are not satisfied, we still expect the system to exhibit essentially the same behavior although there may be some accidental (and irrelevant) degeneracies in the energy eigenvalues.

Other Fermion Operators: Let $\nu =1,2$ specify one of the two chains. We denote by $\mathsf {N}_\nu :=\sum _{x\in \Lambda _\nu }\mathsf {c}^\dagger _{x}\mathsf {c}_{x}$ the number of fermions on the chain $\nu$. We also define

$$\begin{aligned} \mathsf {a}^\dagger _{k,\nu }:=\frac{1}{\sqrt{L}}\sum _{x\in \Lambda _\nu }e^{ikx}\mathsf {c}^\dagger _x, \end{aligned}$$

(10.20)

which creates the state with wave number k only on the chain $\nu$. We obviously have

$$\begin{aligned} \mathsf {a}^\dagger _k=\frac{1}{\sqrt{2}}(\mathsf {a}^\dagger _{k,1}+\mathsf {a}^\dagger _{k,2}), \end{aligned}$$

(10.21)

and

$$\begin{aligned}{}[\mathsf {N}_\nu ,\mathsf {a}^\dagger _{k,\nu '}]=\delta _{\nu ,\nu '}\mathsf {a}^\dagger _{k,\nu }. \end{aligned}$$

(10.22)

For any $k\in \mathcal{K}$, we denote by $\bar{k}$ the unique element in $\mathcal{K}$ such that $|k-\bar{k}|=\pi$. One readily finds $\mathsf {a}^\dagger _{\bar{k},1}=-\mathsf {a}^\dagger _{k,1}$ and $\mathsf {a}^\dagger _{\bar{k},2}=\mathsf {a}^\dagger _{k,2}$. Recalling (10.21), this implies

$$\begin{aligned} \mathsf {a}^\dagger _k\mathsf {a}^\dagger _{\bar{k}}=\frac{1}{2}(\mathsf {a}^\dagger _{k,1}+\mathsf {a}^\dagger _{k,2})(\mathsf {a}^\dagger _{\bar{k},1}+\mathsf {a}^\dagger _{\bar{k},2}) =\frac{1}{2}(\mathsf {a}^\dagger _{k,1}\mathsf {a}^\dagger _{\bar{k},2}+\mathsf {a}^\dagger _{k,2}\mathsf {a}^\dagger _{\bar{k},1}). \end{aligned}$$

(10.23)

From (10.20), we also get the anticommutation relations

$$\begin{aligned} \{\mathsf {a}^\dagger _{k,1},\mathsf {a}_{k',2}\}=0, \quad \{\mathsf {a}^\dagger _{k,1},\mathsf {a}_{k',1}\}= {\left\{ \begin{array}{ll} 1&{}k=k',\\ -1&{}\bar{k}=k',\\ 0&{}\text {otherwise},\\ \end{array}\right. } \quad \{\mathsf {a}^\dagger _{k,2},\mathsf {a}_{k',2}\}= {\left\{ \begin{array}{ll} 1&{}k=k',\\ 1&{}\bar{k}=k',\\ 0&{}\text {otherwise},\\ \end{array}\right. }\nonumber \\ \end{aligned}$$

(10.24)

for any $k,k'\in \mathcal{K}$.

Energy Eigenstate Thermalization: As for the thermodynamic quantity of interest let us take

$$\begin{aligned} \mathsf {M}_V:=\mathsf {N}_1-\mathsf {N}_2, \end{aligned}$$

(10.25)

which is the difference of the particle numbers in the two chains. The equilibrium value of $\mathsf {M}_V$ is obviously zero by the symmetry.

Let us examine the validity of the energy eigenstate thermalization with respect to $\mathsf {M}_V$. For $K\subset \mathcal{K}$ with $|K|=N$, define

$$\begin{aligned} K_0:=\left\{ k\in K\,\Bigl |\,k\le \pi ,\bar{k}=k+\pi \in K\right\} . \end{aligned}$$

(10.26)

We can then write the energy eigenstate (10.16) as

$$\begin{aligned} |\Psi _K\rangle&=\pm \Bigl (\prod _{k\in K_0}\mathsf {a}^\dagger _{k}\mathsf {a}^\dagger _{\bar{k}}\Bigr ) \Bigl (\prod _{k\in K\backslash K_0}\mathsf {a}^\dagger _{k}\Bigr )|\Phi _\mathrm {vac}\rangle \nonumber \\&= \pm \left( \prod _{k\in K_0}\frac{\mathsf {a}^\dagger _{k,1}\mathsf {a}^\dagger _{\bar{k},2}+\mathsf {a}^\dagger _{k,2}\mathsf {a}^\dagger _{\bar{k},1}}{2}\right) \left( \prod _{k\in K\backslash K_0}\frac{\mathsf {a}^\dagger _{k,1}+\mathsf {a}^\dagger _{k,2}}{\sqrt{2}}\right) |\Phi _\mathrm {vac}\rangle , \end{aligned}$$

(10.27)

where we used (10.23) and (10.21).

Let $N_0=2|K_0|$. Noting the commutation relation (10.22), we find that, in the state (10.27), $N_0$ fermions are evenly distributed to the two chains, and each of the remaining $N-N_0$ fermions belongs to one of the two chains with independent probability 1 / 2. The probability distribution for the numbers of fermions in the two chains is then

$$\begin{aligned}&p(N_1,N_2):=\langle \Psi _K|\,\mathsf {P}[\mathsf {N}_1=N_1,\mathsf {N}_2=N_2]\,|\Psi _K\rangle \nonumber \\&\quad ={\left\{ \begin{array}{ll} \dfrac{1}{2^{N-N_0}}\,\dfrac{(N-N_0)!}{\{N_1-\frac{N_0}{2}\}!\,\{N_2-\frac{N_0}{2}\}!}&{} \text {when}\, N_1+N_2=N, N_1\ge \dfrac{N_0}{2},\, \mathrm{and}\, N_2\ge \dfrac{N_0}{2}\\ 0&{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

(10.28)

Given the binomial distribution (10.28) we again see from the standard result in large deviation (see footnote 61) that

$$\begin{aligned}&\langle \Psi _K|\,\mathsf {P}\bigl [\mathsf {M}_V\ge V\delta \bigr ]\,|\Psi _K\rangle =\mathop {\sum _{N_1,N_2}}_{(N_1-N_2\ge V\delta )}p(N_1,N_2) \nonumber \\&{\left\{ \begin{array}{ll} \le \exp \biggl [ -V\,(\rho -\rho _0)\biggl \{\log 2-S_2\Bigl (\dfrac{1}{2}+\dfrac{\delta }{2(\rho -\rho _0)}\Bigr )\biggr \}\biggr ] &{}\text {for}\, \delta \in (0,\rho -\rho _0]\\ =0&{}\text {for}\, \delta \in (\rho -\rho _0,\rho ] \end{array}\right. } \end{aligned}$$

(10.29)

where $\rho _0=N_0/V$. Noting the symmetry $\mathsf {M}_V\rightarrow -\mathsf {M}_V$ and the bound

$$\begin{aligned} (\rho -\rho _0)\biggl \{\log 2-S_2\Bigl (\dfrac{1}{2}+\dfrac{\delta }{2(\rho -\rho _0)}\Bigr )\biggr \} \ge \rho \,\biggl \{\log 2-S_2\Bigl (\dfrac{1}{2}+\dfrac{\delta }{2\rho }\Bigr )\biggr \}, \end{aligned}$$

(10.30)

we find for any $\delta \in (0,\rho ]$ that

$$\begin{aligned} \langle \Psi _K|\,\mathsf {P}\bigl [|\mathsf {M}_V|\ge V\delta \bigr ]\,|\Psi _K\rangle \le 2 e^{-\kappa (\delta ) V}, \end{aligned}$$

(10.31)

where $\kappa (\delta )$ is defined as the right-hand side of (10.30). So the energy eigenstate thermalization hypothesis (7.1) is valid for any energy eigenstate $|\Psi _K\rangle$.

Note that (10.31) readily implies the thermodynamic bound

$$\begin{aligned} \Bigl \langle \mathsf {P}\bigl [|\mathsf {M}_V|\ge V\delta \bigr ]\Bigr \rangle ^\mathrm {mc}_{V,u} \le 2e^{-\kappa (\delta )V}, \end{aligned}$$

(10.32)

for any u.

Thermalization: Suppose that the conditions for the nondegeneracy in Proposition 10.1 are satisfied. Since the energy eigenstate thermalization (10.31) is valid, we see that the conditions for Theorem 7.1 are satisfied. Therefore we have a concrete example in which the approach to thermal equilibrium from an arbitrary initial state $|\varphi (0)\rangle \in \mathcal {H}_{V,u}$ can be proved without any unjustified assumptions.

Nonequilibrium Initial States with a Moderate Energy Distribution: Note that Theorem 6.1, which states thermalization for certain initial states, does not provide any additional information when the stronger Theorem 7.1 is known to be valid. It is nevertheless useful to see explicitly that nonequilibrium initial states with a moderate energy distribution (as required in Theorem 6.1) are possible in this model.⁶⁶

Fix an energy interval $(u- \Delta u,u]$. To avoid technical complexity, we assume that the coupling $\lambda$ satisfies $0<\lambda \ll \Delta u$, and can be neglected when we estimate the energy. We further simplify the discussion by focusing only on the extreme nonequilibrium where $\mathsf {M}_V=\mathsf {N}_1-\mathsf {N}_2$ takes its maximum value N.

Take a subset $\tilde{K}\subset \mathcal{K}$ such that $|\tilde{K}|=N$ and $k\le \pi$ for any $k\in \tilde{K}$. We also assume that the total energy satisfies

$$\begin{aligned} u- \Delta u<\frac{1}{V}\sum _{k\in \tilde{K}}\epsilon _0(k)\le u, \end{aligned}$$

(10.33)

where we ignored the terms including $\lambda$ in (10.18). We denote by $D_{V,u}^\mathrm {neq}$ the total number of $\tilde{K}$ satisfying all these conditions.

We define

$$\begin{aligned} |\Gamma _{\tilde{K}}\rangle :=\Bigl (\prod _{k\in \tilde{K}}\mathsf {a}^\dagger _{k,1}\Bigr )|\Phi _\mathrm {vac}\rangle , \end{aligned}$$

(10.34)

which is in the energy shell $\mathcal {H}_{V,u}$ (under the assumption $\lambda \ll \Delta u$), and is an extreme nonequilibrium state with $\mathsf {M}_V|\Gamma _{\tilde{K}}\rangle =N|\Gamma _{\tilde{K}}\rangle$. We thus find that $D_{V,u}^\mathrm {neq}$ is the dimension of the nonequilibrium subspace in this case. Note that, corresponding to the thermodynamic bound (2.16), we have $D_{V,u}^\mathrm {neq}\sim e^{-\gamma V}D_{V,u}$ (which essentially is the definition of $\gamma >0$).

Since $\mathsf {a}^\dagger _{k,1}=(\mathsf {a}^\dagger _k-\mathsf {a}^\dagger _{\bar{k}})/\sqrt{2}$, we can rewrite (10.34) as

$$\begin{aligned} |\Gamma _{\tilde{K}}\rangle =\Biggl (\prod _{k\in \tilde{K}}\frac{\mathsf {a}^\dagger _k-\mathsf {a}^\dagger _{\bar{k}}}{\sqrt{2}}\Biggr )|\Phi _\mathrm {vac}\rangle . \end{aligned}$$

(10.35)

Expanding the product, we see that this state is a linear combination of $2^N$ energy eigenstates (10.16). This means that $|\Gamma _{\tilde{K}}\rangle$ has the effective dimension $D_\mathrm {eff}=2^N$.

The rest is easy. Consider an initial state

$$\begin{aligned} |\Phi (0)\rangle =\sum _{\tilde{K}}\alpha _{\tilde{K}}|\Gamma _{\tilde{K}}\rangle , \end{aligned}$$

(10.36)

where $\tilde{K}$ is summed over the $D_{V,u}^\mathrm {neq}$ subsets $\tilde{K}$ satisfying the above conditions, and all $|\alpha _{\tilde{K}}|$ are nearly equal. Clearly $|\Phi (0)\rangle$ is in $\mathcal {H}_{V,u}$, is an extreme nonequilibrium state, and has the effective dimension

$$\begin{aligned} D_\mathrm {eff}\sim 2^{N}D_{V,u}^\mathrm {neq}\sim 2^{N}e^{-\gamma V}D_{V,u}= e^{-(\gamma -\rho \log 2)V}D_{V,u}. \end{aligned}$$

(10.37)

By comparing this with (6.2), we can choose $\eta =\gamma -\rho \log 2$. The condition $\gamma >\eta$ required in Theorem 6.1 is thus satisfied.

Proof of Proposition 10.1: To prove the absence of degeneracy, it is convenient to introduce the standard occupation number description. With each $K\subset \mathcal{K}$, we associate a 2L-tuple $\varvec{n}=(n_j)_{j=1,2,\ldots ,2L}$ by

$$\begin{aligned} n_j={\left\{ \begin{array}{ll} 1&{}\text {if}\, \frac{2\pi }{2L}j\in K,\\ 0&{}\text {if}\, \frac{2\pi }{2L}j\not \in K.\\ \end{array}\right. } \end{aligned}$$

(10.38)

Then the energy eigenvalue (10.18) is written as

$$\begin{aligned} E_K=\sum _{k\in K}\bigl \{\cos (2k+\theta )+\lambda \cos (k+\theta )\bigr \} =\mathfrak {R}\Bigl [e^{i\theta }\bigl \{z_0(\varvec{n})+\lambda \,z_\mathrm{coup}(\varvec{n})\bigr \}\Bigr ], \end{aligned}$$

(10.39)

with

$$\begin{aligned} z_0(\varvec{n}):=\sum _{j=1}^{2L}n_j\,\exp \left[ i\frac{2\pi }{L}j\right] ,\quad z_\mathrm{coup}(\varvec{n}):=\sum _{j=1}^{2L}n_j\,\exp \left[ i\frac{2\pi }{2L}j\right] . \end{aligned}$$

(10.40)

In the following lemma, $\varvec{n}=(n_j)_{j=1,2,\ldots ,2L}$ and $\varvec{n}'=(n'_j)_{j=1,2,\ldots ,2L}$ denote general 2L-tuples whose elements are 0 and 1. We also write $|\varvec{n}|=\sum _{j=1}^{2L}n_j$.

Lemma 10.1

Let $L>2$ be prime. Take any $\varvec{n}$ and $\varvec{n}'$ such that $|\varvec{n}|=|\varvec{n}'|<L/2$. Then one has $z_0(\varvec{n})=z_0(\varvec{n}')$ and $z_\mathrm{coup}(\varvec{n})=z_\mathrm{coup}(\varvec{n}')$ simultaneously if and only if $\varvec{n}=\varvec{n}'$.

Proof of Proposition 10.1 given Lemma 10.1

The lemma implies that, when $\varvec{n}\ne \varvec{n}'$, the equality $z_0(\varvec{n})+\lambda \,z_\mathrm{coup}(\varvec{n})=z_0(\varvec{n}')+\lambda \,z_\mathrm{coup}(\varvec{n}')$ may hold only accidentally,⁶⁷ and becomes invalid by an infinitesimal change of $\lambda$. We thus find that, for any $\lambda \in (0,1]$ except for a finite number of points, the complex quantities $z_0(\varvec{n})+\lambda \,z_\mathrm{coup}(\varvec{n})$ (with all possible $\varvec{n}$ such that $|\varvec{n}|=N$) are all distinct.

Suppose that $\lambda$ is fixed to a non-exceptional value. The energy eigenvalue $E_K$ may still degenerate if $e^{i\theta }\{z_0(\varvec{n})+\lambda \,z_\mathrm{coup}(\varvec{n})\}$ and $e^{i\theta }\{z_0(\varvec{n}')+\lambda \,z_\mathrm{coup}(\varvec{n}')\}$ (with $\varvec{n}\ne \varvec{n}'$) happen to have the same real part. Such a degeneracy is lifted by infinitesimally changing $\theta$. Thus degeneracy in $E_K$ can take place only for a finite number of values of $\theta$.

We shall state a mathematical lemma which is the essence of Lemma 10.1. Let $\zeta :=e^{i(2\pi /L)}$. Take an L-tuple $\varvec{m}=(m_j)_{j=1,\ldots ,L}$ with $m_j\in \mathbb {Z}$. Let $|\varvec{m}|=\sum _{j=1}^L|m_j|$ and $\tilde{z}(\varvec{m}):=\sum _{j=1}^Lm_j\zeta ^j$. It is crucial to note that here j runs from 1 to L.

Lemma 10.2

One has $\tilde{z}(\varvec{m})\ne 0$ for any $\varvec{m}$ such that $0<|\varvec{m}|<L$. One also has $\tilde{z}(\varvec{m})\ne \tilde{z}(\varvec{m}')$ for any $\varvec{m},\varvec{m}'$ such that $\varvec{m}\ne \varvec{m}'$ and $|\varvec{m}|+|\varvec{m}'|<L$.

Proof

This lemma is a straightforward consequence of the classical result by Gauss known as “the irreducibility of the cyclotomic polynomials of prime index” (see, for example, Chapter 12, Sect. 3 of [66] or Chapter 13, Sect. 2 of [67]). It implies that the $L-1$ complex numbers $\zeta$, $\zeta ^2$, $\ldots$, $\zeta ^{L-1}$ are rationally independent, i.e., if $\sum _{n=1}^{L-1}m_n\,\zeta ^n=0$ with integers $m_1,\ldots ,m_{L-1}$, one inevitably has $m_1=m_2=\cdots =m_{L-1}=0$.

To show the first claim, we note that $|\varvec{m}|<L$ implies that there is $j_1\in \{1,2,\ldots ,L\}$ such that $m_{j_1}=0$. Then one finds that $\zeta ^{-j_1}\,\tilde{z}(\varvec{m})=\sum _{n=1}^{L-1}\tilde{m}_n\,\zeta ^n$ with $\tilde{m}_n\in \mathbb {Z}$. Since not all of $\tilde{m}_n$ are vanishing, we have $\sum _{n=1}^{L-1}\tilde{m}_n\,\zeta ^n\ne 0$, and hence $\tilde{z}(\varvec{m})\ne 0$.

To show the second claim, we observe that $\tilde{z}(\varvec{m})-\tilde{z}(\varvec{m}')=\tilde{z}(\varvec{m}'')$ with $m''_j=m_j-m'_j$. Since $0<|\varvec{m}''|\le |\varvec{m}|+|\varvec{m}'|<L$, the first claim shows that $\tilde{z}(\varvec{m})-\tilde{z}(\varvec{m}')\ne 0$. $\square$

Proof of Lemma 10.1 given Lemma 10.2

We shall rewrite $z_0(\varvec{n})$ and $z_\mathrm{coup}(\varvec{n})$ in the form of $\tilde{z}(\varvec{m})$. As for $z_0(\varvec{n})$, we readily find

$$\begin{aligned} z_0(\varvec{n})=\sum _{j=1}^{2L}n_j\,\exp \left[ i\frac{2\pi }{L}j\right] =\sum _{j=1}^L(n_j+n_{j+L})\zeta ^j. \end{aligned}$$

(10.41)

To deal with $z_\mathrm{coup}(\varvec{n})$ we note that $e^{i(\pi /L)j}=\zeta ^{j/2}$ for even j, and $e^{i(\pi /L)j}=-\zeta ^{(j\pm L)/2}$ for odd j. Then we get

$$\begin{aligned} z_\mathrm{coup}(\varvec{n})=\sum _{j=1}^{2L}n_j\,\exp \Bigl [i\frac{\pi }{L}j\Bigr ] =\mathop {\sum _{j=1}^L}_{(j\,\text {even})}(n_j-n_{j+L})\zeta ^{j/2} -\mathop {\sum _{j=1}^L}_{(j\,\text {odd})}(n_j-n_{j+L})\zeta ^{(j+L)/2}.\nonumber \\ \end{aligned}$$

(10.42)

Take $\varvec{n}$ and $\varvec{n}'$ such that $|\varvec{n}|=|\varvec{n}'|<L/2$. Then, from the expression (10.41) and Lemma 10.2, we see that $z_0(\varvec{n})=z_0(\varvec{n}')$ if and only if $n_j+n_{j+L}=n'_j+n'_{j+L}$ for all $j=1,2,\ldots ,L$. Similarly from (10.42) and Lemma 10.2, we see that $z_\mathrm{coup}(\varvec{n})=z_\mathrm{coup}(\varvec{n}')$ if and only if $n_j-n_{j+L}=n'_j-n'_{j+L}$ for all $j=1,2,\ldots ,L$. Therefore $z_0(\varvec{n})=z_0(\varvec{n}')$ and $z_\mathrm{coup}(\varvec{n})=z_\mathrm{coup}(\varvec{n}')$ are simultaneously valid if and only if $\varvec{n}=\varvec{n}'$. $\square$

1.3 Toy Model for Two Identical Bodies in Contact

Finally we shall see an artificial model of two identical bodies exchanging energy, the situation treated in Sect. 3.1. We should warn the reader that, unlike the two simple models that we have discussed in Sects. 1.1 and 1.2, the present example is “made up” so that our scenario of typicality and thermalization works perfectly. Nevertheless we hope that this concrete example will be of help in developing intuitions about nontrivial models.

Let us specify the first subsystem. We assume that the eigenvalues of the Hamiltonian $\mathsf {H}^{(1)}$ is $\epsilon _0V n$ with $n=1,2,\ldots$, where $\epsilon _0>0$ is a fixed constant. To mimic the behavior of a macroscopic system, we require that each level with n is $\Omega ^{(1)}_n$ fold degenerate, where

$$\begin{aligned} \Omega ^{(1)}_n=\exp [Vs_n]. \end{aligned}$$

(10.43)

We assume that the “entropy density” $s_n$ is strictly increasing in n, and strictly concave, i.e.,

$$\begin{aligned} 2s_n>s_{n-1}+s_{n+1}, \end{aligned}$$

(10.44)

for any $n=2,3,\ldots$. We denote the eigenstate of $\mathsf {H}^{(1)}$ as $|\psi ^{(1)}_{n,j}\rangle$ where $n=1,2,\ldots$, and $j=1,2,\ldots ,\Omega ^{(1)}_n$. It satisfies $\mathsf {H}^{(1)}|\psi ^{(1)}_{n,j}\rangle =\epsilon _0V n|\psi ^{(1)}_{n,j}\rangle$.

The second subsystem is an exact copy of the first, and we denote by $|\psi ^{(2)}_{n',j'}\rangle$ the energy eigenstate of the Hamiltonian $\mathsf {H}^{(2)}$.

For $m=2,3,\ldots$, let $\mathcal{N}_m:=\{(n,n')\,|\,n,n'\in \{1,2,\ldots \},\ n+n'=m\}$. Then for any $(n,n')\in \mathcal{N}_m$, the tensor product $|\psi ^{(1)}_{n,j}\rangle \otimes |\psi ^{(2)}_{n',j'}\rangle$ is an eigenstate of the noninteracting Hamiltonian $\mathsf {H}^{(1)}\otimes \mathsf {1}+\mathsf {1}\otimes \mathsf {H}^{(2)}$ with the eigenvalue $\epsilon _0V m$. The degeneracy of this eigenvalue is given by

$$\begin{aligned} \Omega _m=\sum _{(n,n')\in \mathcal{N}_m}\Omega ^{(1)}_n\,\Omega ^{(2)}_{n'} =\sum _{(n,n')\in \mathcal{N}_m}\exp [V(s_n+s_{n'})]. \end{aligned}$$

(10.45)

We also denote by $\mathcal{H}_m$ the corresponding $\Omega _m$ dimensional eigenspace.

Suppose that m is even. Take $(n,n')\in \mathcal{N}_m$, and write $n=(m/2)+r$ and $n'=(m/2)-r$. From concavity (10.44), it follows that the quantity $s_n+s_{n'}=s_{(m/2)+r}+s_{(m/2)-r}$ attains its maximum at $r=0$ and decreases strictly⁶⁸ as r deviates from 0. We thus find that

$$\begin{aligned} \frac{\Omega ^{(1)}_{(m/2)+r}\,\Omega ^{(2)}_{(m/2)-r}}{\Omega _{m}} \le \frac{\Omega ^{(1)}_{(m/2)+r}\,\Omega ^{(2)}_{(m/2)-r}}{\Omega ^{(1)}_{m/2}\,\Omega ^{(2)}_{m/2}} =e^{-\tilde{\kappa }(m,r)\,V}, \end{aligned}$$

(10.46)

for any $|r|\ge 1$, where

$$\begin{aligned} \tilde{\kappa }(m,r):=2s_{m/2}-\{s_{(m/2)+r}+s_{(m/2)-r}\}>0, \end{aligned}$$

(10.47)

is strictly increasing in |r| (for a fixed m). This bound will be useful below.

We shall design the interaction Hamiltonian $\mathsf {H}_\mathrm {int}$ so that to leave each subspace $\mathcal{H}_m$ invariant, and mix up all the basis states in it. To make the model trivially solvable, we shall go through the following highly artificial construction. For each $m=2,3,\ldots$, list up all the basis states $|\psi ^{(1)}_{n,j}\rangle \otimes |\psi ^{(2)}_{n',j'}\rangle$ with $(n,n')\in \mathcal{N}_m$, and renumber them⁶⁹ as $|\Phi _{m,\ell }\rangle$, where $\ell =1,2,\ldots ,\Omega _m$. We then define $\mathsf {H}_\mathrm {int}$ by

$$\begin{aligned} \langle \Phi _{m,\ell }|\mathsf {H}_\mathrm {int}|\Phi _{m',\ell '}\rangle = {\left\{ \begin{array}{ll} (V\epsilon _1/2)\,e^{i\theta }&{}\text {if}\, m=m' \,\mathrm{and}\, \ell '=\ell +1\\ (V\epsilon _1/2)\,e^{-i\theta }&{}\text {if}\, m=m' \,\mathrm{and}\, \ell '=\ell -1\\ 0&{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

(10.48)

where we take the “periodic boundary condition” and identify $\ell =\Omega _m+1$ with $\ell =1$. With this artificial choice, the interaction Hamiltonian $\mathsf {H}_\mathrm {int}$, restricted on $\mathcal{H}_m$, is exactly the Hamiltonian of the tight-binding model on a chain of length $\Omega _m$. The phase $\theta$ is introduced to avoid degeneracy.

Then the energy eigenstate of the full Hamiltonian $\mathsf {H}^{(1)}\otimes \mathsf {1}+\mathsf {1}\otimes \mathsf {H}^{(2)}+\mathsf {H}_\mathrm {int}$ is readily obtained as

$$\begin{aligned} |\Psi _{m,q}\rangle =\frac{1}{\sqrt{\Omega _m}} \sum _{\ell =1}^{\Omega _m}\exp \Bigl [i\frac{2\pi q\ell }{\Omega _m}\Bigr ]|\Phi _{m,\ell }\rangle , \end{aligned}$$

(10.49)

where $q=1,\ldots ,\Omega _m$ for each $m=2,3,\ldots$. The corresponding energy eigenvalue is

$$\begin{aligned} E_{m,q}=V\biggl \{\epsilon _0m+\epsilon _1\cos \Bigl [\frac{2\pi q}{\Omega _m}+\theta \Bigr ]\biggr \}. \end{aligned}$$

(10.50)

By taking $\epsilon _0>\epsilon _1>0$ and assuming that $\theta /\pi$ is irrational, we find that the energy eigenvalues are nondegenerate.

Take, for simplicity, an even m, and choose u and $\Delta u$ so that $u- \Delta u=\epsilon _0m-\epsilon _1$ and $u=\epsilon _0m+\epsilon _1$. Then the energy shell $\mathcal {H}_{V,u}$ coincides with the subspace $\mathcal{H}_m$. We shall again look at the energy difference $\mathsf {M}_V=\mathsf {H}^{(1)}\otimes \mathsf {1}-\mathsf {1}\otimes \mathsf {H}^{(2)}$. By construction each $|\Phi _{m,\ell }\rangle$, which is indeed $|\psi ^{(1)}_{n,j}\rangle \otimes |\psi ^{(2)}_{n',j'}\rangle$, is an eigenstate of $\mathsf {M}_V$, i.e., $\mathsf {M}_V|\psi ^{(1)}_{n,j}\rangle \otimes |\psi ^{(2)}_{n',j'}\rangle =V\epsilon _0(n-n')|\psi ^{(1)}_{n,j}\rangle \otimes |\psi ^{(2)}_{n',j'}\rangle$. Since the energy eigenstate $|\Psi _{m,q}\rangle$ is a linear combination of all $|\psi ^{(1)}_{n,j}\rangle \otimes |\psi ^{(2)}_{n',j'}\rangle$ with $(n,n')\in \mathcal{N}_m$ as in (10.49), we readily see that

$$\begin{aligned} \langle \Psi _{m,q}|\,\mathsf {P}[\mathsf {M}_V=V\epsilon _0s]\,|\Psi _{m,q}\rangle = \frac{\Omega ^{(1)}_{(m+s)/2}\,\Omega ^{(2)}_{(m-s)/2}}{\Omega _{m}} \le e^{-\tilde{\kappa }(m,s/2)\,V}, \end{aligned}$$

(10.51)

where the inequality follows from (10.46). Then we immediately see that the energy eigenstate thermalization hypothesis (7.1) holds as⁷⁰

$$\begin{aligned} \langle \Psi _{m,q}|\,\mathsf {P}[|\mathsf {M}_V|\ge V\delta ]\,|\Psi _{m,q}\rangle \le e^{-\kappa (m,\delta )\,V}, \end{aligned}$$

(10.52)

where $\kappa (m,\delta )\simeq \tilde{\kappa }(m,\delta /(2\epsilon _0))$.

We can thus conclude from Theorem 7.1 that the present model exhibits thermalization (in the sense that the energy is almost evenly distributed into the two subsystems) from any initial state.

It is also instructive to see that one can take (initial) states with moderate energy distribution in this model. From (10.49), one finds that any $|\Phi _{m,\ell }\rangle$ can be written in terms of the energy eigenstates as

$$\begin{aligned} |\Phi _{m,\ell }\rangle =\frac{1}{\sqrt{\Omega _m}} \sum _{q=1}^{\Omega _m}\exp \Bigl [-i\frac{2\pi q\ell }{\Omega _m}\Bigr ]|\Psi _{m,q}\rangle . \end{aligned}$$

(10.53)

Since all the expansion coefficients have the same amplitude, the effective dimension of any $|\Phi _{m,\ell }\rangle$, which is indeed $|\psi ^{(1)}_{n,j}\rangle \otimes |\psi ^{(2)}_{n',j'}\rangle$, takes the maximum possible value $D_\mathrm {eff}=D_{V,u}$. This means that there are many nonequilibrium states which satisfies the condition (6.2) with $\eta =0$. We also see that the condition for Theorem 6.2 is satisfied in this case, and hence an overwhelming majority of nonequilibrium states satisfy (6.2).

Appendix 2: Treatment of Non-extensive Quantities

In the main body of the present paper we have treated only macroscopic (extensive) quantities $\mathsf {M}_V^{(1)},\ldots ,\mathsf {M}_V^{(n)}$ of a macroscopic system. Although this is sufficient for our motivation to reproduce equilibrium thermodynamics, one can, if necessary, treat quantities which are not extensive by a slight modification.

Correlation Functions: We concentrate on a model defined on the d-dimensional $L\times \cdots \times L$ hypercubic lattice $\Lambda$ whose sites are denoted as $x,y,\ldots \in \Lambda$, and write $V=L^d$. We assume that the Hamiltonian $\mathsf {H}_V$ is translationally invariant.

Let $\mathsf {f}_o$ and $\mathsf {g}_o$ be operators which act only on a finite number of sites, and denote by $\mathsf {f}_x$ and $\mathsf {g}_x$ their translations. Suppose that one is interested in the correlation function

$$\begin{aligned} c_r(u):=\lim _{V\uparrow \infty }\Bigl \langle \mathsf {f}_x\,\mathsf {g}_{x+r}+(\mathsf {f}_x\,\mathsf {g}_{x+r})^\dagger \Bigr \rangle ^\mathrm {mc}_{V,u}, \end{aligned}$$

(11.1)

for $r\in \mathbb {Z}^d$. We shall argue that the value $c_r(u)$ (for limited r) can be treated as the equilibrium value of a macroscopic quantity.

For a fixed r, we define

$$\begin{aligned} \mathsf {C}_{V,r}:=\sum _{x\in \Lambda }\bigl \{\mathsf {f}_x\,\mathsf {g}_{x+r}+(\mathsf {f}_x\,\mathsf {g}_{x+r})^\dagger \bigr \}, \end{aligned}$$

(11.2)

which is regarded as an extensive quantity. Because of the translation invariance, we have

$$\begin{aligned} c_r(u)=\lim _{V\uparrow \infty }\frac{1}{V}\langle \mathsf {C}_{V,r}\rangle ^\mathrm {mc}_{V,u}. \end{aligned}$$

(11.3)

We then take a sufficiently large subset $\Lambda _0\subset \mathbb {Z}^d$ (which is independent of V), and include all $\mathsf {C}_{V,r}$ with $r\in \Lambda _0$ into the list of macroscopic quantities to consider.⁷¹ We expect that the thermodynamic bound (2.16) is still valid in general after including $\mathsf {C}_{V,r}$. In fact Proposition 3.2 for quantum spin systems extends to this case as it is (with a worse constant).

In this manner we can treat, within our scheme, the correlation function $c_r(u)$ as the equilibrium value of the macroscopic quantity $\mathsf {C}_{V,r}$. All the results about typicality (Sect. 4) and thermalization (Sects. 5, 6, and 7) can be applied as they are when the assumptions are verified. In most cases it is enough to take $\Lambda _0$ sufficiently large (to exceed the correlation length) in order to recover essential physics described by the correlation function.

Probability Distribution in a Small System: Consider a quantum mechanical system defined on a region (which can be a lattice) with a small volume $V_0$. Physical quantities in this system should exhibit relatively large fluctuation in thermal equilibrium. With a little trick (see, e.g., [26]), one can also treat the probability distribution of such a fluctuating quantity within our scheme.

Let a self-adjoint operator $\mathsf {f}$ be the quantity of interest of the small system. We prepare N identical copies of the small system, and consider a combined system of all the copies. There are no interactions between small subsystems. Denoting by $\mathsf {f}^{(j)}$ the quantity $\mathsf {f}$ in the j-th copy, we define, for $a<b$, the operator

$$\begin{aligned} \mathsf {N}_{[a,b]}:=\sum _{j=1}^N\mathsf {P}\bigl [\mathsf {f}^{(j)}\in [a,b]\bigr ], \end{aligned}$$

(11.4)

which counts the number of copies in which the value of $\mathsf {f}$ falls in to the interval [a, b].

Let $\langle \cdots \rangle ^\mathrm{mc}_{N,u}$ be the microcanonical expectation corresponding to the energy range $[(u- \Delta u)N,uN]$ for the whole system. Then it is easily found that⁷²

$$\begin{aligned} p_{\beta (u)}(a,b):=\lim _{N\uparrow \infty }\frac{1}{N}\langle \mathsf {N}_{[a,b]}\rangle ^\mathrm{mc}_{N,u} \end{aligned}$$

(11.5)

is the probability that the value of $\mathsf {f}$ falls into [a, b] in a single small system described by the canonical distribution with $\beta (u)$.

Let us divide the spectrum of $\mathsf {f}$ in to n intervals as $[f_\mathrm{min},f_\mathrm{max}]=\bigcup _{j=1}^n[a_{j-1},a_j]$. We then regard $\mathsf {N}_{[a_{j-1},a_j]}$ with $j=1,\ldots ,n$ as our macroscopic quantities. It is again not hard to prove that the thermodynamic bound (2.16) is valid for any u.

From the results in Sect. 4, we can thus essentially recover the probability distribution $p_\beta (a,b)$ from a single pure state of a large system (constructed by combining copies of the original small system). Unfortunately the large system, as it is, never exhibit thermalization since small parts do not interact with each other. It is likely that the system thermalizes if we add weak interactions between the small systems, but this is not easy to prove.

Appendix 3: Mixed Initial State

Our results about thermalization in Sects. 5, 6, and 7 readily extends to the case where the initial state is a mixed state. In what follows we only consider density matrices whose supports are the energy shell $\mathcal {H}_{V,u}$. Corresponding to Definitions 2.1 or 2.2, we say that a state $\rho$ represents thermal equilibrium if

$$\begin{aligned} \mathrm{Tr}[\rho \,\mathsf {P}\!_\mathrm {neq}]\le e^{-\alpha V}, \end{aligned}$$

(12.1)

where $\mathsf {P}\!_\mathrm {neq}$ is defined by (2.8), (2.12) or (2.15) depending on the situation and the treatment.

Take an initial state $\rho (0)$, and let $\rho (t)=e^{-i\mathsf {H}_Vt}\rho (0)\,e^{i\mathsf {H}_Vt}$ be its time evolution. Then the statement corresponding to Lemma 5.1 reads

Lemma 12.1

Suppose that there is $\tau >0$ and it holds that

$$\begin{aligned} \frac{1}{\tau }\int _0^\tau dt\,\mathrm{Tr}[\rho (t)\,\mathsf {P}\!_\mathrm {neq}] \le e^{-(\alpha +\nu ) V}. \end{aligned}$$

(12.2)

Then there exists a collection of intervals $\mathcal{G}\subset [0,\tau ]$ such that $|\mathcal{G}|/\tau \ge 1-e^{-\nu V}$, and we have for any $t\in \mathcal{G}$ that

$$\begin{aligned} \mathrm{Tr}[\rho (t)\,\mathsf {P}\!_\mathrm {neq}]\le e^{-\alpha V}, \end{aligned}$$

(12.3)

which means that $\rho (t)$ represents thermal equilibrium in the sense of (12.1).

To discuss the extension of Theorem 6.1, it is useful to define two effective dimensions. The first is

$$\begin{aligned} D_\mathrm {eff}^\mathrm{full}:=\frac{1}{\mathrm{Tr}[\{\rho (t)\}^2]}, \end{aligned}$$

(12.4)

which is the inverse of the purity $\mathrm{Tr}[\{\rho (t)\}^2]$, and is clearly independent of t. Note that one has $D_\mathrm {eff}^\mathrm{full}=1$ when $\rho (t)$ represents a pure state.

The effective dimension which corresponds to $D_\mathrm {eff}$ of (6.2) is defined using the energy eigenstate basis $\{|\psi _j\rangle \}_{j=1,\ldots ,D_{V,u}}$ as

$$\begin{aligned} D_\mathrm {eff}^\mathrm{diag}:=\Bigl \{\sum _j\bigl (\langle \psi _j|\rho (t)|\psi _j\rangle \bigr )^2\Bigr \}^{-1}=\frac{1}{\mathrm{Tr}[(\rho _\mathrm{diag})^2]}, \end{aligned}$$

(12.5)

where

$$\begin{aligned} \rho _\mathrm{diag}:=\sum _k|\psi _j\rangle \langle \psi _j|\rho (t)|\psi _j\rangle \langle \psi _j| \end{aligned}$$

(12.6)

is the density matrix for the “diagonal ensemble” obtained by deleting the off-diagonal elements of $\rho (t)$. Note that $\rho _\mathrm{diag}$ and $D_\mathrm {eff}^\mathrm{diag}$ are independent of t.

These effective dimensions satisfy the bound $D_\mathrm {eff}^\mathrm{full}\le D_\mathrm {eff}^\mathrm{diag}$ because of the monotonicity of the purity.⁷³

We first note that the state is in thermal equilibrium to begin with if $D_\mathrm {eff}^\mathrm{full}$ is sufficiently large.

Theorem 12.1

If the thermodynamic bound (2.16) is valid, and one has

$$\begin{aligned} D_\mathrm {eff}^\mathrm{full}\ge e^{-\eta V}D_{V,u}, \end{aligned}$$

(12.7)

with $\eta$ satisfying $\gamma -\eta >2(\alpha +\nu )$, then $\rho (t)$ represents thermal equilibrium for any t (including $t=0$).

Proof

From the Schwarz inequality, we get

$$\begin{aligned} \mathrm{Tr}[\rho (t)\mathsf {P}\!_\mathrm {neq}]&=\mathrm{Tr}_{\mathcal {H}_{V,u}}[\rho (t)\mathsf {P}\!_\mathrm {neq}] \le \sqrt{ \mathrm{Tr}_{\mathcal {H}_{V,u}}[\{\rho (t)\}^2]\,\mathrm{Tr}_{\mathcal {H}_{V,u}}[\mathsf {P}\!_\mathrm {neq}] } \nonumber \\&=\sqrt{\frac{D_{V,u}\langle \mathsf {P}\!_\mathrm {neq}\rangle ^\mathrm {mc}_{V,u}}{D_\mathrm {eff}^\mathrm{full}}}. \end{aligned}$$

(12.8)

Then the statement follows exactly as in the proof of Theorem 6.1. $\square$

Of course it is much more interesting if (12.7) is not valid. The following is a straightforward extension of Theorem 6.1.

Theorem 12.2

If the thermodynamic bound (2.16) is valid, and one has $D_\mathrm {eff}^\mathrm{diag}\ge e^{-\eta V}D_{V,u}$ with $\eta$ satisfying $\gamma -\eta >2(\alpha +\nu )$, then $\rho (t)$ approaches thermal equilibrium (in the sense of Lemma 5.1).

Proof

Note that the nondegeneracy of $E_j$ implies

$$\begin{aligned} \lim _{\tau \uparrow \infty }\frac{1}{\tau }\int _0^\tau dt\,\mathrm{Tr}[\rho (t)\,\mathsf {P}\!_\mathrm {neq}]&= \lim _{\tau \uparrow \infty }\frac{1}{\tau }\int _0^\tau dt\sum _{j,j'\in J_{V,u}}e^{i(E_j-E_{j'})t}\langle \psi _{j'}|\rho (0)|\psi _j\rangle \langle \psi _j|\mathsf {P}\!_\mathrm {neq}|\psi _{j'}\rangle \nonumber \\&=\sum _{j\in J_{V,u}}\langle \psi _{j}|\rho (0)|\psi _j\rangle \langle \psi _j|\mathsf {P}\!_\mathrm {neq}|\psi _{j}\rangle =\mathrm{Tr}[\rho _\mathrm{diag}\mathsf {P}\!_\mathrm {neq}]. \end{aligned}$$

(12.9)

Then the rest of the proof is the same as that of Theorem 12.1. $\square$

Theorem 7.1, which makes use of the energy eigenstate thermalization hypothesis, also extends to the case with mixed initial state. We omit the details since the extension is trivial.

Appendix 4: Typicality of the Canonical Expectation Values

We have exclusively discussed the microcanonical setting in the present paper. Here we apply some of the techniques in the present paper to the setting where the system of interest is coupled to a heat bath, and show the typicality of the canonical expectation values.

Setting: We consider a macroscopic quantum system with volume V, and denote by $\mathcal{H}_\mathrm {S}$ and $\mathsf {H}_\mathrm {S}$ the Hilbert space and the Hamiltonian, respectively. The system is coupled to a heat bath (reservoir) which itself is a macroscopic quantum system with volume $V_\mathrm {B}=\lambda V$, Hilbert space $\mathcal{H}_\mathrm {B}$, and Hamiltonian $\mathsf {H}_\mathrm {B}$. Here $\lambda$ is a fixed constant which is usually taken to be⁷⁴ $\lambda \gg 1$.

The whole system, i.e., the system plus the heat bath, has the volume ${V_\mathrm {tot}}=(1+\lambda )V$, the Hilbert space $\mathcal{H}_\mathrm {tot}=\mathcal{H}_\mathrm {S}\otimes \mathcal{H}_\mathrm {B}$, and the Hamiltonian

$$\begin{aligned} \mathsf {H}_\mathrm {tot}:=\mathsf {H}_\mathrm {S}\otimes \mathsf {1}+\mathsf {1}\otimes \mathsf {H}_\mathrm {B}+\mathsf {H}_\mathrm {int}, \end{aligned}$$

(13.1)

where $\mathsf {H}_\mathrm {int}$ describes the interaction between the system and the bath. We assume $\left\| \mathsf {H}_\mathrm {int}\right\| \le h_0V^\zeta$ with constants $h_0>0$ and $0<\zeta <1$. The energy shell $\mathcal {H}_{{V_\mathrm {tot}},u}$ for the whole system is defined as in Sect. 2.1 by replacing V with ${V_\mathrm {tot}}$.

Canonical Typicality: Popescu, Short, and Winter [12] and Goldstein, Lebowitz, Tumulka, and Zanghì [13] independently stated the important result known as the canonical typicality (see also Sugita [14]).

Let ${\rho }^\mathrm {mc}_{{V_\mathrm {tot}},u}$ be the microcanonical density matrix for the whole system, defined as in (2.5) by replacing V with ${V_\mathrm {tot}}$. Let $\rho _\mathrm {S}:=\mathrm{Tr}_\mathrm {B}[\,{\rho }^\mathrm {mc}_{{V_\mathrm {tot}},u}\,]$ be the reduced density matrix for the system, where $\mathrm {Tr}_\mathrm {B}$ denotes the trace in $\mathcal{H}_\mathrm {B}$. It is usually expected (and can be proved with suitable assumptions) that $\rho _\mathrm {S}$ is close to the canonical density matrix for the system with the inverse temperature $\beta (u)$ defined in (2.2).

Take an arbitrary normalized state $|\varphi \rangle \in \tilde{\mathcal {H}}_{{V_\mathrm {tot}},u}$ from the energy shell, and write the corresponding density matrix for the system as $\rho _\varphi :=\mathrm{Tr}_\mathrm{B}[\,|\varphi \rangle \langle \varphi |\,]$. It has been shown that, when the state $|\varphi \rangle$ is sampled from $\tilde{\mathcal {H}}_{{V_\mathrm {tot}},u}$ randomly according to the uniform measure as in Sect. 4.1, the density matrices $\rho _\mathrm {S}$ and $\rho _\varphi$ are very close to each other with probability close to one. This is the canonical typicality.

Therefore, when one is only interested in physical quantities of the system, it is typical that the state of the system is described by the canonical distribution. We believe that this provides a satisfactory characterization and justification of the canonical distribution.

Main Result: To complete the justification of the canonical distribution from the operational point of view, we still need to show that (i) the result of a single measurement of a macroscopic quantity of the system almost coincides with the expectation value with respect to $\rho _\mathrm {S}$, and (ii) $\rho _\mathrm {S}$ is indeed close to the canonical density matrix.

Both (i) and (ii) can be done starting from the canonical typicality. But let us here present a result (which does not make an explicit use of the canonical typicality) which attains the goal directly.

Define the canonical expectation for the system as

$$\begin{aligned} \langle \cdots \rangle ^\mathrm {can}_{V,\beta }:= \frac{\mathrm{Tr}_\mathrm{S}[\,(\cdots )\,e^{-\beta \mathsf {H}_\mathrm{S}}\,]}{\mathrm{Tr}_\mathrm{S}[\,e^{-\beta \mathsf {H}_\mathrm{S}}\,]}, \end{aligned}$$

(13.2)

where $\mathrm{Tr}_\mathrm{S}[\cdots ]$ denotes the trace over the space $\mathcal{H}_\mathrm{S}$. Note that neither $\mathsf {H}_\mathrm{int}$ nor $\mathsf {H}_\mathrm{B}$ appears in the definition (13.2).

We assume that the whole system satisfies the condition for the number of states (2.1), with V replaced by ${V_\mathrm {tot}}$.

As in Sect. 2.2, we let $\mathsf {M}_V^{(1)},\ldots ,\mathsf {M}_V^{(n)}$ be extensive quantities and define the nonequilibrium projection $\mathsf {P}\!_\mathrm {neq}$ as (2.8), (2.12) or (2.15) , but by replacing $m^{(i)}(u)\simeq \langle \mathsf {M}_V^{(i)}\rangle ^\mathrm{mc}_{V,u}/V$ by the canonical expectation value $\langle \mathsf {M}_V^{(i)}\rangle ^\mathrm{can}_{V,\beta }/V$. We then make a crucial assumption that the canonical version of the thermodynamic bound

$$\begin{aligned} \langle \mathsf {P}\!_\mathrm {neq}\rangle ^\mathrm{can}_{V,\beta }\le e^{-\gamma '(\beta )\,V} \end{aligned}$$

(13.3)

is valid for sufficiently large V with $\gamma '(\beta )>0$. This is almost the standard large deviation upper bound, which is expected to be valid in general, and can be proved for models treated in Sects. 3.2 and 3.3.

Theorem 13.1

Take the energy density u such that (3.1) is valid, and let $\beta =\beta (u)$. Assume that the bound (13.3) holds. We choose a normalized state $|\varphi \rangle \in \tilde{\mathcal {H}}_{{V_\mathrm {tot}},u}$ randomly according to the uniform measure as in Theorem 4.1. Then with probability larger than $1-e^{-\nu 'V}$, we have

$$\begin{aligned} \langle \varphi |\mathsf {P}\!_\mathrm {neq}\otimes \mathsf {1}|\varphi \rangle \le e^{-\alpha 'V}, \end{aligned}$$

(13.4)

for sufficiently large V, where the constants satisfy $\nu '\simeq \gamma '(\beta )-\alpha '$.

The theorem says that, for an overwhelming majority of the states in the energy shell, the result of a single measurement of $\mathsf {M}_V^{(i)}$ almost coincides with the canonical expectation value $\langle \mathsf {M}_V^{(i)}\rangle ^\mathrm{can}_{V,\beta }$ with probability close to one. This provides a rather satisfactory justification of the canonical distribution.

As we noted before the ration $\lambda$ need not be large. This is because the proof makes use of the equivalence of the microcanonical and the canonical ensembles. When $\lambda$ is large, however, we see that the inverse temperature $\beta$ is essentially determined by the properties and the energy of the heat bath.

Proof of Theorem 13.1

We shall prove that

$$\begin{aligned} \overline{\langle \varphi |\mathsf {P}\!_\mathrm {neq}\otimes \mathsf {1}|\varphi \rangle }\le e^{-\gamma ''V}, \end{aligned}$$

(13.5)

where the left-hand side is the average over $|\varphi \rangle \in \tilde{\mathcal {H}}_{{V_\mathrm {tot}},u}$ as defined in (4.1) and $\gamma ''\simeq \gamma '(\beta )$. Then by using the Markov inequality as in the proof of Theorem 4.1, we get the desired (13.4).

To bound the average, we note that

$$\begin{aligned} \overline{\langle \varphi |\mathsf {P}\!_\mathrm {neq}\otimes \mathsf {1}|\varphi \rangle }= \langle \mathsf {P}\!_\mathrm {neq}\otimes \mathsf {1}\rangle ^\mathrm{mc}_{{V_\mathrm {tot}},u} \le \eta (u){V_\mathrm {tot}}\langle \mathsf {P}\!_\mathrm {neq}\otimes \mathsf {1}\rangle ^\mathrm{can}_{{V_\mathrm {tot}},\beta (u)}, \end{aligned}$$

(13.6)

where $\langle \cdots \rangle ^\mathrm{mc}_{{V_\mathrm {tot}},u}$ and $\langle \cdots \rangle ^\mathrm{can}_{{V_\mathrm {tot}},\beta }$ are the microcanonical and the canonical expectations, respectively, of the whole system with Hamiltonian (13.1). The equality and the inequality in (13.6) follow from (4.3) and (8.8), respectively. Then exactly as in (8.31), the final expectation is bounded as

$$\begin{aligned} \langle \mathsf {P}\!_\mathrm {neq}\otimes \mathsf {1}\rangle ^\mathrm{can}_{{V_\mathrm {tot}},\beta }\le e^{2\beta h_0V^\zeta }\langle \mathsf {P}\!_\mathrm {neq}\rangle ^\mathrm{can}_{V,\beta }, \end{aligned}$$

(13.7)

where the expectation in the right-hand side is the one defined in (13.2). By combining (13.6), (13.7), and the assumption (13.3), we get (13.5). $\square$

It is a pleasure to thank Shelly Goldstein and Takashi Hara, my collaborators in closely related topics, for valuable discussions and inspirations, Shin Nakano, Yoshiko Ogata, and Luc Rey-Bellet for their indispensable help in mathematical issues, and Marcus Cramer, Fabian Essler, Tatsuhiko Ikeda, Joel Lebowitz, Elliott Lieb, Takashi Mori, Hidetoshi Nishimori, Peter Reimann, Marcos Rigol, Takahiro Sagawa, Udo Seifert, Akira Shimizu, and Yu Watanabe for useful discussions and comments. The present work was supported in part by JSPS Grants-in-Aid for Scientific Research no. 25400407.