Skip to main content
SpringerLink
Log in

Patchiness and Demographic Noise in Three Ecological Examples

  • Published:
Journal of Statistical Physics Aims and scope Submit manuscript

Abstract

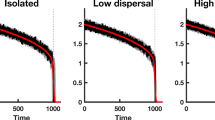
Understanding the causes and effects of spatial aggregation is one of the most fundamental problems in ecology. Aggregation is an emergent phenomenon arising from the interactions between the individuals of the population, able to sense only—at most—local densities of their cohorts. Thus, taking into account the individual-level interactions and fluctuations is essential to reach a correct description of the population. Classic deterministic equations are suitable to describe some aspects of the population, but leave out features related to the stochasticity inherent to the discreteness of the individuals. Stochastic equations for the population do account for these fluctuation-generated effects by means of demographic noise terms but, owing to their complexity, they can be difficult (or, at times, impossible) to deal with. Even when they can be written in a simple form, they are still difficult to numerically integrate due to the presence of the “square-root” intrinsic noise. In this paper, we discuss a simple way to add the effect of demographic stochasticity to three classic, deterministic ecological examples where aggregation plays an important role. We study the resulting equations using a recently-introduced integration scheme especially devised to integrate numerically stochastic equations with demographic noise. Aimed at scrutinizing the ability of these stochastic examples to show aggregation, we find that the three systems not only show patchy configurations, but also undergo a phase transition belonging to the directed percolation universality class.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. Even worse, in some cases, the described derivation of continuous approaches relying on standard field-theoretical techniques does not produce any Langevin equation, i.e. the resulting generating functional cannot be cast into any standard stochastic equation.

  2. In the assumption of D and D 2 being constant, it is implicitly assumed that there is no intraspecific variability or other kind of heterogeneity in the distribution of these dispersal rates.

  3. Of course, active aggregation must be added on top of this to bring the patterns to a more realistic scenario. However, our objective is to show that there may be two complementary origins of pattern that must be integrated, one arising from stochastic demographic fluctuations and the other owing to active aggregation.

  4. Note that, in this case, we are using as a reference at the microscopic level the real interactions and patterns observed in Nature (see [17, 18, 36] for some illustrative examples).

References

  1. Durrett, R., Levin, S.A.: The importance of being discrete (and spatial). Theor. Popul. Biol. 46, 363–394 (1994)

    Article  MATH  Google Scholar 

  2. Cantrell, R.S., Cosner, C.: Deriving reaction-diffusion models in ecology from interacting particle systems. J. Math. Biol. 48, 187–217 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  3. Amit, D., Martín-Mayor, V.: Field Theory, the Renormalization Group, and Critical Phenomena, 3rd edn. World Scientific, Singapore (2005)

    Book  Google Scholar 

  4. Turing, A.M.: The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond., Ser. B 237, 37–72 (1952)

    Article  ADS  Google Scholar 

  5. Steele, J.: Spatial heterogeinity and population stability. Nature 248, 83 (1974)

    Article  ADS  Google Scholar 

  6. Okubo, A.: Tech. Rept 86, Chesapeake Bay Inst. Johns Hopkins University, Baltimore (1974)

  7. Levin, S.A., Segel, L.A.: Hypothesis for origin of planktonic patchiness. Nature 259, 659 (1976)

    Article  ADS  Google Scholar 

  8. Steele, J., Henderson, E.W.: A simple model for plankton patchiness. J. Plankton Res. 14, 1397–1403 (1992)

    Article  Google Scholar 

  9. Butler, T., Goldenfeld, N.: Robust ecological pattern formation induced by demographic noise. Phys. Rev. E 80, 030902(R) (2009)

    ADS  Google Scholar 

  10. Butler, T., Goldenfeld, N.: Fluctuation-driven Turing patterns. Phys. Rev. E 84, 011112 (2011)

    Article  ADS  Google Scholar 

  11. Doi, M.: Second quantization representation for classical many-particle systems. J. Phys. A 9, 1465–1479 (1976)

    Article  ADS  Google Scholar 

  12. Peliti, L.: Path integral approach to birth-death processes on a lattice. J. Phys. 46, 1469–1483 (1985)

    Article  MathSciNet  Google Scholar 

  13. Grassberger, P., Scheunert, M.: Fock-space methods for identical classical objects. Fortschr. Phys. 28, 547–578 (1980)

    Article  MathSciNet  Google Scholar 

  14. DeDominicis, C.J.: Techniques de renormalisation de la théorie des champs et dynamique des phénomènes critiques. J. Phys. 37, 247–257 (1976)

    Google Scholar 

  15. Janssen, H.K.: On a Lagrangian for classical field dynamics and renormalization group calculations of dynamical critical properties. Z. Phys. B 23, 377–380 (1976)

    Article  ADS  Google Scholar 

  16. Martin, P.C., Siggia, E.D., Rose, H.A.: Statistical dynamics of classical systems. Phys. Rev. A 8, 423–437 (1973)

    Article  ADS  Google Scholar 

  17. Klausmeier, C.: Regular and irregular patterns in semiarid vegetation. Science 284, 1826–1828 (1999)

    Article  Google Scholar 

  18. von Hardenberg, J., Meron, E., Shachak, M., Zarmi, Y.: Diversity of vegetation patterns and desertification. Phys. Rev. Lett. 87(198101), 1–4 (2001)

    Google Scholar 

  19. Manor, A., Shnerb, N.M.: Facilitation, competition, and vegetation patchiness from scale free distribution to patterns. J. Theor. Biol. 253, 838–842 (2008)

    Article  MathSciNet  Google Scholar 

  20. Hernández-García, E., López, C.: Clustering, advection and patterns in a model of population dynamics with neighborhood-dependent rates. Phys. Rev. E 70, 016216 (2004)

    Article  ADS  Google Scholar 

  21. López, C., Hernández-García, E.: Fluctuations impact on a pattern-forming model of population dynamics with non-local interactions. Physica D 199, 223–234 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  22. Hernández-García, E., López, C.: Birth, death and diffusion of interacting particles. J. Phys. Condens. Matter 17, S4263–4274 (2005)

    Article  Google Scholar 

  23. Ramos, F., López, C., Hernández-García, E., Muñoz, M.A.: Crystallization and melting of bacteria colonies and Brownian bugs. Phys. Rev. E 77, 011116 (2008)

    Article  ADS  Google Scholar 

  24. Täuber, U.C.: Stochastic population oscillations in spatial predator-prey models. J. Phys. Conf. Ser. 319, 012019 (2011)

    Article  ADS  Google Scholar 

  25. Dickman, R.: Numerical study of a field theory for directed percolation. Phys. Rev. E 50, 4404–4409 (1994)

    Article  ADS  Google Scholar 

  26. Dornic, I., Chaté, H., Muñoz, M.A.: Integration of Langevin equations with multiplicative noise and the viability of field theories for absorbing phase transitions. Phys. Rev. Lett. 94, 100601 (2005)

    Article  ADS  Google Scholar 

  27. Moro, E.: Numerical schemes for continuum models of reaction-diffusion systems subject to internal noise. Phys. Rev. E 70, 045102(R) (2004)

    Article  ADS  Google Scholar 

  28. Hinrichsen, H.: Nonequilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 49, 815–958 (2000)

    Article  ADS  Google Scholar 

  29. Odor, G.: Universality classes in nonequilibrium lattice systems. Rev. Mod. Phys. 76, 663–724 (2004)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  30. Grinstein, G., Muñoz, M.A.: In: Garrido, P., Marro, J. (eds.) Fourth Granada Lectures in Computational Physics. Lecture Notes in Physics, vol. 493, p. 223. Springer, Berlin (1997)

    Chapter  Google Scholar 

  31. Marro, J., Dickman, R.: Nonequilibrium Phase Transitions in Lattice Models. Cambridge University Press, Cambridge (1999)

    Book  Google Scholar 

  32. Van Kampen, N.G.: Stochastic Processes in Physics and Chemistry, 6th edn. North-Holland, Elsevier, Amsterdam (1990)

    Google Scholar 

  33. McKane, A.J., Newman, T.J.: Predator-prey cycles from resonant amplification of demographic stochasticity. Phys. Rev. Lett. 94, 218102 (2005)

    Article  ADS  Google Scholar 

  34. Levin, S.A., Withfield, M.: Patchiness in marine and terrestrial systems from individuals to populations. Philos. Trans. R. Soc. Lond. B, Biol. Sci. 343, 99–103 (1994)

    Article  ADS  Google Scholar 

  35. Shnerb, N.M., Sarah, P., Lavee, H., Solomon, S.: Reactive glass and vegetation patterns. Phys. Rev. Lett. 90, 038101 (2003)

    Article  ADS  Google Scholar 

  36. Shnerb, N.M.: Pattern formation and nonlocal logistic growth. Phys. Rev. E 69, 061917 (2004)

    Article  ADS  Google Scholar 

  37. Manor, A., Shnerb, M.N.: Dynamical failure of Turing patterns. Europhys. Lett. 74, 837–843 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  38. Fuentes, M.A., Kuperman, M.N., Kenkre, V.M.: Nonlocal interaction effects on pattern formation in population dynamics. Phys. Rev. Lett. 91, 158104 (2003)

    Article  ADS  Google Scholar 

  39. Sayama, M.A., de Aguiar, M., Bar-Yam, Y., Baranger, M.: Spontaneous pattern formation and genetic invasion in locally mating and competing populations. Phys. Rev. E 65, 051919 (2002)

    Article  ADS  Google Scholar 

  40. Maruvka, Y.E. Shnerb, N.M.: Nonlocal competition and logistic growth: patterns, defects, and fronts. Phys. Rev. E73, 011903 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  41. Pigolotti, S., López, C., Hernández-García, E.: Species clustering in competitive Lotka-Volterra models. Phys. Rev. Lett. 98, 258101 (2007)

    Article  ADS  Google Scholar 

  42. Levin, S.A., Segel, L.A.: Pattern generation in space and aspect. SIAM Rev. 27, 2–67 (1985)

    Article  MathSciNet  Google Scholar 

  43. Brigatti, E., Schwammle, V., Neto, M.A.: Individual-based model with global competition interaction: fluctuation effects in pattern formation. Phys. Rev. E 77, 021914 (2008)

    Article  ADS  Google Scholar 

  44. Janssen, H.K.: On the nonequilibrium phase transition in reaction-diffusion systems with an absorbing stationary state. Z. Phys. B 42, 151–154 (1981)

    Article  ADS  Google Scholar 

  45. Grassberger, P.: On phase transitions in Schlögl’s second model. Z. Phys. B 47, 365–374 (1982)

    Article  MathSciNet  ADS  Google Scholar 

  46. Muñoz, M.A., Grinstein, G., Dickman, R., Livi, R.: Critical behavior of systems with many absorbing states. Phys. Rev. Lett. 76, 451–454 (1996)

    Article  ADS  Google Scholar 

  47. Muñoz, M.A., Grinstein, G., Dickman, R.: Phase diagram of systems with an infinite number of absorbing states. J. Stat. Phys. 91, 541–569 (1998)

    Article  MATH  Google Scholar 

  48. Muñoz, M.A., Grinstein, G., Dickman, R., Livi, R.: Infinite numbers of absorbing states: critical behavior. Physica D 103, 485–490 (1997)

    Article  ADS  MATH  Google Scholar 

  49. Grinstein, G., Lai, Z.-W., Browne, D.A.: Critical phenomena in a nonequilibrium model of heterogeneous catalysis. Phys. Rev. A 40, 4820–4823 (1989)

    Article  ADS  Google Scholar 

  50. Janssen, H.K.: Directed percolation with colors and flavors. J. Stat. Phys. 103, 801–839 (2001)

    Article  MATH  Google Scholar 

  51. Vespignani, A., Dickman, R., Muñoz, M.A., Zapperi, S.: Driving, conservation and absorbing states in sandpiles. Phys. Rev. Lett. 81, 5676–5679 (1998)

    Article  ADS  Google Scholar 

  52. Dickman, R., Muñoz, M.A., Vespignani, A., Zapperi, S.: Paths to self-organized-criticality. Braz. J. Phys. 30, 27–41 (2000)

    Article  ADS  Google Scholar 

  53. Vespignani, A., Dickman, R., Muñoz, M.A., Zapperi, S.: Absorbing phase transitions in fixed-energy sandpiles. Phys. Rev. E 62, 4564–4582 (2000)

    Article  ADS  Google Scholar 

  54. Maia, D.S., Dickman, R.: Diffusive epidemic process: theory and simulation. J. Phys. Condens. Matter 19, 065143 (2007)

    Article  ADS  Google Scholar 

  55. van Wijland, F., Oerding, K., Hilhorst, H.J.: Wilson renormalization of a reaction-diffusion process. Physica A 251, 179–201 (1998)

    Article  Google Scholar 

  56. Lübeck, S.: Universal scaling behavior of non-equilibrium phase transitions. Int. J. Mod. Phys. B 18, 3977 (2004)

    Article  ADS  Google Scholar 

  57. Muñoz, M.A., Dickman, R., Vespignani, A., Zapperi, S.: Avalanche and spreading exponents in systems with absorbing states. Phys. Rev. E 59, 6175–6179 (1999)

    Article  ADS  Google Scholar 

  58. López, C., Ramos, F., Hernández-García, E.: An absorbing phase transition from a structured active particle phase. J. Phys. Condens. Matter 19, 065133 (2007)

    Article  Google Scholar 

Download references

Acknowledgements

We gratefully acknowledge support from the Cooperative Institute for Climate Science (CICS) of Princeton University and the National Oceanographic and Atmospheric Administration’s (NOAA) Geophysical Fluid Dynamics Laboratory (GFDL), the National Science Foundation (NSF) under grant OCE-1046001, the Spanish MICINN-FEDER under project FIS2009-08451, and from Junta de Andalucía (Proyecto de Excelencia P09FQM-4682). MAM thanks I. Dornic, H. Chaté and, C. López, and F. Ramos, for a long term collaboration on some of the issues presented here.

Author information

Authors and Affiliations

  1. Department of Ecology and Evolutionary Biology, Princeton University, Princeton, NJ, 08544-1003, USA

    Juan A. Bonachela & Simon A. Levin

  2. Instituto Carlos I de Física Teórica y Computacional, Facultad de Ciencias, Universidad de Granada, 18071, Granada, Spain

    Miguel A. Muñoz

Authors
  1. Juan A. Bonachela
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Miguel A. Muñoz
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Simon A. Levin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Juan A. Bonachela.

Appendix

Appendix

We have numerically shown that the critical exponents measured in all of the examples discussed in this paper are directed-percolation like. Here we justify that result by analyzing their corresponding Langevin equations Eqs. (3), Eqs. (5), and Eq. (7).

As conjectured years ago by Janssen and Grassberger [44, 45] all systems exhibiting a phase transition into a unique absorbing state, with a single-component order parameter, and no extra symmetry or conservation law, belong to the same universality class whose most distinguished representative is directed percolation (DP). In a field theoretical description this universality class is represented by the Reggeon Field theory (RFT), [44, 45] which in terms of a Langevin equation reads:

$$ {\displaystyle{\partial\rho(\mathbf {x},t) \over\partial t}} = \nabla^2 \rho (\mathbf {x},t) + a \rho(\mathbf {x},t) -b \rho^2(\mathbf {x},t) + \sqrt{\rho(\mathbf {x},t)} \eta(\mathbf {x},t) , $$
(9)

where ρ(x,t) is the density field at position x and time t, a and b are parameters, and η(x,t) is a delta-correlated Gaussian noise, 〈η(x,t)η(x′,t′)〉=Dδ(x−x′)δ(t−t′).

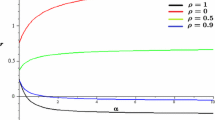
The previous conjecture was confirmed in a large number of computer simulations, series expansion analysis, field theoretical studies, etc. Indeed, the DP universality class has proved to be extremely robust against the modification of many details in the microscopic models. The conjecture of universality has been extended systems with an infinite number of absorbing states [46, 47] (see also [48]). Also, Grinstein et al. extended the conjecture to the case of multicomponent systems [49] (see also [50]). Considering, for the sake of simplicity a two-component system with absorbing states, it can generically be described by a set of Langevin equations whose linearized dynamics (ignoring the Laplacian terms and the noise) is generically:

$$ \begin{array}{ll} \partial_{t}\rho_1(\mathbf {x},t)=a_{1,1}\rho_1+ a_{1,2}\rho_2 \cr\noalign{\vspace{3pt}} \partial_{t}\rho_2(\mathbf {x},t)= a_{2,1}\rho_1 + a_{2,2}\rho_2 \end{array} $$
(10)

and diagonalizing the matrix of the linear coefficients:

$$ \begin{array}{@{}ll} \partial_{t}\xi_1(\mathbf {x},t)=\lambda_1\xi_1 \cr\noalign{\vspace{3pt}} \partial_{t}\xi_2(\mathbf {x},t)= \lambda_{2}\xi_2 \end{array} $$
(11)

where λ 1 and λ 2 are the associated eigenvalues and ξ 1 and ξ 2 are the corresponding eigenvectors. The existence of the absorbing state implies that the two eigenvalues are negative. At the critical point one of the two eigenvalues, say λ 1 vanishes. If the other one does not, it remains negative, and then fluctuations in ξ 2 continue to decay exponentially with time. This implies that ξ 2 does not experience critical fluctuations in the vicinity of the transition, and so can be integrated out of the problem. Hence, asymptotically, the set of Langevin equations can be reduced to single relevant equation which is precisely Eq. (9), ensuing DP behavior.

On the other hand, if the secondary field is conserved (which, in particular, enforces a 2,1 and a 2,2 to vanish) or there is a hidden symmetry imposing λ 1 and λ 2 to vanish at the same point, this conclusion can break down. In both of these cases, at the system critical point, the two fields are simultaneously critical (or “massless” or “gapless” using the field theory jargon).

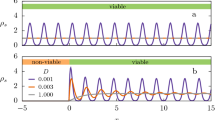
Systems in which the density field is coupled to a secondary conserved field indeed exhibit non-DP critical behavior. This is the case of, for instance, (i) systems related to self-organized criticality in which the activity field is coupled to a conserved non-diffusive background field [51–53] and (ii) systems in which the secondary field is conserved but diffusive [54, 55].

Let us now return to the three models discussed in this paper.

  1. (a)

    Let us first scrutinize the simpler case of vegetation patterns as described by Eqs. (5). At the critical point the expectation value of ρ vanishes, while ϕ converges on average to a value R/κ and, for generic values of ρ, it converges to ϕ st =(R−w 2 ρ)/κ. Let us remark that these are the noiseless or mean-field expectation values. Defining a new field ψ=ϕ−ϕ st and linearizing the dynamics as above, it is straightforward to see that this is an instance of the non-symmetric case discussed above in which the linear terms in both equations do not vanish simultaneously: DP behavior is predicted. Observe also that, after shifting the secondary field, a standard saturation term proportional to −ρ 2 appears in the first equation, i.e. the competition for the available resource (water) acts as an inhibitor generating the necessary effective carrying capacity term (see main text).

  2. (b)

    The case of the stochastic Levin-Segel model, as defined by Eqs. (3) is a bit trickier. Observe that on average one expects (at a noiseless or mean-field level) ϕ=ρw 2/λ, which implies that when ρ vanishes so does ϕ opening the door to non-DP scaling. However, closer inspection reveals that the noise in the equation for ϕ is a higher order one as it is proportional to \(\sqrt{\rho\phi}\). It is therefore irrelevant in the renormalization group sense around the DP-like fixed point (indeed, we have verified numerically that the critical exponents of the modified version of Eqs. (3) without such a term coincide, within error bars, with those of the original ones—results not shown). In this way, the equation for ∂ t ϕ becomes asymptotically a deterministic one. Then, ϕ(x) can be written as a function of ρ(x,t), i.e. ϕ(x,t)=F(ρ(x,t)) where F is an unspecified function which can be formally obtained by integration of the equation for ∂ t ϕ. Expanding such a function in power series of ρ, plugging in the result in the equation for ∂ t ρ and neglecting higher-order terms, one readily recovers Eq. (9), and hence DP scaling. The field ϕ is just a slave mode of ρ (proportional to it up to leading order), inheriting all its critical properties from it.

  3. (c)

    Finally, for the non-local Langevin model for Brownian bugs, it is easy to see that by performing a coarse graining in which scales below l are scaled-up, one recovers effectively Eq. (9). The main point is that nonlocal but finite-range interaction becomes local in the renormalization group perspective once a sufficient amount of coarse graining has been considered. See [23] for further details.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bonachela, J.A., Muñoz, M.A. & Levin, S.A. Patchiness and Demographic Noise in Three Ecological Examples. J Stat Phys 148, 724–740 (2012). https://doi.org/10.1007/s10955-012-0506-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10955-012-0506-x

Keywords

Search

Navigation