Abstract
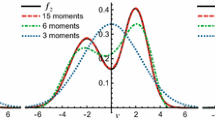
We describe a hierarchy of formal expansions that represent the Fourier transform of a solution of the Boltzmann equation. The constructed approximations are based on the family of weighted Taylor expansions. The first two representations correspond to the Maxwellian and to the Gaussian expansions. The third representation has a weight that generalizes the Gaussian and it depends on the first 13 moments of the Boltzmann density f. It can be shown that this weight is Galilean invariant and it is close to the Gaussian, providing that the heat fluxes are not too large. The 13 moment weight yields a revised form of Grad’s 13 moment expansion for the Boltzmann equation. In search for the entropy dissipation inequality, we also examine the relation between Levermore’s 14 moment density and Grad’s 13 moment expansion. First, we show that the coefficients of the Godunov potential are described by a system of partial differential equations, with coefficients that depend on the Fourier transform of the Levermore’s density f Λ itself. Then, we argue that the same Taylor expansion exploited in the Grad’s scheme, can be used to approximate Levermore’s 14 moment density. We also show that the weighted Taylor expansions are related to a formal solution of the Hamburger problem.
Similar content being viewed by others
References
R. Alexandre, L. Desvillettes, C. Villani, and B. Wennberg. Entropy dissipation and long range interactions, Arch. Rational Mech. Anal. 152:327–355 (2000).
A. V. Bobylev, The theory of the nonlinear spatially uniform Boltzmann equation for Maxwell molecules. Sov. Sci. Rev. C. Math. Phys. 7:111–233 (1988).
A. V. Bobylev, The Chapman-Ensgok and Grad methods for solving the Boltzmann equation. Sov. Phys. Dokl. 27:29–31 (1982).
C. Cercignani, The Boltzmann Equation and its Applications, Springer-Verlag, New York (1988).
S. Chapman and T. G. Cowling, The Mathematical Theory of Non-Uniform Gases, 3rd edn. Cambridge Math. Library (1970).
W. Dreyer, Maximization of the entropy in non-equlibrium, J.Phys. A: Math. Gen. 20:6505–6517 (1987).
W. Dreyer, M. Junk, and M. Kunik, On the approximation of the Fokker-Planck equation by moment systems. Nonlinearity 14:881–906 (2001).
S. K. Godunov, An interesting class of quasilinear systems. Sov. Phys. Math. 2:947–949 (1961).
S. Goldstein and J. Lebowitz, On the Boltzman entropy of nonequlibrium systems. Physica D193:53–66 (2004).
H. Grad, On the kinetic theory of rarefied gases. Commun. Pure. Apply. Math. 2:331–407 (1949).
H. Grad, Principles of the kinetic theory of gases. In: S. Flügge, ed., Handbuch der Physik, Band XII, Springer-Verlag, Berlin 1958, pp. 205–294.
A. Greven, G. Keller, and G. Warnecke (eds.), Entropy, Princeton University Press, Princeton, Oxford (2003).
M. N. Kogan, Rarefied Gas Dynamics, Plenum Press, New York (1969).
M. Junk, Domain of definition of Levermore’s five moment system. J. Stat. Phys. 93:1143–1167 (1988).
M. Junk and A. Unterreiter, Maximum entropy moment systems and Galilean invariance. Continuum Mech. Thermodyn. 14:563–576 (2002).
D. Levermore, Moment closure hierarchies for kinetic theories. J. Stat. Phys. 83(1–2):1021–1065 (1996).
D. Levermore and W. Morokoff, The Gaussian moment closure for gas dynamics. SIAM J. Apply. Math. 59(1):72–96 (1998).
E. Lukacs, Characteristic Functions, Griffin & Company Limited, London (1960).
I. Müller and T. Ruggeri, Rational Extended Thermodynamics, 2nd edn. Springer-Verlag, New York (1998).
T. Ruggeri, Galilean invariance and entropy principle for systems of balance laws. The structure of extended thermodynamics. Continuum Mechanics and Thermodynamics 1(1):3–27 (1989).
B. Simon, The classical moment problem as self-adjont finite difference operator. Adv. Math. 137:82–203 (1998).
E. M. Stein, Harmonic Analysis: Real Variable Methods, Orthogonality and Oscillatory Integrals, Priceton University Press, Princeton, New Jersey (1993).
R. Strichartz, A Guide to Distribution Theory and Fourier Transforms, World Scientific Pubisher Co. Pfe. Ltd., Singapore (2003).
C. Villani, A reviev of mathematical topics in collisional kinetic theory. In Hanbook of Mathematical Fluid Dynamics. S. Friedlender, D. Serre, Eds. Elsevier, vol 1, Chapter 2, 2002, pp. 71–305. (the web version updated in September 2005).
L. Zalcman, Mean-values and Differential Equations. Israel J. Math. 14:339–352 (1973).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Karwowski, A. Grad’s 13 Moment Equations in a Modified Form. J Stat Phys 128, 667–698 (2007). https://doi.org/10.1007/s10955-006-9216-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-006-9216-6