Globally Hyperbolic Moment Model of Arbitrary Order for One-Dimensional Special Relativistic Boltzmann Equation

Abstract

This paper extends the model reduction method by the operator projection to the one-dimensional special relativistic Boltzmann equation. The derivation of arbitrary order globally hyperbolic moment system is built on our careful study of two families of the complicate Grad type orthogonal polynomials depending on a parameter. We derive their recurrence relations, calculate their derivatives with respect to the independent variable and parameter respectively, and study their zeros and coefficient matrices in the recurrence formulas. Some properties of the moment system are also proved. They include the eigenvalues and their bound as well as eigenvectors, hyperbolicity, characteristic fields, linear stability, and Lorentz covariance. A semi-implicit numerical scheme is presented to solve a Cauchy problem of our hyperbolic moment system in order to verify the convergence behavior of the moment method. The results show that the solutions of our hyperbolic moment system converge to the solution of the special relativistic Boltzmann equation as the order of the hyperbolic moment system increases.

Appendices

Appendix 1: Proofs in Section 2

1.1 Proof of Theorem 2.1

Proof

For the nonnegative distribution f(x, p, t), which is not identically zero, using (2.3) gives

$$\begin{aligned} T^{\alpha \alpha }>0, \alpha =0,1;\quad T^{00}+T^{11}{\pm }2T^{01}={c}\int _{\mathbb {R}}\big (p^{0}{\pm } p^{1}\big )^2f\frac{dp}{p^{0}}>0, \end{aligned}$$

which implies the first inequality in (2.22).

Using the definition of $\Delta ^{\alpha \beta }$ in (2.6) and the tensor decomposition of $T^{\alpha \beta }$ in (2.5) gives (2.23), which is a quadratic equation with respect to u. The first inequality in (2.22) tells us that (2.23) has two different solutions whose product is equal to ${c^{2}}$, while one of them with a smaller absolute value is (2.24).

Using further (2.3) gives

$$\begin{aligned} {N^{0}-c^{-1}u N^{1}=c\int _{\mathbb {R}}\big (p^{0}-c^{-1}up^{1}\big )f\frac{dp}{p^{0}}}>0, \end{aligned}$$

i.e. the second inequality in (2.22), and then using the tensor decomposition of $N^\alpha$ in (2.4) gives

$$\begin{aligned} \rho ={c^{-1}m\frac{N^{0}-c^{-1}u N^{1}}{\sqrt{1-c^{-2}u^2}}}>0. \end{aligned}$$

Moreover, using the second identity in (2.17) and (2.3) can give (2.26).

The inequality ${E\ge mc^{2}}$ holds because

$$\begin{aligned} E=U_{\alpha }p^{\alpha }={(1-c^{-2}u^2)^{-\frac{1}{2}}\left( c\sqrt{m^2c^2+p^2}-up\right) }>0, \end{aligned}$$

and

$$\begin{aligned} {E^2-m^2c^4=(1-c^{-2}u^2)^{-1}\left( u\sqrt{m^2c^2+p^2}-cp\right) ^2=\left( \frac{c^2}{U^{0}}p_{{\langle }1{\rangle }}\right) ^2}\ge 0. \end{aligned}$$

Thus, it holds

$$\begin{aligned} T^{00}-c^{-1}uT^{01}-c^{2}\rho= & {} \frac{T^{00}- 2c^{-1}u T^{01}+ c^{-2}u^2 T^{11}}{1-c^{-2}u^2} -c^{2}\rho \\= & {} c^{-1}\int _{\mathbb {R}}E\big (E-mc^2\big )f\frac{dp^1}{p^{0}}>0, \end{aligned}$$

which gives the third inequality in (2.22), and implies that $G(\theta ^{-1})-\theta >1$ for $\theta \in (0,+\infty )$.

On the other hand, one has

$$\begin{aligned} \lim _{\theta \rightarrow 0}\left( G(\theta ^{-1})-\theta \right) =1,\ \lim _{\theta \rightarrow +\infty }\left( G(\theta ^{-1})-\theta \right) =\lim _{\theta \rightarrow +\infty }\theta = +\infty , \end{aligned}$$

and

$$\begin{aligned} \frac{\partial (G(\theta ^{-1})-\theta )}{\partial \theta } =&-\theta ^{-2} \left( G(\theta ^{-1})^2-3G(\theta ^{-1})\theta +\theta ^{2}-1\right) =:\tilde{\psi }(G(\theta ^{-1}),\theta ). \end{aligned}$$

Because

$$\begin{aligned} 0&<c^{-1}\int _{\mathbb {R}}(E-mc^2)f^{(0)}\frac{dp}{p^{0}}=-m^{-1}\rho (G(\theta ^{-1})-2\theta -1),\\ 0&<c^{-1}\int _{\mathbb {R}}(E-mc^2)^2f^{(0)}\frac{dp}{p^{0}}=\rho c^{2}(2G(\theta ^{-1}) - 3\theta -2),\\ 0&<c^{-1}\int _{\mathbb {R}}(E-mc^2)^3f^{(0)}\frac{dp}{p^{0}}=-\rho mc^{4}((4 - \theta )G(\theta ^{-1}) - 5\theta -4), \end{aligned}$$

one obtains

$$\begin{aligned} \frac{3}{2}\theta +1< G(\theta ^{-1})< {\left\{ \begin{array}{ll} \min \left\{ 2\theta +1,(4-\theta )^{-1}(5\theta +4)\right\} ,&{} 0<\theta <4,\\ 2\theta +1,&{} \theta \ge 4, \end{array}\right. } \end{aligned}$$

which is equivalent to the following inequality

$$\begin{aligned} \frac{3}{2}\theta +1&<G(\theta ^{-1})< {\left\{ \begin{array}{ll} (4-\theta )^{-1}(5\theta +4), &{} 0<\theta <1,\\ 2\theta +1, &{} \theta \ge 1. \end{array}\right. } \end{aligned}$$

Thus, one has

$$\begin{aligned} \tilde{\psi }(G(\theta ^{-1}),\theta )> {\left\{ \begin{array}{ll} \tilde{\psi }\left( 2\theta +1,\theta \right)>\theta ^{3}(\theta -1)>0, &{}\theta \ge 1,\\ \\ \tilde{\psi }\left( (4-\theta )^{-1}(5\theta +4),\theta \right)>(4-\theta )^{-2}\theta ^4(\theta +8)(1-\theta )>0, &{}\theta <1, \end{array}\right. } \end{aligned}$$

i.e.

$$\begin{aligned} \frac{\partial (G(\theta ^{-1})-\theta )}{\partial \theta }>0, \end{aligned}$$

which implies that $G(\theta ^{-1})-\theta$ is a strictly monotonic function of $\theta$ in the interval $(0,+\infty )$.

Thus (2.26) has a unique solution in the interval $(0,+\infty )$. The proof is completed. $\square$

1.2 Proof of Theorem 2.2

Proof

Under Theorem 2.1, for the nonnegative distribution f(x, p, t), which is not identically zero, one obtains $\{\rho ,u,\theta \}$ satisfying

$$\begin{aligned} \rho>0, \quad |u|<{c}, \quad \theta >0. \end{aligned}$$

(8.1)

Due to the last equations in (2.7) and (2.20), one obtains

$$\begin{aligned} {\Pi =-\int _{\mathbb {R}}\Delta _{\alpha \beta }p^{\alpha }p^{\beta }f\frac{dp}{p^{0}}-c^{2}\rho \theta =c^{-1}\int _{\mathbb {R}}\big (E^2-m^2c^4\big )f\frac{dp}{p^{0}}-\rho c^{2}\theta >-\rho c^{2}\theta }, \end{aligned}$$

which completes the proof. $\square$

Appendix 2: Proofs in Section 3

1.1 Proof of Theorem 3.2

Proof

• (i) For $k\le n+2$, taking the inner product with respect to $\omega ^{(0)}$ between the polynomials $P_{k}^{(0)}(x;\zeta )$ and $(x^2-1)P_{n}^{(1)}(x;\zeta )$ gives

  $$\begin{aligned}&\left( (x^2-1)P_{n}^{(1)},P_{n+2}^{(0)}\right) _{\omega ^{(0)}}=\left( c_{n}^{(1)}x^{n+2},P_{n+2}^{(0)}\right) _{\omega ^{(0)}}= \frac{c_{n}^{(1)}}{c_{n+2}^{(0)}}\left( P_{n+2}^{(0)},P_{n+2}^{(0)}\right) _{\omega ^{(0)}}=r_{n+1},\\&\left( (x^2-1)P_{n}^{(1)},P_{n+1}^{(0)}\right) _{\omega ^{(0)}}\\&\quad = \left( c_{n}^{(1)}\left( x^{n+2}-\sum _{i=1}^{n+2}x_{i,n+2}^{(0)}x^{n+1}+ \left( \sum _{i=1}^{n+2}x_{i,n+2}^{(0)}-\sum _{i=1}^{n}x_{i,n}^{(1)}\right) x^{n+1}\right) ,P_{n+1}^{(0)}\right) _{\omega ^{(0)}}\\&\quad =r_{n+1}\left( P_{n+2}^{(0)},P_{n+1}^{(0)}\right) _{\omega ^{(0)}}+ q_{n}\left( P_{n+1}^{(0)},P_{n+1}^{(0)}\right) _{\omega ^{(0)}}=q_{n},\\&\left( (x^2-1)P_{n}^{(1)},P_{n+1}^{(0)}\right) _{\omega ^{(0)}}\\&\quad =\left( P_{n}^{(1)},c_{n+1}^{(0)} \left( x^{n+1}-\sum _{i=1}^{n+1}x_{i,n+1}^{(1)}x^{n}+ \left( \sum _{i=1}^{n+1}x_{i,n+1}^{(1)}-\sum _{i=1}^{n+1}x_{i,n+1}^{(0)}\right) x^{n}\right) \right) _{\omega ^{(1)}}\\&\quad =p_{n+1}\left( P_{n}^{(1)},P_{n+1}^{(1)}\right) _{\omega ^{(1)}}+\frac{c_{n+1}^{(0)}}{c_{n}^{(1)}}\left( \sum _{i=1}^{n+1}x_{i,n+1}^{(1)}- \sum _{i=1}^{n+1}x_{i,n+1}^{(0)}\right) \left( P_{n}^{(1)},P_{n}^{(1)}\right) _{\omega ^{(1)}}\\&\quad =\frac{c_{n+1}^{(0)}}{c_{n}^{(1)}} \sum _{i=1}^{n+1} \left( x_{i,n+1}^{(1)}-x_{i,n+1}^{(0)}\right) =q_{n}, \\&\left( (x^2-1)P_{n}^{(1)},P_{n}^{(0)}\right) _{\omega ^{(0)}} =\left( P_{n}^{(1)},P_{n}^{(0)}\right) _{\omega ^{(1)}}= \left( P_{n}^{(1)},c_{n}^{(0)}x^{n}\right) _{\omega ^{(1)}}\\&\qquad \qquad \qquad \qquad \qquad \qquad \quad =p_{n}\left( P_{n}^{(1)},P_{n}^{(1)}\right) _{\omega ^{(1)}}= p_{n},\\&\left( (x^2-1)P_{n}^{(1)},P_{k}^{(0)}\right) _{\omega ^{(0)}} =\left( P_{n}^{(1)},P_{k}^{(0)}\right) _{\omega ^{(1)}}=0, \quad k\le n-1, \end{aligned}$$

  Substituting them into (3.3) gives (3.9).

• (ii) Taking the inner product with respect to $\omega ^{(1)}$ between $P_{n+1}^{(0)} (x;\zeta )$ and $P_{k}^{(1)} (x;\zeta )$ with $k\le n+1$

  $$\begin{aligned} \left( P_{n+1}^{(0)},P_{n+1}^{(1)}\right) _{\omega ^{(1)}}&= \left( c_{n+1}^{(0)}x^{n+1},P_{n+1}^{(1)}\right) _{\omega ^{(1)}} =p_{n+1}\left( P_{n+1}^{(1)},P_{n+1}^{(1)}\right) _{\omega ^{(1)}}=p_{n+1},\\ \left( P_{n+1}^{(0)},P_{n}^{(1)}\right) _{\omega ^{(1)}}&= \left( P_{n+1}^{(0)},(x^2-1)P_{n}^{(1)}\right) _{\omega ^{(0)}}=q_{n}, \\ \left( P_{n+1}^{(0)},P_{n-1}^{(1)}\right) _{\omega ^{(1)}}&=\left( P_{n+1}^{(0)},(x^2-1)P_{n-1}^{(1)}\right) _{\omega ^{(0)}}= r_{n}\left( P_{n+1}^{(0)},P_{n+1}^{(0)}\right) _{\omega ^{(0)}}=r_{n},\\ \left( P_{n+1}^{(0)},P_{k}^{(1)}\right) _{\omega ^{(1)}}&=\left( P_{n+1}^{(0)},(x^2-1)P_{k}^{(1)}\right) _{\omega ^{(0)}}=0, \quad k\le n-2. \end{aligned}$$

  Similarly, substituting them into (3.3) gives (3.10).

• (iii) If using (3.6) to eliminate $P_{n+2}^{(0)}$ and $P_{n+1}^{(1)}$ in (3.9) and (3.10) respectively, then one obtains

  $$\begin{aligned} (x^2-1)P_{n}^{(1)}=\tilde{p}_{n}(x+\tilde{q}_{n})P_{n+1}^{(0)}+\tilde{r}_{n}P_{n}^{(0)},\quad P_{n+1}^{(0)}=\frac{1}{\tilde{\tilde{p}}_{n}}\big (x-\tilde{\tilde{q}}_{n}\big )P_{n}^{(1)}-\frac{a_{n-1}^{(1)}}{a_{n}^{(0)}}\tilde{\tilde{r}}_{n}P_{n-1}^{(1)}, \end{aligned}$$

  with

  $$\begin{aligned} \tilde{p}_{n}= & {} \frac{r_{n+1}}{a_{n+1}^{(0)}}=\frac{c_{n}^{(1)}}{c_{n+1}^{(0)}}=\frac{a_{n}^{(1)}}{p_{n+1}}=\tilde{\tilde{p}}_{n},\\ \tilde{q}_{n}= & {} \frac{1}{\tilde{p}_{n}}q_{n}-b_{n+1}^{(0)}=\sum _{i=1}^{n+1}x_{i,n+1}^{(0)}-\sum _{i=1}^{n}x_{i,n}^{(1)}=b_{n}^{(1)}-\tilde{p}_{n}q_{n}=\tilde{\tilde{q}}_{n},\\ \tilde{r}_{n}= & {} p_{n}-\tilde{p}_{n}a_{n}^{(0)}={p_{n}(1-\tilde{p}_{n}^{2})} =\frac{a_{n}^{(0)}}{a_{n-1}^{(1)}}\left( -r_{n}+\frac{1}{\tilde{p}_{n}}a_{n-1}^{(1)}\right) = \tilde{\tilde{r}}_{n}. \end{aligned}$$

  The proof is completed.

$\square$

1.2 Proof of Theorem 3.3

Proof

With the aid of definition and recurrence relation of the second kind modified Bessel function in (2.18) and (2.19), one has

$$\begin{aligned} \frac{\partial }{\partial \zeta }\omega ^{(\ell )}(x;\zeta )&=\frac{K_{2}(\zeta )+K_{0}(\zeta )-2xK_{1}(\zeta )}{2K_{1}(\zeta )}\left( \frac{1}{K_{1}(\zeta )}(x^2-1)^{\ell -\frac{1}{2}}\exp (-\zeta x)\right) \\&=\left( G(\zeta )-\zeta ^{-1}-x\right) \omega ^{(\ell )}(x;\zeta ). \end{aligned}$$

Taking the partial derivative of both sides of identities

$$\begin{aligned} \left( P_{n+1}^{(\ell )},P_{k}^{(\ell )}\right) _{\omega ^{(\ell )}}=\delta _{n+1,k}, k=0,\ldots ,n+1, \end{aligned}$$

with respect to $\zeta$ and using (3.8) gives

$$\begin{aligned} \frac{\partial }{\partial \zeta } \left( P_{n+1}^{(\ell )},P_{n+1}^{(\ell )}\right) _{\omega ^{(\ell )}} =\,&2\left( \frac{\partial }{\partial \zeta }P_{n+1}^{(\ell )},P_{n+1}^{(\ell )}\right) _{\omega ^{(\ell )}} +\left( G(\zeta )-\zeta ^{-1}\right) \left( P_{n+1}^{(\ell )},P_{n+1}^{(\ell )}\right) _{\omega ^{(\ell )}}\\&-\,\left( xP_{n+1}^{(\ell )},P_{n+1}^{(\ell )}\right) _{\omega ^{(\ell )}}\\ =\,&2\left( \frac{\partial }{\partial \zeta }P_{n+1}^{(\ell )},P_{n+1}^{(\ell )}\right) _{\omega ^{(\ell )}} +\left( G(\zeta )-\zeta ^{-1}-b_{n+1}^{(\ell )}\right) =0,\\ \frac{\partial }{\partial \zeta } \left( P_{n+1}^{(\ell )},P_{n}^{(\ell )}\right) _{\omega ^{(\ell )}} =\,&\left( \frac{\partial }{\partial \zeta }P_{n+1}^{(\ell )},P_{n}^{(\ell )}\right) _{\omega ^{(\ell )}} +\left( P_{n+1}^{(\ell )},\frac{\partial }{\partial \zeta }P_{n}^{(\ell )}\right) _{\omega ^{(\ell )}}\\&+\,\left( G(\zeta )-\zeta ^{-1}\right) \left( P_{n+1}^{(\ell )},P_{n}^{(\ell )}\right) _{\omega ^{(\ell )}}-\left( xP_{n}^{(\ell )},P_{n+1}^{(\ell )}\right) _{\omega ^{(\ell )}}\\ =\,&\left( \frac{\partial }{\partial \zeta }P_{n+1}^{(\ell )},P_{n}^{(\ell )}\right) _{\omega ^{(\ell )}} -a_{n}^{(\ell )}=0,\\ \frac{\partial }{\partial \zeta } \left( P_{n+1}^{(\ell )},P_{k}^{(\ell )}\right) _{\omega ^{(\ell )}} =\,&\left( \frac{\partial }{\partial \zeta }P_{n+1}^{(\ell )},P_{k}^{(\ell )}\right) _{\omega ^{(\ell )}} +\left( P_{n+1}^{(\ell )},\frac{\partial }{\partial \zeta }P_{k}^{(\ell )}\right) _{\omega ^{(\ell )}}\\&\,+\left( G(\zeta )-\zeta ^{-1}\right) \left( P_{n+1}^{(\ell )},P_{k}^{(\ell )}\right) _{\omega ^{(\ell )}}-\left( xP_{k}^{(\ell )},P_{n+1}^{(\ell )}\right) _{\omega ^{(\ell )}}\\ =\,&\left( \frac{\partial }{\partial \zeta }P_{n+1}^{(\ell )},P_{k}^{(\ell )}\right) _{\omega ^{(\ell )}} =\,0,\quad k\le n-1. \end{aligned}$$

Thus one has

$$\begin{aligned} \left( \frac{\partial }{\partial \zeta }P_{n+1}^{(\ell )},P_{n+1}^{(\ell )}\right) _{\omega ^{(\ell )}}&=-\frac{1}{2}\left( G(\zeta )-\zeta ^{-1}-b_{n+1}^{(\ell )}\right) ,\\ \left( \frac{\partial }{\partial \zeta }P_{n+1}^{(\ell )},P_{n}^{(\ell )}\right) _{\omega ^{(\ell )}}&= a_{n}^{(\ell )},\quad \left( \frac{\partial }{\partial \zeta }P_{n+1}^{(\ell )},P_{k}^{(\ell )}\right) _{\omega ^{(\ell )}} =0,\quad k\le n-1. \end{aligned}$$

Because $\frac{\partial P_{n+1}^{(\ell )}}{\partial \zeta }$ is a polynomial and its degree is not larger than $n+1$, using (3.3) gives (3.17). The proof is completed. $\square$

1.3 Proof of Theorem 3.4

Proof

Similar to the proof of Theorem 3.3, one has

$$\begin{aligned} {\frac{\partial }{\partial x}\omega ^{(1)}(x;\zeta ) =x\omega ^{(0)}(x;\zeta )-\zeta \omega ^{(1)}(x;\zeta ).} \end{aligned}$$

Because the degrees of polynomials $\frac{\partial P_{n+1}^{(0)}}{\partial x}$ and $(x^2-1)\frac{\partial P_{n}^{(1)}}{\partial x}+xP_{n}^{(1)}$ are not larger than n and $n+1$, respectively, and

$$\begin{aligned}&\lim _{x\rightarrow +\infty }P_{i}^{(0)}(x;\zeta )P_{j}^{(1)}(x;\zeta )\omega ^{(1)}(x;\zeta )=0,\\&\quad \lim _{x\rightarrow 1}P_{i}^{(0)}(x;\zeta )P_{j}^{(1)}(x;\zeta )\omega ^{(1)}(x;\zeta )=0,\quad \forall i,j\in \mathbb {N}, \end{aligned}$$

one can calculate the expansion coefficients in (3.3) as follows

$$\begin{aligned} \left( \frac{\partial }{\partial x}P_{n+1}^{(0)},P_{n}^{(1)}\right) _{\omega ^{(1)}}=&\left( (n+1)c_{n+1}^{(0)}x^{n},P_{n}^{(1)}\right) _{\omega ^{(1)}}= \frac{n+1}{\tilde{p}_{n}}\left( P_{n}^{(1)},P_{n}^{(1)}\right) _{\omega ^{(1)}} =\frac{n+1}{\tilde{p}_{n}},\\ \left( \frac{\partial }{\partial x}P_{n+1}^{(0)},P_{n-1}^{(1)}\right) _{\omega ^{(1)}}=&\int _{1}^{+\infty }\frac{\partial }{\partial x}\left( P_{n+1}^{(0)}P_{n-1}^{(1)}\omega ^{(1)}\right) dx -\left( P_{n+1}^{(0)},(x^2-1)\frac{\partial }{\partial x}P_{n-1}^{(1)}\right) _{\omega ^{(0)}}\\&-\left( P_{n+1}^{(0)},xP_{n-1}^{(1)}\right) _{\omega ^{(0)}}+\zeta \left( P_{n+1}^{(0)},(x^2-1)P_{n-1}^{(1)}\right) _{\omega ^{(0)}} =\zeta r_{n},\\ \left( \frac{\partial }{\partial x}P_{n+1}^{(0)},P_{k}^{(1)}\right) _{\omega ^{(1)}}=&\int _{1}^{+\infty }\frac{\partial }{\partial x}\left( P_{n+1}^{(0)}P_{k}^{(1)}\omega ^{(1)}\right) dx -\left( P_{n+1}^{(0)},(x^2-1)\frac{\partial }{\partial x}P_{k}^{(1)}\right) _{\omega ^{(0)}}\\&-\left( P_{n+1}^{(0)},xP_{k}^{(1)}\right) _{\omega ^{(0)}} +\zeta \left( P_{n+1}^{(0)},(x^2-1)P_{k}^{(1)}\right) _{\omega ^{(0)}} \!=0,k{\le } n{-}2{,} \end{aligned}$$

and

$$\begin{aligned} \left( (x^2-1)\frac{\partial }{\partial x}P_{n}^{(1)}+xP_{n}^{(1)},P_{n+1}^{(0)}\right) _{\omega ^{(0)}}=&\left( (n+1)c_{n}^{(1)}x^{n+1},P_{n+1}^{(0)}\right) _{\omega ^{(0)}}\\ =&(n+1)\tilde{p}_{n}\left( P_{n+1}^{(0)},P_{n+1}^{(0)}\right) _{\omega ^{(0)}} =(n+1)\tilde{p}_{n},\\ \left( (x^2{-}1)\frac{\partial }{\partial x}P_{n}^{(1)}{+}xP_{n}^{(1)},P_{n}^{(0)}\right) _{\omega ^{(0)}}=&\int _{1}^{+\infty }\frac{\partial }{\partial x}\left( P_{n}^{(1)}P_{n}^{(0)}\omega ^{(1)}\right) dx{-}\left( \!P_{n}^{(1)},\frac{\partial }{\partial x}P_{n}^{(0)}\!\right) _{\omega ^{(1)}}\\&+\zeta \left( P_{n}^{(1)},P_{n}^{(0)}\right) _{\omega ^{(1)}}=\zeta \left( P_{n}^{(1)},P_{n}^{(0)}\right) _{\omega ^{(1)}}=\zeta p_{n},\\ \left( \!(x^2{-}1)\frac{\partial }{\partial x}P_{n}^{(1)}{+}xP_{n}^{(1)},P_{k}^{(0)}\right) _{\omega ^{(0)}}=&\int _{1}^{+\infty }\!\!\frac{\partial }{\partial x}\left( P_{n}^{(1)}P_{k}^{(0)}\omega ^{(1)}\right) dx{-}\left( P_{n}^{(1)},\frac{\partial }{\partial x}P_{k}^{(0)}\right) _{\omega ^{(1)}}\\&+\zeta \left( P_{n}^{(1)},P_{k}^{(0)}\right) _{\omega ^{(1)}}=0,k\le n-1.\\ \end{aligned}$$

The proof is completed. $\square$

1.4 Proof of Theorem 3.6

Proof

Substituting $\{x_{i,n+1}^{(0)}\}_{i=1}^{n+1}$ into (3.14) gives

$$\begin{aligned} \left( (x_{i,n+1}^{(0)})^2-1\right) P_{n}^{(1)}(x_{i,n+1}^{(0)};\zeta ) =\tilde{r}_{n}P_{n}^{(0)}(x_{i,n+1}^{(0)};\zeta ){,} \end{aligned}$$

which implies that $\tilde{r}_{n}\ne 0$. In fact, if assuming $\tilde{r}_{n}=0$, then the above identity and the fact that $(x_{i,n+1}^{(0)})^2-1>0$ imply $P_{n}^{(1)}(x_{i,n+1}^{(0)};\zeta )=0$, which contradicts with $P_{n}^{(1)}$ being a polynomial of degree n.

Using Theorem 3.5 gives

$$\begin{aligned} \mathrm{sign}\left( P_{n}^{(1)}(x_{i,n+1}^{(0)};\zeta )P_{n}^{(1)}(x_{i+1,n+1}^{(0)};\zeta )\right) =\mathrm{sign}\left( P_{n}^{(0)}(x_{i,n+1}^{(0)};\zeta )P_{n}^{(0)}(x_{i+1,n+1}^{(0)};\zeta )\right) <0. \end{aligned}$$

Thus there exists at least one zero of the polynomial $P_{n}^{(1)}$ in each subinterval $\left( x_{i,n+1}^{(0)},x_{i+1,n+1}^{(0)}\right)$. The proof is completed. $\square$

1.5 Proof of Corollary 1

Proof

It is obvious that

$$\begin{aligned} p_{n}=\frac{c_{n}^{(0)}}{c_{n}^{(1)}}>0,\quad r_{n}=\frac{c_{n-1}^{(1)}}{c_{n+1}^{(0)}}>0,\quad \tilde{p}_{n}=\frac{c_{n}^{(1)}}{c_{n+1}^{(0)}}>0. \end{aligned}$$

Using Theorems 3.1 and 3.6 gives

$$\begin{aligned} \tilde{q}_{n}&=\sum _{i=1}^{n+1}x_{i,n+1}^{(0)}-\sum _{i=1}^{n}x_{i,n}^{(1)}=\sum _{i=1}^{n}\left( x_{i+1,n+1}^{(0)}-x_{i,n}^{(1)}\right) +x_{1,n+1}^{(0)}>0,\\ q_{n}&=\tilde{p}_{n}\left( \sum _{i=1}^{n+2}x_{i,n+2}^{(0)}-\sum _{i=1}^{n}x_{i,n}^{(1)}\right) =\tilde{p}_{n}\left( b_{n+1}^{(0)}+\tilde{q}_{n}\right) >0, \end{aligned}$$

which imply $q_{n}>0$ and $\tilde{q}_{n}>0$.

Comparing the coefficients of the nth order terms at two sides of (3.14) gives

$$\begin{aligned} \tilde{r}_{n}&=p_{n}^{-1} \left( \sum _{i=1}^{n}\sum _{j=i+1}^{n}x_{i,n}^{(1)}x_{j,n}^{(1)}-1- \sum _{i=1}^{n+1}\sum _{j=i+1}^{n+1}x_{i,n+1}^{(0)}x_{j,n+1}^{(0)}\right. \\&\quad + \left. \left( \sum _{i=1}^{n+1}x_{i,n+1}^{(0)}-\sum _{i=1}^{n}x_{i,n}^{(1)}\right) \sum _{i=1}^{n+1}x_{i,n+1}^{(0)}\right) \\&= p_{n}^{-1} \left( \sum _{i=1}^{n}\sum _{j=i+1}^{n}x_{i,n}^{(1)}x_{j,n}^{(1)}+\sum _{i=1}^{n+1}\sum _{j=i}^{n+1}x_{i,n+1}^{(0)}x_{j,n+1}^{(0)} -\sum _{i=1}^{n}x_{i,n}^{(1)}\sum _{i=1}^{n+1}x_{i,n+1}^{(0)}-1\right) \\&=p_{n}^{-1} \left( \sum _{i=1}^{n}x_{i+1,n+1}^{(0)}(x_{i+1,n+1}^{(0)}-x_{i,n}^{(1)})+(x_{1,n+1}^{(0)})^{2}-1\right. \\&\left. \quad +\sum _{i=0}^{n}\sum _{j=i+1}^{n}(x_{i+1,n+1}^{(0)}-x_{i,n}^{(1)})(x_{j+1,n+1}^{(0)}-x_{j,n}^{(1)})\right) , \end{aligned}$$

where $x_{0,n}^{(1)}=0$.

Combining it with Theorem 3.6 gives $\tilde{r}_{n}>0$. The proof is completed. $\square$

1.6 Proof of Corollary 3

Proof

Taking partial derivative of $P_{n}^{(\ell )}(x_{i,n}^{(\ell )};\zeta )$ with respect to $\zeta$ and using Theorem 3.3 gives

$$\begin{aligned}&\frac{\partial x_{i,n}^{(\ell )}}{\partial \zeta }=-\left( \frac{\partial P_{n}^{(\ell )}}{\partial x}(x_{i,n}^{(\ell )};\zeta )\right) ^{-1} \left( \frac{\partial P_{n}^{(\ell )}}{\partial \zeta }(x_{i,n}^{(\ell )};\zeta )\right) \\&=-a_{n-1}^{(\ell )}\left( \frac{\partial P_{n}^{(\ell )}}{\partial x}(x_{i,n}^{(\ell )};\zeta )\right) ^{-1}P_{n-1}^{(\ell )}(x_{i,n}^{(\ell )};\zeta ). \end{aligned}$$

Due to Theorem 3.5, one has

$$\begin{aligned} \mathrm{sign}(P_{n-1}^{(\ell )}(x_{i,n}^{(\ell )};\zeta ))=(-1)^{n+i}=\mathrm{sign}\left( \frac{\partial P_{n}^{(\ell )}}{\partial x}(x_{i,n}^{(\ell )};\zeta )\right) . \end{aligned}$$

Combining them completes the proof. $\square$

1.7 Proof of Lemma 1

Proof

According to the definition of $Q_{2n}(x;\zeta )$ in (3.30), it is not difficult to know that $Q_{2n}(x;\zeta )$ is an even function and a polynomial of degree 2n.

If taking x in (3.30) as the zero of $P_{n+1}^{(0)}(x;\zeta )$, i.e. $x=x_{i,n+1}^{(0)}$, $i=1,\ldots ,{n+1}$, then one has

$$\begin{aligned} Q_{2n}(x_{i,n+1}^{(0)};\zeta )=P_{n+1}^{(0)}(-x_{i,n+1}^{(0)};\zeta )P_{n}^{(1)}(x_{i,n+1}^{(0)};\zeta ). \end{aligned}$$

Since

$$\begin{aligned} \mathrm{sign}\left( P_{n+1}^{(0)}(-x_{i,n+1}^{(0)};\zeta )\right) =(-1)^{n+1}, \quad i=1,\ldots , n+1, \end{aligned}$$

using Theorem 3.6 gives

$$\begin{aligned} \mathrm{sign}\left( Q_{2n}(x_{i,n+1}^{(0)};\zeta )Q_{2n}(x_{i+1,n+1}^{(0)};\zeta )\right) =\mathrm{sign}\left( P_{n}^{(1)}(x_{i,n+1}^{(0)};\zeta )P_{n}^{(1)}(x_{i+1,n+1}^{(0)};\zeta )\right) <0, \end{aligned}$$

for $i=1,\ldots ,n$, which implies that there exists at least one zero of $Q_{2n}(x;\zeta )$ in each subinterval $(x_{i,n+1}^{(0)},x_{i+1,n+1}^{(0)})$, $i=1,\ldots ,n$. Because $Q_{2n}(x;\zeta )$ is an even polynomial of degree 2n, there exists exactly one zero of $Q_{2n}(x;\zeta )$ in each subinterval $(x_{i,n+1}^{(0)},x_{i+1,n+1}^{(0)})$, $i=1,\ldots ,n$. The proof is completed. $\square$

1.8 Proof of Lemma 2

Proof

According to the definition of $Q_{2n}(x;\zeta )$ in (3.30), one has

$$\begin{aligned} \frac{\partial Q_{2n}}{\partial \zeta }(z_{i,n};\zeta )=\,&\frac{\partial P_{n+1}^{(0)}}{\partial \zeta }\Big |_{x=z_{i,n}} P_{n}^{(1)}(-z_{i,n};\zeta ) +\frac{\partial P_{n}^{(1)}}{\partial \zeta }\Big |_{x=z_{i,n}} P_{n+1}^{(0)}(-z_{i,n};\zeta )\\&+\frac{\partial P_{n+1}^{(0)}}{\partial \zeta } \Big |_{x=-z_{i,n}} P_{n}^{(1)}(z_{i,n};\zeta ) +\frac{\partial P_{n}^{(1)}}{\partial \zeta }\Big |_{x=-z_{i,n}} P_{n+1}^{(0)}(z_{i,n};\zeta ). \end{aligned}$$

Using Theorem 3.3 gives

$$\begin{aligned} \frac{\partial Q_{2n}}{\partial \zeta }(z_{i,n};\zeta )=\,&a_{n}^{(0)}\left( P_{n}^{(0)}(z_{i,n};\zeta )P_{n}^{(1)}(-z_{i,n};\zeta )+P_{n}^{(0)}(-z_{i,n};\zeta )P_{n}^{(1)}(z_{i,n};\zeta )\right) \\&+a_{n-1}^{(1)}\left( P_{n-1}^{(1)}(z_{i,n};\zeta )P_{n+1}^{(0)}(-z_{i,n};\zeta )+P_{n-1}^{(1)}(-z_{i,n};\zeta )P_{n+1}^{(0)}(z_{i,n};\zeta )\right) \\&+\left( \frac{1}{2}(b_{n+1}^{(0)}+b_{n}^{(1)})-(G(\zeta )-\zeta ^{-1})\right) Q_{2n}(z_{i,n};\zeta )\\ =\,&a_{n}^{(0)}\left( P_{n}^{(0)}(z_{i,n};\zeta )P_{n}^{(1)}(-z_{i,n};\zeta )+P_{n}^{(0)}(-z_{i,n};\zeta )P_{n}^{(1)}(z_{i,n};\zeta )\right) \\&+a_{n-1}^{(1)}\left( P_{n-1}^{(1)}(z_{i,n};\zeta )P_{n+1}^{(0)}(-z_{i,n};\zeta )+P_{n-1}^{(1)}(-z_{i,n};\zeta )P_{n+1}^{(0)}(z_{i,n};\zeta )\right) . \end{aligned}$$

Substituting (3.14) and (3.15) into it gives

$$\begin{aligned} \frac{\partial Q_{2n}}{\partial \zeta }(z_{i,n};\zeta ) =\,&\frac{2a_{n}^{(0)}}{\tilde{r}_{n}}\left( ((z_{i,n})^2-1)P_{n}^{(1)}(z_{i,n};\zeta )P_{n}^{(1)}(-z_{i,n};\zeta )\right. \\&\quad \left. + \tilde{p}_{n}z_{i,n}P_{n+1}^{(0)}(-z_{i,n};\zeta )P_{n}^{(1)}(z_{i,n};\zeta )\right) \\&\,-\frac{2a_{n}^{(0)}}{\tilde{r}_{n}}\left( P_{n+1}^{(0)}(z_{i,n};\zeta )P_{n+1}^{(0)}(-z_{i,n};\zeta )- \tilde{p}_{n}^{-1}z_{i,n}P_{n+1}^{(0)}(-z_{i,n};\zeta )P_{n}^{(1)}(z_{i,n};\zeta )\right) \\ =\,&2\frac{P_{n}^{(1)}(z_{i,n};\zeta )}{P_{n}^{(1)}(-z_{i,n};\zeta )} \frac{a_{n}^{(0)}}{\tilde{r}_{n}}\left( (\tilde{p}_{n}+ \tilde{p}_{n}^{-1})z_{i,n}P_{n}^{(1)}(-z_{i,n};\zeta )P_{n+1}^{(0)}(-z_{i,n};\zeta )\right. \\&\left. +(z_{i,n}^2-1)P_{n}^{(1)}(-z_{i,n};\zeta )^2 +P_{n+1}^{(0)} (-z_{i,n};\zeta )^2\right) \\ =\,&2\frac{P_{n}^{(1)}(z_{i,n};\zeta )}{P_{n}^{(1)}(-z_{i,n};\zeta )} \frac{a_{n}^{(0)}}{\tilde{r}_{n}}\left( (c_{n+1}^{(0)})^2\prod _{j=1}^{n+1}(z_{i,n}+x_{j,n+1}^{(0)}) \tilde{I}_{1}-(c_{n}^{(1)})^2\prod _{j=1}^{n}(z_{i,n}+x_{j,n}^{(1)}) \tilde{I}_{2}\right) \!, \end{aligned}$$

where

$$\begin{aligned} \tilde{I}_{1}:=\prod _{j=1}^{n+1}\left( z_{i,n}+x_{j,n+1}^{(0)}\right) -z_{i,n}\prod _{j=1}^{n}\left( z_{i,n}+x_{j,n}^{(1)}\right) , \end{aligned}$$

$$\begin{aligned} \tilde{I}_{2}:=z_{i,n}\prod _{j=1}^{n+1}\left( z_{i,n}+x_{j,n+1}^{(0)}\right) -(z_{i,n}^2-1)\prod _{j=1}^{n}\left( z_{i,n}+x_{j,n}^{(1)}\right) . \end{aligned}$$

Similarly, using Theorem 3.4 and (3.14)-(3.15) gives

$$\begin{aligned} \frac{\partial Q_{2n}}{\partial x}(z_{i,n};\zeta ) =\,&\zeta \frac{c_{n-1}^{(1)}}{c_{n+1}^{(0)}}\left( P_{n-1}^{(1)}(z_{i,n};\zeta )P_{n}^{(1)}(-z_{i,n};\zeta )-P_{n-1}^{(1)}(-z_{i,n};\zeta )P_{n}^{(1)}(z_{i,n};\zeta )\right) \\&+(z_{i,n}^2-1)^{-1}\zeta \frac{c_{n}^{(0)}}{c_{n}^{(1)}}\left( P_{n}^{(0)}(z_{i,n};\zeta )P_{n+1}^{(0)}(-z_{i,n};\zeta )\right. \\&\left. -P_{n}^{(0)}(-z_{i,n};\zeta )P_{n+1}^{(0)}(z_{i,n};\zeta )\right) \\ =\,&2\zeta \frac{P_{n}^{(1)}(z_{i,n};\zeta )}{P_{n}^{(1)}(-z_{i,n};\zeta )} \frac{a_{n}^{(0)}}{\tilde{r}_{n}}\left( z_{i,n}P_{n}^{(1)}(-z_{i,n};\zeta )^{2}\right. \\&\left. +(\tilde{p}_{n}+\tilde{p}_{n}^{-1})P_{n+1}^{(0)}(-z_{i,n};\zeta )P_{n}^{(1)}(-z_{i,n};\zeta )\right. \\&\left. +(z_{i,n}^2-1)^{-1}z_{i,n}P_{n+1}^{(0)}(-z_{i,n};\zeta )^2 \right) \\ =\,&2\zeta \frac{P_{n}^{(1)}(z_{i,n};\zeta )}{P_{n}^{(1)}(-z_{i,n};\zeta )}\\&\frac{a_{n}^{(0)}}{\tilde{r}_{n}}\left( (c_{n+1}^{(0)})^2\frac{\prod _{j=1}^{n+1}(z_{i,n}+x_{j,n+1}^{(0)})}{z_{i,n}^2-1} \tilde{I}_{2}-(c_{n}^{(1)})^2\prod _{j=1}^{n}(z_{i,n}+x_{j,n}^{(1)})\tilde{I}_{1}\right) . \end{aligned}$$

Using Theorem 3.6 gives

$$\begin{aligned} z_{i,n}+x_{j+1,n+1}^{(0)}>z_{i,n}+x_{j,n}^{(1)} ,\quad j=1,\ldots ,n, \\ z_{i,n}+x_{1,n+1}^{(0)}>z_{i,n}+1>z_{i,n}>z_{i,n}-1, \end{aligned}$$

for $i=1,\ldots ,n$, which imply

$$\begin{aligned} \tilde{I}_{1}>0,\quad \tilde{I}_{2}>0. \end{aligned}$$

Thus one has

$$\begin{aligned} \prod _{j=1}^{n+1}&(z_{i,n}+x_{j,n+1}^{(0)})\tilde{I}_{1}-\prod _{j=1}^{n}(z_{i,n}+x_{j,n}^{(1)}) \tilde{I}_{2}\\ =&\left( \prod _{j=1}^{n+1}(z_{i,n}+x_{j,n+1}^{(0)})-(z_{i,n}-1)\prod _{j=1}^{n}(z_{i,n}+x_{j,n}^{(1)} )\right) \\&\times \left( \prod _{j=1}^{n+1}(z_{i,n}+x_{j,n+1}^{(0)})-(z_{i,n}+1)\prod _{j=1}^{n}(z_{i,n}+x_{j,n}^{(1)})\right) >0, \end{aligned}$$

$$\begin{aligned} \prod _{j=1}^{n+1}&(z_{i,n}+x_{j,n+1}^{(0)}) \tilde{I}_{2}-((z_{i,n})^2-1)\prod _{j=1}^{n}(z_{i,n} +x_{j,n}^{(1)})\tilde{I}_{1}\\ =&z_{i,n}{\left( \prod _{j=1}^{n+1}(z_{i,n}+x_{j,n+1}^{(0)})\tilde{I}_{1}-\prod _{j=1}^{n}(z_{i,n}+x_{j,n}^{(1)}) \tilde{I}_{2}\right) }\\&+2\prod _{j=1}^{n+1}(z_{i,n}+x_{j,n+1}^{(0)})\prod _{j=1}^{n}(z_{i,n}+x_{j,n}^{(1)})>0. \end{aligned}$$

Using Corollaries 1 and 2, and the above results gives (3.31).

The proof is completed. $\square$

1.9 Proof of Lemma 3

Proof

Taking partial derivative of $Q_{2n}(z_{i,n};\zeta )$ with respect to $\zeta$ gives

$$\begin{aligned} \frac{\partial z_{i,n}}{\partial \zeta }=-\left( \frac{\partial Q_{2n}}{\partial x}\Big |_{x=z_{i,n}}\right) ^{-1} \left( \frac{\partial Q_{2n}}{\partial \zeta }\Big |_{x=z_{i,n}}\right) , i=1,\ldots ,n. \end{aligned}$$

Using Lemma 2 completes the proof. $\square$

1.10 Proof of Theorem 3.7

Proof

Obviously, both vectors $\mathbf {u}_{i,n}$ and $\mathbf {v}_{i,n}$ defined in (3.35) are not zero at the same time, $i=\pm 1,\ldots ,\pm n$. The nonzero eigenvalues and eigenvectors of the matrix pair $\mathbf {A}^{0}_{n}$ and $\mathbf {A}^{1}_{n}$ in (3.32) and (3.34) can be obtained with the aid of (3.28)-(3.29) and Lemma 1. Using Lemma 3 further gives (3.33).

In the following, let us discuss the eigenvector $\mathbf {y}_{0,n}$. Multiplying (3.12) by $P_{n+1}^{(0)}(-x;\zeta )$ gives

$$\begin{aligned}&(x^2-1)\mathbf {P}_{n-1}^{(1)}(x;\zeta )P_{n+1}^{(0)}(-x;\zeta )\nonumber \\&=\mathbf {J}_{n-1}\mathbf {P}_{n}^{(0)}(x;\zeta )P_{n+1}^{(0)}(-x;\zeta ) +r_{n}P_{n+1}^{(0)}(x;\zeta )P_{n+1}^{(0)}(-x;\zeta )\mathbf {e}_{n}. \end{aligned}$$

(9.1)

Transforming (9.1) by x to $-x$ and then subtracting it from (9.1) and letting $x=1$ gives as follows

$$\begin{aligned} 0=\mathbf {J}_{n-1}\left( \mathbf {P}_{n}^{(0)}(1;\zeta )P_{n+1}^{0}(-1;\zeta )-\mathbf {P}_{n}^{(0)}(-1;\zeta )P_{n+1}^{(0)}(1;\zeta )\right) =\mathbf {J}_{n-1}\mathbf {u}_{0,n}, \end{aligned}$$

which is a special case of (3.21) with $\hat{\lambda } =0$.

The proof is completed. $\square$

Appendix 3: Proofs in Section 4

1.1 Proof of Lemma 4

Proof

• (i) Due to the definition of E and $p_{{\langle }1{\rangle }}$, it is obvious that each component of $\mathbf {\mathcal {P}}_{\infty }[u,\theta ]$ (resp. $\mathbf {\mathcal {P}}_{M}[u,\theta ]$) belongs to $\mathbb {H}^{g^{(0)}_{[u,\theta ]}}$ (resp. $\mathbb {H}^{g^{(0)}_{[u,\theta ]}}_{M}$).

• (ii) The mathematical induction is used to prove that any element in the space $\mathbb {H}^{g^{(0)}_{[u,\theta ]}}$ (resp. $\mathbb {H}^{g^{(0)}_{[u,\theta ]}}_{M}$) can be expressed as a linear combination of vectors in $\mathbf {\mathcal {P}}_{\infty }[u,\theta ]$ (resp. $\mathbf {\mathcal {P}}_{M}[u,\theta ]$) . For $M=1$, it is clear to have the linear combination

  $$\begin{aligned} p^{\alpha }g^{(0)}_{[u,\theta ]}\overset{(2.9)}{=}&\left( p^{{\langle }\alpha {\rangle }}+U^{\alpha }E\right) g^{(0)}_{[u,\theta ]} \overset{(2.8)}{=} \left( -(U^{0})^{-1}U^{1-\alpha }p_{{\langle }1{\rangle }}+U^{\alpha }E\right) g^{(0)}_{[u,\theta ]}\\ \overset{(3.5)}{=}&-(c_{0}^{(1)})^{-1}U^{1-\alpha }\tilde{P}_{0}^{(1)}[u,\theta ]+ (c_{1}^{(0)})^{-1}U^{\alpha }\tilde{P}_{1}^{(0)}[u,\theta ]\\&+(c_{0}^{(0)})^{-1}U^{\alpha }x_{1,1}^{(0)}\tilde{P}_{0}^{(0)}[u,\theta ], \end{aligned}$$

  where the decomposition of the particle velocity vector (2.9) has been used. Assume that the linear combination

  $$\begin{aligned} p^{\mu _{1}}p^{\mu _{2}}\ldots p^{\mu _{M}}g^{(0)}_{[u,\theta ]}=&\sum _{i=0}^{M}c_{i,0}^{\mu _{1},\ldots ,\mu _{M}}\tilde{P}_{i}^{(0)}[u,\theta ] +\sum _{i=0}^{M-1}c_{i,1}^{\mu _{1},\ldots ,\mu _{M}}\tilde{P}_{i}^{(1)}[u,\theta ],\\&\mu _{i}=0,1, i\in \mathbb {N}, i\le M, \quad c_{i,0}^{\mu _{1},\ldots ,\mu _{M}},c_{i,1}^{\mu _{1},\ldots ,\mu _{M}}\in \mathbb {R}, \end{aligned}$$

  holds. One has to show that $p^{\mu _{1}}p^{\mu _{2}}\ldots p^{\mu _{M+1}}g^{(0)}_{[u,\theta ]}$ can be expressed as a linear combination of components of $\mathbf {\mathcal {P}}_{M+1}[u,\theta ]$. Because

  $$\begin{aligned}&p^{\mu _{1}}p^{\mu _{2}}\ldots p^{\mu _{M+1}}g^{(0)}_{[u,\theta ]}\\&=\left( \sum _{i=0}^{M}c_{i,0}^{\mu _{1},\ldots ,\mu _{M}}\tilde{P}_{i}^{(0)}[u,\theta ] +\sum _{i=0}^{M-1}c_{i,1}^{\mu _{1},\ldots ,\mu _{M}}\tilde{P}_{i}^{(1)}[u,\theta ]\right) \\&\times \left( -(U^{0})^{-1}U^{1-\mu _{M+1}}p_{{\langle }1{\rangle }}+U^{\mu _{M+1}}E\right) \\&=\sum _{i=0}^{M}c_{i,0}^{\mu _{1},\ldots ,\mu _{M}}U^{\mu _{M+1}}E\tilde{P}_{i}^{(0)}[u,\theta ] -\sum _{i=0}^{M-1}c_{i,1}^{\mu _{1},\ldots ,\mu _{M}}U^{1-\mu _{M+1}}(E^2-1)P_{i}^{(1)}(E;\zeta )\\&\quad -\sum _{i=0}^{M}c_{i,0}^{\mu _{1},\ldots ,\mu _{M}}(U^{0})^{-1}U^{1-\mu _{M+1}}P_{i}^{(0)}(E;\zeta )p_{{\langle }1{\rangle }}+ \sum _{i=0}^{M-1}c_{i,1}^{\mu _{1},\ldots ,\mu _{M}}U^{\mu _{M+1}}\tilde{P}_{i}^{(1)}[u,\theta ], \end{aligned}$$

  one has

  $$\begin{aligned}&p^{\mu _{1}}p^{\mu _{2}}\ldots p^{\mu _{M+1}}g^{(0)}_{[u,\theta ]}\\&\quad =\sum _{i=0}^{M}c_{i,0}^{\mu _{1},\ldots ,\mu _{M}}U^{\mu _{M+1}} \left( a_{i-1}^{(0)}\tilde{P}_{i-1}^{(0)}[u,\theta ]+b_{i}^{(0)}\tilde{P}_{i}^{(0)}[u,\theta ]+a_{i}^{(0)}\tilde{P}_{i+1}^{(0)}[u,\theta ]\right) \\&\qquad -\sum _{i=0}^{M-1}c_{i,1}^{\mu _{1},\ldots ,\mu _{M}}U^{1-\mu _{M+1}} \left( p_{i}\tilde{P}_{i}^{(0)}[u,\theta ]+q_{i}\tilde{P}_{i+1}^{(0)}[u,\theta ]+r_{i+1}\tilde{P}_{i+2}^{(0)}[u,\theta ]\right) \\&\qquad -\sum _{i=0}^{M}c_{i,0}^{\mu _{1},\ldots ,\mu _{M}}U^{1-\mu _{M+1}} \left( r_{i-1}\tilde{P}_{i-2}^{(1)}[u,\theta ]+q_{i-1}\tilde{P}_{i-1}^{(1)}[u,\theta ]+p_{i}\tilde{P}_{i}^{(1)}[u,\theta ]\right) \\&\qquad +\sum _{i=0}^{M-1}c_{i,1}^{\mu _{1},\ldots ,\mu _{M}}U^{\mu _{M+1}} \left( a_{i-1}^{(1)}\tilde{P}_{i-1}^{(1)}[u,\theta ]+b_{i}^{(1)}\tilde{P}_{i+1}^{(1)}[u,\theta ]+a_{i}^{(1)}\tilde{P}_{i+1}^{(1)}[u,\theta ]\right) \\&\quad =:\sum _{i=0}^{M+1}c_{i,0}^{\mu _{1},\ldots ,\mu _{M+1}}\tilde{P}_{i}^{(0)}[u,\theta ] +\sum _{i=0}^{M}c_{i,1}^{\mu _{1},\ldots ,\mu _{M+1}}\tilde{P}_{i}^{(1)}[u,\theta ]{,} \end{aligned}$$

  by using the three-term recurrence relations (3.6), (3.9), and (3.10) for the orthogonal polynomials $\{P_{n}^{(\ell )}(x;\zeta ), \ell =0,1\}$.

• (iii) Using (3.1) gives

  $$\begin{aligned} {\langle }\tilde{P}_{i}^{(\ell )}[u,\theta ],\tilde{P}_{j}^{(\ell )}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}}= \left( P_{i}^{(\ell )},P_{j}^{(\ell )}\right) _{ \omega ^{(\ell )}}=\delta _{i,j},\ \ell =0,1. \end{aligned}$$

  (10.1)

  Because of (2.9), one has

  $$\begin{aligned} \frac{dp}{p^{0}}=dp_{{\langle }1{\rangle }}\frac{-1+u(U^{0}E)^{-1}p_{{\langle }1{\rangle }}}{-up_{{\langle }1{\rangle }}+U^{0}E}=-\frac{dp_{{\langle }1{\rangle }}}{U^{0}E}, \quad E=\sqrt{\left( (U^{0})^{-1}p_{{\langle }1{\rangle }}\right) ^2+1}. \end{aligned}$$

  Thus it holds

  $$\begin{aligned} \nonumber {\langle }\tilde{P}_{i}^{(0)}[u,\theta ],\tilde{P}_{j}^{(1)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}}=&\int _{\mathbb {R}}g^{(0)}_{[u,\theta ]}P_{i}^{(0)}(E;\zeta )P_{j}^{(1)}(E;\zeta )(U^{0})^{-1}p_{{\langle }1{\rangle }}\frac{dp}{p^{0}}\\ =&-\int _{\mathbb {R}}g^{(0)}_{[u,\theta ]}P_{i}^{(0)}(E;\zeta )P_{j}^{(1)}(E;\zeta )(U^{0})^{-1}p_{{\langle }1{\rangle }}\frac{dp_{{\langle }1{\rangle }}}{U^{0}E}=0. \end{aligned}$$

  (10.2)

  Combining (i) and (ii) with (iii) completes the proof.

$\square$

1.2 Proof of Lemma 5

Proof

For $s=t$ and x, it is clear to have

$$\begin{aligned} \frac{\partial E}{\partial s}=\frac{\partial u}{\partial s}\frac{1}{(1-u^2)}(U^{0})^{-1}p_{{\langle }1{\rangle }},\quad \frac{\partial \left( (U^{0})^{-1}p_{{\langle }1{\rangle }}\right) }{\partial s}=\frac{\partial u}{\partial s}\frac{1}{1-u^2}E. \end{aligned}$$

Using the above identities and (4.1) gives

$$\begin{aligned} \frac{\partial g^{(0)}_{[u,\theta ]}}{\partial s}=-\left( \frac{\partial \theta }{\partial s}\zeta ^2\left( G(\zeta )-\zeta ^{-1}-E\right) + \frac{\partial u}{\partial s}\frac{1}{\theta (1-u^2)}(U^{0})^{-1}p_{{\langle }1{\rangle }}\right) g^{(0)}_{[u,\theta ]}. \end{aligned}$$

The derivation rule of compound function gives

$$\begin{aligned} \frac{\partial \tilde{P}_{n}^{(0)}[u,\theta ]}{\partial s}=&\frac{\partial P_{n}^{(0)}}{\partial E}\frac{\partial E}{\partial s}g^{(0)}_{[u,\theta ]} -\zeta ^2\frac{\partial P_{n}^{(0)}}{\partial \zeta }\frac{\partial \theta }{\partial s}g^{(0)}_{[u,\theta ]} +P_{n}^{(0)}\frac{\partial g^{(0)}_{[u,\theta ]}}{\partial s},\\ \frac{\partial \tilde{P}_{n-1}^{(1)}[u,\theta ]}{\partial s}=&\frac{\partial P_{n-1}^{(1)}}{\partial E}\frac{\partial E}{\partial s}(U^{0})^{-1}p_{{\langle }1{\rangle }}g^{(0)}_{[u,\theta ]} -\zeta ^2\frac{\partial P_{n-1}^{(1)}}{\partial \zeta }\frac{\partial \theta }{\partial s}(U^{0})^{-1}p_{{\langle }1{\rangle }}g^{(0)}_{[u,\theta ]}\\&+P_{n-1}^{(1)}\frac{\partial \left( (U^{0})^{-1}p_{{\langle }1{\rangle }}\right) }{\partial s}g^{(0)}_{[u,\theta ]} +P_{n-1}^{(1)}(U^{0})^{-1}p_{{\langle }1{\rangle }}\frac{\partial g^{(0)}_{[u,\theta ]}}{\partial s}{.} \end{aligned}$$

Combining them and using Theorems 3.1–3.4 complete the proof. $\square$

1.3 Proof of Lemma 6

Proof

Using the three-term recurrence relations (3.7), (3.11), and (3.12) gives

$$\begin{aligned} E\mathbf {\mathcal {\tilde{P}}}_{M}[u,\theta ]&=\mathbf {A}^{0}_{M} \mathbf {\mathcal {\tilde{P}}}_{M}[u,\theta ]+a_{M}^{(0)}\tilde{P}_{M+1}^{(0)}[u,\theta ]\mathbf {e}_{2M+1}^{3} +a_{M-1}^{(1)}\tilde{P}_{M}^{(1)}[u,\theta ]\mathbf {e}_{2M+1}^{2}, \\ (U^{0})^{-1}p_{{\langle }1{\rangle }}\mathbf {\mathcal {\tilde{P}}}_{M}&=\mathbf {A}^{1}_{M}\mathbf {\mathcal {\tilde{P}}}_{M}[u,\theta ] +p_{M}\tilde{P}_{M}^{(1)}[u,\theta ]\mathbf {e}_{2M+1}^{3} +r_{M}\tilde{P}_{M+1}^{(0)}[u,\theta ]\mathbf {e}_{2M+1}^{2}, \end{aligned}$$

where $\mathbf {e}_{2M+1}^{3}$ is the $(M+1)$th column of the identity matrix of order $(2M+1)$. Thus one has

$$\begin{aligned} E\mathbf {\mathcal {P}}_{M}[u,\theta ]&= \mathbf {P}_{M}^{p}\mathbf {A}^{0}_{M}(\mathbf {P}_{M}^{p})^{T} \mathbf {\mathcal {P}}_{M}[u,\theta ]{+}a_{M}^{(0)}\tilde{P}_{M+1}^{(0)}[u,\theta ]\mathbf {e}_{2M+1}^{1} {+}a_{M-1}^{(1)}\tilde{P}_{M}^{(1)}[u,\theta ]\mathbf {e}_{2M+1}^{2},\\ (U^{0})^{-1}p_{{\langle }1{\rangle }}\mathbf {\mathcal {P}}_{M}&= \mathbf {P}_{M}^{p}\mathbf {A}^{1}_{M}(\mathbf {P}_{M}^{p})^{T}\mathbf {\mathcal {P}}_{M}[u,\theta ] +p_{M}\tilde{P}_{M}^{(1)}[u,\theta ]\mathbf {e}_{2M+1}^{1} +r_{M}\tilde{P}_{M+1}^{(0)}[u,\theta ]\mathbf {e}_{2M+1}^{2}. \end{aligned}$$

Combining them with (2.9) completes the proof. $\square$

1.4 Proof of Lemma 7

Proof

It is obvious that $\Pi _{M}[u,\theta ]$ is a linear bounded operator and $\Pi _{M}[u,\theta ]f\in \mathbb {H}^{g^{(0)}_{[u,\theta ]}}_{M}$ for all $f\in \mathbb {H}^{g^{(0)}_{[u,\theta ]}}$.

For all $f\in \mathbb {H}^{g^{(0)}_{[u,\theta ]}}_{M}$, besides (4.7), by using Lemma 4 one has

$$\begin{aligned} f=&\sum _{i=0}^{M}\tilde{f}_{i}^{0}\tilde{P}_{i}^{(0)}[u,\theta ]+ \sum _{j=0}^{M-1}\tilde{f}_{j}^{1}\tilde{P}_{j}^{(1)}[u,\theta ]. \end{aligned}$$

Taking respectively the inner product with $\tilde{P}_{i}^{(0)}[u,\theta ]$ and $\tilde{P}_{j}^{(1)}[u,\theta ]$ from both sides of the last equation gives

$$\begin{aligned} f_{i}^{0}={\langle }f,\tilde{P}_{i}^{(0)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}},i\le M,\quad f_{j}^{1}={\langle }f,\tilde{P}_{j}^{(1)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}},j\le M-1. \end{aligned}$$

Comparing them with the coefficients in (4.9) shows that $\tilde{f}_{i}^{0}=f_{i}^{0}$, $\tilde{f}_{j}^{1}=f_{j}^{1}$,

$i=0,\ldots , M$, $j=1,\ldots ,M-1$. The proof is completed. $\square$

Appendix 4: Proofs in Section 5

1.1 Proof of Lemma 8

Proof

It is obvious that for $M=1$, the matrix $\mathbf {D}_M$ is invertible because

$\det (\mathbf {D}_M)=\rho \zeta ^2c_0^{(1)}(c_0^{(0)}c_1^{(0)}(1-u^2))^{-1}>0$. For $M\ge 2$, according to the form of $\mathbf {D}_M$ in Sect. 4.2, one has

$$\begin{aligned} \det (\mathbf {D}_{M})=\det (\mathbf {D}_{2})=\zeta ^3c_{2}^{(0)}c_{1}^{(1)}(x_{1,2}^{(0)}+x_{2,2}^{(0)})(\rho G(\zeta )+\Pi )\rho (c_{1}^{(0)}c_{0}^{(0)}(1-u^2))^{-1}. \end{aligned}$$

Using $\Pi >-\rho \theta$ gives

$$\begin{aligned} \det (\mathbf {D}_{M})>\zeta ^3c_{2}^{(0)}c_{1}^{(1)}(x_{1,2}^{(0)}+x_{2,2}^{(0)})\rho ^2( G(\zeta )-\zeta ^{-1})(c_{1}^{(0)}c_{0}^{(0)}(1-u^2))^{-1}>0. \end{aligned}$$

The proof is completed. $\square$

1.2 Proof of Theorem 5.1

Proof

Consider the following generalized eigenvalue problem (2nd sense): Find a vector $\mathbf {r}$ that obeys $\lambda \mathbf {B}_{M}^{0}\mathbf {r}=\mathbf {B}_{M}^{1}\mathbf {r}$ or $\lambda \mathbf {M}_{M}^{t}\mathbf {D}_{M}\mathbf {r}=\mathbf {M}_{M}^{x}{\mathbf {D}}_{M}\mathbf {r}$. Thanks to (4.5), this eigenvalue problem is equivalent to

$$\begin{aligned} (\lambda -u) \mathbf {A}_{M}^{0}(\mathbf {P}_{M}^{p})^{T}\mathbf {D}_{M}\mathbf {r}= (\lambda u-1) \mathbf {A}_{M}^{1}(\mathbf {P}_{M}^{p})^{T}\mathbf {D}_{M}\mathbf {r}. \end{aligned}$$

Because Theorem 3.7 tells us that $\hat{\lambda } _{i,M}$ and $\mathbf {y}_{i,M}$ satisfy

$$\begin{aligned} \hat{\lambda } _{i,M}\mathbf {A}_{M}^{0}\mathbf {y}_{i,M}=\mathbf {A}_{M}^{1}\mathbf {y}_{i,M},\ | \hat{\lambda } _{i,M}|<1, \end{aligned}$$

the scalar $\lambda _{i,M}$ in (5.1) and vector $\mathbf {r}_{i,M}$ in (5.2) solve the above generalized eigenvalue problem,

and satisfy

$$\begin{aligned} |\lambda _{i,M}|<\frac{1-u}{1-u}=1. \end{aligned}$$

The proof is completed. $\square$

1.3 Proof of Lemma 9

Proof

Because $U^{0}\mathbf {M}_{M}^{t}-U^{1}\mathbf {M}_{M}^{x}=\mathbf {P}_{M}^{p}A_{M}^{0}(\mathbf {P}_{M}^{p})^{T}$ and the permutation matrix $\mathbf {P}_{M}^{p}$ in (4.6) satisfies $\mathbf {P}_{M}^{p}(\mathbf {P}_{M}^{p})^{T}=(\mathbf {P}_{M}^{p})^{T}\mathbf {P}_{M}^{p}={\mathbf {I}}$, two matrices $U^{0}\mathbf {M}_{M}^{t}-U^{1}\mathbf {M}_{M}^{x}$ and $\mathbf {A}_{M}^{0}$ are similar and thus have the same eigenvalues. The definition of $\mathbf {A}_{M}^{0}$ in (3.20) tells us that the eigenvalues of $\mathbf {A}_{M}^{0}$ are the zeros of $P_{M+1}^{(0)}(x;\zeta )$ and $P_{M}^{(1)}(x;\zeta )$ which are larger than one [43, Theorem 3.4], so the matrix $U^{0}\mathbf {M}_{M}^{t}-U^{1}\mathbf {M}_{M}^{x}$ is positive definite.

Theorem 3.7 implies

$$\begin{aligned} \rho \left( (\mathbf {A}_{M}^{0})^{-\frac{1}{2}}\mathbf {A}_{M}^{1}(\mathbf {A}_{M}^{0})^{-\frac{1}{2}}\right) =\rho \left( (\mathbf {A}_{M}^{0})^{-1}\mathbf {A}_{M}^{1}\right) <1, \end{aligned}$$

where $\rho (\cdot )$ is the spectral radius of the matrix. Then $[{\mathbf {I}}-\left( (U^{0}\mathbf {A}_{M}^{0})^{-\frac{1}{2}}U^{1}\mathbf {A}_{M}^{1}(U^{0}\mathbf {A}_{M}^{0})^{-\frac{1}{2}}\right)$ is positive definite, so the matrix ${\mathbf {M}}_{M}^{t}$ is positive definite. $\square$

1.4 Proof of Theorem 5.2

Proof

Lemmas 8 and 9 show that the matrix $\mathbf {B}_{M}^{0}=\mathbf {M}^{t}_{M}\mathbf {D}_{M}$ is invertible, and Theorem 5.1 implies that $\mathbf {B}_{M}$ is diagonalizable with real eigenvalues and the spectral radius of $\mathbf {B}_{M}$ is less than one. The proof is completed. $\square$

1.5 Proof of Theorem 5.3

Proof

Because

$$\begin{aligned} \nabla _{\mathbf {W}_{M}}\lambda _{i,M}=\frac{1}{\left( 1-u \hat{\lambda } _{i,M}\right) ^{2}}\left( 0,1- \hat{\lambda } _{i,M}^2, -(1-u^2)\frac{\partial \hat{\lambda } _{i,M}}{\partial \theta },0\ldots ,0\right) ^{T},\ \end{aligned}$$

and $\mathbf {r}_{i,M}=\mathbf {D}_{M}^{-1}\mathbf {P}_{M}^{p}\left( (\mathbf {u}_{i,M})^{T},(\mathbf {v}_{i,M})^{T}\right) ^{T}$, $i=-M,\ldots , M$, one has

$$\begin{aligned} \nabla _{\mathbf {W}_{M}}\lambda _{i,M}\cdot \mathbf {r}_{i,M}=\frac{1}{\left( 1-u \hat{\lambda } _{i,M}\right) ^{2}}\left( \left( 1- \hat{\lambda } _{i,M}^2\right) \mathbf {d}_{2}\mathbf {P}_{2}^{p}\tilde{\mathbf {r}}_{i}^{M} -(1-u^2)\frac{\partial \hat{\lambda } _{i,M}}{\partial \theta }\mathbf {d}_{3}\mathbf {P}_{2}^{p}\tilde{\mathbf {r}}_{i}^{M}\right) , \end{aligned}$$

(11.1)

where $\tilde{\mathbf {r}}_{i}^{M}=\left( (\mathbf {u}_{i,M}^{(3)})^{T},(\mathbf {v}_{i,M}^{(2)})^{T}\right) ^{T}$, $\mathbf {u}_{i,M}^{(3)}$ and $\mathbf {v}_{i,M}^{(2)}$ denote two vectors formed by first three and two components of $\mathbf {u}_{i,M}$ and $\mathbf {v}_{i,M}$ respectively, and $\mathbf {d}_{2}$ and $\mathbf {d}_{3}$ are the second and third row of $\mathbf {D}_{2}^{-1}$, specifically

$$\begin{aligned} \mathbf {d}_{2}=&-\frac{G(\zeta )(1-u^2)}{(\rho G(\zeta )+\Pi )\sqrt{\zeta }}\left( 0,0,G(\zeta ),0,\sqrt{-G(\zeta )^{2}+3\zeta ^{-1}G(\zeta )+1}\right) , \\ \mathbf {d}_{3}=&\frac{1}{\rho \zeta (G(\zeta )^2\zeta ^2{-}3G(\zeta )\zeta {-}\zeta ^2{+}1)}\left( 0, \frac{\sqrt{G(\zeta ){-}2\zeta ^{-1}}(G(\zeta )^2\zeta ^2{-}3G(\zeta )\zeta {-}\zeta ^2{+}1)}{\sqrt{G(\zeta )^2\zeta ^2{-}3G(\zeta )\zeta {-}\zeta ^2{+}2}}, \right. \\&\left. \frac{(G(\zeta )\zeta -1)\tilde{n}^{1}G(\zeta )}{\sqrt{\zeta }(\rho G(\zeta )+\Pi )}, -\frac{\sqrt{2G(\zeta )^3\zeta ^2-7G(\zeta )^2\zeta -2G(\zeta )\zeta ^2+6G(\zeta )+\zeta }}{\sqrt{G(\zeta )^2\zeta ^2-3G(\zeta )\zeta -\zeta ^2+2}},\right. \\&\left. \frac{(G(\zeta )-\zeta ^{-1})\sqrt{-G(\zeta )+3\zeta ^{-1}G(\zeta )+1}}{\rho G(\zeta )+\Pi }\right) . \end{aligned}$$

The identity (11.1) always holds, because $\hat{\lambda } _{0,M}=0$ and $\mathbf {u}_{0,M}$ and $\mathbf {v}_{0,M}$ are given in (3.36).

The proof is completed. $\square$

1.6 Explanation of Remark 11

In fact, in order to judge by numerical experiments whether the sign of $\nabla _{\mathbf {W}_{M}}\lambda _{i,M}\cdot \mathbf {r}_{i,M}$ is constant or not, (11.1) should be reformed. For $i=\pm 1,\pm 2,\ldots ,\pm M$, Theorem 3.7 and (11.1) give

$$\begin{aligned} \frac{ \nabla _{\mathbf {W}_{M}}\lambda _{i,M}\cdot \mathbf {r}_{i,M}}{ -(1-u^2) } =&\left( \frac{z_{i,M}^2-1}{\rho G(\zeta )+\Pi } -\zeta \frac{\partial z_{i,M}}{\partial \zeta }\frac{1}{\rho (G(\zeta )^2\zeta ^2-3G(\zeta )\zeta -\zeta ^2+1)}\right. \\&\quad \times \left. \left( G(\zeta )\zeta -1-\zeta z_{i,M}-\frac{(G(\zeta )\zeta -1)\tilde{n}^{1}\sqrt{z_{i,M}^2-1}}{\rho G(\zeta )+\Pi }\right) \right) P_{M}^{(1)}(-z_{i,M};\zeta ) \\&+\left( \frac{z_{i,M}^2-1}{\rho G(\zeta )+\Pi } + \zeta \frac{\partial z_{i,M}}{\partial \zeta }\frac{1}{\rho (G(\zeta )^2\zeta ^2-3G(\zeta )\zeta -\zeta ^2+1)}\right. \\&\quad \times \left. \left( G(\zeta )\zeta -1+\zeta z_{i,M} + \frac{(G(\zeta )\zeta -1)\tilde{n}^{1}\sqrt{z_{i,M}^2-1}}{\rho G(\zeta )+\Pi }\right) \right) P_{M}^{(1)}(z_{i,M};\zeta ). \end{aligned}$$

Only a simple case is discussed in the following. As shown in Remark 2, at the local thermodynamic equilibrium, $\Pi =0$ and $n^\alpha =0$, thus one has

$$\begin{aligned} \frac{ \nabla _{\mathbf {W}_{M}}\lambda _{i,M}\cdot \mathbf {r}_{i,M} }{-(1-u^2)} =&\left( \frac{z_{i,M}^2-1}{\rho G(\zeta )} -\zeta \frac{\partial z_{i,M}}{\partial \zeta } \frac{G(\zeta )\zeta -1-\zeta z_{i,M} }{\rho (G(\zeta )^2\zeta ^2-3G(\zeta )\zeta -\zeta ^2+1)}\right) P_{M}^{(1)}(-z_{i,M};\zeta ) \\&+\left( \frac{z_{i,M}^2-1}{\rho G(\zeta )} +\zeta \frac{\partial z_{i,M}}{\partial \zeta } \frac{G(\zeta )\zeta -1+\zeta z_{i,M} }{\rho (G(\zeta )^2\zeta ^2-3G(\zeta )\zeta -\zeta ^2+1)}\right) P_{M}^{(1)}(z_{i,M};\zeta ). \end{aligned}$$

Using the term

$$\begin{aligned} \frac{\rho (G(\zeta )^2\zeta ^2-3G(\zeta )\zeta -\zeta ^2+1)}{(z_{i,M}^2-1)(G(\zeta )\zeta -1) P_{M}^{(1)}(-z_{i,M};\zeta )}, \end{aligned}$$

to normalize the above identity and noting that

$$\begin{aligned} \mathrm{sign}(G(\zeta )^2\zeta ^2-3G(\zeta )\zeta -\zeta ^2+1)=-\mathrm{sign}(x_{1,2}^{(0)}x_{2,2}^{(0)})<0{,} \end{aligned}$$

gives

$$\begin{aligned} \mathrm{sign}\left( \nabla _{\mathbf {W}_{M}}\lambda _{i,M}\cdot \mathbf {r}_{i,M}\right) =(-1)^{M}\mathrm{sign}\left( \hat{g}(z_{i,M};\zeta )\right) , \end{aligned}$$

where $\hat{g}(z_{i,M};\zeta )$ is defined by

$$\begin{aligned} \hat{g}(z_{i,M};\zeta )=&\frac{G(\zeta )^2\zeta ^2-3G(\zeta )\zeta -\zeta ^2+1}{ G(\zeta )\left( G(\zeta )\zeta -1\right) }\left( 1+\frac{P_{M}^{(1)}(z_{i,M};\zeta )}{P_{M}^{(1)}(-z_{i,M};\zeta )}\right) \\&-\frac{\zeta }{(z_{i,M})^2-1} \left( 1-\frac{P_{M}^{(1)}(z_{i,M};\zeta )}{P_{M}^{(1)}(-z_{i,M};\zeta )}\right) \frac{\partial z_{i,M}}{\partial \zeta }\\&+\frac{\zeta ^2 z_{i,M}}{ \big ( (z_{i,M})^2-1\big ) \left( G(\zeta )\zeta -1\right) }\left( 1+\frac{P_{M}^{(1)}(z_{i,M};\zeta )}{P_{M}^{(1)}(-z_{i,M};\zeta )}\right) \frac{\partial z_{i,M}}{\partial \zeta }, \ i\ge 1, \end{aligned}$$

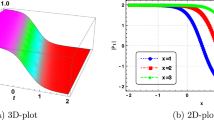
and $\hat{g}(z_{i,M};\zeta ):=\hat{g}(z_{-i,M};\zeta )$ for $i\le -1$. It is relatively easy to judge by numerical experiments whether the sign of $\hat{g}(z_{i,M};\zeta )$ is constant or not. Figure 6 shows plots of $\hat{g}(z_{1,4};\zeta )$ and $\hat{g}(z_{1,7};\zeta )$ in terms of $\zeta$. Similar to the special case of $M=4$ and 7, our observation in numerical experiments is that the sign of $\hat{g}(z_{1,M};\zeta )$ is not constant when $M\ge 4$ so that both $\lambda _{1,M}$ and $\lambda _{-1,M}$ characteristic fields are neither linearly degenerate nor genuinely nonlinear when $M\ge 4$. Such phenomenon is still not found in the case of $M\le 3$.

Fig. 6

Plots of $\hat{g}(z_{1,M};\zeta )$ in terms of $\zeta$ for $M=4$ (left) and 7 (right)

1.7 Proof of Theorem 5.4

Proof

Because the matrix $\mathbf {D}_M$ in (4.14) at $\mathbf {W}_{M}=\mathbf {W}_{M}^{(0)}$ can be reformed as follows

$$\begin{aligned} \mathbf {D}_{M}=\begin{pmatrix} \mathbf {D}_{3\times 3}^{11} &{}\mathbf {D}_{3\times 2}^{12} &{} \mathbf {O}\\ \mathbf {O} &{} \mathbf {D}_{2\times 2}^{22} &{} \mathbf {O}\\ \mathbf {O} &{} \mathbf {O} &{} \mathbf {I}_{2M-4} \end{pmatrix}, \end{aligned}$$

and its inverse is given by

$$\begin{aligned} \mathbf {D}_{M}^{-1}=\begin{pmatrix} \left( \mathbf {D}_{3\times 3}^{11}\right) ^{-1} &{} -\left( \mathbf {D}_{3\times 3}^{11}\right) ^{-1}\mathbf {D}_{3\times 2}^{12}\left( \mathbf {D}_{2\times 2}^{22}\right) ^{-1} &{} \mathbf {O}\\ \mathbf {O} &{} \left( \mathbf {D}_{2\times 2}^{22}\right) ^{-1} &{} \mathbf {O}\\ \mathbf {O} &{} \mathbf {O} &{} \mathbf {I}_{2M-4} \end{pmatrix}, \end{aligned}$$

as well as

$$\begin{aligned} \tilde{\mathbf {D}}_{M}^{W}=\begin{pmatrix} \mathbf {O} &{}\mathbf {D}_{3\times 2}^{12} &{} \mathbf {O}\\ \mathbf {O} &{} \mathbf {D}_{2\times 2}^{22} &{} \mathbf {O}\\ \mathbf {O} &{} \mathbf {O} &{} \mathbf {I}_{2M-4} \end{pmatrix}, \end{aligned}$$

the product of $\tilde{\mathbf {D}}_{M}^{W}$ and $\mathbf {D}_{M}^{-1}$ is of the form

$$\begin{aligned} \tilde{\mathbf {D}}_{M}^{W}\mathbf {D}_{M}^{-1}=\begin{pmatrix} \mathbf {O}_{3\times 3}&{} \mathbf {D}_{3\times 2}^{12}\left( \mathbf {D}_{2\times 2}^{22}\right) ^{-1} &{} \mathbf {O}_{3\times (2M-4)}\\ \mathbf {O}_{2\times 3}&{} \mathbf {I}_{2}&{} \mathbf {O}_{2\times (2M-4)}\\ \mathbf {O}_{(2M-4)\times 3}&{}\mathbf {O}_{(2M-4)\times 2}&{}\mathbf {I}_{2M-4} \end{pmatrix}, \end{aligned}$$

where $\mathbf {D}_{3\times 3}^{11}$ is the $3\times 3$ subblock of $\mathbf {D}_{2}$ in the upper left corner, $\mathbf {D}_{3\times 2}^{12}$ denotes the $3\times 2$ subblock of $\mathbf {D}_{2}$ in the upper right corner, and $\mathbf {D}_{2\times 2}^{22}$ is $2\times 2$ subblock of $\mathbf {D}_{2}$ in the bottom right corner. It is obvious that each eigenvalue of $-\tilde{\mathbf {D}}_{M}^{W}\mathbf {D}_{M}^{-1}$ is non-positive, so does the matrix

$$\begin{aligned} \bar{\mathbf {Q}}_{M}:=-\frac{1}{\tau }\left( U^{0}\mathbf {M}_{M}^{t}-U^{1}\mathbf {M}_{M}^{x}\right) ^{\frac{1}{2}}\tilde{\mathbf {D}}_{M}^{W}\mathbf {D}_{M}^{-1}\left( U^{0}\mathbf {M}_{M}^{t}-U^{1}\mathbf {M}_{M}^{x}\right) ^{-\frac{1}{2}}. \end{aligned}$$

The matrix $U^{0}\mathbf {M}_{M}^{t}-U^{1}\mathbf {M}_{M}^{x}$ can be written as follows

$$\begin{aligned} \begin{pmatrix} \mathbf {M}_{3\times 3}^{11}&{}\mathbf {M}_{3\times 2}^{12}&{}\mathbf {O}_{3,2M-4}\\ (\mathbf {M}_{3\times 2}^{12})^{T}&{}\mathbf {M}_{2\times 2}^{22}&{}\mathbf {M}_{2\times (2M-4)}^{23}\\ \mathbf {O}_{2M-4,3}&{}(\mathbf {M}_{2\times (2M-4)}^{23})^{T}&{}\mathbf {M}_{(2M-4)\times (2M-4)}^{33} \end{pmatrix}, \end{aligned}$$

where $\mathbf {M}_{3\times 3}^{11}$ is the $3\times 3$ subblock of $\mathbf {P}_{2}^{p}\mathbf {A}_{2}^{0}(\mathbf {P}_{2}^{p})^{T}$ in the upper left corner, $\mathbf {M}_{3\times 2}^{12}$ denotes the $3\times 2$ subblock of $\mathbf {P}_{2}^{p}\mathbf {A}_{2}^{0}(\mathbf {P}_{2}^{p})^{T}$ in the upper right corner, and $\mathbf {M}_{2\times 2}^{22}$ is $2\times 2$ subblock of $\mathbf {P}_{2}^{p}\mathbf {A}_{2}^{0}(\mathbf {P}_{2}^{p})^{T}$ in the bottom right corner, the rest subblocks form the $(2M-2)\times (2M-2)$ bottom right corner of $\mathbf {P}_{2}^{p}\mathbf {A}_{M}^{0}(\mathbf {P}_{M}^{p})^{T}$. Thus one has

$$\begin{aligned} \mathbf {M}_{D}:=(\mathbf {M}_{3\times 2}^{12})^{T}\mathbf {D}_{3\times 2}^{12}\left( \mathbf {D}_{2\times 2}^{22}\right) ^{-1} =-\left( \mathbf {D}_{3\times 2}^{12}\left( \mathbf {D}_{2\times 2}^{22}\right) ^{-1}\right) ^{T}\mathbf {M}_{3\times 3}^{11} \left( \mathbf {D}_{3\times 2}^{12}\left( \mathbf {D}_{2\times 2}^{22}\right) ^{-1}\right) , \end{aligned}$$

which is symmetric because $\mathbf {M}_{3\times 3}^{11}\mathbf {D}_{3\times 2}^{12}\left( \mathbf {D}_{2\times 2}^{22}\right) ^{-1}+ \mathbf {M}_{3\times 2}^{12}=\mathbf {O}_{3\times 2}.$

On the other hand, because the first three components of $\mathbf {S}(\mathbf {W}_M)$ are zero, all elements in the first three rows and the first three columns of the matrix

$$\begin{aligned} \mathbf {Q}_{M}=-\frac{1}{\tau }\left( U^{0}\mathbf {M}_{M}^{t}-U^{1}\mathbf {M}_{M}^{x}\right) \tilde{\mathbf {D}}_{M}^{W}\mathbf {D}_{M}^{-1}, \end{aligned}$$

are zero, and the matrix $\mathbf {Q}_{M}$ is of form

$$\begin{aligned} \mathbf {Q}_{M}=-\frac{1}{\tau } \begin{pmatrix} \mathbf {O}_{3,3}&{}\quad \mathbf {O}_{3,2}&{}\quad \mathbf {O}_{3,2M-4}\\ \mathbf {O}_{2,3}&{}\quad \mathbf {M}_{2\times 2}^{22}+\mathbf {M}_{D}&{}\quad \mathbf {M}_{2\times (2M-4)}^{23}\\ \mathbf {O}_{2M-4,3}&{}\quad (\mathbf {M}_{2\times (2M-4)}^{23})^{T}&{}\quad \mathbf {M}_{(2M-4)\times (2M-4)}^{33} \end{pmatrix}. \end{aligned}$$

Hence the matrix $\mathbf {Q}_{M}$ is symmetric. It is obvious that $\mathbf {Q}_{M}$ is congruent with $\bar{\mathbf {Q}}_{M}$, so it is negative semi-definite.

Because both matrices $\mathbf {D}_{M}$ and $\mathbf {M}_{M}^{t}$ are invertible, and $\mathbf {M}_{M}^{t}$ is positive definite, (5.4) is equivalent to

$$\begin{aligned} \det \left( i\omega \mathbf {I}-ik\mathbf {M}_{M}-\hat{\mathbf {Q}}_{M}\right) =0, \end{aligned}$$

(11.2)

where

$$\begin{aligned} \hat{\mathbf {Q}}_{M}:=&\left( \mathbf {M}_{M}^{t}\right) ^{-\frac{1}{2}}\mathbf {Q}_{M}\left( \mathbf {M}_{M}^{t}\right) ^{-\frac{1}{2}}, \end{aligned}$$

and

$$\begin{aligned} \mathbf {M}_{M}:=\left( \mathbf {M}_{M}^{t}\right) ^{-\frac{1}{2}}\mathbf {M}_{M}^{x}\left( \mathbf {M}_{M}^{t}\right) ^{-\frac{1}{2}}. \end{aligned}$$

It is obvious that the matrix $\hat{\mathbf {Q}}_{M}$ is congruent with $\mathbf {Q}_{M}$ and negative semi-definite, and $\mathbf {M}_{M}$ is symmetric. Using Lemmas 1 and 2 in [15] completes the proof. $\square$

1.8 Proof of Lemma 10

Proof

• (i) Under the given Lorentz boost (x direction)

  $$\begin{aligned} t'=\gamma (v) (t-vx),\ x'=\gamma (v)(x-vt),\ \gamma (v)=(1-v^2)^{-\frac{1}{2}}, \end{aligned}$$

  where v is the relative velocity between frames in the x-direction, one has

  $$\begin{aligned}&(p^{0})'=\gamma (v)(p^{0}-p^{1}v),\quad (p^{1})'=\gamma (v)(p^{1}-p^{0}v), \\&(U^{0})'=\gamma (v)(U^{0}-U^{1}v),\quad (U^{1})'=\gamma (v)(U^{1}-U^{0}v). \end{aligned}$$

  Thus one further obtains

  $$\begin{aligned} E'= (U^{0})'(p^{0})'-(U^{1})'(p^{1})'=U^{0}p^{0}-U^{1}p^{1}=E, \end{aligned}$$

  and

  $$\begin{aligned} \left( \frac{p_{{\langle }1{\rangle }}}{U^{0}}\right) '=&\frac{-(p^{{\langle }1{\rangle }})'}{(U^{0})'}=-\frac{p^{{\langle }0{\rangle }}-p^{{\langle }1{\rangle }}v}{U^{1}-U^{0}v}=-\frac{(U^{0})^{-1}U^{1}p^{{\langle }1{\rangle }}-p^{{\langle }1{\rangle }}v}{U^{1}-U^{0}v}=\frac{p_{{\langle }1{\rangle }}}{U^{0}}, \\ \left( \frac{dp}{p^{0}}\right) '=&\frac{d(p^{1})'}{(p^{0})'}=\frac{dp^{0}-dp^{1}v}{p^{1}-p^{0}v}=\frac{(p^{0})^{-1}p^{1}dp^{1}-dp^{1}v}{p^{1}-p^{0}v}=\frac{dp}{p^{0}}. \end{aligned}$$

  Combining them with (4.9) gives that each component of $\mathbf {f}_{M}$ is Lorentz invariant, so that the last $(2M-4)$ components of $\mathbf {W}_{M}$ are also Lorentz invariant. From (2.17) and (2.20), it is not difficult to prove that $\rho$ and $\theta$ are Lorentz invariant. On the other hand, because

  $$\begin{aligned} \tilde{n}^{1}=\int _{\mathbb {R}}\frac{p^{{\langle }1{\rangle }}}{U^{0}}f\frac{dp}{p^{0}}, \end{aligned}$$

  the quantity $\tilde{n}^{1}$ is Lorentz invariant. Moreover, one has

  $$\begin{aligned} \left( \frac{du}{1-u^2}\right) '=\frac{d(U^{1})'}{(U^{0})'}=\frac{dU^{0}-dU^{1}v}{U^{1}-U^{0}v}=\frac{(U^{0})^{-1}U^{1}dU^{1}-dU^{1}v}{U^{1}-U^{0}v}=\frac{dU^{1}}{U^{0}}=\frac{du}{1-u^2}. \end{aligned}$$

  Using the above results completes the proof of the first part.

• (ii) Because $\mathbf {A}_{M}^{0}$ and $\mathbf {A}_{M}^{1}$ only depend on $\theta$, they are Lorentz invariant. The source term $\mathbf {S}(\mathbf {W}_{M})$ in (4.21) can be rewritten into

  $$\begin{aligned} \mathbf {S}(\mathbf {W}_{M})=-\frac{1}{\tau }\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{0}(\mathbf {P}_{M}^{p})^{T}\left( \mathbf {f}_{M}-\mathbf {f}^{(0)}_{M}\right) , \end{aligned}$$

  which has been expressed in terms of the Lorentz covariant quantities. In fact, the general source term $\mathbf {S}(\mathbf {W}_{M})$ in the moment system (4.20) is also Lorentz invariant. The proof is completed.

$\square$

1.9 Proof of Theorem 5.5

Proof

From the 3rd step in Sec. 4.2 and Lemma 10, one knows that $\hat{\mathbf {D}}_{M}=\mathbf {D}_M(\mathbf {D}_{M}^{u})^{-1}$ can be expressed in terms of the Lorentz covariant quantities, so it is Lorentz invariant. Because

$$\begin{aligned} (\mathbf {M}_{M}^{t})'&=-\gamma (v)(U^{1}-U^{0}v)\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{1}(\mathbf {P}_{M}^{p})^{T}+\gamma (v)(U^{0}-U^{1}v)\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{0}(\mathbf {P}_{M}^{p})^{T},\\ (\mathbf {M}_{M}^{x})'&=-\gamma (v)(U^{0}-U^{1}v)\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{1}(\mathbf {P}_{M}^{p})^{T}+\gamma (v)(U^{1}-U^{0}v)\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{0}(\mathbf {P}_{M}^{p})^{T}, \end{aligned}$$

and

$$\begin{aligned} \left( \frac{\partial }{\partial t}\right) '=\gamma (v)\left( \frac{\partial }{\partial t}+v\frac{\partial }{\partial x}\right) ,\quad \left( \frac{\partial }{\partial x}\right) '=\gamma (v)\left( \frac{\partial }{\partial x}+v\frac{\partial }{\partial t}\right) , \end{aligned}$$

one has

$$\begin{aligned} \left( \mathbf {D}_{M}^{u}\frac{\partial \mathbf {W}_{M}}{\partial t}\right) '=\,&\mathrm{diag}\left\{ 1,\big ((U^{0})^2\big )',1,\ldots ,1\right\} \gamma (v)\left( \frac{\partial (\rho ,u',\theta ,\Pi ,\tilde{n}^{1},f_{3}^{0},\ldots ,f_{M-1}^{1})^{T}}{\partial t}\right. \\&+\left. v\frac{\partial (\rho ,u',\theta ,\Pi ,\tilde{n}^{1},f_{3}^{0},\ldots ,f_{M-1}^{1})^{T}}{\partial x}\right) \\ =\,&\mathrm{diag}\left\{ 1,\big ((U^{0}\big )^{-1})',1,\ldots ,1\right\} \gamma (v)\left( \frac{\partial (\rho ,(U^{1})',\theta ,\Pi ,\tilde{n}^{1},f_{3}^{0},\ldots ,f_{M-1}^{1})^{T}}{\partial t}\right. \\&+\left. v\frac{\partial (\rho ,(U^{1})',\theta ,\Pi ,\tilde{n}^{1},f_{3}^{0},\ldots ,f_{M-1}^{1})^{T}}{\partial x}\right) \\ =\,&\mathbf {D}_{M}^{u}\gamma (v)\left( \frac{\partial \mathbf {W}_{M}}{\partial t}+v\frac{\partial \mathbf {W}_{M}}{\partial x}\right) , \end{aligned}$$

where the last equal sign is derived by following the proof of Lemma 10. Similarly, one has

$$\begin{aligned} \left( \mathbf {D}_{M}^{u}\frac{\partial \mathbf {W}_{M}}{\partial x}\right) '=\mathbf {D}_{M}^{u}\gamma (v)\left( \frac{\partial \mathbf {W}_{M}}{\partial x}+v\frac{\partial \mathbf {W}_{M}}{\partial t}\right) . \end{aligned}$$

Thus it holds

$$\begin{aligned}&\left( \mathbf {B}_{M}^{0}\frac{\partial \mathbf {W}_{M}}{\partial t} + \mathbf {B}_{M}^{1}\frac{\partial \mathbf {W}_{M}}{\partial x}\right) '\\&\quad =\,(\mathbf {M}_{M}^{t})'\left( \mathbf {D}_{M}\frac{\partial \mathbf {W}_{M}}{\partial t}\right) '+(\mathbf {M}_{M}^{x})'\left( \mathbf {D}_{M}\frac{\partial \mathbf {W}_{M}}{\partial x}\right) '\\&\quad =\left( -(U^{1})'\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{1}(\mathbf {P}_{M}^{p})^{T}+ (U^{0})'P_{M}^{p}\mathbf {A}_{M}^{0}(P_{M}^{p})^{T}\right) \mathbf {D}_{M}\left( \gamma (v)\left( \frac{\partial \mathbf {W}_{M}}{\partial t}+v\frac{\partial \mathbf {W}_{M}}{\partial x}\right) \right) \\&\qquad +\,\left( -(U^{0})'\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{1}(\mathbf {P}_{M}^{p})^{T}+ (U^{1})'\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{0}(\mathbf {P}_{M}^{p})^{T}\right) \mathbf {D}_{M}\left( \gamma (v)\left( \frac{\partial \mathbf {W}_{M}}{\partial x}+v\frac{\partial \mathbf {W}_{M}}{\partial t}\right) \right) \\&\quad =\left( -U^{1}v\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{1}(\mathbf {P}_{M}^{p})^{T}+U^{0}\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{0}(\mathbf {P}_{M}^{p})^{T}\right) \mathbf {D}_{M}\frac{\partial \mathbf {W}_{M}}{\partial t}\\&\qquad +\,\left( -U^{0}\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{1}(\mathbf {P}_{M}^{p})^{T}+U^{1}\mathbf {P}_{M}^{p}\mathbf {A}_{M}^{0}(\mathbf {P}_{M}^{p})^{T}\right) \mathbf {D}_{M}\frac{\partial \mathbf {W}_{M}}{\partial x}\\&\quad =\mathbf {B}_{M}^{0}\frac{\partial \mathbf {W}_{M}}{\partial t} + \mathbf {B}_{M}^{1}\frac{\partial \mathbf {W}_{M}}{\partial x}. \end{aligned}$$

Combining it with Lemma 10 completes the proof. $\square$

Appendix 5: Proofs in Section 6

1.1 Proof of Lemma 11

Proof

Using Lemmas 4 and 7 gives

$$\begin{aligned} \tilde{f}g^{(0)}_{[u,\theta ]}=&\sum _{i=0}^{M}\tilde{f}_{i}^{0}\tilde{P}_{i}^{(0)}[u,\theta ]+\sum _{j=0}^{M-1}\tilde{f}_{j}^{1}\tilde{P}_{j}^{(1)}[u,\theta ],\\ \Pi _{M}[u,\theta ] f=&\sum _{i=0}^{M}f_{i}^{0}\tilde{P}_{i}^{(0)}[u,\theta ]+\sum _{j=0}^{M-1}f_{j}^{(1)}\tilde{P}_{j}^{(1)}[u,\theta ], \end{aligned}$$

where

$$\begin{aligned} f_{i}^{0}&={\langle }f,\tilde{P}_{i}^{(0)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}},\quad \tilde{f}_{i}^{0}={\langle }\tilde{f}g^{(0)}_{[u,\theta ]},\tilde{P}_{i}^{(0)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}},\quad i\le M,\\ f_{j}^{1}&={\langle }f,\tilde{P}_{j}^{(1)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}},\quad \tilde{f}_{j}^{1}={\langle }\tilde{f}g^{(0)}_{[u,\theta ]},\tilde{P}_{j}^{(1)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}},\quad j\le M-1. \end{aligned}$$

Therefore one has

$$\begin{aligned}&{\langle }\tilde{f}g^{(0)}_{[u,\theta ]},\Pi _{M}[u,\theta ]f{\rangle }_{g^{(0)}_{[u,\theta ]}}={\langle }\tilde{f}f,\Pi _{M}[u,\theta ]f{\rangle }_{f}\\&\quad =\sum _{i=0}^{M}f_{i}^{0}{\langle }\tilde{f}f,\tilde{P}_{i}^{(0)}[u,\theta ]{\rangle }_{f}+ \sum _{j=0}^{M-1}f_{j}^{1}{\langle }\tilde{f}f,\tilde{P}_{j}^{(1)}[u,\theta ]{\rangle }_{f}\\&\quad =\sum _{i=0}^{M}f_{i}^{0}{\langle }\tilde{f}g^{(0)}_{[u,\theta ]},\tilde{P}_{i}^{(0)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}}+ \sum _{j=0}^{M-1}f_{j}^{1}{\langle }\tilde{f}g^{(0)}_{[u,\theta ]},\tilde{P}_{j}^{(1)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}}\\&\quad =\sum _{i=0}^{M}f_{i}^{0}\tilde{f}_{i}^{0}+ \sum _{j=0}^{M-1}f_{j}^{1}\tilde{f}_{j}^{1}\\&\quad =\sum _{i=0}^{M}{\langle }f,\tilde{f}_{i}^{0}\tilde{P}_{i}^{(0)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}}+ \sum _{j=0}^{M-1}{\langle }f,\tilde{f}_{j}^{1}\tilde{P}_{j}^{(1)}[u,\theta ]{\rangle }_{g^{(0)}_{[u,\theta ]}}\\&\quad ={\langle }f,\tilde{f}g^{(0)}_{[u,\theta ]}{\rangle }_{g^{(0)}_{[u,\theta ]}}={\langle }f,\tilde{f}f{\rangle }_{f}. \end{aligned}$$

The proof is completed. $\square$

1.2 Proof of Lemma 12

Proof

Using Lemma 7 gives

$$\begin{aligned}&\Pi _{M}[u_{1},\theta _{1}]f=\sum _{i=0}^{M}f_{i}^{0}\tilde{P}_{i}^{(0)}[u_{1},\theta _{1}]+ \sum _{j=0}^{M-1}f_{j}^{1}\tilde{P}_{i}^{(1)}[u_{1},\theta _{1}],\\&\Pi _{M}[u_{1},\theta _{1}]\Pi _{M}[u_{2},\theta _{2}]f=\sum _{i=0}^{M}\tilde{f}_{i}^{0}\tilde{P}_{i}^{(0)}[u_{1},\theta _{1}]+ \sum _{j=0}^{M-1}\tilde{f}_{j}^{1}\tilde{P}_{j}^{(1)}[u_{1},\theta _{1}], \end{aligned}$$

$$\begin{aligned} f_{i}^{0}&={\langle }f,\tilde{P}_{i}^{(0)}[u_{1},\theta _{1}]{\rangle }_{g^{(0)}_{[u_{1},\theta _{1}]}}= {{\langle }f,{P}_{i}^{(0)}(u_{1},\zeta _{1})f{\rangle }_{f}},i\le M,\\ f_{j}^{1}&={\langle }f,\tilde{P}_{j}^{(1)}[u_{1},\theta _{1}]{\rangle }_{g^{(0)}_{[u_{1},\theta _{1}]}}= {{\langle }f,{P}_{j}^{(1)}(u_{1},\zeta _{1})(U_{0})_{1}^{-1}p_{{\langle }1{\rangle }}f{\rangle }_{f}},j\le M-1, \end{aligned}$$

$$\begin{aligned} \tilde{f}_{i}^{0}&={\langle }\Pi _{M}[u_{2},\theta _{2}]f,\tilde{P}_{i}^{(0)}[u_{1},\theta _{1}]{\rangle }_{g^{(0)}_{[u_{1},\theta _{1}]}}= {{\langle }\Pi _{M}[u_{2},\theta _{2}]f,{P}_{i}^{(0)}(u_{1},\zeta _{1})f{\rangle }_{f}},i\le M,\\ \tilde{f}_{j}^{1}&={\langle }\Pi _{M}[u_{2},\theta _{2}]f,\tilde{P}_{j}^{(1)}[u_{1},\theta _{1}]{\rangle }_{g^{(0)}_{[u_{1},\theta _{1}]}}\\&= {{\langle }\Pi _{M}[u_{2},\theta _{2}]f,{P}_{j}^{(1)}(u_{1},\zeta _{1})(U_{0})_{1}^{-1}p_{{\langle }1{\rangle }}f{\rangle }_{f}},j\le M-1{.} \end{aligned}$$

Because both ${P}_{i}^{(0)}(u_{1},\zeta _{1})f$ and ${P}_{j}^{(1)}(u_{1},\zeta _{1})(U_{0})_{1}^{-1}p_{{\langle }1{\rangle }}f$ belong to the space $\mathbb {H}_{M}^{f}$, using Lemma 11 completes the proof. $\square$

1.3 Proof of Theorem 6.1

Proof

Because Eq. (6.3) is equivalent to

$$\begin{aligned} \left( \mathbf {I}+\frac{\Delta t}{\tau _{i}^{*}}\left( \mathbf {M}_{i,M}^{t*}\right) ^{-1}\left( U_{i}^{0*}\mathbf {M}_{i,M}^{t*}-U_{i}^{1*} \mathbf {M}_{i,M}^{x*}\right) \left( \mathbf {I}-\mathbf {D}_{i,M}^{f_{i}^{(0)*}}\right) \right) \mathbf {f}_{i,M}^{n+1}=\mathbf {f}_{i,M}^{*}, \end{aligned}$$

it is unconditionally stable if and only if the modulus of each eigenvalue of the matrix

$$\begin{aligned} \mathbf {I}+\frac{\Delta t}{\tau _{i}^{*}}\left( \mathbf {M}_{i,M}^{t*}\right) ^{-1}\left( U_{i}^{0*}\mathbf {M}_{i,M}^{t*}-U_{i}^{1*} \mathbf {M}_{i,M}^{x*}\right) \left( \mathbf {I}-\mathbf {D}_{i,M}^{f_{i}^{(0)*}}\right) , \end{aligned}$$

is not less than one. It is true if the real part of each eigenvalue of the matrix

$$\begin{aligned} \left( \mathbf {M}_{i,M}^{t*}\right) ^{-1}\left( U_{i}^{0*}\mathbf {M}_{i,M}^{t*}-U_{i}^{1*}\mathbf {M}_{i,M}^{x*}\right) \left( \mathbf {I}-\mathbf {D}_{i,M}^{f_{i}^{(0)*}}\right) =:\left( \mathbf {M}_{i,M}^{t*}\right) ^{-1}\bar{\mathbf {M}}_{D}^{*}, \end{aligned}$$

(12.1)

is non-negative.

In fact, thanks to (6.4), the characteristic polynomial of the upper triangular matrix $\mathbf {I}-\mathbf {D}_{i,M}^{f_{i}^{(0)*}}$ is explicitly given by

$$\begin{aligned} 0=\det \left( \lambda \mathbf {I}-\left( \mathbf {I}-\mathbf {D}_{i,M}^{f_{i}^{(0)*}}\right) \right) = \det \left( (\lambda -1)\mathbf {I}+\mathbf {D}_{i,M}^{f^{(0)*}}\right) =\lambda (\lambda -1)^{2M}, \end{aligned}$$

and $\bar{\mathbf {M}}_{D}^{*}$ is a symmetric matrix and congruent with

$$\begin{aligned} \left( U_{i}^{0*}\mathbf {M}_{i,M}^{t*}-U_{i}^{1*}\mathbf {M}_{i,M}^{x*}\right) ^{\frac{1}{2}} \left( \mathbf {I}-\mathbf {D}_{i,M}^{f_{i}^{(0)*}}\right) \left( U_{i}^{0*} \mathbf {M}_{i,M}^{t*}-U_{i}^{1*}\mathbf {M}_{i,M}^{x*}\right) ^{-\frac{1}{2}}, \end{aligned}$$

which is similar to the matrix $\mathbf {I}-\mathbf {D}_{i,M}^{f_{i}^{(0)*}}$. Thus the matrix $\bar{\mathbf {M}}_{D}^{*}$ is positive semi-definite and each eigenvalue of the matrix $\left( \mathbf {M}_{i,M}^{t*}\right) ^{-1}\bar{\mathbf {M}}_{D}^{*}$ is non-negative because of the relation $\left( \mathbf {M}_{i,M}^{t*}\right) ^{-1}\bar{\mathbf {M}}_{D}^{*} =\left( \mathbf {M}_{i,M}^{t*}\right) ^{-\frac{1}{2}} \big ( \left( \mathbf {M}_{i,M}^{t*}\right) ^{-\frac{1}{2}} \bar{\mathbf {M}}_{D}^{*} \left( \mathbf {M}_{i,M}^{t*}\right) ^{-\frac{1}{2}}\big ) \left( \mathbf {M}_{i,M}^{t*}\right) ^{\frac{1}{2}}$. The proof is completed. $\square$