Advertisement

Journal of Scientific Computing

, Volume 61, Issue 2, pp 398–423 | Cite as

An Analysis of Solution Point Coordinates for Flux Reconstruction Schemes on Triangular Elements

  • F. D. Witherden
  • P. E. Vincent
Open Access
Article
First Online:

Abstract

The flux reconstruction approach offers an efficient route to high-order accuracy on unstructured grids. The location of the solution points plays an important role in determining the stability and accuracy of FR schemes on triangular elements. In particular, it is desirable that a solution point set (i) defines a well conditioned nodal basis for representing the solution, (ii) is symmetric, (iii) has a triangular number of points and, (iv) minimises aliasing errors when constructing a polynomial representation of the flux. In this paper we propose a methodology for generating solution points for triangular elements. Using this methodology several thousand point sets are generated and analysed. Numerical performance is assessed through an Euler vortex test case. It is found that the Lebesgue constant and quadrature strength of the points are strong indicators of stability and performance. Further, at polynomial orders \(\wp = 4,6,7\) solution points with superior performance to those tabulated in literature are discovered.

Keywords

Flux reconstruction High-order methods Nodal discontinuous Galerkin method Computational fluid dynamics 

1 Introduction

Theoretical studies and numerical experiments suggest that unstructured high-order methods can provide solutions to otherwise intractable fluid flow problems within the vicinity of complex geometries. In 2007 Huynh proposed the flux reconstruction (FR) approach [1], a unifying framework for high-order schemes that encompasses several existing methods while simultaneously admitting an efficient implementation. Using FR it is possible to recover nodal discontinuous Galerkin (DG) methods of the type described by Hesthaven and Warburton [2], and the spectral difference schemes, original proposed by Kopriva and Kolias in 1996 [3] and later popularised by Sun et al. [4]. Unlike traditional DG methods, which are based on a weak formulation, and hence require integration, the FR approach is based on the differential form of the governing system. As a consequence, implementations of FR forego having to perform numerical quadrature within each element. This not only reduces complexity, but can also lead to decreased computational cost.

One problem with the FR approach is that for a non-linear flux function aliasing driven instabilities may develop. The severity of these instabilities depends upon the degree to which the flux is under resolved within each element. This is particularly problematic within the context of the Euler and Navier–Stokes equations. Here the flux is not only non-linear with respect to the solution but also non-polynomial. It has been demonstrated, both theoretically [5] and empirically [6] that the degree of aliasing driven instabilities depends upon the location of the solution points inside each element. Specifically, it has been found that placing points at the abscissa of strong Gaussian quadrature rules has a positive impact on their performance.

In this paper we describe a methodology for generating sets of candidate solution points for triangular elements. With this methodology we obtain a range of point sets for polynomial orders \(\wp = 3,4,5,6,7\). The performance of these points is then analysed, both theoretically and experimentally, and compared against those in literature. The paper is set out as follows. In Sect. 2 we give a short overview of previous work on the subject. Existing point sets proposed by Hesthaven and Warburton [2] and Williams and Jameson [7] are discussed. We also take the opportunity to elaborate on the constraints that candidate points must fulfil. The methodology used to derive our point sets is described in Sect. 3. Based on the approach of Zhang et al. [8], we show how it can be employed to generate quadrature rules in triangular elements. In Sect. 4 mathematical tools for analysing the rules that are produced will be presented. Potential issues regarding the lack of unisolvency are discussed. Candidate solution point sets are presented in Sect. 5. A two dimensional Euler vortex test case is introduced in Sect. 6. This test case, along with the metrics of Sect. 4 are then used to evaluate, compare and contrast the various rules with the results being presented in Sect. 7. Finally, in Sect. 8 conclusions are drawn and guidance on the choice of points is given.

2 Solution Point Requirements

Hesthaven and Warburton [2] identify three key criteria that solution point sets for nodal DG must satisfy. The first is that the points define a well conditioned nodal basis. This property ensures any nodal expansions based on the points will be well suited to the task of polynomial interpolation. The second is that the points be arranged symmetrically inside of each element. This eliminates any potential for the solution to be biased towards one region of an element depending on the global-to-local mapping. The third is that the number of solution points must be equivalent to the rank of the polynomial basis used to represent the solution. For triangular elements this fixes the number of points to be a triangle number as shown in Table 1. To satisfy the aforementioned criteria Hesthaven and Warburton suggest [2] using Gauss–Legendre–Lobatto (GLL) points in one dimension and propose a multidimensional analogue of these points in triangles and tetrahedra. The nodal sets proposed are constructive and parameterised by a single scalar constant \(\alpha \). For each polynomial order values of \(\alpha \) which yield the best conditioned bases are tabulated. The corresponding points are known as \(\alpha \)-optimised nodal sets.
Table 1

Relationship between polynomial order, \(\wp \), and solution point count, \(N_p(\wp )\), in triangular elements

\(\wp \)

1

2

3

4

5

6

7

\(N_p(\wp )\)

3

6

10

15

21

28

36

In 2011 Castonguay et al. [6] used the FR approach to solve the Euler equations on triangular grids. While evaluating the performance of the schemes on a Euler vortex test problem the \(\alpha \)-optimised points were found to exhibit extremely poor performance. However, similar test cases on quadrilateral meshes—with nodes placed at a tensor product of either Gauss–Legendre or Gauss–Legendre–Lobatto points—were found to be stable. One difference between the tensor produced points used in quadrilaterals and the \(\alpha \)-optimised points in triangles is that the latter do not correspond to the abscissa of good quadrature rules. Noting this the authors proceeded to use the abscissa of the (mildly asymmetric) quadrature rules presented in [9] as the solution points. Unlike the \(\alpha \)-optimised points which are designed for polynomial interpolation these points are designed for polynomial integration. By using good quadrature points as the solution points a marked improvement in the stability of the Euler vortex simulation was observed. Also in 2011 Jameson et al. [5] published a technical note investigating the non-linear stability of FR schemes in one dimension. In this paper a connection between solution point placement and non-linear stability was derived. It was found that instabilities associated with the projection (at the solution points) of a non-linear flux onto the polynomial space can be minimised by placing solution points at the abscissa of strong quadrature rules. This is in accordance with the empirical findings of Castonguay et al. [6].

In summary, for FR we seek solution points which fulfil dual roles: those of polynomial interpolation and of non-linear flux projection. Hence, we require solution points which satisfy four criteria. In addition to fulfilling the three requirements of Hesthaven and Warburton they must also be located at the abscissa of strong Gaussian quadrature rules.

3 Rule Derivation

3.1 Background

There is an extremely large body of literature on the derivation of Gaussian quadrature rules for triangular domains. Along with the aforementioned paper by Taylor et al. [9] a collection of near-optimal symmetric rules were discovered by Dunavant [10]. When deriving pure quadrature rules the objective is usually to obtain a rule which utilises a minimal number of points for a given integration strength. However, seldom are these minima coincident with the triangular number of points required by nodal schemes. A consequence of this is that few of the rules presented by Dunavant feature a triangular number of points. It is therefore not possible to repurpose these rules as FR solution points. An additional complication arises on account of the fact that basis functions on a triangle are not unisolvent [11]. This means that there exists configurations of distinct points inside of a triangle for which the associated basis set is linearly dependent. While this does not affect the suitability of a given set of points for numerical quadrature it does prevent them from being used for polynomial interpolation. Hence, such nodes are unsuitable candidates for solution points. These three constraints: symmetry, unisolvency and a triangular number of points serve to exclude almost all existing rules.

More recently Shunn and Ham [12] presented a set of quadrature rules for tetrahedra derived using a cubic close packed (CCP) lattice arrangement. One advantage of the CCP methodology employed is that all of the rules have, by construction, a tetrahedral number of points. By applying this approach to triangles Williams [13] was able to generate a suitable set of solution points for \(1 \le \wp \le 11\). Following Williams we will refer to these herein as the Williams–Shunn (WS) points. Further, in [7] Williams and Jameson proceeded to analyse the points by Shunn and Ham [12] for solving unsteady flow problems on tetrahedral meshes. (In these experiments the corresponding set of WS points were used on the faces of the tetrahedra.) It was found that the symmetric quadrature points outperformed the \(\alpha \)-optimised points in all of the test cases.

3.2 Methodology

To identify solution points in this paper we will employ the methodology of Zhang et al. [8] which provides a simple means of generating symmetric quadrature rules on triangles with a prescribed number of points. This will give us a means of generating candidate solution point sets which fulfil three of the four requirements described in Sect. 2. Namely those of being symmetric, having a triangular number of points, and with abscissa that correspond to a quadrature rule.

We take our triangular domain to be \(\mathcal {T} = \mathcal {T}(\varvec{\mathrm{v}}_1, \varvec{\mathrm{v}}_2, \varvec{\mathrm{v}}_3)\) where \(\varvec{\mathrm{v}}_i\) are the three defining vertices. Given a function \(f(\varvec{\mathrm{r}})\) where \(\varvec{\mathrm{r}} = (p,q)^T\) we can approximate its integral as
$$\begin{aligned} \int \int \limits _{\mathcal {T}} f(\varvec{\mathrm{r}}) \,\mathrm{d}\varvec{\mathrm{r}} \approx |\mathcal {T}| \sum \limits _{i}^{N_p} f(\varvec{\mathrm{r}}_i) \omega _i, \end{aligned}$$
(1)
where \(\{\varvec{\mathrm{r}}_i\}\) are a set of \(N_p\) quadrature points, \(\{\omega _i\}\) the set of associated weights, and \(|\mathcal {T}|\) the area of \(\mathcal {T}\). Next, we shall introduce the set of monomials on \(\mathcal {T}\) as being
$$\begin{aligned} P_\varphi = \bigl \{p^iq^j \mid 0 \le (i, j) \le \varphi , i + j \le \varphi \bigr \}, \end{aligned}$$
(2)
which consists of all polynomials of degree \(\le \varphi \). A quadrature rule can be said to be of order \(\varphi \) if \(\forall f \in P_\varphi \) the relation in Eq. 1 is exact. This definition also provides us with a direct mechanism for evaluating the strength of a rule.
As was mentioned in the previous section it is important that any set of solution points be symmetric. The symmetry group of the triangle consists of two rotations, three reflections, and the identity transformation. A simple means of realising these symmetries is to transform from Cartesian to barycentric coordinates; which we introduce as
$$\begin{aligned} (\lambda _1,\lambda _2,\lambda _3)^T \quad 0 \le \lambda _i \le 1, \lambda _1 + \lambda _2 + \lambda _3 = 1, \end{aligned}$$
(3)
and being related to Cartesian coordinates via
$$\begin{aligned} \varvec{\mathrm{r}} = \lambda _1\varvec{\mathrm{v}}_1 + \lambda _2\varvec{\mathrm{v}}_2 + \lambda _3\varvec{\mathrm{v}}_3. \end{aligned}$$
(4)
A key property of this system is that the symmetries of the triangle can be encoded as the (unique) permutations of \((\lambda _1,\lambda _2,\lambda _3)^T\). The number of permutations of a barycentric coordinate is dependent on the number of unique components. This leads us directly to the notion of symmetry orbits as defined in Table 2. A point where \(\lambda _1 = \lambda _2 = \lambda _3 = \tfrac{1}{3}\) gives rise to an \(S_3\) orbit and one degree of freedom, the weight. Similarly, a point where any two barycentric components are identical corresponds to an \(S_{21}\) orbit which has three unique permutations and two degrees of freedom: the repeated component \(\alpha \) and a weight. Any symmetric set of points can be written as a combination of these orbits. From this it follows that \(N_p = n_3 + 3n_{21} + 6n_{111}\) where \(n_3 \in \{0,1\}\) and \((n_{21},n_{111}) \ge 0\). The above expression is simply a linear Diophantine equation. Hence, by solving it we can decompose an \(N_p\) into orbits. For example in the case of \(N_p = 15\) we obtain
$$\begin{aligned} \begin{aligned} n_3{:}n_{21}{:}n_{111}&= 0{:}5{:}0\\ n_3{:}n_{21}{:}n_{111}&= 0{:}3{:}1\\ n_3{:}n_{21}{:}n_{111}&= 0{:}1{:}2, \end{aligned} \end{aligned}$$
(5)
with the total number of degrees of freedom being 10, 9, and 8 respectively.
Table 2

Symmetry orbits inside of a triangle

Orbit

\(n_{\mathrm{pts}}\)

\(n_{\mathrm{dof}}\)

Barycentric coordinates

\(S_3(\alpha =\tfrac{1}{3})\)

1

1

\({{\mathrm{Perm}}}(\alpha ,\alpha ,\alpha )\)

\(S_{21}(\alpha )\)

3

2

\({{\mathrm{Perm}}}(\alpha ,\alpha ,1-2\alpha )\)

\(S_{111}(\alpha ,\beta )\)

6

3

\({{\mathrm{Perm}}}(\alpha ,\beta ,1-\alpha -\beta )\)

The number of points (unique permutations) contributed by each orbit is given by \(n_{\mathrm{pts}}\) while the number of degrees of freedom contributed to the quadrature rule is indicated by \(n_{\mathrm{dof}}\)

To generate a series of candidate solution points three input parameters are required: the number of points, \(N_p\), the desired rule order, \(\varphi \), and the maximum number of attempts, \(N_t\). The first stage of the algorithm consists of computing the permitted decompositions of \(N_p\). For each decomposition the idea is to generate a random set of points, \(\mathcal {G}\), inside of \(\mathcal {T}\) and then attempt to minimise—in the least squares sense—the error incurred when using these points to integrate the basis set, \(P_{\varphi }\). If the minimisation process is successful then the points are validated to ensure that they are all inside of \(\mathcal {T}\). This procedure is then repeated until \(N_t\) attempts have been made. Due to the large number of local minima it is not unusual for hundreds or even thousands of attempts to be required to find a single rule. However, as the minimum number of points required to construct a rule of order \(\varphi \) is almost never coincident with the desired point counts of Table 1 it usually possible to obtain a very large number of distinct rule sets. This is a direct consequence of the presence of additional degrees of freedom in such cases. In accordance with the recommendations of Zhang et al. [8] we have opted to treat the quadrature weights as dependent variables. As a consequence the weights are not included as degrees of freedom in the non-linear least squares problem. Rather, they are computed dynamically at each iteration of the non-linear solve. This is accomplished by taking the abscissa as given and then finding a set of weights which minimise the integration error. Since the only free parameters are the weights this is a linear least squares problem. This reduces the size of the non-linear least squares problem from \(n_1 + 2n_2 + 3n_3\) unknowns to \(n_2 + 2n_3\) unknowns [8]. This modification has been found to increase the probability that a given initial guess will converge to a solution. A description of the algorithm can be found in Algorithm 1.
Further refinements to the above procedure are possible: it turns out that the number of equations required to specify a quadrature rule of strength \(\varphi \) is less than the number of polynomials in Eq. 2. Specifically, by exploiting symmetries in the basis the number of equations can be reduced from
$$\begin{aligned} \frac{1}{2}(\varphi + 1)(\varphi + 2) = \frac{\varphi ^2}{2} + \frac{3\varphi }{2} + 1, \end{aligned}$$
to [14]
$$\begin{aligned} \frac{\varphi ^2}{12} + \frac{\varphi }{2} + \frac{7}{9} + \frac{2}{9}\cos {\frac{2\varphi \pi }{3}}. \end{aligned}$$
This greatly decreases the size of the non-linear least squares problem. Moreover, it can also be used to exclude decompositions in cases where the associated number of degrees of freedom is less than the number of equations.

4 Metrics

4.1 Background

By employing the algorithm of the previous section it is possible to readily generate a large number of quadrature rules. However, while the methodology guarantees that the rules will be symmetric, of a given power and with a prescribed (triangular) number of points, it does not ensure that they will be suitable for polynomial interpolation. In this section we will introduce two mathematical constants that can be used a priori to compare the generated solution point candidates. The first of these, the Lebesgue constant, will allow us to assess how well suited a set of solution points are to the task of polynomial interpolation. The second quantity, an approximation of the truncation error, will permit us to evaluate the performance of a quadrature rule when it is used to integrate a basis of order \(\varphi ^{+} > \varphi \).

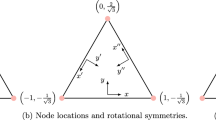
Without loss of generality we shall take our reference triangle \(\mathcal {T}_{s}\) to be that of Fig. 1. Inside of this triangle we introduce the Proriol–Koornwinder–Dubiner–Owens (PKDO) basis as
$$\begin{aligned} \psi _{n} \equiv \psi _{ij}(\varvec{\mathrm{r}}) = \sqrt{2}\hat{P}_i\bigl (2\tfrac{1 + p}{1 - q} - 1\bigr )\hat{P}_j^{(2i + 1, 0)}(q)(1 - q)^i, \end{aligned}$$
(6)
where \(\hat{P}^{(\alpha ,\beta )}_i\) is a normalised Jacobi polynomial as specified in §18.3 of [15], \(i + j \le N_p\), and \(n\) is a bijective mapping onto \((i,j)\). Using the orthogonality of the Jacobi polynomials it can be readily shown that
$$\begin{aligned} \int \int \limits _{\mathcal {T}_{s}} \psi _{ij}(\varvec{\mathrm{r}}) \,\mathrm{d}\varvec{\mathrm{r}} = \delta _{i0}\delta _{j0}\sqrt{2} \end{aligned}$$
(7)
where \(\delta _{ij}\) is the Kronecker delta.
Fig. 1

Standard triangle \(\mathcal {T}_{s}\) and the relevant coordinate system

4.2 Lebesgue constant

Consider an arbitrary scalar function \(u(\varvec{\mathrm{r}})\) on \(\mathcal {T}_{s}\). By expanding this function in terms of a nodal basis set we can construct an interpolating polynomial
$$\begin{aligned} u^{\delta }(\varvec{\mathrm{r}}) = \sum \limits _i^{N_p} u(\varvec{\mathrm{r}}_i)\ell _i(\varvec{\mathrm{r}}), \end{aligned}$$
(8)
where \(u^{\delta }(\varvec{\mathrm{r}}) \approx u(\varvec{\mathrm{r}})\), \(\{\varvec{\mathrm{r}}_i\}\) are a set of points, and \(\{\ell _i(\varvec{\mathrm{r}})\}\) is a nodal basis set with the property that \(\ell _i(\varvec{\mathrm{r}}_j) = \delta _{ij}\). To obtain such a set we compute the elements of the generalised Vandermonde matrix
$$\begin{aligned} \mathcal {V}_{ij} = \psi _{i}(\varvec{\mathrm{r}}_j), \end{aligned}$$
(9)
and let
$$\begin{aligned} \ell _i(\varvec{\mathrm{r}}) = \sum \limits _k^{N_p} \mathcal {V}^{-1}_{ik}\psi ^{}_{k}(\varvec{\mathrm{r}}), \end{aligned}$$
(10)
where \(\mathcal {V}^{-1}\) denotes the matrix inverse of \(\mathcal {V}\), hence
$$\begin{aligned} \ell _i(\varvec{\mathrm{r}}_j) = \sum \limits _{k}^{N_p} \mathcal {V}^{-1}_{ik}\psi ^{}_{k}(\varvec{\mathrm{r}}^{}_j) = \sum \limits _{k}^{N_p} \mathcal {V}^{-1}_{ik}\mathcal {V}^{}_{kj} = \delta ^{}_{ij}, \end{aligned}$$
(11)
as required. We note here that in constructing the nodal basis set we have required the generalised Vandermonde matrix to be invertible. A matrix is invertible so long as \(\det \mathcal {V} \ne 0\). However, on triangular elements there exists sets of points where this is not the case [11]. In such instances it is simply not possible to form a nodal basis set associated with these points, and therefore it is not possible to utilise such points in nodal schemes.
Assuming that a nodal basis can be constructed for a given set of points it is interesting to consider how the resulting interpolating polynomial, \(u^{\delta }(\varvec{\mathrm{r}})\), compares to the best approximating polynomial, \(u^{*}(\varvec{\mathrm{r}})\), in the \(L^{\infty }\) sense for \(\varvec{\mathrm{r}} \in \mathcal {T}_{s}\). We do this by noting that
$$\begin{aligned} \begin{aligned} \Vert u - u^{\delta }\Vert _{\infty }&= \Vert u - u^{*} + u^{*} - u^{\delta }\Vert _{\infty }\\&\le \Vert u - u^{*}\Vert _{\infty } + \Vert u^{*} - u^{\delta }\Vert _{\infty }\\&\le (1 + \Lambda )\Vert u - u^{*}\Vert _{\infty }, \end{aligned} \end{aligned}$$
(12)
where in the second step we have employed the triangle inequality and have defined
$$\begin{aligned} \Lambda = \max _{\varvec{\mathrm{r}} \in \mathcal {T}_{s}} \sum \limits _{i}^{N_p} |\ell _i(\varvec{\mathrm{r}})|, \end{aligned}$$
(13)
which is known as the Lebesgue constant [2, 16]. The task of finding an ideal set of points for polynomial interpolation is therefore equivalent to minimising the Lebesgue constant. As it is not usually possible to compute \(\Lambda \) analytically we must instead determine it numerically. We can accomplish this by discretising \(\mathcal {T}_{s}\) onto a fine mesh with \(\mathcal {O}(10^5)\) points. At each point the absolute sum of each basis function can be evaluated and the maxima of these taken.

4.3 Truncation error

A quadrature rule of order \(\varphi \) is, by definition, one which can integrate all polynomials of degree \(\le \varphi \). It therefore follows that for a rule to be of order \(\varphi \) and not \(\varphi + 1\) there must exist at least one polynomial of order \(\varphi + 1\) which it can not integrate exactly. Given an evaluation order, \(\varphi ^{+} > \varphi \), we define the truncation error as
$$\begin{aligned} \xi ^2(\varphi ^{+}) = \sum \limits _{i,j}^{i + j \le \varphi ^{+}} \Bigg \{\sum \limits _{k}^{N_{p}}\psi _{ij}(\varvec{\mathrm{r}}_k)\omega _k - \delta _{i0}\delta _{j0}\sqrt{2}\Bigg \}^2, \end{aligned}$$
(14)
where the summation inside the curly braces is the quadrature approximation of Eq. 7. Here we will take \(\varphi ^{+} = \varphi + 1\). However, one problem with this choice arises when \(N_p\) is close to the number of abscissa required for a strength \(\varphi + 1\) rule. This is the case when \(N_p(\wp = 4) = 15\) and \(N_p(\wp = 7) = 36\) since there exists higher strength rules with 16 and 37 points respectively [8, Table 4.1]. At these point counts the majority of rules will be capable of integrating most of the polynomials of order \(\varphi + 1\). Hence, in these instances we chose \(\varphi ^{+} = \varphi + 2\). As a metric the truncation error gives us a means of comparing two otherwise identical (in terms of order) quadrature rules.

5 Candidate Point Sets

Using the algorithm of Sect. 3 a large number of symmetric quadrature rules with a triangular number of points were generated. This was accomplished by a variant of the codes developed by Zhang et al. [8] modified to produce an entire family of rules. A summary of the rules found can be seen in Table 3. The quadrature rule strengths were selected to be the strongest obtainable for the specified number of points. However, at polynomial orders five and six many/all of the highest strength rules were found yield singular Vandermonde matrices. Hence, in both instances the derivation procedure was repeated with a lower target rule strength.
Table 3

Number of rules, \(N_r\), discovered at each polynomial order, \(\wp \), and the associated quadrature strengths, \(\varphi \)

\(\wp \)

3

4

5

5

6

6

7

\(\varphi \)

5

7

8

9

10

11

12

\(\varphi ^{+}\)

6

9

10

10

12

12

14

\(N_r\)

95

66

722

473

412

12

136

\(N_r(\det \mathcal {V} \ne 0)\)

24

64

452

2

236

0

100

The basis order used for computing the truncation error is indicated by \(\varphi ^{+}\). Only rules with \(\det \mathcal {V} \ne 0\) are viable solution point candidates

6 Numerical Experiments

6.1 Euler Equations

The two dimensional Euler equations govern the flow of an inviscid compressible fluid. They are both time-dependent and non-linear. Expressed in conservative form they read
$$\begin{aligned} \frac{\partial u}{\partial t} + \varvec{\nabla } \cdot \varvec{\mathrm{f}} = 0, \end{aligned}$$
(15)
where
$$\begin{aligned} u = \left\{ \begin{array}{l} \rho \\ \rho v_x\\ \rho v_y\\ E \end{array}\right\} , \qquad \varvec{\mathrm{f}} = \left\{ \begin{array}{l@{\quad }l} \rho v_x &{} \rho v_y \\ \rho v_x^2 + p &{} \rho v_yv_x \\ \rho v_xv_y &{} \rho v_y^2 + p\\ v_x(E + p) &{} v_y(E + p) \end{array}\right\} . \end{aligned}$$
(16)
Here \(\rho \) is the mass density of the fluid, \(\varvec{\mathrm{v}} =(v_x,v_y)^T\) is the fluid velocity vector, \(E\) is the total energy per unit volume, and \(p\) is the pressure. For a perfect gas the pressure and total energy are related by
$$\begin{aligned} E = \frac{p}{\gamma - 1} + \frac{1}{2}\rho \varvec{\mathrm{v}}\cdot \varvec{\mathrm{v}}, \end{aligned}$$
(17)
with \(\gamma \simeq 1.4\). To solve such a system using the FR approach it is necessary to chose both a time integration scheme and an approximate Riemann solver to evaluate the normal fluxes at element interfaces.
Following [6, 7, 17] we will evaluate the numerical performance of our solution points by modelling an isentropic Euler vortex in a free-stream. The initial conditions for this numerical experiment are given by
$$\begin{aligned} \rho (x,y,t=0)&= \left\{ 1 - \frac{S^2M^2(\gamma - 1)\exp 2f}{8\pi ^2}\right\} ^{\frac{1}{\gamma -1}},\end{aligned}$$
(18)
$$\begin{aligned} v_x(x,y,t=0)&= \frac{Sy\exp {f}}{2\pi R},\end{aligned}$$
(19)
$$\begin{aligned} v_y(x,y,t=0)&= 1 - \frac{Sx\exp {f}}{2\pi R},\end{aligned}$$
(20)
$$\begin{aligned} p(x,y,t=0)&= \frac{\rho ^{\gamma }}{\gamma M^2}, \end{aligned}$$
(21)
where \(f = (1 - x^2 - y^2)/2R^2\), \(S\) is the strength of the vortex, \(M\) is the free-stream Mach number and \(R\) is the radius. In a domain \(\varvec{\mathrm{\Omega }} = \{(x,y) \mid -10 < x < 10, -10 < y < 10\}\) we chose to take \(S = 13.5\), \(M = 0.4\), and \(R = 1.5\). To complete the system we will apply periodic boundary conditions in the \(x\)- and \(y\)-directions. These conditions, however, result in the modelling of an infinite grid of coupled vortices [17]. The impact of this is mitigated by the observation that the exponentially-decaying vortex has a radius which is far smaller than the extent of the domain. Neglecting these effects the analytic solution of the system at a time \(t\) is simply a translation of the initial conditions.

6.2 Error Estimation

Using the analytical solution we can define an \(L^2\) error as
$$\begin{aligned} \sigma (t)^2 = \int \limits _{-2}^{2} \int \limits _{-2}^{2}\Bigl (\rho ^{\delta }(x, y + \Delta _y(t), t) - \rho (x, y + \Delta _y(t), t)\Bigr )^2 \,\mathrm{d} x \,\mathrm{d} y, \end{aligned}$$
(22)
where \(\rho ^{\delta }(x,y,t)\) is the numerical mass density, \(\rho (x,y,t)\) the analytic mass density, and \(\Delta _y(t)\) is the ordinate corresponding to the centre of the vortex at a time \(t\) and accounts for the fact that the vortex is translating in a free stream velocity of unity in the \(y\) direction. The initial mass density along with the \((-2,-2)\times (2,2)\) region used to evaluate the error can be seen in Fig. 2. For the general case of an instructed triangular mesh the evaluation of Eq. 22 is extremely cumbersome. However, if a mesh is constructed such that there are times, \(\tilde{t}\), when the error box does not straddle any mesh elements then at these times
$$\begin{aligned} \sigma (\tilde{t}\,)^2&= \sum \limits _i \int \int \limits _{\mathcal {T}_{s}}\Bigl (\rho ^{\delta }_{i}(p, q, \tilde{t}\,) - \rho \bigl (x_i(\varvec{\mathrm{r}}), y_i(\varvec{\mathrm{r}}), \tilde{t}\bigr )\Bigr )^2 J_i(\varvec{\mathrm{r}}) \,\mathrm{d} \varvec{\mathrm{r}} \end{aligned}$$
(23)
$$\begin{aligned}&\approx 2 \sum \limits _i \sum \limits _j^{N_p} \Bigl (\rho ^{\delta }_{i}(p_j, q_j, \tilde{t}\,) - \rho \bigl (x_i(\varvec{\mathrm{r}}_j), y_i(\varvec{\mathrm{r}}_j), \tilde{t}\bigr )\Bigr )^2 J_i(\varvec{\mathrm{r}}_j)\omega _j, \end{aligned}$$
(24)
where the sum is over all elements inside of the box, \(\rho ^{\delta }_{i}(p, q, t)\) is the approximate solution inside of the \(i\)th element, \(x_i(\varvec{\mathrm{r}})\) and \(y_i(\varvec{\mathrm{r}})\) are suitable local-to-global coordinate mappings for the element and \(J_i(\varvec{\mathrm{r}})\) is the associated Jacobian. In the second line we have simply applied the quadrature formula of Eq. 1 to approximate the integral. So long as the rule used—which need not be symmetric or consist of a triangular number of points—is of adequate strength then this will be a very accurate approximation of the true \(L^2\) error. For experiments conducted herein a 55-point rule of order \(\varphi = 16\) is used for the purpose. The requirement that there exist times when the grid and bounding box conform has been satisfied by using the mesh of Fig. 3.
Fig. 2

Initial density profile for the vortex in \(\varvec{\mathrm{\Omega }}\). The black box shows the area where the error is calculated at \(t = 0\). This box remains centered on the vortex as it progress in the \(+y\) direction

Fig. 3

The mesh used for the vortex test case consisting of 800 triangles

To completely specify the proposed numerical experiment it is also necessary to specify the time-marching algorithm/time-step, the approximate Riemann solver, and the choice of flux points along each edge. Here we choose to use a classical fourth order Runge–Kutta (RK4) scheme with \(\Delta t = 0.0005\). For computing the numerical fluxes at element interfaces we use a Rusanov type Riemann solver, as presented in [4]. Finally, at the edges of the triangles, we take the flux points to be at Gauss–Legendre points.

7 Results and Discussion

For each order, all derived point sets were subjected to the test case detailed in Sect. 6 using a validated FR code based on approach of [18] with correction functions chosen to recove a collocation based nodal DG scheme. Simulations were run until \(t = 100\); equivalent to five passes of the vortex through the domain. Measurements of the error were made every time unit with the simulation being terminated should NaNs be encountered. For each rule we therefore have three direct metrics: the Lebesgue constant, \(\Lambda \), the truncation error, \(\xi \), and the binary measure of whether the simulation made it to \(t = 100\) or not. Further, for those rules where the vortex does not break down we can compute the \(L^2\) error at \(t = 100\), \(\sigma \), and the average \(L^2\) error over the entire simulation, \(\langle \sigma \rangle \). We shall denote the rule with the smallest \(L^2\) error at \(t = 100\) as being the \(\sigma \)-optimal point set and the rule with the smallest average \(L^2\) error as being the \(\langle \sigma \rangle \)-optimal set. The range of Lebesgue constants and truncation errors at each order can be seen in Fig. 4. Plots of the \(L^2\) error against time are shown in Fig. 5. The points themselves are graphically illustrated, within the context of an equilateral triangle, in Fig. 6.
Fig. 4

Semi-log plots of the Lebesgue constant, \(\Lambda \), against truncation error, \(\xi \), for all point sets. Rules which do not make it to \(t = 100\) are indicated by hollow markers. \(\Lambda \)-optimal points are denoted by a gold circle, \(\xi \)-optimal by a green diamond, \(\sigma \)-optimal by a teal ‘\(+\)’, \(\langle \sigma \rangle \)-optimal by a blue ‘\(\times \)’ and WS by a pink triangle (Color figure online)

Fig. 5

\(L^2\) error against time for the \(\alpha \)-optimised, \(\Lambda \)-optimal, \(\xi \)-optimal, \(\sigma \)-optimal, \(\langle \sigma \rangle \)-optimal and WS points. Quantitative details of the \(L^2\) error at \(t = 100\) for all point sets shown can be found in Table 4

Fig. 6

Plots of \(\alpha \)-optimised, \(\Lambda \)-optimal, \(\xi \)-optimal, \(\sigma \)-optimal, \(\langle \sigma \rangle \)-optimal, and WS rules on an equilateral triangle for various orders. The location of these points are tabulated, along with the associated quadrature weights, in Appendix. They are also available in Online Resource 1

Starting with the Lebesgue-truncation plots, we note that for all orders except \(\wp = 4\) the \(\sigma \)- and \(\langle \sigma \rangle \)-optimal point sets—along with those of [13]—feature both low Lebesgue constants and low truncation errors. At higher orders it is evident that points with either high Lebesgue constants or high truncation errors are more likely to either become unstable before \(t = 100\) or perform poorly. A good example of this is the \(\Lambda \)-optimal points at orders \(\wp = 3,5,6\). At these orders the \(\Lambda \)-optimal points all have truncation errors within the upper-quartile and exhibit markedly worse performance than the \(\sigma \)-optimal or WS points. Conversely, at \(\wp = 7\) (when the \(\Lambda \)-optimal point set has a truncation error which lies in the lower-quartile of the distribution) the performance of the set is extremely good. These three results all serve to reaffirm the dual role that solution points play in FR schemes.

From the error-time plots it is observed that for all polynomial orders the performance of the \(\alpha \)-optimised points is significantly worse than those which are good quadrature rules. This is in good agreement with [6]. It is also observed from Table 4 that at orders \(\wp = 4, 6, 7\) the \(\sigma \)-optimal rule sets outperform the WS points by 73, 33, and 34 %, respectively.

The relationship between the Lebesgue constant, truncation error and \(L^2\) error is not perfect, however. A clear example of this can be seen when \(\wp = 6\) where there exist serval point sets with \(\Lambda \lesssim 100\) and truncation errors \(\xi \lesssim 2\) which fail to reach \(t = 100\). Similarly, it is also possible to find examples of points with either high Lebesgue constants/truncation errors which do finish. The case of \(\wp = 4\) is also extremely interesting. From Fig. 5 we see the \(\sigma \)-optimal points outperforming the others by a sizeable margin. However, the set ranks only moderately in terms of its Lebesgue constant and poorly in terms of truncation error (as indicated by Fig. 4). In addition, at this order, there appears to be a direct, although non-trivial, relation between the two metrics. As plotted the rules appear to form two distinct branches with each branch not too dissimilar in shape to the third order case. This branching appears to occur as a result of there being two distinct point configurations at order four. Looking at Fig. 6 we note that the fourth order \(\xi \)-, \(\sigma \)-, and \(\langle \sigma \rangle \)-optimal rules have three points in the second ‘row’ (from the top) whereas the \(\alpha \)-optimised, \(\Lambda \)-optimal and WS points only have two. Further analysis showed that many other points in this branch also exhibited similar characteristics. Despite these differences all of the unisolvent forth-order points share a common topological configuration of the form \(n_3{:}n_{21}{:}n_{111} = 0{:}3{:}1\) (c.f. Eq. 5). This suggests that there are other factors at work. The somewhat anomalous behaviour of the fourth-order point sets warrants further exploration in the future.
Table 4

\(L^2\) errors at \(t = 100\) for \(\Lambda \)-optimal, \(\xi \)-optimal, \(\sigma \)-optimal, \(\langle \sigma \rangle \)-optimal, and WS point sets

\(\wp \)

\(\sigma (t = 100)\)

3

 

   \(\alpha \)-opt

DNF \(t = 81.40\)

   \(\Lambda \)-opt

\(2.58 \times 10^{-2}\)

   \(\xi \)-opt

\(8.20 \times 10^{-3}\)

   \(\sigma \)-opt

\(8.20 \times 10^{-3}\)

   \(\langle \sigma \rangle \)-opt

\(8.61 \times 10^{-3}\)

   WS

\(8.27 \times 10^{-3}\)

4

 

   \(\alpha \)-opt

DNF \(t = 13.30\)

   \(\Lambda \)-opt

\(1.20 \times 10^{-3}\)

   \(\xi \)-opt

\(2.09 \times 10^{-3}\)

   \(\sigma \)-opt

\(6.59 \times 10^{-4}\)

   \(\langle \sigma \rangle \)-opt

\(6.76 \times 10^{-4}\)

   WS

\(1.15 \times 10^{-3}\)

5

 

   \(\alpha \)-opt

DNF \(t = 18.95\)

   \(\Lambda \)-opt

\(2.64 \times 10^{-3}\)

   \(\xi \)-opt

\(1.36 \times 10^{-4}\)

   \(\sigma \)-opt

\(9.69 \times 10^{-5}\)

   \(\langle \sigma \rangle \)-opt

\(9.69 \times 10^{-5}\)

   WS

\(6.92 \times 10^{-5}\)

6

 

   \(\alpha \)-opt

DNF \(t = 22.24\)

   \(\Lambda \)-opt

\(2.02 \times 10^{-4}\)

   \(\xi \)-opt

\(4.16 \times 10^{-5}\)

   \(\sigma \)-opt

\(2.38 \times 10^{-5}\)

   \(\langle \sigma \rangle \)-opt

\(2.42 \times 10^{-5}\)

   WS

\(3.16 \times 10^{-5}\)

7

 

   \(\alpha \)-opt

DNF \(t = 12.50\)

   \(\Lambda \)-opt

\(5.95 \times 10^{-6}\)

   \(\xi \)-opt

\(1.10 \times 10^{-5}\)

   \(\sigma \)-opt

\(5.95 \times 10^{-6}\)

   \(\langle \sigma \rangle \)-opt

\(5.95 \times 10^{-6}\)

   WS

\(8.00 \times 10^{-6}\)

Those which do not finish are indicated by DNF along with the time at which the simulation blows up

8 Conclusion

In this paper we have investigated how solution point placement contributes to the stability and accuracy of FR schemes on triangular elements. To begin we described a simple methodology for generating candiate solution point sets. After analysing the performance of these points for an Euler vortex test problem the main findings can be summarised as follows. Firstly, the requirement that points be at the abscissa of a quadrature rule appears to be necessary but not sufficient for a good numerical scheme. As a corollary to this we have reaffirmed previous findings that the \(\alpha \)-optimised points are unsuitable for non-linear problems. Secondly, both the Lebesgue constant and truncation error associated with a point set are very strong indicators of stability. Finally, we have demonstrated that existing quadrature-optimised solution points are not necessarily optimal. Specifically, at orders \(\wp = 4, 6, 7\) we have discovered rules which outperform those of Williams [13].

Notes

Acknowledgments

The authors would like to thank the Engineering and Physical Sciences Research Council for their support via a Doctoral Training Grant and an Early Career Fellowship (EP/K027379/1).

Supplementary material

10915_2014_9832_MOESM1_ESM.zip (15 kb)
Supplementary material 1 (zip 15 KB)

References

  1. 1.
    Huynh, H.T.: A flux reconstruction approach to high-order schemes including discontinuous galerkin methods. AIAA Paper 4079, 2007 (2007)Google Scholar
  2. 2.
    Hesthaven, J.S., Tim, W.: Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications, vol. 54. Springer, Berlin (2008)Google Scholar
  3. 3.
    Kopriva, D.A., Kolias, J.H.: A conservative staggered-grid chebyshev multidomain method for compressible flows. J. Comput. Phys. 125(1), 244–261 (1996)Google Scholar
  4. 4.
    Sun, Y., Wang, Z.J., Liu, Y.: High-order multidomain spectral difference method for the Navier–Stokes equations on unstructured hexahedral grids. Commun. Comput. Phys. 2(2), 310–333 (2007)MathSciNetzbMATHGoogle Scholar
  5. 5.
    Jameson, A., Vincent, P.E., Castonguay, P.: On the non-linear stability of flux reconstruction schemes. J. Sci. Comput. 50(2), 434–445 (2011)Google Scholar
  6. 6.
    Castonguay, P., Vincent, P.E., Jameson, A.: Application of high-order energy stable flux reconstruction schemes to the euler equations. In: 49th AIAA Aerospace Sciences Meeting, vol. 686 (2011)Google Scholar
  7. 7.
    Williams, D., Jameson, A: Nodal points and the nonlinear stability of high-order methods for unsteady flow problems on tetrahedral meshes. In: 43rd AIAA Fluid Dynamics Conference (2013)Google Scholar
  8. 8.
    Zhang, L., Cui, T., Liu, H.: A set of symmetric quadrature rules on triangles and tetrahedra. J. Comput. Math. 27(1), 89–96 (2009)MathSciNetzbMATHGoogle Scholar
  9. 9.
    Taylor, M.A., Wingate, B.A., Bos, L.P.: Several new quadrature formulas for polynomial integration in the triangle. ArXiv Mathematics e-prints, Jan 2005Google Scholar
  10. 10.
    Dunavant, D.A.: High degree efficient symmetrical Gaussian quadrature rules for the triangle. Int. J. Numer. Methods Eng. 21(6), 1129–1148 (1985)Google Scholar
  11. 11.
    Bos, L.: On certain configurations of points in \(\mathbb{R}^n\) which are unisolvent for polynomial interpolation. J. Approx. Theory 64(3), 271–280 (1991)Google Scholar
  12. 12.
    Shunn, L., Ham, F.: Symmetric quadrature rules for tetrahedra based on a cubic close-packed lattice arrangement. J. Comput. Appl. Math. 236(17), 4348–4364 (2012)MathSciNetCrossRefzbMATHGoogle Scholar
  13. 13.
    Williams, D.M.: Energy stable high-order methods for simulating unsteady, viscous, compressible flows on unstructured grids. Ph.D. thesis, Stanford University (2013)Google Scholar
  14. 14.
    Cohen, G., Joly, P., Roberts, J.E., Tordjman, N.: Higher order triangular finite elements with mass lumping for the wave equation. SIAM J. Numer. Anal. 38(6), 2047–2078 (2001)MathSciNetCrossRefzbMATHGoogle Scholar
  15. 15.
    Olver, F.W.J.: NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge, MA (2010)zbMATHGoogle Scholar
  16. 16.
    Blyth, M.G., Pozrikidis, C.: A lobatto interpolation grid over the triangle. IMA J. Appl. Math. 71(1), 153–169 (2006)MathSciNetCrossRefzbMATHGoogle Scholar
  17. 17.
    Vincent, P.E., Castonguay, P., Jameson, A.: Insights from von neumann analysis of high-order flux reconstruction schemes. J. Comput. Phys. 230(22), 8134–8154 (2011)MathSciNetCrossRefzbMATHGoogle Scholar
  18. 18.
    Castonguay, P., Vincent, P.E., Antony, J.: A new class of high-order energy stable flux reconstruction schemes for triangular elements. J. Sci. Comput. 51(1), 224–256 (2012)MathSciNetCrossRefzbMATHGoogle Scholar

Copyright information

© The Author(s) 2014

Open AccessThis article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.

Authors and Affiliations

  1. 1.Department of AeronauticsImperial College LondonLondonUK

Personalised recommendations