On the role of specific drug binding in modelling arterial eluting stents

Abstract

In this paper we consider drug binding in the arterial wall following delivery by a drug-eluting stent. Whilst it is now generally accepted that a non-linear saturable reversible binding model is required to properly describe the binding process, the precise form of the binding model varies between authors. Our particular interest in this manuscript is in assessing to what extent modelling specific and non-specific binding in the arterial wall as separate phases is important. We study this issue by extending a recently developed coupled model of drug release and arterial tissue distribution, and comparing simulated profiles of drug concentration and drug mass in each phase within the arterial tissue.

1 Introduction

Arterial stents are medical devices designed to widen the lumen of vessels which have become narrowed as a result of atherosclerosis. It is now standard for these stents to release antiproliferative/anti-inflammatory drugs into the arterial wall to control the proliferation and migration of smooth muscle cells, which is linked to the development of restenosis (re-narrowing). These drug-eluting stents (DES) consist of a wired scaffold, typically coated with a polymer that encapsulates the therapeutic drug. The coating may include a rate-limiting barrier that provides a more controlled release. Both the stent geometry and coating design should be optimized so that therapeutic levels of drug are delivered to the arterial wall for the correct period of time. The evolution from drug-free bare metal stents to DES has resulted in significantly reduced restenosis rates, with the result that only around 5 % of patients [1] now suffer from this setback. However, there is still considerable scope to reduce restenosis rates further. Another potentially more serious problem is the occurrence of late-stent thrombosis, which has been associated with delayed healing of the arterial wall. This may result from drug being retained in the arterial wall for longer than necessary, at concentrations which prevent re-endothelialisation. Before one can fully optimise the release kinetics, it is therefore essential to fully understand the binding of drug to components in the wall.

Mathematical and computational (in silico) modelling has emerged as an extremely useful tool to study the drug-release process and binding kinetics and to optimize the stent design and physico-chemical parameters (see e.g. [2, 3]). However, in silico models alone are not sufficient. Indeed, a combination of models, ranging from in vitro to ex vivo and in vivo are required if this problem is to be fully addressed [4]. Many in-silico model parameter values have been derived from experimental in vitro and ex vivo studies whilst model validation typically requires in vivo measurements of drug mass remaining on the stent and in the tissue [5].

It is generally accepted that drug transport within the stent coating is governed by diffusion and possibly dissolution/degradation/erosion (depending on the physico-chemical properties of the polymer carrier and of the drug), whilst transport within the arterial wall is governed by diffusion, convection and binding. Early models of binding assumed either equilibrium reactions or linear first order kinetics [6]. However, these have been shown to result in elevated and delayed peak wall concentrations [7] which are inconsistent with experimental results. There is a plethora of literature on more advanced non-linear mathematical models of drug binding. Whilst it is not our intention to provide a review of the various published models, we mention here some examples of non-linear binding models which have been applied to a variety of different situations. Groh et al. [8] considered the interaction of a chemotherapeutic agent with the microenvironment of cells in tumour drug delivery. They devised a three compartment model which included a non-linear reaction to describe binding to binding sites within cells. Vo and Meere [9] modelled the release of heparin-binding growth factors from an affinity-based delivery system using a non-linear reversible binding model. Ferreira et al. [10] presented a series of non-linear binding models to describe the degradation of a PLA stent coating into lactic acid and oligomers. A non-linear saturable binding model was adopted by Tzafriri et al. [11] and later by Bozsak et al. [3, 7] to describe drug binding to arterial tissue sites. The model included two phases of drug in the tissue: free and bound. However, it is well established that in addition to binding to specific receptors (SR), there is also the occurrence of non-specific binding caused by association of drug with membrane constituents or by trapping of drug in the extracellular medium [12]. Most recently, Tzafriri et al. [5] included two equations for drug binding in arterial tissue: one for specific binding to receptors and another for non-specific binding to general extracellular matrix (ECM) sites. The result is three phases in the tissue: two bound (SR and ECM) and one free.

In a recent paper [13], we outlined and emphasized the significance of modelling release from a drug delivery device and the consequent transport in the contiguous biological tissue as an intrinsically coupled system. In this manuscript we extend that work to the particular application of DES to assess the importance (or otherwise) of modelling specific and non-specific saturable binding in the arterial wall as separate phases.

2 The mathematical model

We adopt the recent modelling framework of McGinty and Pontrelli [13] and extend their model to include two distinct bound phases within the tissue. The model consists of equations which describe drug diffusion and dissolution in the polymer coating, diffusion, convection and saturable binding in the arterial wall, as well as interface conditions to fully couple the release-uptake system and a series of initial and boundary conditions. We briefly summarize the model here and, for full details, the reader is referred to [13].

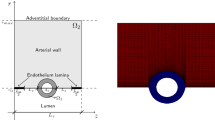
The coating is modelled as a planar slab, enclosed on one side with the impermeable strut and having the other side faced to the wall. In this configuration, as most of the mass transport occurs in the direction normal to the tissue surface, we consider a simplified one-dimensional case. Since the arterial wall thickness is very small compared to the arterial radius, it is reasonable to use a Cartesian coordinate system, with the x-axis representing the radial direction normal to the layer surface. The location of the interface is given by $x=0$, and $l_0$, $l_1$ are the thicknesses of the coating and wall, respectively, with $l_1 \gg l_0$ (Fig. 1).

Fig. 1

Schematic diagram showing the geometrical configuration and the reference system. The stent is coated with a polymer which contains the drug. Following dissolution and diffusion in the coating, dissolved drug enters the arterial wall. Here drug exists in the free phase, but also binds to non-specific general extracellular matrix (ECM) sites and to specific receptors (SR)

2.1 Modelling drug dynamics in the coating

Let $b_0$ and $c_0$ represent the concentrations of drug bound within the polymer matrix and dissolved in the free phase, respectively. Initially all of the drug exists in solid form in the bound phase at concentration B. When exposed to plasma, we assume that the polymer becomes fully wetted, initiating a dissolution process whereby bound drug dissolves into the free phase and subsequently diffuses through plasma before being released into the arterial tissue. Since the diffusion of drug in the solid phase is negligible, the equations for the drug dynamics in terms of concentrations $b_0$ and $c_0$ are

$$\begin{aligned}&\frac{\partial b_0}{\partial t} = -\beta _0 b_0^{\frac{2}{3}}\left( S-c_0\right) \quad \qquad \qquad \quad \! \text{ in } \, \, (-l_0, 0), \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial c_0}{\partial t} = D_0 \frac{\partial ^2 c_0}{\partial x^2} + \beta _0 b_0^{\frac{2}{3}}\left( S-c_0\right) \quad \text{ in }\, \, (- l_0, 0), \end{aligned}$$

(2)

where $D_0$ ($\mathrm{cm}^2\,\mathrm{s}^{-1}$) is the effective diffusion coefficient of the solute, $\beta _0$ ($1/(\mathrm{s}\,(\mathrm{mol}\, \mathrm{cm}^{-3})^{2/3})$) is the dissolution rate and S is the solubility limit [14].

2.2 Modelling drug dynamics in the arterial wall

In the arterial wall, the free drug ($c_1$) undergoes diffusion and convection due to a pressure difference across the wall. In addition, the drug binds reversibly to components of the tissue. Denoting the concentration of drug which is bound to non-specific general ECM sites and SR by $b_1$ and $b_2$, respectively, then assuming the wall comprises a single homogeneous layer with isotropic diffusion properties, the equations of drug transport in the tissue are given by:

$$\begin{aligned} \frac{\partial c_1}{\partial t}&=D_1 \frac{\partial ^2 c_1}{\partial x^2} -v_1 \frac{\partial c_1}{\partial x}- k_1^f c_1\left( b^{max}_1-b_1\right) + k_1^r b_1 \nonumber \\&\quad -\,k_2^f c_1\left( b^{max}_2-b_2\right) + k_2^r b_2 \qquad \text{ in } \, \, (0 , l_1), \end{aligned}$$

(3)

$$\begin{aligned} \frac{\partial b_1}{\partial t}&= k_1^f c_1\left( b^{max}_1-b_1\right) - k_1^r b_1\qquad \quad \text{ in } \, \, (0 , l_1), \end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial b_2}{\partial t}&= k_2^f c_1\left( b^{max}_2-b_2\right) - k_2^r b_2 \qquad \quad \text{ in } \, \, (0 , l_1), \end{aligned}$$

(5)

where $D_1$ is the diffusivity of the unbound drug and $v_1$ ($\mathrm{cm}\,\mathrm{s}^{-1}$) is the magnitude of the convection which is assumed to act in the positive x direction. In the above equations, $k^f$ and $k^r$ represent the forward and backward rate constants, $b^{max}$ is the local density of binding sites, and the subscripts 1 and 2 denote parameters with respect to the ECM and SR phases, respectively. We note that by choosing $k_2^f=k_2^r=0$ we return the single bound phase model [13] (with the parameters $k_1^f$ and $k_1^r$ redefined to incorporate both phases of binding).

2.3 Boundary, interface and initial conditions

To close the two-layer coupled mass transfer system given by (1)–(5) we need to assign appropriate boundary, interface and initial conditions. At the boundary with the impermeable stent ($x=-l_0$) and the adventitia ($x=l_1$) we choose zero flux and infinite sink conditions, respectively:

$$\begin{aligned} -D_0\frac{\partial c_0}{\partial x}&=0 \quad \text{ at } x=-l_0, \end{aligned}$$

(6)

$$\begin{aligned} c_1&= 0 \quad \text{ at } \, \, x=l_1. \end{aligned}$$

(7)

The zero-flux condition at $x=-l_0$ assumes that no drug is lost to the flowing blood in the lumen. This, of course, is a simplification, although it is not clear how much drug is lost, given the limited solubility of the compounds used on DES and the fact that many devices are now only coated with drug abluminally. Other authors [5] have considered ‘efficiency factors’ to try to address this issue. One may also use a more general Robin boundary condition. At the interface between the stent coating and the arterial tissue we need two conditions. We impose continuity of flux and allow for a possible concentration jump:

$$\begin{aligned}&-D_0\frac{\partial c_0}{\partial x}= -D_{1}\frac{\partial c_1}{\partial x} + v_1 c_1 \quad \text{ at } \, \, x=0, \end{aligned}$$

(8)

$$\begin{aligned}&-D_1 \frac{\partial c_1}{\partial x}= P \left( c_0 -c_1\right) \qquad \,\,\quad \text{ at } \, \, x=0, \end{aligned}$$

(9)

with $P (\mathrm{cm}\,\mathrm{s}^{-1})$ the overall mass transfer coefficient. As initial conditions, we consider that all drug is at maximum concentration in encapsulated form ($b_0=B$) in the coating, and all the other concentrations are zero ($c_0=c_1=b_1=b_2=0$).

3 Results

Before solving the model equations, we follow the nondimensionalization presented in [13], with all concentrations scaled by the initial bound drug concentration in the coating (B), spatial variables scaled by the thickness of the arterial wall ($l_1$) and temporal variables scaled by the diffusion timescale in the tissue ($l_1^2/D_1$). The resulting system of nondimensionalized partial differential equations are then spatially discretized using a standard finite difference scheme. At $x=0$ no unique value for concentration exists and no derivative can be computed across the interface, due to a possible discontinuity. The procedure proposed by [15] is adopted to get the concentration values across the interface. The resulting non-linear system of ordinary differential equations is solved by a Runge-Kutta type method with backward differentiation formulas, and an adaptive time step. For full details of the solution method, we refer the reader to [13].

Table 1 Dimensional parameter values used in the simulations [5, 13]

Fig. 2

Nondimensional concentration profiles in the arterial wall at three times. Free ($c_1$), ECM bound ($b_1$) and SR bound drug ($b_2$) are displayed

In Table 1 we summarize the parameter values used in the simulations. These are representative of a first generation DES (Cypher) which elutes the drug sirolimus. In order to examine the effect of treating specific and non-specific binding as two separate phases, in Fig. 2 we plot simulated concentration profiles of free drug, ECM bound drug and SR bound drug. Drug enters the arterial wall (at $x=0$) in the free-phase and is rapidly bound to both ECM and SR sites. The free and ECM bound drug concentration profiles rise to a peak (not shown) before decaying with time as drug traverses through the tissue, is bound to SR and is absorbed at the adventitial boundary ($x=1$). Although the $c_1$ and $b_1$ profile shapes are similar, drug concentrations within the ECM bound phase are an order of magnitude greater than the SR bound phase which in turn are tenfold greater than the free drug concentrations. Within the first hour, SR spanning half the thickness of the tissue are saturated: these remain saturated for the duration of the 30 days studied (Fig. 3). The remaining SR sites become saturated in the subsequent hours and they too remain at saturation levels for the duration of the 30 days.

Fig. 3

Nondimensional concentration profiles in the arterial wall at three times. Drug bound to non-specific ECM sites ($b_1$) and SR ($b_2$) are displayed as a % of their respective saturation levels

Fig. 4

Nondimensional drug mass in each phase as a function of time. $M_{c1}$, $M_{b1}$ and $M_{b2}$ represent the nondimensional mass of drug contained within the free, ECM bound and SR bound phases, respectively. The inset is a magnification of the SR bound and free drug mass over the first 24 h

However, Fig. 3 reveals that ECM sites are not saturated. Indeed, ECM bound concentrations are only around 30 % of saturation levels close to the lumen at 1 h, and this percentage decreases rapidly with increasing x. By 30 days, ECM bound concentrations are at ${<}10\,\%$ of saturation levels throughout the arterial wall. Therefore, our results demonstrate that drug delivered to the arterial wall from the stent is too low to occupy a large proportion of ECM binding sites, yet is high enough to saturate SR. This is in agreement with Tzafriri et al. [5].

It is also possible to simulate the mass of drug contained within each phase in the arterial wall. This can be achieved easily from the model by simply integrating the various concentrations over the spatial domain. In Fig. 4 we observe that significantly more drug is contained within the ECM bound phase than the other two phases, with the free drug phase containing the lowest amounts of drug. The peak of the free drug mass and the ECM bound drug mass occurs at the same time (approximately 10 h): however, the mass of drug in the SR bound phase peaks at saturation levels within the first 4 h.

4 Discussion

The goal of this work was to determine the importance (or otherwise) of modelling specific and non-specific saturable reversible binding in the arterial wall as separate phases. Our results have demonstrated (at least for the case of sirolimus elution) that the simulation of ECM bound and SR bound phases separately is indeed important if the aim of the model is to demonstrate receptor saturation. When binding is simulated as a single phase, it is not possible to capture the SR saturation: the single bound phase (which includes ECM binding and SR binding) never reaches saturation due to the large total number of binding sites. Since receptor saturation has been associated with therapeutic effect [5], this has important implications if one is using the model a priori to predict DES efficacy. The saturation of SR is a result of the combined high binding rate and low binding site density. The significantly higher capacity of ECM binding sites means that they are never saturated, at least for the rate of drug elution from the Cypher stent. The relatively fast ECM unbinding rate (an order of magnitude greater than the SR unbinding rate) results in ECM bound drug dissociating relatively rapidly, and effectively acting as a further source for SR binding, thus ensuring that SR saturation levels are maintained.

It is worth mentioning that the lack of ECM binding site saturation has implications in terms of the type of binding model required. A saturable binding model is clearly unnecessary and so ECM binding can reasonably be approximated by a first order linear binding model (which has been shown to be a special case of the saturable model [13]). This simplifies the mathematics and may potentially significantly reduce computation time if the model presented here is extended to more complex geometries in higher dimensions.

If, however, the aim of the mathematical model is to make comparisons with in vivo experimental results, then our results show that it may not be important to model specific and non-specific binding as separate phases. The reason for this is that, to the best of our knowledge, it is not possible to discriminate between the mass of drug that is bound to ECM sites and the mass of drug that is bound to SR. The current standard is to measure the total mass of drug in the wall (often expressed as $\upmu \mathrm{g}$ drug/g tissue) [5]. We have demonstrated that the vast majority of drug is contained within the ECM bound phase and so the simulation of a single bound phase (as in [13]) is sufficient to compare with these experimental results.

5 Conclusions

A deeper understanding of drug release kinetics and tissue absorption is necessary for the rational optimization of stent-based drug delivery systems. One of the methods available to evaluate the characteristics of drug elution from the coating into the arterial wall and to optimize the physico-chemical parameters is mathematical modelling and numerical simulation. In this paper we have built upon a previously published model [13] and focused on the reversible and saturable binding processes in the vascular tissue. The model is based on a two-layer multiple-phase system where a system of partial differential equations describes both the dissolution and diffusion processes in the polymeric layer as well as diffusion, convection and reaction in the tissue layer.

A number of simplifying assumptions have been made in the model. For example, we have considered a one-dimensional model which cannot account for anisotropy. Additionally, the arterial wall has a typical multi-layered structure, whereas we model only one layer (the media). However, we believe that all the modeling assumptions we have made are appropriate for studying the question addressed in this manuscript.

We point out that the results presented here are for the simulated case of sirolimus release and absorption from the Cypher stent. Although sirolimus-derived compounds are currently the most used drugs on DES, other drugs (e.g. paclitaxel) with different modes of action are also used. Notwithstanding, when the ratios of SR to ECM binding site density ($b_2^{max}/b_1^{max}$) and of SR to ECM unbinding rate ($k_2^r/k_1^r$) are both small, these conclusions likely hold.

Data

The data associated with this paper consists of the mathematical model which is detailed in the text.