1 Introduction

One of the most important problems of quantum mechanics and quantum chemistry is to solve the Schrödinger equation with the potentials, which properly describe the vibrational and vibrational-rotational motions of atomic nuclei, occurring in diatomic molecules. Determination of the internuclear potentials, that accurately reproduce the rovibrational spectra of diatomic molecules is a very important quantum procedure, providing useful information on the internal molecular structure and physical properties such as dipole moment, equilibrium internuclear distance and polarizability. To describe motions of nuclei in diatomic systems a method based on the analytic potential expansions has been developed [1]. In quantum chemistry computations the most frequently applied expansion forms are Dunham’s [2], Simons–Parr–Finlan’s [3] and Coolidge–James–Vernon’s [4]. By introducing these expansions into rovibrational Schrödinger equation one may obtain the energy eigenvalues expressions that depend on potential parameters and the equilibrium configuration of the rotationless state. Applying the semiclassical Dunham approach [2], hypervirial theorem [5], supersymmetric quantum mechanics [6] as well as the variational [7] or perturbation method [8] the rovibrational Schrödinger equation can be solved exactly or in approximate scheme. Recently, a quantum method based on a so-called deformable body model has been developed by Molski [9, 10]. This method assumes that interatomic distances depend on the vibrational momenta and overall angular momentum as a result of the Coriolis and centrifugal forces. Furthermore, according to this method in many diatomic molecules the centrifugal force leads to the vibrational-deformational displacements of atoms. Besides, in this theoretical model the magnitudes of the deformational displacements of atoms from the original reference configuration are calculated with the use of dynamic equilibrium state between deforming and restoring potential forces.

It should be stressed that exact solutions of the Schrödinger equation are possible for certain physical potentials such as: Morse, Kratzer, Coulomb, Wei-Hua and pseudoharmonic potentials [11–16]. Also, various methods have been applied successfully for one-dimensional anharmonic oscillator with different types of anharmonicities [17, 18]. Moreover, the Hill determinant method generates excellent results for both polynomial and nonpolynomial potentials [19]. In the last few years many quantum methods have been developed to solve the Schrödinger equation within the use of algebraic approach. One of the most important procedures is to solve the second-order Schrödinger differential equation using its transformation into the same commonly known differential equations, whose exact solutions can be specified as the confluent hypergeometric functions, associated with the Kummer function, Whittaker functions and Laguerre polynomials. Also, supersymmetric quantum mechanics (SUSY QM) procedure is strictly correlated with analytical solutions of eigenproblems for many anharmonic potentials [20, 21]. Applying the ideas of supersymmetry (SUSY) and an integrability condition called the shape invariance condition for a whole class of shape invariant potentials exact spectrum of energy levels can be determined [22, 23]. It should be emphasized that the concept of the shape invariant potentials within the SUSY QM method has been introduced by Gendenshtein [24].

Apart from analytical methods of solving the Schrödinger equation many numerical methods, mostly basing on the routine Numerov procedure, are widely used [25]. For example, the available for free computer code LEVEL developed by LeRoy is one of the most commonly used in quantum computations. Also matrix methods are usually used [26] and derive from either basis set expansions or from the discrete variable representation. In the several past decades, many efforts have been undertaken to investigate the stationary Schrödinger equation with the central potentials containing negative powers of the radial coordinate [27, 28]. Recently, the Schrödinger equation with higher order central potentials has been carefully studied. For example the sextic potential, the mixed (harmonic + linear + Coulomb) potential and singular even-power potential have been widely used in molecular physics, field theory, structural phase transitions and quantum optics. There is a need to emphasize that model potentials have come a long way since the simple forms introduced by Morse and his successors.

With the wide demand for highly accurate anharmonic potentials, which can be applied in theoretical spectroscopy to determine energy levels spacings, it seems reasonable to introduce new potentials and to solve the radial Schrödinger equation, including these potential functions. Therefore, we are concerned with determination of new internuclear potential functions, for which the Schrödinger equation can be easily converted to the second-order exact solvable differential equation. In particular, we are interested in solutions of the Schrödinger equation for the proposed potentials.

2 Proposed potentials and quantum calculations

2.1 Five-parameter potentials

The first of the potentials studied has the following form:

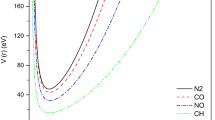
$$\begin{aligned} U(r)=D_e\left\{ {\frac{1-\exp \left\{ {-\alpha \!\left[ {\left( {\frac{r}{r_e}}\right) ^{m}-1}\right] }\right\} }{1-c\exp \left\{ {-\alpha \!\left[ {\left( {\frac{r}{r_e}}\right) ^{m}-1}\right] } \right\} }}\right\} ^{\!2} \end{aligned}$$
(1)

An exemplary plot of this function is presented in Fig. 1. In the formula (1) \(\hbox {D}_\mathrm{e}\) stands for dissociation energy of diatomic molecule and \(\hbox {r}_\mathrm{e}\) refers to the equilibrium distance between two nuclei. Adjustable parameters \(m>0\) and \(c\in (-1;1)\) have been introduced to correct the shape of the Rydberg–Klein–Rees potential energy curve. These parameters can be determined for each particular chemical system using a direct fit to energy level spacings. Consider a following nonlinear variable:

$$\begin{aligned} y=\exp \left[ {-\alpha \left( {\frac{r}{r_e}-1}\right) }\right] , \quad y\in [0,1] \end{aligned}$$
(2)

After simple algebraic manipulations we obtain the following relationships:

$$\begin{aligned} \left( {\frac{r}{r_e}}\right) ^{m}=\left( {1\!-\!\frac{\ln y}{\alpha }} \right) ^{m},\quad \exp \left\{ {-\alpha \left[ {\left( {\frac{r}{r_e}}\right) ^{m}\!-\!1}\right] }\right\} =b\exp \left[ {-\alpha \left( {\frac{\alpha -\ln y}{\alpha }}\right) ^{m}} \right] ,\nonumber \\ \end{aligned}$$
(3)

where \(b=\exp \alpha \).

Adopting Taylor series for (3) with \(r\in (r_{e}-\varepsilon ;r_{e}+\varepsilon ),\varepsilon \rightarrow 0\) and taking into consideration only the first and second terms we receive:

$$\begin{aligned} \exp \left\{ {-\alpha \left[ {\left( {\frac{r}{r_e}}\right) ^{m}-1} \right] }\right\} =a_0+a_1y+a_2y^{2}, \end{aligned}$$
(4)

where

$$\begin{aligned} a_0&= be^{-\alpha m}\left( {1-\frac{3m}{2}+\frac{m^{2}}{2}}\right) , \quad a_{1}=be^{-\alpha m}[2m-m^{2}],\nonumber \\ a_2&= be^{-\alpha m}\left[ {\frac{m^{2}}{2}-\frac{m}{2}}\right] . \end{aligned}$$
(5)

In further considerations we will examine only the \(a_{0}\) and \(a_{1}y\) terms. The vibrational Schrödinger equation for the nuclear motion of a diatomic systems, expressed in terms of the \(y\) variable can be rewritten in the following form:

$$\begin{aligned} \left\{ {-\frac{\hbar ^{2}\alpha ^{2}}{2\mu r_e^2 }y^{2}\frac{d^{2}}{dy^{2}}-\frac{\hbar ^{2}\alpha ^{2}}{2\mu r_e^2 }y\frac{d}{dy}+D_e\left[ {\frac{1-\left( {a_0+a_1y} \right) }{1-c\left( {a_0+a_1y}\right) }}\right] ^{2}}\right\} \Psi \left( y\right) _\upsilon =E_\upsilon \Psi \left( y\right) _\upsilon ,\nonumber \\ \end{aligned}$$
(6)

in which \(\mu \) denotes the reduced mass of a diatomic system. Assuming that \(1-a_{0}=\delta _{0}\) and \(1-ca_{0}=\delta _{1}\) we receive:

$$\begin{aligned} \left[ {-\frac{\hbar ^{2}\alpha ^{2}}{2\mu r_e^2 }y^{2}\frac{d^{2}}{dy^{2}}-\frac{\hbar ^{2}\alpha ^{2}}{2\mu r_e^2 }y\frac{d}{dy}+D_e\left( {\frac{\delta _0-a_1y}{\delta _1-ca_1 y}}\right) ^{2}}\right] \Psi \left( y\right) _\upsilon =E_\upsilon \Psi \left( y\right) _\upsilon . \end{aligned}$$
(7)

After Changing the variable \(x=\frac{ca_1}{\delta _1}y\) and applying simple manipulations we get:

$$\begin{aligned} \left[ {-\frac{\hbar ^{2}\alpha ^{2}}{2\mu r_e^2 }x^{2}\frac{d^{2}}{dx^{2}}-\frac{\hbar ^{2}\alpha ^{2}}{2\mu r_e^2 }x\frac{d}{dx}+D_e\left( {\frac{\delta _0}{\delta _1}} \right) ^{2}\left( {\frac{1-\frac{\delta _1}{c\delta _0}x}{1-x}} \right) ^{2}}\right] \Psi \left( x\right) _\upsilon =E_\upsilon \Psi \left( x\right) _\upsilon .\nonumber \\ \end{aligned}$$
(8)

Introducing following designations:

$$\begin{aligned} t=\frac{\delta _0 r_e\sqrt{2D_e\mu }}{\delta _1\hbar \alpha }, \quad \beta =\frac{\delta _1}{c\delta _0},\quad \lambda _\upsilon =\frac{2E_\upsilon \mu r_e^2}{\hbar ^{2}\alpha ^{2}} \end{aligned}$$
(9)

we obtain the Eq. (8) in the following form:

$$\begin{aligned} \left[ {\frac{d^{2}}{dx^{2}}+\frac{1}{x}\frac{d}{dx}-t^{2}\frac{\left( {1-\beta x}\right) ^{2}}{\left( {1-x} \right) ^{2}x^{2}}+\frac{\lambda _\upsilon }{x^{2}}}\right] \Psi \left( x\right) _\upsilon =0. \end{aligned}$$
(10)

We can now easily notice that the differential Eq. (10) has the same form as the one derived by Hua [15]. After bringing Eq. (10) to the standard form of hypergeometric Gauss equation and taking into consideration the regularity of wave function in the point \(x=0\), we can express the solution in terms of Jacoby polynomial in the following manner:

$$\begin{aligned} \Psi (x)_\upsilon =N_\upsilon x^{\rho _\upsilon }(1-x)^{\frac{1}{2}-\rho }P\left( {-\upsilon ,\omega _\upsilon ,\gamma _\upsilon ,x}\right) , \end{aligned}$$
(11)

where

$$\begin{aligned} \rho _{\upsilon }&= (t^{2}-\lambda _{\upsilon })^{1/2},\rho =\left[ {\frac{1}{4}+t^{2}\left( {\beta -1}\right) ^{2}}\right] ^{1/2},\nonumber \\ \omega _\upsilon&= \frac{1}{2}+\rho _\upsilon +\rho +t^{2}\left( {\beta ^{2}-\lambda _\upsilon }\right) ^{1/2},\quad \gamma _{\upsilon }=1+2\rho _{\upsilon }. \end{aligned}$$
(12)

We can also calculate energy levels from the following relationship:

$$\begin{aligned} E_\upsilon&= \frac{\hbar ^{2}\alpha ^{2}\left( {\rho +\upsilon +\frac{1}{2}}\right) ^{-2}}{2\mu r_e^2}\left\{ \beta t^{2}\left[ {\left( {\upsilon +\frac{1}{2}} \right) ^{2}+2\left( {\upsilon +\frac{1}{2}}\right) \rho +\frac{1}{4}} \right] \right. \nonumber \\&\left. -\,\frac{1}{4}\left[ {\left( {\upsilon +\frac{1}{2}} \right) ^{2}+\frac{1}{4}+2\rho \left( {\upsilon +\frac{1}{2}}\right) } \right] ^{2}\right\} . \end{aligned}$$
(13)

We propose also a second five-parameter potential:

$$\begin{aligned} U(r)=D_e\frac{1-\exp \left\{ {-\alpha \left[ {\left( {\frac{r}{r_e }}\right) ^{m}-1}\right] }\right\} }{\left\{ {1-c\exp \left[ {-\alpha \left( {\frac{r}{r_e}-1}\right) }\right] }\right\} ^{2}} \end{aligned}$$
(14)

The main aim of our further investigation will be to determine analytically the eigenvalue associated with this potential and to show that it can be expanded into Taylor series and that we can neglect the terms above the 2nd one.

Fig. 1
figure 1

An exemplary plot of the function presented in Eq. (1). Parameters used: \(\alpha =2;r_{e}=1,8;m=0,9; c=0,001;D_{e}=1\)

Full size image

2.2 Six-parameter potentials

Let’s now consider a six-parameter potential in the following form:

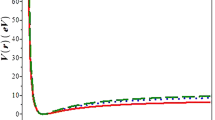
$$\begin{aligned} U(r)=D_e\left\{ {\frac{1-\exp \left\{ {-\alpha \left[ {\left( {\frac{r}{r_e}}\right) ^{m}-1}\right] }\right\} }{1-c\exp \left\{ {-\alpha \left[ {\left( {\frac{r}{r_e}}\right) ^{k}-1}\right] } \right\} }}\right\} ^{2}. \end{aligned}$$
(15)

An exemplary plot of this function is presented in Fig. 2. In the formula (15) \(k>0\) and \(m>0\) play the same role as in (1). After some calculations, similar to the ones applied in the previous cases, we obtain a following second-order differential equation:

$$\begin{aligned} \left[ {\frac{d^{2}}{dx^{2}}+\frac{1}{x}\frac{d}{dx}-f^{2}\frac{\left( {1-\kappa x}\right) ^{2}}{\left( {1-x} \right) ^{2}x^{2}}+\frac{\varepsilon _\upsilon }{x^{2}}}\right] \Psi \left( x\right) _\upsilon =0, \end{aligned}$$
(16)

where

$$\begin{aligned} f&= \frac{\delta _0^{{\prime }}r_e\sqrt{D_e 2\mu }}{\delta ^{{\prime }}_1\hbar \alpha },\; \kappa =\frac{\delta _1^{{\prime }} a_1^{\prime }}{c\delta _0^{{\prime }}a_1^{{\prime }{\prime }}},\; 1-a_{0}^{{\prime }}=\delta _{0},1-ca_{0}^{{\prime }{\prime }}=\delta _{1}^{{\prime }},\nonumber \\ a_0^{{\prime }}&= be^{-\alpha m}\left( {1-\frac{3m}{2}+\frac{m^{2}}{2}} \right) ,a_0^{{\prime }{\prime }}=be^{-\alpha k}\left( {1-\frac{3k}{2}+\frac{k^{2}}{2}}\right) ,\nonumber \\ a_{1}^{{\prime }}&= { be}^{-\alpha m}[2m-m^{2}], a_{1}^{{\prime }{\prime }}={ be}^{-\alpha k}[2k-k^{2}]. \end{aligned}$$
(17)
Fig. 2
figure 2

An exemplary plot of the function presented in Eq. (15). Parameters used: \(\alpha =3;r_{e}=1,1;m=2; c=0,1;k=3;D_{e}=1\)

Full size image

Wave function of the vibrational bound states takes the following form:

$$\begin{aligned} \Psi (x)_\upsilon =N_\upsilon x^{\rho _\upsilon ^{{\prime }}}(1-x)^{\frac{1}{2}-\rho ^{{\prime }}}P\left( {-\upsilon ,\omega _\upsilon ^{{\prime }},\gamma _\upsilon ^{{\prime }},x}\right) , \end{aligned}$$
(18)

where

$$\begin{aligned} \rho _{\upsilon }^{{\prime }}&= (f^{2}-\lambda _{\upsilon })^{1/2},\rho ^{{\prime }}=\left[ {\frac{1}{4}+f^{2}\left( {\kappa -1}\right) ^{2}}\right] ^{1/2},\nonumber \\ \omega _\upsilon ^{{\prime }}&= \frac{1}{2}+\rho _\upsilon ^{{\prime }} +\rho ^{{\prime }}+f^{2}\left( {\kappa ^{2}-\varepsilon _\upsilon } \right) ^{1/2},\gamma _{\upsilon }^{{\prime }}=1+2\rho _{\upsilon }^{{\prime }}. \end{aligned}$$
(19)

We can also calculate eigenvalues from the following relationship:

$$\begin{aligned} E_\upsilon&= \frac{\hbar ^{2}\alpha ^{2}\left( \rho ^{\prime }+\upsilon +\frac{1}{2}\right) ^{-2}}{2\mu r_e^2} \left\{ \kappa f^{2}\left[ \left( {\upsilon +\frac{1}{2}} \right) ^{2}+2\left( {\upsilon +\frac{1}{2}}\right) \rho ^{{\prime }}+\frac{1}{4}\right] \right. \nonumber \\&\left. -\frac{1}{4}\left[ {\left( {\upsilon +\frac{1}{2}}\right) ^{2}+\frac{1}{4}+2\rho ^{{\prime }}\left( {\upsilon +\frac{1}{2}}\right) }\right] ^{2} \right\} . \end{aligned}$$
(20)

We additionally propose one more six-parameter potential in the form:

$$\begin{aligned} U(r)=D_e\left\{ {\frac{1-b\exp \left[ {-\alpha ^{m}\left( {r^{m}-r_e ^{m}}\right) }\right] }{1-c\exp \left[ {-\alpha \left( {r-r_e}\right) }\right] }}\right\} ^{2}. \end{aligned}$$
(21)

Also in this case an appropriate choice of the parameters (which can be done with the use of direct fit to measured energy level spacings) provides a good shape of the potential energy curve.

3 Concluding remarks

In this paper the stationary radial Schrödinger equation with novel energy potential functions has been solved analytically in approximate scheme, applying the algebraic approach. The corresponding eigenvalues and wave functions have been derived. It has been shown that by adopting simple Taylor expansion for exponential functions the Schrödinger equation can be converted to analytically solvable form. We hope that these potentials can be employed to investigate quantum nature of vibrational nuclear motions in diatomic molecules. Moreover, the potentials considered will be used in the future study to compare their accuracy with those available in the literature. The next studies are planned to verify whether these potential functions describe properly the weak attractive van der Waals effect in long-range and short-range electrostatic interactions. In the future paper we will study the application of these potential functions towards computation of dissociation energies of several diatomic molecules and compare the results obtained with those derived with the use of other generalized expansions for the potential energy curve. For a more accurate description of nuclear motions in diatomic molecules the further calculations including rotational term in the Schrödinger equation are needed.