Basics of Joule–Thomson Liquefaction and JT Cooling

Abstract

This paper describes the basic operation of Joule–Thomson liquefiers and Joule–Thomson coolers. The discussion is based on the first law of thermodynamics mainly using hT-diagrams. It is limited to single-component fluids. A nitrogen liquefier and a helium cooler are discussed as important examples.

1 Introduction

This paper discusses the basic operation principles of Joule–Thomson (JT) liquefiers and JT coolers, schematically represented in Fig. 1. It should be considered as an extension of Ref. [1] which treats the basic operation principle of other types of coolers. The important JT coolers got only marginal attention in Ref. [1].

Fig. 1

JT liquefier (left) and JT cooler (right). In the liquefier, the mass flows in the CHEX at the two sides differ while in the cooler they are equal (Color figure online)

Joule–Thomson (JT) coolers are invented by Carl von Linde and William Hampson so these coolers are also called Linde–Hampson coolers [2]. Basically cooling, obtained by the JT process, is very simple and is widely applied in household refrigerators, air conditioners, cryocoolers, and as the final stage of liquefiers. They can be miniaturized [3,4,5], but they are also used on a very large scale in the liquefaction of natural gas [6, 7]. Even though this way of cooling is more than 160 years old published measurements of the cooling power of JT cryocoolers are rare. A critical comparison between theory and experiment is missing. For example, Ref. [5] does not contain one single plot of the measured cooling performance of a JT cooler. As a consequence, system properties discussed in this paper, such as in Fig. 16, are theoretical predictions.

The JT systems are often discussed using temperature–entropy (Ts) diagrams. However, entropies are needed mainly in loss analyses which will not be part of this paper. The basic principles can be understood much better with enthalpy–temperature (hT)-diagrams. Therefore, we will mainly deal with hT-diagrams. Irreversible processes and high pressures in JT coolers can be reduced by using gas mixtures instead of pure fluids [7, 8]. However, we will discuss pure fluids only. For the liquefier, we discuss nitrogen, and for the cooler we will treat helium four as the working fluid as important examples.

As shown in Fig. 1, JT systems contain a Counterflow Heat EXchanger (CHEX). Inside the CHEX, the temperature T of the fluid, the density $\rho$, the velocity v, and specific enthalpy h vary over the cross section. The mass flow rate $\overset{*}{m}$ is given by

$$\begin{aligned} \overset{*}{m}=\int \rho v{\mathrm {d}}A. \end{aligned}$$

(1)

The integral is taken over the cross section A of a channel perpendicular to the flow. What we call “the” temperature $T_{\mathrm {l}}$ of the gas in the low-pressure channel is defined by the relation

$$\begin{aligned} \overset{*}{m}h\left( T_{\mathrm {l}},p\right) =\int \rho vh{\mathrm {d}}A_{ {\mathrm {l}}}. \end{aligned}$$

(2)

A similar relation holds for the high-pressure channel defining the temperature $T_{\mathrm {h}}$.

In this paper, the following approximations and/or assumptions will be made:

• 1. Just like in Ref. [1], kinetic and potential energies of the fluid are neglected.

• 2. The CHEX has no flow resistance. This condition is easier satisfied at the high-pressure side than at the low-pressure side. At the low-pressure side, the flow resistance immediately affects the value of the low temperature.

• 3. We consider only the steady state.

• 4. Heat conduction in the flow direction is neglected. This is justified since the heat flows in the flow direction usually are much smaller than the heat flows between the two sides of the CHEX.

These assumptions are justified in many situations, so we consider realistic systems. No assumptions are made about the heat flow resistance between the hot and the cold sides. Our discussion is based on energy conservation so the relations are very powerful and have general validity. For example, they are independent of the detailed design of the CHEX.

2 JT Liquefier

2.1 System Description

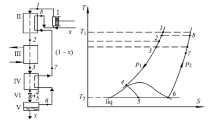
A schematic diagram of a JT liquefier is shown in Fig. 2. It consists of a compressor, a CHEX, a JT valve, and a reservoir. The parts below room temperature are contained in a vacuum chamber. The gas enters the compressor at point a which is at room temperature and (atmospheric) pressure $p_{ \mathrm {l}}$. The compressor can be multistage and contains one or more heat exchangers that cool the gas to room temperature. The gas leaves the compressor with pressure $p_{\mathrm {h}}$ and ambient temperature entering the vacuum chamber at point b. Next it passes the high-pressure side of the CHEX leaving it at point c. In going from c to d, it passes a JT valve which is an adiabatic flow resistance which can be a needle valve, a porous plug, a narrow slit, etc. In the case of a liquefier, the fluid at d consists of a mixture of gas and liquid with liquid mass fraction x,  which enters a reservoir. The reservoir can be used to collect liquid for some time with the exit valve at e closed. This valve can be opened to drain liquid from the reservoir when needed. Here we will discuss the steady state where all liquid, formed after the expansion in the JT valve, is removed from the reservoir instantaneously at e. The remaining gas flows into the low-pressure side of the CHEX at point f, leaving it at point g. In general, $T_{\mathrm {g}}\ne T_{\mathrm {a}},$ so there will be some heat exchange with ambient in the line from g to a.

Fig. 2

Schematic diagram of a JT liquefier. A mass fraction x of the compressed gas is removed as liquid. At room temperature, it is supplied as gas at 1 bar, so that the system is in the steady state (Color figure online)

Fig. 3

hT-diagram of nitrogen with several isobars obtained with Ref. [8]. The indicated points correspond with Fig. 2 for the case that $p_{\mathrm {h}}=200$ bar. The JT expansion is represented by a red dotted horizontal line (Color figure online)

In Fig. 2, the pressures refer to typical values for a nitrogen liquefier. At the inlet of the compressor, the gas is at room temperature (taken here at 300 K) and a pressure of 1 bar (point a).¹ After compression, it is at 300 K and 200 bar (point b). In point d, it has a temperature $T_{\mathrm {d}}=$ 77.244 K and a pressure of 1 bar.

2.2 The Maximum Liquefaction Rate

First we assume that the gas at the low-pressure side leaves the CHEX at point g with a temperature equal to room temperature so $T_{\mathrm {g}}=T_{ \mathrm {a}}$. Later on, we will see that this means that we calculate the maximum liquid fraction $x_{{\mathrm {\max }}}$. The thermodynamic properties of nitrogen are obtained from Ref. [9] from which the hT-diagram (Fig. 3) is derived.

The calculation of $x_{{\mathrm {\max }}}$ becomes surprisingly simple if we consider the content of the vacuum chamber as indicated in Fig. 2 as the thermodynamic system. This is an adiabatic system (no heat exchange with its surroundings) with rigid walls, and it is in the steady state. For such a system, the first law (Ref. [1]) reduces to a conservation law for the enthalpy

$$\begin{aligned} h_{\mathrm {b}}=x_{{\mathrm {\max }}}h_{\mathrm {e}}+\left( 1-x_{{\mathrm {\max }} }\right) h_{\mathrm {a}}. \end{aligned}$$

(3)

So

$$\begin{aligned} x_{{\mathrm {\max }}}=\frac{h_{\mathrm {a}}-h_{\mathrm {b}}}{h_{\mathrm {a}}-h_{ \mathrm {e}}}. \end{aligned}$$

(4)

Clearly there can only be liquefaction if $x_{{\mathrm {\max }}}>0$. As $h_{ \mathrm {a}}>h_{\mathrm {e}}$ this means

$$\begin{aligned} h_{\mathrm {a}}>h_{\mathrm {b}}. \end{aligned}$$

(5)

For nitrogen with the low pressure $p_{\mathrm {l}}=1$ bar and $T_{\mathrm {a} }=T_{\mathrm {b}}=300$ K, this is true if the high pressure $1<p_{\mathrm {h} }<1130$ bar.

Table 1 Thermodynamic values of the JT nitrogen liquefier [9]

With the enthalpy values, obtained from Table 1, and Eq. (4), we get

$$\begin{aligned} x_{{\mathrm {\max }}}=0.074. \end{aligned}$$

(6)

Now $h_{\mathrm {d}}$ and $h_{\mathrm {c}}$ can be calculated with

$$\begin{aligned} h_{\mathrm {d}}=x_{{\mathrm {\max }}}h_{\mathrm {e}}+\left( 1-x_{{\mathrm {\max }} }\right) h_{\mathrm {f}} \end{aligned}$$

(7)

or

$$\begin{aligned} h_{\mathrm {c}}=h_{\mathrm {d}}=62.3\text { kJ/kg.} \end{aligned}$$

(8)

The temperature $T_{\mathrm {c}}$ can be found by following a horizontal line in the hT-diagram from point d to the 200 bar isobar and turns out to be $T_{ \mathrm {c}}=165$ K. This temperature is much higher than the temperature after the expansion (in this case $T_{\mathrm {d}}=\hbox {77.244 K}$). In this respect, the JT expansion in the liquefier differs from the JT expansion in the ideal JT cooler which is isothermal as will be discussed later on.

2.3 More Detailed Analysis

So far we assumed that $T_{\mathrm {g}}=T_{\mathrm {a}}$, but this is not generally true, e.g., due to the finite length of the CHEX. In this subsection, we will drop this assumption and also derive relations for the temperatures inside the CHEX.

Energy conservation, applied to the dotted rectangle in Fig. 4, reads

$$\begin{aligned} h\left( p_{\mathrm {h}},T_{\mathrm {h}}\right) =xh_{\mathrm {e}}+\left( 1-x\right) h\left( p_{\mathrm {l}},T_{\mathrm {l}}\right) \end{aligned}$$

(9)

where $T_{\mathrm {h}}$ and $T_{\mathrm {l}}$ are the temperatures at the high-pressure and low-pressure sides at opposing sides of the CHEX, respectively, as defined in Eq. (2). We can write Eq. (9) as

$$\begin{aligned} h\left( p_{\mathrm {h}},T_{\mathrm {h}}\right) -h_{\mathrm {e}}=\left( 1-x\right) \left( h\left( p_{\mathrm {l}},T_{\mathrm {l}}\right) -h_{\mathrm {e} }\right) . \end{aligned}$$

(10)

Introducing

$$\begin{aligned} h^{\prime }=h-h_{\mathrm {e}} \end{aligned}$$

(11)

this becomes

$$\begin{aligned} h^{\prime }\left( p_{\mathrm {h}},T_{\mathrm {h}}\right) =\left( 1-x\right) h^{\prime }\left( p_{\mathrm {l}},T_{\mathrm {l}}\right) . \end{aligned}$$

(12)

This is a relation between the high- and low-pressure enthalpies with $h_{ \mathrm {e}}$ set to zero and connects the temperatures $T_{\mathrm {l}}$ and $T_{\mathrm {h}}$ as a function of the liquid fraction x. An example is given for $x=0.04$ in Fig. 5. In this case, the temperature at the exit $T_{ \mathrm {g}}\approx 286$ K. Improving the CHEX will increase x and “lower” the low-pressure curve through the factor $1-x$ in Eq. (12) until it touches the high-pressure curve at room temperature if $x=x_{{\mathrm {\max }}}$ . This is the maximum production rate of the liquefier as given in Eq. (6).

Fig. 4

Diagram showing the system which determines the $T_{\mathrm {l}}{-}T_{\mathrm {h} }$ relationship inside the CHEX of a liquefier (Color figure online)

Fig. 5

Demonstration of the operation of Eq. (10) for $x=0.04$ and $x=x_{{\mathrm { \max }}}$. The circle at 300 K indicates the pinch point (Color figure online)

Fig. 6

JT cooler. The solid and dotted rectangles define thermodynamic systems discussed in the text (Color figure online)

Fig. 7

hT-diagram for $^{4}\hbox {He}$ with isobars in red. The 1 bar isobar usually plays a special role and is in black. Data obtained from Ref. [8] (Color figure online)

3 JT Coolers

Now we turn our attention to JT coolers. In this case, there is no liquid production, but the JT cooling effect is used in a cryocooler to cool a particular application.

3.1 System Description

The right-hand side in Figs. 1 and 6 represents a JT cooler. In some applications, there is no compressor, but the gas is supplied by a high-pressure container and the gas leaves the system at 1 atm (open cycle), but for the thermodynamics this makes no difference. A heating power $\dot{Q} _{\mathrm {L}}$ is applied at the low temperature $T_{\mathrm {L}}=T_{\mathrm {f }}$ at the coldest point which usually is called the evaporator.² As mentioned before, we will take helium as an important example of a cooling medium. It is necessary to precool the helium with a cryocooler or a (pumped) liquid hydrogen bath. Figure 7 shows the hT-diagram of helium with several isobars.

3.2 Exit Temperature

We consider the system, indicated in Fig. 6 by the solid rectangle, in the steady state. The first law demands

$$\begin{aligned} \dot{Q}_{\mathrm {L}}+\overset{*}{m}h_{\mathrm {b}}=\overset{*}{m}h_{ \mathrm {g}}. \end{aligned}$$

(13)

Introducing the specific cooling power (strictly speaking it is the specific cooling energy as it is expressed in J/kg and not in W/kg)

$$\begin{aligned} q_{\mathrm {L}}=\frac{\dot{Q}_{\mathrm {L}}}{\overset{*}{m}} \end{aligned}$$

(14)

Eq. (13) gives

$$\begin{aligned} q_{\mathrm {L}}+h_{\mathrm {b}}=h_{\mathrm {g}}. \end{aligned}$$

(15)

In case $q_{\mathrm {L}}=0$, the system inside the vacuum chamber is, thermodynamically, nothing more than a complicated JT valve for which holds

$$\begin{aligned} h_{\mathrm {b}}=h_{\mathrm {g}}. \end{aligned}$$

(16)

Once $p_{\mathrm {l}},p_{\mathrm {h}},$ and $T_{\mathrm {b}}$ are fixed this relation determines $T_{\mathrm {g}}$. Figure 8 shows $T_{\mathrm {g}}$ as function of $p_{\mathrm {h}}$ with $T_{\mathrm {b}}=15$ K and $p_{\mathrm {l} }=1$ bar. Perhaps one might expect that one can force $T_{\mathrm {b}}=T_{ \mathrm {g}}$ by making the CHEX long enough (like in the case of a liquefier), but in a cooler with zero heating power, in general, $T_{\mathrm { b}}\ne T_{\mathrm {g}}$ even with a perfect CHEX.

Fig. 8

$T_{\mathrm {g}}$ versus $p_{\mathrm {h}}$ for helium with $T_{\mathrm {b}}=15$ K and $p_{\mathrm {l}}=1$ bar for $\dot{Q}_{\mathrm {L}}=0$ (Color figure online)

Fig. 9

Two isobars in the hT-diagram of $^{4}$He. The little circles indicate the relationship between $T_{\mathrm {h}}=15$ K and the corresponding $T_{\mathrm { l}}$ for zero applied heating power (Color figure online)

3.3 Temperature Profiles

The first law, applied to the system indicated by the dotted rectangle in Fig. 6, demands that

$$\begin{aligned} q_{\mathrm {L}}+h\left( T_{\mathrm {h}},p_{\mathrm {h}}\right) =h\left( T_{ \mathrm {1}},p_{\mathrm {l}}\right) . \end{aligned}$$

(17)

For given $p_{\mathrm {h}}$ and $p_{\mathrm {l}}$, Eq. (17) relates $T_{ \mathrm {l}}$ to $T_{\mathrm {h}}$ for a given cooling power. As we will see below, this is a very powerful relationship for analyzing the system properties.

3.4 Zero Heat Load

We start with $q_{\mathrm {L}}=0$. In that case, Eq. (17) reduces to

$$\begin{aligned} h\left( T_{\mathrm {h}},p_{\mathrm {h}}\right) =h\left( T_{\mathrm {1}},p_{ \mathrm {l}}\right) . \end{aligned}$$

(18)

So we can derive the $T_{\mathrm {l}}-T_{\mathrm {h}}$ relationship directly from the isobars at $p_{\mathrm {l}}$ and $p_{\mathrm {h}}$. Figure 9 shows an example for helium with $p_{\mathrm {h}}=40$ bar and $p_{\mathrm {l}}=1$ bar. At 15 K and 40 bar, $h=$ 67.66 J/g. The same value of h (horizontal line in the diagram) can be found on the 1 bar isobar at about $T_{\mathrm {l}}=$ 12.3 K. A $T_{\mathrm {h}}$ of 14 K gives a $T_{\mathrm {l}}$ of about 11 K, etc. In this way, the $T_{\mathrm {l}}-T_{\mathrm {h}}$ dependence can be constructed and is shown in Fig. 10. It is important to note that we know the $T_{\mathrm {l}}-T_{\mathrm {h}}$ relationship, but we do not know at which position in the CHEX we have these particular values of $T_{\mathrm {l}}$ and $T_{\mathrm {h}}.$ This is determined by the design of the CHEX (shape and size of the channels, wall material, $\ldots$) and the mass flow rate.

Other $T_{\mathrm {l}}-T_{\mathrm {h}}$ dependences are given in Fig. 11 for various $p_{\mathrm {h}}$ all with $p_{\mathrm {l}}=1$ bar and $T_{\mathrm {b} }=15$ K. The points where the high-pressure isobars cross the 1 bar isobar are pinch points and determine the minimum temperature $T_{{\mathrm {Lim}}}$ the ideal system can reach with a given inlet temperature (in this case 15 K)

$$\begin{aligned} h\left( p_{\mathrm {h}},T_{{\mathrm {Lim}}}\right) =h\left( p_{\mathrm {l}},T_{ {\mathrm {Lim}}}\right) . \end{aligned}$$

(19)

Figure 12 shows these points for 10, $\ldots$, 90, 100 bar by little circles. The maximum $p_{\mathrm {h}}$ with which a temperature of 4.2 K can be reached is 42 bar. The maximum pressure that results in a temperature reduction at all is about 91 bar. It is interesting to note that Kamerlingh Onnes, based on the law of corresponding states, started the liquefaction of helium at 95 atm and obtained liquefaction only after he, more or less accidently, reduced the inlet pressure to 40 atm [10].

Fig. 10

Red curve $T_{\mathrm {l}}-T_{\mathrm {h}}$ dependence for $p_{\mathrm {h} }=40$ bar, $p_{\mathrm {l}}=1$ bar, and $\dot{Q}_{\mathrm {L}}=0$. The blue line, representing $T_{\mathrm {h}}$, is drawn for reference (Color figure online)

Fig. 11

$T_{\mathrm {l}}-T_{\mathrm {h}}$ dependences for $p_{\mathrm {l}}=1$ bar and various values of $p_{\mathrm {h}}$ (indicated in bar) for $\dot{Q}_{\mathrm {L }}=0$ (Color figure online)

Fig. 12

hT-diagram of $^{4}\hbox {He}$ with isobars. The circles mark the points where the high-pressure isobars cross the 1 bar isobar. These are pinch points which determine the minimum temperatures $T_{{\mathrm {Lim}}}$ that can be reached at the corresponding $p_{\mathrm {h}}$ and $\dot{Q}_{\mathrm {L}}=0$ (Color figure online)

Fig. 13

$h\left( p,T\right) =h\left( 40\text { bar},T=T_{{\mathrm {Lim}}}\right)$ isenthalp in the pT-diagram, showing T as function of p for an isenthalpic expansion from $p_{\mathrm {h}}=40$ bar to 1 bar for the ideal case that $T_{\mathrm {c}}=T_{\mathrm {d}}=T_{{\mathrm {Lim}}}$ (in this case 4.2 K). The black line is the saturated vapor line. The dotted horizontal line is $T_{{\mathrm {Lim}}}$ (Color figure online)

So, at $T_{{\mathrm {Lim}}}$, the expansion is both isenthalpic and isothermal.³ For example, for $p_{\mathrm {h}}=40$ bar and $T=T_{{\mathrm {Lim}}}=4.2$ K, $h=19.5$ J/g. In the pT-diagram in Fig. 13, the $T-p$ relationship for this isenthalp is given. Usually only the beginning and the end of the curve are relevant since, inside the flow constriction, the velocities usually are very high (speed of sound). If the diameters of the supply and drain lines are large enough (which is usually the case), the velocities at the ends are small and the kinetic energy can be neglected. If the flow resistance would consist of, e.g., a long porous plug, where the gas velocity would remain far below the speed of sound, one would actually see that the temperature goes up to 7.5 K in the middle of the plug. In Fig. 13, it can be seen that the expansion follows the saturated vapor line in the pT-diagram after it “hits” this line at 1.6 bar. At the low-pressure side, the curve ends just inside the two-phase region as shown in Fig. 12.

Fig. 14

Temperature profiles as functions of the CHEX length in arbitrary units (Color figure online)

As noted before, we know the $T_{\mathrm {l}}{-}T_{\mathrm {h}}$ relationship inside the CHEX, but we do not know at which point in the CHEX we have a particular $T_{\mathrm {l}}$–$T_{\mathrm {h}}$ combination. Figure 14 shows the temperatures $T_{\mathrm {l}}$ and $T_{\mathrm {h}}$ in a CHEX with $p_{ \mathrm {h}}=$ 40 bar and $p_{\mathrm {l}}=$ 1 bar as function of the position with the length l in arbitrary units. With zero heat load, as discussed in this section, the fluid leaves the evaporator with the same composition as after the JT expansion. For $p_{\mathrm {h}}<42$ bar and if the heat exchanger is long enough, this means that two-phase flow enters the low-pressure side of the CHEX at the cold end. When this gas–liquid mixture flows further inside the CHEX, the liquid evaporates until, at some point, only gas remains. In the region of two-phase flow, $p_{\mathrm {l}}$ and $T_{ \mathrm {l}}$ are constant. In this part of the CHEX, $T_{\mathrm {h}}$ approaches $T_{\mathrm {l}}$ exponentially. If the CHEX is not as long as assumed in Fig. 14, the temperature profile is simply a part of the curves shown. So the figure can also be regarded as giving the temperatures at the cold end as functions of the CHEX length.

The maximum amount of heat that can be exchanged in the counterflow CHEX is $h\left( p_{\mathrm {h}},T_{\mathrm {b}}\right) -h\left( p_{\mathrm {h}},T_{{ \mathrm {Lim}}}\right)$ while the actual amount is $h\left( p_{\mathrm {h}},T_{ \mathrm {b}}\right) -h\left( p_{\mathrm {h}},T_{\mathrm {c}}\right)$. The efficiency of the CHEX is defined as

$$\begin{aligned} \eta _{{\mathrm {ex}}}=\frac{h\left( p_{\mathrm {h}},T_{\mathrm {b}}\right) -h\left( p_{\mathrm {h}},T_{\mathrm {c}}\right) }{h\left( p_{\mathrm {h}},T_{ \mathrm {b}}\right) -h\left( p_{\mathrm {h}},T_{{\mathrm {Lim}}}\right) }. \end{aligned}$$

(20)

Usually this efficiency is very close to one.

3.5 Finite Heat Load

If heat is supplied to the cold heat exchanger, Eq. (13) shows that we have to add $q_{\mathrm {L}}$ to the high-pressure enthalpy in order to get the $T_{\mathrm {h}}-T_{\mathrm {l}}$ relationship inside the CHEX. If $q_{ \mathrm {L}}$ goes up, $T_{\mathrm {g}}$ goes up as one might expect. In particular, we can construct the $q_{\mathrm {L}}-T_{\mathrm {L}}$ (cooling power characteristic) for a long CHEX by following the intersection point of the low-pressure isobar and the high-pressure isobar lifted by $q_{ \mathrm {L}}$. An example is shown in Fig. 15 for $p_{\mathrm{h}}=20$ bar. If $q_{\mathrm {L}}$ is equal to

$$\begin{aligned} q_{{\mathrm {\max }}}\left( T_{\mathrm {b}}\right) =h\left( T_{\mathrm {b}},p_{ \mathrm {l}}\right) -h\left( T_{\mathrm {b}},p_{\mathrm {h}}\right) \end{aligned}$$

(21)

there are two intersection points, one at the low-temperature and one at the high-temperature end. In this case also the temperatures at the high- and low-pressure sides at the hot end of the CHEX are the same ($T_{ \mathrm {g}}=T_{\mathrm {b}},$ pinch point) so there is no temperature difference any more to drive the cooler to temperatures below the entrance temperature. Hence, Eq. (21) is the relation for the maximum specific heat load. If $q_{\mathrm {L}}$ is increased from below $q_{{\mathrm {\max }}}$ to above $q_{{\mathrm {\max }}}$, the cooler “suddenly” stops working in the sense that the temperature starts to drift away indefinitely. This is unlike other cryocoolers, such as pulse tube or GM coolers, where the cooling power smoothly increases with $T_{\mathrm {L}}$ until room temperature is reached. The strange behavior of JT coolers can only be observed in its pure form in an infinitely long CHEX. For a CHEX of finite length, $T_{\mathrm {c}}$ increases with $q_{\mathrm {L}}$ especially if $T_{\mathrm {g}}$ approaches $T_{\mathrm {b}}$. The specific enthalpy of the saturated vapor at 1 bar is 20.648 J/g. The isenthalp in the pT-diagram (compare Fig. 13) has a maximum at 7.674 K at a pressure of 13.8 bar. So the highest temperature with which 4.2 K can be reached is 7.7 K and is realized if $p_{\mathrm {h}}=13.8$ bar. For all other $p_{\mathrm {h}}$, the $T_{\mathrm {c}}$ with which 4.2 K can be reached is lower. So, in any case, $T_{\mathrm {L}}>4.2$ K if $T_{\mathrm {c} }>7.7$ K (Fig. 15).

Fig. 15

hT-diagram of $^{4}$He wit h isobars of 1 and 20 bar and with various $q_{ \mathrm {L}}$ as indicated with the curves in J/g. The curve with $q_{ \mathrm {L}}=q_{{\mathrm {\max }}}\left( 15\,\text {K}\right)$ gives the situation with maximum heat load. The circle at 15 K indicates the high-temperature pinch point (Color figure online)

Fig. 16

Specific cooling powers $q_{\mathrm {L}}$ for various $p_{\mathrm {h}}$ as functions of $T_{\mathrm {L}}$. The little circles indicate $q_{{\mathrm {\max }} }$ for the corresponding $p_{\mathrm {h}}$. In the 4.2 K region, the curves overlap so they are shifted a bit (Color figure online)

Figure 16 shows calculated plots of $q_{\mathrm {L}}$ as functions of $T_{ \mathrm {L}}$ for four values of $p_{\mathrm {h}}$. The $q_{{\mathrm {\max }}}$ values are indicated with the little circles. For $p_{\mathrm {h}}$ below about 19 bar, $T_{\mathrm {L}}$ remains constant and equal to the boiling point value of 4.2 K until $q_{{\mathrm {\max }}}$ is reached. If $p_{\mathrm {h} }>19$ bar, the $q_{\mathrm {L}}$ curve contains a part of constant $T_{\mathrm { L}}$ and one where $T_{\mathrm {L}}$ increases above 4.2 K (see also Fig. 15). It is often suggested that the fluid that leaves the cold heat exchanger (at point f) is saturated vapor (see, e.g., Ref. [5] Fig.3.3, [11] Fig. 1, [12] Fig. 1). This is correct for the liquefier (almost by definition) but incorrect for the cooler. In a cooler, the composition of the fluid that leaves the “evaporator” is either a liquid-gas mixture or superheated gas. The case that saturated gas leaves the cold CHEX is accidental.

Consider the case of $p_{\mathrm {h}}=30$ bar in Fig. 16 where $q_{{\mathrm { \max }}}=14.9$ J/g. At $q_{\mathrm {L}}=6.5$ J/g, the temperature starts to rise above 4.2 K. If $q_{\mathrm {L}}=q_{{\mathrm {\max }}}$, then $T_{\mathrm {L}}$ is as high as 6.4 K. For cooling, it is desirable to keep $T_{\mathrm {L}}$ as low as possible. The region where $T_{\mathrm {L}}$ remains at 4.2 K can be extended by having an intermediate JT expansion from 30 bar to, e.g., 10 bar as shown in the left figure in Fig. 17 [13]. How this works can be understood using Fig. 18 which gives the isobars of 1, 10, and 30 bar. At about 8.7 K, a JT expansion from 30 to 10 bar is both isothermal and isenthalpic. The high-temperature part of the 30 bar isobar and the low-temperature part of the 10 bar isobar replace the high pressure isenthalp in the previous discussion with no intermediate expansion. In Fig. 18, the thick combined blue and red curves represent the situation of a double expansion while $q_{{\mathrm {\max }}}$ is applied. The combined curve is below the 1 bar isenthalp over the entire temperature range (except at the pinch points at 4.2 and 15 K). Therefore, with the double expansion, $T_{ \mathrm {L}}$ remains at 4.2 K over the entire cooling power range from zero up to $q_{{\mathrm {\max }}}$.

Fig. 17

Schematic diagrams of possible JT coolers; left the serial double throttling; right the partly continuous JT expansion (Color figure online)

Fig. 18

Isenthalps with serial double throttling from 30 bar to 10 bar. Red 10 bar and the 10 bar curve plus $q_{{\mathrm {\max }}}$ at 30 bar. Blue 30 bar and the 30 bar curve plus $q_{{\mathrm {\max }}}$. The thick curves represent the situation with maximum heat load (Color figure online)

Instead of a discrete expansion by a JT valve, one might consider a continuous expansion by having a high flow resistance at the low-temperature side of the high-pressure channel. The continuous JT expansion is shown in the right figure in Fig. 17. In this case, there is heat exchange between the expanding fluid and its surroundings, so, strictly speaking, this is not a JT expansion. The flow resistance inside the CHEX is of the same order as the flow resistance of the final expansion. That means that one can make the high-pressure channel very narrow, e.g., as a narrow gap between a capillary and a wire which closely fits into the capillary. As a result, the thermal resistance in the fluid at the high-pressure side will be practically zero which enhances the heat exchange at this side of the CHEX. Also the tube diameters can be very small which may decrease the thermal mass at the low-temperature side of the cooler and speed up all processes. Care should be taken that the heat exchange at the low-pressure side remains adequate. It may be interesting to analyze the case where the whole expansion takes place inside the high-pressure channel so that there is no final expansion.

4 COP

If $T_{\mathrm {a}}=T_{\mathrm {b}}$ and equal to ambient temperature the first law, applied to the compressor, reads

$$\begin{aligned} \overset{*}{m}h_{\mathrm {a}}+P=\overset{*}{m}h_{\mathrm {b}}+\dot{Q}_{ {\mathrm {co}}} \end{aligned}$$

(22)

where $\dot{Q}_{{\mathrm {co}}}$ is the heat removed from the compressor by air cooling or cooling water and P the electrical power supplied to the compressor. The second law reads

$$\begin{aligned} 0=\overset{*}{m}s_{\mathrm {a}}-\overset{*}{m}s_{\mathrm {b}}-\frac{ \dot{Q}_{{\mathrm {co}}}}{T_{\mathrm {a}}}+\dot{S}_{{\mathrm {ci}}} \end{aligned}$$

(23)

where $\dot{S}_{{\mathrm {ci}}}$ is the rate of entropy production in the compressor including the heat exchanger. Eliminating $\dot{Q}_{{\mathrm {co}}}$ gives

$$\begin{aligned} P=\overset{*}{m}\left( T_{\mathrm {a}}\left( s_{\mathrm {a}}-s_{\mathrm {b} }\right) -h_{\mathrm {b}}+h_{\mathrm {a}}\right) +T_{\mathrm {b}}\dot{S}_{ {\mathrm {ci}}}. \end{aligned}$$

(24)

The P, where $\dot{S}_{{\mathrm {ci}}}=0$, satisfies

$$\begin{aligned} \frac{P_{{\mathrm {\min }}}}{\overset{*}{m}}=T_{\mathrm {a}}\left( s_{ \mathrm {a}}-s_{\mathrm {b}}\right) -h_{\mathrm {b}}+h_{\mathrm {a}}. \end{aligned}$$

(25)

At room temperature $T_{\mathrm {a}}\left( s_{\mathrm {a}}-s_{\mathrm {b} }\right) \gg \left| h_{\mathrm {b}}-h_{\mathrm {a}}\right|$ so, in good approximation,

$$\begin{aligned} P_{{\mathrm {\min }}}\approx \overset{*}{m}T_{\mathrm {a}}\left( s_{\mathrm {a }}-s_{\mathrm {b}}\right) . \end{aligned}$$

(26)

For working fluids like nitrogen, there is no precooler in the JT cooler. With Eqs. (14) and (21), the maximum cooling power is given by

$$\begin{aligned} \dot{Q}_{{\mathrm {L\max }}}=\overset{*}{m}\left( h\left( T_{\mathrm {a}},p_{ \mathrm {l}}\right) -h\left( T_{\mathrm {a}},p_{\mathrm {h}}\right) \right) . \end{aligned}$$

(27)

The COP is defined by

$$\begin{aligned} \xi =\frac{\dot{Q}_{\mathrm {L}}}{P}. \end{aligned}$$

(28)

In the case of maximum cooling power and minimum applied power, $\xi$ is a maximum and given by

$$\begin{aligned} \xi _{{\mathrm {\max }}}\approx \frac{h\left( T_{\mathrm {a}},p_{\mathrm {l} }\right) -h\left( T_{\mathrm {a}},p_{\mathrm {h}}\right) }{T_{\mathrm {a} }\left( s_{\mathrm {a}}-s_{\mathrm {b}}\right) }. \end{aligned}$$

(29)

In the case of helium as the working fluid, precooling is required (not shown in Fig. 6), e.g., by a cryocooler or (pumped) liquid hydrogen. For the compressor power, Eq. (25) can still be used and for the maximum cooling power a relation similar to Eq. (27) holds where the points a and b in Eq. (25) are at room temperature and differ from the points a and b in Eq. (27) which are at low temperatures. In the determination of the COP of the entire system, the energy consumption by the precooler has to be taken into account.

5 Measured Cooling Powers

As mentioned before, good cooling power measurements of JT coolers are rare. The group in Hangzhou recently has measured the cooling power of a JT cooler for the liquid-helium temperature range precooled by a GM cooler [14]. The measured temperatures before and after the JT valve were the same so the JT expansion isothermal and the CHEX was close to ideal. The maximum heating power was 49 mW. At higher heat loads, the system drifted to higher temperatures indefinitely in accordance with Sect. 3.5. When a heating power below the maximum value was applied, the temperatures were equal to the saturated temperature at 1 atm so there was two-phase flow in the cold heat exchanger all the time. In this experiment (zone E in Ref. [14]), $p_{ \mathrm {h}}=11.37$ bar and $T_{\mathrm {b}}=17.3$ K resulting in $h_{\mathrm {b }}=87.251$ J/g. The low pressure was $p_{\mathrm {l}}=1.036$ bar. At this pressure and the measured $T_{\mathrm {g}}$ of 17.1 K, we have $h_{\mathrm {g} }=93.171$ J/g [15]. With these values, Eq. (21) gives $q_{{\mathrm {\max }}}=93.171-87.251=5.920$ J/g. The flow rate was 9.1 mg/s so the theoretical $\dot{Q}_{{\mathrm {\max }}}$ is $9.1\times 5.920=53.872$ mW. The difference between the calculated 54 mW and the measured 49 mW is within the uncertainty.

Fig. 19

Cooling power of the CryoTiger PT30[15] as function of $T_{\mathrm {L}}$. The dotted part indicates the unstable region as explained in the main text (Color figure online)

Another source of a measured JT cooling power is the CryoTiger manual (Ref. [16]). Figure 19 shows its cooling power characteristic. The CryoTiger is a JT cooler which operates not with a pure fluid but with a gas mixture. There is no part in the $T_{\mathrm {L}}-\dot{Q}_{\mathrm {L}}$ where $T_{ \mathrm {L}}$ is constant as shown in Fig. 16. The $\dot{Q}_{\mathrm {L}}-T_{\mathrm {L }}$ plot has a maximum of 24.2 W at about 140 K. If the heating power would be increased above 24.2 W, the temperature would rise unlimited in accordance with the behavior described above.

For temperatures above 140 K, the slope in the $\dot{Q}_{\mathrm {L}}-T_{ \mathrm {L}}$ plot is negative. This region is unstable. This can be understood by considering the situation at 160 K as an example. At 160 K, the cooling power is 19 W. If we would apply a bit smaller heating power, e.g., $\dot{Q}=18.9$ W at this temperature, then the cooling power $\dot{Q}_{ \mathrm {L}}$ is larger than the heating power $\dot{Q}$ and the temperature will go down. As a result of the negative slope, the net cooling power $\dot{Q }_{\mathrm {L}}-\dot{Q}$ will be even higher, so the system will cool down even faster. The process will stop at 133 K, where the cooling power is 18.9 W in the region with the positive slope. If, initially, we would have applied a heating power which is a bit higher than 19 W then the system would have run away to high temperatures. So the region of negative slope is unstable and can only be derived from the transient behavior such as during cool down using the relation

$$\begin{aligned} \dot{Q}_{\mathrm {L}} =-C_{\mathrm {L}}\frac{\mathrm {d}T_{\mathrm {L}}}{\mathrm {d }t} \end{aligned}$$

(30)

where $C_{\mathrm {L}}$ is the heat capacity of the low-temperature end.

During cool down, one has to be aware of the fact that the flows in the CHEX may differ from point to point due to the changing density distribution. If there is a reservoir in the system there may be a phase in the cool down during which it is filling with liquid. In that case, the flows at the warm and cold sides differ significantly. Also the finite heat capacity of the CHEX comes into play. If there is a big thermal mass at the cold end, the cool down is very slow and we are dealing with a quasi-steady situation.

6 Conclusion

The first law of thermodynamics is a very powerful tool for analyzing JT liquefiers and JT coolers. Important properties such as liquefaction rates, cooling powers, temperature distributions, and system limitations can be easily visualized using hT-diagrams.