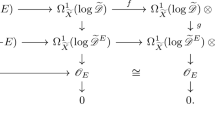Skip to main content
SpringerLink
Log in

Euler characteristics of moduli spaces of torsion free sheaves on toric surfaces

  • Original Paper
  • Published:
Geometriae Dedicata Aims and scope Submit manuscript

Abstract

Given a smooth toric variety \(X\), the action of the torus \(T\) lifts to the moduli space \({\mathcal {M}}\) of stable sheaves on \(X\). Using the pioneering work of Klyacho, a fairly explicit combinatorial description of the fixed point locus \({\mathcal {M}}^T\) can be given (as shown by earlier work of the author). In this paper, we apply this description to the case of torsion free sheaves on a smooth toric surface \(S\). A general expression for the generating function of the Euler characteristics of such moduli spaces is obtained. The generating function is expressed in terms of Euler characteristics of certain moduli spaces of stable configurations of linear subspaces appearing in classical GIT. The expression holds for any choice of \(S\), polarization, rank, and first Chern class. Specializing to various examples allows us to compute some new as well as known generating functions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. For the definition of Gieseker stability, see [12, Def. 1.2.4].

  2. Recall that the notion of stability depends on the choice of polarization.

  3. In this paper, we work with varieties, schemes, and stacks over ground field \({\mathbb {C}}\).

  4. For the definition of \(\mu \)-stability, also known as slope or Mumford-Takemoto stability, see [12, Def. 1.2.12].

  5. Configurations of linear subspaces and their moduli spaces are a classical topic in GIT. See [4, Ch. 11] for a discussion.

  6. This example was considered independently around the same time by Weist using techniques of toric geometry and quivers [29].

  7. We always assume \(\Delta \) contains cones of dimension \(d\).

  8. For gluing conditions for general \(T\)-equivariant coherent sheaves see [26, Sect. 5.2].

  9. The precise statement is this. The category of \(T\)-equivariant torsion free sheaves on \(U_{\sigma _i}\) is equivalent to the category of finite \(\sigma _i\)-families with all maps \(\chi _{m,m'}^{\sigma _i}\) injective. This category is equivalent to its full subcategory of finite \(\sigma _i\)-families with all maps \(\chi _{m,m'}^{\sigma _i}\) inclusions.

  10. It should be clear how the gluing conditions read when the rays of \(\sigma _i \cap \sigma _j\) do not necessarily correspond to the first \(p\) rays of \(\sigma _i\) and \(\sigma _j\).

  11. Large parts of this section hold for \(T\)-equivariant pure sheaves in general [20].

  12. As usual, two such families \(\mathcal {F}_{1}\), \(\mathcal {F}_{2}\) are identified if there exists a line bundle \(L\) on \(S\) and a \(T\)-equivariant isomorphism \(\mathcal {F}_{1} \cong \mathcal {F}_{2} \otimes p_{S}^{*}L\). See [20, Sect. 3.1] for details.

  13. In the previous sections, we followed Perling’s convention of ascending directions for the maps between the weight spaces as opposed to Klyachko’s convention of descending directions. This results in some minus signs compared to Klyachko’s original formula.

  14. Note that for any finite product of Grassmannians \(\prod _{i} \mathrm{Gr}(n_{i},N)\), the map \(\{p_{i}\}_i \mapsto \mathrm{dim}\left( \bigcap _{i} p_{i} \right) \) is upper semicontinuous.

  15. The terminology “wall” might be slightly confusing in this context as \(W\) lies dense in \({\mathbb {Q}}_{>a}\).

  16. The cited theorem also holds for \(\mu \)-stability instead of Gieseker stability.

  17. In the case \(f_3=f_4=0 \mod 2\), we have \(\Lambda = \varnothing \). However, for \(r=2\) and fixed \(c_1, c_2\) one can show that \(\mathrm{Obj}_{ss}^{\mathrm{ch}}(\mu ) \setminus \mathrm{Obj}_{s}^{\mathrm{ch}}(\mu )\) is the same for any polarization not on a wall of type \((c_1,c_2)\). Therefore, formula (14) also holds in this case, because strictly \(\mu \)-semistables on either side of a wall cancel (compare [9, Thm. 2.9]).

  18. During the final preparations of the first version of this paper, the author found out about recent independent work of Weist [29], which also computes the case \(r=3\) and \(S = {\mathbb {P}}^{2}\) using techniques of toric geometry and quivers. Weist has communicated to the author that his results are consistent with the expansions given at the end of this section.

References

  1. Bruzzo, U., Poghossian, R., Tanzini, A.: Poincaré polynomial of moduli spaces of framed sheaves on (stacky) Hirzebruch surfaces. Commun. Math. Phys. 304, 395–409 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  2. Choi, J.: Genus Zero BPS Invariants for Local \({\mathbb{P}}^1\), IMRN advance access (2012)

  3. Choi, J., Maican, M.: Torus action on the moduli spaces of plane sheaves, arXiv:1304.4871

  4. Dolgachev, I.: Lectures on Invariant Theory. Cambridge University Press, Cambridge (2003)

    Book  MATH  Google Scholar 

  5. Ellingsrud, G., Strømme, S.A.: On the homology of the Hilbert scheme of points in the plane. Invent. Math. 87, 343–352 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  6. Fulton, W.: Introduction to Toric Varieties. Princeton University Press, Princeton (1993)

    MATH  Google Scholar 

  7. Gómez, T.L.: Algebraic stacks. Proc. Indian Acad. Sci. Math. Sci. 111, 1–31 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  8. Göttsche, L.: The Betti numbers of the Hilbert scheme of points on a smooth projective surface. Math. Ann. 286, 193–207 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  9. Göttsche, L.: Change of polarization and Hodge numbers of moduli spaces of torsion free sheaves on surfaces. Math. Z. 223, 247–260 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  10. Göttsche, L.: Theta functions and Hodge numbers of moduli spaces of sheaves on rational surfaces. Commun. Math. Phys. 206, 105–136 (1999)

    Article  MATH  Google Scholar 

  11. Hartshorne, R.: Stable reflexive sheaves. Math. Ann. 254, 121–176 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  12. Huybrechts, D., Lehn, M.: The Geometry of Moduli Spaces of Sheaves. Vieweg, Braunschweig (1997)

    Book  MATH  Google Scholar 

  13. Joyce, D.: Motivic invariants of Artin stacks and ‘stack functions’. Q. J. Math. 58, 345–392 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  14. Joyce, D.: Configurations in abelian categories. IV. Invariants and changing stability conditions. Adv. Math. 217, 125–204 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  15. Kaneyama, T.: On equivariant vector bundles on an almost homogeneous variety. Nagoya Math. J. 57, 65–86 (1975)

    MATH  MathSciNet  Google Scholar 

  16. Klyachko, A.A.: Toric bundles and problems of linear algebra. Funct. Anal. Appl. 23, 135–137 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  17. Klyachko, A.A.: Equivariant bundles on toral varieties. Math. USSR Izvestiya 35, 337–375 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  18. Klyachko, A.A.: Stable bundles, representation theory and Hermitian operators. Sel. Math. 4, 419–445 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  19. Klyachko, A.A.: Vector Bundles and Torsion Free Sheaves on the Projective Plane, preprint Max Planck Institut für Mathematik (1991)

  20. Kool, M.: Fixed point loci of moduli spaces of sheaves on toric varieties. Adv. Math. 227, 1700–1755 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  21. Kool, M.: Moduli spaces of sheaves on toric varieties, D.Phil. thesis University of Oxford (2010)

  22. Manschot, J.: The Betti numbers of the moduli space of stable sheaves of rank 3 on \({\mathbb{P}}^2\). Lett. Math. Phys. 98, 65–78 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  23. Manschot, J.: BPS invariants of \(N=4\) gauge theory on a surface. Commun. Num. Theor. Phys. 6, 497–516 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  24. Manschot, J.: BPS invariants of semi-stable sheaves on rational surfaces. arXiv:1109.4861

  25. Mozgovoy, S.: Invariants of moduli spaces of stable sheaves on ruled surfaces. arXiv:1302.4134

  26. Perling, M.: Graded rings and equivariant sheaves on toric varieties. Math. Nachr. 263–264, 181–197 (2004)

    Article  MathSciNet  Google Scholar 

  27. Qin, Z.: Equivalence classes of polarizations and moduli spaces of sheaves. J. Diff. Geom. 37, 397–413 (1993)

    MATH  Google Scholar 

  28. Vakil, R.: Murphy’s law in algebraic geometry: badly-behaved deformation spaces. Invent. Math. 164, 569–590 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  29. Weist, T.: Torus fixed points of moduli spaces of stable bundles of rank three. J. Pure Appl. Algebra 215, 2406–2422 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  30. Yoshioka, K.: The Betti numbers of the moduli space of stable sheaves of rank 2 on \({\mathbb{P}}^{2}\). J. Reine Angew. Math. 453, 193–220 (1994)

    MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

Many of the guiding ideas of this paper come from Klyachko’s wonderful preprint [19]. I would like to thank Tom Bridgeland, Frances Kirwan, Sven Meinhardt, Yinan Song, Balázs Szendrői, Yukinobu Toda and Richard Thomas for useful discussions and my supervisor Dominic Joyce for his continuous support. The author would also like to thank the referee very useful suggestions on improving the exposition of this paper. This paper is part of the author’s D.Phil. project funded by an EPSRC Studentship, which is part of EPSRC Grant EP/D077990/1.

Author information

Authors and Affiliations

  1. Pacific Institute for the Mathematical Sciences, University of British Columbia, 4176–2207 Main Mall, Vancouver, BC, V6T 1Z4, Canada

    Martijn Kool

Authors
  1. Martijn Kool
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Martijn Kool.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kool, M. Euler characteristics of moduli spaces of torsion free sheaves on toric surfaces. Geom Dedicata 176, 241–269 (2015). https://doi.org/10.1007/s10711-014-9966-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10711-014-9966-2

Keywords

Mathematical Subject Classification

Search

Navigation