Regularized boundary integral equations for two-dimensional crack problems in multi-field media

Abstract

A systematic procedure is followed to develop a set of regularized boundary integral equations for modeling cracks in 2D linear multi-field media. The class of media treated is quite general and includes, as special cases, anisotropic elasticity, piezoelectricity and magnetoelectroelasticity. Of particular interest is the development of a pair of weakly-singular, weak-form integral equations for ‘generalized displacement’ and ‘generalized stress’; these serve as the basis for a weakly-singular symmetric Galerkin boundary element method.

Appendices

Appendix A: Somigliana’s identity

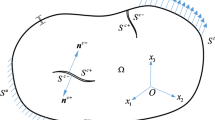
Consider a homogeneous finite 2D domain $\varOmega$ as shown schematically in Fig. 3. The boundary $\varGamma$ of the domain is composed of two parts: $\varGamma _t$ on which traction is prescribed and $\varGamma _u$ on which displacement is prescribed (i.e. $\varGamma =\varGamma _t\cup \varGamma _u$ and $\varGamma _t\cap \varGamma _u=\emptyset$). In the absence of body force, the displacement $u_J$ satisfies the governing equilibrium equation

$$\begin{aligned} E_{\alpha IJ\beta }\frac{\partial ^2}{\partial \xi _\alpha \partial \xi _\beta }u_J({\varvec{\xi }})&= 0. \end{aligned}$$

(80)

Fig. 3

Schematic of homogeneous finite domain under general boundary conditions

We will have a need for the displacement fundamental solution $U_{J}^{P}({\varvec{\xi }}-{{\varvec{x}}})$ which satisfies

$$\begin{aligned} E_{\alpha IJ\beta }\frac{\partial ^{2}}{\partial \xi _{\alpha }\partial \xi _{\beta }}U_{J}^{P}({\varvec{\xi }}-{{\varvec{x}}})=-\delta _{IP} \, \delta ({\varvec{\xi }}-{{\varvec{x}}}) \end{aligned}$$

(81)

where $\delta ({\varvec{\xi }}-{{\varvec{x}}})$ is the 2D Dirac delta, and where $\delta _{IP}$ is a generalized Knonecker delta defined such that $\delta _{IP}=1$ when $I=P$ and $\delta _{IP}=0$ when $I \ne P$. For future reference we note that the stress fundamental solution follows from the displacement fundamental solution by

$$\begin{aligned} S_{\alpha I}^{P}({\varvec{\xi }}-{{\varvec{x}}}) = E_{\alpha IJ\beta }\frac{\partial }{\partial \xi _\beta }U_{J}^{P}({\varvec{\xi }}-{{\varvec{x}}}). \end{aligned}$$

(82)

Now, multiply Eq. (80) with the fundamental solution and integrate over the domain $\varOmega$ to find

$$\begin{aligned} \int \limits _{\Omega }{E_{\alpha IJ\beta }\frac{\partial ^2 u_J({\varvec{\xi }})}{\partial \xi _\alpha \partial \xi _\beta }U_I^P({\varvec{\xi }}-{{\varvec{x}}})dA({\varvec{\xi }})}&= 0 \end{aligned}$$

(83)

where ${{\varvec{x}}}$ is the source point of the fundamental problem, and $dA$ is the infinitesimal area. After integration by parts twice, Eq. (83) becomes

$$\begin{aligned}&-\int \limits _{\Omega }{E_{\alpha IJ\beta }u_J({\varvec{\xi }})\frac{\partial ^2 U_I^P({\varvec{\xi }}-{{\varvec{x}}})}{\partial \xi _{\alpha }\partial \xi _{\beta }}dA({\varvec{\xi }})}\nonumber \\&\quad \quad =\int \limits _{\varGamma }{E_{\alpha IJ\beta }\frac{\partial u_J({\varvec{\xi }})}{\partial \xi _\beta }U_{I}^P({\varvec{\xi }}-{{\varvec{x}}})n_{\alpha }({\varvec{\xi }})ds({\varvec{\xi }})}\nonumber \\&\quad \quad \quad -\int \limits _{\varGamma }{E_{\alpha IJ\beta }u_J({\varvec{\xi }})\frac{\partial U_I^P({\varvec{\xi }}-{{\varvec{x}}})}{\partial \xi _\alpha }n_{\beta }({\varvec{\xi }})ds({\varvec{\xi }})} \nonumber \\ \end{aligned}$$

(84)

where $n_\alpha$ is the unit normal to the boundary $\varGamma$ at point ${\varvec{\xi }}$. Utilizing the equilibrium Eq. (81) and the symmetry property of the material constants (i.e. $E_{\alpha IJ\beta }=E_{\beta JI\alpha }$), one obtains an integral equation for the displacement at a source point ${{\varvec{x}}}$ in terms of the data on the boundary, i.e. Somigliana’s identity generalized to multi-field media, as

$$\begin{aligned} u_P({{\varvec{x}}})&= \int \limits _{\varGamma }{U_{I}^P({\varvec{\xi }}-{{\varvec{x}}})t_I({\varvec{\xi }})ds({\varvec{\xi }})} \nonumber \\&-\int \limits _{\varGamma }{S_{\beta J}^P({\varvec{\xi }}-{{\varvec{x}}})n_\beta ({\varvec{\xi }})u_J({\varvec{\xi }})ds({\varvec{\xi }})}. \end{aligned}$$

(85)

Appendix B: Demonstration that $H_{\alpha J}^P n_\alpha = \text{ O }(1)$

This section establishes that the dot product of the kernel $H_{\alpha J}^P$ with the normal vector at either the source point ${{\varvec{x}}}$ or the field point ${\varvec{\xi }}$ is regular as $r\rightarrow 0$. This is demonstrated in a fashion similar to the work of Xiao (1998) for 3D isotropic elastic media, and is included for completeness. For convenience, the expression for kernel $H_{\alpha J}^P$ (Eq. (16)) is restated as

$$\begin{aligned} H_{\alpha J}^{P}({\varvec{\xi }}-{{\varvec{x}}}) = -\delta _{JP}\frac{\partial }{\partial \xi _{\alpha }}\Bigl (\frac{\ln r}{2\pi }\Bigr ) = -\delta _{JP}\frac{\xi _\alpha -x_\alpha }{2\pi r^2}, \nonumber \\ \end{aligned}$$

(86)

then the dot product $H_{\alpha J}^P n_\alpha$ becomes

$$\begin{aligned} H_{\alpha J}^{P}n_\alpha = -\delta _{JP}\frac{{{\varvec{r}}}\cdot {{\varvec{n}}}}{2\pi r^2}. \end{aligned}$$

(87)

Fig. 4

Local coordinate system employed for the demonstration

For purposes of the demonstration, consider a point ${{\varvec{x}}}$ on a (locally smooth) curve $\varGamma$ as shown in Fig. 4. At this point, introduce a coordinate system $(\xi _1,\xi _2)$ such that $\xi _2$ is directed along the opposite direction of the normal ${{\varvec{n}}}({{\varvec{x}}})$ to the curve $\varGamma$ at the point ${{\varvec{x}}}$. In the vicinity of ${{\varvec{x}}}$, $\varGamma$ can be represented as

$$\begin{aligned} \xi _2=f(\xi _1) \end{aligned}$$

(88)

where $f$ is a function to define the curve $\varGamma$. Then

$$\begin{aligned} {{\varvec{n}}}({{\varvec{x}}})\cdot {{\varvec{r}}}=-\xi _2=-f(\xi _1). \end{aligned}$$

(89)

To proceed, a Taylor expansion of $f$ about ${{\varvec{x}}}$ is given as

$$\begin{aligned} f(\xi _1)={1\over 2}f^{\prime \prime }(0)\xi _1^2+\mathcal O (\xi _1^3) \end{aligned}$$

(90)

where we used the fact that $f^{\prime }(0)=0$ since the normal vector ${{\varvec{n}}}({{\varvec{x}}})$ is in the direction of the $\xi _2$-axis. Note that $\xi _1=r\cos \theta$, so Eq. (90) becomes

$$\begin{aligned} f(\xi _1)={1\over 2}f^{\prime \prime }(0)r^2\cos ^2\theta +\mathcal O (r^3). \end{aligned}$$

(91)

The combination of Eqs. (89) and (91) leads to the result

$$\begin{aligned} \frac{{{\varvec{n}}}({{\varvec{x}}})\cdot {{\varvec{r}}}}{r^2}=\mathcal O (1) \quad \text{ as } r\rightarrow 0. \end{aligned}$$

(92)

Now consider the case of the normal vector at the field point ${\varvec{\xi }}$. With the expression for $\varGamma$ given by Eq. (88), components of the normal vector ${{\varvec{n}}}$ at the field point ${\varvec{\xi }}$ are as follows

$$\begin{aligned} {{\varvec{n}}}({\varvec{\xi }})=\bigl (f^{\prime }(\xi _1),-1\bigr ). \end{aligned}$$

(93)

Note that, in (93), the normal vector ${{\varvec{n}}}({\varvec{\xi }})$ is not normalized to become a unit vector yet. The dot product of ${{\varvec{n}}}({\varvec{\xi }})$ and ${{\varvec{r}}}$ becomes

$$\begin{aligned} {{\varvec{n}}}({\varvec{\xi }})\cdot {{\varvec{r}}}= f^{\prime }(\xi _1)\xi _1-\xi _2 = f^{\prime }(\xi _1)\xi _1 - f(\xi _1). \end{aligned}$$

(94)

Forming a Taylor expansion of $f^{\prime }(\xi _1)$ about ${{\varvec{x}}}$, we have

$$\begin{aligned} f^{\prime }(\xi _1) = f^{\prime \prime }(0)\xi _1+\mathcal O (\xi _1^2). \end{aligned}$$

(95)

Combining Eqs. (90), (94) and (95), we have

$$\begin{aligned} {{\varvec{n}}}({\varvec{\xi }})\cdot {{\varvec{r}}}&= \frac{1}{2}f^{\prime \prime }(0)\xi _1^2+\mathcal O (\xi _1^3) \quad \text{ as } r\rightarrow 0. \end{aligned}$$

(96)

Similarly to the previous case, noting $\xi _1=r\cos \theta$, Eq. (96) leads to

$$\begin{aligned} \frac{{{\varvec{n}}}({\varvec{\xi }})\cdot {{\varvec{r}}}}{r^2}=\mathcal O (1) \quad \text{ as } r\rightarrow 0. \end{aligned}$$

(97)

Appendix C: Radon transform

We provide a summary of certain properties of the Radon transform that are relevant to our development. More details of the Radon transform and its applications can be found in Deans (1983). The Radon transform involves two independent transform parameters: a unit vector ${{\varvec{z}}}$ and a scalar $p$. In a 2D Euclidean plane, a line $L$ that is perpendicular to ${{\varvec{z}}}$ and has a distance of $p$ to the origin of the coordinate system, as shown in Fig. 5, is defined by the equation ${{\varvec{z}}}\cdot {\varvec{\xi }}=p$. Let $f=f({\varvec{\xi }})$ be a function defined on a domain $\varOmega \in \mathbb{R }^2$. Then the Radon transform of $f({\varvec{\xi }})$ is defined as the integral of $f({\varvec{\xi }})$ along this line, provided the integral exists, i.e.

$$\begin{aligned} \hat{f}({{\varvec{z}}},p) = \mathcal R f({\varvec{\xi }}) = \int \limits _{{{\varvec{z}}}\cdot {\varvec{\xi }}=p}f({\varvec{\xi }})ds = \int \limits _{\mathbb{R }^2}f({\varvec{\xi }})\delta (p-{{\varvec{z}}}\cdot {\varvec{\xi }})dA\nonumber \\ \end{aligned}$$

(98)

where $ds$ and $dA$ denote infinitesimal length and area respectively, and $\delta (p-{{\varvec{z}}}\cdot {\varvec{\xi }})$ is the 2D Dirac delta ‘centered’ at the line ${{\varvec{z}}}\cdot {\varvec{\xi }}=p$.

Fig. 5

Line $L$ and its parameters utilized in the definition of the Radon transform

The function $f({\varvec{\xi }})$ is then given in terms of its Radon transform $\hat{f}({{\varvec{z}}},p)$ defined in (98) by the inversion formula

$$\begin{aligned} f({\varvec{\xi }})=\frac{1}{4\pi ^2}\oint \limits _{\Vert {{\varvec{z}}}\Vert =1}{\int \limits _{-\infty }^{\infty }{\frac{\partial ^2 \hat{f}({{\varvec{z}}},p)}{\partial p^2}\ln |p-{{\varvec{z}}}\cdot {\varvec{\xi }}|\,dp}}\,ds \nonumber \\ \end{aligned}$$

(99)

in which the outer integration is taken over a unit circle.

Certain useful properties and results of the Radon transform that pertain to our development are summarized below.

• 1. Shifting property: The Radon transform of a function $f({\varvec{\xi }}-{{\varvec{x}}})$ where ${{\varvec{x}}}$ is a fixed point is given by

  $$\begin{aligned} \mathcal R f({\varvec{\xi }}-{{\varvec{x}}})&= \int \limits _{\mathbb{R }^2}{f({\varvec{\xi }}-{{\varvec{x}}})\delta (p-{{\varvec{z}}}\cdot {\varvec{\xi }})dA} \nonumber \\&= \hat{f}({{\varvec{z}}},p-{{\varvec{z}}}\cdot {{\varvec{x}}}). \end{aligned}$$

  (100)

  Then application of the inversion formula (99) for the function $f({\varvec{\xi }}-{{\varvec{x}}})$ gives

  $$\begin{aligned}&f({\varvec{\xi }}-{{\varvec{x}}}) = \nonumber \\&\ \frac{1}{4\pi ^2}\oint \limits _{\Vert {{\varvec{z}}}\Vert =1}\int \limits _{-\infty }^{\infty }\frac{\partial ^2 \hat{f}({{\varvec{z}}},p\!-\!{{\varvec{z}}}\cdot {{\varvec{x}}})}{\partial p^2}\ln |p\!-\!{{\varvec{z}}}\cdot {\varvec{\xi }}|dp \, ds. \nonumber \\ \end{aligned}$$

  (101)

• 2. For a particular case where the function $\frac{\partial ^2 \hat{f}({{\varvec{z}}},p-{{\varvec{z}}}\cdot {{\varvec{x}}})}{\partial p^2}$ in (101) is expressed as

  $$\begin{aligned} \frac{\partial ^2 \hat{f}({{\varvec{z}}},p-{{\varvec{z}}}\cdot {{\varvec{x}}})}{\partial p^2}=g({{\varvec{z}}})\delta (p-{{\varvec{z}}}\cdot {{\varvec{x}}}) \end{aligned}$$

  (102)

  where $g({{\varvec{z}}})$ is a suitably well-behaved function of ${{\varvec{z}}}$, then (101) becomes

  $$\begin{aligned} f({\varvec{\xi }}-{{\varvec{x}}})=\frac{1}{4\pi ^2}\oint \limits _{\Vert {{\varvec{z}}}\Vert =1}{g({{\varvec{z}}})\ln |{{\varvec{z}}}\cdot ({\varvec{\xi }}-{{\varvec{x}}})|\,ds}. \nonumber \\ \end{aligned}$$

  (103)

  This special inversion formula plays a key role in our development; while it is readily obtained from standard inversion formulas for the Radon transform, we are unaware of it being pointed out previously in the literature. It is analogous to a result for the 3D Radon transform that is, however, widely known (and in that case is associated with functions $f({\varvec{\xi }}-{{\varvec{x}}})$ having a $1/r$ singularity where $r=\Vert {\varvec{\xi }}-{{\varvec{x}}}\Vert$).

• 3. The Radon transform of the derivative of a function satisfies

  $$\begin{aligned} \mathcal R \biggl (\frac{\partial f({\varvec{\xi }})}{\partial \xi _\alpha }\biggr )=z_\alpha \frac{\partial \hat{f}({{\varvec{z}}},p)}{\partial p}. \end{aligned}$$

  (104)

• 4. The Radon transform of a 2D Dirac delta is given by

  $$\begin{aligned} \mathcal R \delta ({\varvec{\xi }}-{{\varvec{x}}})=\delta (p-{{\varvec{z}}}\cdot {{\varvec{x}}}). \end{aligned}$$

  (105)