Credit Card Competition and Naive Hyperbolic Consumers

Abstract

I explain the credit card market’s observed systematic pricing patterns by examining time-inconsistent consumers. I find that time inconsistency steers the competition from long-term borrowing contingent prices to short-term noncontingent ones. This pattern occurs because the consumer in the contracting period underestimates the future charges, and therefore pays attention only to short-term price elements, such as annual fees. The consumer’s risk of default also plays a role in determining who gets which contract.

Appendix

1.1 A.1 Naive hyperbolic consumer underestimates future consumption

If the consumer is not planning to default, the consumer pays all of his debt back by the last period. Therefore, only the first period borrowing will create interest revenue, but not the second period borrowing. Therefore, I analyze only first-period new borrowing. First, I analyze the exponential consumer as the benchmark (0≤δ≤1 and β=1). The exponential consumer is time consistent, and therefore the first-period borrowing according to the contracting-period self (${n_{1}^{0}},$ believed amount of borrowing) and according to the period-one self (${n_{1}^{1}},$ actual amount of borrowing) is the same (${n_{1}^{0}}={n_{1}^{1}}$). Exponential consumers can either be borrowers or convenience users, but cannot switch between these roles. There is a δ ^∗ such that the contracting-period self correctly knows that he will not pay interest for δ≥δ ^∗ (convenience user). Therefore, this self is unresponsive to interest rates. Nevertheless, being unresponsive to interest rates does not hurt him because he will not pay interest in the future anyway. The companies earn zero profit even without competition on interest rates. If δ<δ ^∗, then the contracting-period self correctlyknows that he will pay interest (borrower). Therefore, this self looks for the lowest interest rate. As a result, a Bertrand competition drives the interest rates down to zero. A naive hyperbolic consumer, on the other hand, has a self-control problem and is not aware of it (β<1). Consequently, this consumer underestimates his future borrowings $\left ({n_{1}^{0}}<{n_{1}^{1}}\right )$. The following proposition shows that there is a naive hyperbolic consumer (specified by δ and β) who has a contracting-period self that plans to use the card for transactions only, but who has a period-one self that ends up using it for borrowing.

Proposition 5

For a naive hyperbolic consumer, there is a δ ^∗ , such that ${n_{1}^{0}}\leq m$ for all δ≥δ ^∗ . There is also a $\beta _{r=1}^{\ast }(\delta )>0,$ such that ${n_{1}^{0}}\leq m<{n_{1}^{1}}$ for all $\left (\delta ,\beta \right )$ where δ≥δ ^∗ and $\beta <\beta _{r=1}^{\ast }(\delta )$.

Proof

We start the analysis with an exponential consumer. It is a dominant strategy for the consumer to pay off as much of his borrowing in the grace period as possible. Therefore, if$~{n_{1}^{t}}\leq m,$ then ${p_{2}^{t}}={n_{1}^{t}}$ and ${p_{3}^{t}}={n_{2}^{t}}$; if$\ {n_{1}^{t}}>m,$ then ${p_{2}^{t}}=m$ and ${p_{3}^{t}}=\left ({n_{1}^{t}}-m\right ) \left (1+r\right ) +{n_{2}^{t}}$. As a result, the consumer’s utility function is as follows:

• If ${n_{1}^{t}}\leq m,$ then $U_{{n_{1}^{t}}\leq m}=\delta \left [u\left (m+{n_{1}^{t}}\right )+\delta u\left (m-{n_{1}^{t}}+{n_{2}^{t}}\right )+\delta ^{2}u\left (m-{n_{2}^{t}}\right )\right ]$.

• If ${n_{1}^{t}}>m,$ then $U_{{n_{1}^{t}}>m}=\delta \left [u\left (m+{n_{1}^{t}}\right )+\delta u\left ({n_{2}^{t}}\right )+\delta ^{2}u\left (m-\left ({n_{1}^{t}}-m\right ) \left (1+r\right ) -{n_{2}^{t}}\right )\right ]$.

The solutions to these two utility functions show that

• $\max U_{{n_{1}^{0}}\leq m}\geq \max U_{{n_{1}^{0}}>m}$ for δ≥δ ^∗, irrespective of the interest rate, and

• $\max U_{{n_{1}^{0}}\leq m}\leq \max U_{{n_{1}^{0}}>m}$ for $\delta <\delta _{r=1}^{\ast }$.

Completing the proof demonstrates that $\delta _{r=1}^{\ast }<\delta ^{\ast }$.

• 1. For $U_{{n_{1}^{0}}\leq m}$, the consumer’s maximization problem at time zero is given by:

  $$\begin{array}{@{}rcl@{}} &&\underset{{n_{1}^{0}},~{n_{2}^{0}}}{\max }~\delta \left[ u\left(m+{n_{1}^{0}}\right)+\delta u\left(m-{n_{1}^{0}}+{n_{2}^{0}}\right)+\delta^{2}u\left(m-{n_{2}^{0}}\right)\right] \\ &&s.t.~{n_{1}^{0}}\leq m,~-{n_{1}^{0}}\leq 0,~and~-{n_{2}^{0}}\leq 0. \end{array} $$

  (3)

  The Lagrangian is given by

  $$\begin{array}{@{}rcl@{}}\mathcal{L}&=&\delta \left[ u\left(m+{n_{1}^{0}}\right)+\delta u\left(m-{n_{1}^{0}}+{n_{2}^{0}}\right)+\delta^{2}u\left(m-{n_{2}^{0}}\right)\right] \\ &&-\lambda_{1}\left({n_{1}^{0}}-m\right)-\lambda_{2}\left(-{n_{1}^{0}}\right)-\lambda _{3}\left(-{n_{2}^{0}}\right) \end{array} $$

  The set of FOCs is as follows:

  $$\begin{array}{@{}rcl@{}} &&\frac{\partial}{\partial {n_{1}^{0}}}=\delta u^{\prime }\left(m+{n_{1}^{0}}\right)-\delta^{2}u^{\prime }\left(m-{n_{1}^{0}}+{n_{2}^{0}}\right)-\lambda_{1}+\lambda_{2}=0 \end{array} $$

  (4)
  $$\begin{array}{@{}rcl@{}} &&\frac{\partial}{\partial {n_{2}^{0}}}=\delta^{2}u^{\prime }\left(m-{n_{1}^{0}}+{n_{2}^{0}}\right)-\delta^{3}u^{\prime }\left(m-{n_{2}^{0}}\right)+\lambda_{3}=0 \\ &&\lambda_{1}\left({n_{1}^{0}}-m\right)=0,~\lambda_{2}\left(-{n_{1}^{0}}\right)=0,~and~\lambda_{3}\left(-{n_{2}^{0}}\right)=0 \\ &&\lambda_{1}\geq 0,~\lambda_{2}\geq 0,~and~\lambda_{3}\geq 0 \\ &&{n_{1}^{0}}\leq m,~-{n_{1}^{0}}\leq 0,~and~-{n_{2}^{0}}\leq 0 \end{array} $$

  (5)

  If ${n_{1}^{0}}=m,$ then λ ₁≥0 and λ ₂=0. If ${n_{2}^{0}}=0,$ then Eq. 5 creates a contradiction; therefore ${n_{2}^{0}}>0$ and λ ₃=0. Then, by Eqs. 4 and 5,

  $$\begin{array}{@{}rcl@{}} u^{\prime }(2m) &=&\delta u^{\prime }\left({n_{2}^{0}}\right)+\lambda_{1} \end{array} $$

  (6)
  $$\begin{array}{@{}rcl@{}} u^{\prime }({n_{2}^{0}}) &=&\delta u^{\prime }\left(m-{n_{2}^{0}}\right) \end{array} $$

  (7)

  There is a δ ^∗ such that Eqs. 6 and 7 both hold for δ≤δ ^∗ where δ ^∗ is determined by $u^{\prime }(2m)=\delta u^{\prime }\left ({n_{2}^{0}}\right )$ and $u^{\prime }\left ({n_{2}^{0}}\right )=\delta u^{\prime }\left (m-{n_{2}^{0}}\right )$. However, Eqs. 6 and 7 cannot simultaneously hold for δ>δ ^∗. Hence, ${n_{1}^{0}}\leq m$ for δ≥δ ^∗.

• 2. For $U_{{n_{1}^{0}}>m}$, the consumer’s maximization problem at time zero is given by:

  $$\begin{array}{@{}rcl@{}} &&\underset{{n_{1}^{0}},~{n_{2}^{0}}}{\max }~\delta \left[ \begin{array}{c} u\left(m+{n_{1}^{0}}\right)+\delta u\left({n_{2}^{0}}\right) \\ +\delta^{2}u\left(m-\left( {n_{1}^{0}}-m\right) (1+r) -{n_{2}^{0}}\right) \end{array} \right] \\ &&s.t.~-{n_{1}^{0}}<-m,~-{n_{1}^{0}}\leq 0,~and~-{n_{2}^{0}}\leq 0. \end{array} $$

  (8)

  The Lagrangian is given by

  $$\begin{array}{@{}rcl@{}}\mathcal{L}&=&\delta \left[ u\left(m+{n_{1}^{0}}\right)+\delta u\left({n_{2}^{0}}\right)+\delta ^{2}u\left(m-\left( {n_{1}^{0}}-m\right) \left( 1+r\right) -{n_{2}^{0}}\right)\right] \\ &&-\lambda_{1}\left(-{n_{1}^{0}}+m\right)-\lambda_{2}\left(-{n_{1}^{0}}\right)-\lambda _{3}\left(-{n_{2}^{0}}\right)\end{array} $$

  The set of FOCs is as follows:

  $$\begin{array}{@{}rcl@{}} &&\frac{\partial}{\partial {n_{1}^{0}}}=\delta u^{\prime }(m+{n_{1}^{0}})\,-\,\delta^{3}(1\,+\,r)u^{\prime }\left(m\,-\,\left( {n_{1}^{0}}\,-\,m\right) \left( 1\,+\,r\right) -{n_{2}^{0}}\right)+\lambda_{1}\,+\,\lambda_{2}\,=\,0 \end{array} $$

  (9)
  $$\begin{array}{@{}rcl@{}} &&\frac{\partial}{\partial {n_{2}^{0}}}=\delta^{2}u^{\prime }\left({n_{2}^{0}}\right)-\delta^{3}u^{\prime }\left(m-\left( {n_{1}^{0}}-m\right) \left( 1+r\right) -{n_{2}^{0}}\right)+\lambda_{3}=0 \\ &&\lambda_{1}\left(-{n_{1}^{0}}+m\right)=0,~\lambda_{2}\left(-{n_{1}^{0}}\right)=0,~and~\lambda_{3}\left(-{n_{2}^{0}}\right)=0 \\ &&\lambda_{1}\geq 0,~\lambda_{2}\geq 0,~and~\lambda_{3}\geq 0 \\ &&-{n_{1}^{0}}\leq -m,~-{n_{1}^{0}}\leq 0,~and~-{n_{2}^{0}}\leq 0 \end{array} $$

  (10)

  If ${n_{1}^{0}}=m,$ then λ ₁≥0 and λ ₂=0. If ${n_{2}^{0}}=0,$ then Eq. 10 cannot hold; therefore ${n_{2}^{0}}>0$ and λ ₃=0. Then, by Eqs. 9 and 10:

  $$\begin{array}{@{}rcl@{}} u^{\prime }(2m) &=&\delta^{2}(1+r)u^{\prime }(m-{n_{2}^{0}})-\lambda_{1} \end{array} $$

  (11)
  $$\begin{array}{@{}rcl@{}} u^{\prime }({n_{2}^{0}}) &=&\delta u^{\prime }(m-{n_{2}^{0}}) \end{array} $$

  (12)

  For a given r, there is a $\delta _{r}^{\ast }$ such that Eqs. 11 and 12 both hold for $\delta \geq \delta _{r}^{\ast }$ where $\delta _{r}^{\ast }$ is determined by $u^{\prime }(2m)=\delta (1+r)u^{\prime }\left (m-{n_{2}^{0}}\right )$ and $u^{\prime }\left ({n_{2}^{0}}\right )=\delta u^{\prime }\left (m-{n_{2}^{0}}\right )$. However, Eqs. 11 and 12 cannot simultaneously hold for $\delta <\delta _{r}^{\ast }$. Thus, ${n_{1}^{0}}>m$ for $\delta <\delta _{r}^{\ast }$.

  Therefore, $\delta _{r}^{\ast }$ decreases with r and $\delta _{r=1}^{\ast }<\delta _{r}^{\ast }<\delta _{r=0}^{\ast }=\delta ^{\ast }$. In summary, the consumer borrows less than or equal to m if δ≥δ ^∗ and more than m if $\delta <\delta _{r}^{\ast }$.

  An exponential consumer with δ≥δ ^∗ correctly believes that he will borrow less than his income. A naive hyperbolic consumer with an exponential discount factor δ≥δ ^∗ possesses the exact same belief $\left ({n_{1}^{0}}\leq m\right )$, but his belief might not be correct, depending on his hyperbolic discount factor. I now analyze the first-period-self of the naive hyperbolic consumer with δ≥δ ^∗. As before, the consumer’s utility function is as follows:

• If ${n_{1}^{t}}\leq m,$ then $U_{{n_{1}^{t}}\leq m}=u\left (m+{n_{1}^{t}}\right )+\beta \delta u\left (m-{n_{1}^{t}}+{n_{2}^{t}}\right )+\beta \delta ^{2}u\left (m-{n_{2}^{t}}\right )$.

• If ${n_{1}^{t}}>m,$ then $U_{{n_{1}^{t}}>m}=u\left (m+{n_{1}^{t}}\right )+\beta \delta u\left ({n_{2}^{t}}\right )+\beta \delta ^{2}u(m-\left ({n_{1}^{t}}-m\right ) \left (1+r\right ) -{n_{2}^{t}})]$.

I follow similar steps as before and solve these two utility functions separately and show that $\max U_{{n_{1}^{1}}>m}\geq \max U_{{n_{1}^{1}}\leq m}$ for all $\left (\delta ,\beta \right )$ where δ≥δ ^∗ and$~\beta <\beta _{r=1}^{\ast \ast }(\delta )$.

• 1. For $U_{{n_{1}^{1}}\leq m}$, the consumer’s maximization problem at time one is as follows:

  $$\begin{array}{@{}rcl@{}} &&\underset{{n_{1}^{1}},~{n_{2}^{1}}}{\max }~u\left(m+{n_{1}^{1}}\right)+\beta \delta u\left(m-{n_{1}^{1}}+{n_{2}^{1}}\right)+\beta \delta^{2}u\left(m-{n_{2}^{1}}\right) \\ &&s.t.~{n_{1}^{1}}\leq m,~-{n_{1}^{1}}\leq 0,~and~-{n_{2}^{1}}\leq 0. \end{array} $$

  (13)

  The Lagrangian is given by

  $$\mathcal{L}=u\left(m+{n_{1}^{1}}\right)+\beta \delta u\left(m-{n_{1}^{1}}+{n_{2}^{1}}\right)+\beta \delta^{2}u\left(m-{n_{2}^{1}}\right)-\lambda_{1}\left({n_{1}^{1}}-m\right)-\lambda _{2}\left(-{n_{1}^{1}}\right)-\lambda_{3}\left(-{n_{2}^{1}}\right) $$

  The set of FOCs is as follows:

  $$\begin{array}{@{}rcl@{}} &&\frac{\partial}{\partial {n_{1}^{1}}}=u^{\prime }(m+n_{1})-\beta \delta u^{\prime }\left(m-{n_{1}^{1}}+{n_{2}^{1}}\right)-\lambda_{1}+\lambda_{2}=0 \end{array} $$

  (14)
  $$\begin{array}{@{}rcl@{}} &&\frac{\partial}{\partial {n_{2}^{1}}}=\beta \delta u^{\prime }\left({n_{2}^{1}}\right)-\beta \delta^{2}u^{\prime }\left(m-{n_{2}^{1}}\right)+\lambda_{3}=0 \end{array} $$

  (15)
  $$\begin{array}{@{}rcl@{}} &&\lambda_{1}({n_{1}^{1}}-m)=0,~\lambda_{2}\left(-{n_{1}^{1}}\right)=0,~and~\lambda_{3}\left(-{n_{2}^{1}}\right)=0 \\ &&\lambda_{1}\geq 0,~\lambda_{2}\geq 0,~and~\lambda_{3}\geq 0 \\ &&{n_{1}^{1}}\leq m,~-{n_{1}^{1}}\leq 0,~and~-{n_{2}^{1}}\leq 0 \end{array} $$

  For δ>δ ^∗ and β=1, the constraints are not binding, and hence λ ₁,λ ₂,λ ₃=0. Moreover, one can show that $\frac {\partial {n_{1}^{1}}}{\partial \beta }<0$ and that there is a β ^∗(δ) such that the constraint (${n_{1}^{1}}\leq m$) is binding for β<β ^∗(δ).

• 2. For $U_{{n_{1}^{1}}>m}$, the consumer’s maximization problem at time one is as follows:

  $$\begin{array}{@{}rcl@{}} &&\underset{{n_{1}^{1}},~{n_{2}^{1}}}{\max }~\left[ \begin{array}{c} u\left(m+{n_{1}^{1}}\right)+\beta \delta u\left({n_{2}^{1}}\right) \\ +\beta \delta^{2}u\left(m-\left( {n_{1}^{1}}-m\right) (1+r)-{n_{2}^{1}}\right) \end{array} \right] \\ &&s.t.~-{n_{1}^{1}}<-m,~-{n_{1}^{1}}\leq 0,~and~-{n_{2}^{1}}\leq 0. \end{array} $$

  (16)

  The Lagrangian is given by

  $$\begin{array}{@{}rcl@{}}\mathcal{L}&=&\delta \left[ u\left(m+{n_{1}^{0}}\right)+\delta u\left(m-{n_{1}^{0}}+{n_{2}^{0}}\right)+\delta^{2}u\left(m-{n_{2}^{0}}\right)\right] \\ &&-\lambda_{1}\left({n_{1}^{0}}-m\right)-\lambda_{2}\left(-{n_{1}^{0}}\right)-\lambda _{3}\left(-{n_{2}^{0}}\right) \end{array} $$

  The set of FOCs is as follows:

  $$\begin{array}{@{}rcl@{}} &&\frac{\partial}{\partial {n_{1}^{1}}}=u^{\prime }\left(m+{n_{1}^{1}}\right)-\beta \delta^{2}(1+r)u^{\prime }\left(m-\left( {n_{1}^{1}}-m\right) \left( 1+r\right) -{n_{2}^{1}}\right)+\lambda_{1}+\lambda_{2}=0 \end{array} $$

  (17)
  $$\begin{array}{@{}rcl@{}} &&\frac{\partial}{\partial {n_{2}^{1}}}=\beta \delta u^{\prime }\left({n_{2}^{1}}\right)-\beta \delta^{2}u^{\prime }\left(m-\left( {n_{1}^{1}}-m\right) \left( 1+r\right) -{n_{2}^{1}}\right)+\lambda_{3}=0 \\ &&\lambda_{1}\left(-{n_{1}^{1}}+m\right)=0,~\lambda_{2}\left(-{n_{1}^{1}}\right)=0,~and~\lambda_{3}\left(-{n_{2}^{1}}\right)=0 \\ &&\lambda_{1}\geq 0,~\lambda_{2}\geq 0,~and~\lambda_{3}\geq 0 \\ &&-{n_{1}^{1}}\leq -m,~-{n_{1}^{1}}\leq 0,~and~-{n_{2}^{1}}\leq 0 \end{array} $$

  (18)

  For δ>δ ^∗,r=1, and β=1, the constraint $\left (-{n_{1}^{1}}\leq -m\right )$ is binding, and it can also be shown that $\frac { \partial {n_{1}^{1}}}{\partial \beta }<0$. Moreover, there is a $\beta _{r=1}^{\ast }(\delta )$ such that the constraint $\left (-{n_{1}^{1}}\leq -m\right )$ is not binding for $\beta <\beta _{r=1}^{\ast }(\delta )$.²³

  Thus, I conclude that the contracting-period self believes that he will borrow less than or equal to m in the future consumption periods, but the period-one self ends up borrowing more than m for all (δ,β) where δ≥δ ^∗ and $\beta <\beta _{r=1}^{\ast }(\delta )$.

  In Fig. 2, I demonstrate how a naive hyperbolic consumer’s period-one self might end up borrowing more than his income even though his contracting-period self plans not to. The x-axis shows the δ discount factor in [0,1]. The y-axis shows the β hyperbolic discount factor in [0,1]. The contracting-period self believes that the β discount factor does not affect his future consumption plans. If the parameter values that define the consumer are in region A ₁ or A ₂, then the consumer believes that he will not accumulate interest-bearing debt. If the parameter values are in region C, the consumer believes that he will accumulate interest-bearing debt and pay interest even if the interest is at the highest possible rate. On the other hand, the period-one self takes β into account when deciding how much to borrow. For the period-one self, the interest rate (r) and the exponential discount factor (δ) are no longer the only determinants of borrowing; the hyperbolic discount factor (β) plays a role as well. Therefore, the vertical line at $\delta _{r=1}^{\ast }$ separating the interest payers from convenience users at the highest interest rate transforms into the downward sloped line in the diagram. If the consumer is in region A ₂,B ₁, or C, his period-one self accumulates interest-bearing debt even at the highest interest rate. However, there is a conflict between what the contracting-period self believes and what the period-one self ends up doing if the parameter values are in region A ₂, irrespective of the interest rate. Proposition 1 shows the existence of consumers in this region. I analyze only the consumers in region A ₂ throughout the paper. Although the contracting-period self is unresponsive to interest rates, the period-one self ends up paying interest.

  Fig. 2

  

  β and δ cutoffs for a naive hyperbolic consumer’s borrowing

□

1.2 A.2 Contract choice depending on credit limits

In summary, if the offered credit limits are l ₁ and l ₂:

• if $\max \left \{ l_{1},l_{2}\right \} \geq n^{0}>\min \{l_{1},l_{2}\}$, then the consumer accepts the contract with the higher credit limit only.

• If $\min \left \{ l_{1},l_{2}\right \} \geq n^{0}$, then the consumer accepts one contract randomly.

• If $\max \left \{ l_{1},l_{2}\right \} <n^{0}$, then the consumer accepts both contracts.

1.3 A.3 Default consideration according to different period selves

Lemma 1

Suppose that l ₁ and l ₂ are in the appropriate ranges, such that the consumer chooses only one contract. Then, the unselected contract’s interest rate does not affect the gain from default. The gain from default is G ₀ (l ₁ ,l ₂ ) with $\frac {\partial G_{0}}{\partial l_{1}}=\frac {\partial G_{0}}{\partial l_{2}}>0,$ according to the contracting-period self, and is G _c (l ₁ ,r ₁ ) with $\frac { \partial G_{c}}{\partial l_{1}}>0$ and $\frac {\partial G_{c}}{\partial r_{1}} >0,$ according to the consumption-period selves if the selected contract is (l ₁ ,r ₁ ). Moreover, G ₀ (l ₁ ,l ₂ )<G _c (l ₁ ,r ₁ ) for low enough values of l ₂ and for all r ₁ ∈[0,1].

Proof

• 1. In the contracting period, the consumer’s total utility is

  $$\begin{array}{@{}rcl@{}} U_{t=0,~d=-1}=\underset{{n_{1}^{0}}}{\max }\beta \delta \left[ u(m+{n_{1}^{0}})+\delta u(m+l_{1}+l_{2}-{n_{1}^{0}})+\delta^{2}u(m)-\delta^{2}C \right] \end{array} $$

  if he plans to default, and

  $$\begin{array}{@{}rcl@{}} U_{t=0,~d=0}=\underset{n_{1}^{0}\leq m,~n_{2}^{0}}{\max }\beta \delta \left[ u(m+n_{1}^{0})+\delta u(m-n_{1}^{0}+n_{2}^{0})\right.\\ \phantom{-00}+\left.\delta^{2}u(m-n_{2}^{0})\right] \end{array} $$

  if he does not plan to default.

  Therefore, the gain from defaulting according to the contracting-period self is given by $G_{0}=\frac {1}{\beta \delta ^{3}}\left (U_{t=0,~d=-1}-U_{t=0,~d=0}\right )$ and $\frac {\partial G_{0}}{\partial l_{1} }=\frac {\partial G_{0}}{\partial l_{2}}>0$ (adjusted according to the last period self).

• 2. When the consumer reaches the first period with the chosen contract (which is (l ₁,r ₁)), he realizes that his actual debt is more than his income. Therefore, the consumer’s total utility is as follows:

  $$\begin{array}{@{}rcl@{}} U_{t=1,~d=-1}=\underset{{n_{1}^{1}}\leq l_{1}}{\max }\left[ u\left(m+{n_{1}^{1}}\right)+\beta \delta u\left(m+l_{1}-{n_{1}^{1}}\right)+\beta \delta^{2}u(m)-\beta \delta^{2}C\right] \end{array} $$
  $$\begin{array}{@{}rcl@{}} if he plans to default, and U_{t=1,~d=0}&=&\underset{{n_{1}^{1}}\leq l_{1},~{n_{2}^{1}}}{\max }\left[ u\left(m+{n_{1}^{1}}\right)+\beta \delta u\left({n_{2}^{1}}\right)\right.\\ &&+\left.\beta \delta^{2}u\left(m-\left({n_{1}^{1}}-m\right)(1+r_{1})-{n_{2}^{1}}\right)\right] \end{array} $$

  if he does not plan to default.

  Therefore, the gain from defaulting planned in the first period is

  $G_{1}=\frac {1}{\beta \delta ^{2}}\left (U_{t=1,~d=-1}-U_{t=1,~d=0}\right )$.

• 3. When the consumer reaches the second period, the total utility is

  $$\begin{array}{@{}rcl@{}} U_{t=2,~d=-1}=\left[ u\left(m+l_{1}-n_{1}^{1\ast }\right)+\beta \delta u(m)-\beta \delta C\right] \end{array} $$

  if he plans to default, and

  $$\begin{array}{@{}rcl@{}} U_{t=2,~d=0}=\underset{{n_{2}^{2}}}{\max }\left[ u\left({n_{2}^{2}}\right)\,+\,\beta \delta u\left(m\,-\,(n_{1}^{1\ast }\,-\,m)(1\,+\,r)\-{n_{2}^{2}}\right)\right] \end{array} $$

  if he does not plan to default.

  Therefore, the gain from defaulting planned in the second period is $G_{2}= \frac {1}{\beta \delta }\left (U_{t=2,~d=-1}-U_{t=2,~d=0}\right )$. As a result, the gain from defaulting according to the consumption period selves is $G_{c}=\max \{G_{1}(l_{1},r),G_{2}(l_{1},r)\}$ with $\frac {\partial G_{c} }{\partial l_{1}}>0$ and $\frac {\partial G_{c}}{\partial r_{1}}>0$.

  If l ₂=0 and β=1; then U _{t=0, d=−1} and U _{t=1, d=−1} are equal, and consequently any difference between G ₀ and G ₁ is due to the difference between U _{t=0, d=0} and U _{t=1, d=0}. From Proposition 1, the profit maximizing n ₁ is less than m for δ>δ ^∗. Therefore, U _{t=0, d=0} is greater than U _{t=1, d=0} for δ>δ ^∗. Consequently, G ₀<G ₁ for β=1. Additionally, $\frac {\partial G_{1}}{\partial \beta }=-\frac { \left [ u(m+n_{1}^{1\ast })-u(m+n_{1}^{1\ast \ast })\right ] }{\left (\beta \delta \right )^{2}}<0$ such that $n_{1}^{1\ast }$ and $n_{1}^{1\ast \ast }$ represent the profit maximizing n ₁ in the case of planning and not planning default, respectively. As a result, G ₀(l ₁,l ₂=0)<G ₁(l ₁,r ₁)≤G _c (l ₁,r ₁) for all r ₁∈[0,1].

□

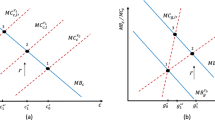
The reasoning behind this lemma is as follows. The contracting-period self believes that he will not pay interest; therefore, the gain from defaulting is not affected by interest rates. Moreover, a marginal gain from each credit limit increase is the same because the credit limits always appear as a sum in the gain function. Consumption-period selves, on the other hand, realize that they pay interest; therefore, the gain from defaulting increases with the interest rate of the chosen contract. The credit limit offered by the contract that is not chosen does not affect the gain because the contracting period has already passed, and the consumer has only the chosen contract on hand. As a result, the set of credit limits that do not induce the consumer to default are shown by the shaded area in Fig. 3.²⁴

Fig. 3

The no-default-region if only one contract is chosen

If I further investigate the gain functions from different selves’ point of view, I find that two different effects determine the gain. One is “the credit effect” and the other is “the spending effect”. The credit effect is the effect of the potential credit limit to default at; it may be larger in the contracting period than in the consumption period depending on other companies’ offers. The spending effect is the effect of the expenditure level, and it is larger in the consumption periods since the consumer spends more than what he had planned earlier. Depending on the contract terms, the credit effect might offset the spending effect or vice versa. For example, G _c (l _i ,r) is the restrictive constraint for the lower values of l _j (the credit effect is smaller). However, if the consumer chooses both contracts, then the credit effect is the same in all periods (the potential credit limit to default at is constant at l ₁+l ₂), although the spending effect is greater in the consumption periods. Therefore, the gain from defaulting is determined according to the consumption-period selves, namely, G _c (l ₁,l ₂,r).

Lemma 2

Suppose that l ₁ and l ₂ are in the appropriate ranges such that the consumer chooses both contracts, and suppose that r ₁ ≤r ₂ . Then, the gain from defaulting is G _c (l ₁ ,l ₂ ,r ₁ ), with $\frac {\partial G_{c}}{\partial l_{1}}, \frac {\partial G_{c}}{\partial l_{2}},\frac {\partial G_{c}}{\partial r_{1}} >0$ and $\frac {\partial G_{c}(l_{1},l_{2},r_{1}=0)}{\partial l_{1}}=\frac { \partial G_{e}(l_{1},l_{2},r_{1}=0)}{\partial l_{2}}>0$.

Proof

The gain from defaulting according to the contracting-period self is the same as before, namely, G ₀(l ₁,l ₂). But, the gain from defaulting according to the consumption-period selves depends on the credit limit offers of both companies instead of only one, namely, G _c (l ₁,l ₂,r ₁) if the lower interest rate contract is (l ₁,r ₁). The consumer pays the contract with the higher interest rate fully to minimize the cost of borrowing, which eliminates the higher interest rate from the gain function.

By using the same arguments as in the previous proof: $G_{0}(l_{1},l_{2})<G_{c}(l_{1},l_{2},r_{1}),\frac {\partial G_{c}(l_{1},l_{2},r_{1})}{\partial r_{1}}>0,$ and $\frac {\partial G_{c}(l_{1},l_{2},r_{1}=0)}{\partial l_{1}}=\frac {\partial G_{c}(l_{1},l_{2},r_{1}=0)}{\partial l_{2}}>0$. □

When the consumer has two contracts on hand, the no-default-region is determined by G _c (l ₁,l ₂,r ₁=0)≤C. This is shown in Fig. 4.

Fig. 4

The shaded region is the no-default-region if two contracts are chosen

1.4 A.4 Equilibrium results

Proof (Proposition 1)

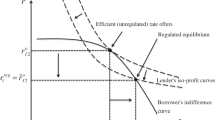
By referring to Fig. 1, I will first illustrate the number of contracts that the consumer will choose under different contract offers and determine whether the consumer will pay interest on them. Afterward, I will determine the equilibria. If the offered contracts lie in region one, the consumer chooses only one contract and pays the agreed interest on that contract. If the offered contracts are in region two, the consumer chooses only one contract but does not pay interest, because the chosen contract’s credit limit prevents him from spending more. If the contracts are in region three, the consumer chooses both contracts but does not pay interest (even the total credit limit offered by these contracts does not allow the consumer to accumulate interest-bearing debt). If the contracts are in region four, the consumer chooses both contracts and pays interest on the contract with the lower interest rate (the total credit limit allows the consumer to accumulate interest-bearing debt and the first-period self pays the contract with higher interest rate within the grace period).

Each company offers a monopoly contract (l ^∗,r ^∗) if there is no risk of default. But, when there is risk of default, the companies might not be able to offer the credit limits they want without triggering default. For convenience, from this point on, I analyze the problem from the first company’s point of view. The second company’s problem is similar. The default constraints are G _c (l ₁,r ₁)≤C and G ₀(l ₁,l ₂)≤C assuming that only one contract is chosen in equilibrium. Additionally, G ₀(l ₁,l ₂)≤G _c (l ₁,r ₁)≤C for lower values of l ₂. Suppose that $(l_{1}^{\ast \ast },r_{1}^{\ast \ast })$ is the first company’s profit-maximizing contract offer when the other company offers a zero credit limit. Let $l_{2}^{\prime }$ be the solution to $G_{0}(l_{1}^{\ast },l_{2})=C$ and $r_{2}^{\prime }= \underset {G_{c}(l_{2},r_{2})\leq C}{\arg \max }(l_{2}^{\prime }-m)r_{2}$. Each company’s contract offer is affected by the other company’s offer only if G ₀(l ₁,l ₂)=C.

Let C ^∗=G _c (l ₁=m,r ₁=0) and C ^∗∗=G _c (l ₁=n ⁰,r ₁=0).

• Consider the case C>C ^∗; I now demonstrate that a company offers a large enough credit limit with a positive interest rate when the other company offers a zero credit limit. If C>C ^∗, then G _c (l ^∗,r ^∗)≤C might or might not be satisfied. If $G_{c}(l_{1}^{\ast }=l^{\ast },r_{1}^{\ast }=r^{\ast })\leq C,$ then the monopoly contract is feasible. Otherwise, the company offers $l_{1}^{\ast }>m$ and $r_{1}^{\ast }>0$ as the profit-maximizing contract with $G_{c}(l_{1}^{\ast },r_{1}^{\ast })=C$. The argument is as follows. Suppose that $l_{1}^{\ast }=m$ and $r_{1}^{\ast }=0$. The company can obtain a higher profit by slightly increasing l ₁ and r ₁ because the constraints C>G _c (l ₁=m,r ₁=0)>G ₀(l ₁=m,l ₂=0) are not binding for $l_{1}^{\ast }=m$ and $r_{1}^{\ast }=0$. Suppose that $l_{1}^{\ast }=m$ and $r_{1}^{\ast }>0$. The company can increase its profit by slightly decreasing the interest rate and slightly increasing the credit limit. Last, suppose that $l_{1}^{\ast }>m$ and $r_{1}^{\ast }=0$. The company can increase its profit by slightly decreasing the credit limit and slightly increasing the interest rate. I now show the existence of different equilibria depending on where $G_{0}(l_{1}^{\ast },l_{2})\leq C$ starts to bind.

  • If $l_{2}^{\prime }\geq l_{1}^{\ast },$ then $(l_{1}^{\ast \ast },r_{1}^{\ast \ast })$ and $(l_{2}^{\ast }=l_{1}^{\ast \ast },r_{2}^{\ast }=r_{1}^{\ast \ast })$ is the unique symmetric equilibrium in region 1. This is because $G_{0}(l_{1}^{\ast \ast },l_{2}^{\ast })<C,$ and each company offers the profit-maximizing contract without triggering default.

  • If $m<l_{2}^{\prime }<l_{1}^{\ast },$ then $(l_{1}^{\ast \ast },r_{1}^{\ast \ast })$ and $(l_{2}^{\ast },r_{2}^{\ast })$ is an equilibrium such that $m<l_{2}^{\ast }\leq l_{2}^{\prime }$ and $r_{2}^{\ast }>0$. This is because the second company cannot offer more than $l_{2}^{\prime }$ and does not have an incentive to offer less than m. Moreover, the second company can offer a positive interest rate without triggering default, as $G_{0}(l_{1}^{\ast \ast },l_{2}^{\ast })\leq C$ and $G_{c}(l_{2}^{\ast },r_{1}^{\ast })<G_{c}(l_{1}^{\ast \ast },r_{1}^{\ast })\leq C$.

  • If $l_{2}^{\prime }\leq m,$ then $(l_{1}^{\ast \ast },r_{1}^{\ast \ast })$ and $(l_{2}^{\ast },r_{2}^{\ast })$ is an equilibrium such that $l_{2}^{\ast }\leq l_{2}^{\prime }$ and $r_{2}^{\ast }\geq 0$. This is because the second company cannot offer more than m, and consequently makes zero profit.

• If C ^∗∗≤C≤C ^∗. $(l_{1}^{\ast },r_{1}^{\ast })$ and $(l_{2}^{\ast },r_{2}^{\ast })$ are then an equilibrium where $0\leq l_{1}^{\ast }\leq l_{1}^{\ast \ast },r_{1}^{\ast }\geq 0,$ and $0\leq l_{2}^{\ast }\leq l_{2}^{\prime },r_{2}^{\ast }\geq 0$. The companies cannot offer more than m without triggering default, and consequently there is no profitable deviation (region 2 or region 4). Companies make zero profits with or without competition on interest rates. In region 4, the equilibrium contracts are zero-interest contracts, because the consumer accepts two contracts in this region and pays the higher interest rate within the grace period.

• If $C\leq C^{\ast \ast },(l_{1}^{\ast },r_{1}^{\ast })$ and $(l_{2}^{\ast },r_{2}^{\ast })$ are then an equilibrium where $l_{1}^{\ast }+l_{2}^{\ast }\leq n^{0},r_{1}^{\ast }\geq 0,$ and $r_{2}^{\ast }\geq 0$. There is no profitable deviation, as the total credit limit to be offered to the consumer without triggering default is not more than the consumer’s income (region 3).

□

Proof (Proposition 2)

The naive hyperbolic consumer’s contracting-period self does not plan to borrow more than his income at any consumption period, but his period-one self ends up borrowing. The exponential consumer, on the other hand, correctly believes that he will not borrow on the credit card. But, in equilibrium, noncompetitive interest rates can be observed depending on the default risk. This follows from the fact that neither the exponential consumer nor the naive consumer’s contracting-period self are responsive to interest rates. Being unresponsive to interest rates neither hurts the exponential consumer nor benefits the companies since the consumer does not borrow anyway and consequently there are no profits from lending. But, when it comes to naive hyperbolic consumers, being unresponsive to interest rates hurts the consumer and benefits the companies as showed in 1. With probability p, the consumer is naive hyperbolic, and the company earns profit with the of probability $\frac {p}{2}$ by offering a positive interest rate and a high enough credit limit. With probability 1−p, the consumer is exponential, and the company does not earn a profit from him independent of the interest rate. As a result, the companies do not have an incentive to compete on the interest rates. □

Proof (Proposition 3)

If companies offer positive interest rates for one-period-loans, then the company with the higher interest for the one-period loan can profitably deviate by offering a smaller interest for the one-period-loan. Therefore, no equilibrium contract will have a positive one-period-loan interest. The consumer is not responsive to interest rates for two-period loans, the companies can safely offer a monopoly interest rate for two-period loans if the default risk is low enough. □

Proof (Proposition 4)

According to both the contracting-period self and the period-one self, the consumer’s utility when he reaches the period-two is given by

• $u(m-n_{1}+n_{2})+\widehat {\beta }u(m-n_{2})$ if n ₁≤m, and

• $u(n_{2})+\widehat {\beta }u(m-(n_{1}-m)r-n_{2})$ if n ₁>m.

I denote the optimal period-two borrowing as $n_{2}^{\ast }(n_{1}, \widehat {\beta })$.

According to the period-one self, the consumer’s utility when he reaches this period is:

• $u(m+{n_{1}^{1}})+\beta \left [ u(m-{n_{1}^{1}}+n_{2}^{\ast }({n_{1}^{1}}, \widehat {\beta }))+u(m-n_{2}^{\ast }({n_{1}^{1}},\widehat {\beta }))\right ]$ if ${n_{1}^{1}}\leq m,$ and

• $u(m+{n_{1}^{1}})+\beta \left [ u(n_{2}^{\ast }({n_{1}^{1}},\widehat {\beta } ))+u(m-({n_{1}^{1}}-m)(1+r)-n_{2}^{\ast }({n_{1}^{1}},\widehat {\beta }))\right ]$ if ${n_{1}^{1}}>m$.

I denote the optimal period-one borrowing according to the period-one self as $n_{1}^{1\ast }(\beta ,\widehat {\beta })$.

But, according to the contracting-period self, the consumer’s utility when he reaches the first period is:

• $u(m+{n_{1}^{0}})+\widehat {\beta }\left [ u(m-{n_{1}^{0}}+n_{2}^{\ast }({n_{1}^{0}},\widehat {\beta }))+u(m-n_{2}^{\ast }({n_{1}^{0}},\widehat {\beta })) \right ]$ if ${n_{1}^{0}}>m,$ and

• $u(m+{n_{1}^{0}})+\widehat {\beta }\left [ u(n_{2}^{\ast }({n_{1}^{0}}, \widehat {\beta }))+u(m-({n_{1}^{0}}-m)(1+r)-n_{2}^{\ast }({n_{1}^{0}},\widehat { \beta }))\right ]$ if ${n_{1}^{0}}\leq m$.

I denote the optimal period-one borrowing according to the contracting-period self as $n_{1}^{0\ast }(\widehat {\beta })$.

Let us consider the case when $\beta =\widehat {\beta }$ (sophisticated hyperbolic consumer). If $\widehat {\beta }=1,$ then ${n_{1}^{0}}={n_{1}^{1}}=0$. As $\widehat {\beta }$ decreases, ${n_{1}^{0}}={n_{1}^{1}}$ increase and there is a cutoff β ^∗ such that the ${n_{1}^{0}}={n_{1}^{1}}\leq m$ for $\widehat {\beta }\geq \beta ^{\ast }$ and ${n_{1}^{0}}={n_{1}^{1}}>m$ for $\widehat {\beta }<\beta ^{\ast }$. Now, $\widehat {\beta }\geq \beta ^{\ast }$ stays the same but β decreases starting from $\widehat {\beta }$. Decreasing β does not affect the optimal period-one borrowing according to the contracting-period self, but does increase the optimal period-one borrowing according to the period-one self. As $\beta \rightarrow 0, {n_{1}^{1}}\rightarrow \infty$. Therefore, there is a $(\beta _{r=1}^{\ast \ast }(\widehat {\beta }),\beta ^{\ast })$ such that ${n_{1}^{0}}\leq m$ and ${n_{1}^{1}}>m$ for $\beta <\beta _{r=1}^{\ast \ast }(\widehat {\beta })$ and $\widehat {\beta }>\beta ^{\ast }$. This means that there are partially hyperbolic consumers with a contracting-period self who believes he will not borrow more than his income and with a period-one self who ends up borrowing more than his income even at the highest interest rate of r=1. □