Effects of Jumps and Small Noise in High-Frequency Financial Econometrics

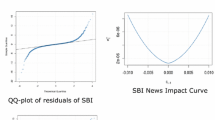
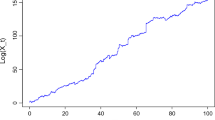
Abstract

Several new statistical procedures for high-frequency financial data analysis have been developed to estimate risk quantities and test the presence of jumps in the underlying continuous-time financial processes. Although the role of micro-market noise is important in high-frequency financial data, there are some basic questions on the effects of presence of noise and jump in the underlying stochastic processes. When there can be jumps and (micro-market) noise at the same time, it is not obvious whether the existing statistical methods are reliable for applications in actual data analysis. We investigate the misspecification effects of jumps and noise on some basic statistics and the testing procedures for jumps proposed by Ait-Sahalia and Jacod (Ann Stat 37–1:184–222 2009; 38–5:3093–3123 2010) as an illustration. We find that their first test (testing the presence of jumps as a null-hypothesis) is asymptotically robust in the small-noise asymptotic sense against possible misspecifications while their second test (testing no-jumps as a null-hypothesis) is quite sensitive to the presence of noise.

Appendices

Appendix 1 : Mathematical Derivations

In this “Appendix 1” we give some details of the proofs of mathematical results omitted in previous sections. Since the derivations are often slight modifications of Jacod and Protter (2012), and Ait-Sahalia and Jacod (2009), we refer to their book and some related papers for some mathematical details on the underlying arguments. We need some additional arguments because of the presence of noise in the following arguments.

Proof of Lemma 1

From (2.12) we represent that for $t_{i-1}^n<t\le t_i^n$ and $t_i^n-t_{i-1}^n=1/n \;(i=1,\ldots ,n),$

$$\begin{aligned} \sigma _t=\sigma (t_{i-1}^n)+\int _{t_{i-1}^n}^t\mu _s^{\sigma }ds + \int _{t_{i-1}^n}^t\omega _s^{\sigma }dB_s^{\sigma }\;\;. \end{aligned}$$

(6.2)

Then we have

$$\begin{aligned} \int _{t_{i-1}^n}^t\sigma _u du =\frac{1}{n}\sigma (t_{i-1}^n) +O_p\left( \frac{1}{n\sqrt{n}}\right) \; . \end{aligned}$$

(6.3)

It is because

$$\begin{aligned} \int _{t_{i-1}^n}^{t_i^n}\int _{t_{i-1}^n}^{u}\mu _s^{\sigma } ds du = O_p\left( \frac{1}{n^2}\right) \end{aligned}$$

(6.4)

due to the assumption that $\mu _s^{\sigma }$ is bounded and

$$\begin{aligned} \int _{t_{i-1}^n}^{t_i^n}\int _{t_{i-1}^n}^{u}\omega _s^{\sigma } dB_s^{\sigma }du = \int _{t_{i-1}^n}^{t_i^n}\left( \int _s^{t_{i}^n} du \right) \omega _s^{\sigma } dB_s^{\sigma }= O_p\left( \frac{1}{n\sqrt{n}}\right) \;\;. \end{aligned}$$

(6.5)

Then by using It${\hat{o}}^{'}$s Lemma

$$\begin{aligned}&\int _{t_{i-1}^n}^{t_i^n}\sigma _u^2 du -(t_i^n-t_{i-1}^n)\sigma ^2(t_{i-1}^n)\nonumber \\&\quad = \int _{t_{i-1}^n}^{t_i^n}\int _{t_{i-1}^n}^{u}\left[ 2\sigma _u\mu _s^{\sigma } +(\omega _s^{\sigma } )^2 ds \right] du + \int _{t_{i-1}^n}^{t_i^n}\left[ \int _{t_{i-1}^n}^u 2 \sigma _u\omega _s^{\sigma } dB_s^{\sigma }\right] du\;. \end{aligned}$$

(6.6)

Again by interchanging the integrations, using (6.3–6.5) and evaluating two terms separately, we find the result. $\square$

Proof of Lemma 2

We use the notation that $\omega ^{\sigma }(t_{i}^n)=\omega ^{\sigma }_s$ at $s=t_{i}^n$.

• (i) From (2.12) we find that for $t_{i-1}^n<t\le t_i^n$ and $t_i^n-t_{i-1}^n=1/n \;(i=1,\ldots ,n),$

  $$\begin{aligned} \sigma _t=\sigma (t_{i-1}^n)+\omega ^{\sigma }(t_{i-1}^n) [ B^{\sigma }(t) -B^{\sigma }(t_{i-1}^n) ] +o_p\left( \frac{1}{\sqrt{n}}\right) \; \end{aligned}$$

  (6.7)

  because

  $$\begin{aligned} \mathcal{E}[ \int _{t_{i-1}^n}^t (\omega ^{\sigma }(s)-\omega ^{\sigma }(t_{i-1}^n))^2ds ] =o\left( \frac{1}{n}\right) \;. \end{aligned}$$

  (6.8)

  Then we write

  $$\begin{aligned} X_i-X_{i-1}= & {} \int _{t_{i-1}^n}^{t_i^n}\sigma _s dB_s\\= & {} \int _{t_{i-1}^n}^{t_i^n} \left[ \sigma (t_{i-1}^n)+\omega ^{\sigma }(t_{i-1}^n) ( B^{\sigma }(s) -B^{\sigma }(t_{i-1}^n) ) \right] dB_s + o_p\left( \frac{1}{n}\right) \;, \end{aligned}$$

  where we denote $X_i=X(t_i^n)\;(i=1,\ldots ,n)$. Here we decompose for $s\ge t_{i-1}^n$

  $$\begin{aligned} B^{\sigma }(s) -B^{\sigma }(t_{i-1}^n) =\rho [B_s -B(t_{i-1}^n)]+ \sqrt{1-\rho ^2}[B_s^{*} -B^{*}(t_{i-1}^n)] \end{aligned}$$

  to make $B_s^{*}$ and $B_s$ being independent ($\rho$ is the correlation coefficient of $B_s$ and $B_s^{*}$), and we use the fact that

  $$\begin{aligned} \int _{t_{i-1}^n}^{t_i^n}[B_s-B(t_{i-1}^n)] dB_s =\frac{1}{2} \left[ (B_s-B(t_{i-1}^n))^2 -(s-t_{i-1}^n)^2\right] _{t_{i-1}^n}^{t_i^n}\;, \end{aligned}$$

  (6.9)

  which is $O_p(n^{-1})$. Hence we have (2.15).

• (ii) We write $(X_i-X_{i-1})^2=X_i^2-X_{i-1}^2-2X_{i-1}(X_i-X_{i-1})$ and apply Ito’s Lemma to $X_i^2$. Then we have

  $$\begin{aligned} (X_i-X_{i-1})^2= & {} \int _{t_{i-1}^n}^{t_i^n}2X_s dX_s +\int _{t_{i-1}^n}^{t_i^n}d[X_s,X_s] -2X_{i-1}(X_i-X_{i-1})\\= & {} \int _{t_{i-1}^n}^{t_i^n}2(X_s-X_{i-1}) dX_s +[X_i,X_i]-[X_{i-1},X_{i-1}]\;, \end{aligned}$$

  where $[X_i,X_i]$ is the quadratic variation of $X_i\;(i=1,\ldots ,n)$ with the notation $[X_0,X_0]=0$. Since

  $$\begin{aligned} {[}X_i,X_i]-[X_{i-1},X_{i-1}] =\int _{t_{i-1}^n}^{t_i^n}\sigma _s^2 ds\;, \end{aligned}$$

  (6.10)

  we have

  $$\begin{aligned} \sum _{i=1}^n(X_i-X_{i-1})^2 -\int _{t_{i-1}^n}^{t_i^n}\sigma _s^2 ds =\sum _{i=1}^n\int _{t_{i-1}^n}^{t_i^n}2(X_s-X_{i-1}) dX_s \;. \end{aligned}$$

  (6.11)

  Because the right-hand side is a martingale,

  $$\begin{aligned} \left[ \int _{t_{i-1}^n}^{t_i^n}(X_s-X_{i-1}) dX_s , \int _{t_{i-1}^n}^{t_i^n}(X_s-X_{i-1}) dX_s \right] =\int _{t_{i-1}^n}^{t_i^n}(X_s-X_{i-1})^2 \sigma _s^2 ds\;, \end{aligned}$$

  and $(X_s-X_{i-1})^2=O_p(n^{-1}) ,$ we have the result of (2.16).

$\square$

Proof of Theorem 1

We use the fact that the limiting random variables of $U_{in}\;(i=1,2,3)$ follow the ($\mathcal{F}-$conditionally) Gaussian distributions, which are mutually independent, by using the central limit theorem. Because we can apply the arguments in Jacod and Protter (2012), we have the stable convergence of the underlying random variables and then $U_i\;(i=1,2,3)$ are $\mathcal{F}-$conditionally independent. Since $\mathbf{Var}[Z_i^2-1]=2 ,$ we find that

$$\begin{aligned} \mathbf{Var} [ U_{1n}]\sim & {} 2 \int _0^1\sigma _s^4ds\;, \end{aligned}$$

(6.12)

$$\begin{aligned} \mathbf{Var} [ U_{2n}]\sim & {} 8c \int _0^1\sigma _s^2ds\;, \end{aligned}$$

(6.13)

Also the asymptotic variance of the third term $U_{3n}$ is approximately equal to $(1/n)\mathcal{E}\left[ 4\sum _{i=2}^n(v_i^2-1)^2+4\sum _{i=2}^nv_{i}^2v_{i-1}^2\right]$. It is because we use a simple relation

$$\begin{aligned} \left[ \sum _{i=1}^n(v_i-v_{i-1})^2-2n\right] ^2\sim & {} \left[ 2\sum _{i=1}^n(v_i^2-1)-2\sum _{i=1}^nv_iv_{i-1}\right] ^2\\= & {} 4\left[ \sum _{i=1}^n(v_i^2-1)^2+\sum _{i=1}^nv_i^2v_{i-1}^2 -2\sum _{i=1}^n(v_i^2-1)\sum _{i=1}^nv_iv_{i-1}\right] \end{aligned}$$

and $4[ \mathcal{E}(v_i^4)-(\mathcal{E}(v_i^2))^2)]+4(\mathcal{E}(v_i^2))^2) =4[2+\kappa _4]+4$. Thus we find that

$$\begin{aligned} \mathbf{Var} [ U_{3n}] \sim [ 12+4\kappa _4 ]c^2\;. \end{aligned}$$

(6.14)

Since $U_i\;(i=1,2,3)$ are $\mathcal{F}-$conditionally uncorrelated, they are $\mathcal{F}-$conditionally independent. By applying the stable convergence theorem and the central limit theorem (CLT), we have the desired result. $\square$

Derivations of (2.24–2.26) We use the relation that

$$\begin{aligned} \sum _{i=1}^n(X_i-X_{i-1})^2 =\sum _{i=1}^n \left[ \int _{t_{i-1}^n}^{t_i^n}\mu _s ds + \int _{t_{i-1}^n}^{t_i^n} \sigma _s dB_s + \sum _{t_{i-1}^n<s\le t_i^n}\Delta X_s \right] ^2 \;. \end{aligned}$$

We note that the last term does make sense because we have assumed the boundedness of jumps and $t_i^n-t_{i-1}^n=1/n\;(i=1,\ldots ,n)$. Since the effect of the drift term is $o_p(1)$, which is stochastically negligible, by using the standard result on semi-martingales we have

$$\begin{aligned} \sum _{i=1}^n(X_i-X_{i-1})^2 \mathop {\longrightarrow }\limits ^{p} \int _0^1 \sigma _s^2 ds +\sum _{0<s\le 1} (\Delta X_s)^2\;. \end{aligned}$$

(6.15)

Then we have (2.24) by using LLN (the law of large numbers) to $\left( 1/n)\sum _{i=1}^n(v_i-v_{i-1}\right) ^2$.

Let

$$\begin{aligned} Z_n= \sqrt{n}\left[ \sum _{i=1}^n(X_i-X_{i-1})^2 -\left( \int _0^1 \sigma _s^2 ds +\sum _{0<s\le 1} (\Delta X_s)^2\right) \right] \;, \end{aligned}$$

(6.16)

which is approximately equal to

$$\begin{aligned}&\sqrt{n} \left( \sum _{i=1}^n\left[ \sigma (t_{i-1}^n)(B(t_i^n)-B(t_{i-1}^n)) +\sum _{t_{i-1}^n<s\le t_i^n}\Delta X_s \right] ^2 \right. \nonumber \\&\left. \qquad -\left[ \int _0^1 \sigma _s^2 ds +\sum _{0<s\le 1} (\Delta X_s)^2 \right] \right) \;. \end{aligned}$$

(6.17)

Then the additional term of the constant order in probability from (6.16) is given by

$$\begin{aligned} 2 \sum _{i=1}^n\left[ \sum _{t_{i-1}^n<s\le t_i^n}\Delta X_s\right] \sqrt{n} \sigma (t_{i-1}^n)(B(t_i^n)-B(t_{i-1}^n ) )\;. \end{aligned}$$

(6.18)

The additional cross product of jump term and the noise term from the second term of $V_n(2),$ i.e. $2\epsilon _n \sum _{i=2}^n(X_i-X_{i-1})(v_i-v_{i-1})$ is given by

$$\begin{aligned} \sqrt{n}\times \frac{2\sqrt{c}}{\sqrt{n}} \left[ \sum _{i=1}^n\sum _{t_{i-1}^n<s\le t_i^n}\Delta X_s\right] (v_i-v_{i-1})\;. \end{aligned}$$

(6.19)

If we assume the Gaussianity on $v_i\;(i=1,\ldots ,n),$ we have the $\mathcal{F}-$conditional Gaussianity.

The remaining arguments of the stable convergence are followed by the corresponding ones of Jacod and Protter (2012). $\square$

Proof of Lemma 3

Let $Y(t)=[X(t)-X(t_{i-1}^n)]^p$ for $p\ge 2$ and we apply It${\hat{o}}^{'}$s lemma for the general Ito semi-martingale to Y(t). (Theorem 32 of Protter (2003), for instance.) For $p\ge 3$, (3.2) is $o_p(1)$.

Then we have

$$\begin{aligned}&(X_i-X_{i-1})^p-\left[ \sum _{t_{i-1}^n\le s\le t_i^n} (\Delta X_s)^p\right] \\&\quad = \int _{t_{i-1}^n}^{t_i^n} p(X_{s-}-X_{i-1})^{p-1}dX_s +\int _{t_{i-1}^n}^{t_i^n} \frac{p(p-1)}{2}(X_{s-}-X_{i-1})^{p-2} d [X_s,X_s]^c \\&\qquad +\,\sum _{t_{i-1}^n \le s< t_i^n} \left[ (X_s-X_{i-1})^p-(X_{s-}-X_{i-1})^p -p(X_{s-}-X_{i-1})^{p-1} \Delta X_s \right] \\&\qquad -\, \sum _{t_{i-1}^n\le s<t_i^n} \left[ (X_s-X_{i-1})-(X_{s-}-X_{i-1})\right] ^p\;\;. \end{aligned}$$

In the above derivation we use the relation $(X_s-X_{i-1})^p-(X_{s-}-X_{i-1})^p =[\Delta +(X_{s-}-X_{i-1})]^p-(X_{s-}-X_{i-1})^p ,$ which equal to $\sum _{j=2}^{p-1} {}_p C_j (X_{s-}-X_{i-1})^{p-j}(\Delta X_s)^j$. Then by taking the summation with respect to $i=1,\ldots ,n,$ we have the result. $\square$

Proof of Theorem 2

By using Lemma 3, we have

$$\begin{aligned} \sum _{i=1}^n(X_i-X_{i-1})^4 \mathop {\longrightarrow }\limits ^{p} \sum _{0\le s <1} (\Delta X_s)^4\;. \end{aligned}$$

(6.20)

By using the similar arguments as (6.15) and (6.16), we can express

$$\begin{aligned}&\sqrt{n}\left[ \sum _{i=1}^n(X_i-X_{i-1})^4 - \sum _{0\le s<1} (\Delta X_s)^4 \right] \nonumber \\&\quad = \frac{4}{\sqrt{n}}\sum _{i=1}^n\sum _{t_{i-1}^n\le s < t_i^n} \sigma ({\tau }_{i-1}^n) Z({\tau }_i^n) (\Delta X_s)^3 +o_p(\frac{1}{\sqrt{n}}) \;, \end{aligned}$$

(6.21)

where $\tau _i^n\;(i=1,2,\ldots )$ correspond to the stopping times for jumps of the It${\hat{o}}$ semimartingale (and if there were no jumps in $t_{i-1}^n\le s < t_i^n,$ they do not appear). The remaining term in the decomposition we need to evaluate is

$$\begin{aligned} U_{2n}= & {} \frac{4\sqrt{c}}{\sqrt{n}}\sum _{i=1}^n (X_i-X_{i-1})^3 (v_i-v_{i-1})\nonumber \\= & {} \frac{4\sqrt{c}}{\sqrt{n}}\sum _{0\le s \le 1} (\Delta X_s)^3 [ v({\tau }_i^n)-v({\tau }_{i-1}^n) ]+O_p(\frac{1}{\sqrt{n}}) \;, \end{aligned}$$

(6.22)

where

we have used the notation $\Delta _n=1/n ,$ $\Delta _i^n X=X_i-X_{i-1}\;(i=2,\ldots ,n)$. We set

$$\begin{aligned} U_{2n}^{'}= & {} \sqrt{\epsilon _n} \left[ \sum _{i=1}^n(\Delta _i^nX)^3v_i-\sum _{i=1}^n(\Delta _i^nX)^3v_{i-1} \right] \\= & {} \sqrt{\epsilon _n} \left[ \sum _{i=1}^{n-1} [ (\Delta _i^nX)^3-(\Delta _{i+1}^nX)^3 ]v_i +(\Delta _n^nX)^3v_n-(\Delta _1^nX)^3v_0 \right] \;. \end{aligned}$$

Then by using the Cauchy-Swartz inequality, we evaluate the conditional expectation $\mathcal{E}[ (U_{2n}^{'})^2\vert X],$ which is given by

$$\begin{aligned} \mathcal{E}[ (U_{2n}^{'})^2\vert X ]= & {} \epsilon _n \left[ \sum _{i=1}^{n-1}[(\Delta _i^nX)^3-(\Delta _{i+1}^nX)^3]^2 + (\Delta _n^nX)^6 (\Delta _1^nX)^6 \right] \\= & {} 2\epsilon _n \left[ \sum _{i=1}^n(\Delta _i^nX)^6 -\sum _{i=1}^{n-1}(\Delta _i^nX)^3(\Delta _{i+1}^nX)^3 \right] \\\le & {} 4\epsilon _n \sum _{i=1}^n(\Delta _i^nX)^6\;. \end{aligned}$$

We notice that $\sum _{i=1}^n(\Delta _i^nX)^6=O_p(1) ,$ $\sum _{i=1}^{n-1}(\Delta _i^nX)^3(\Delta _{i+1}^n X)^3=o_p(1) ,$ and then we have $\mathcal{E}[(U_{2n}^{'})^2]=O(n^{-1})$. In these relations the most important step is to show that $\sum _{i=1}^{n-1}(\Delta _i^nX)^3(\Delta _{i+1}^n X)^3=o_p(1) ,$ which can be proven by applying Theorem 8.2.1 of Jacod and Protter (2012). We set $F(x_1,x_2)=x_1^3x_2^3, f_1(x)=F(x_1,0), f_2(x)=F(0,x_2)$ and $f_1*\mu _1+f_2*\mu _1=0$ (here $\mu _1$ is the associated jump measure) in their notation.

Then we have

$$\begin{aligned} \mathcal{E}[ (\Delta _n^{-1/2}U_{2n}^{'})^2\vert X] \mathop {\longrightarrow }\limits ^{p} 2c \mathcal{E}[v_1^2]\sum _{0<s\le 1 }(\Delta X_s)^6\;. \end{aligned}$$

(6.23)

Finally, since $U_{1n}$ and $U_{2n}$ are $\mathcal{F}-$conditionally uncorrelated, they are $\mathcal{F}-$conditionally independent. By using the stable convergence arguments in Jacod and Protter (2012), we have the desired result. $\square$

Proof of Theorem 3

We follow Ait-Sahalia and Jacod (2009) for basic method of their proof, but we need some additional arguments because we have the effects of noise as well as jumps in the underlying processes.

[Part 1]: We apply Lemma 3 with a general k($\;k\ge 1$) and $p\ge 4$ to $[ \Delta _i^n Y(k)]^p,$ and then we can express that

$$\begin{aligned}&\sum _{i=1}^{[n/k]}[Y({ik\Delta _n})-Y({(i-1)k\Delta _n})]^p \\&\quad = \sum _{i=1}^{[n/k]}[X({ik\Delta _n})-X({(i-1)k\Delta _n})]^p \\&\qquad +\, p\epsilon _n \sum _{i=1}^{[n/2]}[X({ik\Delta _n})-X({(i-1)k\Delta _n})]^{p-1} [v(ik\Delta _n)-v({(i-1)k\Delta _n})] \\&\qquad +\,o_p(\frac{1}{\sqrt{n}}) \\&\quad = \sum _{0\le s<1}(\Delta X_s)^p + p\sqrt{\frac{k}{n}} [ \sum _{i=1}^{[n/k]}\sum _{ t_{(i-1)k}^n\le s< t_{ik}^n } \sigma ({t_{(i-1)k}^n)} Z_i^n(k)(\Delta X_s)^{p-1} ] \\&\qquad +\,\frac{ p\sqrt{c}}{\sqrt{n}} [\sum _{i=1}^{[n/k]} \sum _{t_{(i-1)k}^n\le s < t_{ik}^n } (\Delta X_s)^{p-1}[v(ik\Delta _n)-v({(i-1)k\Delta _n}) ] ] +o_p(\frac{1}{\sqrt{n}})\;, \end{aligned}$$

where we denote that $Z_i^n(k)=\sqrt{n/k} \left[ B(t_{ik}^n)-B(t_{(i-1)k}^n)\right]$ and then $Z_i^n=Z_i^n(1)$ in (2.7).

For the ease of exposition we shall use the notations that $\Delta _i^nX(k)=X(ik\Delta _n)-X((i-1)k\Delta _n) ,$ $\Delta _i^nB(k)=B(ik\Delta _n)-B((i-1)k\Delta _n) ,$ and $\Delta _i^nv(k)=v(ik\Delta _n)-v((i-1)k\Delta _n)=v_{ik}-v_{(i-1)k}$ in the following analysis.

By taking the $p-$the realized variation with $k\;(k\ge 2)$ and the $p-$the realized variation with $k\;(k=1)$ for $p=4 ,$ we decompose

$$\begin{aligned} \sqrt{n} \left[ \sum _{i=1}^{[n/k]} [Y({ik\Delta _n})-Y({(i-1)k\Delta _n})]^4 - \sum _{i=1}^{n}[Y({i\Delta _n})-Y({(i-1)\Delta _n})]^4\right] \nonumber \\ \end{aligned}$$

(6.24)

into four terms except other negligible terms asymptotically, which are given by

$$\begin{aligned} W_{1n}= & {} 4\sum _{i=1}^{[n/k]}\sigma ({t_{(i-1)k}^n}) [ \sqrt{k} Z_i^n(k) \sum _{\tau _{(i-1)k}^n\le s<\tau _{ik}^n } (\Delta X_s)^3]\;, \\ W_{2n}= & {} -4\sum _{i=1}^{n}\sigma (t_{(i-1)}^n) [ Z_i^n(1) \sum _{\tau _{(i-1)}^n\le s<\tau _{i}^n}(\Delta X_s)^3]\;, \\ W_{3n}= & {} 4 \sqrt{c}\sum _{i=1}^{[n/k]}\sum _{t_{(i-1)k}^n\le s <t_{ik}^n } (X({ik\Delta _n})-X({(i-1)k\Delta _n})]^3 \Delta _i^n v(k) \end{aligned}$$

and

$$\begin{aligned} W_{4n}=-4\sqrt{c} \sum _{i=1}^{n}\sum _{t_{(i-1)}^n \le s <t_{i}^n}[X({i\Delta _n})-X({(i-1)\Delta _n})]^3 \Delta _i^n v(k)\;, \end{aligned}$$

(6.25)

respectively, where

$Z_i^n(k)\;(i=1,\ldots ,n)$ are Gaussian random variables with N(0, 1).

In order to obtain the asymptotic distribution of (6.24), we need to evaluate the asymptotic variances of $W_{1n}+W_{2n}$ and $W_{3n}+W_{4n},$ respectively. Since the asymptotic covariance of $W_{1n}+W_{2n}$ and $W_{3n}+W_{4n}$ are asymptotically negligible, we need to evaluate the variance of $W_{1n}+W_{2n}$ (and that of $W_{3n}+W_{4n}$). For this purpose we decompose $W_{1n}+W_{2n}=4 \sum _{i=1}^{[n/k]}U_{i,k}^n ,$ where we further decompose $U_{i,k}^{(n)}=U_{i,k}^n(1)-U_{i,k}^n(2)$ as

$$\begin{aligned} U_{i,k}^n(1)= & {} \sigma (t_{(i-1)k}^n) \sum _{t_{(i-1)k}^n\le s<t_{ik}^n } (\Delta X_s)^{p-1} \sum _{l=0}^{k-1} [B(t_{ (i-l)k}^n)- B(t_{(i-1)k-1}) ],\\ U_{i,k}^n(2)= & {} \sum _{l=0}^{k-1} \sigma (t_{(i-1))k+l}^n) \sum _{t_{(i-1)k+l}^n\le s <t_{(i-1)k+l+1}^n } (\Delta X_s)^{p-1} [B(t_{(i-1)k+l+1}^n)\\&- B(t_{(i-l)k+l}^n)] . \end{aligned}$$

Then it is straightforward to evaluate that for $p=4$

$$\begin{aligned} \mathbf{Var}[U_{i,k}^n(1)\vert \mathcal{F}_{(i-1)k}]\sim & {} \frac{k}{n}[\sigma (t_{(i-1)k}^n)]^2 [\sum _{t_{(i-1)k}^n\le s<t_{ik}^n } (\Delta X_s)^{6}],\\ \mathbf{Var}[U_{i,k}^n(2)\vert \mathcal{F}_{(i-1)k} ]\sim & {} \frac{1}{n} \sum _{l=0}^{k-1} [ \sigma (t_{(i-1)k+l}^n)]^2 [\sum _{t_{(i-1)k+l}^n\le s<t_{(i-1)k+l+1}^n } (\Delta X_s)^{6}],\\ \mathbf{Cov}[U_{i,k}^n(1) U_{i,k}^n(2)\vert \mathcal{F}_{(i-1)k}]\sim & {} \frac{1}{n} \sum _{l=0}^{k-1} \sigma (t_{(i-1)k}^n)\sigma (t_{(i-1)k+l}^n) \sum _{t_{(i-1)k+l}^n\le s <t_{(i-1)k+l+1}^n } (\Delta X_s)^{6}, \end{aligned}$$

where we have used the notation that $\mathcal{F}_{(i-1)k}$ is the $\sigma -$field given at $t=(i-1)k\Delta _n$ in the discretization of the underlying continuous time processes.

Because we have assumed the volatility process as (2.12), we find that

$$\begin{aligned} \mathbf{Var}[U_{i,k}^n\vert \mathcal{F}_{(i-1)k}]= & {} \mathbf{Var}[U_{i,k}^n(1)\vert \mathcal{F}_{(i-1)k}] +\mathbf{Var}[U_{i,k}^n(2)\vert \mathcal{F}_{(i-1)k}]\\&-\,2\mathbf{Cov}[U_{i,k}^n(1),U_{i,k}^n(2)\vert \mathcal{F}_{(i-1)k}] \end{aligned}$$

is approximately

$$\begin{aligned} \mathbf{Var}[U_{i,k}^{n,*}\vert \mathcal{F}_{(i-1)k}] = [\frac{k-1}{n}][ \sigma (t_{(i-1)k}^n)]^2 [\sum _{ t_{(i-1)k}^n\le s <t_{ik}^n } (\Delta X_s)^{6} ]\;. \end{aligned}$$

(6.26)

By taking the summation with respect to $i=1,\ldots , [n/k],$ we can obtain (4.5). By applying the similar arguments to $W_{3n}+W_{4n}$, we also obtain (4.6). Since the remaining arguments are similar to the proof of Theorem 2 as we have done in the derivations of Theorem 2, we have the first part of Theorem 3.

[Part 2$]\;:\;$ We re-write $V_n(4,k),$ which can be decomposed into five terms as

$$\begin{aligned} V_n(4,k)= & {} \sum _{i=1}^{[n/k]} ( Y({ik\Delta _n})-Y({(i-1)k\Delta _n}) )^4 \\= & {} \sum _{i=1}^{[n/k]} ( X({ik\Delta _n})-X({(i-1)k\Delta _n}) )^4 \\&+\,4 \epsilon _n\sum _{i=1}^{[n/k]} (X({ik\Delta _n})-X({(i-1)k\Delta _n}))^3 (v_{ik}-v_{(i-1)k}) \\&+\,6 \epsilon _n^2\sum _{i=1}^{[n/k]} (X({ik\Delta _n})-X({(i-1)k\Delta _n}))^2 (v_{ik}-v_{(i-1)k})^2\\&+\,4 \epsilon _n^3\sum _{i=1}^{[n/k]} (X({ik\Delta _n})-X({(i-1)k\Delta _n})) (v_{ik}-v_{(i-1)k})^3 \\&+\, \epsilon _n^4\sum _{i=1}^{[n/k]} (v_{ik}-v_{(i-1)k})^4 \\= & {} (I) +(II) +(III)+(IV)+(V)\;\;(\hbox {say}). \end{aligned}$$

Then we evaluate the stochastic order of each terms and we find that $(I)=O_p(n^{-1}) ,$ $(II) = (F_{2n}, say) =O_p(n^{-3/2}) ,$ $(III)=O_p(n^{-1}) ,$ $(IV) = (F_{4n}, say) =O_p(n^{-3/2})$ and $(V)=O_p(n^{-1})$. Because

$$\begin{aligned} n\times & {} (I)\sim k(k/n)\sum _{i=1}^{[n/k]}[\Delta _i^nX(k)/\sqrt{k\Delta _n}]^4,\\ n\times & {} (III)\sim n\times 6(c/n) \sum _{i=1}^{[n/k]}[\Delta _i^nX(k)/\sqrt{k\Delta _n}]^2[\Delta _iv(k)]^2 \end{aligned}$$

and

$$\begin{aligned} n\times (V)\sim n(c/n)^2\sum _{i=1}^{[n/k]}[\Delta _iv(k)]^2 , \end{aligned}$$

we can obtain the limiting random variable as (4.8).

Then we set

$$\begin{aligned} F_{1n}= & {} n\times (I) - k m_4 \int _0^1\sigma _s^4ds\;, \end{aligned}$$

(6.27)

$$\begin{aligned} F_{3n}= & {} n\times (III) - 6c \times 2\int _0^1\sigma _s^2ds\;, \end{aligned}$$

(6.28)

and

$$\begin{aligned} F_{5n}=n\times (V) - \frac{c^2}{k} \times \mathcal{E}[(\Delta _i v(k))^4]\;, \end{aligned}$$

(6.29)

which are $O_p(n^{-1/2})$.

For the ease of expositions we shall use the notations that $U_{in}$ correspond to $F_{in}$ for $i=2,3,4$ except constant terms. Then we need to evaluate the limiting random variables of $U_{in}\;(i=2,\ldots ,4)$ and the limiting random variables of $\sqrt{n}\times F_{1n},$ $n\sqrt{n}\times (II),$ $\sqrt{n}\times F_{3n},$ $n\sqrt{n}\times (IV)$ and $\sqrt{n}\times F_{5n} ,$ separately.

The explicit evaluations of these terms are straightforward, but they are a little bit tedious especially for $F_{3n}$. Since careful calculations at several places are needed, we give some details of those points.

First, it is straightford to find that the limiting random variable of $\mathbf{Var}[ \sqrt{n} F_{1n}]$ as $\mathcal{E}[(U_1^{*}(4,k))^4\vert \mathcal{F}] \sim k^3(m_8-m_4^2)\int _0^1\sigma _s^8ds$ in (4.10).

Second, let

$$\begin{aligned} U_{2n}= & {} k^{3/2}\Delta _n^2\sum _{i=1}^{[n/k]}[\frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}}]^3 [\Delta _i v(k)]\nonumber \\= & {} k^{3/2}\Delta _n^2\sum _{i=1}^{[n/k]}[ (\frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}})^3 -(\frac{\Delta _{i+1}^n X(k)}{\sqrt{k\Delta _n}})^3][\Delta _i v(k)] \nonumber \\&+\,k^{3/2}\Delta _n^2 [(\frac{\Delta _{n}^n X(k)}{\sqrt{k\Delta _n}})^3 v_{n} -(\frac{\Delta _1^n X(k)}{\sqrt{k\Delta _n}})^3v_{0} ], \end{aligned}$$

(6.30)

Then we have the conditional expectation given X as

$$\begin{aligned}&\Delta _n^{-3}\mathcal{E}[ (U_{2n})^2\vert X]\\&\quad = k^{3}\Delta _n\sum _{i=1}^{[n/k]} [(\frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}})^3 -(\frac{\Delta _{i+1}^n X(k)}{\sqrt{k\Delta _n}})^3]^2\\&\qquad +\, k^{3}\Delta _n [(\frac{\Delta _{[n/k]} X(k)}{\sqrt{k\Delta _n}})^6 + (\frac{\Delta _{1}^n X(k)}{\sqrt{k\Delta _n}})^6]\\&\quad = 2k^2 \left[ k\Delta _n \sum _{i=1}^{[n/k]} (\frac{\Delta _{n/k} X(k)}{\sqrt{k\Delta _n}} )^6 -k\Delta _n \sum _{i=1}^{[n/k]}(\frac{ \Delta _{i}^n X(k)}{\sqrt{k\Delta _n}})^3 (\frac{\Delta _{i+1}^n X(k)}{\sqrt{k\Delta _n}})^3 \right] , \end{aligned}$$

which converges in probability to $2k^2\int _0^1\sigma _s^6ds$ because the second term is stochastically negligible. By multiplying $4^3c$ to $\mathbf{Var}[U_{2n}],$ we have (4.11) as the second term. Third, we set

$$\begin{aligned} U_{3n}= k\Delta _n^2 \sum _{i=1}^{[n/k]}[\frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}}]^2 [\Delta _i v(k)]^2\;, \end{aligned}$$

(6.31)

which is the order $O_p(\Delta _n)\;(=O_p(n^{-1}))$. (The explicit calculation of the limiting random variables of $U_{3n}$ involves some complications because of the evaluation of the associated discretization errors and auto-correlation structures.) For this evaluation we define a sequence of random variables $W_n=nU_{3n}-2\mathcal{E}[v_1^2]m_2\int _0^1\sigma _s^2d;,$ which can be re-written as

$$\begin{aligned} W_n= & {} k\Delta _{n}\left[ \sum _{i=1}^{[n/k]-1} \left( (\Delta _{i}^{n}X(k)/\sqrt{k\Delta _{n}})^{2} +(\Delta _{i+1}^{n}X(k)/\sqrt{k\Delta _{n}})^{2}\right) v_{ik}^{2}\right] \\&\quad -\, 2\mathcal{E}[v_{1}^{2}]m_{2}\int _{0}^{1}\sigma _{s}^{2}ds \\&\quad -\, 2k\Delta _{n}\sum _{i=1}^{[n/k]-1}(\Delta _{i}^{n}X(k)/\sqrt{k\Delta _{n}})^{2} v_{ik}v_{(i-1)k} + o_{p}(\frac{1}{\sqrt{n}})\;, \end{aligned}$$

where we have used the relation

$$\begin{aligned} \int _{0}^{1}\sigma _{s}^{2}ds = \frac{k}{n}\sum _{i=1}^{[n/k]}\sigma _{t_{(i-1)k}}^{2} + O_{p}(\frac{1}{n}) \;. \end{aligned}$$

We further decompose $W_{n}$ as

$$\begin{aligned} W_{n}= & {} \frac{k}{n}\left[ \sum _{i=1}^{[n/k]-1} (\Delta _{i}^{n}X(k)/\sqrt{k\Delta _{n}})^{2}(v_{ik}^{2} - \mathcal{E}[v_{ik}^{2}])\right] \\&\quad +\, \frac{k}{n}\left[ \sum _{i=1}^{[n/k]-1} (\Delta _{i+1}^{n}X(k)/\sqrt{k\Delta _{n}})^{2} (v_{ik}^{2}- \mathcal{E}[v_{ik}^{2}])\right] \\&\quad +\, \mathcal{E}[v_{1}^{2}]\frac{k}{n} \left[ \sum _{i=1}^{[n/k]-1}\left( (\Delta _{i}^{n}X(k)/\sqrt{k\Delta _{n}})^{2} +(\Delta _{i+1}^{n}X(k)/\sqrt{k\Delta _{n}})^{2} - 2\sigma _{t_{k(i-1)}}^{2}\right) \right] \\&\quad -\,2\frac{k}{n}\left[ \sum _{i=1}^{[n/k]-1}(\Delta _{i}^{n}X(k) /\sqrt{k\Delta _{n}})^{2}v_{ik}v_{(i-1)k}\right] + o_{p}(\frac{1}{\sqrt{n}})\\= & {} {W}_I + W_{II} + W_{III} + W_{IV} + o_{p}(\frac{1}{\sqrt{n}})\quad (say). \end{aligned}$$

Then we shall evaluate the asymptotic variances and covariances of each terms in the following analysis.

• (i) Evaluation of $W_{I}$

  We set

  $$\begin{aligned} \xi _{i}^{n,\mathbf {I}} = {k \over n}\left( {\Delta _{i}^{n}X(k) \over \sqrt{k\Delta _{n}}}\right) ^{2} [v_{ik}^2 - \mathcal{E}(v_{ik}^{2})]\;, \end{aligned}$$

  and

  $$\begin{aligned} \widetilde{\xi _{i}}^{n,\mathbf {I}} = {k \over n}\sigma _{(i-1)k}^{2}(Z_{i}^n(k))^{2}[v_{ik}^2 - \mathcal{E}(v_{ik}^{2})]\;. \end{aligned}$$

  Since $(\Delta _{i}^{n}X(k)/\sqrt{k\Delta _{n}})^{2} = \sigma _{(i-1)k}^{2}(Z_{i}^n(k))^{2} + O_{p}(\frac{1}{\sqrt{n}})$ by the result of Lemma 2, we find that $n\sum _{i=1}^{[n/k]-1}((\xi _{i}^{n,\mathbf {I}})^{2} - (\widetilde{\xi }_{i}^{n,\mathbf {I}})^{2})$ is asymptotically negligible. Therefore we can replace $\xi _{i}^{n,\mathbf {I}}$ with $\widetilde{\xi }_{i}^{n,\mathbf {I}}$ in $W_{n}$. Moreover,

  $$\begin{aligned} k\times \frac{1}{(\frac{k}{n})} \sum _{i=1}^{[n/k]-1}\mathcal{E}[(\widetilde{\xi }_{i}^{n,\mathbf {I}})^{2}|\mathcal {F}_{k(i-1)}]= & {} k\mathbf{Var}[v_{1}^{2}]m_{4} \left( k\Delta _{n}\sum _{i=1}^{[n/k]-1}\sigma _{(i-1)k}^{4}\right) \\&\mathop {\longrightarrow }\limits ^{p} k\mathbf{Var}[v_{1}^{2}]m_{4}\int _{0}^{1}\sigma _{s}^{4}ds\; ( \equiv V_{\mathbf{I}}=V_{\mathbf{II}})\;. \end{aligned}$$

  Hence we have the stable convergence as

  $$\begin{aligned} \sqrt{n} \times W_{I} \mathop {\longrightarrow }\limits ^{\mathcal {L}-s} \mathbf{N}\left( 0,k\mathbf{Var}[v_{1}^{2}]m_{4}\int _{0}^{1}\sigma _{s}^{4}ds\right) \,. \end{aligned}$$

  (6.32)

• (ii) Evaluation of $W_{II}$

  We set

  $$\begin{aligned} \xi _{i}^{n,\mathbf{II}} = {k \over n}\left( {\Delta _{i+1}^{n}X(k) \over \sqrt{k\Delta _{n}}}\right) ^{2} [v_{ik}^2 - \mathcal{E}(v_{ik}^{2})], \end{aligned}$$

  and

  $$\begin{aligned} \widetilde{\xi _{i}}^{n,\mathbf{II}} = {k \over n}\sigma _{(i-1)k}^{2}(Z_{i+1}^n(k))^{2} (v_{ik}^2 - \mathcal{E}[v_{ik}^{2}])\;. \end{aligned}$$

  By using Lemma 1, we can evaluate $\mathbf {II}$ in the same way as $W_I$.

• (iii) Evaluation of $W_{III}$

  We use the fact that $\sqrt{n} W_{III}$ is approximately equivalent to

  $$\begin{aligned} 2\sqrt{k}\times \frac{1}{\sqrt{\frac{n}{k}}} \sum _{i=1}^{[\frac{n}{k}]} \left[ \left( \frac{\Delta _i^n X(k)}{ k\Delta _n} \right) ^2 - \sigma ^2_{t_{k(i-1)}} \right] \;. \end{aligned}$$

  Then by applying CLT, we have that $\sqrt{n}\times W_{III}\mathop {\longrightarrow }\limits ^{\mathcal {L}-s} \mathbf{N}\left( 0,V_{\mathbf{III}}\right) \; ,$ where $V_{ \mathbf{III}} = 4k (m_{4}-m_{2}^{2})\int _{0}^{1}\sigma _{s}^{4}ds$.

• (iv) Evaluation of $W_{IV}$

  Let

  $$\begin{aligned} \xi _{i}^{n,\mathbf{IV}} = {k \over n}\left( {\Delta _{i}^{n}X(k) \over \sqrt{k\Delta _{n}}}\right) ^{2} v_{ik}v_{(i-1)k} ,\; \widetilde{\xi _{i}}^{n, \mathbf{IV}} = {k \over n}\sigma _{(i-1)k}^{2}(Z_{i}^n(k))^{2}v_{ik}v_{(i-1)k}\;. \end{aligned}$$

  By using the similar argument of the evaluation of $W_I$, we obtain,

  $$\begin{aligned} 4 n\sum _{i=1}^{[n/k]-1}\mathcal{E} [(\widetilde{\xi }_{i}^{n,\mathbf{IV}})^{2}|\mathcal {F}_{k(i-1)}]= & {} 4k\mathcal{E}[v_{1}^{2}]^{2}m_{4} \left( k\Delta _{n}\sum _{i=1}^{[n/k]-1}\sigma _{(i-1)k}^{4}\right) \\&\mathop {\longrightarrow }\limits ^{p} 4k m_{4}\int _{0}^{1}\sigma _{s}^{4}ds\; ( \equiv V_{\mathbf{IV}}). \end{aligned}$$

  Also we find that the correlations of $W_I$ and $W_{III}$, $W_I$ and $W_{IV}$, $W_{II}$ and $W_{III}$, $W_{II}$ and $W_{IV}$, $W_{III}$ and $W_{IV}$ is asymptotically negligible.

• (v) Evaluation of the correlation of $W_I$ and $W_{II}$

  From the similar arguments of the evaluation of $W_{I}$, we know that $n\sum _{i=1}^{[n/k]-1}(\xi _{i}^{n,\mathbf{I}}\xi _{i}^{n,\mathbf{II}} - \widetilde{\xi }_{i}^{n,\mathbf{I}}\widetilde{\xi }_{i}^{n,\mathbf{II}})$ is asymptotically negligible. Moreover,

  $$\begin{aligned}&n\sum _{i=1}^{[n/k]-1}\left( \mathcal{E}[ \widetilde{\xi }_{i}^{n,\mathbf{I}}\widetilde{\xi }_{i}^{n,\mathbf{II}}|\mathcal {F}_{k(i-1)}] - \mathcal{E}[ \widetilde{\xi }_{i}^{n,\mathbf{I}}|\mathcal {F}_{k(i-1)}] \mathcal{E}[ \widetilde{\xi }_{i}^{n,\mathbf{II}}|\mathcal {F}_{k(i-1)}] \right) \\&\quad = k\mathbf{Var}[v_{1}^{2}]m_{2}^{2} \left( k\Delta _{n}\sum _{i=1}^{[n/k]-1}\sigma _{(i-1)k}^{4}\right) \\&\mathop {\longrightarrow }\limits ^{p} k\mathbf{Var} [v_{1}^{2}]m_{2}^{2}\int _{0}^{1}\sigma _{s}^{4}ds ( \equiv V_{\mathbf{I},\mathbf{II}}) \end{aligned}$$

  Then by summarizing (i–v), we conclude that $\sqrt{n}W_{n} \mathop {\longrightarrow }\limits ^{\mathcal {L}-s} \mathbf{N}\left( 0,V_{W}\right) \;,$ where

  $$\begin{aligned} V_{W}= & {} V_{\mathbf{I}} +V_{\mathbf{I}} + V_{\mathbf{III}} + V_{\mathbf{IV}} + 2V_{\mathbf{I},\mathbf{II}}\\= & {} k\left[ \mathbf{Var}(v_1^2)m_4+\mathbf{Var}(v_1^2)m_4+4\mathbf{Var}(v_1^2) +4m_4 +2\mathbf{Var}(v_1) \right] \int _{0}^{1}\sigma _{s}^{4}ds\;. \end{aligned}$$

(We have the relation that $\mathbf{Var}[(\Delta v)^2]= 2\mathcal{E}(v_1^4)+2$ and it is 8 for the Gaussian case.) Then by multiplying $6^2c^2$ to $V_W ,$ we finally have (4.12) as the third term.

Fourth, we set

$$\begin{aligned} U_{4n}= & {} k^{1/2}\Delta _n^2\sum _{i=1}^{[n/k]}\left( \frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}}\right) (\Delta v_{i}(k))^3\\= & {} k^{1/2}\Delta _n^2\sum _{i=1}^{[n/k]}\left[ \left( \frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}}\right) -\left( \frac{\Delta _{i+1}^n X(k)}{\sqrt{k\Delta _n}}\right) \right] v_{ik}^3\\&+ k^{1/2}\Delta _n^2 \left[ \left( \frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}}\right) v^3_{k[n/k]}- \left( \frac{\Delta _1^n X(k)}{\sqrt{k\Delta _n}}\right) v^3_{0}\right] \\&-3k^{1/2}\Delta _n^2 \left[ \left( \frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}}\right) v_{ik}^2v_{(i-1)k} - \left( \frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}}\right) v_{ik}v_{(i-1)k}^2\right] . \end{aligned}$$

Then we find that

$$\begin{aligned}&\Delta _n^{-3} \mathcal{E}[ (U_{4n})^2 \vert X ] \\&\quad = 2\mathcal{E}[v_1^6]k\Delta _n \left[ \sum _{i=1}^{[n/k]}\left( \frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}}\right) ^2 -2\sum _{i=1}^{[n/k]}\left( \frac{\Delta _{i+1}^n X(k)}{\sqrt{k\Delta _n}}\right) \right] \\&\qquad +\,2\times 9\mathcal{E}[v_1^4]\mathcal{E}[v_1^2]k\Delta _n \sum _{i=1}^{[n/k]}\left( \frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}}\right) ^2 \\&\qquad -\,2\times 3\mathcal{E}[v_1^4]\mathcal{E}[v_1^2]k\Delta _n \sum _{i=1}^{[n/k]}\left( \frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}} -\frac{\Delta _{i+1}^n X(k)}{\sqrt{k\Delta _n}}\right) \left( \frac{\Delta _{i+1}^n X(k)}{\sqrt{k\Delta _n}}\right) \\&\qquad +\,2\times 3\mathcal{E}[v_1^4]\mathcal{E}[v_1^2]k\Delta _n \sum _{i=1}^{[n/k]}\left( \frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}} -\Delta _{i+1}^n \frac{X}{\sqrt{k\Delta _n}}\right) \left( \frac{\Delta _{i}^n X(k)}{\sqrt{k\Delta _n}}\right) \\&\qquad -\,2\times 9(\mathcal{E}[v_1^2])^3 k\Delta _n \sum _{i=1}^{[n/k]-1} \left( \frac{\Delta _i^n X(k)}{\sqrt{k\Delta _n}}\right) \left( \frac{\Delta _{i+1}^n X}{\sqrt{k\Delta _n}}\right) \\&\qquad +\,o_p(1) \\&\quad \mathop {\longrightarrow }\limits ^{p} [2 \mathcal{E}[v_1^6]+30\mathcal{E}[v_1^4]\mathcal{E}[v_1^2]]\int _0^1\sigma _s^2ds\;, \end{aligned}$$

which is $\mathbf{Var}([\Delta v])^3]\int _0^1\sigma _s^2ds$. By multiplying $4^2(c\sqrt{c})^2$, we have (4.13).

Fifth, we use the relation that

$$\begin{aligned} \epsilon _n^4\sum _{i=1}^{[n/k]} [ (\Delta v_{i}(k))^4-\mathcal{E}(\Delta v_{i}(k))^4 ] \sim \frac{c^2}{n} \sqrt{\frac{n}{k}} \frac{1}{\sqrt{\frac{n}{k}} } \sum _{i=1}^{[n/k]} [(\Delta v_{i}(k))^4-\mathcal{E}(\Delta v_{i}(k))^4 ], \end{aligned}$$

whose asymptotic variance is the limit of $1/n^3 times [c^2\sqrt{k} ]\mathbf{Var}(\Delta v)^4$. Then it becomes (4.14) as the limit of $\mathbf{Var}[\sqrt{n} F_{5n}]$.

Finally, because $F_{1n}$ includes the sum of $[Z_i^n(k)]^4$ essentially, $F_{2n}$ includes the sum of $[Z_i^n]^3\Delta _i v(k)$ essentially, $F_{3n}$ includes the sum of $[Z_i^n]^2[\Delta _i v(k)]^2$ essentially, $F_{4n}$ includes the sum of $[Z_i^n][\Delta _i v(k)]^3$ and $F_{5n}$ includes the sum of $[\Delta _i v(k)]^3$ essentially. Then they are asymptotically and $\mathcal{F}-$conditionally uncorrelated and thus they are $\mathcal{F}-$conditionally independent. By using the stable convergence and summarizing the limiting random variables of each terms, we have the result. $\square$

Proof of Corollary 4

Because of (4.17), we have

$$\begin{aligned} \hat{S}(p ,k) -1 =\frac{ \hat{B}(p,k\Delta _n)_1-\hat{B}(p,\Delta _n)_1}{\hat{B}(p,\Delta _n)_1}\;. \end{aligned}$$

(6.33)

Then by applying Theorem 3, we have the first part.

For the second part, we consider

$$\begin{aligned}&\frac{\hat{B}(p,k\Delta _n)_1}{\hat{B}(p,\Delta _n)_1} -k^{p/2-1}\\&\quad = \frac{ \left[ \Delta _n^{1-p/2}\hat{B}(p,k\Delta _n)_1-k^{p/2-1}m_pA(p)\right] -k^{p/2-1}[ \Delta _n^{1-p/2}\hat{B}(p,\Delta _n)_1-m_pA(p)] }{ [\Delta _n^{1-p/2}\hat{B}(p,\Delta _n)_1-m_pA(p)] +m_p A(p) }\\&\qquad -\, k^{p/2-1}. \end{aligned}$$

Then by applying Theorem 3, we have the second part. $\square$

Appendix 2: Some Figures

In this “Appendix 2” we have given several figures we mentioned to in Sects. 5 and 6. We have given the empirical density of the normalized (limiting) random variables for each normalized statistics based on a set of simulations. (The details are explained in Sect. 5.) For the comparative purpose, the density of the limiting normal density has been drawn by bold (red) curves in each figures.