Reconstruction of Contraction Operators

Abstract

An operator of belief change is reconstructible as another such operator if and only if any outcome that can be obtained with the former can also be obtained with the latter (not necessarily using the same input). Two operators are mutually reconstructible if they generate exactly the same set of outcomes. The relations of reconstructibility among fifteen operators of contraction, including the common AGM contraction operators, are completely characterized. Furthermore, the additional such relations are characterized that arise if all belief sets are required to be finite-based or if the language is finite. These results are significant for the choice of a formal model to represent how real-world agents change their beliefs. In particular, if two contraction operators are mutually reconstructible, then that limits the types of considerations that can legitimately be invoked in favour of one over the other.

Appendix: Proofs

Definition 2

For any set A of sentences:

${\textsf {nimp}} (A) = \{ x \in A \mid (\forall y \in A) ({\text {If}}\;x \vdash y\;{\text {then}}\;y \vdash x) \}$

In other words, a sentence is in ${\textsf {nimp}} (A)$ (the “non-impliers” in A) if and only if it is an element of A that implies no other element of A than itself (or elements to which it is equivalent).

Lemma 1

${\mathrm {Cn}}(\{a \vee b\}) = {\mathrm {Cn}}(\{a\}) \cap {\mathrm {Cn}}(\{b\})$

Proof of Lemma 1

See Hansson (1999, p. 28).$\square$

Lemma 2

If compactness and Zorn’s lemma hold, then: If $X \subseteq A$ and $X \nvdash _{\exists } B$, then there is some $X'$ such that $X \subseteq X' \in A \perp B$. (upper bound property)

Proof of Lemma 2

See Alchourrón and Makinson (1981, p. 129).$\square$

Lemma 3

$K \perp (p \vee q) = (K \perp p) \cap (K \perp q)$ when $p, q \in K = {\mathrm {Cn}}(K)$.

Proof of Lemma 3

See Rott (1993) or Hansson (1999, pp. 49–50).$\square$

Lemma 4

Let K be a logically closed set and let $p, q \in K$. Then $K\perp p \subseteq K\perp q$ if and only if $\vdash q\rightarrow p$.

Proof of Lemma 4

See Hansson (1999, p. 49).$\square$

Lemma 5

Let $K'$ and K be belief sets such that $K' \subseteq K$. Then $\{K'\} = K\perp (K \backslash K' )$.

Proof of Lemma 5

Part 1 We are first going to show that $K' \in K \bot (K \backslash K')$. (i) We have $K'\subseteq K$ by the conditions. (ii) Suppose that $K'$ implies some element q of $K\backslash K'$. It follows from $K' \vdash q$ and the logical closure of $K'$ that $q \in K'$. Contradiction. (iii) Let $K' \subset Y \subseteq K$. Then there is some $z \in Y$ such that $z \in K{\setminus}K'$, hence $Y \vdash _\exists K{\setminus}K'$.$\square$

It remains to be shown that $K'$ is the only element of $K\perp (K{\setminus}K')$. Let $Z \in K\perp (K {\setminus}K')$. Then $Z \subseteq K$ and $Z \cap (K \backslash K') = \emptyset$. From this and $K' \subseteq K$ it follows set-theoretically that $Z\subseteq K'$. It follows from $Z\in K \bot (K \backslash K')$ and $K' \in K \bot (K \backslash K')$ that $Z \not \subset K'$, and we can conclude that $Z = K'$.

Lemma 6

If $z \vdash _\exists B$ for all $z \in Z$, then $A \perp (B \cup Z) = A \perp B$

Proof of Lemma 6

See Hansson (1999, pp. 39–41).$\square$

Lemma 7

Let K be a belief set and let $p \in K$. Then $K \sim p = K \cap {\mathrm {Cn}}(\{ \lnot p\})$.

Proof of Lemma 7

See Alchourrón and Makinson (1982) or Hansson (1999, pp. 125–126).$\square$

Lemma 8

Let X and K be logically closed. If $K \sim p \subseteq X \subseteq K$ and $X \nvdash p$, then $X = \bigcap \{ Y \in K \perp p \mid X \subseteq Y\}$.

Proof of Lemma 8

For one direction, note that due to Lemma 2, there is some Y such that $X \subseteq Y \in K \perp p$. This is sufficient to show that $X \subseteq \bigcap \{ Y \in K \perp p \mid X \subseteq Y\}$.

For the other direction suppose to the contrary that $\bigcap \{ Y \in K \perp p \mid X \subseteq Y\} \nsubseteq X$. Then there is some r such that (i) for all $Y \in K \perp p$, if $X \subseteq Y$ then $Y \vdash r$ and (ii) $X \nvdash r$. It follows from $r \in K$, $K \sim p \subseteq X$ and Lemma 7 that $X \vdash \lnot p \vee r$. If follows from (i) that:

If $Y \in K \perp p$ and $Y \nvdash r$, then $X \nsubseteq Y$

If $Y \in K \perp p$ and $Y \in K \perp r$, then $X \nsubseteq Y$

If $Y \in K \perp (p \vee r)$, then $X \nsubseteq Y$       (Lemma 3)

If $X \subseteq Y$ then $Y \notin K \perp (p \vee r)$

$p \vee r \in X$       (Lemma 2)

We have now obtained $X \nvdash r$, $X \vdash \lnot p \vee r$, and $p \vee r \in X$. We can conclude from this contradiction that $\bigcap \{ Y \in K \perp p \mid X \subseteq Y\} \subseteq X$, and with this the proof is finished.$\square$

Lemma 9

1.:

If A is finite then $K \simeq A = K \simeq \textit{ \& }A$

2.:

If A is infinite then $K \simeq A = {\mathrm {Cn}}(\varnothing )$

3.:

If A is finite then $K \simeq A = {\mathrm {Cn}}(\varnothing )$ if and only if $K \subseteq {\mathrm {Cn}}(A)$

Proof of Lemma 9

Part 1 Let $A = \{a_1,\ldots a_n\}$. Then:

$K \simeq A = K \cap {\mathrm {Cn}}(\{\lnot a_1\}) \cap \cdots {\mathrm {Cn}}(\{\lnot a_n\})$

$= K \cap {\mathrm {Cn}}(\{\lnot a_1 \vee \cdots \vee \lnot a_n\})$       (Lemma 1)

$= K \cap {\mathrm {Cn}}(\{\lnot \textit{ \& }A \})$

$= K \simeq \textit{ \& }A$

Part 2 Let A contain an infinite number of non-equivalent elements and let $r \in K \simeq A$. It follows from the definition of $\simeq$ that $\lnot a \vdash r$ for all $a \in A$, thus $\lnot r \vdash a$ for all $a \in A$. Since A contains an infinite number of non-equivalent elements, its elements contain an infinite number of atoms of the language.³ Therefore $\lnot r$ can imply all of them only if it is a contradiction, thus $r \in {\mathrm {Cn}}(\varnothing )$.

Part 3

$K \simeq A = {\mathrm {Cn}}(\varnothing )$

iff $K \simeq \textit{ \& }A = {\mathrm {Cn}}(\varnothing )$       (Part 1 of the present observation)

iff $K \cap {\mathrm {Cn}}(\{\lnot \textit{ \& }A\}) = {\mathrm {Cn}}(\varnothing )$       (Definition of $\simeq$)

iff for all $z \in K$, $\vdash z \vee \lnot \textit{ \& }A$       (Lemma 1)

iff for all $z \in K$, $\textit{ \& }A \vdash z$

iff $K \subseteq {\mathrm {Cn}}(\{\textit{ \& }A\})$

iff $K \subseteq {\mathrm {Cn}}(A)$ $\square$

Lemma 10

$K \sim A = K \simeq {\textsf {nimp}} (K \cap A)$.

Proof of Lemma 10

It follows from the definition of remainders and the logical closure of K that $K \perp A = K \perp (K \cap A)$ and thus $K \sim A = K \sim (K \cap A)$. It follows from Lemma 6 that $K \sim (K \cap A) = K \sim {\textsf {nimp}} (K \cap A)$. To complete the proof we need to show that if $A = {\textsf {nimp}} (A) \subseteq K$, then $K \sim A = K \simeq A$. Let $A = {\textsf {nimp}} (A) \subseteq K$.

In order to prove that $K \sim A \subseteq K \simeq A$, suppose to the contrary that there is some $e \in (K \sim A) {\setminus}(K \simeq A)$. It follows from the definition of eradication and $K \sim A \subseteq K$ that there is some $x \in A$ such that $e \notin {\mathrm {Cn}}(\{\lnot x\})$, thus $x \vee \lnot e \nvdash x$.

Suppose that $x \vee \lnot e \vdash y$ for some $y \in A {\setminus}\{x\}$. Then $x \vdash y$, contrary to our condition that $A = {\textsf {nimp}} (A)$. Thus $x \vee \lnot e \nvdash _\exists A$. It follows from the upper bound property (Lemma 2) that there is some X such that $x \vee \lnot e \in X \in K \perp A$. Furthermore, since $\{x \vee \lnot e\} \cup \{e\} \vdash x$, we have $e \notin X$. It follows that $e \notin \bigcap (K \perp A)$, i.e. $e \notin K \sim A$, contrary to the conditions.

In order to prove that $K \simeq A \subseteq K \sim A$, suppose to the contrary that there is some $e \in (K \simeq A) {\setminus}( K \sim A)$. It follows from $e \in K {\setminus}(K \sim A)$ that there is some Y such that $e \notin Y \in K \perp A$. Since $e \in K$ this means that $Y \cup \{e\} \vdash _\exists A$. Let z be an element of A such that $Y \cup \{e\} \vdash z$.

Since $z \in A$ and $e \in K \simeq A$ it follows from the definition of $\simeq$ that $\lnot z \vdash e$, thus $\lnot e \vdash z$. From this and $Y \cup \{e\} \vdash z$ it follows that $Y \vdash z$, contrary to our assumption that $Y \in K \perp A$ and $z \in A$. We can conclude from this contradiction that $K \simeq A \subseteq K \sim A$.$\square$

Lemma 11

Let $\sim _\gamma$ be an operator of finitely multiple partial meet contraction on the belief set K and let A be a finite set. Then there is a sentence y and a set $Y \subseteq K\perp y$ such that $K\sim _\gamma A=\bigcap Y$.

Proof of Lemma 11

Let $\sim _\gamma$ be an operator of finitely multiple partial meet contraction and let A be a finite set. Then:

$K \sim \textit{ \& }{\textsf {nimp}} (K \cap A) = K \simeq \textit{ \& }{\textsf {nimp}} (K \cap A)$       (Lemma 7)

$= K \simeq {\textsf {nimp}} (K \cap A)$       (Lemma 9, part 1)

$= K \sim A$       (Lemma 10)

$\subseteq K \sim _\gamma A$.

Using Lemma 8 we can conclude from $K \sim \textit{ \& }{\textsf {nimp}} (K \cap A) \subseteq K \sim _\gamma A$ and $K \sim _\gamma A \nvdash \textit{ \& }{\textsf {nimp}} (K \cap A)$ that:

$K \sim _\gamma A = \bigcap \{ X \in K \perp (\textit{ \& }{\textsf {nimp}} (K \cap A)) \mid K \sim _\gamma A \subseteq X\}$.$\square$

Lemma 12

Let ${\mathcal {L}}$ be based on an infinite number of atoms. Let K be a belief set and let $y\in K$ and ${\mathrm {Cn}}(\{y\})\ne K$. Then there is an infinite set of pairwise logically non-equivalent sentences $y'$ such that

$K\perp y \subseteq K\perp y'$

Proof of Lemma 12

Case (i), K is finite-based: We can use the set of sentences that are formed as $y \ \& \ (\textit{ \& }K \vee s)$, where s is an atom that is absent from both y and from a finite base of K. It follows from Lemma 4 that

$K\perp y \subseteq K \perp (y \ \& \ (\textit{ \& }K \vee s))$.

Case (ii), K is not finite-based: We can use the set of sentences formed as $y \ \& \ z$ with $z \in K{\setminus}{\mathrm {Cn}}(\{y\})$. To see that this set is logically infinite it is sufficient to note that otherwise $K={\mathrm {Cn}}((K{\setminus}{\mathrm {Cn}}(\{y\}))\cup \{y\})$ is finite-based, contrary to the assumptions. It follows from Lemma 4 that

$K\perp y \subseteq K \perp (y \ \& \ z)$.$\square$

Lemma 13

1.:

Let K be finite-based and let $K'$ be a logically closed finite-based subset of K. Then there is a sentence p such that $K' = K \sim p$.

2.:

Let ${\mathcal {L}}$ be infinite. Let K be a finite-based belief set and A a finite set of sentences, and let $K' \in K \perp A$. Then $K'$ is not finite-based.

3.:

Let ${\mathcal {L}}$ be finite and let $K'$ be a logically closed subset of K. Then there is a finite set A such that $K' \in K \perp A$.

4.:

Let ${\mathcal {L}}$ be finite and let $K' \in K \perp A$ for some set A. It does not hold in general that there is a sentence p such that $K' \in K \perp p$.

Proof of Lemma 13

Part 1 Let $p = \textit{ \& }K' \rightarrow \textit{ \& }K$. Then:

$K \sim p = K \sim (\textit{ \& }K' \rightarrow \textit{ \& }K)$

$= {\mathrm {Cn}}(\{\textit{ \& }K \vee \lnot (\textit{ \& }K' \rightarrow \textit{ \& }K)\})$       (Lemmas 1 and 7)

$= {\mathrm {Cn}}(\{\textit{ \& }K' \})$       (Since $K \vdash \textit{ \& }K'$)

$= K'$

Part 2 Suppose to the contrary that $K'$ is finite-based. Then there is some atom t that is not included in $\textit{ \& }K$, in $\textit{ \& }K'$ or in any of the elements of A. Since $K' \nvdash _\exists A$, the atomic structure yields $K' \cup \{t\} \nvdash _\exists A$ from which follows $K' \cup \{\textit{ \& }K \vee t\} \nvdash _\exists A$. Since $\textit{ \& }K \vee t \in K$ and $K' \in K \perp A$ it follows that $\textit{ \& }K \vee t \in K'$, hence $\textit{ \& }K' \vdash \textit{ \& }K \vee t$, hence $\lnot t \vdash \textit{ \& }K' \rightarrow \textit{ \& }K$. The atomic structure yields $\vdash \textit{ \& }K' \rightarrow \textit{ \& }K$, hence $K' = K$, contrary to the conditions.

Part 3 Let $K'$ be a logically closed subset of K. It follows from Lemma 5 that $\{K'\} = K \perp (K {\setminus}K')$. Since the language is finite, so is $K {\setminus}K'$.

Part 4 Let ${\mathcal {L}}$ consist of the truth-functional combinations of the two atoms $s_1$ and $s_2$. Let $K = {\mathrm {Cn}}(\{s_1, s_2\})$. Then ${\mathrm {Cn}}(\{s_1 \vee s_2\}) \in K \perp \{s_1,s_2\}$.⁴ But suppose that there is some p such that ${\mathrm {Cn}}(\{s_1 \vee s_2\}) \in K \perp p$. Since $s_1 \in K {\setminus}{\mathrm {Cn}}(\{s_1 \vee s_2\})$ we have ${\mathrm {Cn}}(\{s_1 \vee s_2\}) \cup \{s_1\} \vdash p$. Similarly, ${\mathrm {Cn}}(\{s_1 \vee s_2\}) \cup \{s_2\} \vdash p$. Hence $s_1 \vee s_2 \vdash p$, contrary to ${\mathrm {Cn}}(\{s_1 \vee s_2\}) \in K \perp p$.$\square$

Proof of Observation 1

For all operations mentioned in the observation there is some input (such as a set containing only a tautology) that yields the original belief set as outcome. This limiting case will not be further discussed.

Part 1 Since the outcomes of closed subtraction coincide with the set of logically closed subsets of K, the other three operations are reconstructible as closed subtraction. It remains to be shown that these operations have the same outcome range, i.e. that for all logically closed subsets $K'$ of K there is a set A of sentences such that $K \div A = K'$.

Let $A = K {\setminus}K'$. It follows from Lemma 5 that $\{K' \} = K \perp A$. It follows directly that $K \sim _\gamma A = K'$, for any multiple partial meet contraction, multiple maxichoice contraction, or multiple full meet contraction $\sim _\gamma$.

Part 2 Singleton partial meet contraction is a subcase of finitely multiple partial meet contraction. We have to prove that finitely multiple partial meet contraction is reconstructible as singleton partial meet contraction. Let $\sim _\gamma$ be an operator of finitely multiple partial meet contraction for K.

Case (i), ${\mathcal {L}}$ is finite: For this case we can prove the stronger statement that finitely multiple partial meet contraction is reconstructible as singleton full meet contraction:

$K\sim _\gamma A = K \cap {\mathrm {Cn}}(\{\textit{ \& }(K\sim _\gamma A)\})$

$= K \sim \lnot \textit{ \& }(K\sim _\gamma A)$       (Lemma 7)

Case (ii), ${\mathcal {L}}$ is infinite: Since ${\mathcal {L}}$ is countable, so is the set of its finite subsets. Let $X_1, X_2, \dots$ be a list containing all the finite subsets of ${\mathcal {L}}$, i.e. all the inputs of $\sim _\gamma$. Furthermore, let $y_1, y_2,\dots$ be a list containing all sentences in ${\mathcal {L}}$. We are going to construct a function h from elements on the first of these lists to elements on the second, and at the same time construct a selection function $\gamma^{\prime}$ on K for singleton partial meet contraction. We do this inductively, first for $X_1$, then for $X_2$, etc., according to the following three rules:

(a) If $K\sim _\gamma X_m = {\mathrm {Cn}}(\varnothing )$ then let $h(X_m) = \textit{ \& }{\textsf {nimp}} (K \cap X_m)$. Let $\gamma^{\prime}(K\perp \textit{ \& }{\textsf {nimp}} (K \cap X_m))= K\perp \textit{ \& }{\textsf {nimp}} (K \cap X_m)$. (Note that it follows from $K\sim _\gamma X_m = {\mathrm {Cn}}(\varnothing )$ that $K\sim X_m = {\mathrm {Cn}}(\varnothing )$ and that using Lemmas 10 and 9, Part 1, we have $K \sim X_m = K\simeq {\textsf {nimp}} (K \cap X_m) = K\simeq \textit{ \& }{\textsf {nimp}} (K \cap X_m) = K\sim \textit{ \& }{\textsf {nimp}} (K \cap X_m)$.)

(b) For all other $X_m$, let $h(X_m)$ be the first sentence $y_n$ on our list of sentences in ${\mathcal {L}}$ such that (i) $K\sim _\gamma X_m=\bigcap Y$ for some $Y \subseteq K\perp y_n$ and (ii) $y_n \ne h(K_k)$ for all $k<m$. (Due to Lemma 11 there is at least one sentence $y_n$ on the list satisfying (i), and due to Lemma 12 there is an infinite number of them so that (ii) can always also be satisfied.) Let $\gamma^{\prime}(K\perp y_n) = Y$.

(c) For any $y_n$ on the list of sentences for which the value of $\gamma^{\prime}(K\perp y_n)$ is not assigned according to rules (a) and (b), let $\gamma^{\prime}(K\perp y_n) = K\perp y_n$.

The verification that $K\sim _\gamma X_m = K\sim _{\gamma^{\prime}}h(X_m)$ for all $X_m$ is straight-forward.

Part 3 Singleton full meet contraction is a special case of both finitely multiple full meet contraction and internal finitely multiple eradication. It remains to be shown that the latter two types of operations are reducible to singleton full meet contraction. For internal finitely multiple eradication we have $K \simeq A = K \simeq \textit{ \& }A$ according to Lemma 9, part 1. For finitely multiple full meet contraction we have:

$K \sim A = K \simeq {\textsf {nimp}} (K \cap A)$       (Lemma 10)

$= K \simeq \textit{ \& }{\textsf {nimp}} (K \cap A)$       (Lemma 9, part 1)

$= K \sim \textit{ \& }{\textsf {nimp}} (K \cap A)$       (Lemma 7)

Part 4 Due to the subcase relationships it is sufficient to show that multiple eradication is reconstructible as singleton eradication. If A is infinite, then let p be a sentence such that $\vdash \lnot p$. It follows from Lemma 9, part 2, that $K \simeq A = {\mathrm {Cn}}(\varnothing )$ and from the definition of $\simeq$ that $K \simeq p = {\mathrm {Cn}}(\varnothing )$. If A is finite, then let $A = \{a_1,\ldots a_n \}$. We have:

$$\begin{aligned}K \simeq A & = K \cap \bigcap \{{\mathrm {Cn}}(\{\lnot p\}) \mid p \in A\})\\ & \; = K \cap {\mathrm {Cn}}(\{\lnot a_1 \vee \cdots \vee \lnot a_n\}) \qquad ({\text{Lemma}}\,1)\\ & \; = K \simeq \textit{ \& }A \quad \square \end{aligned}$$

Proof of Observation 2

Throughout the proof, $S = \{s_1, s_2\cdots \}$ is an infinite series of atoms in ${\mathcal {L}}$.

Part 1 Let $K = A = {\mathrm {Cn}}(S)$. Then closed subtraction of K by A yields the outcome ${\mathrm {Cn}}(\varnothing )$. Suppose that there is a finite set B and a selection function $\gamma$ such that ${\mathrm {Cn}}(\varnothing ) = K \sim _\gamma B$. Due to the recovery property for finitely multiple partial meet contraction (Hansson 1999, pp. 135–136) we have $K \subseteq {\mathrm {Cn}}((K\sim _\gamma B) \cup B)$, i.e. $K \subseteq {\mathrm {Cn}}(B)$, which is impossible since B contains only a finite number of the elements of S.

Part 2 Let $K = {\mathrm {Cn}}(S)$. Then K has uncountably many logically closed subsets, but there is only a countable number of sentences and therefore only a countable number of subsets of K that can be formed through singleton eradication.

Part 3 Let p be an atom such that $p \notin S$. Let $K = {\mathrm {Cn}}(S \cup \{p\})$ and suppose that $K \sim p$ can be obtained from K through maxichoice contraction by some finite set Y. Then $K \sim p \in K \perp Y$. Since Y is finite it follows from the recovery lemma (Hansson 1999, p. 47) that $(K\sim p) \cup Y \vdash s_k$ for all $s_k \in K$. Due to Lemma 7 $K\sim p \subseteq {\mathrm {Cn}}(\{\lnot p\})$, and we then have $\{\lnot p\} \cup Y \vdash s_k$ for all $s_k \in K$, but this is impossible since Y only contains a finite number of atoms.

Part 4 Let p and q be atoms, and let $p, q \in K$. It follows from Lemma 2 that there is some X such that $p \vee q \in X \in K \perp \{p, q\}$. Suppose that $X \in K \perp z$ for some z. It follows from the definition of $\perp$, since $p \in K {\setminus}X$, that $X \cup \{p\} \vdash z$, and similarly $X \cup \{q\} \vdash z$. It follows from $X \cup \{p\} \vdash z$ and $X \cup \{q\} \vdash z$ that $X \cup \{p \vee q\} \vdash z$, hence $X \vdash z$, contrary to the conditions.

Part 5 Let p be an atom such that $p \notin S$ and let $K = {\mathrm {Cn}}(S \cup \{p\})$. It follows from Lemma 2 that there is some X such that $S \subseteq X \in K \perp p$. Let $\gamma$ be a maxichoice selection function such that $\gamma (K \perp p) = \{X\}$. Then $K \sim _\gamma\,p = X$.

Now suppose that X can be obtained from K through multiple eradication. Then there is some A such that $X = K \simeq A$. Since $X \ne {\mathrm {Cn}}(\varnothing )$ it follows from Lemma 9, part 2, that A is finite and from Lemma 9, part 1, that $X = K \simeq \textit{ \& }A$. The definition of $\simeq$ yields $X \subseteq {\mathrm {Cn}}(\{\lnot \textit{ \& }A \})$, and since $S \subseteq X$ we then have $\lnot \textit{ \& }A \vdash s_k$ for all $s_k \in S$, which is impossible due to the atomic structure.

Part 6 Let $K = {\mathrm {Cn}}(S)$ and let p be an atom such that $p \notin S$. Suppose that there is some $A \subseteq K$ such that $K \simeq p = K \simeq A$.

Since $K \simeq p \ne {\mathrm {Cn}}(\varnothing )$ it follows from Lemma 9, part 2, that A is finite, and then from Lemma 9, part 1 that $K \simeq p = K \simeq \textit{ \& }A$. We then have for all $s_k \in S$:

$\textit{ \& }A \rightarrow s_k \in K \simeq \textit{ \& }A$       (Definition of $\simeq$)

$\textit{ \& }A \rightarrow s_k \in K \simeq p$       (Assumption)

$\textit{ \& }A \rightarrow s_k \in {\mathrm {Cn}}(\{\lnot p\})$       (Definition of $\simeq$)

$\lnot p \vdash \textit{ \& }A \rightarrow s_k$

$\textit{ \& }A \vdash p \vee s_k$

which cannot hold for all $s_k \in S$ due to the atomic structure. It follows that there can be no such set A.

Part 7 Let $K = A = {\mathrm {Cn}}(S)$. Due to Lemma 9, part 2, $K \simeq A = {\mathrm {Cn}}(\varnothing )$. Let $\gamma$ be a selection function. Suppose that for some finite B, $K \sim _\gamma B = {\mathrm {Cn}}(\varnothing )$. Due to the recovery property of $\sim _\gamma$ (Hansson 1999, pp. 135–136) we have $K \subseteq {\mathrm {Cn}}((K \sim _\gamma B) \cup B)$, i.e. $K \subseteq {\mathrm {Cn}}(B)$ which is impossible since B contains only a finite number of elements of S.$\square$

Proof of Observation 3

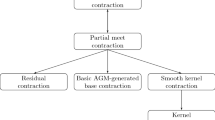
The mutual reconstructibilities indicated in the diagram are exactly those proved in Observation 1. The one-directed reconstructibilities are all obtainable from subcase relationships. It remains to show that no additional reconstructibility relationships hold. This will be done by showing for each potential additional such relationship that if it held, then it would give rise to a chain of reconstructions that would produce a reconstruction relationship that is known from Observation 2 not to hold. In what follows, the same abbreviations of the names of operators will be used as in the diagram.

If closed subtraction were reconstructible as any operation in addition to those indicated in the diagram, then it would be reconstructible either as finite pmc or as singleton eradication. This is impossible due to Observation 2, parts 1 respectively 2.

If finite pmc were reconstructible as any operation in addition to those indicated in the diagram, then it would be reconstructible as either finite maxichoice or multiple eradication. This is impossible due to Observation 2, parts 3 respectively 5.

If finite maxichoice were reconstructible as any operation in addition to those indicated in the diagram, then it would be reconstructible either as singleton maxichoice or multiple eradication. This is impossible due to Observation 2, parts 4 respectively 5.

If singleton maxichoice were reconstructible as any operation in addition to those indicated in the diagram, then it would be reconstructible as multiple eradication. This is impossible due to Observation 2, part 5.

If singleton eradication were reconstructible as any operation in addition to those indicated in the diagram, then it would be reconstructible either as finite pmc or as internal multiple eradication. This is impossible due to Observation 2, parts 7 respectively 6.

If internal multiple eradication were reconstructible as any operation in addition to those indicated in the diagram, then it would be reconstructible as finite pmc, which is impossible due to Observation 2, part 7.

Finally, if singleton fmc were reconstructible as any operation in addition to those indicated in the diagram, then it would be reconstructible as finite maxichoice, contrary to Observation 2, part 3.$\square$

Proof of Observation 4

In addition to what was shown in Observation 3 it is suffcient to show that if K is finite-based, then any operation that yields finite-based and logically closed sets as outputs for all inputs is reconstructible as full meet contraction. This follows from Lemma 13, part 1.$\square$

Proof of Observation 5

Part 1 In addition to what was shown in Observations 3 and 4 it is sufficient to show that singleton partial meet contraction is reconstructible as finitely multiple maxichoice contraction. This follows from Lemma 13, part 3.

Part 2 The non-trivial direction follows from Lemma 13, part 4.$\square$