Planar Rayleigh–Taylor instabilities: outflows from a binary line-source system

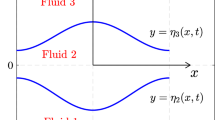
Abstract

Rayleigh–Taylor instabilities occur when a light fluid lies beneath a heavier one, with an interface separating them. Under the influence of gravity, the two fluid layers attempt to exchange positions, and as a result, the interface between them is unstable, forming fingers and plumes. Here, an analogous problem is considered, but in cylindrical geometry. Two line sources are present within an inner region of lighter fluid, and each of them has an inwardly directed gravity field. The surrounding fluid is heavier and is pushed outward by the light inner fluid ejected from the two sources. Nonlinear inviscid solutions are calculated and compared with the results of a linearized inviscid theory. In addition, the problem is formulated as a weakly compressible viscous outflow and modeled with Boussinesq theory. It is found that vorticity is generated in the viscous interfacial zone but that overturning plumes do not develop. However, the solution growth is highly sensitive to initial conditions.

Appendix

In this Appendix, the integrals defining the constants ${\mathcal {C}}_n (\beta )$ and ${\mathcal {S}}_n (\beta )$ in Eq. (28) are calculated in closed form, using the calculus of residues. For convenience, attention is focussed purely on the two integrals in these definitions, which are written here as

$$\begin{aligned} K_n (\beta ) = \int _{- \pi }^{\pi } \frac{\cos \theta \sin ( n\theta )}{ 1 - 2\beta \sin \theta + \beta ^2} \, \mathrm{{d}}\theta , \quad L_n (\beta ) = \int _{- \pi }^{\pi } \frac{\cos \theta \cos ( n\theta )}{ 1 - 2\beta \sin \theta + \beta ^2} \, \mathrm{{d}}\theta . \end{aligned}$$

(60)

These are converted into contour integrals in a complex $z$-plane, in the standard manner (see Saff and Snider [37, Sect.  6.2]). The integrals can be regarded as describing a single revolution on the unit circle $|z| = 1$, parametrized as $z = \exp (\mathrm{i}\theta )$. The two trigonometric functions are eliminated according to the formulae

$$\begin{aligned} \cos \theta = \frac{1}{2} \left( z + \frac{1}{z}\right) ; \quad \sin \theta = \frac{1}{2\mathrm{i}} \left( z - \frac{1}{z}\right) , \end{aligned}$$

and the terms in Eq. (60) are expressed as

$$\begin{aligned} K_n (\beta ) = \frac{\mathrm{i}}{4\beta } \big [ J_1 - J_2 + J_3 - J_4 \big ], \quad L_n (\beta ) = - \frac{1}{4\beta } \big [ J_1 + J_2 + J_3 + J_4 \big ]. \end{aligned}$$

(61)

In this expression, the four terms

$$\begin{aligned}&J_1 = \oint \frac{z^{n+1}}{\big ( z - \mathrm{i}\beta \big ) \big ( z - \mathrm{i}/ \beta \big )} \, \mathrm{{d}}z, \quad J_2 = \oint \frac{z^{1-n}}{\big ( z - \mathrm{i}\beta \big ) \big ( z - \mathrm{i}/ \beta \big )} \, \mathrm{{d}}z,\quad J_3 = \oint \frac{z^{n-1}}{\big ( z - \mathrm{i}\beta \big ) \big ( z - \mathrm{i}/ \beta \big )} \, \mathrm{{d}}z,\nonumber \\&J_4 = \oint \frac{z^{-n-1}}{\big ( z - \mathrm{i}\beta \big ) \big ( z - \mathrm{i}/ \beta \big )} \, \mathrm{{d}}z \end{aligned}$$

(62)

have been defined for convenience. Each of them is a contour integral about the unit circle traversed once in the positive direction, as illustrated in Fig. 15.

Fig. 15

The contour used in the complex plane, along which the integrals in Eq. (62) are evaluated. The (red) stars denote the possible locations of pole singularities. (Color figure online)

The two terms $J_1$ and $J_3$ appearing in Eq. (62) are straightforward to evaluate, since they each only contain a simple pole at the single point $z = \mathrm{i}\beta$ within the unit circle (since $\beta < 1$). The residue at this point is easily obtained, and it follows that

$$\begin{aligned} J_1 = 2\pi \big (\mathrm{i}^{n+1} \big ) \frac{\beta ^{n+2}}{\beta ^2 - 1},\quad J_3 = 2\pi \big ( \mathrm{i}^{n-1} \big ) \frac{\beta ^n}{\beta ^2 - 1}. \end{aligned}$$

(63)

The integrand of the term $J_2$ in Eq. (62) has both a simple pole at $z = \mathrm{i}\beta$ as well as a pole of order $n-1$ at the origin $z = 0$. The residue of the simple pole is easy to calculate, but that of the high-order pole at the origin is more difficult. It is appropriate to use partial fractions to re-write this expression as

$$\begin{aligned} J_2 = \frac{\beta }{\mathrm{{i}} \big ( \beta ^2 - 1 \big )} \oint \frac{1}{z^{n-1}} \left[ \frac{1}{z - \mathrm{{i}}\beta } - \frac{1}{z - \mathrm{i} / \beta } \right] \, \mathrm{{d}}z. \end{aligned}$$

In this form, the residue of the pole of order $n-1$ at the origin may now be obtained by differentiation, and a little algebra gives the simple final form

$$\begin{aligned} J_2 = 2\pi \big (\mathrm{{i}}^{1-n} \big ) \frac{\beta ^n}{\beta ^2 - 1}. \end{aligned}$$

(64)

A similar use of partial fractions is applied to the expression for $J_4$ in (62), since it too involves a simple pole at the point $z = \mathrm{{i}}\beta$ and a pole of order $n+1$ at the origin $z=0$. This quantity can therefore be calculated to be

$$\begin{aligned} J_4 = 2\pi \frac{\beta ^{n+2}}{\mathrm{i}^{n+1} \big ( \beta ^2 - 1 \big )}. \end{aligned}$$

(65)

These four expressions in Eqs. (63), (64), (65) are now substituted into the expressions (61) for $K_n$ and $L_n$, and yield the results

$$\begin{aligned} K_n = - \pi \beta ^{n-1} \cos \big ( n\pi / 2 \big ), \quad L_n = \pi \beta ^{n-1} \sin \big ( n\pi / 2 \big ). \end{aligned}$$

These formulae now give the final forms (29) in the text.