1 Introduction

In modern engineering applications involving thermal shock and high strain rate loading conditions, structures based on homogeneous materials are becoming inadequate because the requirements for thermal insulability and mechanical strength can not be satisfied simultaneously. The trend in materials design for these applications is to adopt composite materials such as thermal barrier coating (TBC) in which a ceramic micro-crystalline coating is joined onto a metallic substrate [1]. In this approach, dissimilar materials are combined to take advantage of the strengths of each material, such as high mechanical strength and toughness in metals and high thermal oxidation and corrosive resistances in ceramics. To further enhance the robustness of the composite structure, the concept of functionally graded materials (FGMs) is introduced such that the discontinuities in material properties across the interface and the associated stress built up can be reduced [2].

For TBCs under typical operating conditions, a strong temperature gradient across the coating thickness would lead to high thermal stress in the dissimilar or functionally graded interface region. Stress- or other environmental effect-induced cracking defects in this region would further increase the local thermal gradient and, consequently, lead to higher thermal stress and crack growth driving force. Thermal and thermomechanical problems of cracks and defects in regular and functionally graded TBCs have been investigated by many researchers because of their important implications for structural performance and reliability. Sih [3] studied the problem of an infinite cracked medium subjected to uniform heat flow and derived the solution for the crack-tip heat flux with a singularity of \(1/{\sqrt{r}}\). Tzou [4] also investigated the temperature distribution around a macrocrack tip in an infinite medium and defined a temperature gradient intensity factor to quantify the thermal energy accumulated in the neighborhood of the crack tip. It was also shown that the power of the temperature gradient singularity was not affected by the discontinuous jumps of the thermal properties across the materials’ interface. For characterizing the inherent behavior of the singular heat flow at a crack-tip, Chao and Chang [5] defined the heat flux intensity factor to quantify the heat flux accumulated in the vicinity of the crack tip. The heat flux intensity factor and the full field temperature solution were also given for the problem of a crack on the interface of two dissimilar anisotropic media. Chao and Kuo [6] studied the thermal problem of a circular-arc crack embedded in dissimilar materials under a point heat source. It was shown that the heat flux intensity factor reduced as the crack length reduced. Noda and Jin [7] studied the problem of a perfectly insulated crack embedded in an infinite nonhomogeneous elastic medium under steady-state heat flux through the crack surfaces. The effects of material inhomogeneity on the temperature field and the stress intensity factors for a perfectly insulated crack were presented. El-Borgi et al. [8] investigated the thermal and thermoelastic problems of an infinite plane containing a partially insulated crack perpendicular to the direction of material grading. The effect of material inhomogeneity on crack surface temperatures and the stress intensity factors were provided.

In addition to the analytical treatments of the thermal crack problems, domain- or boundary-based numerical discretizations were also implemented for investigating thermal problems involving more complex geometries. Wang et al. [9] presented a boundary-based meshless numerical procedure utilizing a virtual boundary collocation method in conjunction with radial basis function approximations and the analog equation method to analyze transient heat conduction problem in FGMs. A hybrid graded finite element method was developed by Cao et al. [10]. In this approach, a fundamental solution in the Laplace transform domain is first constructed for a FGM with an exponential, quadratic, or trigonometric grading profile under transient heat conduction. The field solutions are then obtained by the hybrid graded element formulation and the Stehfest inverse transform algorithm.

In this paper, the thermal problem of an infinite functionally graded medium containing an arbitrarily oriented crack under uniform remote heat flux is considered. Using the theory of thermal conduction and Fourier transformation, the field equations with mixed boundary conditions are reduced to a system of integral equations and solved numerically. A temperature solution for the cracked medium and the crack-tip heat flux intensity factors are then calculated from the solution of the singular integral equation. The effects of grading inhomogeneity and crack orientation on the temperature distribution in the cracked medium and the heat flux intensity factors are also discussed.

2 Formulation of problem

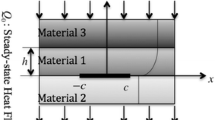
The two-dimensional thermal problem of a functionally graded infinite medium containing an arbitrarily oriented crack under uniform remote heat flow (Fig. 1) is considered. It is assumed that the thermal conductivity of the infinite medium is functionally graded with an exponential variation along the \(y\)-direction and is given by

$$\begin{aligned} k=k_0 \exp (\delta y/a), \end{aligned}$$
(2.1)

where \(k_{0}\) is the thermal conductivity at \(y=0\), and \(\delta \) is the inhomogeneity parameter. The crack is assumed to be perfectly insulated and is of length 2\(a\) and centered on \((x,y)=(0,0)\). The crack surface plane is along the \(s\)-axis, which is rotated counterclockwise with an angle \(\theta \) from the \(x\)-axis.

Fig. 1
figure 1

Schematic of the problem

Full size image

Under a uniform steady-state heat flux applied away from the cracked region, the temperature of the nonhomogeneous medium must satisfy the following Poisson equation:

$$\begin{aligned} \nabla ^{2}T+\frac{\delta \sin \theta }{a}\frac{\partial T}{\partial s}+\frac{\delta \cos \theta }{a}\frac{\partial T}{\partial r}=0. \end{aligned}$$
(2.2)

The boundary conditions for the temperature field on crack surfaces for the perfectly insulated crack are given by

$$\begin{aligned} k_0 \text {e}^{({{s\delta \sin \theta })/{a}}}\frac{\partial T(s,0^{+})}{\partial r}=k_0 \text {e}^{({{s\delta \sin \theta })/{a}}}\frac{\partial T(s,0^{-})}{\partial r}=0, \quad -a<s<a. \end{aligned}$$
(2.3)

For the problem as shown in Fig. 1, the temperature solution can be obtained using a superposition approach in which the original problem is divided into two cases: the first one is an uncracked infinite nonhomogeneous medium subjected to a remote heat flux (Fig. 2a), and the second one is a cracked infinite nonhomogeneous medium with boundary heat flux \(Q^{*}\) on the crack surfaces (Fig. 2b). From the concept of superposition, the sum of \(Q^{*}\) and the heat flux across the dotted line \((-a<s<a,r=0)\) (Fig. 2a) should be equal to the crack surface condition given in Eq. (2.3) such that \(Q^{*}=Q_0\cos \theta \). The temperature fields for the problems as shown in Fig. 2a, b are denoted by \(T_{1}\) and \(T_{2}\), respectively. To formulate the thermal problems, a set of normalized quantities are first introduced:

$$\begin{aligned} (\bar{{x}},\bar{{y}})={(x,y)}/a,\quad (\bar{{s}},\bar{{r}})={(s,r)}/a,\quad \bar{{T}}=\left( {\frac{k_0 }{Q_0 a}} \right) T. \end{aligned}$$
(2.4)

For the problem as shown in Fig. 2a, because the heat flux and material gradient are both along the \(y\)-direction, it is obvious that the dimensionless temperature field \(\bar{{T}}_1 \) is a function of \(y\) only, and \(\bar{{T}}_1 \) must satisfy the corresponding governing equation and boundary conditions given as follows:

$$\begin{aligned} \frac{\text {d}^{2}\bar{{T}}_1 }{\text {d}\bar{{y}}^{2}}+\delta \frac{\text {d}\bar{{T}}_1 }{\text {d}\bar{{y}}}&= 0, \end{aligned}$$
(2.5)
$$\begin{aligned} \frac{\text {d}\bar{{T}}_1 }{\text {d}\bar{{y}}}&= \text {e}^{-\delta \bar{{y}}}\text {, }\quad \bar{{y}}\rightarrow \pm \infty . \end{aligned}$$
(2.6)

By assuming \(\bar{{T}}_1 =0\) on \(\bar{{y}}=0\) without loss of generality, the normalized temperature field that satisfies Eqs. (2.5) and (2.6) is given by

$$\begin{aligned} \bar{{T}}_1 \left( {\bar{{s}},\bar{{r}}} \right) =\frac{1-\text {e}^{-\left( {\bar{{s}}\delta \sin \theta +\bar{{r}}\delta \cos \theta } \right) }}{\delta }. \end{aligned}$$
(2.7)

For the problem as shown in Fig. 2b, the governing equation for the normalized temperature \(\bar{{T}}_2 \) is given by

$$\begin{aligned} \nabla ^{2}\bar{{T}}_2 +\delta \sin \theta \frac{\partial \bar{{T}}_2 }{\partial \bar{{s}}}+\delta \cos \theta \frac{\partial \bar{{T}}_2 }{\partial \bar{{r}}}=0. \end{aligned}$$
(2.8)

In addition, \(\bar{{T}}_2 \) must satisfy the following boundary and continuity conditions:

$$\begin{aligned} \frac{\partial \bar{{T}}_2 }{\partial \bar{{r}}}&= 0, \quad \bar{{r}}\rightarrow \pm \infty , \end{aligned}$$
(2.9)
$$\begin{aligned} \frac{\partial \bar{{T}}_2 (\bar{{s}},0^{+})}{\partial \bar{{r}}}&= \frac{\partial \bar{{T}}_2 (\bar{{s}}, 0^{-})}{\partial \bar{{r}}},\quad \left| {\bar{{s}}} \right| <\infty , \end{aligned}$$
(2.10)
$$\begin{aligned} \bar{{T}}_2 (\bar{{s}},0^{+})&= \bar{{T}}_2 (\bar{{s}},0^{-}), \quad \left| {\bar{{s}}} \right| \ge 1, \end{aligned}$$
(2.11)
$$\begin{aligned} \text {e}^{\bar{{s}}\delta \sin \theta }\frac{\partial \bar{{T}}_2 (\bar{{s}},0^{+})}{\partial \bar{{r}}}&= \text {e}^{\bar{{s}}\delta \sin \theta }\frac{\partial \bar{{T}}_2 (\bar{{s}},0^{-})}{\partial \bar{{r}}}=-\cos \theta , \quad -1<\bar{{s}}<1. \end{aligned}$$
(2.12)

Equations (2.11) and (2.12) represent a set of mixed boundary conditions along the crack surface plane \((\bar{{r}}=0)\). Applying Fourier transform to Eq. (2.8) and solving the resulting differential equation, the normalized temperature \(\bar{{T}}_2 \) can be expressed as

$$\begin{aligned} \bar{{T}}_2 (\bar{{s}},\bar{{r}})=\left\{ {{\begin{array}{l} {\displaystyle \int \nolimits _{-\infty }^\infty {\left[ {C_1 (\omega )\mathrm{{e}}^{n_1 \bar{{r}}}+C_2 (\omega )\mathrm{{e}}^{n_2 \bar{{r}}}} \right] \mathrm{{e}}^{-\text {i}\bar{{s}}\omega }\,\text {d}\omega } \quad \bar{{r}}>0,} \\ {\displaystyle \int \nolimits _{-\infty }^\infty {\left[ {C_3 (\omega )\mathrm{{e}}^{n_1 \bar{{r}}}+C_4 (\omega )\mathrm{{e}}^{n_2 \bar{{r}}}} \right] \mathrm{{e}}^{-\text {i}\bar{{s}}\omega }\,\text {d}\omega } \quad \bar{{r}}<0,} \\ \end{array} }} \right. \end{aligned}$$
(2.13)

where \(C_{1},{\ldots }, C_{4}(\omega )\) are unknown functions of \(\omega \), and \(n_{1}\) and \(n_{2}\) are the roots of the characteristic equation and are found to be

$$\begin{aligned} n_1 =\frac{-\delta \cos \theta +\sqrt{({\delta \cos \theta })^{2}+4({\omega ^{2}+\text {i}\omega \delta \sin \theta })}}{2},\end{aligned}$$
(2.14a)
$$\begin{aligned} n_2 =\frac{-\delta \cos \theta -\sqrt{( {\delta \cos \theta } )^{2}+4({\omega ^{2}+\text {i}\omega \delta \sin \theta })}}{2}. \end{aligned}$$
(2.14b)

Three of the four unknowns \(C_j \text { ( }j=1,\ldots ,4)\) may be eliminated by substituting Eq. (2.13) into the homogeneous equation (2.9) and (2.10); it follows that

$$\begin{aligned} C_1 =C_4 =0,\quad C_3 (\omega )=\frac{n_2 }{n_1 }C_2 (\omega ). \end{aligned}$$
(2.15)

By further defining an unknown density function

$$\begin{aligned} \psi (\bar{{s}})=\frac{\partial }{\partial \bar{{s}}}\left[ {\bar{{T}}_2 (\bar{{s}},0^{+})-\bar{{T}}_2 (\bar{{s}},0^{-})} \right] , \quad -\infty <\bar{{s}}<\infty , \end{aligned}$$
(2.16)

and observing from Eq. (2.11) that

$$\begin{aligned} \psi (\bar{{s}})=0,\quad \left| {\bar{{s}}} \right| >1, \end{aligned}$$
(2.17)

it can be seen that the density function must satisfy the following single-valuedness condition:

$$\begin{aligned} \int _{-1}^1 {\psi (t)\,\text {d}t=0}. \end{aligned}$$
(2.18)

By substituting the normalized temperatures (2.13) into the definition of the unknown density function (2.16), the remaining unknown constant in Eq. (2.15) can be expressed in terms of the unknown density function as

$$\begin{aligned} C_2 (\omega )=\frac{\text {i}}{2\pi \omega }\!\left( {\frac{n_1 }{n_1 -n_2 }} \right) \int _{-1}^1 {\psi (t)\mathrm{{e}}^{\text {i}\omega t}\text {d}t}. \end{aligned}$$
(2.19)

From the remaining mixed boundary condition (2.12), the unknown density function must satisfy the following relation:

$$\begin{aligned} \frac{1}{\pi }\int _{-1}^1 {\psi (t)K(\bar{{s}},t)\,\text {d}t} =-2\text {e}^{-\bar{{s}}\delta \sin \theta }\cos \theta , \quad -1<\bar{{s}}<1, \end{aligned}$$
(2.20)

where the kernel is given by

$$\begin{aligned} K(\bar{{s}},t)=\mathop {\lim }\limits _{\bar{{r}}\rightarrow 0^{+}} \int _0^\infty \big \{ {\mathrm{Re} [{D(\omega ,\bar{{r}})}]\cos \omega ({t-\bar{{s}}})-\mathrm{Im} [{D(\omega ,\bar{{r}})}]\sin \omega ({t-\bar{{s}}})} \big \}\,\text {d}\omega \end{aligned}$$
(2.21)

and

$$\begin{aligned} D(\omega ,\bar{{r}})=\frac{\text {2i}}{\omega }\!\left( {\frac{n_1 n_2 }{n_1 -n_2 }} \right) \text {e}^{n_2 \bar{{r}}}. \end{aligned}$$
(2.22)

By observing that the asymptotic leading term of \(D\) as \(\omega \rightarrow \infty \) is

$$\begin{aligned} D^{\infty }=\mathop {\lim }\limits _{\omega \rightarrow \infty } D=-\text {ie}^{\big [ {-\frac{1}{2}\delta \left( {\cos \theta +\text {i}\sin \theta } \right) -\omega } \big ]\bar{{r}}}, \end{aligned}$$
(2.23)

and evaluating the integrals involving the leading term using the relation

$$\begin{aligned} \mathop {\lim }\limits _{\bar{{r}}\rightarrow 0^{+}} \int _0^\infty {\text {e}^{\big [ {-\frac{1}{2}\delta \left( {\cos \theta +\text {i}\sin \theta } \right) \!-\!\omega } \big ]\bar{{r}}}\sin \omega \left( {t-\bar{{s}}} \right) } \text {d}\omega&= \mathop {\lim }\limits _{\bar{{r}}\rightarrow 0^{+}} \left[ {\frac{t-\bar{{s}}}{\bar{{r}}^{2}+\left( {t-\bar{{s}}} \right) ^{2}}} \right] \text {e}^{\big [-\frac{1}{2}\delta \left( {\cos \theta \!+\!\text {i}\sin \theta } \right) \big ]\bar{{r}}} =\frac{1}{t-\bar{{s}}}, \end{aligned}$$
(2.24)

the integral equation (2.20) can be rewritten as a Cauchy singular integral equation given by

$$\begin{aligned} \frac{1}{\pi }\int _{-1}^1 {\left[ {\frac{1}{t-\bar{{s}}}+K_\mathrm{F} (\bar{{s}},t)} \right] \psi (t)\text {d}t} =-2\text {e}^{-\bar{{s}}\delta \sin \theta }\cos \theta , \quad -1<\bar{{s}}<1. \end{aligned}$$
(2.25)

In Eq. (2.25), \(K_\mathrm{F}\) denotes a Fredholm kernel and is given by

$$\begin{aligned} K_\mathrm{F} (\bar{{s}},t)=\int _0^\infty {\left[ {F_1 (\omega )\sin \left( {t-\bar{{s}}} \right) \omega +F_2 (\omega )\cos \left( {t-\bar{{s}}} \right) \omega } \right] \text {d}\omega } , \end{aligned}$$
(2.26)

where

$$\begin{aligned} F_1 (\omega )&= -\text {Im}\left[ {\frac{\text {2i}}{\omega }\left( {\frac{n_1 n_2 }{n_1 -n_2 }} \right) } \right] -1,\end{aligned}$$
(2.27a)
$$\begin{aligned} F_2 (\omega )&= \text {Re}\left[ {\frac{\text {2i}}{\omega }\left( {\frac{n_1 n_2 }{n_1 -n_2 }} \right) } \right] . \end{aligned}$$
(2.27b)

Note that, for the case where \(\theta =0\), Eq. (2.25) can be reduced to the integral equation for a perfectly insulated crack given in [8].

Fig. 2
figure 2

Schematics of problems used for superposition a Case 1: uncracked medium under remote heat flux b Case 2: cracked medium under crack surface heat flux

Full size image

3 Solution of singular integral equation

It can be shown that the general solution of the integral equation (2.25) with a Cauchy singularity is of the form [11]

$$\begin{aligned} \psi (t)=\frac{g(t)}{\sqrt{1-t^{2}}},\quad -1<t<1, \end{aligned}$$
(3.1)

where the bounded unknown function \(g(t)\) is Hölder-continuous and can be expressed in terms of infinite series of orthogonal polynomials. Using the Chebyshev polynomials of the first kind \(\text {T}_{k }(t),\; k = 0, 1, {\ldots },\) it follows that

$$\begin{aligned} g(t)=\sum _{k=0}^\infty {B_k } \text {T}_k (t). \end{aligned}$$
(3.2)

Substituting Eqs. (3.1) and (3.2) into the single-valuedness condition (2.18) and from the orthogonality conditions of T\(_{k}(t)\), it can be shown that \(B_0 =0\). Truncating the infinite series, the density function can be approximated as

$$\begin{aligned} \psi (t)\cong \frac{1}{\sqrt{1-t^{2}}}\sum _{k=1}^N {B_k } \text {T}_k (t). \end{aligned}$$
(3.3)

The unknown constants \(B_{k},\; k = 1, {\ldots },N,\) can be determined by substituting equation (3.3) into the singular integral Eq. (2.25) and using the following relations:

$$\begin{aligned} \frac{1}{\pi }\int _{-1}^1 {\frac{\text {T}_k (t)}{(t-\bar{{s}})\sqrt{1-t^{2}}}\text {d}t} =\left\{ {{\begin{array}{ll} {0} \qquad \qquad \qquad \quad \,\, \quad \, {k=0, \quad \left| {\bar{{s}}} \right| <1,} \\ {\text {U}_{k-1} (\bar{{s}})} \quad \,\,\,\,\, \qquad \quad {k>0, \quad \left| {\bar{{s}}} \right| <1,} \\ {-\frac{\left( {\bar{{s}}-\, \frac{\left| {\bar{{s}}} \right| }{\bar{{s}}}\sqrt{\bar{{s}}^{2}-1}} \right) ^{k}}{\frac{\left| {\bar{{s}}} \right| }{\bar{{s}}}\sqrt{\bar{{s}}^{2}-1}}}\quad {k\ge 0, \quad \left| {\bar{{s}}} \right| >1,} \\ \end{array} }} \right. \end{aligned}$$
(3.4)

and the Cauchy singularity can be regularized and the integral equation can be rewritten as

$$\begin{aligned} \sum _{k=1}^N {B_k\!\left( {\text {U}_{k-1} (\bar{{s}})+\frac{1}{\pi }\int _{-1}^1 {\frac{\text {T}_k (t)}{\sqrt{1-t^{2}}}K_\mathrm{F} (\bar{{s}},t)\,\text {d}t} } \right) } =-2\text {e}^{-\bar{{s}}\delta \sin \theta }\cos \theta , \quad -1<\bar{{s}}<1, \end{aligned}$$
(3.5)

where \(\text {U}_{k}\) denotes the Chebyshev polynomial of the second kind. The Fredholm kernel \(K_\mathrm{F} (\bar{{s}},t)\) in Eq. (3.5) is considered by separating integral (2.26) as

$$\begin{aligned} K_\mathrm{F} (\bar{{s}},t)&= \int _0^V {\left[ {F_1 (\omega )\sin (t-\bar{{s}})\omega +F_2 (\omega )\cos (t-\bar{{s}})\omega } \right] \text {d}\omega }\nonumber \\&\!+\int _V^\infty \left[ {F_1 (\omega )\sin (t-\bar{{s}})\omega +F_2 (\omega )\cos (t-\bar{{s}})\omega } \right] \text {d}\omega . \end{aligned}$$
(3.6)

In Eq. (3.6) the first integral is evaluated numerically by using the Gauss–Chebyshev integration formula, whereas the second integral is estimated by applying series approximations for \(F_1 (\omega )\) and \(F_2 (\omega )\). By applying a suitable 32-term asymptotic expansion for \(F_1 (\omega )\) and \(F_2 (\omega )\) as \(\omega \,\rightarrow \,\infty \), and choosing a large enough value of \(V\), it follows that

$$\begin{aligned} K_\mathrm{F} (\bar{{s}},t)&\cong \int _0^V {\left[ {F_1 (\omega )\sin (t-\bar{{s}})\omega +F_2 (\omega )\cos (t-\bar{{s}})\omega } \right] \text {d}\omega } \nonumber \\&\quad +\sum _{k=1}^{16} {\xi _k \int _V^\infty {\frac{\sin (t-\bar{{s}})\omega }{\omega ^{2k}}\text {d}\omega } } +\sum _{k=1}^{16} {\eta _k \int _V^\infty {\frac{\cos (t-\bar{{s}})\omega }{\omega ^{2k-1}}\text {d}\omega ,} } \end{aligned}$$
(3.7)

where \(\xi _k \) and \(\eta _k \), \(k\) = 1, ..., 16, are the coefficients of the asymptotic expansions of \(F_{1}\) and \(F_{2}\), respectively, and \(\xi _1 ,\xi _2 ,\xi _3 ,\eta _1 ,\eta _2 ,\) and \(\eta _3\) are given by

$$\begin{aligned} \xi _1&= -\frac{\delta ^{2}\cos 2\theta }{8}, \end{aligned}$$
(3.8a)
$$\begin{aligned} \xi _2&= -\frac{\delta ^{4}\left( {-4\cos 2\theta +\cos 4\theta } \right) }{128}, \end{aligned}$$
(3.8b)
$$\begin{aligned} \xi _3&= -\frac{\delta ^{6}\left( {25\cos 2\theta -16\cos 4\theta +\cos 6\theta } \right) }{2048}, \end{aligned}$$
(3.8c)
$$\begin{aligned} \eta _1&= \frac{\delta \sin \theta }{2}, \end{aligned}$$
(3.8d)
$$\begin{aligned} \eta _2&= \frac{\delta ^{3}\cos 2\theta \sin \theta }{16}, \end{aligned}$$
(3.8e)
$$\begin{aligned} \eta _3&= \frac{\delta ^{5}\left( {-2-8\cos 2\theta +\cos 4\theta } \right) \sin \theta }{256}. \end{aligned}$$
(3.8f)

Because the difference between the expressions of the Fredholm kernel given in Eqs. (3.6) and (3.7) are of order \(1/V^{32}\), Eq. (3.6) can be replaced by Eq. (3.7), provided that a large enough value of \(V\) is selected. By further defining

$$\begin{aligned}&C_k (t-\bar{{s}})=\int _V^\infty {\frac{\cos (t-\bar{{s}})\omega }{\omega ^{k}}\mathrm{d}\omega }, \quad k=1,2,\dots , \end{aligned}$$
(3.9)
$$\begin{aligned}&S_k (t-\bar{{s}})=\int _V^\infty {\frac{\sin (t-\bar{{s}})\omega }{\omega ^{k}}\mathrm{d}\omega }, \quad k=1,2,\dots , \end{aligned}$$
(3.10)

and using the recursive relations

$$\begin{aligned} C_1 (t-\bar{{s}})&= -\text {Ci}(\left| {t-\bar{{s}}} \right| V), \end{aligned}$$
(3.11)
$$\begin{aligned} S_1 (t-\bar{{s}})&= \frac{\left| {t-\bar{{s}}} \right| }{t-\bar{{s}}}\left[ {\frac{\pi }{2}-\text {Si}(\left| {t-\bar{{s}}} \right| V)} \right] , \end{aligned}$$
(3.12)
$$\begin{aligned} C_k (t-\bar{{s}})&= \frac{1}{k-1}\left[ {\frac{\cos (\left| {t-\bar{{s}}} \right| V)}{V^{k-1}}+\left( {t-\bar{{s}}} \right) S_{k-1} (t-\bar{{s}})} \right] , \quad k>1, \end{aligned}$$
(3.13)
$$\begin{aligned} S_k (t-\bar{{s}})&= \frac{1}{k-1}\left[ {\frac{\left| {t-\bar{{s}}} \right| }{t-\bar{{s}}}\frac{\sin (\left| {t-\bar{{s}}} \right| V)}{V^{k-1}}+\left( {t-\bar{{s}}} \right) C_{k-1} (t-\bar{{s}})} \right] , \quad k>1, \end{aligned}$$
(3.14)

the Fredholm kernel (3.7) can be rewritten as

$$\begin{aligned} K_\mathrm{F} (\bar{{s}},t)&= \int _0^V {\Bigg [ {F_1 (\omega )\sin (t-\bar{{s}})\omega +F_2 (\omega )\cos (t-\bar{{s}})\omega } \Bigg ]\text {d}\omega }+\sum _{k=1}^{16} {\Bigg [ {\xi _k S_{2k} (t-\bar{{s}})+\eta _k C_{2k-1} (t-\bar{{s}})} \Bigg ]}. \end{aligned}$$
(3.15)

In Eqs. (3.11) and (3.12) Ci and Si are the cosine and sine integrals, respectively, and are given by

$$\begin{aligned} \text {Ci}(x)&= \gamma _0 +\ln x+\int _0^x {\frac{\cos \tau -1}{\tau }\text {d}\tau }, \quad x>0, \end{aligned}$$
(3.16)
$$\begin{aligned} \text {Si}(x)&= \int _0^x {\frac{\sin \tau }{\tau }\text {d}\tau }, \quad x>0, \end{aligned}$$
(3.17)

where \(\gamma _{0}\) is Euler’s constant. From Eqs. (3.11) and (3.16) it can be seen that a logarithmic singularity is present in the Fredholm kernel (3.15). To avoid the numerical difficulty associated to this singularity, the logarithmic term is extracted from the Fredholm kernel and is considered by using the following relation:

$$\begin{aligned} \int _{-1}^1 {\frac{\text {T}_k (t)}{\sqrt{1-t^{2}}}\ln \left| {t-\bar{{s}}} \right| \text {d}t} =-\frac{\pi }{k}\text {T}_k (\bar{{s}}), \quad k\ge 1. \end{aligned}$$
(3.18)

Consequently, the integral equation given in Eq. (3.5) can be regularized and is expressed as

$$\begin{aligned}&\sum _{k=1}^N {B_k \left( {\text {U}_{k-1} (\bar{{s}})+\frac{\eta _1 }{k}\text {T}_k (\bar{{s}})+\frac{1}{\pi }\int _{-1}^1 {\frac{\text {T}_k (t)}{\sqrt{1-t^{2}}}K^{*}(\bar{{s}},t)\text {d}t} } \right) }=-2\text {e}^{-\bar{{s}}\delta \sin \theta }\cos \theta , \quad -1<\bar{{s}}<1, \end{aligned}$$
(3.19)

where

$$\begin{aligned} K^{*}(\bar{{s}},t)&= \int _0^V {\left[ {F_1 (\omega ,\bar{{s}})\sin (t-\bar{{s}})\omega +F_2 (\omega ,\bar{{s}})\cos (t-\bar{{s}})\omega } \right] \text {d}\omega }-\eta _1 \left[ {\gamma _0 +\int _0^{\left| {t-\bar{{s}}} \right| V} {\frac{\cos \tau -1}{\tau }\text {d}\tau } } \right] +\xi _1 S_2 (t-\bar{{s}})\nonumber \\&+\sum _{k=2}^{16} {\left[ {\xi _k S_{2k} (t-\bar{{s}})+\eta _k C_{2k-1} (t-\bar{{s}})} \right] }. \end{aligned}$$
(3.20)

The unknown constants \(B_k ,k=1,\dots ,N,\) can be determined by using a suitable collocation technique to convert Eq. (3.19) into a set of linear simultaneous equations and then solving numerically for \(B_{k}\). The collocation points selected in this study are

$$\begin{aligned} \bar{{s}}_j =\cos \frac{(2j-1)\pi }{2N}, \quad j=1,\dots ,N, \end{aligned}$$
(3.21)

which are roots of the Chebyshev polynomials. These collocation points seem to give better convergence in numerical analysis. Numerical convergence of the collocation procedure is examined by comparing calculated values of the density function \(\psi \) at \(\bar{{s}}=0\) for various numbers of collocation points. Shown in Table 1 are the numerical values of \(\psi (0)\) for some special cases. It can be seen from Table 1 that a five-digit convergence is achieved by choosing as few as 15 collocation points. The subsequent analyses for the remaining cases are therefore computed with \(N\) = 15.

Table 1 Convergence of calculated density function \(\psi (0)\)
Full size table

4 Temperature field and heat flux intensity factor

4.1 Temperature field

By substituting Eq. (2.13) into Eqs. (2.9), (2.10), (2.16), and (2.17) with some straightforward algebraic manipulations, the normalized temperature field \(\bar{{T}}_2 \) can be expressed in terms of the density function \(\psi \),

$$\begin{aligned} \bar{{T}}_2 (\bar{{s}},\bar{{r}})=\left\{ {\begin{array}{l} \int _{-1}^1 {K_1 (\bar{{s}},\bar{{r}},t)\psi (t)\,\text {d}t} \quad \bar{{r}}>0, \\ \int _{-1}^1 {K_2 (\bar{{s}},\bar{{r}},t)\psi (t)\,\text {d}t} \quad \bar{{r}}<0, \\ \end{array}} \right. \end{aligned}$$
(4.1)

where \(K_{1}\) and \(K_{2}\) are given by

$$\begin{aligned} \begin{array}{lll} K_1 (\bar{{s}},\bar{{r}},t)&{}=&{}\displaystyle \int _0^\infty {{\text {Re}}\left[ \frac{\text {i}n_1 }{\pi \omega \left( {n_1 -n_2 } \right) }{\text {e}}^{n_2 \bar{{r}}}\text {e}^{\text {i}(t-\bar{{s}})\omega } \right] \text {d}\omega },\\ K_2 (\bar{{s}},\bar{{r}},t)&{}=&{}\displaystyle \int _0^\infty {\text {Re}}\left[ {\frac{\text {i}n_2 }{\pi \omega \left( {n_1 -n_2 } \right) }{\text {e}}^{n_1 \bar{{r}}}\text {e}^{\text {i}(t-\bar{{s}})\omega }} \right] \text {d}\omega . \end{array} \end{aligned}$$
(4.2)

The solution of the dimensionless temperature field \(\bar{{T}}_2 \) at a specific location in a nonhomogeneous medium can be obtained by substituting the series expression (3.3) into (4.1) and integrating the resulting equation by using the Gauss–Chebyshev integration formula. The temperature solution for the problem described in Fig. 1 can then be superpositioned from Eq. (2.7) and \(\bar{{T}}_2 \).

4.2 Heat flux intensity factor

For the problem as depicted in Fig. 2b, it can be seen from Eq. (2.12) that Eq. (2.25) is proportional to the dimensionless heat flux outside \((\left| {\bar{{s}}} \right| >1)\) as well as within \((\left| {\bar{{s}}} \right| <1)\) the crack. By using the Plemelj formula, the term with a Cauchy singularity in Eq. (2.25) can be expressed as follows:

$$\begin{aligned} \frac{1}{\pi }\int _{-1}^1 {\frac{\psi (t)}{t-\bar{{s}}}\text {d}t} =\frac{g(-1)}{\sqrt{2(-1-\bar{{s}})}}-\frac{g(1)}{\sqrt{2(\bar{{s}}-1)}}+F_0 (\bar{{s}}), \quad \left| {\bar{{s}}} \right| >1, \end{aligned}$$
(4.3)

where \(F_{0}\) has a singularity of less than 1/2. Equation (4.3) implies that the near-tip heat fluxes always possess a square-root singularity in terms of the distance from the crack tip \((\bar{{s}}=\pm 1)\). Because the heat flux for the problem as depicted in Fig. 2a is finite, the superpositioned heat flux solution for the problem as depicted in Fig. 1 contains a square-root singularity at the crack tip. To characterize the singular heat flux around the crack tips, the heat flux intensity factor [5], given by

$$\begin{aligned} H=\mathop {\lim }\limits _{\left| s \right| \rightarrow a^{+}} \sqrt{2\left| {s-a} \right| }q_r (s,0), \end{aligned}$$
(4.4)

is applied to estimate the intensity of the singular flux at both crack tips. By substituting Eqs. (2.25), (3.3), and (4.3) into Eq. (4.4), the heat flux intensity factors at both crack tips can be expressed as

$$\begin{aligned} H(a)=\frac{1}{2}Q_0 \sqrt{a}\text {e}^{\delta \sin \theta }\sum _{k=1}^N {B_k } \text {T}_k (1),\quad H(-a)=-\frac{1}{2}Q_0 \sqrt{a}\text {e}^{-\delta \sin \theta }\sum _{k=1}^N {B_k } \text {T}_k (-1). \end{aligned}$$
(4.5)

5 Results and discussion

To investigate the effects of material grading and crack insulation on heat flow, the temperature and heat flux intensity factor solutions for various grading inhomogeneities and crack orientations are calculated. Without loss of generality, the temperature is set to be zero at \(x\rightarrow \pm \infty ,y=0\). In the case of a homogeneous medium, i.e., \(\delta =0\), the nonhomogeneous formulation given in the previous sections could not render a temperature solution due to numerical difficulties, and therefore the solution is approximated by substituting \(\delta =-1\times 10^{-6}\) into the nonhomogeneous formulation. To validate the approximation and verify the accuracy of the numerical procedure, numerical results obtained with \(\delta =-1\times 10^{-6}\) are compared to the exact temperature solution given in the appendix for the homogeneous medium. A comparison between the approximate and exact temperature solutions along the crack surface plane \((\bar{{r}}=0)\) is given in Table 2, from which it can be seen that the approximate solution agrees very well with the exact solution.

Table 2 Numerical and closed-form solutions of crack surface temperatures for the case of a homogeneous medium
Full size table
Fig. 3
figure 3

Isothermal contours for homogeneous medium, \(\theta =0\)

Full size image

The temperature solutions around the insulated crack for various grading inhomogeneities and crack orientations are presented in Figs. 3–5. Shown in Fig. 3 are the isothermal contours around the crack in a homogeneous medium under uniform remote heat flux in the direction perpendicular to the crack. From Fig. 3 it can be seen that the temperature field is symmetric with respect to the \(y\)-axis and antisymmetric with respect to the \(x\)-axis. It can also be seen from Fig. 3 that the temperature solutions agree very well with the benchmark solutions from [5]. Note that the signs of the benchmark solutions shown in Fig. 3 are opposite to the signs of the original solutions given in [5]. The adjustment is intended to compensate the opposite remote heat flux directions assumed in [5] and this study.

Fig. 4
figure 4

Effect of material inhomogeneity on isothermal contours for the case of \(\theta =36^{\circ }\) a \(\delta =0\) b \(\delta =-1\) c \(\delta =-2\) d \(\delta =-3\)

Full size image

Shown in Fig. 4 are the isothermal contours around an inclined crack of angle \(\theta =36^{\circ }\). It can be seen from Fig. 4a that when the medium is homogeneous, the temperatures above and below the crack surface plane on the right side of the medium (\(\bar{{x}}>0\)) are equal in value but opposite in sign to the temperatures below and above the crack surface plane on the left side of the medium (\(\bar{{x}}<0)\). The antisymmetry in the temperature field (Fig. 4a) may be attributed to the geometrical configuration about the coordinates. As the medium becomes nonhomogeneous, it can be seen from Figs. 4b–d that the temperature field is no longer antisymmetric. Instead, the temperature gradient becomes more significant and skews toward the top side of the crack as the material inhomogeneity increases. The higher temperature change is related to the lower thermal conductivity. Under a uniform remote heat flux, it is expected that a higher temperature gradient would exist in the region of lower conductivity.

Fig. 5
figure 5

Effect of crack orientations on isothermal contours for the case of \(\delta =-1\) a \(\theta =0^{\circ }\) b \(\theta =18^{\circ }\) c \(\theta =54^{\circ }\) d \(\theta =72^{\circ }\) e \(\theta =89^{\circ }\)

Full size image

The effect of crack orientation on heat flow in a nonhomogeneous medium is shown in Fig. 5, in which the isothermal contours for the FGM inhomogeneity parameter \(\delta =-1\) and crack orientations of \(\theta = \) 0, 18, 54, 72, 89\(^{\circ }\) are presented. It can be seen from Figs. 4b and 5 that the temperature gradient decreases and skews toward the right side of the crack as the crack orientation angle increases. As expected, the corresponding reduction in the flux-insulating capability of the crack has a more dominant influence and causes the temperature gradient to drop. When the crack orientation approaches \(90^{\circ }\), i.e., coincides with the direction of the remote heat flux, the insulating effect of the crack becomes absent and the temperature difference across crack surfaces diminishes.

The heat flux intensity factors for selected FGM inhomogeneity parameter and crack orientation angles are given in Tables 3 and 4, in which the negative signs of the heat flux intensity factors are associated to the uniform remote heat flux in the negative \(y\)-direction. For the case of a crack of orientation \(\theta =0^{\circ }\) in a homogeneous medium \((\delta =0)\), the heat flux intensity factors shown in Table 3 and the values given in [5] are identical in magnitude but with a sign difference, which again can be attributed to the opposite remote heat flux direction.

Table 3 Heat flux intensity factors for right (\(s=a)\) and left (\(s=-a)\) crack tips
Full size table
Table 4 Heat flux intensity factors for small \(\theta \)
Full size table

For the case of a crack with orientation angle \(\theta =0^{\circ }\) in a FGM, it can be seen from Table 3 that the heat flux intensity factor increases as the absolute value of the inhomogeneity parameter increases (i.e., as the medium becomes more nonhomogeneous). Furthermore, the crack-tip heat flux intensity factors in cases of heat flowing in the directions of increasing or decreasing conductivity are the same, as long as \(|\delta |\) are identical. Also for the case of \(\theta =0^{\circ }\), because of the symmetry of the geometry and loading with respect to the \(y\)-axis, \(H(a)\) is equal to \(H(-a)\).

From Table 3 it also can be seen that as the crack orientation angle increases from \(\theta =0^{\circ }\) to higher values, the crack-tip heat flux intensity factor is shifting from a symmetric function of \(\delta \) to a monotonic one. Furthermore, for the nonzero crack orientation angles shown in Table 3, the absolute value of the heat flux intensity factor at the right crack tip increases as the material inhomogeneity increases. The higher flux intensity can be attributed to the higher thermal conductivity locally around the crack tip. Similarly, as the material inhomogeneity parameter increases, the absolute value of the heat flux intensity factor at the left crack tip decreases because of the reducing thermal conductivity locally around the crack tip. By comparing the values of \(H(a)\) and \(H(-a)\) for any specific crack orientation, it can further be seen from Table 3 that \(H(a)\) in a FGM with a particular \(\delta \) value equals \(H(-a)\) in a medium with a \(\delta \) value that is the same in magnitude but opposite in sign.

The effect of crack orientation angle on the heat flux intensity factors can also be observed from Tables 3 and 4, from which it can be seen that, except for some of the cases where \(0^{\circ }<\theta <\text {1}8^{\circ }\), the magnitude of the heat flux intensity factor decreases as \(\theta \) increases. The variation in the heat flux intensity factor as the crack orientation changes may be attributed to two influencing factors: the local thermal conductivity around the crack tip and the heat flow insulability of the crack. For a FGM with positive \(\delta \), the local thermal conductivity around the right crack tip increases as \(\theta \) increases, and as a consequence, the higher thermal conductivity would enhance the heat flux intensification; on the other hand, the higher \(\theta \) would lead to lower \(Q^{*}\) (less heat insulation) and the magnitude of \(H\) would be reduced. For the cases of FGM with positive \(\delta \) and \(\theta >\text {1}8^{\circ }\), the decreasing \(\left| {H(a)} \right| \) as \(\theta \) increases as shown in Table 3 indicates that the reduction in flux insulability of the crack has a more dominant influence than the increase in the local thermal conductivity, and it causes the magnitude of the heat flux intensity factor to drop. But when \(\delta >0\) and \(\theta <\text {1}8^{\circ }\), as can be seen in Table 4, the competing influences of the local thermal conductivity and heat flux insulability lead to a local maximum of \(\left| {H(a)} \right| \). As an example, the results for \(\delta =1\) as given in Table 4 indicate that the local thermal conductivity associated with the material inhomogeneity is the dominant influence for the flux intensification, and \(\left| {H(a)} \right| \) increases as \(\theta \) increases from \(0^{\circ }\) to \(11^{\circ }\); but when \(\theta >11^{\circ }\), the decrease in heat flux insulability dominates the increase in local thermal conductivity, and the \(\left| {H(a)} \right| \) decreases as \(\theta \) increases. A maximum value of \(\left| {H(a)} \right| \) therefore occurs when \(\theta =11^{\circ }\) for the case where \(\delta =1\). Because the local thermal conductivity around the right crack tip increases as the inhomogeneity parameter \(\delta \) increases, the maximum of \(\left| {H(a)} \right| \) is reached at a larger crack orientation angle \(\theta \) for higher values of \(\delta \), and it can be seen from Table 4 that the maximum of \(\left| {H(a)} \right| \) occurs at \(\theta =\) 11, 15, and \(16^{\circ }\) when \(\delta =1\), 2, and 3, respectively.

For cases where \(\delta <0\), because both the heat flow insulability and the local thermal conductivity around the right crack tip decrease as \(\theta \) increases, \(\left| {H(a)} \right| \) decreases monotonically as \(\theta \) increases from \(0^{\circ }\) to \(90^{\circ }\). For the limiting case of \(\theta = 89^{\circ }\), due to the drastically decreasing heat flux insulability of the crack, the absolute intensity factor \(H\) approaches zero for either positive or negative values of \(\delta \).

6 Concluding remarks

The thermal conduction problem of a functionally graded medium containing an arbitrarily oriented crack under uniform remote heat flux was considered. Isothermal temperature contours and the heat flux intensity factors were presented to characterize the heat flow in the vicinity of the crack and the singular intensifications of heat flux at the crack tip. Some conclusions from this study are given as follows:

  1. 1.

    As the grading inhomogeneity increases, the temperature gradient on the side of the crack that has lower thermal conductivity increases, but the magnitude of the heat flux intensity factor at the crack tip on the side of lower thermal conductivity decreases.

  2. 2.

    The temperature gradient around the crack decreases as the crack orientation angle increases. When the crack orientation becomes more coincident with the direction of the remote heat flux, the insulating effect of the crack diminishes, and as a result, the temperature difference across crack surfaces and the heat flux intensity factors at crack tips approach zero.

  3. 3.

    As the crack orientation becomes less perpendicular to the direction of remote heat flux and material grading, the magnitude of the heat flux intensity factor at the crack tip on the side of higher thermal conductivity first increases and then decreases; while the magnitude of the heat flux intensity factor at the crack tip on the side of lower thermal conductivity decreases monotonically.