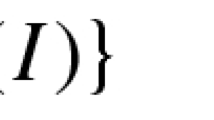The Second-Order L ²-Flow of Inextensible Elastic Curves with Hinged Ends in the Plane

Abstract

In this article, we study the evolution of open inextensible planar curves with hinged ends. We obtain long time existence of C ^∞-smooth solutions during the evolution, given the initial curves that are only C ²-smooth with vanishing curvature at the boundary. Moreover, the asymptotic limits of this flow are inextensible elasticae. Our method and result extend the work by Wen (Duke Math. J. 70(3):683–698, 1993).

Appendix

Lemma 13

Let $\ell\in\mathbb{N}$, and

$$\begin{aligned} \gamma_{\ell}(s,t) :=\int_{0}^{t}\int _{-\infty}^{\infty} \partial_s^{\ell}K(s- \xi,t-\tau) \cdot(h\circ\varphi) (\xi,\tau) d\xi d\tau . \end{aligned}$$

Then, under the assumption in Lemma  10, $\gamma_{\ell}: D_{0}^{b}\rightarrow\mathbb{R}$ is well-defined for any ℓ∈{1,2,…,m+1}. Moreover, for any δ∈(0,t), the following properties hold,

$$\begin{aligned} \bigl\vert \gamma_\ell(s,t)\bigr\vert &\leq C_{\ell}^{\prime\prime} (b, \delta) ,\quad \forall (s, t)\in D_\delta^b , \end{aligned}$$

(4.1)

$$\begin{aligned} \bigl\vert \gamma_\ell(s_2, t) - \gamma_\ell(s_1, t) \bigr\vert &\le C_{\ell}^{\prime\prime} (b, \delta) \cdot |s_2-s_1| ,\quad \forall (s_1, t), (s_2, t) \in D_\delta^b , \end{aligned}$$

(4.2)

$$\begin{aligned} \gamma_\ell &\in C^{0}\bigl(D_0^b \bigr) , \end{aligned}$$

(4.3)

where $C_{\ell}^{\prime\prime}(b, \delta)$ is a constant.

Proof

Note that since $\varphi\in\mathfrak{B}_{b}^{L}(d_{0},M_{0})$, we may apply (3.34), (3.32), (3.33), and (3.20), and verify easily that, for any ℓ∈{1,2,…,m},

$$\begin{aligned} \partial_\xi^\ell(h\circ\varphi) &\in C^{0} \bigl(D_0^b\bigr) , \\ \bigl|\partial_\xi^\ell(h\circ\varphi) (\xi, \tau)\bigr| &\le C( \ell, b, \delta) , \end{aligned}$$

(4.4)

$$\begin{aligned} \bigl|\partial_\xi^\ell(h\circ\varphi) (\xi_2, \tau)-\partial_\xi^\ell(h\circ \varphi) (\xi_1, \tau)\bigr| &\le C (\ell, b, \delta)\cdot|\xi_2 -\xi_1| , \end{aligned}$$

(4.5)

for all $(\xi,\tau)\in D_{\delta}^{b}$, $(\xi_{i},\tau) \in D_{\delta}^{b}$, i∈{1,2}, and some positive constants C(ℓ,b,δ). For convenience, we may assume without loss of generality that, for fixed ℓ and b, C(ℓ,b,δ)↗+∞ as δ↘+0.

From the definition of fundamental solution K in (3.12), it is easy to verify that K is infinitely differentiable in $\mathbb{R}\times(0, \infty)$ and its derivatives of any order is uniformly bounded in $\mathbb{R}\times[\epsilon, \infty)$ for any fixed ϵ>0. In fact, for any $k\in\mathbb{N}$,

$$\begin{aligned} \partial_x^k K(x,t)=P_t^k(x) \cdot K(x,t), \end{aligned}$$

(4.6)

where $P_{t}^{k}(x)$ is a polynomial of degree k whose coefficients depend continuously on t and could tend to infinity only if t→+0. From using (4.6), it is easy to verify that, for any fixed t>0, $s\in\mathbb{R}$, and t ₁,t ₂≥0,

$$\begin{aligned} &\int_{-\infty}^{\infty} \bigl\vert \partial_s^k K(s-\xi,t)\bigr\vert d \xi< C_K(k,t) , \end{aligned}$$

(4.7)

$$\begin{aligned} &\int_{t_1}^{t_2}\int_{-\infty}^{\infty} \bigl\vert \partial_s K(s-\xi,\tau)\bigr\vert d\xi d\tau = \frac{2(\sqrt{t_2}-\sqrt{t_1})}{\sqrt{\pi}} , \end{aligned}$$

(4.8)

where the constant C _K (k,t)→+∞ as t→+0.

To show (4.1) when ℓ∈{1,2,…,m+1}, observe that, with a change of variables and an integration by parts with respect to the space variables,

$$\begin{aligned} \gamma_{\ell}(s,t) &=\int_{0}^{\epsilon^\prime}\int _{-\infty}^{\infty} \partial_s^\ell K(s-\xi,t-\tau) \cdot(h\circ\varphi) (\xi,\tau) d\xi d\tau \\ & \quad{} +\int_{\epsilon^\prime}^{t}\int_{-\infty}^{\infty} \partial_s^{\ell-1}K(s-\xi,t-\tau) \cdot\frac{\partial(h\circ\varphi )}{\partial\xi}( \xi,\tau) d\xi d\tau \\ & \quad{} - \int_{\epsilon^\prime}^{t} \bigl[ \partial_s^{\ell-1}K(s-\xi,t-\tau) \cdot(h\circ\varphi) (\xi, \tau) \bigr]_{-\infty}^{\infty} d\tau , \end{aligned}$$

(4.9)

for any fixed ϵ′∈(0,t). Note that, for any fixed τ∈(ϵ′,t), one can infer from (4.6) and (3.20) that the integrand in the last term is null. As we continue to integrate by parts in (4.9), using (4.4) and the property of exponentially vanishing rate of $[\partial_{s}^{j}K](x, t^{\prime})$, we obtain that

$$\begin{aligned} \gamma_{\ell}(s,t) &=\int_{0}^{\epsilon^\prime}\int _{-\infty}^{\infty} \partial_s^\ell K(s-\xi,t-\tau) \cdot(h\circ\varphi) (\xi,\tau) d\xi d\tau \\ & \quad{} +\int_{\epsilon^\prime}^{t}\int_{-\infty}^{\infty} \partial_s K(s-\xi,t-\tau) \cdot\bigl[\partial_\xi^{\ell-1}(h \circ\varphi )\bigr](\xi,\tau) d\xi d\tau \end{aligned}$$

(4.10)

for any ℓ∈{1,2,…,m+1} and any fixed ϵ′∈(0,t). Now, (4.1) follows on applying (3.20), (4.4), (4.7), and (4.8). Furthermore, since (4.1) holds for any δ∈(0,b), $\gamma_{\ell}: D_{0}^{b}\rightarrow\mathbb{R}$ is well-defined.

To show (4.2), we use the formula (4.10) and write

$$\begin{aligned} &\gamma_{m+1}(s_2, t) - \gamma_{m+1}(s_1, t) \\ &\quad=\int_{0}^{\epsilon^\prime}\int_{-\infty}^{\infty} \bigl( \partial_s^{m+1} K(s_2-\xi,t-\tau) - \partial_s^{m+1} K(s_1-\xi,t-\tau) \bigr) \\ & \qquad{} \cdot(h\circ\varphi) (\xi,\tau) d\xi d\tau \\ &\qquad{} +\int_{\epsilon^\prime}^{t}\int_{-\infty}^{\infty} \bigl( \partial_s K(s_2-\xi,t-\tau) - \partial_s K(s_1-\xi,t-\tau) \bigr) \\ &\qquad{} \cdot \partial_\xi^{m}(h\circ \varphi) (\xi,\tau) d\xi d\tau , \end{aligned}$$

(4.11)

for some fixed ϵ′∈(0,t). The first integral in (4.11) can be rewritten as

$$\begin{aligned} \int_{0}^{\epsilon^\prime}\int_{-\infty}^{\infty} \int_{s_1}^{s_2} \partial_s^{m+2} K(s-\xi,t-\tau) \cdot(h\circ\varphi) (\xi,\tau) ds d\xi d\tau . \end{aligned}$$

(4.12)

For fixed t,τ satisfying t−τ≥t−ϵ′>0, one can conclude from (4.6) and (3.20) that the function $K_{(t,\tau)}^{m+2}(\xi,s):=\partial_{s}^{m+2} K(s-\xi,t-\tau) \cdot (h\circ\varphi)(\xi,\tau)$ is uniformly bounded, integrable over the subset $\mathbb{R}\times [s_{1},s_{2}]\subset\mathbb{R}^{2}$ and

$$\begin{aligned} \iint_{\mathbb{R}\times[s_1,s_2]} \bigl\vert K_{(t,\tau)}^{m+2}(\xi,s) \bigr\vert d(\xi,s) < +\infty . \end{aligned}$$

(4.13)

By using Fubini’s Theorem, the integral in (4.12) can be written as

$$\begin{aligned} \int_{0}^{\epsilon^\prime}\int_{s_1}^{s_2} \int_{-\infty}^{\infty} \partial_s^{m+2} K(s-\xi,t-\tau) \cdot(h\circ\varphi) (\xi,\tau) d\xi ds d\tau . \end{aligned}$$

(4.14)

The second integral in (4.11) can be written as

$$\begin{aligned} &\int_{\epsilon^\prime}^{t}\int_{-\infty}^{\infty} \partial_s K \bigl(s_1-\xi^\prime,t-\tau\bigr) \\ &\quad{} \cdot \bigl[ \partial_{\xi^\prime}^{m} (h\circ\varphi) \bigl(\xi^\prime+\Delta s,\tau\bigr) - \partial_{\xi^\prime}^{m} (h\circ\varphi) \bigl(\xi^\prime, \tau\bigr) \bigr] d\xi^\prime d\tau , \end{aligned}$$

(4.15)

by the change of variables, ξ′=ξ−Δs, where Δs:=s ₂−s ₁≥0. Thus, by applying (3.20), (4.7) to the integral (4.14), and by applying (4.5), (4.8) to the integral (4.15), we obtain

$$\begin{aligned} &\bigl\vert \gamma_{m+1}(s_2, t) - \gamma_{m+1}(s_1, t)\bigr\vert \\ &\quad\le \Delta s \cdot \biggl( C_{K}\bigl(m+2, t- \epsilon^\prime\bigr) \cdot2C_3 \cdot\epsilon^\prime + C(m, t, \delta) \cdot\bigl(t-\epsilon^\prime\bigr) \cdot \frac{2(\sqrt{t}-\sqrt{\epsilon^\prime})}{\sqrt{\pi}} \biggr) . \end{aligned}$$

(4.16)

Therefore, (4.16) implies the continuity of γ _m+1 in the domain $D_{0}^{b}$ along the s-direction, i.e., we have proved (4.2).

To show (4.3), we only need to prove the continuity of γ _m+1 at any point in $D_{0}^{b}$ along the t-direction, because of the result in (4.2). Now, for a fixed t ₁∈(0,b), we assume that ϵ>0 satisfies

$$\begin{aligned} b>t_1+\epsilon>t_1-\epsilon>0 \end{aligned}$$

(4.17)

and choose t ₂≠t ₁ so that

$$\begin{aligned} |t_2-t_1|< \epsilon/2 . \end{aligned}$$

(4.18)

From using (4.10), we write

$$\begin{aligned} &\gamma_{m+1}(s, t_2) - \gamma_{m+1}(s, t_1) \\ &\quad=\int_{0}^{t_1-\epsilon}\int_{-\infty}^{\infty} \bigl( \partial_s^{m+1} K(s-\xi, t_2-\tau) - \partial_s^{m+1} K(s-\xi, t_1-\tau) \bigr) \\ &\qquad{} \cdot(h\circ\varphi) (\xi,\tau) d\xi d\tau \\ &\qquad{} +\int_{t_1-\epsilon}^{t_2}\int_{-\infty}^{\infty} \partial_s K(s-\xi, t_2-\tau) \cdot \partial_\xi^{m}(h\circ\varphi) (\xi,\tau) d\xi d\tau \\ &\qquad{} - \int_{t_1-\epsilon}^{t_1}\int_{-\infty}^{\infty} \partial_s K(s-\xi, t_1-\tau) \cdot \partial_\xi^{m}(h\circ\varphi) (\xi,\tau) d\xi d\tau . \end{aligned}$$

(4.19)

By the property $\partial_{t} K(x,t)=\partial_{x}^{2} K(x,t)$, the first integral in (4.19) can be written as

$$\begin{aligned} &\int_{0}^{t_1-\epsilon} \int_{-\infty}^{\infty} \int_{t_1}^{t_2} \partial_s^{m+3} K(s-\xi, t-\tau) \cdot(h\circ\varphi) (\xi,\tau) dt d\xi d\tau . \end{aligned}$$

(4.20)

For fixed $s\in\mathbb{R}$, τ∈[0,t ₁−ϵ], one can conclude from (4.6) and (3.20) that the function $L_{(s,\tau)}^{m+3}(\xi,t):=\partial_{s}^{m+3} K(s-\xi,t-\tau) \cdot (h\circ\varphi)(\xi,\tau)$ is uniformly bounded, integrable over the subset $\mathbb{R}\times [t_{1},t_{2}]\subset\mathbb{R}^{2}$ and

$$\begin{aligned} \iint_{\mathbb{R}\times[t_1,t_2]} \bigl\vert L_{(s,\tau)}^{m+3}(\xi,t) \bigr\vert d(\xi,t) < +\infty . \end{aligned}$$

(4.21)

By using Fubini’s Theorem, we may rewrite the integral in (4.20) as

$$\begin{aligned} &\int_{0}^{t_1-\epsilon} \int_{t_1}^{t_2} \int_{-\infty}^{\infty} \partial_s^{m+3} K(s-\xi, t-\tau) \cdot(h\circ\varphi) (\xi,\tau) d\xi dt d\tau =:I_1 . \end{aligned}$$

(4.22)

By applying (4.7), (4.17), (4.18), we note that t−τ≥ϵ/2 in the integrand of (4.22) and thus

$$\begin{aligned} |I_1|\le|t_2-t_1| \cdot(t_1- \epsilon) \cdot2C_3 \cdot\sup_{t\in[\epsilon/2, b]}\bigl\{ C_{K}(m+3, t)\bigr\} . \end{aligned}$$

(4.23)

Denote the second integral in (4.19) by I ₂. Then, by applying (4.4), (4.8), (4.18), we obtain

$$\begin{aligned} |I_2|\le\bigl(|t_2-t_1|+\epsilon\bigr) \cdot \frac{2}{\sqrt{\pi t_1}} \cdot C(m, b, t_1-\epsilon) . \end{aligned}$$

(4.24)

Similarly, we may denote the third integral in (4.19) by I ₃ and obtain

$$\begin{aligned} |I_3|\le\epsilon \cdot\frac{2}{\sqrt{\pi t_1}} \cdot C(m, b, t_1-\epsilon) . \end{aligned}$$

(4.25)

Notice that sup _t∈[ϵ/2,b]{C _K (m+3,t)}→+∞, as ϵ→+0, while C(m,b,t ₁−ϵ) in (4.24) and (4.25) would remain bounded as ϵ→+0. Now, for any sufficiently small ϵ>0, we choose any t ₂∈(t ₁−ϵ/2,t ₁+ϵ/2) such that

$$|t_2-t_1|^{1/2} \cdot\sup_{t\in(\epsilon/2, b)}\bigl\{ C_{K}(m+3, t)\bigr\} \le1 . $$

Then, from (4.23)–(4.25), we obtain

$$\begin{aligned} &\bigl|\gamma_{m+1}(s,t_2) - \gamma_{m+1}(s,t_1)\bigr| \\ &\quad< \biggl\{ |\Delta t| ^{\frac{1}{2}}\cdot t_1 \cdot2C_3 + \bigl(|\Delta t|+2\epsilon\bigr) \cdot\frac{2}{\sqrt{\pi t_1}} \cdot C(m, b, t_1-\epsilon) \biggr\} , \end{aligned}$$

where |Δt|:=|t ₂−t ₁|<ϵ/2. Now, we have the continuity of γ _m+1 along t-direction at any point in $D_{0}^{b}$. Thus, the proof of (4.3) is obtained. □

Proof of Lemma 10

We want to show that

$$\begin{aligned} \partial_s^{\ell}H_{0}^{\varphi}(\cdot,t) = \gamma_{\ell}(\cdot,t) ,\quad \forall t\in(0,b] ,\ \ell\in \{1,2,\ldots,m+1\} . \end{aligned}$$

(4.26)

Let

$$\begin{aligned} J_\epsilon(s,t) :=\int_0^{t-\epsilon}\int _{-\infty}^{\infty} K(s-\xi,t-\tau) \cdot(h\circ\varphi) ( \xi,\tau) d\xi d\tau . \end{aligned}$$

Note that, for fixed t∈(0,b] and fixed ϵ∈(0,t), J _ϵ (⋅,t) is smooth over $\mathbb{R}$, and we may exchange the operation of differentiation and integration below,

$$\begin{aligned} \partial_s^{\ell}J_\epsilon(s,t) &=\int _0^{t-\epsilon}\int_{-\infty}^{\infty} \partial_s^{\ell}K(s-\xi,t-\tau) \cdot(h\circ\varphi) (\xi, \tau) d\xi d\tau . \end{aligned}$$

Then, for any fixed t∈(0,b] and ℓ∈{1,2,…,m+1}, we first show that, on any bounded and closed interval of $\mathbb{R}$,

$$\partial_s^{\ell}J_\epsilon(\cdot, t)\rightarrow \gamma_{\ell}(\cdot, t) \text{ uniformly as } \epsilon\rightarrow+0 . $$

Observe that, from (4.10), choosing sufficiently small ϵ>0 so that t−ϵ>δ>0, and applying (4.8), we have

$$\begin{aligned} &\bigl\vert \gamma_{\ell}(s, t) - \partial_s^{\ell}J_\epsilon(s, t) \bigr\vert \\ &\quad= \biggl\vert \int_{t-\epsilon}^{t}\int _{-\infty}^{\infty} \partial_s K(s-\xi,t-\tau) \cdot \partial_\xi^{\ell-1}(h\circ\varphi) (\xi,\tau) d\xi d\tau\biggr\vert \\ &\quad \leq C(\ell-1, b, \delta)\cdot\frac{2(\sqrt{t}-\sqrt{t-\epsilon })}{\sqrt{\pi}} . \end{aligned}$$

Thus, over any compact subset $[s_{0}, s]\subset\mathbb{R}$ and for any fixed t∈(0,b],

$$\begin{aligned} \partial_s^{\ell}J_\epsilon(\cdot, t)\rightarrow \gamma_{\ell}(\cdot, t) \text{ uniformly,}\quad \forall \ell\in \{1,2,\ldots,m+1\} , \end{aligned}$$

(4.27)

as ϵ→+0. Moreover, γ _ℓ (⋅,t) is uniformly continuous on [s ₀,s], for all ℓ∈{1,2,…,m+1}.

Now, we prove (3.37) by induction argument. Namely, we assume that

$$\begin{aligned} \partial_s^{\ell}H_{0}^{\varphi}(\cdot,t) = \gamma_{\ell}(\cdot,t) ,\quad \forall \ell\in\{0,1,\ldots,m\},\ \forall t\in(0,b] . \end{aligned}$$

(4.28)

Notice that, as ℓ=0, the equality holds by the definition of function γ _ℓ . Since

$$\begin{aligned} \partial_s^{\ell} J_\epsilon(s, t) &=\int _{s_0}^{s} \partial_s^{\ell+1} J_\epsilon(x, t) dx + \partial_s^{\ell} J_\epsilon(s_0, t) , \end{aligned}$$

(4.29)

∀ℓ∈{1,…,m}, fixed t∈(0,b], and sufficiently small ϵ>0. By letting ϵ→+0 and applying (4.27) in (4.29), we derive

$$\begin{aligned} \gamma_{\ell}(s, t) =\int_{s_0}^{s} \gamma_{\ell+1}(x, t) dx + \gamma_{\ell}(s_0, t) , \quad \forall \ell\in\{1,\ldots,m\} . \end{aligned}$$

(4.30)

By applying (4.28) to the L.H.S. of (4.30), we obtain

$$\begin{aligned} \partial_s^{\ell}H_{0}^{\varphi}(s, t) = \int_{s_0}^{s} \gamma_{\ell+1}(x, t) dx + \gamma_{\ell}(s_0, t) , \quad\forall \ell\in\{1, \ldots,m\} . \end{aligned}$$

Then, by applying the fundamental theorem of calculus above, we have proved (4.26).

The proof of Lemma 10 is now completed by using an induction argument on m, and applying Lemma 13 and (4.26). Note that when m=1, (3.34), (3.32), (3.33) hold from the fact that $\varphi\in\mathfrak{B}_{t_{0}}$, for some t ₀∈(0,b ₀], and applying Lemma 6. □