1 Introduction

Ecological research and conservation and management efforts rely on estimates of population and species abundance and the ability to detect changing trends in abundance over space and time. Capture-recapture (CR; also referred to as mark-recapture) methods are widely used in population studies and come with a long history of developments for analyzing the size of animal populations (e.g., Buckland et al. 2000; Cormack 1968; Pollock et al. 1990; Pollock 1990; Seber 1982, 1986, 1992). The framework for such methods relies on the ability of one to recapture or resight marked individuals over time, accounting for capture probability. For many species and natural populations, an accurate measure of abundance can be very challenging to obtain due to variations in individual detection probabilities. Such variation can come from a variety of sources such as individual behavioral differences (e.g., trap responses), temporally dependent variables (e.g., survey conditions, time of day, etc.) and numerous other forms of persistent heterogeneity between individuals. Heterogeneity in detection probability is one of the most common and unavoidable sources of error in natural biological populations but also one of the more serious issues leading to biased abundance estimates (Carothers 1973).

After pioneering papers by Jolly (1965) and Seber (1965), a considerable amount of ecological literature has focused on extending classic models to account for implicit heterogeneity and other modern sampling issues found in animal populations (e.g., Norris and Pollock 1995, 1996; Otis et al. 1978; Pledger 2000; Pledger and Efford 1998; Pollock 1982; Royle 2004a, b; Wegner and Freeman 2008). Most of these approaches utilize variations of the maximum likelihood (ML) function. Issues arise however, because each sampling nuance leads to increasing number of parameters being introduced which may vary on space/time—something that is very hard to incorporate. While statistically powerful, the drawback can be an overly parameterized model and unintended consequences (e.g., positive birth/death rates in closed systems where this is impossible). Another concern is that the multinomial ML approach exploits independence of trials and this becomes an issue when cluster sampling is encountered. Non-independence in individual detection is likely to occur across numerous taxa, relevant especially to any species that tends to occur in groups (e.g., cetaceans, birds, amphibians, and ungulates), resulting in an overestimation in abundance. Royle (2008) attempts to handle cluster sampling bias in a Bayesian hierarchical modeling framework with uniform prior to generate a fixed dataset on each encounter. He uses Markov Chain Monte Carlo (MCMC) to complete the data using posterior distribution of the dataset. Royle demonstrates the application using varying cluster size distribution. While a powerful illustration of the effects of cluster sampling, the model is not compared with existing models to demonstrate its convergence rate and performance. The use of a diffuse prior in a Bayesian model and its performance is also not discussed. Martin et al. (2011) develop a beta-binomial mixture model that accounts for corrected Bernoulli outcomes. Both approaches add additional parameters to be modeled and require an assumed underlying distribution for these parameters.

We consider a non-parametric frequentist framework for capture-recapture data based on a simple ratio estimator, which offers several advantages. As a non-parametric model, it does not require a known underlying distribution for parameters nor the assumptions that come with parametric models (such as of equal probability of detection between individuals), eliminating the need for post-hoc corrections or additional modeling to account for heterogeneity and other violated assumptions. Instead, we allow for implicit heterogeneity when units being sampled are hard to identify. Our approach explicitly deals with dependence of trials by considering trials to be dependent; therefore, cluster sampling is handled naturally and additional adjustments are not necessary.

This model fills a critical oversight and gap in the literature which does not currently take into account the ordering of recaptures. Order is being simply ignored in the estimation process. Our estimator accounts for ordering, utilizing the fact that a system with a small population will have a greater frequency of recaptures “early” in the survey work compared to an identical system with a larger population. Classically, within a given closed mark or recapture time period, the primary goal is to detect all individuals at least once. If individuals were seen or captured multiple times, the additional captures are ignored. This leads to loss of useful data points. With the new model, we utilize the entire data set to obtain abundance estimates. We provide mathematical proof that our estimator attains asymptotic minimum variance (i.e., population variance) under open systems. Additionally, a formula for population variance provides insights into the underlying system variance.

Here we develop and present a new nonparametric model for estimating abundance. The proposed model is described in Sect. 2. Open and closed systems are discussed in Sect. 3. A simulation study of cluster sampling on a closed system to validate the estimator and analyze its properties is presented in Sect. 4. Finally, we consider the application of the model to a mark-recapture dataset of bottlenose dolphins (Tursiops truncatus) in Northwest Florida in Sect. 5.

2 Model

We use mathematical “operator” notation instead of functional notation. All captures/recaptures are Bernoulli trials with each trial resulting in capture of a single unit. This is relaxed in cluster sampling situation (open systems) and we let the reader know accordingly. Thus each trial is a simple random sample of one unit.

  • \(q_i =\) Probability of catching a marked unit in ith recapture (computed at end of ith trial);

  • \(i=1 \ldots n\)

  • \(Y_i =\) Random # of marked units at end of ith recapture

  • \(Y_o =\) Initial known # of marked units at time zero

  • \(\tau =\) Total population to be estimated

    Then

  • \(q_i =\frac{Y_i }{\tau }\) with \(Y_i\) always random and \(\tau \) random in open system only. With \(x_i =bernoulli(q_i )\) trials,

    $$\begin{aligned} Ex_i =q_i ;Varx_i =q_i (1-q_i );E\mathop x\limits ^- =\mathop q\limits ^- \end{aligned}$$

    Using our definitions and non iid version of Strong Law of Large Numbers (SLLN),

    $$\begin{aligned} \mathop {x}\limits ^- =\frac{x_1 +x_2 + \ldots x_n }{n}\mathop {\rightarrow } \limits ^{SLLN} E\frac{x_1 +x_2 + \ldots x_n }{n}=\frac{q_1 +q_2 + \ldots q_n }{n}=\mathop {q}\limits ^{-} \end{aligned}$$
Fig. 1
figure 1

Schematic flow

Full size image

All values are reported at the end of the period. For example for the ith interval, the data \(x_i\) is collected throughout the interval but we assume that values are reported at the end of the interval. This assumption is made out of mathematical convenience only (Fig. 1).

The results presented are asymptotic. At the same time the populations are finite. Thus \(n\rightarrow \infty \) means sampling all population units in the system.

2.1 Capture history as an ordered string

One the key aspect of the model is to capture the sequence or ordering of the capture-recapture history. Assuming no implicit heterogeneity issues, we do not care about “unique” histories and their frequencies and instead focus on the collective sampling history. This is different than current literature that relies on unique capture history of each unit, regardless of heterogeneity. In the case of heterogeneity, our model also requires these capture histories of each unit to be recorded. To illustrate, suppose we assign 0 to a capture and 1 to a recapture (first or subsequent). Then the entire sampling history of 20 encounters could be denoted by a single string such as:

$$\begin{aligned}&x_i :00010101001011000101\\&Y_i :1,2,3,3,4,4,5,5,6,7,7,8,8,8,9,10,11,11,12,12 \end{aligned}$$

Note that ordering is relevant as\(\sum {Y_i }\) and \(\sum {x_i } \)will change on a different ordering. Thus permutations on this string will produce different estimates of the population.

2.2 Cluster sampling

Throughout our development, we have assumed draw by draw with replacement. Cluster sampling situation arises when more than one unit is caught at a time, such as when the experimenter is using a net to catch fish. In a cluster sampling situation, a unit cannot be captured twice (recaptured) in a single trial since many units are caught at once and this eliminates the opportunity for a unit to be released and possibly recaptured.

The open system results under Appendices A, B and C apply to cluster sampling situations. Thus in our model, even for truly real world closed systems, under cluster sampling, we would use open system results. The closed system results in our model apply to closed systems under non-cluster situations. This is not a model limitation but an artifact of the way theorems are developed. In cluster sampling situations, we model each individual recapture as an immediate exit from the system. In other words, these individuals are no longer available for further recaptures. We continue to note these individual “exits” as if they were individual experiments and we allow all of them to return at once (entry) into the system before the start of the next cluster trial. A typical data setup is shown below as an example.

Suppose the end of ith trial is a cluster trial with 3 recaptures (bold rows) and 2 captures (un-bolded rows). Translated in terms of our “individualized model” the data would appear as in Table 1.

Table 1 Data table under cluster sampling
Full size table

The first two rows reflect the adjusted data to account for first two recaptures due to cluster sampling. The last row reflects the last recaptured unit which is treated as a singleton trial with no adjustment. The ordering is important as after the last recapture, the experiment is repeated. The exited units re-enter the system at the end of the trial \(k_i =5\).

Note that clustering data adjustments to the data are needed only when more than one unit is captured/recaptured. Additionally, since the ordering information in a cluster sample is lost, a random ordering is suggested between captures and recaptures within a cluster since there is no reason to assume any specific ordering.

2.3 Open system model (under cluster sampling)

We start by repeating the experiment. The number of marked units at the end of time \(i-1\) (beginning of timei) is \(Y_{i-1}\) . At the end of timeithe marked population is updated due to \(x_i =0\) recaptures, \(s_i\) marked units leaving the system (including deaths), \(k_i\) marked units re-enter the system due to cluster trials. The marked population at the end of time i is \(Y_i\) . Formally,

$$\begin{aligned} Y_i= & {} Y_{i-1} +1-x_i -s_i +k_i ;i=1\ldots n \\ Y_i= & {} Y_{i-1} +1-(x_i +s_i -k_i ) \end{aligned}$$

Net marked exits \(s_i \) : = Random marked exits – Random marked re-entries + Cluster marked exits Cluster marked re-entries \(k_i \) : = number of marked units re-entering the system as a result of cluster trials. The quantity, \(k_i \ge 0\) is completely known once \(s_i\) is known. Thus \(P\left( {\left. {K_i =k_i } \right| s_i } \right) =1\). We will thus treat \(k_i\) as a constant whose values are known.

Also note the following:

  1. 1.

    We draw the distinction between “random” re-entries of marked units and “cluster re-entries” that were explained above. The cluster re-entries are non-random and arise due to model specification.

  2. 2.

    The exits \(s_i\) are modeled as binomial trials with a given average probability of exit over all available marked units. We thus require that each trial is random.

  3. 3.

    The random variable\(s_i\) is non-negative. This does not mean that we assume that there are more marked exits than random re-entries on each trial. If there are more marked exits than random re-entries, the case is explained below in detail.

  4. 4.

    Unmarked units can leave or enter the system, including births, as these are unmarked.

2.4 Excess random marked re-entries

Random re-entries are netted against marked exits and are therefore “handled” by the quantity \(s_i \ge 0\). The limitation on non-negative \(s_i\) leads us to consider the case where “excess” random re-entries have to be considered. We do not specifically model these excess random re-entries. Instead we treat them as unmarked units when they re-enter the system. This has no effect on our estimation but the price we pay is that this marked data is lost and we have to start fresh. In other words, when these previously marked units are caught again, we remove the old marks and remark them.

3 Open and closed systems

Theorems 1 and 2 are given in appendixes A, B and C. Appendix D discusses provides a useful discussion on the Theorems. The closed system results are discussed in Appendix E.

4 Simulations

The closed form results of the order of convergence of the estimator could not be obtained (Appendix F). This is an artifact of the complexity of algebra and not a model limitation. Therefore, a simulation study of cluster sampling on a closed system was performed to validate the estimator and analyze its properties. First, a Monte Carlo simulation was implemented in R, in which clusters of samples were sequentially selected from a fixed population (closed system). The sequence of captures for each simulation was saved for later analysis. The variance estimator was initially implemented in R, but had to be re-implemented in Python to improve the speed of calculations for large sample sizes. The STOKES high performance compute cluster at the University of Central Florida was used to run calculations in parallel.

4.1 Results for closed system under cluster sampling

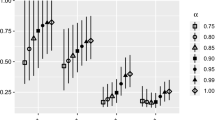
The simulator was used to estimate four population sizes: 10\(^{3}\), 10\(^{4}\), 10\(^{5}\), and 10\(^{6}\). For each population size, the cluster size was fixed at 10, and various numbers of clusters were used: 10, 20, 50, and 100. Each population/sample size combination was tested 250 times. The mean of these 250 trials was used as the estimator’s mean value. Results show that the population estimates converge to the known population as the number of clusters increased (Fig. 2). The confidence intervals in the plots were computed based on the estimated variance.

Fig. 2
figure 2

Convergence of population estimator for a simulation study of a closed system under cluster sampling for four different population sizes. Confident intervals (CI) based on estimated variance

Full size image

The simulations demonstrated that the estimator was able to produce useful estimates of population and variance with sample sizes less than 10 % of the population size. The minimum sample size for this is estimator is determined by the necessity to re-capture at least some individuals. For the largest population studied, the estimator is anticipated to produce useful estimates for sample sizes less than 1 % of the population size.

5 Case study: estimating a dolphin population

We applied the new nonparametric model to survey data on bottlenose dolphins in Northwest Florida. These data are from a mark-recapture project conducted through the University of Central Florida. Our purpose is not to provide a detailed analysis of this data set but to illustrate the application of the new model to real data. This system offers a useful example for several reasons. First, this data set offers an example of cluster sampling since bottlenose dolphins are typically seen together in groups. The new model does not assume independence and therefore handles cluster sampling directly. Second, traditional analyses of dolphin abundances can result in data loss, a concern that may be alleviated by the new model. Instead of a physical mark, dolphin mark-recapture research utilizes images that are taken of individuals and used to track individuals over time. Re-sights of individuals across a given mark or recapture period are traditionally ignored since it only matters whether or not an individual was detected, not how many times. Dolphins are fast moving animals that can traverse large areas quickly. Although surveys are designed to minimize the chance of re-encountering individuals again in the same mark or recapture time frame, often it cannot be avoided. This data set used in the new model includes all resights of individuals, even within a given mark or recapture period, and the new model takes order into account, utilizing that information directly instead of discarding it.

5.1 Study area and survey method

Bottlenose dolphin surveys were completed in June, 2013 using a small vessel (18–21 ft) and using both line (2 km apart) and contour transects to guide coverage of the Pensacola Bay system. Sampling consisted of a primary mark period (3 days) followed by two secondary recapture periods (3 days each), using established photo-identification methods (Würsig and Jefferson 1990; Würsig and Würsig 1977). Each mark and recapture period were separated by 2 days each to allow mixing between sampling events (a total of 14 days for a complete mark-recapture-recapture session). The order of coverage was stratified so that bays were surveyed in a different order each time and the direction of coverage (north to south or vice versa) was random. All track lines for a given survey were completed in the shortest time possible to meet the assumption of a closed population and under optimal sighting conditions (\(\le \) Beaufort Sea State 3) to maximize detection probabilities. Photos were graded on fin distinctiveness and photo quality and cataloged according to established methods using program FinBase (Urian et al. 1999, 2014; Melancon et al. 2011).

5.2 Statistical analyses

Abundance from single mark recapture session was estimated using both the classic closed models (Otis et al. 1978) in program MARK and the new nonparametric method presented here. Data used for MARK were only of distinct individuals with high quality images that were seen at least once during a mark or recapture period. The data used in the nonparametric estimator were the same, except that we also included any additional resights of individuals within a given mark or recapture session (a feature of the data that classic closed models ignore). Using MARK, four models were selected to estimate abundance: Mo, Mh, Mt, and Mth. The behavioral models (e.g., Mb, Mtb, Mbh, Mbth) were not included since they are not considered biologically relevant models for this data set (i.e., there’s no indication of trap dependence). Akaike’s Information Criteria (AIC) values were used to evaluate model selection in program MARK.

5.3 Results

Table 4 presents the results from the classic closed model abundance estimates analyzed in MARK, listed in order of AIC\(_{c }\)value. Based on AIC\(_{c }\)and model deviance values alone, the Mth model has the most support. Model averaged estimates of N have become more commonly used and have shown better properties over a single-model estimate (Stanley and Burnham 1998). The MARK model average, which also takes into account the weight of each model, provided an abundance estimate of 216.73 (69.70 SE; Table 4). The non-parametric model produces a point estimate of 157.0 with SE of 23.5. This estimate was produced using Theorems 1 and 2 (Appendices A and B) under cluster sampling. Note that our cluster sampling requires using open system theorems even through the system itself is closed. This is because of exits and entries required under Table 1 under cluster sampling.

Table 2 Estimated population as a percentage of the actual population for a simulation study of a closed system under cluster sampling
Full size table
Table 3 Estimated formula based variance (of estimator) as a percentage of the true variance for a simulation study of a closed system under cluster sampling
Full size table
Table 4 Bottlenose dolphin case study results
Full size table

6 Discussion

Our simulation study shows that our estimator is asymptotically unbiased with a conservative estimate of the confidence intervals. Tables 2 and 3 as well as Fig. 2 illustrate a desirable property of the proposed model: the rate of convergence of the estimator is a monotonically increasing function of sample size and not the proportion of the population sampled. Hence the model scales nicely for larger populations - to attain the same degree of accuracy, one can sample a smaller proportion of the population. The simulations were done with sample sizes of up to 1000 which was limited only due to computational convenience. With the Normal Approximation results (Appendix C) and higher computational power, the sample sizes can be increased, which is why the simulation results are incomplete in Fig. 2 and Tables 2 and 3 for the largest two population sizes (i.e., N = 10\(^{5}\) and N = 10\(^{6})\). While it may be theoretically relevant, it may not be biologically realistic to have such a high sample size. Therefore, we did not deem it necessary to demonstrate for purposes of this paper.

Table 3 illustrates the fact that generally asymptotic confidence intervals are overstated by the model and hence conservative. A reversal occurs in entry (3,1} in Table 3 where the true standard deviation would be \(\left( {\sqrt{\frac{1}{0.82}}-1} \right) =+10.4\,\% \)of the estimated standard deviation.

The asymptotic results rely on Central Limit Theorem (non-iid case) and that itself depends on the underlying random variables or the system in question. No convincing mathematical answer exists for the “acceptable minimum size” and simulations are the best way to gain insights. Tables 2 and 3 are intended to achieve this but more can be done. We suggest a future study to include MARK based model estimates in these simulations so that comparison be made with the benchmark being the known true population.

Results from the dolphin case study dataset are mixed. One can see from Table 4 that there were a wide range of abundance estimates provided in MARK, depending on the model used and no single model was strongly supported over the other competing options. The Mth model had the lowest AIC\(_{c-}\) value and highest AIC\(_{c}\) weight, suggesting it was the most parsimonious model. However, the null model (Mo) was a closely competing model with very similar AIC\(_{c }\)value and AIC\(_{c}\) weight. The low model deviance for the Mth model also indicates stronger support for this model, however, this is likely due to the nature of it being a fully parameterized model which one would expect to fit better simply because there are more parameters to estimate. Many of the probability of first capture (\(p_{i})\) and recapture probability (\(c_{i})\) parameters were not estimated properly in either of the heterogeneity models, further indicating that these models may not be estimating N appropriately (see Table 5 found in Supplementary material, Appendix G). Given this much variability in model outputs, it is difficult to choose one model over another for providing an appropriate abundance estimate. If is also challenging to decipher whether or not variations in the model output are due to the model itself or true violations of assumptions from the data. While model averaging is commonly employed to help with these issues, any model that is artificially inflated (e.g., due to lack of independent sampling or violated assumptions) will also influence the model average. The MARK model average here was likely inflated due to the large abundance estimate from the Mth model and the large error associated with this model.

As discussed earlier, there are a variety of ways to correct for various violated assumptions but one may need multiple corrections to address multiple issues in the dataset. On the other hand, the abundance estimate from the non-parametric model presented here was comparable with three out of the four closed model results from MARK with comparable standard error. Given the simulation study results, we suggest that the nonparametric model estimates from the dolphin data were reasonable. With the number of caught units (including recaptures) at 80 % of the population (126 total units and abundance estimate of 157), we can lookup simulation Table 2 entry in cell {3,1} and guess that the true population would be \(\pm 3\,\%\) of 157.0. The true bias would higher as Table 2 entry is based on 500 samples which improves the conditions for Central Limit Theorem and at the same time lower because we have 80 % sampled instead of 50 %. On the contrary, the first MARK based model is completely incorrect while the last is substantially off. The new model is faster to run, does not risk violating strong assumptions, and is less susceptible to the human interpretation required by other approaches.

From a purely mathematical perspective, there are similarities between proposed model and the asymptotic maximum likelihood model. Both use Taylor First Order Approximation. However, the functions approximated are different and thus approximations are different for Maximum Likelihood (ML) and the new model. They are similar in that the rates of convergence and performance of estimators can be similar under closed systems, singleton trials. However, we argue that the non-parametric model developed here can be considered a better alternative for several reasons. First, the ML model requires maximizing a multivariate function over Euclidean space. That is not computationally simple and for large cohorts the maximization variables are large (recall that each cohort adds a new variable) and thus computational time is large. Our approach is primarily concerned with repetitive calculations involving the “choose” function and as simulations show, it is faster.

Second, the ML estimator requires independence of observations. In sampling (especially cluster sampling) such independence assumption is violated as the same unit can be caught repeatedly. To avoid this key violation, ML based models deploy cohort formations. Essentially each cohort is an independent sample and thus makes ML estimation feasible. The “cost” is three-fold. First, a new cohort adds one more parameter to be estimated. This results in large computational time (above point) and makes the model less attractive due to large number of parameters to be estimated. Second and more importantly, it invokes the First Order Taylor approximation again and each time the larger number of approximations decreases the convergence rate of the ML estimator. Third, there is minor loss of data in under each cohort and that reduces the efficiency of the ML estimator. The number of cohorts under ML is a balancing act. The researcher must have as few cohorts as possible but they have to form a new cohort when the same captures start occurring frequently. Our estimator on the other hand uses Taylor approximation only once and does not make any independence assumptions. Hence situations where large number of cohorts are needed (as in cluster sampling where n/N is large) ML estimator will not perform as well as ours. In cases such as cluster sampling where n/N is large and the researcher has not formed enough cohorts (as this requires extra physical effort and cost) there is loss of data as well as violation on independence assumption in ML, in which case our estimator will perform better. Finally, parametric models often utilize model fitting procedures but that is not necessary for a non-parametric model. The true test is the performance of the model in real life situations. Everything else is secondary to this objective.

6.1 Adaptability

Future research can be done to adapt the model in abundance estimation situations where capture-recapture is feasible. Examples include healthcare related problems (disease control) and heterogeneity (see below). This model strength is due to its simplicity and non-biological model structure that permits such adaptations.

6.1.1 Sampling under implicit heterogeneity

In most practical sampling situations the researcher gathers data on many different types of units at once. Such a heterogeneous dataset involves different types of units with varying probability of capture/recapture. This of course is not an issue for our model as long as we can identify different types of individuals and separate our datasets accordingly.

The “implicit” effect arises when the population is heterogeneous but the researcher cannot identify the various classes of units that generated the dataset. In this situation our standard model needs to be augmented and we must first develop an approach to identify these classes.

6.1.2 Complete capture history

A row vector comprising of complete capture and recapture history of each unit is recorded. Note that in many instances there will be missing values as the same unit is not captured in that trial. Thus a unit with more frequent recaptures will likely have a higher probability of recapture and thus possibly belong to a different class, at least from a recapture probability viewpoint. Next, we group similar capture histories and index them bym. The order of captures is irrelevant and we simply care about total count of captures/recaptures. Our goal will be to use this extended dataset to identify the classes of individuals, thereby converting our implicit heterogeneity problem into explicit. Our standard model then applies individually to each explicit class. However, we will now need to “rebuild” the ordered data set for this class and know the capture-recapture sequence of each class separately.

An example is shown below. Typically, several such strings would be recorded, one for each unique string:

figure a

6.1.3 Multinomial likelihood model

Let there bemdistinct patterns (capture histories) and there are a total ofnindependent singleton trials. The cell probabilities \(p_i ,i=1 \ldots m\) are such that \(\sum _{i=1}^m {p_i } =1\). We note the frequency of patterns, \(x_i ,i=1 \ldots m\) and the likelihood function of the observed set \(\left\{ {x_1 ,x_2 \ldots x_m } \right\} \) is given by,

$$\begin{aligned} L(p_1 \ldots p_m )=\frac{n!}{x_1 ! \ldots x_m !}\prod _{i=1}^m {p_i ^{x_i }} \end{aligned}$$

Using standard maximum likelihood estimation the parameters \(p_1 \ldots p_m\) and their respective confidence intervals are obtained. Classes with overlapping confidence intervals are combined and the process continued until classes with distinct capture histories are identified. This classification is based on distinct probability of observed capture history.

6.2 Conclusion

We present a novel approach to the capture recapture problem that is different than maximum likelihood based models. It has the advantage that it considers ordering, dependence, minimum variance, non-parametric and accounts for exits and entries. It has an impressive rate of convergence. Perhaps the test of a good model is how closely it mirrors reality and in that sense we have shown that our model works well. A large number of assumptions and parameters to estimate often leads to loss of “reality” (McCullagh and Nelder 1989). We suggest using specialized separate models to measure mortality and other quantities of interest in order to avoid this problem.

In the future, we aim to make this model continuous in time. We could obtain explicit formulae for population estimators and its variance as a function of time. Second, the model could also be enhanced to measure mortality and other quantities of interest to biologists. Third, model adaptations to other fields such as healthcare (disease control) should be explored.