When the use of cognitive conflict is ineffective—problematic learning situations in geometry

Abstract

Problematic learning situations (PLS) arise when students encounter learning difficulties and their teacher encounters difficulties assisting them. The current study looks at student and teacher difficulties revealed during PLS, in the course of instruction of basic geometrical concepts for average and below-average junior high school students, when teachers apply the strategy of cognitive conflict spontaneously and inefficiently. Re-analyzing three PLS detected while observing three student teachers (Gal in Educational Studies in Mathematics, 78 (2), 183–203, 2011), I found that the teachers intuitively attempted to create a cognitive conflict but were mostly unaware of the inefficiency of this approach when students were not cognitively prepared. The findings point to the importance of enhancing teachers’ awareness of how their students think, helping them interpret their students’ understanding and encouraging them to seek the origins of student difficulties, so that teachers may be better prepared to reach a rational decision about an appropriate way to handle PLS. It is recommended to include these issues in teacher preparation and development programs.

Appendix: extended analysis of PLS 3

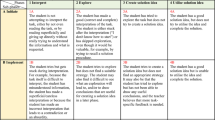
PLS often require multidimensional analysis of both student and teacher difficulties, using more than one theory or research approach simultaneously (for more examples of multidimensional analysis, see Gal & Linchevski, 2010; Gal, 2011). The following suggests additional perspectives for analyzing PLS 3.

1.1 Logical analysis

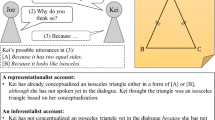
A logical analysis of the PLS suggests two difficulties. The first is a two-way implication fallacy. The student learned that if triangles are congruent, then angles are correspondingly equal; due to the fallacy, she now claims that if angles are correspondingly equal, then triangles are congruent. The teacher fails to convince her that this is not always true.

The second possible difficulty is the implication of the negation fallacy, whereby the student interprets “does not necessarily imply” congruence, as suggested by the teacher’s counter-example, to mean “negatively implies” lack of congruence. According to Harel, “Many propositions in mathematics seem trivial to students because they judge them in terms of epistemic values rather than logical values” (2008, p. 497). Moreover, it is accepted that difficulties in logical thinking make it difficult to experience cognitive conflict (Kang et al., 2004). There also seem to be differences between the teacher’s (expert) proof scheme, which is probably deductive, and the one clearly attempted by the student, based on external conviction, i.e., where proving depends on an authority such as the teacher (Harel & Sowder, 1998).

1.2 Mismatch between level of instruction and student’s level of geometrical thinking

Van Hiele (1986) considers the cognitive skills of proving to be levels 3 and 4. Students at level 3 perceive relationships between properties and figures, can create meaningful definitions, and can provide informal arguments to justify their reasoning. Those at level 4 can construct proofs, understand the role of axioms and definitions, and know the meaning of necessary and sufficient conditions. In our case, however, the student only understood that this activity required using a side, an angle, and another side. Because you can see in the figure that these parts are (correspondingly) equal, she could point them out, even though they were not given as data. Her reactions point to van Hiele’s first or second level of thinking. A student at level 1 recognizes figures by their global appearance, often by comparing them to a known prototype. The properties of a figure are not perceived until level 2. The student’s reactions (e.g., “But I do see it. I’m not blind.”) are all explanations based on viewing the figures either by their global appearance or by partial analysis of their properties. The dialogue indicates that proofs and postulates are not a meaningful justification for the student and that the teacher’s attempt to apply these modalities (e.g., “There is no ‘to see’ in geometry.”) results in pseudo-conceptual and pseudo-analytical behavior. The student’s way of handling the assignment (folding the triangles to show they are congruent) suggests she is involved in Natural Geometry (Geometry I) and not Formalist Geometry (Geometry III) or even Natural Axiomatic Geometry (Geometry II) (Kuzniak & Rauscher, 2011). The passage from Geometry I to II “is the first time in mathematics that the mental perspective on the object has to change drastically, without any ‘visual’ change, symbol or pictorial aid” (Houdement & Kuzniak, 2003, p. 6).

1.3 Difficulties in visual perception

Gestalt principles guide the organization of shapes and objects which were extracted from the visual scene into groups to form the object (Wertheimer, 1958). The factor of proximity suggests that grouping occurs on the basis of small distance (Wertheimer, 1958; see Fig. 7).

Fig. 7

Decomposing the configuration into two triangles contradicts the principle of proximity

This makes it difficult to decompose the configuration of two triangles sharing a common side. When the teacher directed the student’s attention, she was able to find the common side.