1 Introduction

Sinclair et al. (2016) reviewed over 200 research papers about the teaching and learning of geometry published since 2008, and identified six themes, including the understanding of the teaching and learning of definitions. They state that one research question to be investigated is about students’ understanding of hierarchically defining and classifying shapes (p. 706). Indeed, students find the understanding of hierarchically defining and classifying shapes difficult at a cognitive (e.g., de Villiers, 1994; Fujita, 2012) and a discourse level (e.g., Wang & Kinzel, 2014). The difficulties in defining and classifying in geometry might be overcome if students undertake problems collaboratively because they might have opportunities to share their ideas about the geometrical shapes. Our paper is concerned with this issue; in the context of hierarchically defining and classifying shapes, can collaborative learning settings be productive ways to develop mathematical thinking and understanding? This approach is particularly used in computer-supported collaborative learning (CSCL) contexts, and the findings so far suggest that with careful design, scaffolding and teachers’ interventions, small group work can promote students’ geometrical thinking and understanding (e.g., Stahl, 2015; Schwarz et al., 2018).

By taking suggestions from CSCL, we take a further step in studying students’ collaborative decision making processes in geometry. For example, Stahl (2015) wrote that the synthesis of physical, verbal and social involvement is crucial in collaborative work (p. 226), but it still remains unclear how we capture such involvement holistically. In this paper, we take semiotic (e.g., Duval, 2006, 2017; Godino Batanero, & Font, 2007; Font, Godino, & Gallardo, 2013) and dialogic approaches (Radford, 2003; Wegerif, 2011; Kazak, Wegerif, & Fujita, 2015; Kazak, Fujita, & Wegerif, 2016). We take a semiotic approach because this provides us with a powerful way of elucidating sensemaking processes which involve multiple presentations such as diagrams, language, definitions, etc. (Godino et al., 2007; Font et al., 2013), which can be applied both with or without computer learning contexts. In addition to this semiotic approach, we take dialogic approaches inspired by Bakhtin (1963/1984) which take dialogues between voices and switching in perspectives as essential, with understanding emerging in the context of a relationship between two or more voices (e.g., Wegerif, 2011; Kazak et al., 2015; Barwell, 2016). Our approach understands thinking as dialogue and so is very close to Anna Sfard’s “comognition” approach to mathematics which understands thinking as “internal communication” (Sfard, 2008). It is possible that the two approaches are compatible. However, the choice of the term “dialogue” over the term “communication” does signal one key difference. Whereas Sfard focuses more on mathematics as a discourse, or way of speaking, we focus more on learning as switching perspective in a dialogue to see things from another point of view around a gap of difference. The gap of difference between perspectives in dialogue is understood by us to be a source of creativity, making new understandings available not simply as new ways of talking, but as sparks of insight or mutual illumination in dialogues in a way that precedes and exceeds talking and other forms of communicating (Wegerif, 2011).

The purpose of this paper is to investigate the following research question: “What learning processes will be involved when students are working together in various ways with problems related to hierarchical defining and classifying shapes, and what obstacles will be recognised?” We attempt to answer these questions by undertaking a finer interpretative microanalysis. We first propose our theoretical framework derived from:

  1. 1.

    The developmental model for collective thinking processes (Pirie & Kieren, 1994; Martin & Towers, 2015);

  2. 2.

    Semiotic representation approaches by Duval (2006, 2017) and onto-semiotic approaches (e.g., Godino et al., 2007; Font et al., 2013);

  3. 3.

    Dialogic theory in collective thinking processes (e.g., Wegerif, 2011; Kazak et al., 2015).

We first provide overviews of each theoretical idea, and then locally integrate these different theoretical perspectives (Bikner-Ahsbahs & Prediger, 2014) for a better understanding of collaborative decision-making processes in defining and classifying shapes, which we call a semiotic/dialogic approach. We do not intend to argue that the semiotic approach is better than dialogic and/or vice versa, but we attempt to discuss how these two approaches can complement each other, potentially providing us with a powerful way of understanding collaborative learning processes in mathematics. We then show how this approach can be used to give a detailed analysis by using data derived from 27 year 7 students (12–13 years old) in a lower secondary school in the UK.

2 Theoretical framework

2.1 Defining and classifying geometrical figures

Herbst, Fujita, Halverscheid, and Weiss (2017) state that the teaching of geometry at the secondary level should provide opportunities for “the progressive sophistication of students’ intellectual means to model, predict, and control geometric representations …” (p. 3). Defining is one such activity in mathematics (Zazkis & Leikin, 2008), as it gives precise and clear meanings for mathematical concepts (Alcock & Simpson, 2017). Definitions provide students with opportunities to engage in the classifying of mathematical objects. Defining is also closely related to classifying. Alcock and Simpson (2017) observed: “Classifying tasks and reasoning tasks (such as proof construction) in which participants should invoke a definition but are not explicitly told to do so; Defining tasks in which participants are asked to state the meaning of a concept, either as a formal definition or as a personal explanation.” (p. 7).

Both hierarchical and partitioned definitions for quadrilaterals are mathematically correct, but hierarchical definitions are preferred as this approach is more economical and appreciated within mathematical reasoning (de Villiers, 1994; Fujita, 2012). However, whilst they can state hierarchically correct definitions of rectangles and parallelograms, these students cannot accept, for example, that rectangles can be a member of the parallelogram group. Their reasoning could be the following: rectangles have 90° angles, but parallelograms should be “slanted” (“visual geometrical images”) and do not have such angles (e.g., Fujita, 2012), influenced by the prototypical images which they gained in their early stage of learning (Hershkowitz, 1990).

2.2 Collaborative learning

Collaborative learning has been recognised as a key topic in mathematics education research (e.g., Martin & Towers, 2015), and this approach might be beneficial in defining and classifying geometrical shapes, in particular in CSCL contexts. For example, Stahl (2015) suggests that with good group work, students can share their visualisation and manipulation with geometrical concepts. Schwarz et al. (2018) reported with teachers’ orchestrations with technological supports that it is possible for even grade 5 students to engage conceptual learning with defining and classifying geometrical shapes.

In order to study students’ collaborative learning process, based on Pirie and Kieren’s model (1994), Martin and Towers (2015) proposed a developmental model for collective thinking in mathematics as (p. 4):

  • Collective image making (CIM)—collectively developing particular initial conceptions and ideas for the meaning of a mathematical concept;

  • Collective image having (CIH)—collectively carrying a general mental plan and use accordingly for solving problems with the mathematical concept;

  • Collective property noticing (CPN)—collectively saying something that works “for all” and of recognising why this is the case.

The learners’ developmental paths from CIM to CPN would not be straightforward. For example, when a group of learners had difficulty in noticing properties during problem solving, they might examine their already made images, and as a result, they remade new images for exploring new paths for problem solving. This is what Pirie and Kieren (1994) call folding back, returning to earlier stages, e.g., when a student noticed that collective images were not useful to recognise something might work to solve a problem (property noticing), they went back to remaking their images (image-making). This is one of the keys for developing mathematical concepts (p. 173) and is crucial in the collective thinking process as well (Martin & Towers, 2015).

2.3 Geometric representations from the semiotic approach

In our collaborative group work, geometrical images play central roles, but how do students interact with these images in their collaborative learning situations? Different semiotic systems such as natural language, mathematical language, definitions, properties, etc. will be involved in such interactions. In order to elucidate social interactions among students, two semiotic approaches are relevant because their images of geometrical figures are “represented” in a variety of different forms including those on a computer screen. The two approaches are registers of semiotic representations (e.g., Duval, 2006, 2017) and the onto-semiotic approach (e.g., Godino et al., 2007; Font et al., 2013), which can be combined to enable us to undertake detailed analysis of students’ sensemaking processes in social contexts (e.g., Pino-Fan, Guzmán, Duval, & Font, 2015).

Duval (2006) claims “Mathematics is the domain within which we find the largest range of semiotic representation systems, both those common to any kind of thinking such as natural language and those specific to mathematics such as algebraic and formal notations” (p. 108). The theoretical essence of Duval’s idea is how to capture relationships between representations in different semiotic systems (e.g., discursive/non-discursive, natural language/symbolic etc.) and knowledge of mathematical objects. “Registers” are semiotic representations of mathematical concepts (symbol, graph, words etc.), and mathematical activities are described as transformations of these registers (pp. 111–2). Two types of transformation of registers are considered: treatment (transformations within the same semiotic system e.g., solving an equation or system of equations) and conversion (transformations of different semiotic systems e.g., transforming algebraic symbols to graphs).

The onto-semiotic approach is described as “an ontology of mathematical objects that takes into account the triple aspect of mathematics as a socially shared problem-solving activity, a symbolic language and a logically organized conceptual system” (Godino et al., 2007, p. 129). The theoretical essence of this approach is that knowledge of mathematical objects merges from rather complex interplays between personal and institutional levels of practice, defined as “The system of practices that a person carries out (personal meaning), or are shared within an institution (institutional meaning), to solve a type of problem-situations in which finding a representative of a set of data is required” (p. 129). Font et al. (2013) further state that “The personal/institutional dialectic is essential in teaching processes, whose aim is to enable students to take on board the institutional objects (i.e. learning). The mathematics classroom makes use of a language game that leads students to distinguish between personal objects and institutional objects” (p. 113). Here, a language game can be defined by following Sáenz-Ludlow (2006), in which “teacher and students constitute themselves as intentional subjects capable of interpreting linguistic, mathematical, and other kinds of signs” (p. 186). Interpreting games is defined as “teacher and students come to express and modify their personal interpretations of mathematical concepts” (p. 200).

Thus, teaching is to provide students with opportunities to participate in the system of practice, sharing meanings shared by certain institutional communities (e.g., schools which follow prescribed formal definitions of geometrical shapes), and learning is the appropriation for students who have their individual understanding of meanings (e.g., their own understanding of geometrical shapes) transformed to institutional ones (Godino et al., 2007, p. 130) through interpreting games. At the microlevel of teaching and learning, participations of practice involves the treatment and conversion of various semiotic representations in a certain system of practice, involving the six multi-facets of mathematical objects: (1) situations–problems, (2) linguistic elements, (3) concepts/definitions, (4) propositions/properties, (5) procedures, and (6) arguments (Pino-Fan et al., 2015, p. 36; see also Godino et al., 2007, p. 131; Font et al., 2013, p. 109). Godino et al. (2007) state that “The students’ errors and difficulties were explained by semiotic conflicts, i.e., as disparities between the student’s interpretation and the meaning in the mathematics Institution” (p. 133); in our case, the disparities in geometrical shapes are related to various semiotic representations of geometrical shapes in a certain system of practice.

Pino-Fan et al. (2015) describe the following constructs related to evaluation processes of the mathematical objects within the onto-semiotic approach (p. 36):

  • Activations of various representations derived from the six facets of mathematical objects (a conglomerate) i.e. situations–problems, languages, concepts, propositions, procedures and arguments, e.g., parallelograms which are represented by words, drawings, properties and arguments around their relationships, etc., which are derived from students who belong to certain institutional contexts.

  • Connecting these representations (configurations) to form mathematical objects shared within the group of students. These formed mathematical objects can be socio-epistemic (networks of institutional objects, which appear in curriculum materials such as textbooks, e.g., “parallelogram is a quadrilateral with two sets of parallel lines”) or cognitive (networks of personal objects, which individual students have, and may or may not correspond to conventional mathematical definitions, e.g., “parallelogram is a slanted rectangle”).

In our case, we are interested in what semiotic discursive/non-discursive representations of parallelograms will be identified within certain institutional systems. We are also interested how these representations are connected to by groups of students in their decision-making processes (examples are provided in 2.5). Before doing this, in the next section, we shall discuss our final twist: a dialogic approach. This approach shares a lot of ideas with semiotics but also suggests different ways of analysing collaborative processes, which focuses on more “relationships” than “signs” in learning processes (Kazak et al., 2015, p. 106).

2.4 Dialogic process in collective learning

Sáenz-Ludlow (2006) states that “Classroom interactions between teacher and students and among students themselves are acts of communication at two levels: acts of communication with oneself and acts of communication with others” (p. 184). Working within a Vygotskian perspective, Mercer and Sams (2006) studied how certain types of talk, which mediate conceptual knowledge, affect students’ ways of collective thinking and problem solving. They particularly consider that exploratory talk (characterised as being critical friends to each other and using explicit reasoning during problem solving e.g., (after an idea/answer was suggested) “you might be correct, but how about this one, because…”) is crucial for developing understanding, comparing to the other types of talk such as disputational (being competitive or disagreeing with each other in egoistical ways, “no, your answer is wrong. It should be this” (without stating any reasons)) or cumulative talk (agreeing each other without constructive criticisms, e.g., after an idea/answer was suggested), “yes, I think your answer is right” (without stating any opinion)). Stahl (2015) also pointed out that asking “why” questions or the use of “maybe” is related to effective group work in geometry in CSCL.

However “nicely children talk together to ask each other questions and give each other reasons, this will not automatically translate into insight” (Kazak et al., 2015, p. 111). They report that an “Aha!” moment occurred after learners had engaged in productive “dialogues,” which include more than exchanging recognisable utterances, but require a genuine inter-animation of different perspectives such that there is a dialogic switch and individuals learn to see the problem “as if through other’s eyes.” Our view, based on Bakhtinian dialogic perspectives (e.g., Bakhtin, 1963/1984), is that dialogical relationships elucidate differences and gaps and encourage learners to see their learning from a different perspective (although explicit verbalisation can be useful, this is more than language use as it requires an almost embodied switch in point of view). Bakhtin also states:

“The idea begins to live, that is, to take shape, to develop, to find and renew its verbal expression, to give birth to new ideas, only when it enters into genuine dialogic relationships with other ideas, with the ideas of others. Human thought becomes genuine thought, that is, an idea, only under conditions of living contact with another and alien thought, a thought embodied in someone else’s voice, that is, in someone else’s consciousness expressed in discourse. At that point of contact between voice-consciousnesses the idea is born and lives.” (ibid., p. 88).

Barwell (2016) also argues “There is no opposition of informal and formal mathematical language/discourse; rather, the simultaneous presence of multiple discourses, voices and languages in every utterance makes it possible for students to express mathematical ideas meaningfully” (pp. 337–8).

From this point of view, in addition to effective collaborative practice (such as building useful representations of geometrical figures for problem solving), seeing a problem “as if through the eyes of another” is important for emergence and development of collective group thinking. The change in subjects’ identifications is what we call a “dialogic switch” (Kazak et al., 2015). This links with Radford (2003) who emphasised the importance of a desubjectification process, which is described as “a process that emphasizes changes in the relation between the object of knowledge and the knowing participant” (p. 55). For the dialogic switch, it is necessary for students to, for example, recognise multiple “voices” in mathematical concepts, see ideas from an “outside” perspective, establish dialogic space, show respect for each other, and so on (Kazak et al., 2015; Wegerif et al., 2017). This is what Wegerif (2011) refers to as dialogic process of conceptual growth.

2.5 The integrated framework

Let us consider how we can theoretically explain complex decision-making processes and students’ obstacles in defining and classifying geometrical shapes. We call this analytic approach a semiotic/dialogic approach.

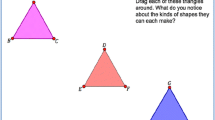
Our mathematical objects are quadrilaterals. We need to clarify the system of practice and the problem–situation first. For example, in our context, the institutional system here is a UK school where students are expected to understand formal definitions of geometrical shapes under the hierarchical classification. Suppose it is a test situation: groups of students are asked to answer a set of questions (Fig. 1; Fujita, 2012) about hierarchical relationships between parallelograms in a context of a “test”.

Fig. 1
figure 1

Tests for geometrical thinking

Full size image

In this system of practice, “disparities between the student’s interpretation and the meaning in the mathematics institution” arise from their own personal concepts/definitions and properties of shapes and formal hierarchical definitions of shapes. An interesting aspect of this situation is that students have to decide their answers without their teachers’ involvement as this is a test for a group, so this interpreting game will be done without a “referee”.

Students are asked to collectively give their answers, e.g., “Is no. 2 in Fig. 1 classified as a parallelogram?” It is expected that they will activate semiotic representations of parallelograms and try to interplay or connect them (Duval, 2006; Pino-Fan et al., 2015). For example, their prototypical (Hershkowitz, 1990) non-discursive representations of parallelograms (e.g., no. 1 in Fig. 1) might be “converted” to a (personal/informal) discursive statement “parallelograms are slanted shapes.” Then, this might be further transformed to other discursive statements related to properties of parallelogram such as “they do not have 90 degree angles.” These two statements might be connected as their temporal (cognitive) definition, and then will be used in their argument to conclude “no. 2 is not a parallelogram”, which is incorrect according to their institutional system (argument 1). However, some students might argue by using a (rather institutional/formal) discursive statement that “parallelograms have two sets of parallel lines.” By this statement, they might fold back (Pirie & Kieren, 1994) to remaking their representations, and by “parallelograms have two sets of parallel lines,” the non-discursive prototypical representation might be transformed to another (e.g., no. 2 in Fig. 1). Now, they face a moment to collectively decide if no. 2 is classified as a rectangle (argument 2).

Next, their dialogic relationships can be considered when scrutinising why some groups might (or might not) accept their peers’ arguments (e.g., argument 2). In the above decision-making process, they might voice “rectangle” or “parallelogram”, but from the dialogic point of view, they will contain “multiple perspectives and agencies” i.e. rectangles based on their own or peers’ informal definitions (a personal level), for the formal definitions which appear in the textbook or for definitions used by teachers (a formal/institutional level), and so on. In their talk, they might agree or disagree in their arguments with each other. If the group of students do not desubjectify their position (Radford, 2003), and see their own personal representations or definitions from an “outside” perspective, they might not be able to reach mutual agreements or reasonable answers or extend their discussions and apply other contexts even when they fold back to their early collective thinking stages.

3 Methodology

3.1 Geometry group test

In order to answer our research question under the semiotic/dialogic framework, we use the data derived from 27 year 7 students (12–13 years old) in a lower secondary school in the UK. Their abilities are recognised by their class teacher as the second highest group in the year group, meaning that their achievements are higher than the average students in the UK school context (institutional practice). They have also studied formal definitions of basic 2-D shapes including parallelograms.

These 27 students first undertook a non-verbal reasoning test developed by Wegerif et al. (2017). Based on their individual test scores, we formed nine groups (three students in each group), and then these students undertook another non-verbal test in groups. They then undertook the geometry group test shown (Fig. 1). It was originally designed to assess the extent to which individual students have prototypical examples when they define and classify parallelograms (we are aware of the methodological concerns raised by Alcock and Simpson (2017), but our questionnaire was implemented (May 2016) prior to the publication of their paper). For each question in Fig. 1, a marking is derived mainly from van Hiele’s model (1999; see also Fujita, 2012), i.e. hierarchical (level 3 informal deduction level), partially hierarchical (level 2 analysis level), but if it was prototypical (level 1, visual level). For example, for Q1, hierarchical for “1, 2, 4, 5, 6, 7, 9, 11, 13, 14, 15,” partially hierarchical for “1, 5, 6, 9, 14, 15,” or “1, 2, 5, 6, 7, 9, 13, 14, 15,” but prototypical for “1, 6, 9, 14”; for Q3, hierarchical for “true for (a), (b), (c), (d) and (e),” partially hierarchical for “true for (a), (b), and (c),” or “true for (b), (c) and (d),” but prototypical for “true for (b) and (c).”

3.2 Data analysis procedure

For the purpose of this paper, we selected four groups (G1, G2, G5 and G8), in total 12 students, and video-recorded their group work on the geometry tests for further analysis. These groups were purposefully chosen based on our initial observations of their group work in the non-verbal reasoning test. For example, G1, G5 and G8 worked well when they undertook the non-verbal reasoning test in groups, whereas G2 did not collaborate well but their group scores for the non-verbal reasoning test were higher than their average individual scores.

We then analysed these video data from their collaborative group work by first extracting a total of 340 utterances from these four groups, and then applying the following analytical points informed by the semiotic/dialogic framework. First, we identified segments of students’ collaborative interactions by using collective image making (CIM, collectively developing images of geometrical shapes), collective image having (CIH, carrying established images for geometrical shapes), and collective property noticing (CPN, using their established images to examine properties of shapes). We then conducted a semiotic/dialogic analysis. For semiotic, we first examined what semiotic representations and arguments were used in their processes of forming their own definitions. For dialogic, we observed the types of talk (disputational, cumulative or explorative) and what “voices” might be included in their dialogue by examining the following: (a) in what contexts the utterances were voiced and (b) how other members of the group reacted to this utterance.

For example, G2’s processes for Q2 were divided into the two segments “CIM→CIH” and “folding back (FB)→CIM” (Fig. 2), because in these stage, they tried to established their collective definition of parallelogram (“CIM→CIH”) but briefly folded back to the earlier question to check if their established definition might be right (“FB→CIM”). From a semiotic point of view, MS voiced his personal statement (discursive representation) “There are two sets of parallels, and ‘an obtuse’.” ST then stated “I think it is obtuse,” and this was transformed to another statement by MS: “two acute and two obtuse right.” These “parallel, obtuse and acute angles” helped them connect the activated representations of parallelograms and write their definition “Two parallels, and two acute and two obtuse angles,” which was now their collective definition in the group (this is different from the institutional one). From a dialogic point of view, their utterances were cumulative as no constructive criticism to student MS was given by students’ ST and CC, but the word “parallel” helped MS “switch” his thought on what parallel lines mean (line 20), and thus the word parallel has multiple voices as this was shared in this group. On the other hand, the word “acute” and “obtuse” by MS might not be fully shared by the other two. MS questioned this (line 24), but the other two did not comment on obtuse and acute much, which was subsequently examined with later interactions when ST actually considered square might be a member of parallelogram (see Sect. 4.3, line G2 57). Thus, these statements, acute and obtuse, might actually not be shared within the group for their collective definition.

Fig. 2
figure 2

Example of analysis

Full size image

After conducting our analysis on all the groups, we then integrated the findings in terms of the semiotic/dialogic framework, which will be shown in the next section.

4 Findings: students’ collaborative decision-making processes

4.1 Overall performance in geometry test

The overall performances summarised in Table 1 might indicate that the students’ answers are also governed by prototypical examples of parallelograms (G1, G2, G3, G4, G5, G8 and G9) or rather underdeveloped (G8 and G10), despite being given opportunities to share their ideas and to work collaboratively to solve the geometry test.

Table 1 Detailed answers for the geometry tests
Full size table

Based on this result, one might conclude that the geometry test was just too difficult for the students. Their answers are either partially hierarchical or prototypical, and therefore, even group work was not particularly helpful for them to answer the questions correctly in the context of the hierarchical defining and classification. This might be true to some extent, but the analysis of four groups’ data seems more interesting and complex than the result in Table 1. For example, one interesting observation is that all groups’ answers were very similar in terms of ways they defined and classified parallelograms, whilst ways of their talk were quite different i.e. G1 was disputational/cumulative type talk; G5 was explorative/cumulative, and G2 and G8 were cumulative. Also, the groups G1, G2 and G5, in particular, often had moments to examine their various semiotic registers around the object parallelogram, but they did not explore these opportunities. In Sects. 4.2 and 4.3, we shall present the examples of students’ dialogues which particularly illustrate their decision-making processes in both semiotic and dialogic obstacles were identified.

4.2 Processes in establishing definitions

Let us take the case from G1 first. In their group learning processes, various representations of parallelograms were activated, but their discussions were argumentative and they could not see their peers’ ideas from the others’ point of view. For example, their discussion for Q2 was as follows:

G1 47.

JC

What is a parallelogram? Write the definition.

G1 48.

AC

A squished up rectangle

G1 49.

JC

No both sides are parallel.

G1 50.

AC

A squashed up rectangle

G1 51.

BS

So that would mean thirteen as well and two.

G1 52.

AC

And a square

G1 53.

BS

And one and

G1 54.

AC

And a square and a rectangle. It’s trash.

This is a collective image making stage, as they were developing their images of parallelogram. In their discussion, we can see that different representations of parallelograms were activated. For example, AC repeatedly used his personal/informal statement “a squished up rectangle.” In line 51, BS questioned if a rectangle or square can be parallelograms based on another discursive statement “both sides are parallel” by JC (line 49). Immediately, AC transformed this to “a square and a rectangle” (line 54), but the other two did not accept the suggestions by BS or JC.

They then continued their discussion, and it is evident that AC and JC’s argument was overtaking in this group (lines 59, 60 or 70).

G1 59.

BS

A squashed up rectangle

G1 60.

JC

No if it’s a squashed up I need to know squeeze it.

G1 61.

AC

[relatively aggressively] That’s what we got told in.

G1 62.

BS

All sides are the same.

G1 63.

AC

No they are not.

G1 64.

BS

No, no, all the sides are parallel.

G1 65.

JC

Yeah.

G1 66.

AC

Yes so is a square.

G1 67.

BS

So that will do one, two (pointing a rectangle image).

G1 68.

JC

No because that’s a quadrilateral not a parallelogram. A parallelograms are like…

G1 69.

AC

A squashed up rectangle.

G1 70.

JC

No parallelograms are like that they are like that they are messed up.

G1 71.

BS

Oh no.

As we see in the above discussion, it seemed that AC and JC could not see each other’s positions. In line 61, AC aggressively said “that’s what we got told in…,” referring to her/his memory in lessons which contains a kind of authoritative tone, trying to refer their personal representations to an “institutional one” (which he thought to be the definition taught by their teacher). In line 64, BS tried to state his idea “all the sides are parallel” and then suggested that a rectangle can be a parallelogram. This was an important moment to be explored, as this suggests that there was a dialogic gap in their ideas between BS and AC/JC. However, JC and AC again referred to their personal statement (line G1 68 and 69) in their argument. BS’s argument was dismissed, and he disappointingly said “Oh no.” Their collaborative explorations stopped here as their collective definition “Both sides are parallel. It’s a squashed up rectangle” was established.

We turn now to G5, who worked well collaboratively in general.

G5 7.

JM

Ok what is a parallelogram?

G5 8.

BH

Oh.

G5 9.

JM

It’s rectangle but

G5 10.

BH

It’s like

G5 11.

TF

Erm like

G5 12.

JM

It’s like, it’s a rectangle but it does not, we are not, it does not have all ninety degrees. It does not have all right angles.

G5 13.

TF

Yeah, yeah yes so it’s a rectangle but it does not have

G5 14.

BH

Two pairs of parallel sides

G5 15.

JM

It’s a rectangle.

G5 16.

BH

Two pairs of parallel sides

G5 17.

JM

Yeah but that erm that a rectangle has two pairs of parallel sides as well.

G5 18.

JM

… (a moment) But it does not have right angles so it’s rectangle without …

G5 19.

TF

Ninety degree angles

In this collective image making stage, JM first voiced his personal statement (line G5 12) which was then TF agreed. Then, BH added “two pairs of parallel sides” (line G5 14). This made JM produce an argument “a rectangle has two pairs of parallel sides” (line G5 17). Although this was a brief moment, this could have been important to scrutinise JM and TF’s personal definition which was based on prototypical, but after another moment, he added “it (parallelogram) doesn’t have right angles” (line G5 18), indicating he could not see BH’s point of view. TF then agreed with JM. BH did not argue back from here. At this point, their collective definition of parallelogram “a rectangle without 90 degree angles” was established.

The other groups (G2 and G8) showed similar processes; a member voiced her/his personal discursive statements, and then, this became their collective definition without critical entanglements or dialogic reflections.

4.3 Collective thinking after establishing definitions

After the students established their collective definitions, these were used throughout the problem solving process (collective property noticing stage, saying what would work in general). The result is that they only chose (b) and (c) of Q3 as true, or in Q4, they formulated it would be impossible to draw a parallelogram whose four vertices are on the circumference of a circle. It is interesting that both G1 and G5, whose talks were disputational or exploratory in Q1 and 2 in Fig. 1, engaged in rather cumulative talk at this stage. This might be due to the fact that they had established their definition of parallelogram, or they just reasoned based on these without much conflict or gaps between the group members. For example, G1 answered very quickly compared to the other questions.

G1 89.

AC

[reading questions] “There’s a type of parallelogram which has right angles”—no. “There is a type of parallelogram which has four sides of equal”—no. “Some parallelograms have more than two lines of symmetry”—it [parallelogram] has no lines of symmetry.

G1 91.

JC

“There is a parallelogram that has right angles”—yes a square (and then JC excluded this from parallelogram).

From a semiotic point of view, the written statement “There is a parallelogram that has right angles” was transformed to “square” (in line G1 91), and this was then rejected as a “true” statement because of their own definition “Both sides are parallel. It’s a squashed up rectangle.” From a dialogic point of view, the word parallelogram was shared as squashed rectangle, but at this phase of problem solving, BS did not join their dialogues anymore, almost having given up stating his opinions.

Similarly, G5 worked very smoothly by using their collective definition, clearly excluding rhombus from parallelogram (line G5 39) with explicit reasoning by JM, and the others agreed with this without any conflicts.

G5 36.

JM

Some parallelograms have more than two lines of symmetry.

G5 37.

BH

Erm…

G5 38.

TF

Erm yeah.

G5 39.

JM

No, no that’s not true, a rhombus does, a parallelogram does not.

G5 40.

BH

Great ok.

All groups had however difficulties in answering Q4 (drawing a parallelogram whose four vertices are on the circumference of a circle), and they often folded back to check what a parallelogram was for them. For example, G5 exchanged various opinions with explicit reasoning, but they concluded it would not be possible to draw a parallelogram on the circle, stating their reasons by “the obtuse angles would not touch the circumference of the circle” (line G5 56), which was derived from their collective definition. G1 and G8 could not explain their reasons, but their decisions were made by referring to their prototypical collective definition.

Interestingly, G1 and G5 did not attempt to convert their discursive statement to non-discursive in Q4, although the question asked to them was to draw their visual images. G8 just drew a very incomplete diagram. In G2, more semiotic representations of parallelograms were recognised. For example, MS’s first thought was that it would be possible to draw a parallelogram on the circle (line G2 51), but he then drew a diagram by himself (i.e. conversion from discursive to non-discursive representation).

G2 49.

MS

So the circumference is a whole circle.

G2 50.

MS

The radius is half, right. Circumference is the whole. No and the diameter is what the circumference is I think the outside.

G2 51.

MS

Yeah I think you could. Yeah you probably could draw a parallel round that could you?

The problem was now represented by the diagram (non-discursive representation), and he noticed two vertices would not touch on the circumference of a circle, and therefore, the answer would be “impossible.”

G2 52.

CC:

No it’s too small oh in the whole thing.

G2 53.

MS:

Yes.

G2 54.

MS

Vertices are these are not they?

G2 56.

MS

Yes so well let me yeah that in that section there and that section could touch there…

G2 57.

ST

Would not that just be a square?

G2 58.

MS

We need to make it into a parallelogram…

A dialogic obstacle was also recognised. ST, who did not comment on MS’s personal definition (two parallels, and two acute and two obtuse angles) before, suggested that a square could be an answer (line G2 57) at this point. Again, this could have been a moment to fold back to reconsider their collective definition, but MS gently rejected ST’s idea without any reasons, and more importantly, not seeing from ST’s point of view why he mentioned “a square” here. Thus, for them, this word “square” contained only ST’s perspective and ended “it is not possible” to draw a parallelogram for Q4.

5 Discussion

In this paper, we examined the research question concerning with students’ decision-making processes and obstacles in defining and classifying geometrical shapes in terms of the semiotic/dialogic framework. By answering this question, our analysis suggests that the decision-making and obstacles were described as semiotic/dialogic transforming their informal/personal representations of parallelogram to collective/institutional ones in the system of practice (in this case, hierarchical classifications in the UK context). Even in group work, students still used prototypical examples (e.g., Hershkowitz, 1990; Fujita, 2012) in their reasoning, but semiotic and dialogic processes were crucial to understand this learning process. As we have seen in our data, the students activated various representations of parallelogram (e.g., a squashed up rectangle or two acute and two obtuse), and these informal representations were argued, negotiated and modified within groups under a kind of a language/interpreting game in the certain system of practice (Sáenz-Ludlow, 2006; Font et al., 2013). Then, these activated representations were connected and gradually became their collective definition (Pino-Fan et al., 2015). These established definitions may or may not correspond to conventional mathematical definitions, but were used as their “institutional” definitions to solve other problems. Our study also suggests that the dialogic aspect was important, and this should be explicitly included in “modelling collaborative practice”. In their group interactions, the students voiced various informal words related to parallelogram. Each word was indeed meaningful for each student (Barwell, 2016). Whilst the observed groups often had opportunities to examine their collective definitions (e.g., lines G1 67 or G5 18–19) in their collective image making/having stages, they did not explore these opportunities because each member did not see what others were saying “as if through the eyes of another” (Kazak et al., 2015). Once they had established their collective definitions, they just referred to these without much discussion (e.g., lines G1 89–91 or G5 36–40, or G2 57–58).

For implications of our findings, we argue that our study suggests that collective image making/having stages of classifying and defining are crucial. Sáenz-Ludlow (2006) wrote “The teacher also understood that students’ interpretations of mathematical meanings were subjective and transitory but in the process of becoming more refined and objective. …” (p, 221). Schwarz et al. (2018) found that, with computer support, it was useful to identify critical moments “in which the teacher’s (lack of) intervention may lead to a particular development” (p. 192) to promote students’ learning in classifying shapes. Through our semiotic/dialogic analysis, we have learnt that even in a short group discussion, students exchange various representations of mathematical objects and negotiate with each other to establish their collective definitions of the objects and use them to solve questions, in particular in their collective image making/having stage of collaborative learning. This can be seen as stages when “critical moments” might be likely to happen. Stahl (2015) wrote that in CSCL learning, it is important to “step users through initial sessions and provide prompting to model collaborative practices” (p. 243). One of the approaches is to teach, for example, “ground rules for talk” explicitly (Mercer & Sams, 2006) so that students can engage in exploratory type talk. However, Kazak et al. (2015) argue that exploratory talk might be not enough to study certain mathematical topics. In the dialogic theory of education, a hypothesis is that seeing things from others’ point of view opens a shared space in which new ways of understanding can emerge that go further than any individual understanding held prior to the dialogue. This process has been theorised as a dialogue with a local “superaddressee” voice, in this case, the “voice of mathematics” as a generalised voice for the community of mathematicians (Wegerif, 2011). This hypothesis about the potential power of dialogue was not realised in our data; we found that the students failed to deepen and open up the dialogue by examining their framing assumptions. In particular, the frame provided by too quickly arrived at collective definitions of parallelogram can be a crucial obstacle preventing the development of students’ collective defining and classifying of geometrical shapes. Therefore, teachers should not only encourage students to exchange semiotic representations in their image making/having stages but also carefully orchestrate students to see different points of view “as if through other’s eyes” in the study of geometrical shapes. We believe that this has not been pointed out in the existing research studies.

We are aware that our sample sizes were small, and the study context (defining and classifying geometrical shapes) is limited. Therefore, it is necessary to examine other learning and teaching contexts by using the semiotic/dialogic framework. Methodologically, we used the test but by reflecting on dialogues by the students (e.g., the utterance G1 89); the ways the test questions were phrased (e.g., “circle correct answers”) might have limited students’ productive dialogues. Rephrasing questions such as “which Figures 1–15 provide a proper response to the query in Q3d?” might be more appropriate to stimulate students’ dialogues. Another challenge is the order of the questions. It is interesting to change the order of the questions, which were suggested by Alcock and Simpson (2017). For example, the current test started from drawings of quadrilaterals, but might their group dynamics and decision-making processes be different if the students started from Q2, defining a parallelogram in discursive ways? This is an interesting issue to pursue in order to enrich our understanding of students’ use of various semiotic registers in geometry.