Energy Transition Under Irreversibility: A Two-Sector Approach

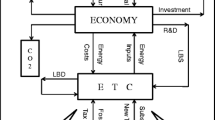
Abstract

This paper analyses the optimal energy transition of a two-sector economy (energy and final goods) under irreversible environmental catastrophe. First, it proposes a general appraisal of optimal switching problems related to energy transition showing: (1) the possibility of a catastrophe due to accumulation of pollution; and (2) technological regimes with the adoption of renewable energy. Second, it numerically shows that for given baseline parameter values, the most profitable energy transition path may correspond to the one in which the economy starts using both resources, crosses the pollution threshold by losing a part of its capital, and never adopts only clean energy. Third, it extends the model to allow for additional investment in energy saving technologies. We then find that this additional investment favours full transition to the sole use of renewable energy. It is then profitable to take advantage of these synergies by jointly promoting deployment of clean energy and providing incentives for investment in energy saving technologies.

Appendix

1.1 Appendix $A_0$

See Table 4.

Table 4 Variables and parameters

1.2 Appendix $A_1$

Let us recall that the equation of capital accumulation is:

$$\begin{aligned} \dot{K}_{t}=Y{}_{t}-C_{t} . \end{aligned}$$

(23)

We also know that: $Y_t=min\{\alpha _{2}K_{Yt},\beta _{2}E_{Yt}\}$, where, $K_{t} = K_{Et} +K_{Yt}$ and $E_{ct} = \eta K_{Et}$. $E_{ct} = \eta K_{Et}$ implies that $K_{Et}=\frac{E_{ct}}{\eta }$. Then,

$$\begin{aligned} K_{Yt} = K_{t}- K_{Et}=K_{t}-\frac{E_{ct}}{\eta } . \end{aligned}$$

(24)

From Leontief conditions in the final goods sector, we have:

$$\begin{aligned} Y_{t}=\alpha _{2}K_{Yt}=\beta _{2}E_{Yt} . \end{aligned}$$

(25)

During the third regime, only the clean source of energy is used so that we have the following equalities: $E_{Yct}= E_{Yt}$, and $E_{Cct}= E_{Ct}.$ By summing up the above two expressions and plugging this into successive Eqs. (24), (25) and into Eq. (23) gives $\dot{K}_{t}=\alpha _{2}K_{t}-\alpha _{2}\frac{E_{Yt}+E_{Ct}}{\eta }-C_{t}.$

1.3 Appendix $A_2$

To determine the expression of capital in the third regime, we need to solve the following equation of capital accumulation for the capital $K_{t}$: $\dot{K}_t=\Lambda K_t-\Theta \lambda _{T_{2}}^{-\frac{1}{\delta }}e^{(\frac{\alpha _{2}-\rho }{\delta })(t-T_{2})}$, where $\Lambda =\frac{\alpha _{2}\beta _{2}\eta }{\alpha _{2}+\beta _{2}\eta }$ and $\Theta =\frac{\alpha _{2}\beta _{2}}{\alpha _{2}+\beta _{2}\eta } (\frac{\alpha _{2}}{\eta })^{-\frac{1}{\delta }}+1.$ By making a change of variables $x_t=K_t e^{-\Lambda (t-T_{2})}$ and using the following transversality conditions $\underset{t\rightarrow \infty }{lim}\lambda _{t}K_{t}e^{-\rho (t-T_{2})}=0$, we get $K_{t}=-\frac{\Theta \delta }{\alpha _{2}-\rho -\delta \Lambda } \lambda _{T_{2}}^{-\frac{1}{\delta }}e^{(\frac{\alpha _{2}-\rho }{\delta })(t-T_{2})},$ for $\alpha _{2}(1-\delta )<\rho .$

Finally, we need to impose the non-negativity condition on $E_{Yt}$ so that:

$$\begin{aligned} E_{Yt}=\frac{\alpha _{2}}{\alpha _{2}+\eta \beta _{2}}(\eta K_t-E_{Ct})>0\Leftrightarrow -\frac{\Theta \delta \eta }{\alpha _{2}-\rho -\delta \Lambda } -\left( \frac{\alpha _{2}}{\eta }\right) ^{-\frac{1}{\delta }}>0. \end{aligned}$$

1.4 Appendix $A_3$

The expression of capital in the second regime is determined from FOCs as follows:

FOCs lead to: $\mu _{t}=\mu _{T_{1}}e^{(\rho -\alpha _{2}(1-\phi ))(t-T_{1})}$, $\nu _{t}=\nu _{T_{1}}e^{\rho (t-T_{1})}$, $C_{t}=\mu _{T_{1}}^{-\frac{1}{\delta }}e^{(\frac{\alpha _{2}(1-\phi )-\rho }{\delta }) (t-T_{1})}$ and $E_{Ct}=(\xi \nu _{T_{1}})^{-\frac{1}{\delta }}e^{-\frac{\rho }{\delta }(t-T_{1})}$. Using the above expression of C, the equation of capital accumulation becomes: $\dot{K}-\alpha _{2}(1-\phi )K=-\mu _{T_{1}}^{ -\frac{1}{\delta }}e^{(\frac{\alpha _{2}(1-\phi )-\rho }{\delta })(t-T_{1})}.$ Using the same variable change as in Appendix B and taking $K_{t}$ at $\hbox {t}=T_{1},$ gives:

$K_{t}=-(\overline{K_{2}}-K_{T_{1}})*e^{(\frac{\alpha _{2}(1-\phi )-\rho }{\delta })(t-T_{1})}+\overline{K_{2}},$ where $\overline{K_{2}}$ is unknown and will be determined using boundary conditions in Sect. 3.1.4.

1.5 Appendix $A_4$

We assume that the dirty source of energy is exhaustible and that we have crossed the second regime after a period of time $T_{1}$. Then, the initial stock of the dirty source of energy $S_{0}$ is equal to the sum of the part of the dirty source of energy that is used during the first regime which corresponds to the total amount of pollution $\overline{Z}$ and the part of the dirty source of energy that the economy uses during the second regime. We have: $S_{0}=\underset{\overline{Z}}{\underbrace{\int _{0}^{T_{1}}\xi (E_{Yt}+E_{Ct})dt}}+\int _{T_{1}}^{T_{2}}\xi (E_{Yt}+E_{Ct})dt$. This implies that: $S_{0}-\overline{Z}=\int _{T_{1}}^{T_{2}}\xi (E_{Yt}+E_{Ct})dt=\frac{\xi \alpha _{2}}{\beta _{2}}\int _{T_{1}}^{T_{2}}K_{t}dt+\xi \int _{T_{1}}^{T_{2}}E_{Ct}dt,$ with $S_{0}>\overline{Z}$.

The above equation gives:

$$\begin{aligned} \frac{1}{\xi }(S_{0}-\overline{Z})= & {} -(\xi \nu _{T_{1}})^{-\frac{1}{\delta }}* \frac{\delta }{\rho }\left[ e^{-\frac{\rho }{\delta }(T_{2}-T_{1})}-1\right] +\frac{\alpha _{2}(1-\phi )}{\beta _{2}}\overline{K_{2}}\left[ (T_{2}-T_{1})\right] \\&-\,\frac{\delta \alpha _{2}}{\beta _{2}(\alpha _{2}(1-\phi )-\rho )}* (\overline{K_{2}}-K_{T_{1}})*\left[ e^{(\frac{\alpha _{2}(1-\phi )-\rho }{\delta }) (T_{2}-T_{1})}-1\right] . \end{aligned}$$

1.6 Appendix $A_5$

The level of capital at each time during the first regime is determined as follows:

FOCs give: $\mu _{t}=\mu _{T_0}e^{(\rho -\alpha _{2}(1-\phi ))t},$ $\nu _{t}=\nu _{T_0}e^{\rho t} ,$ $C_{t}=\mu _{T_0}^{-\frac{1}{\delta }}e^{(\frac{\alpha _{2}(1-\phi )-\rho }{\delta })t}$ and $E_{Ct}=(-\nu _{T_0}\xi )^{-\frac{1}{\delta }}e^{-\frac{\rho }{\delta }t}$. As before, we also replace the expression of $C_t$ in the equation of capital accumulation to get: $\dot{K}_t-\alpha _{2}(1-\phi )K_t=-\mu _{T_0}^{-\frac{1}{\delta }}e^{(\frac{\alpha _{2}(1-\phi )-\rho }{\delta })t}.$ Solving the above equation and taking $K_{t}$ at $t=0$ give $K_{t}=-(\overline{K_{1}}-K_{0})e^{(\frac{\alpha _{2}(1-\phi )-\rho }{\delta })t}+\overline{K_{1}}$. Finally, at the end of the first regime, we cross the pollution threshold so that $\overline{Z}=\int _{0}^{T_{1}}\xi (E_{Yt}+E_{Ct})dt$. This equation then implies that:

$$\begin{aligned} \nu _{T_0}= & {} -\frac{1}{\xi }\left[ \left( -\frac{\overline{Z}}{\xi }+\frac{\alpha _{2}(1-\phi )}{\beta _{2}} \overline{K_{1}}*T_{1}- \frac{\alpha _{2}(1-\phi )\delta }{\beta _{2}(\alpha _{2}(1-\phi ) -\rho )}(\overline{K_{1}}-K_{0})\right. \right. \\&\left. \left. \left[ e^{\left( \frac{\alpha _{2}(1-\phi )-\rho }{\delta }\right) *T_{1}}-1\right] \right) * \frac{\rho }{\delta \left[ e^{-\frac{\rho }{\delta }T_{1}}-1\right] }\right] ^{-\delta } \end{aligned}$$

where $\nu _{T_0}$ and $\overline{K_{1}}$ are unknown and will be determined in Sect. 3.1.4 using boundary conditions.

1.7 Appendix $B_1$

Equations (12), (9) and (11) become respectively:

$$\begin{aligned}&\dot{K}_{t}=Y{}_{t}-C_{t}-q_{t} ,\\&\left\{ \begin{array}{l@{\quad }l} E_{Yt} =min\{\frac{1}{\xi }E_{Ydt}, E_{Yct}\}+\varepsilon _{Y}(q_{t}), &{} t< T_{2}\\ E_{Yt} = E_{Yct}+ \varepsilon _{Y}(q_{t}), &{} t \ge T_{2} \\ \end{array}\right. \nonumber \end{aligned}$$

(26)

and

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} E_{Ct} = min\{\frac{1}{\xi }E_{Cdt}, E_{Cct}\}+\varepsilon _{C}(q_{t}), &{} t< T_{2}\\ E_{Ct} = E_{Cct}+ \varepsilon _{C}(q_{t}), &{} t \ge T_{2} .\\ \end{array}\right. \end{aligned}$$

where $t< T_{2}$ corresponds to the first two regimes, while $t \ge T_{2}$ denotes the third regime.

Also, Eqs. (14), (19) and (20) become respectively:

$$\begin{aligned} \dot{K}_{t}= & {} \alpha _{2}K_{t}-\alpha _{2}\frac{(E_{Yt}+E_{Ct}) -(\varepsilon _{Y}(q_{t})+\varepsilon _{C}(q_{t}))}{\eta }-C_{t}-q_{t}.\\ \dot{S}_{t}= & {} -E_{dt}=- \xi (E_{Yt}+E_{Ct})+\xi (\varepsilon _{Y}(q_{t}) +\varepsilon _{C}(q_{t})) \end{aligned}$$

and

$$\begin{aligned} \dot{Z}_{t}=E_{dt}= \xi (E_{Yt}+E_{Ct})-\xi (\varepsilon _{Y}(q_{t})+\varepsilon _{C}(q_{t})). \end{aligned}$$

1.8 Appendix $B_2$

1.8.1 Second regime

As before, the only change is the FOC with respect to $q_{t}$:

$$\begin{aligned} \varepsilon _{Y}^{\prime }(q_{t})+\varepsilon _{C}^{\prime }(q_{t})=\frac{\mu _{t}}{\xi \nu _{t}} . \end{aligned}$$

(27)

Using the same specifications as before, the solution of Eq. (27) is :

$$\begin{aligned} q^{*}=\left[ \frac{\mu _{t}}{2\sigma \xi \nu _{t}}\right] ^{\frac{1}{\sigma -1}} . \end{aligned}$$

(28)

Equation (28) helps to solve the model during the second regime as before. The expression of the capital during the second regime becomes:

$$\begin{aligned} K_{t}-\overline{K_{2}}= & {} -\mu _{T_{1}}^{-\frac{1}{\delta }}* \frac{\delta }{\alpha _{2}(1-\phi )(1-\delta ) -\rho }e^{\frac{\alpha _{2}(1-\phi )-\rho }{\delta }(t-T_{1})}\\&+\, \left[ \frac{\mu _{T_{1}}}{2\sigma \xi \nu _{T_{1}}}\right] ^{\frac{1}{\sigma -1}}\frac{\sigma -1}{\alpha _{2}(1-\phi )\sigma } e^{-\frac{\alpha _{2}(1-\phi )}{\sigma -1}(t-T_{1})}. \end{aligned}$$

We should also observe here that the level of capital at each period of time during the second regime has a second negative component. As the share of the income that goes to investment is reduced by investment in energy saving technologies, one should expect a decrease in capital.

As in the case without any investment in EST, all the dirty sources of energy are extracted during the first and the second regimes such that:

$$\begin{aligned} S_{0}-\overline{Z}=\int _{T_{1}}^{T_{2}}\xi (E_{Yt}+E_{Ct}-\varepsilon _{Y} -\varepsilon _{C})dt. \end{aligned}$$

Solving the above equation, we get:

where $H_{0}=-\xi ^{\frac{\delta -1}{\delta }}\frac{\delta }{\rho }$, $H_{1}=-\frac{\xi \delta ^{2} \alpha _{2}}{\beta _{2}[\alpha _{2}(1-\phi )(1-\delta )-\rho ][\alpha _{2}(1-\phi )-\rho ]}$, $H_{2}=-\frac{\xi (\sigma -1)^{2} \alpha _{2}}{\beta _{2}(2\sigma \xi )^{\frac{1}{\sigma -1}}\sigma \alpha _{2}^{2}(1-\phi )^{2}}$ and $H_{3}=\frac{2\xi (\sigma -1)}{\alpha _{2}(1-\phi )\sigma (2\sigma \xi )^{\frac{\sigma }{\sigma -1}}}.$

1.8.2 First Regime

As in the second regime the optimal investment in EST is:

$$\begin{aligned} q^{*}=\left[ -\frac{\mu _{t}}{2\sigma \xi \nu _{t}}\right] ^{\frac{1}{\sigma -1}}. \end{aligned}$$

(29)

We then solve the equation of capital accumulation to get the following expression of capital during the first regime:

$$\begin{aligned} K_{t}-\overline{K_{1}}= & {} -\mu _{T_0}^{-\frac{1}{\delta }}\frac{\delta }{\alpha _{2}(1-\phi )(1-\delta )-\rho } e^{\frac{\alpha _{2}(1-\phi )-\rho }{\delta }t}\\&+ \left[ -\frac{\mu _{T_0}}{2\sigma \xi \nu _{T_0}}\right] ^{\frac{1}{\sigma -1}}\frac{\sigma -1}{\sigma \alpha _{2}(1-\phi )}e^{\frac{-\alpha _{2}(1-\phi )}{\sigma -1}t}. \end{aligned}$$

We still have an additional negative component of the capital due to investment in energy saving technologies.

At the end of the first regime, we cross the pollution threshold so that:

$$\begin{aligned} \overline{Z}=\int _{0}^{T_{1}}\xi (E_{Yt}+E_{Ct}-2\varepsilon _{t}^{*})dt. \end{aligned}$$

By solving the above equation as before, we get the following expression:

where $H_{0}$, $H_{1}$ and $H_{3}$ are the same as defined before and $H_{4}=\frac{\xi \delta (\sigma -1)\alpha _{2}}{\beta _{2} \alpha _{2}((1-\phi )\left[ \alpha _{2}(1-\phi )(1-\delta )-\rho \right] }.$

1.8.3 Boundary Conditions

As in the case without any investments in EST, we apply some boundary conditions. Continuity of $\mu _{t}$ and continuity of $K_{t}$ at the switching times $T_{1}$ and $T_{2}$ gives the following equation:

where

$$\begin{aligned} H_{5}= & {} -\frac{\Theta \delta }{\alpha _{2}-\rho -\delta \Lambda }e^{\frac{\alpha _{2}(1-\phi )-\rho }{\delta }T_{2}},\\ H_{6}= & {} \frac{\delta }{\alpha _{2}(1-\phi )(1-\delta )-\rho }\left[ \theta e^{\frac{\alpha _{2}(1-\phi )-\rho }{\delta }T_{1}}+(1-\phi )-e^{\frac{\alpha _{2}(1-\phi )-\rho }{\delta }T_{2}}\right] ,\\ H_{7}= & {} \frac{\sigma -1}{\alpha _{2}\sigma (1-\phi )}\left[ -e^{\frac{\rho -\alpha _{2}(1-\phi )}{\sigma -1}T_{1}} +e^{[{\frac{\rho }{\sigma -1}T_{1}-\frac{\alpha _{2}(1-\phi )}{\sigma -1}T_{2}}]}\right] \hbox { and }\\ H_{8}= & {} \frac{(\sigma -1)(1-\theta )}{\alpha _{2}\sigma (1-\phi )}\left[ -1+e^{\frac{-\alpha _{2}(1-\phi )}{\sigma -1}T_{1}}\right] .\\ \end{aligned}$$

Equations A, B and C express three different relationships between $\mu _{T_0}$, $\nu _{T_0}$ and $\nu _{T_{1}}$ that we can simultaneously solve. Additionally, we simultaneously and numerically solve the equality of Hamiltonians at the switching time $T_{1}$ and $T_{2}$ to get $T_{1}$ and $T_{2}$.