Abstract
Truss decomposition is a popular notion of hierarchical dense substructures in graphs. In a nutshell, k-truss is the largest subgraph in which every edge is contained in at least k triangles. Truss decomposition aims to compute k-trusses for each possible value of k. There are many works that study truss decomposition in deterministic graphs. However, in probabilistic graphs, truss decomposition is significantly more challenging and has received much less attention; state-of-the-art approaches do not scale well to large probabilistic graphs. Finding the tail probabilities of the number of triangles that contain each edge is a critical challenge of those approaches. This is achieved using dynamic programming which has quadratic run-time and thus not scalable to real large networks which, quite commonly, can have edges contained in many triangles (in the millions). To address this challenge, we employ a special version of the Central Limit Theorem (CLT) to obtain the tail probabilities efficiently. Based on our CLT approach we propose a peeling algorithm for truss decomposition that scales to large probabilistic graphs and offers significant improvement over state-of-the-art. We also design a second method which progressively tightens the estimate of the truss value of each edge and is based on h-index computation. In contrast to our CLT-based approach, our h-index algorithm (1) is progressive by allowing the user to see near-results along the way, (2) does not sacrifice the exactness of final result, and (3) achieves all these while processing only one edge and its immediate neighbors at a time, thus resulting in smaller memory footprint. We perform extensive experiments to show the scalability of both of our proposed algorithms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An important category of problems in network analysis is detecting dense or cohesive components in graphs. Studying cohesive subgraphs can reveal important information about connectivity, centrality, and robustness of the network. Among different notions of cohesive subgraphs in the literature, the notion of truss is particularly suited to extracting a hierarchical structure of cohesive subgraphs [1].
In deterministic graphs, the k-truss of a graph G is defined as the largest subgraph in which each edge is contained in at least k triangles (or \((k-2)\) in some works). The highest value of k for which an edge is part of the k-truss is called truss value of that edge. The collection of all k-trusses for different values of k forms the truss decomposition of the graph. This is a hierarchical structure because k-truss is contained in \((k-1)\)-truss for all \(k>1\). Truss decomposition has been used in several important applications such as visualization of complex networks [2] and community modeling [3]. Truss decomposition can also be used to speed up the process of discovering maximum cliques since each k-clique should be in a k-truss.
Probabilistic truss decomposition naturally extends all the applications of deterministic truss decomposition to probabilistic graphs. Another application described in [4] is task-driven team formation in probabilistic social networks. It is thus important to compute truss decomposition in probabilistic graphs. While truss decomposition in deterministic graphs is well studied [1, 3, 5], truss decomposition in probabilistic graphs is more challenging and has received much less attention. Here, we present efficient algorithms for computing truss decomposition in probabilistic graphs; the graphs in which each edge has a probability of existence independent of the other edges. We use the notion of \((k,\eta )\)-truss introduced in [4]. Specifically, we aim to compute the largest subgraph in which each edge is contained in at least k triangles within that subgraph with probability no less than a user specified threshold \(\eta\). The threshold \(\eta\) defines the desired level of certainty of the output trusses.
1.1 Challenges and contributions
The standard approach to computing k-truss decomposition is the edge peeling process, which is based on continuously removing edges with less than k triangles (cf. [4]). This process is repeated after incrementing k until no edges remain [6], which results in finding all k-trusses for different values of k. Counting the number of triangles which contain an edge (the “edge support”) is simple in deterministic graphs. But, in probabilistic graphs, computing the probability that the edge support is above a threshold has a combinatorial nature (see [4, 7]). We refer to this probability as support probability of the edge. Computing the support probability becomes challenging when the input graph is huge. This is because given an edge \(e=(u,v)\) its support probability is computed using dynamic programming (DP) as proposed in [4]. The time complexity of computation using DP is \(O((\min \left\{ d(u), d(v) \right\} )^2)\), where d(u) and d(v) are the deterministic degrees of u and v, respectively. Unfortunately, the values of d(u) and d(v) can be in the millions in many real-world social and web networks, and the quadratic time complexity of DP makes it impractical for such graphs.
In this paper, we model each triangle in a probabilistic graph as a Bernoulli random variable with an existence probability and design a novel approach based on Lyapunov’s special version of the Central Limit Theorem [8] to approximate the probability distribution of the support of an edge. We derive an error bound on the approximation to demonstrate that the computed probabilities are very close to the values obtained through exact computation.
Next, we design a peeling algorithm for probabilistic k-truss decomposition. Our algorithm takes advantage of the fast calculation of edge support probabilities in time \(O(\min \left\{ d(u), d(v) \right\} )\) using the Central Limit Theorem. It also uses optimized array-based data structures for storing edge information of the graph.
While our first approach efficiently computes truss decomposition, it is a peeling approach, nevertheless. Edge peeling is associated with a major drawback: the edges have to be kept sorted by their current triangle support at all times which requires maintaining global information of the graph at each step of the algorithm. Furthermore, if we want to avoid statistical approximations, edge peeling becomes even more challenging, since the exact computation of the support probability of an edge e is done using dynamic programming. The process is repeated each time the edge loses a neighbor during the peeling approach. This leads us to ask whether there is an exact and scalable approach to truss decomposition in probabilistic graphs.
We answer the above question positively by introducing an algorithm which extends the iterative h-index computation, recently introduced for deterministic graphs in [6], to probabilistic graphs.
In deterministic graphs, the triangle supports of the edges are obtained at the beginning, and each edge computes the h-index value for the list of its neighbors’ triangle supports. Neighbors of an edge are those edges which form a triangle with the given edge. This process is repeated on these values until convergence to truss values occurs. Upon termination, the final h-index value of each edge equals its truss value. The authors in [6] prove that convergence of support values to the truss values is guaranteed.
Unfortunately, this idea does not work for probabilistic graphs, since it does not consider uncertainty in such graphs, thus resulting in wrong truss values. In this paper, we introduce an h-index updating algorithm that works for probabilistic graphs. In particular, we design a procedure which considers properties of truss subgraphs in probabilistic graphs and maintains proper upper-bounds on truss value of edges until convergence to true truss values. In summary, our contributions are as follows:
-
We introduce an efficient approach based on Lyapunov’s Central Limit Theorem to compute support probabilities for the edges in the input graph. Using a theoretical analysis based on the Berry-Essen Theorem, we obtain an error bound that formalizes the tightness of our approximation.
-
We develop a peeling algorithm based on recursive edge deletions which, by utilizing CLT and efficient data structures, is able to calculate truss decomposition in large probabilistic graphs not possible to handle with the DP approach.
-
We propose a second algorithm based on h-index updating which works for probabilistic graphs. Our proposed algorithm is exact with respect to final result, but also progressive allowing the user to see near-results along the way, and it works by processing only one edge and its immediate neighbors at a time, resulting in smaller memory requirement.
-
While proving the correctness of the algorithm, we obtain an upper-bound on the number of iterations that the algorithm needs for convergence. It shows that the convergence to truss values can be obtained after a finite number of iterations.
-
We evaluate the performance of our approaches on a wide range of datasets. Our experimental results confirm the scalability and efficiency of our exact algorithm, significantly outperforming the exact algorithm in [4] for large datasets. Furthermore, comparisons with the proposed approximate algorithm show that the running time of our exact algorithm is very close to that of the approximate algorithm. It is indeed surprising that we can achieve efficiency without sacrificing the exactness of the solution. Moreover, we show the usefulness of the probabilistic truss decomposition on the human biomine dataset with respect to COVID-19 protein nodes.
2 Related work
In the literature, much research has been done in the area of mining and querying probabilistic graphs [9,10,11,12,13,14,15], such as the k-nearest neighbor search over probabilistic graphs [16], uncertain graph sparsification [17], and mining top k maximal cliques in probabilistic graphs [18].
Recently k-truss has attracted a lot of attention due to its cohesive structure and the fact that it can be used to compute other definitions of dense subgraphs, such as k-clique. In deterministic graphs, truss decomposition has been studied extensively in different settings (cf. [1, 3, 19, 20]). For instance, Xing et al. in [19], propose a novel traversal in-memory algorithm for truss decomposition in deterministic graphs. In external-memory setting, Wang and Cheng in [1] propose an efficient algorithm for deterministic graphs that do not fit in memory. Huang et al. [3] study truss decomposition of dynamic deterministic graphs.
For probabilistic graphs, the notion of \((k,\eta )\)-truss is introduced by Huang, Lu, and Lakshmanan in [4]. Their algorithm for computing \((k,\eta )\)-truss is based on iterative edge peeling and uses dynamic programming for computing the support probability of the edges. While this algorithm runs in polynomial time, it does not scale well to large graphs, especially those having a high maximum vertex degree. [4] also proposes the notion of global \((k,\eta )\)-truss based on the probability of each edge belonging to a connected k-truss in a possible world. An algorithm based on sampling is proposed in [4] to find global \((k,\eta )\)-trusses. This notion of probabilistic truss decomposition falls in the category of #P-hard problems (Table 1).
3 Background
3.1 Trusses in deterministic graphs
Let \(G=(V,E)\) be an undirected graph with no self-loops. For a vertex \(u \in V\), the set of its neighbors is denoted by \(N_{G}(u)\) and defined as \(N_{G}(u) = \{v: (u,v) \in E\}\). A triangle in G is defined as a set of three vertices \(\{u,v,w\}\subseteq V\) such that all three edges (u, v), (v, w) and (u, w) exist. This triangle is denoted by \(\Delta _{uvw}\). The support of an edge \(e = (u,v)\) in G, denoted by \(\sup _{G}(e)\), is defined as the number of triangles in graph G containing e. Formally, \(\sup _{G}(e) = \left| N_G(u) \cap N_G(v) \right|\).
The k-truss of G is defined as the largest subgraph F of G in which each edge e has \(\textsf {sup}_{F}(e) \ge k\). The set of all k-trusses forms the truss decomposition of G, where \(0 \le k \le k_{\max }\), and \(k_{\max }\) is the largest support of any edge in G.
3.2 Probabilistic graphs
A probabilistic graph is a triple \(\mathcal G= (V, E, p)\), and is defined over a set of vertices V, a set of edges E and a probability function \(p : E \rightarrow (0,1]\) which maps every edge \(e \in E\) to an existence probability p(e). In the most common probabilistic graph model [21], the existence probability of each edge is assumed to be independent of other edges.
To analyze probabilistic graphs, we use the concept of possible worlds, which are deterministic graph instances of \(\mathcal G\). In each possible world only a subset of edges appears. For each possible world \(G = (V, E_G) \sqsubseteq \mathcal G\), where \(E_G \subseteq E\), the probability of observing that possible world is obtained as follows:
Example 1
Consider probabilistic graph \(\mathcal {G}\) in Fig. 1a. A possible world G of \(\mathcal {G}\) is shown in Fig. 1b. \(\text {Pr}(G) = 0.5 \cdot 0.4 \cdot 0.3 \cdot 0.65 \cdot (1-0.25) = 0.02925\).
Given edge \(e = (u,v)\), let \(k_e = \left| N_{\mathcal G}(u) \cap N_{\mathcal G}(v)\right|\). We define an integer random variable \(\textsf {sup}_{\mathcal G}(e)\) with values in \([0,k_e]\) and distribution:
where \(\mathbbm {1}(\sup _{G}(e) = t)\) is an indicator function which takes on 1 if edge e has support equal to t in G, and 0 otherwise.
Given a user-specified threshold \(\eta \in (0,1]\), the probabilistic support of an edge e, denoted by \(\eta\)-\(\textsf {sup}_{\mathcal G}(e)\), is the maximum integer \(t \in [0,k_e]\) for which \(\text {Pr}[ \textsf {sup}_{\mathcal G}(e) \ge t] \ge \eta\).
It should be noted that as t increases (decreases), \(\text {Pr}[ \textsf {sup}_{\mathcal G}(e) \ge t]\) decreases (increases).
Definition 1
Let \(\eta\) be a user defined threshold.
-
\((k,\eta )\)-truss of \(\mathcal G\) is the largest subgraph \(\mathcal F\) of \(\mathcal G\) in which each edge e has probabilistic support in \(\mathcal F\) no less than k, i.e. \(\eta\)-\(\textsf {sup}_{\mathcal F}(e) \ge k\).
-
Truss decomposition of \(\mathcal G\) is the set of all \((k,\eta )\)-trusses, for \(k \in [0,k_{\max , \eta }]\), where \(k_{\max ,\eta }=\max _{e} \{ \eta\)-\(\textsf {sup}_{\mathcal G}(e) \}\).
-
Truss value of an edge e, \(\kappa _{\eta }(e)\), is the largest integer k for which e belongs to a \((k,\eta )\)-truss.
Proposition 1
\((k,\eta )\)-truss of \(\mathcal G\) is the subgraph of \(\mathcal G\) containing all and only the edges e in \(\mathcal G\) with \(\kappa _{\eta }(e) \ge k\).
In this paper (as in [4]) we focus on finding the truss values of the edges in an input graph. Then \((k,\eta )\)-truss for any k is constructed by collecting all edges e with \(\kappa _{\eta }(e) \ge k\).
Example 2
Consider Fig. 2a, edge \(e=(1,2)\), and \(\eta = 0.20\). We have \(\text {Pr}[ \textsf {sup}_{\mathcal G}(e) \ge 3] = 1 \cdot 0.3 \cdot 0.5 = 0.15\) (product of probabilities that \(\bigtriangleup _{012}\), \(\bigtriangleup _{123}\), \(\bigtriangleup _{124}\) exist), and \(\text {Pr}[ \textsf {sup}_{\mathcal G}(e) \ge 2] = 0.65\). Since 0.65 is greater than \(\eta\), \(\eta\)-\(\textsf {sup}_{\mathcal G}(e) = 2\).
Figure 2b shows a (2, 0.15)-truss \(\mathcal F\) of \(\mathcal G\). Each edge \(e \in \mathcal F\), is contained in 2 triangles with probability 0.15.
Consider \(e=(1,2)\) and \(\eta =0.15\). Now, \(\eta\)-\(\textsf {sup}_{\mathcal G}(e) = 3\). Edge e is in (1, 0.15)-truss (\(\mathcal G\) itself) and (2, 0.15)-truss (\(\mathcal F\)). There is no (3, 0.15)-truss, thus, \(\kappa _{\eta }(e)=2\).
3.3 Obtaining \(\eta\)-\(\textsf{\textbf{sup}}_{\mathcal G}(e)\) using dynamic programming
To obtain \(\eta\)-\(\textsf {sup}_{\mathcal G}(e)\), we need to compute \(\text {Pr}[\textsf {sup}_{\mathcal {G}}(e) \ge t]\), which can be written in the form of the following recursive formula:
Computing \(\text {Pr}[\textsf {sup}_{\mathcal {G}}(e) = i]\) for different values of i can be done using dynamic programming as proposed in [4].
4 Central limit theorem framework
In this section, we describe a CLT-based framework to compute truss decomposition in probabilistic graphs.
4.1 Computing \(\eta\)-\(\textsf{\textbf{sup}}_{\mathcal G}(e)\) using Lyapunov CLT
We first show how a special version of Central Limit Theorem (CLT) can be applied to estimate \(\text {Pr} \big [ \textsf {sup}_{\mathcal {G}}(e) \ge k \big ]\). Then, we show theoretical bounds on the accuracy of this approximation.
Specifically, we consider a variant of CLT called Lyapunov CLT that can be applied when random variables are independent, but not necessarily identically distributed. The theorem can be formally stated as follows.
Theorem 1
(Lyapunov CLT [8]) Let \(\zeta _1, \zeta _2, \ldots , \zeta _n\) be a sequence of independent, but non-identically distributed random variables, where \(\zeta _k\) has finite mean \(\mu _k\) and variance \(\sigma _k\). Let
If
for some \(\delta > 0\), then \(\frac{1}{s_n}\sum _{k=1}^{n}(\zeta _k-\mu _k)\) converges in distribution to a standard normal random variable.
Equation (4) is called Lyapunov’s condition which in practice is usually tested for the special case \(\delta = 1\). The proof of this theorem can be found in [22].
Associated with each edge \(e_j\) we define a Bernoulli random variable \(\zeta _{e_j}\) which is 1 with probability \(p(e_j)\) and 0 with probability \(1-p(e_j)\). Since each edge is assumed to exist independently of other edges, \(\zeta _{e_j}\)’s are independent. Given an edge \(e=(u,v)\), let \(\mathcal {T}_e\) be a set of all the common neighbors of u and v in \(\mathcal {G}\). We have,
For each common neighbor \(t_i\) of u and v, let \(\zeta _{u,t_i}\) and \(\zeta _{v,t_i}\) be the Bernoulli random variables corresponding to the edges \((u,t_i)\) and \((v,t_i)\), respectively. Let \(X_i = \zeta _{u,t_i} \cdot \zeta _{v,t_i}\). The following observations hold for random variables \(X_i\): (1) \(X_i\)’s are Bernoulli random variables which take on 1 with probability \(p_i=p(u,t_i) \cdot p(v,t_i)\) and 0 otherwise. Note that \(\mathrm {E}[X_i] = \mu _i = p_i\) and \(\mathrm {Var}[X_i] = p_i (1-p_i)\). (2) \(X_i\)’s are independent, due to the assumption that existence of edges \((u,t_i)\) and \((v,t_i)\) is independent of the existence of edges \((u,t_j)\) and \((v,t_j)\) when \(i \ne j\), and \(X_i\)’s are not identically distributed, as \(p_i \ne p_j\) when \(i \ne j\).
Now, consider triangle \(\bigtriangleup _{uv{t_i}}\). With the assumption that e exists, \(\bigtriangleup _{uv{t_i}}\) exists if both edges \((u,t_i)\) and \((v,t_i)\) exist, which corresponds to \(X_i = 1\). On the other hand, the triangle does not exist if at least one of two edges, \((u,t_i)\) and \((v,t_i)\), does not exist, which corresponds to \(X_i = 0\). Therefore, we have
Random variables \(X_i\)’s are independent, but not identically distributed. Thus, if condition (4) is satisfied, we can conclude that \(\frac{1}{s_{k_e}}\sum _{i=1}^{k_e}(X_i-\mu _i)\), where \(s_{k_e}= \sqrt{\sum _{i=1}^{k_e} p_i(1-p_i)}\), converges to standard normal distribution. We prove this in Theorem 2.
In order to compute the right-hand side of equation (5), we can subtract \(\sum _{i=1}^{k_e} \mu _i\) from both sides of the inequality, and then divide by \(s_{k_e}\) which results in:
Using Lyapunov CLT and setting
we conclude that Z has standard normal distribution. Thus
where \(z= \frac{1}{s_{k_e}} (k - \sum _{i=1}^{k_e} \mu _i)\). Using the complementary cumulative distribution function [23] of standard normal variable Z, we can evaluate the right-hand side of Equation (8) for each value of k. Thus, to find the probabilistic support for an edge, we start with \(k=1\), approximate \(\text {Pr}[\textsf {sup}_{\mathcal {G}}(e) \ge k] = \text {Pr}[\textsf {sup}_{\mathcal {G}}(e) \ge k \bigl |e \text{ exists}] \cdot p(e)\) using Lyapunov CLT (for the first factor), and find the maximum k for which this probability is above threshold \(\eta\). For an edge e, the obtained value of k, which can be in range from one to \(k_e\), is set as initial \(\eta\)-support for that edge. Given an edge \(e = (u,v)\), the time complexity of finding probabilistic support is \(O(k_e)\).
In the following theorem we show that Lyapunov’s condition in Theorem 1 is satisfied for our problem by setting \(\delta = 1\) in Eq. (4).
Theorem 2
Given a sequence of random variables \(X_i\sim \text {Bernoulli}(p_i)\), where \(1 \le i \le n\), the Lyapunov’s condition (4) for \(\delta =1\) is satisfied whenever \(s_{n}= \sqrt{\sum _{k=1}^{n} p_k (1-p_k)} \rightarrow \infty\) as \(n \rightarrow \infty\).
Proof
Note that the variance of each Bernoulli random variable \(X_i\) is \(\sigma _i^2=p_i(1-p_i)\). Thus, we have \(s_n^2=\sum _{k=1}^{n} p_k(1-p_k)\) according to the Eq. (3). Also, the expected value of \(X_i\) is \(\mu _i = p_i\). By setting \(\delta =1\) in (4), \(E [ \bigl |X_k-\mu _k \bigl |^{3}]\) can be written as:
where in inequality (9) we have used the fact that \((1-p_k)^2+p_k^2 \le 1\) for any value of \(p_k\). Thus, \(\sum _{k=1}^{n} E \big [ \bigl |X_k-\mu _k \bigl |^{3}] \le s_n^2\). Setting \(\delta =1\) in the Lyapunov’s condition (4), and substituting (9) in it, we have \(E [ \bigl |X_k-\mu _k \bigl |^{3}]/s_{n}^3 \le s_{n}^{2}/s_{n}^{3}=1/s_{n} \rightarrow 0\) as \(n \rightarrow \infty\) using the assumption that \(s_n \rightarrow \infty\) as \(n \rightarrow \infty\). Thus Eq. (4) holds and the theorem follows. \(\square\)
Corollary 1
For our problem, \(s_{n}= \sqrt{\sum _{k=1}^{n} p_k (1-p_k)} \rightarrow \infty\) as \(n \rightarrow \infty\).
Proof
Observe that \(s_n^2=\sum _{k=1}^{n} p_k(1-p_k)=\sum _{k=1}^{n} \sigma _k^2 \ge n \sigma _{\min }^2.\) Since all the edge probabilities, \(p_i\)’s, are fixed constants, \(\sigma _{\min }^2=\min _k\{\sigma _k^2\}\) is bounded away from zero. Therefore, as n increases, \(n \sigma _{\min }^2\) goes to \(\infty\), resulting in \(s_n \rightarrow \infty\) as \(n \rightarrow \infty\) and hence the assumption needed in Theorem 2 holds for our problem. \(\square\)
From the above corollary and Theorem 2, we conclude that our sequence of \(X_i\) variables satisfies the Lyapunov conditions in Theorem 1.
4.2 Accuracy of the approximation
In order to show the accuracy of the approximation, we use the Berry–Esseen theorem stated as follows.
Theorem 3
[24] Let \(Y_1,Y_2,\ldots , Y_n\) be a sequence of non identically distributed, independent random variables with \(\textit{E}(Y_i) = 0\), \(\textit{E}(Y_i ^2) = \sigma _i ^2\), and \(\textit{E}(\bigl |Y_i ^3 \bigl |) = \rho _i < \infty\), there exists a constant \(C_0\) such that the following inequality is satisfied for all n:
where \(\textit{F}_n\) is the cumulative distribution of \(S_n = \frac{Y_1 + Y_2 + \cdots + Y_n}{\sqrt{\sigma _1^2 + \sigma _2^2 + \cdots + \sigma _n^2}}\), which is the sum of \(Y_i\)’s standardized by the variances, and \(\Phi\) is the cumulative distribution of the standard normal distribution. In the above inequality \(\psi _0\) is a function given by
where \(\overrightarrow{\sigma } = (\sigma _1, \ldots , \sigma _n)\), and \(\overrightarrow{\rho } = (\rho _1, \ldots , \rho _n)\) are the vectors of \(\sigma _i\)’s and \(\rho _i\)’s respectively.
In the following corollary, using the Berry-Esseen theorem, we show how to obtain an upper-bound on the maximal error while approximating the true distribution of the sum of \(X_i\)’s with the normal distribution.
Corollary 2
For each edge e in \(\mathcal {G}\) with \(X_i\)’s defined as above in this section, where \(i=1,\ldots ,k_e\), the error bound on the approximation of the right-hand side of Equation (8) to the standard normal distribution is given as follows:
Proof
Let \(Y_i = X_i - p_i\) in Eq. (7). We can apply the Berry–Essen theorem for random variables \(Y_1,Y_2, \ldots ,Y_{k_e}\), since for each \(Y_i\), \(\mathrm {E}[Y_i] = 0\). In addition,
It should be noted that the random variable
in the Berry–Essen theorem is the same as the random variable Z in Eq. (7).
Substituting \(\sigma _i ^2\) and \(\rho _i\) in Eq. (11), we obtain:
Using the fact that \(1 = (1-p_i+p_i)^2 = (1-p_i)^2 + p_i^2 + 2p_i(1-p_i) \ge (1-p_i)^2 + p_i^2,\) we can simplify (14) to have:
Substituting (15) in (10) the stated claim follows. \(\square\)
4.3 Peeling algorithm
While solving the challenge of computing probabilistic support is an important step forward, we still need an algorithm for computing truss decomposition for large probabilistic graphs.
Our algorithm is based on a concept used in truss computation in deterministic graphs, which we call “edge peeling”. It involves (1) recursively deleting the edge e of smallest support, (2) setting e’s truss value to be equal to its support at the time of deletion, and (3) updating the supports of the edges which form a triangle with e (cf. [25]).
We call our proposed algorithm PAPT (peeling-approximate-truss). It consists of two main parts: (1) initial probabilistic support computation, and (2) probabilistic truss computation which involves deleting the edge of smallest probabilistic support, setting its truss value and updating probabilistic support values of other edges once it is removed.
In the initial support computation step, the probabilistic support of each edge e is computed using CLT and Eq. (8), if \(k_e\), the number of triangles containing e, is greater than a threshold B, otherwise DP is used. We set threshold B to be 100 in our experiments.Footnote 1


Algorithm 1 describes the main steps of PAPT. It sorts the edges in ascending order of their probabilistic support and stores them in sortedEdge array (line 4). Then, the algorithm starts removing edges with the lowest probabilistic support (line 5). The removal of edge \(e=(u,v)\) affects the probabilistic support of all edges that can constitute triangles with (u, v).
Hence, the algorithm finds all the common neighbors w of u and v, i.e., \(\bigtriangleup _{uvw}\) is a triangle containing edge (u, v). Once a common neighbor w is found, we find the edge ID of (u, w) and (v, w) (lines 9-10). Using this information, the probabilistic support of edges (u, w) and (v, w) are updated if their probabilistic supports are greater than e’s probabilistic support (lines 11 and 13). We do the updating part using Algorithm 2. In particular, if the number of remaining triangles which contain an edge is greater than B, we perform update phase using CLT approach. Otherwise, we apply DP (Algorithm 2 lines 2-5).
Since the probabilistic supports of edges (u, w) and (v, w) have changed, we update their position in sortedEdge array in constant time while maintaining the order of the array (line 6 of Algorithm 2). For the details of this step, we refer the reader to [25]. After removing all the edges with probabilistic support equal to k, the program increments k by one, and continues (lines 16-17) until all the edges in the graph are removed.
4.4 Time complexity
The running time of initial probabilistic support computation phase is dominated by computing probabilistic support using Central Limit Theorem which can be done in \(O(k_e)\) time, where \(O(k_e) \subseteq O(\min \left\{ d(u),d(v) \right\} )\). Note that this phase is faster that dynamic programming approach which computes probabilistic supports in \(O(k_e^2)\). In the truss computation phase (lines 5-17), when an edge \(e=(u,v)\) is removed, the support of edges (v, w) and (u, w) should be updated. Thus, for each edge the number of updates is at most \(2 \cdot \left| N_{\mathcal {G}}(u) \cap N_{\mathcal {G}}(v) \right| \in O(\min \left\{ d(u),d(v) \right\} )\). The time complexity of each single update is \(O(k_e) \subseteq O(\min \left\{ d(u),d(v) \right\} )\). Thus, the updating part takes
where \(d_{\max }\) is the maximum degree, m is the number of edges in graph \(\mathcal {G}\), and \(\psi\) is minimum number of spanning forests needed to cover all edges of \(\mathcal {G}\). Therefore, the time complexity of Algorithm 1 is \(O(d_{\max } \psi m )\). It should be noted that this is the worst case running time analysis, our proposed algorithm is quite fast in practice.
5 H-Index framework
Here we propose an algorithm based on h-index updating, which has been introduced in the context of deterministic graphs by [6]. Given a set of real numbers, the h-index of the set is defined as the largest number h such that there are at least h elements in the set that are equal to h or higher. For instance, the h-index of the set \(\left\{ 1,2,3,3,5 \right\}\) is 3 because the set includes three numbers no less than 3.
We also have the notion of the h-index of an edge which is an integer variable initialized to the edge’s initial support (as a first approximation of the edge’s truss value). Then the algorithm iterates multiple times over the edges tightening up their h-index as described below. In fact, truss values are related to h-indices. For instance, truss value of an edge can be defined as the largest k such that it is contained in at least k triangles (or with probability \(\ge \eta\) in the probabilistic context) whose edges have truss value of at least k.
Let e be an edge and \((e,e',e'')\) be a triangle supporting e. For such a triangle, we define its support to e as the minimum of h-indices of \(e'\) and \(e''\). The support values of all triangles supporting e are collected in a set L and its h-index is computed. At each iteration, the h-index of e is updated to the smallest of its current value and the h-index of L.
In our algorithm, we refer to this process as Phase I. This phase corresponds to the h-index based algorithm of [6] for the deterministic case. In deterministic graphs, once the process terminates, the h-index of each edge becomes equal to the truss value of that edge. However, we show that this does not solve our problem.
5.1 Deterministic h-index updating, Phase I
In the following we provide explanation of Phase I of our algorithm, which is based on [6].
Definition 2
Given a set K of natural numbers, \(\mathcal {H}(K)\) is the largest \(k \in \mathbb {N}\) such that at least k elements of K are greater than or equal to k.

Let h(e) denote the h-index value of edge e at each iteration of our algorithm. Phase I tightens h(e) values for each edge e and iterates until no further updates occur for any h(.) value irrespective of edge probabilities. The flag update_Phase I is used to check termination of \(\textit{Phase I}\) (line 3). The flag is initially set to true (line 2), and stays true as long as there is an update on a h(.) value (lines 4,12, and 13). For each triangle \(\bigtriangleup =(e,e',e'')\) which contains e, the algorithm computes its \(\rho _{\bigtriangleup }\) value that is the minimum value of \(h(e')\) and \(h(e'')\) and collects them in a set L (lines 7-10). Then, function \(\mathcal {H}\) is applied on set L (line 11). If the h-index of set L is smaller than h(e), it is assigned as a new index for edge e in array h (line 11). The validity of the assigned value is checked by \(\textit{Phase II}\) in the next iterations of our proposed proHIT algorithm using the scheduled array (line 15).
We demonstrate how Phase I works in the following example:
Example 3
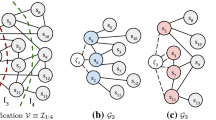
To illustrate how h-index works on deterministic graphs, we refer to Fig. 3. The figure shows a deterministic graph with 6 vertices. Initially, the triangle counts of all the edges are computed and are set as initial values on the h-index of the edges. Let \(h_0\) be the list of these initial values, which are shown with blue color in the figure. Then, the algorithm starts updating the h-indices based on the initial values. Let \(h_1\) be the list of updated values at this step (red). Edge \(e=(0,2)\), for instance, participates in 4 triangles and in each of them, the algorithm finds the edge neighbor to (0, 2) with minimum \(h_0\) value and records this value in an array. Then the algorithm updates the h-index of e. So, \(L = \{ \min (h_0(0,1),h_0(1,2)), \min (h_0(0,3),h_0(2,3)), \min (h_0(0,4), h_0(2,4)),\min (h_0(0,5),h_0(2,5)) \} = \{1,2,3,2 \}\). As a result, \(h_1(0,2) = \mathcal {H}(L) = 2\). The h-index of edges (0, 4) and (2, 4) are updated similarly. No more updates happen in the next iteration. Since the given graph is a deterministic graph, at the end, each edge obtains its truss value (green).
5.2 Phase II
Since Phase I does not take into account an edge having enough support probability to be part of a \((k,\eta )\)-truss, it may not converge to the true truss value of the edge.
For an example, consider Fig. 2a and \(\eta = 0.2\). In Table 2 we show the execution of our algorithm at each phase. The first column shows edges in the graph. The last shows their truss values. Column ph_I shows the h-index values at the end of Phase I. Initially h-index, h(e), of each edge e is set to \(\eta\)-\(\textsf {sup}_{\mathcal G}(e)\) (second column). Now, consider edge \(e = (1,2)\). For each triangle containing e, Phase I finds the minimum h-index of the two edges other than e in the triangle, and adds this minimum to a set L. For e, we have \(L = \{ \min (h(0,1),h(0,2)), \min (h(1,3),h(2,3)), \min (h(1,4),h(2,4)) \} = \{ 1,2,2 \}\).
Since there are two numbers on this list that are equal to 2, Phase I sets 2 as the h-index of edge e. Further execution of Phase I cannot produce any updates. However, the truss value of edge e is in fact 1 (see last column of Table 2) as we explain later in this section. Therefore, Phase I is not able to converge to the truss value of e. Nevertheless, we prove that Phase I can be used to provide upper-bounds to true truss values. The proof of this fact, Theorem 4, is presented in Sect. 5.4.


We tackle the problem by introducing a process we call Phase II. Although Phase I is not able to compute exact truss values, it can provide good upper-bounds which can be used in Phase II. Therefore, we combine Phase II with Phase I to speed up convergence as Phase I runs faster than Phase II.
The major steps of our algorithm, probabilistic h -index truss (proHIT), are summarized in Algorithm 4. At a high level, we maintain an array h indexed by edges where we initially store the h-index value for each edge. Then, we tighten up these values using Phase I and Phase II, and by the end of the iterations, we have the output truss values in array h.
Checking whether an edge requires processing or not is done by array scheduled, which is initialized to true for each edge. Variable updated records whether there is some edge with its h(.) value changed or not. Line 4 invokes Phase I. Then, Phase II starts and processes the h(.) values (upper-bound on truss value) of all the edges for the possibility of gap between current value and truss value (line 7). If after Phase II terminates, there is some edge with its h(.) value updated, Phase I (line 10) starts again. The process continues until each h(.) value achieves convergence (lines 6-10). The final truss value of each edge is set to the final h-index.
Phase II of our approach is given in Algorithm 5. This part crucially differentiates our approach from h-index based algorithms for deterministic graphs.
Let e be an edge. We define \(\Gamma\) to be the set of \((e,e',e'')\) triangles that contain e and \(h(e'), h(e'') \ge h(e)\). It is only the triangles in \(\Gamma\) that can contribute to updating h(e).
Also, we denote by \(\text {Pr} \big [\textsf {sup}(e) \ge h(e) \bigl |\Gamma \big ]\) the probability that e is contained in at least h(e) triangles selected from \(\Gamma\). Now, in order to possibly tighten up the current upper bound value of e, we check the condition
For each scheduled edge e, line 4 constructs the set \(\Gamma\) using function ConstructGamma, and the above condition is checked in line (6). Checking the condition presents its own challenges and is presented in detail later in this section. If the condition fails, integer values less than h(e) are checked one at a time until we find a value for h(e) for which the condition is true. Set \(\Gamma\) is updated each time to correspond to the h(e) value being used for edge e (lines 8-9). This guarantees that the assigned value does not go below the true truss value of each edge. Variable \(h_e\textit{-changed}\) records whether a new h(e)-value for e is obtained or not, and initially is set to false (line 5).
For instance, let us consider again the example in Fig. 2a. For \(e=(1,2)\) in Table 2 with \(h(e) = 2\) (which is obtained by Phase I, see third column in Table 2), we verify the condition \(\text {Pr}[\textsf {sup}(e) \ge 2 \bigl |\Gamma ] \ge \eta\), where \(\Gamma = \{ \bigtriangleup _{123} , \bigtriangleup _{124}\}\) (set of triangles containing e with other edges having an h(.) value of at least 2). We have \(\text {Pr}[\textsf {sup}(e) \ge 2 \bigl |\Gamma ] = 0.3 \cdot 0.5 = 0.15 < 0.2\). As a result, e cannot have a truss value of 2. As such, we update h(e) to be 1 and check the condition again. We have \(\text {Pr}[\textsf {sup}(e) \ge 1 \bigl |\Gamma ] = 1 > \eta\), where \(\Gamma = \{ \bigtriangleup _{012}, \bigtriangleup _{123} , \bigtriangleup _{124}\}\) (set of triangles containing e with other edges having an h(.) value of at least 1). Since the new probability is greater than \(\eta\), h(e) is settled to 1.
Let \(E_{\Gamma }\) be the edges of the triangles in \(\Gamma\). If a new h(e) value is obtained and checked in line 10, the edges in \(E_{\Gamma }\setminus \{e\}\) may change their h(.) values and thus are scheduled to be processed in the next iteration (lines 12-13).
In the following sections we provide the proof of the correctness of the algorithm as well as time complexity analysis.
The main challenge in Phase II is efficient checking of condition 16 for different values of h(e) until a proper value is obtained. For this, we introduce a modified dynamic programming (DP) process to avoid computation of these probabilities from scratch.
5.3 Modified DP
This process is invoked when we check the condition on line 6 of Algorithm 5.
Let \(H=h(e)\), and \(\Gamma\) be the set of \((e,e',e'')\) triangles as defined earlier. For a triangle \(\bigtriangleup = (e,e',e'') \in \Gamma\), we denote by \(\rho _{\bigtriangleup }\) the minimum value of \(h(e'), h(e'')\). We have \(\rho _{\bigtriangleup } \ge H\).
The probability \(\text {Pr}[\textsf {sup}(e) \ge H \bigl |\Gamma ]\) is computed using DP [4]. However, \(\Gamma\) changes in each iteration of the while loop (see line 9). We would like to avoid the computation of \(\text {Pr}[\textsf {sup}(e) \ge H \bigl |\Gamma ]\) from scratch each time. It should be noted that the probability computation is valid if e exists, with existence probability p(e). So, based on statistics we can write:
Initially, the following probabilities are computed
We now cache these probabilities.
Given a \(\Gamma\) set, let \(\text {Pr}_{(H,\Gamma ) } = \text {Pr}[\textsf {sup}(e) \ge H \bigl |\Gamma ]\). For \(H-1\), we define \(\mathcal {T}^{(H-1)} = \left\{ \bigtriangleup _1,\ldots , \bigtriangleup _j \right\}\) to be the set of \(\bigtriangleup\) triangles which contain e, and \(\rho _{\bigtriangleup } = H-1\). Let \(\Gamma ^{new}\) be the set of all triangles \(\bigtriangleup\) which contain e, and have \(\rho _{\bigtriangleup }\ge H-1\). Clearly, \(\Gamma ^{new} = \Gamma \cup \mathcal {T}^{(H-1)}\). Now, we need to compute \(\text {Pr}_{(H-1,\Gamma ^{new}) }\) efficiently using the probabilities in Eq. 18. For this, we only need to look at set \(\mathcal {T}^{(H-1)}\), which is usually small (i.e., not more than 50 in our tested real graphs). As such, the computation is done very fast.
Given an edge \(e=(u,v)\), let us assume that we have computed \(\text {Pr}[\textsf {sup}(e) = k \bigl |\Gamma ,e \text { exists}]\), where \(k=0,\ldots ,H\), and \(\Gamma\) is as before. We have:
By T(j, k) we denote the probability that e participates in k triangles selected from \(\Gamma \cup \left\{ \bigtriangleup _1,\ldots , \bigtriangleup _j \right\}\), given that e exists.
Let \(\bigtriangleup _l = (u,v,w_l)\), where \(l\in [1,j]\), be a triangle in \(\mathcal {T}^{(H-1)}\). With the assumption that e exists, we consider the following two exclusive events (in terms of possible worlds). Event 1: \(\bigtriangleup _l\) exists and e participates in \(k-1\) other triangles of \(\mathcal {T}^{(H-1)}\). Event 2: \(\bigtriangleup _l\) does not exist and e participates in k other triangles of \(\mathcal {T}^{(H-1)}\). The sum of probabilities of events (1) and (2) gives us the probability that e participates in k triangles in \(\mathcal {T}^{(H-1)}\). Formally,
The base cases for the above formula are: (1) \(T(0,k) = \text {Pr} [\textsf {sup}(e) = k \bigl |\Gamma ,e \text { exists} ], \quad 0 \le k \le H\), (2) \(T(j,-1) = 0\).
As can be seen, in the recursive formula, we use the previously computed support probabilities to compute new probability values. This significantly speeds up the process. By multiplying T(j, k) by p(e) we obtain the desired probability \(\text {Pr} [\textsf {sup}(e) = k \bigl |\Gamma ^{new}]\).
5.4 Proofs of correctness
In this section, we present the proofs of correctness of our algorithm, proHIT, propsed in Sect. 5. In particular, we show that convergence can be obtained in a finite number of iterations. We start by showing that the values obtained by Phase I are upper-bounds on the truss values.
Theorem 4
In every iteration, Phase I provides upper-bounds on truss values of edges in the input probabilistic graph. \(\square\)
Proof
Given an edge e, let assume that the index value by Phase I is fixed at H. This means that H is the maximum value such that there exists at least H triangles (regardless of their existence probability), which contain e, and have \(\rho _{\bigtriangleup } \ge H\) for each triangle \(\bigtriangleup\).
Let \(\Gamma\) be the set of \((e,e',e'')\) triangles that contain e and \(h(e'), h(e'') \ge h(e)\).
Given the threshold \(\eta\), the probability \(\text {Pr}[{\textsf {sup}}(e) \ge H \bigl |\Gamma ]\) might be either (1) less than \(\eta\) or (2) greater than or equal to \(\eta\).
If the first case holds, the truss value of e should be in the interval \(\left[ 0, H \right)\).
Now, let us consider the second case. Since H is the maximum value obtained by \(\textit{Phase I}\), e cannot be contained in \(H' > H\) triangles, with \(\rho\)-value at least \(H'\) because otherwise, Phase I would have produced an estimate of \(H'\) for e. Thus, the probability that the truss value of e is equal to \(H'\) is 0. Furthermore, since \(\text {Pr}[\textsf {sup}(e) \ge H \bigl |\Gamma ] \ge \eta\), we can conclude that the truss value of e should be in the interval \(\left[ 0, H \right]\), i.e. the truss value of e can be H but also can be lowered in future iterations.
Therefore, considering the first and second cases, we can conclude that the true truss value of e should be in the interval \(\left[ 0, H \right]\). As a result, the theorem follows. \(\square\)
In the following, we first generalize some definitions and properties of deterministic truss decomposition to the probabilistic context.
Let \(\mathcal G\) be a probabilistic graph, and \(\eta\) be a user-defined threshold. Given an edge e, recall that by \(\kappa _\eta (e)\) we denote the largest integer k for which e belongs to a \((k,\eta )\)-truss. Also, the probabilistic support of e, \(\eta\)-\(\textsf {sup}_{\mathcal G}(e)\), is the maximum integer \(t \in [0,k_e]\) for which \(\text {Pr}[ \textsf {sup}_{\mathcal G}(e) \ge t] \ge \eta\), where \(k_e= \bigl |N_{\mathcal G}(u) \cap N_{\mathcal G}(v) \bigr |\), and \(N_{\mathcal G}(u)\) and \(N_{\mathcal G}(v)\) are the set of neighbor vertices to u and v, respectively. Let \(\delta _\eta (\mathcal G)\) be the minimum probabilistic support in \(\mathcal G\); i.e. \(\delta _\eta (\mathcal G) = \min _{e}\){\(\eta\)-\(\textsf {sup}_{\mathcal G}(e)\)} . Thus, we have:
We use \(E(\mathcal {G})\) to denote the set of edges in graph \(\mathcal G\). Moreover, let W be the set of all the triangles in \(\mathcal G\) which contain e. We note that the computation of \(\Pr [{\textsf {sup}}_{\mathcal G}(e) \ge k]\) is done by considering the triangles which contain e. Thus, the values obtained by \(\Pr [{\textsf {sup}}_{\mathcal G}(e) \ge k]\) and \(\text {Pr}[{\textsf {sup}}(e) \ge k \bigl |W]\) are basically the same, and as a result we use \(\Pr [{\textsf {sup}}_{\mathcal G}(e) \ge k]\) interchangeably with \(\text {Pr}[{\textsf {sup}}(e) \ge k \bigl |W]\) to refer to same concept. We have the following proposition.
Proposition 2
Given a subgraph \(\mathcal G' \subseteq \mathcal G\) and an edge \(e=(u,v)\) in \(\mathcal G'\), let W and \(W'\) be the sets of all the triangles in \(\mathcal G\) and \(\mathcal G'\), respectively, which contain e. We have that \(\Pr [{\textsf {sup}}(e) \ge k \bigl |W'] \le \Pr [{\textsf {sup}}(e) \ge k \bigl |W ]\), where \(k=0,\ldots ,k_e\). (As mentioned earlier, this is equivalent to \(\Pr [{\textsf {sup}}_{\mathcal G'}(e) \ge k] \le \Pr [{\textsf {sup}}_{\mathcal G}(e) \ge k]\)) [4].
The following Lemma is a generalization of a property of truss values in deterministic graphs [6] to the probabilistic context.
Lemma 1
Given threshold \(\eta\), for all \(e \in E(\mathcal G)\), we have
where \(\mathcal {G}'\) is a subgraph of \(\mathcal {G}\) which contains e (i.e. \(e \in E(\mathcal {G}'))\).
Proof
Let \(\mathcal {F}\) be the \((\kappa _{\eta }(e),\eta )\)-truss which contains e. By the definition of truss subgraph we have: \(\delta _\eta ({F}) = \kappa _{\eta }(e)\). Thus, \(\kappa _{\eta }(e) \le \max _{\mathcal G'} \delta _\eta (\mathcal G')\), for any \(\mathcal G'\) which contains e.
Now, we show that \(\kappa (e) \ge \max _{\mathcal G'} \delta _\eta (\mathcal G')\). We use proof by contradiction. Let \(\mathcal G''\) be the largest subgraph of \(\mathcal G\) that contains e and has \(\delta _\eta (\mathcal G'') > \kappa _{\eta }(e)\). Based on Eq. 20 we have \(\text {Pr}[{\textsf {sup}}_{\mathcal G''}(e') \ge \delta _\eta (\mathcal G'')] \ge \eta\), for any edge \(e' \in E(\mathcal G'')\), including e. Hence, \(\mathcal G''\) is a \((\delta _\eta (\mathcal G''),\eta )\)-truss and contains e. This is a contradiction by the definition of \(\kappa _{\eta }(e)\) which is the largest value of k such that e is contained in a \((k,\eta )\)-truss. \(\square\)
Following [6], we define the concept of degree (support) levels of edges in a probabilistic graph. First, we start with some technical definitions. Let \(\mathcal G\) be a probabilistic graph, and \(\eta\) be a user-defined threshold. Also, let \(\mathcal {C}(\mathcal G)\) be the set of edges and their containing triangles. We define the following features for edges and triangles in \(\mathcal {C}(\mathcal G)\):
-
Triangle \(\bigtriangleup \in \mathcal {C}(\mathcal G)\), if \(\forall e \in \bigtriangleup\), \(e \in \mathcal {C}(\mathcal G)\).
-
If e is removed from \(\mathcal {C}(\mathcal G)\), all \(\bigtriangleup \supset e\) are also removed from \(\mathcal {C}(\mathcal G)\).
Remark 1
We could have created two separate sets for edges and triangles, but doing so would significantly complicate the notation and its use in the proof as maintaining the relationship between these two sets would be cumbersome. This definition of C(G) is chosen purely for notational convenience and is similar to the definition used in [6] where it is defined as the set of all r-cliques and s-cliques.
Definition 3
(Degree Levels) We define degree levels in a recursive way in a probabilistic graph \(\mathcal G\). Let set \(L_i\) denote the i-th degree level. \(L_0\) is defined as the set of edges e which have minimum probabilistic support in \(\mathcal {C}(\mathcal G)\). \(L_1\) is defined as the set of edges which have minimum probabilistic support in \(\mathcal {C}(\mathcal G) \setminus L_0\), and so on. In general, \(L_i\) contains the set of edges which have minimum probabilistic support in \(\mathcal {C}(\mathcal G) \setminus \bigcup _{j<i}L_j\). The maximum value of i for which \(L_i\) can be non-empty is equal to \(k_{\max ,\eta }\). We recall that \(k_{\max ,\eta } = \max _{e} \{ \eta\)-\(\textsf {sup}_{\mathcal G}(e) \}\).
Theorem 5
Given integers i and j such that \(i\le j\) and a threshold \(\eta\), for any \(e_i \in L_i\) and \(e_j \in L_j\), \(\kappa _{\eta }(e_i) \le \kappa _{\eta }(e_j)\).
Proof
Let \(L'= \bigcup _{r\ge i}L_r\) be the union of all levels i and above. Also, let \(\mathcal G'\) be the graph such that \(L'=E(\mathcal G')\). Based on definition of levels, for \(e_i \in L_i\), we have \(\eta\)-\(\textsf {sup}_{\mathcal G'}(e_i) = \delta _\eta (\mathcal G')\). Moreover, \(e_j \in L_j\) implies \(\eta\)-\(\textsf {sup}_{\mathcal G'}(e_j) \ge \eta \text {-}\textsf {sup}_{\mathcal G'}(e_i)\). Since the truss value of \(e_i\) is \(\kappa _{\eta }(e_i)\), there should exist a \((\kappa _{\eta }(e_i), \eta )\)-truss \(\mathcal {F}\) which contains \(e_i\). We can have two following cases:
(1) \(E(\mathcal {F}) \subseteq L'\). Using Proposition 2 and the fact that each edge in \(\mathcal {F}\) is in \(\mathcal G'\) (because \(L'=E(\mathcal G')\)), we have \(\text {Pr}[{\textsf {sup}}_{\mathcal {F}}(e) \ge k] \le \text {Pr}[{\textsf {sup}}_{\mathcal G'}(e) \ge k]\). For edge \(e_i\), \(\kappa _{\eta }(e_i) = \delta _\eta (\mathcal {F})\). Thus, setting \(k=\delta _\eta (\mathcal {F})\), we have \(\eta \le \text {Pr}[{\textsf {sup}}_{\mathcal {F}}(e_i) \ge \delta _\eta (\mathcal {F})] \le \text {Pr}[{\textsf {sup}}_{\mathcal G'}(e_i) \ge \delta _\eta (\mathcal {F})]\). Since \(\eta\)-\(\textsf {sup}_{\mathcal G'}(e_i)\) is the maximum value of k such that \(\text {Pr}[{\textsf {sup}}_{\mathcal G'}(e_i) \ge k] \ge \eta\), we have \(\eta \text {-}\textsf {sup}_{\mathcal G'}(e_i) \ge \delta _\eta (\mathcal {F})\). Thus, we obtain that \(\eta \text {-}\textsf {sup}_{\mathcal G'}(e_i) = \delta _\eta (\mathcal G') \ge \delta _\eta (\mathcal {F}) = \kappa _{\eta }(e_i)\). On the other-hand, based on Lemma 1, for \(\mathcal G' \subseteq \mathcal G\) which contains \(e_j\), \(\delta _\eta (\mathcal G') \le \kappa _{\eta }(e_j)\). Combining the above, \(\kappa _{\eta }(e_i) \le \kappa _{\eta }(e_j)\).
(2) \(E(\mathcal {F}) \setminus L' \ne \emptyset\). This means that there should exist at least one edge in \(E(\mathcal {F})\), but not in \(L'\) (e.g. in the levels \(< i\)). Let \(e'\) be one of these edges such that \(e' \in E(\mathcal {F}) \cap L_b\) with the minimum value of b, where \(b<i\). Since \(e' \in \mathcal {F}\) and \(\mathcal {F}\) is a \((\kappa _{\eta }(e_i), \eta )\)-truss, then \(\eta\)-\(\textsf {sup}_{\mathcal {F}}(e') \ge \kappa _{\eta }(e_i)\). Set \(M = \bigcup _{r\ge b}L_r\). It should be noted that \(E(\mathcal {F}) \subseteq M\). Let \(\mathcal {Q}\) be the corresponding subgraph such that \(M=E(\mathcal {Q})\). We have \(\eta\)-\(\textsf {sup}_{\mathcal {Q}}(e') \ge \eta \text {-}\textsf {sup}_{\mathcal {F}}(e') \ge \kappa _{\eta }(e_i)\). Also, \(\eta \text {-}\textsf {sup}_{\mathcal {Q}}(e') = \delta _\eta (\mathcal {Q})\), because \(e' \in L_b\). Since \(j > b\) and \(e_j \in M\), \(\kappa _{\eta }(e_j) \ge \delta _\eta (\mathcal {Q})\) (based on Lemma 1). Combining the above, we conclude \(\kappa _{\eta }(e_i) \le \kappa _{\eta }(e_j)\). \(\square\)
We prove the convergence of our proposed algorithm using ideas similar to the proof of deterministic h-index algorithm in [6]. In Theorem 4 we showed that Phase I provides upper-bounds on truss values of the input probabilistic graph. In the following, we prove that upper-bounds are monotonically non-increasing and are lower-bounded by truss values.
Theorem 6
For all t and all edges e in \(\mathcal G\), we have (1) \(h_{t+1}(e) \le h_t(e)\), (2) \(h_{t}(e) \ge \kappa _{\eta }(e)\), where by \(h_t(e)\) we denote the h-index of e after the t-th iteration of Phase I and Phase II together.
Proof
(1) We prove this by induction on t. Initially, when \(t=0\), \(h_0(e)\) is equal to \(\eta\)-\(\textsf {sup}_{\mathcal G}(e)\) . Let \(h_1^p(\cdot )\) be the processed values after completion of Phase I at iteration 1. As shown in [6], throughout Phase I, the upper-bounds can only decrease, so \(h_1^p(e) \le h_0(e)\), for each edge e. The \(h_1^p(\cdot )\) values are passed to Phase II. The block of steps 6–9 of Phase II (Algorithm 5) checks all the values equal or less than \(h_1^p(e)\) for each edge e, and finds the maximum value for which the condition in line 6 holds. Let \(h_1(e)\) be the obtained maximum value. Thus, we have \(h_1(e) \le h_1^p(e) \le h_0(e)\). Assume the property is true up to t. For iteration \(t+1\), Phase I needs to process the values \(h_t(\cdot )\) obtained from the previous iteration (i.e. t) by Phase II. Let \(h_{t+1}^p(e)\) be the processed values after completion of Phase I at iteration \(t+1\). For an edge e, by the induction hypothesis, and monotonicity of Phase I itself [6], we have \(h_{t+1}^p(e) \le h_{t}(e) \le h_{t-1}(e)\). Then, this value is passed through Phase II. As discussed above, this value is processed using lines 6–9 in Algorithm 5 which make sure that \(h_{t+1}(e) \le h_t^p(e)\). Thus, we have \(h_{t+1}(e) \le h_{t}(e)\).
(2) We prove the property by induction on t. For \(t=0\), \(h_0(e) = \eta \textsf {-sup}_{\mathcal G}(e) \ge \kappa _{\eta }(e)\). Let us assume that for t, \(h_{t}(e) \ge \kappa _{\eta }(e)\). Now, we focus on the computation of \(h_{t+1}(e)\). Using the induction step and the fact that Phase I provides an upper-bound on \(\kappa _{\eta }(e)\) for each edge e (please refer to Theorem 4), we can write: \(h_{t+1}^p(e) \ge \kappa _{\eta }(e)\). Consider the computation of \(h_{t+1}(e)\) by Phase II which is based on the value produced by Phase I (i.e. \(h_{t+1}^p(e)\)). Let \(\mathcal {F}\) be \((\kappa _{\eta }(e),\eta )\)-truss which contains e. Also, let S be the set of all supporting triangles \(\bigtriangleup\) in \(\mathcal {F}\) for edge e, such that \(\forall e',e''\ne e \in \bigtriangleup\), \(\min (\kappa _\eta (e'), \kappa _\eta (e'')) \ge \kappa _\eta (e)\). Using the property of truss value we know that \(\text {Pr}[{\textsf {sup}}(e) \ge \kappa _{\eta }(e) \bigl |S] \ge \eta\). To obtain \(h_{t+1}(e)\), Phase II checks the condition \(\text {Pr}[{\textsf {sup}}(e) \ge h_{t+1}^p(e) \bigl |\Gamma ] \ge \eta\) (line 6, Algorithm 5), where \(\Gamma\) is the set of all the triangles that contain e, and is detected by Phase II since \(\rho _{\bigtriangleup } \ge h_{t+1}^p(e)\), for each \(\bigtriangleup \in \Gamma\), where \(\rho _{\bigtriangleup }\) is the minimum h-index value of the edges other than e in \(\bigtriangleup\) (line 19, Algorithm 5). If \(\text {Pr}[{\textsf {sup}}(e) \ge h_{t+1}^p(e) \bigl |\Gamma ] \ge \eta\) holds, then \(h_{t+1}(e) = h_{t+1}^p(e) \ge \kappa _{\eta }(e)\). Otherwise, all the k values smaller than \(h_{t+1}^p(e)\) are checked. In the worst case, consider the computation of the probability when k becomes equal to \(\kappa _{\eta }(e)\). Let \(\Gamma\) be the updated set to contain all \(\bigtriangleup\) with \(\rho _{\bigtriangleup } \ge k\). We claim that \(S \subseteq \Gamma\). For each triangle \(\bigtriangleup \in S\), and \(\forall e',e''\ne e \in \bigtriangleup\), we have \(\kappa _{\eta }(e'), \kappa _{\eta }(e'') \ge \kappa _{\eta }(e)\). In addition, based on Theorem 4, \(h_{t+1}^p(e') \ge \kappa _{\eta }(e') \ge \kappa _{\eta }(e) = k\), and \(h_{t+1}^p(e'') \ge \kappa _{\eta }(e'') \ge \kappa _{\eta }(e) = k\). Thus, \(\rho _{\bigtriangleup } = \min (h_{t+1}^p(e'),h_{t+1}^p(e'')) \ge k = \kappa _{\eta }(e)\), which results in \(\bigtriangleup \in \Gamma\). Using Proposition 2, \(\text {Pr}[{\textsf {sup}}(e) \ge k \bigl |\Gamma ] \ge \text {Pr}[{\textsf {sup}}(e) \ge k \bigl |S]\). If for \(k=\kappa _{\eta }(e)\), \(\text {Pr}[{\textsf {sup}}(e) \ge \kappa _{\eta }(e) \bigl |\Gamma ] < \eta\), then \(\text {Pr}[{\textsf {sup}}(e) \ge \kappa _{\eta }(e) \bigl |S] < \eta\), which is a contradiction with the definition of \(\kappa _{\eta }(e)\). As a result, we should have \(\text {Pr}[{\textsf {sup}}(e) \ge \kappa _{\eta }(e) \bigl |\Gamma ] \ge \eta\). Thus, \(h_{t+1}(e) \ge \kappa _{\eta }(e)\). \(\square\)
Theorem 7
Given any level \(L_i\), for all \(t \ge i\), and \(e \in L_i\), we have \(h_t(e) = \kappa _{\eta }(e)\).
Proof
We prove this by induction on i. For \(i=0\), let us consider the set of edges e with minimum \(\eta\)-\(\textsf {sup}_{\mathcal G}(e)\) in \(\mathcal G\). For these edges, \(h_t(e) = \eta\)-\(\textsf {sup}_{\mathcal G}(e) = \max _k \{ \text {Pr}[{\textsf {sup}}_{\mathcal G}(e) \ge k] \ge \eta \} = \kappa _{\eta }(e)\). Assume that the theorem is true up to level i. As a result, \(\forall t \ge i\), and \(\forall e \in \bigcup _{j \le i}L_j\), \(h_t(e) = \kappa _{\eta }(e)\). Let \(e_a\) be an arbitrary edge in level \(i+1\), and \(L' = \bigcup _{j \ge i+1}L_j\).
Consider the partition of all the triangles which contain \(e_a\) into two sets \(S_l\) and \(S_h\). Triangles in \(S_l\) contain some edge outside \(L'\), and those in \(S_h\) have all their edges contained in \(L'\). For each triangle \(\bigtriangleup \in S_l\), there is some \(e_b \ne e_a \in \bigtriangleup\) such that \(e_b \in L_k\), where \(k \le i\). Using induction hypothesis, we have \(h_t(e_b) = \kappa _{\eta }(e_b)\). Also, since \(e_a \in L_{i+1}\), using Theorem 5, we have \(h_t(e_b) = \kappa _{\eta }(e_b) < \kappa _{\eta }(e_a) \le h_{t}(e_a)\), where for the last inequality we have used the property (2) in Theorem 6.
Let us focus on the computation of \(h_{t+1}(e_a)\) (lines 6–9, Algorithm 5). The algorithm checks the condition \(\text {Pr}[{\textsf {sup}}(e_a) \ge r \bigl |\Gamma ] \ge \eta\), where \(\Gamma\) is the set of triangles \(\bigtriangleup\) which contain \(e_a\), and have \(\rho _{\bigtriangleup } \ge r\), where \(r = h_{t}(e_a)\). We recall that \(\rho _{\bigtriangleup } = \min \{ h_t(e'),h_t(e'')\}\) (line 19, Algorithm 5), where \(e',e'' \ne e_a \in \bigtriangleup\). Set \(\Gamma\) is updated each time to correspond to the r value being used for computation of the condition. For every \(\bigtriangleup \in S_l\), by the previous argument, there is some \(e_b \ne e_a \in \bigtriangleup\), such that \(h_{t}(e_b) < h_{t}(e_a)\). Thus, \(\rho _{\bigtriangleup } < h_{t}(e_a)\), and these triangles are not considered in the computation. As a result set \(\Gamma\) will consist of triangles from set \(S_h\) only; \(\Gamma \subseteq S_h\). Let \(\mathcal G'\) be the graph such that \(L'=E(\mathcal G')\). Using Proposition 2, we can write
Since \(e_a \in L_{i+1}\), \(\eta\)-\(\textsf {sup}_{\mathcal G'}(e_a) = \delta _\eta (\mathcal G')\). Thus, we have
The above equations are based on the definition of probabilistic support of an edge: \(\eta\)-\(\textsf {sup}_{\mathcal G'}(e_a) = \max _k \{ \text {Pr}[{\textsf {sup}}_{\mathcal G'}(e_a) \ge k] \ge \eta \}\). By definition of \(S_h\), edges contained in the triangles of \(S_h\) are part of \(L'=E(\mathcal G')\). Thus, triangles in \(S_h\) are contained in \(\mathcal G'\). As mentioned earlier, since computation of \(\text {Pr}[{\textsf {sup}}_{\mathcal G'}(e_a) \ge r']\) is done by considering triangles in \(S_h\), the values of \(\text {Pr}[{\textsf {sup}}_{\mathcal G'}(e_a) \ge r']\) and \(\text {Pr}[{\textsf {sup}}(e_a) \ge r' \bigl |S_h]\) are the same. Therefore, \(\text {Pr}[{\textsf {sup}}(e_a) \ge r' \bigl |S_h] < \eta\). Combining this with Eq. 22, for \(r > \delta _\eta (\mathcal G')\) we obtain:
Since \(\text {Pr}[{\textsf {sup}}(e_a) \ge r \bigl |\Gamma ] <\eta\), the algorithm checks r values less than or equal to \(\delta _\eta (\mathcal G')\), thus \(h_{t+1}(e_a) \le \delta _\eta (\mathcal G')\). In addition, based on Lemma 1, we have \(\delta _\eta (\mathcal G') \le \kappa _{\eta }(e_a)\). Thus, \(h_{t+1}(e_a) \le \kappa _{\eta }(e_a)\). On the other-hand, based on property (2) in Theorem 6, we have \(h_{t+1}(e_a) \ge \kappa _{\eta }(e_a)\). Combining \(h_{t+1}(e_a) \le \kappa _{\eta }(e_a)\) and \(h_{t+1}(e_a) \ge \kappa _{\eta }(e_a)\), we conclude that \(h_{t+1}(e_a) = \kappa _{\eta }(e_a)\). Since \(e_a\) was an arbitrary edge in \(L_{i+1}\), this concludes the proof by induction. \(\square\)
Based on the above theorem, we can express the following corollary which shows that convergence is guaranteed in a finite number of iterations.
Corollary 3
Given a probabilistic graph \(\mathcal G\), and threshold \(\eta\), let l be the maximum value for the degree level, such that \(L_l \ne \emptyset\). There exists some \(t \le l\) such that \(h_t(e) = \kappa _{\eta }(e)\), for all edges.
5.5 Complexity analysis
In this section we present the time complexity of our proposed algorithm, proHIT.
Theorem 8
Given a probabilistic graph \(\mathcal G\), proHIT computes the truss decomposition of \(\mathcal G\) in \(O\big ( t k_{\max ,\eta } \psi m \big )\), where t is the total number of iterations \(k_{\max ,\eta }=\max _{e} \{ \eta\)-\(\textsf {sup}_{\mathcal G}(e) \}\), \(\psi\) is the minimum number of spanning forests needed to cover all edges of \(\mathcal G\) , and m is the number of the edges.
Proof
The time complexity of Algorithm 4 is dominated by the time complexity of Phase II, since h-index computation of edges is done by dynamic programming (DP) algorithm which has quadratic time complexity. In contrast, the h-index computation in Phase I can be done in linear time.
To analyze the time complexity of Phase II (given in Algorithm 5), we should note that for each edge \(e=(u,v)\), the first time computation of the probability \(\text {Pr}[{\textsf {sup}}(e) \ge H \bigl |\Gamma ]\) in line 6 (Algorithm 5), takes \(O(Hj_0)\) time, where \(j_0 = \bigl |\Gamma \bigr |\), \(H=h(e)\), and \(\Gamma\) is as given in the algorithm. For the next iterations in the while loop (line 6, Algorithm 5), using Modified DP, the computation is performed on \(\mathcal {T}^{i}\) only, where \(i=H-1,\ldots ,0\), and \(\mathcal {T}^{i}\) is as before. In the worst case, the while loop is repeated H times. Let us assume that \(j_1 = \bigl |\mathcal {T}^{H-1} \bigr |\), \(j_2 = \bigl |\mathcal {T}^{H-2} \bigr |\), \(\ldots\), \(j_{k_e} = \bigl |\mathcal {T}^{0} \bigr |\). It is obvious that \(j_0+j_1+\cdots + j_{k_e} = k_e\), where \(k_e\) is the number of common neighbors of u and v. We have that \(k_e \subseteq O(\min \left\{ d(u),d(v) \right\} )\), where d(u) and d(v) are the degree of vertices u and v, respectively. Therefore, the while loop takes \(O(j_0H) + O(j_1(H-1)) + \cdots + O(j_{k_e-1}1)\) time. In the worst case then, the time complexity of the while loop is bounded by \(O(j_0 k_{\max ,\eta }) + O(j_1 k_{\max ,\eta }) + \cdots + O(j_{k_e-1} k_{\max ,\eta })\), which is equal to \(O(k_{\max ,\eta } k_e) \subseteq O(k_{\max ,\eta } \min \left\{ d(u),d(v) \right\} )\).
Moreover, the iteration over each neighbor of edge e in line 12 (Algorithm 5), takes \(O(\min \left\{ d(u),d(v) \right\} )\). As a resul, the time complexity of Phase II is bounded by
Thus, the time complexity becomes:
It should be noted that \(\psi \le \min \left\{ d_{\max }, \sqrt{m} \right\}\), where \(d_{\max }\) is the maximum degree in the graph. Let t be the total number of iterations. The total time complexity is \(O\big ( t k_{\max ,\eta } \psi m \big )\). In the worst case the number of iterations, t, is bounded by the degree levels as discussed in Theorem 7 and Corollary 3 in Sect. 5.4. The number of degree levels are bounded by \(\beta = k_{\max ,\eta }\). \(\square\)
The running times of the baseline algorithms, PDT and PAPT are dominated by \(O(d_{max} \psi m)\). However, proHit algorithm performs much better in practice. This is because \(\beta\) in the above proof is worst-case upper-bound on t, the number of iterations, and is not representative of practical performance. As shown in our experiments t is much less than \(\beta\) in practice as the h-index of several edges will decrease simultaneously in each iteration.
For example, let us consider the flickr dataset, with \(\beta = k_{\max ,\eta }=49\). However, as can be seen in Fig. 7, for flickr with \(\eta = 0.1\), the total number of iterations is about 18 which is much smaller than \(\beta\). This trend is also evident for other datasets.
6 Experiments
In this section, we present our experimental results. Our implementations are in Java and the experiments are conducted on a machine with Intel i7, 2.2Ghz CPU, and 12Gb RAM, running Ubuntu 18.04. The statistics for the datasets are shown in Table 3. We report the number of vertices \(\bigl |V \bigl |\), the number of edges \(\bigl |E \bigl |\), and the number of triangles \(\bigl |\bigtriangleup \bigl |\). Datasets with real probability values are flickr, dblp, and biomine.
flickr is a popular online community for sharing photos. Nodes are users in the network, and the probability of an edge between two users is obtained based on the Jaccard coefficient of the interest groups of the two users [16, 21].
dblp comes from the well-known bibliography website. Nodes correspond to authors, and there is an edge between two authors if they co-authored at least one publication. The existence probability of each edge is measured based on an exponential function of the number of collaborations between two users [16, 21].
biomine contains biological interactions between proteins. The probability of an edge represents the confidence level that the interaction actually exists [21].
The rest of the datasets are social networks and web graphs which are obtained from Laboratory of Web Algorithms [26, 27]. For these datasets we generated probability values uniformly distributed in (0, 1].
6.1 Efficiency evaluation
In this section, we report the running time of our proposed algorithms, PAPT and proHIT, versus the state-of-the-art peeling algorithm, which we refer to as PDT (peeling-DP-truss). PDP is based on an iterative edge removal process which removes edges e with smallest probabilistic support, \(\eta\)-\(\textsf {sup}_{\mathcal G}(e)\), and updating probabilistic support, \(\eta\)-\(\textsf {sup}_{\mathcal G\setminus \{e \} }(e')\), of the affected edges \(e'\) in \(\mathcal G\setminus \{ e \}\). PDT uses dynamic programming for computing and updating probabilistic support of edges. We use DP as an abbreviation for dynamic programming.
In our experiments, we set threshold \(\eta =0.1,\ldots , 0.5\). The running times in log-scale are shown in Figs. 4 and 5. In Fig. 4 we present the running times for flickr, dblp, biomine, and ljournal-2008 using \(\eta = 0.1\) as an example. In Fig. 5, we separate the running times for the rest of the datasets due to different scales in their plot of running times. For these datasets we show the results for \(\eta =0.2,\ldots ,0.5\), since PDT cannot complete in reasonable time for \(\eta =0.1\). Moreover, for each dataset, we obtain the average of the maximum probabilistic support, \(\text{ avg}_{\eta }\{k_{\max ,\eta }\}\), and the average of maximum truss value, \(\text{ avg}_{\eta } \{ {\max _{e} \{\kappa _{\eta } (e)\}} \}\), over \(\eta =0.1, \ldots , 0.5\). These statistics are shown in Table 4, second and third columns, respectively.
As can bee seen in Figs. 4 and 5, proHIT and PAPT algorithms are significantly faster than PDT, especially on networks containing a large number of triangles, and having large value of \(\text{ avg}_{\eta }\{k_{\max ,\eta }\}\). For instance, for biomine (Fig. 4) which is such a dataset, the gain of proHIT and PAPT compared to PDT is 84% and 67%, respectively. This makes proHIT and PAPT six and three times faster than PDT. For biomine with \(\eta\) equal to 0.1 and 0.2, proHIT is better than the approximate algorithm PAPT, which, we recall, is an approximate algorithm. For the other \(\eta\)’s for biomine, proHIT is slightly slower than PAPT. To reiterate, this is a welcome surprise because proHIT achieves a similar performance as PAPT, but without sacrificing the exactness of the solution.
In terms of running time on the smaller datasets, flickr and dblp, proHIT produces the results in 1.5 minutes and 1 minute, respectively. The number of triangles in flickr is twice larger than in dblp while having much less edges. We observe that proHIT has a similar performance as PAPT. Both proHIT and PAPT are faster than PDT, except on dblp. We recall that dblp is the smallest dataset in terms of probabilistic support and truss value of its edges, and as such it does not cause too much work for Dynamic Programming needed for PDT. As we see in the rest of the charts in Fig. 5proHIT significantly outperforms PDT and PAPT as the datasets get larger.
The running times of all algorithms increase for ljournal-2008, which is reasonable, because this graph has 49 million edges with \(\text{ avg}_{\eta }\{k_{\max ,\eta }\}\) equal to 911. For ljournal-2008, proHIT computes truss decomposition faster than PDT with a gain of 40 percent.
The running times continue to increase for the remaining datasets. This is because for these datasets \(\text{ avg}_{\eta }\{k_{\max ,\eta }\}\) is much larger as shown in Table 4. For instance, for itwiki-2013, \(\text{ avg}_{\eta }\{k_{\max ,\eta }\}\) is 4574. Moreover, for uk-2014-tpd and in-2004 the ratio of the number of triangles to the number of edges is much higher than \(\textit{ljournal-2008}\).
As can be seen, for these graphs, proHIT is again significantly faster than its counterpart PDT (as an exact method). For instance, for uk-2014 and itwiki-2013 with \(\eta =0.3\), proHIT is about 2 and 3 times faster than PDT. Comparing proHIT with PAPT (which is an approximate method) shows that proHIT is on average 24% faster than PAPT without sacrificing the exactness of the solution. For itwiki-2013 with \(\eta =0.5\), proHIT can complete truss decomposition in about 4 h, while PAPT takes about 7 h. Also, truss decomposition of in-2004 using proHIT is 30 min faster than the one using PAPT. A similar trend can be observed for other values of \(\eta\).
In general, as the number of edges and triangles in the input graph increase, the running times of the algorithms become larger. The conclusion that we get is that for large graphs the performance of the proHIT algorithm is better than the peeling approaches since they require updating probabilistic supports many times during the algorithm process to obtain the truss values of the edges. Also, our PAPT which uses Lyapunov CLT for approximating tail probability of support of edges outperforms PDT approach.
6.1.1 Effect of \(\eta\) values
It should be noted that as \(\eta\) increases, probabilistic support and truss values of edges decrease which lead to decrease in the running times of the algorithms. In Table 5, we show the trend for one of our dataset, \(\textit{biomine}\), in which \(k_{\max ,\eta }\) and \({\max _{e} \{ \kappa _{\eta } (e) \} }\) decrease as \(\eta\) increases.
Next, we discuss why proHIT is faster than PDT. The most expensive part of both algorithms is executing DP routines, with quadratic run-times in the number of triangles containing each edge. However, their number and sizes are different in proHIT and PDT. Step 6 in Phase II (Algorithm 5) of proHIT uses DP to check the validity of the upper-bounds on the truss value of edges at each iteration of the algorithm. Also, at the beginning of proHIT, the upper-bound of each edge e is set to its \(\eta\)-\(\textsf {sup}_{\mathcal G}(e)\) which is obtained using DP (Algorithm 4, line 3). In PDT, DP is used after each edge removal, and all the edges that are neighbors of a peeled edge need to have their probabilistic support recomputed using DP.
Given a probabilistic graph \(\mathcal G\), and edge \(e=(u,v)\), let \(k_e\) be the number of common neighbors of u and v used for computing probabilistic support of e in \(\mathcal {G}\). The time complexity of the computation by DP is \(O(k_e^2)\) [4]. We refer to \(k_e\) as the size of DP. In proHIT, in Phase II, not all neighbors of u and v are used for DP but rather only those neighbors that can contribute to the final truss value of e (recall set \(\Gamma\) and Eq. 16 in Sect. 5). As such, in proHIT, the size of DP is typically smaller than the total number of all the common neighbors of u and v. This is in contrast to PDT, which runs DP using all the remaining neighbors of an edge at that point in the peeling process. In essence, proHIT performs DP on smaller and only the effective set of neighbours for each edge, resulting in a considerable speedup.
We report the average and maximum sizes of DP for both algorithms in Table 6, for flickr, dblp, biomine, and \(\textit{ljournal-2008}\). As can be seen, for all the selected datasets, these sizes are much smaller for proHIT than for PDT. This is particularly important in large datasets, biomine and \(\textit{ljournal-2008}\), in which the average size for proHIT is about 3.5 and 4 times smaller than for PDT. In addition, in the last column of Table 6, we report the number of times DP is performed for both PDT and proHIT algorithms. The difference is noticeable for large datasets. For instance, on ljournal-2008, the number of executions of DP by proHIT is half of those performed by PDT.
6.1.2 Memory usage
In Fig. 6, we compare the memory consumption of proHIT and PAPT versus that of PDT on selected datasets. The trend can be verified for other datasets as well. Our PAPT approach requires a slightly more memory compared to PDT since it stores mean and standard deviation of distribution of the support of edges during execution of the algorithm. On the other hand, proHIT consumes much smaller memory compared to PDT and PAPT. For instance, for biomine the memory consumption of proHIT is 12 times and 6 times smaller than those of PAPT and PDT, respectively. This also holds for other datasets such as ljournal-2008. This is because PDT and PAPT are edge peeling based algorithms which require maintaining the global information of the graph at each step of the algorithm, while proHIT uses local information only.
6.2 Convergence speed
In this section we further evaluate the execution of proHIT as it unfolds with time. We look at the average distance from the truss values over the sequence of iterations for selected small to large datasets (see Fig. 7). The average distance decreases fast for flickr, dblp, and biomine, and more gradually for ljournal-2008, in-2004, and uk-2014-tpd. These results show that proHIT can produce high-quality near-results in only a fraction of iterations needed for completion. For instance, for ljournal-2008 with \(\eta = 0.1\), the average distance becomes less than 0.01 at iteration 20, about one third of the total number of required iterations (about 60, see the end of the curve). This can be a desirable property in graph mining where the user would like to see near-results as the execution progresses.
6.3 Case study
In this section, we show an application of the probabilistic truss notion. Most of applications showcased for probabilistic core and truss decompositions in the literature are based on datasets in which the edge probabilities may be synthetic or not conditionally independent. Here, we consider the human biomine dataset [28], which has 861,812 nodes and 8,666,287 edges. The nodes are proteins and the edges represent protein interactions and their probability of occurrence. We investigate how probabilistic truss can be used in detecting proteins/genes that interact with the SARS-CoV-2 coronavirus. Bouhaddou et al. [29] found that during the SARS-CoV-2 virus infection, changes in activities can happen for human kinases. We consider two tyrosine kinase-related proteins, P17844 and P0CG48. They come from UniProt, which is a freely accessible database of protein sequences and functional information. These proteins have received literature support for interaction with the SARS-CoV-2 coronavirus [30, 31]. We refer to them as proteins of interest and we find the probabilistic truss subgraph which contains these proteins of interest. Also, we compare the obtained subgraph with its counterpart, the probabilistic core subgraph [21], in terms of the number of vertices and edges, and probabilistic density and clustering coefficient. Probabilistic density (PD) is the ratio of the sum of edge probabilities to the possible number of edges in the graph \(\mathcal {G}\) [4]:
Probabilistic clustering coefficient (PCC) measures the level of tendency of the nodes to cluster together [4, 32]:
PD and PCC are important measures of cohesiveness in a probabilistic graph.
Table 7 shows the size of the graphs obtained by probabilistic truss and core as well as their cohesiveness values. We set threshold \(\eta =0.1\). We find the largest value of k for which the subgraph contains the proteins of interest. As can be seen, probabilistic truss gives much higher quality results than probabilistic core in terms of density and clustering coefficient. For instance, PCC for the probabilistic truss subgraph is about 4.5 times larger than the one obtained for the probabilistic core subgraph. Moreover, in terms of the nodes and edges, the probabilistic truss subgraph is much smaller than the probabilistic core subgraph.
Furthermore, using gene enrichment analysis through Metascape,Footnote 2 we see which kind of biology function/process our detected probabilistic truss subgraph represents. Metascape [33] is a web-based portal that provides comprehensive gene list annotation and analysis resources. Figure 8 shows the top disease terms related to the proteins in the detected probabilistic truss subgraph. For instance, the top associated diseases are Anemia and Diamond-Blackfan (a kind of rare anemia disease). The p-value of the association is about \(10^{-30}\), which is statistically very significant. These findings are useful to biologists in order to perform targeted tests for checking whether drugs for the treatment of these diseases can also be repurposed for treating COVID-19 [30].
Note Metascape was unable to process the max core due to its excessive size hence the need for a smaller and denser subgraph, such as the one produced by truss decomposition.
7 Conclusions
We presented a peeling algorithm, PAPT, for computing truss decomposition for large probabilistic graphs. A novel contribution of our work is the use of Lyapunov’s Central Limit Theorem to obtain the probabilistic support for an edge. Unlike the DP approach, PAPT does not rely on incremental evaluation of support probabilities. We evaluated PAPT and showed that it is significantly faster than DP for large datasets. We believe that the CLT techniques we proposed in this paper are of independent interest and can find new applications to other computationally intensive tasks on probabilistic data.
Next we presented proHIT a truss decomposition algorithm based on an h-index updating approach. Unlike the edge peeling strategy, proHIT accesses the edges in a local fashion which makes it memory efficient. proHIT includes two main phases. Phase I is responsible for updating the edges’ h-index without considering edge probabilities. This phase can provide a fast-to-compute upper-bound on truss values of the edges. Phase II takes care of the probabilistic nature of truss decomposition and further tightens the upper-bounds obtained in the previous phase. While being an exact algorithm, proHIT can also produce near-results in only a fraction of iterations needed for computing the full exact solution.
Notes
This value was chosen because it was large enough to keep the approximation error obtained from Corollary 2 small.
References
Wang, J., Cheng, J.: Truss decomposition in massive networks. VLDB 5(9), 812–823 (2012)
Zhao, F., Tung, A.K.: Large scale cohesive subgraphs discovery for social network visual analysis. Proc. VLDB Endow. 6(2), 85–96 (2012)
Huang, X., Cheng, H., Qin, L., Tian, W., Yu, J.: Querying k-truss community in large and dynamic graphs. In: Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, pp. 1311–1322 (2014)
Huang, X., Lu, W., Lakshmanan, L.V.: Truss decomposition of probabilistic graphs: Semantics and algorithms. In: Proceedings of the 2016 ACM SIGMOD International Conference on Management of Data, pp. 77–90 (2016)
Zhang, Y., Parthasarathy, S.: Extracting analyzing and visualizing triangle k-core motifs within networks. In: 2012 IEEE International Conference on Data Engineering, pp. 1049–1060 (2012). IEEE
Sarıyüce, A., Seshadhri, C., Pinar, A.: Local algorithms for hierarchical dense subgraph discovery. VLDB (2019)
Zou, Z., Zhu, R.: Truss decomposition of uncertain graphs. KAIS 50(1), 197–230 (2017)
Lyapunov, A.: Nouvelle forme de la théoreme dur la limite de probabilité. Mémoires de l’Academie Impériale des Sci. de St. Petersbourg 12, 1–24 (1901)
Chen, L., Lian, X.: Query processing over uncertain databases. Synth. Lect. Data Manag. 4(6), 1–101 (2012)
Khan, A., Bonchi, F., Gullo, F., Nufer, A.: Conditional reliability in uncertain graphs. IEEE Trans. Knowl. Data Eng. 30(11), 2078–2092 (2018)
Parchas, P., Gullo, F., Papadias, D., Bonchi, F.: The pursuit of a good possible world: extracting representative instances of uncertain graphs. In: Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, pp. 967–978 (2014)
Yuan, Y., Wang, G., Chen, L., Wang, H.: Efficient keyword search on uncertain graph data. IEEE Trans. Knowl. Data Eng. 25(12), 2767–2779 (2013)
Yuan, Y., Wang, G., Wang, H., Chen, L.: Efficient subgraph search over large uncertain graphs. Proc. VLDB Endow. 4(11), 876–886 (2011)
Zou, Z., Gao, H., Li, J.: Discovering frequent subgraphs over uncertain graph databases under probabilistic semantics. In: Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 633–642 (2010)
Jin, R., Liu, L., Ding, B., Wang, H.: Distance-constraint reachability computation in uncertain graphs. Proc. VLDB Endow. 4(9), 551–562 (2011)
Potamias, M., Bonchi, F., Gionis, A., Kollios, G.: K-nearest neighbors in uncertain graphs. Proc. VLDB Endow. 3(1–2), 997–1008 (2010)
Parchas, P., Papailiou, N., Papadias, D., Bonchi, F.: Uncertain graph sparsification. IEEE Trans. Knowl. Data Eng. 30(12), 2435–2449 (2018)
Zou, Z., Li, J., Gao, H., Zhang, S.: Finding top-k maximal cliques in an uncertain graph. In: 2010 IEEE 26th International Conference on Data Engineering, pp. 649–652 (2010). IEEE
Xing, Y., Xiao, N., Lu, Y., Li, R., Yu, S., Gao, S.: Fast truss decomposition in memory. In: International Conference on Security, Privacy and Anonymity in Computation, Communication and Storage, pp. 719–729 (2017)
Che, Y., Lai, Z., Sun, S., Wang, Y., Luo, Q.: Accelerating truss decomposition on heterogeneous processors. Proc. VLDB Endow. 13(10), 1751–1764 (2020)
Bonchi, F., Gullo, F., Kaltenbrunner, A., Volkovich, Y.: Core decomposition of uncertain graphs. In: Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1316–1325 (2014)
Cramér, H. (ed.): Mathematical Methods of Statistics (PMS-9), vol. 9. Princeton University Press, Princeton (2016)
Zwillinger, D., Kokoska, S.: CRC Standard Probability and Statistics Tables and Formulae. Chapman and Hall/CRC, Boca Raton (2000)
Berry, A.C.: The accuracy of the gaussian approximation to the sum of independent variates. Trans. Am. Math. Soc. 49(1), 122–136 (1941)
Wu, J., Goshulak, A., Srinivasan, V., Thomo, A.: K-truss decomposition of large networks on a single consumer-grade machine. In: Proc. ASONAM, pp. 873–880 (2018). IEEE
Boldi, P., Vigna, S.: The WebGraph framework I: Compression techniques. In: Proceedings of the 13th International Conference on World Wide Web, pp. 595–602 (2004)
Boldi, P., Rosa, M., Santini, M., Vigna, S.: Layered label propagation: a multiresolution coordinate-free ordering for compressing social networks. In: Proceedings of the 20th International Conference on World Wide Web, pp. 587–596 (2011)
Podpe\(\check{c}\)an, V., Ram\(\check{s}\)ak, c., Gruden, K., Toivonen, H., Lavra\(\check{c}\), N.: Interactive exploration of heterogeneous biological networks with biomine explorer. Bioinformatics (2019). https://doi.org/10.1093/bioinformatics/btz509
Bouhaddou, M., Memon, D., Meyer, B., White, K.M., Rezelj, V.V., Marrero, M.C., Polacco, B.J., Melnyk, J.E., Ulferts, S., Kaake, R.M., et al.: The global phosphorylation landscape of sars-cov-2 infection. Cell 182(3), 685–712 (2020)
Guo, Y., Esfahani, F., Shao, X., Srinivasan, V., Thomo, A., Xing, L., Zhang, X.: Integrative COVID-19 biological network inference with probabilistic core decomposition. Brief. Bioinform. (2021). https://www.biorxiv.org/content/10.1101/2021.06.23.449535v1.full.pdf
Dirmeier, S., Dächert, C., van Hemert, M., Tas, A., Ogando, N.S., van Kuppeveld, F., Bartenschlager, R., Kaderali, L., Binder, M., Beerenwinkel, N.: Host factor prioritization for pan-viral genetic perturbation screens using random intercept models and network propagation. PLoS Comput. Biol. 16(2), 1007587 (2020)
Pfeiffer, J.J., Neville, J.: Methods to determine node centrality and clustering in graphs with uncertain structure. In: Fifth International AAAI Conference on Weblogs and Social Media (2011)
Zhou, Y., Zhou, B., Pache, L., Chang, M., Khodabakhshi, A.H., Tanaseichuk, O., Benner, C., Chanda, S.K.: Metascape provides a biologist-oriented resource for the analysis of systems-level datasets. Nat. Commun. 10(1), 1–10 (2019)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Esfahani, F., Daneshmand, M., Srinivasan, V. et al. Scalable probabilistic truss decomposition using central limit theorem and H-index. Distrib Parallel Databases 40, 299–333 (2022). https://doi.org/10.1007/s10619-022-07415-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10619-022-07415-9