Contrarian Behavior, Information Networks and Heterogeneous Expectations in an Asset Pricing Model

Abstract

This paper studies the emergence of contrarian behavior in information networks in an asset pricing model. Financial traders coordinate on similar behavior, but have heterogeneous price expectations and are influenced by friends. According to a popular belief, they are prone to herding. However, in laboratory experiments subjects use contrarian strategies. Theoretical literature on learning in networks is scarce and cannot explain this conundrum (Panchenko et al. in J Econ Dyn Control 37(12):2623–2642, 2013). The paper follows Anufriev et al. (CeNDEF Working paper 15–07, 2015) and investigates an agent-based model, in which agents forecast price with a simple general heuristic: adaptive and trend extrapolation expectations, with an additional term of (dis-)trust towards their friends’ mood. Agents independently use Genetic Algorithms to optimize the parameters of the heuristic. The paper considers friendship networks of symmetric (regular lattice, fully connected) and asymmetric architecture (random, rewired, star). The main finding is that the agents learn contrarian strategies, which amplifies market turn-overs and hence price oscillations. Nevertheless, agents learn similar behavior and their forecasts remain well coordinated. The model therefore offers a natural interpretation for the difference between the experimental stylized facts and market surveys.

1 Introduction

In this paper, I study the effect of information networks on learning in a non-linear asset pricing model. The main question of this work is how agents react to optimism or pessimism of their friends: do they learn herding, or rather contrarian behavior? And how does this affect the emerging market dynamics and stability of the fundamental equilibrium? In order to address this issue, I consider a model, in which the agents apply genetic algorithm (GA) to optimize a simple linear price forecasting rule. The agents learn whether to follow the observed price trend, but also whether to trust the past trading decisions of their friends, which allows for an explicit learning of either herding or contrarian behavior.

One of the fundamental debates of contemporary economics is whether economic agents can learn rational expectations (RE), that is model-consistent predictions of future market prices (Muth 1961). In the context of financial markets, RE require the agents to form a self-fulfilling infinite sequence of forecasts (Blanchard and Watson 1982). Even under a linear relation between the expectations and realized prices, this task is far from being trivial (Sims 2002; Lubik and Schorfheide 2003; Anderson 2008). Furthermore, agents may face additional information constraints (Kormilitsina 2013) or lack the knowledge about the underlying law of motion of the market (Carravetta and Sorge 2010), which further complicates finding the RE solution. Therefore, real economic actors may be unable to bear the cognitive load that is required to form RE. In this case, they would have to learn to predict prices, which does not necessarily lead to ‘as if’ rational expectations equilibria (Hommes and Zhu 2014; Anufriev et al. 2015).

Among other evidence, experiments suggest that people use simple forecasting heuristics (Hommes 2011; Heemeijer et al. 2009; Hommes et al. 2005). In the case of asset markets, this leads to price oscillations that repeatedly over- and undershoot the fundamental (RE) equilibrium. Nevertheless, many economists question the empirical validity of such experiments, as these are based on economies with no or limited information flows between the agents. An informal (yet popular) belief is that in real financial markets the agents can share knowledge about efficient and inefficient trading strategies, and so an information network facilitates convergence towards RE.

Informal information sharing is indeed common among financial traders (Nofsinger 2005; Bollen et al. 2011). Being closer to the core of an information network leads to higher profits (Cohen et al. 2008), but some researches have also argued that networks are a cause of herding (Shiller and Pound 1989; Acemoglu and Ozdaglar 2011). The latter argument became popular after the 2007 crisis in the non-academic discussion¹ and in behavioral economics (for example Akerlof and Shiller 2010, refer to animal spirits as the driving force of financial bubbles). This leads back to the two conflicting views on the rationality of financial agents, which can be associated with Keynes (Akerlof and Shiller 2010) and Muth (1961). How important is therefore herding for market stability, and is herding propagated by information networks? There is no clear answer neither from theoretical nor from empirical work.

Herding is understood as behavior such that individuals, facing strategic uncertainty, disregard their individual information and instead follow the ‘view of the others’, such as the mood of their friends or general market sentiment (see also Sect. 2.6 for a detailed discussion). From the RE perspective, market price should contain all necessary information about the stocks, hence perfect rationality rarely leaves room for herding or networking. The exception would be the case of significant private information (Park and Sabourian 2011) or sequential trading (with the famous example of information cascades, see Anderson and Holt (1997), for a discussion), but neither approach has a clear empirical motivation.

Alternatively, models that depart from rational expectations often investigate some form of social learning. The seminal paper by Kirman (1993) stands as the benchmark for the studies of economic herding (see Alfarano et al. 2005, for a more recent example and a literature review). In this ‘ant-model’, agents are paired at random and imitate each others choices with some exogenous probability, which leads to interesting herding dynamics. The problem with this approach, however, is that individual imitation is assumed as given, instead of being learned by the agents.

Another approach comes with the classical Brock-Hommes heuristic switching model (HSM; Brock and Hommes 1997), in which agents coordinate on price prediction heuristics that have a better past forecasting performance. A more general, agent-based counterpart of HSM comes with genetic algorithm (GA) based models of social learning (see Arifovic et al. 2013, for an example and a literature overview). This approach can explicitly account for social learning (agents switch to better strategies), but does not fit our intuition of herding, which is understood as following the beliefs of others, instead of using similar trading or forecasting strategies.

Empirical studies give ambiguous results on the existence or importance of herding, with the main issue being that such behavior cannot be directly observed in market data. Chiang and Zheng (2010) show that the stock indices between industries are sometimes more correlated than the fundamentals would imply, which can be understood as a sign of herding. However, this effect is absent in Latin America and US data, and its interpretation is subject to debate. An alternative approach is to use experiments, where the information structure is controlled by the researcher. This leads to a surprising result, however: experiments suggest that contrarian (anti-herding) behavior is more common than herding. Two such experiments, both including professional traders as subjects, were reported by Drehmann et al. (2005) and Cipriani and Guarino (2009).

As a result, existence of herding or contrarian behavior in financial markets is not a clear-cut fact. Furthermore, it is not clear whether herding would bring economic agents closer to the rational outcome, or rather to volatile price dynamics (Shiller and Pound 1989). In order to understand the empirical evidence, we require a theoretical inquiry into how herding or contrarian behavior may be learned. Furthermore, such a learning may depend on the structure of ‘information flows’, and thus we need to study it in a context of different information networks.

Recent years have seen a rising popularity of studies devoted to the agent interaction within networks. Probably the most famous example comes with the Siena model (Snijders et al. 2010), which offers a valuable insight into peer effects on the individual decision making. In the financial literature, researchers became interested in the balance sheet interconnections of financial agents such as banks (in’t Veld and van Lelyveld 2014; Fricke and Lux 2014). Nevertheless, theoretical studies of networks in the economic literature typically focus on static environments (such as the mentioned balance sheet connections). Models with explicit learning and expectations formation are scarce, and tend to rely on simple behavioral rules of imitation, since adding realistic learning features into such models easily makes them analytically intractable (see Jadbabaie et al. 2012, for a discussion).

To the best of my knowledge, Panchenko et al. (2013) (henceforth PGP13) are the only authors who conduct a full-fledged theoretical study of the effect of the information network on expectation formation in an asset pricing model. The authors use a HSM model to show that price oscillations are not tamed by the presence of the network. Their interesting paper is, however, subject to some limitations from the perspective of the research problem of this paper. First, in PGP13 the agents can only choose between two predefined forecasting heuristics, leaving little space for any real learning. Second, these two heuristics (chartist and fundamental rules) do not depend on the decisions or beliefs of agent’s friends, but only on realized aggregate market conditions (prices). Third, in PGP13 the network provides information about the realized profitability of the two heuristics, but no insight into the beliefs of one’s friends. The agents are then assumed to fully incorporate this information into their heuristic choice, instead of learning whether to trust it or not. As a result, PGP13 offer a valuable insight into spread of chartist strategies, but not into learning of herding or contrarian behavior itself, which is the topic of this paper. Finally, PGP13 limit their attention to random networks, whereas information networks in many real markets may be much more complicated.

The goal of my paper is to investigate a much more involved learning model. I will use the GA model proposed by Anufriev et al. (2015) (henceforth AHM15), which explains well the individual forecasting heterogeneity of Learning to Forecast experiments. This approach has two advantages: (1) I will work with a realistic, experimentally tested model and (2) I will obtain further insight into the original experiments: to what extent their results (such as the price bubbles) depend on the lack of information networks.

The GA model by Anufriev et al. (2015) is an agent-based model (ABM) based on the work of Hommes and Lux (2011). Its idea is that agents, who are asked to predict a price, follow a simple linear forecasting rule, which is a mixture of adaptive and trend extrapolation expectations. This rule requires specific parametrization, and each agent is endowed with a list of possible specifications of the general heuristic. The agents then observe the market prices and update the list of rules with the use of the GA stochastic evolutionary operators. For instance, if the market generates persistent price oscillations, the agents will experiment with higher trend extrapolation coefficients. Since the agents use the GA procedure independently, the model allows for explicit individual learning. Anufriev et al. (2015) show that the model replicates well the experimental degree of individual heterogeneity, as well as aggregate price dynamics.

In this paper I extend the GA model of Anufriev et al. (2015), to include an information network in such a way that agents may learn herding or contrarian strategies. Agents observe the past trading behavior of their friends and can learn whether to trust it, just as they learn whether to extrapolate the price trend. The model by its ABM structure can evaluate the effects of different, also asymmetric, information networks on price dynamics. Furthermore, the model explicitly accounts for individual learning, and so I can also study the formation of herding/contrarian behavior at the individual level.

The paper is organized in the following way. Section 2 will introduce the theoretical agent-based model, describing a two-period ahead non-linear asset pricing model with GA agents and robotic trader. The third section will present the parametrization of the model, including the investigated network structures, and the setup of the Monte Carlo numerical study of the model. Section 5 will be devoted to small networks of six agents, with which I will highlight the emerging properties of individual learning and resulting price dynamics. The fifth section will move to large networks of up to 1000 agents. Finally, the last section will sum up my results and indicate potential extensions.

2 Theoretical Model

In this section I present the building blocks of the model: an asset market with heterogeneous agents and an information network. The model is based on the standard two-period ahead asset market, used for example by Hommes et al. (2005). For the sake of presentation, most of the analytical results concerning the rational solution of the model are given in Appendix 1.

2.1 Market

Consider I myopic mean-variance agents who can choose between a safe bond with a gross return $R=1+r$ (with $r>0$) or a risky asset. The asset can be bought at price $p_t$ in period t, yields a stochastic dividend $y_t$ and hence can be sold at price $t+1$ in the next period $t+1$. It is commonly known that $y_t\sim NID(y,\sigma _y^2)$. Then the expected return on a unit of the asset bought at $p_t$ is

$$\begin{aligned} \mathbf {E}_{i,t}\left\{ \rho _{t+1}\right\} \equiv \rho ^e_{i,t+1} = \mathbf {E}_{i,t}\{p_{t+1}\} + y - Rp_t, \end{aligned}$$

(1)

where $\mathbf {E}_{i,t}\{\cdot \}$ stands for the individual forecast, which does not have to coincide with the (true) conditional expected value operator $\mathbb {E}\{\cdot \}$.

Denote the agent i’s expectation of the price in the next period $t+1$ as $\mathbf {E}_{i,t}\left( p_{t+1} \right) \equiv p^e_{i,t+1}$. We assume that the agent perceives the variance of one unit of the asset return as a constant, $Var_t(\rho _{t+1})=\sigma _a^2$.² Conditional on the realized price in the current period t, the agent’s i risk adjusted utility at period t is given by

$$\begin{aligned} U_{i,t+1}&= U_{i,t} + z_{i,t}\mathbf {E}_{i,t}\left( \rho _{t+1} \right) - \frac{a}{2}Var_{t}(z_{i,t}\rho _{t+1})\nonumber \\&= U_{i,t} + z_{i,t}\left( p^e_{i,t+1} + y -Rp_{t} \right) - \frac{a}{2}\sigma _a^2 z_{i,t}^2, \end{aligned}$$

(2)

where a is the risk-aversion factor. Hence, define agents’ i optimal demand at period t as $z_{i,t}$, which becomes a linear demand schedule of the form

$$\begin{aligned} z_{i,t}(p_t) \equiv \frac{p^e_{i,t+1} + y -Rp_t}{a\sigma _a^2} = \frac{p^e_{i,t+1} + y}{a\sigma _a^2} - \frac{R}{a\sigma _a^2}p_t. \end{aligned}$$

(3)

For simplicity I assume that the agents face no further liquidity constraints. Agents can take short positions, so $z_{i,t}<0$ is viable.

The market operates in the following fashion. At the beginning of every period t, each agent i has to provide her demand schedule $z_{i,t}$ (3). Notice that because the agents are asked for a demand schedule, they do not have to forecast the contemporaneous price $p_t$. Next to the agents’ demands, there is no additional exogenous supply/demand of the asset. The market clears if the following equilibrium condition is fulfilled:

$$\begin{aligned} \text{ Demand }_t = \sum _{i=1}^I z_{i,t} = 0 = \text{ Supply }_t. \end{aligned}$$

(4)

Denote the average prediction of the agents of the price at $t+1$ as $\bar{p}^e_{t+1}\equiv \frac{1}{I}\sum _{i=1}^I p^e_{i,t+1}$. Substituting the demand schedules (3) into the market equilibrium condition (4), we have that the realized market clearing price is given by

$$\begin{aligned} p_t = \frac{\bar{p}^e_{t+1} + y}{R} + \eta _t \geqslant 0, \end{aligned}$$

(5)

where $\eta _t\sim NID(0,\sigma _{\eta }^2)$ is a small idiosyncratic price shock.³ The price cannot be negative, so it is capped from below at zero. Furthermore, the price $p_t$ is capped at level $p_t \leqslant M$ for any period t and some arbitrary large constant M, which excludes explosive rational solutions (Blanchard and Watson 1982).

This market has a straightforward RE stationary solution such that $p^e_{i,t+1} = \mathbb {E}\{p_{t+1}\} = p^f$ with

$$\begin{aligned} p^f = \frac{y}{r}. \end{aligned}$$

(6)

Without any additional assumptions, the model could explode under non-rational expectations (c.f. Hommes et al. 2008). Following the experimental design of Hommes et al. (2005), I introduce a robotic trader to act as a stabilizing force on the market.

Robotic trader at period t trades as if the next price would be at the fundamental, i.e. his price forecast is $p^e_{ROBO,t+1} = p^f$. He becomes more active when the realized asset price $p_t$ moves away from the fundamental solution. Define

$$\begin{aligned} n_t = 1 - \exp \left( -\phi \left| p_{t-1} - p^f\right| \right) \end{aligned}$$

(7)

as the relative trading share of the robotic trader, which depends on his sensitivity $\phi$. Denote

$$\begin{aligned} \hat{p}^e_{t+1} \equiv n_t p^f + (1-n_t)\bar{p}^e_{t+1} = p^f n_t + \frac{1-n_t}{I}\sum _{i=1}^Ip^e_{i,t+1}, \end{aligned}$$

(8)

that is $\hat{p}^e_{t+1}$ denotes the ‘total’ market price expectations, averaged over the robotic trader and the GA agents. Then the actual realized price including the robotic trader becomes

$$\begin{aligned} p_t&= \frac{(1-n_t)\bar{p}^e_{t+1}+n_tp^f + y}{R} + \eta _t \nonumber \\&= \frac{\hat{p}^e_{t+1} + y}{R} + \eta _t \end{aligned}$$

(9)

which is a two-period ahead nonlinear price-expectations feedback system. Notice that the introduction of the robotic trader does not change the steady state RE solution (see Appendix 1). Importantly, in the model simulations the robotic trader will prevent exploding price paths (c.f. Hommes et al. 2005).⁴

2.2 Network

The agents are not fully isolated. Instead, they are positioned on an unweighted symmetric, irreflexive and a-transitive information network $\mathbf {I}$. Let $\mathbf {I}_{i}$ denote the set of friends of agent i and $\hat{I}_i\equiv |\mathbf {I}_i|$ denote the number of her friends. Throughout the paper, I assume that for a particular market this information network is fixed and exogenous. A natural extension is to relax this assumption and allow for endogenous network formation, but I leave this for future research. See Albert and Barabási (2002), Newman (2003), Goyal (2002) for a general introduction into networks and Bala and Goyal (2000) for endogenous network formation. In the next section I will discuss the specific networks used in the numerical simulations of the model.

Within the network, an agent cannot directly observe the price expectations of her friends, but she knows whether in the recent past they were buying or selling the asset. This is a realistic setting, as real asset traders are likely to share only qualitative information (‘this stock is profitable, I just bought it!’). I emphasize that an agent cannot see the contemporary trade decisions of her friends, and moreover agents have no private information about the future price shocks $\eta _t, \eta _{t+1},\eta _{t+2},\ldots$. Consider agent j and define

$$\begin{aligned} m_{j,s} = {\left\{ \begin{array}{ll} +1 &{} \text{ if } z_{j,s} > 0,\\ 0 &{} \text{ if } z_{j,s} = 0,\\ -1 &{} \text{ if } z_{j,s} < 0 \end{array}\right. } \end{aligned}$$

(10)

a simple sign function of her realized demand in period s.

The agents have memory length $\tau$ and use the simplest possible index $\text{ Mood }_{j,t-1}$, defined as the average mood of agent j in periods $[t-\tau ,t-1]$

$$\begin{aligned} \text{ Mood }_{j,t-1} = \frac{1}{\tau }\sum _{s=t-\tau }^{t-1} m_{j,s}. \end{aligned}$$

(11)

For instance, if during the last $\tau$ periods the agent j was always buying (selling) the asset, her index is $+1$ ($-1$). If she was more likely to buy (sell) the asset, her mood index is positive (negative) and so a positive (negative) index means that the agent j remained optimistic (pessimistic) about the asset profitability. A special case of short memory is $\tau =1$ when the mood index becomes the sign of the agent’s j very last transaction at period $t-1$.

By assumption, the mood of agent $j\,\text{ Mood }_{j,t-1}$ is visible to all of her friends, that is agent i can access all $\text{ Mood }_{j,t-1}$ for which $j\in \mathbf {I}_{i}$. However, in order to study the effect of herding, I assume that the agents do not distinguish between their friends and instead rely on the mood of their peers, that is the mood index (11) averaged among all $\hat{I}_i$ of their friends:

$$\begin{aligned} \text{ Peer }_{i,t-1}&\equiv \frac{1}{\hat{I}_i}\sum _{j\in \mathbf {I}_{i}}\text{ Mood }_{j,t-1} \nonumber \\&= \frac{1}{\tau \hat{I}_i}\sum _{j\in \mathbf {I}_{i}}\sum _{s=t-\tau }^{t-1} m_{j,s}. \end{aligned}$$

(12)

I will refer to (12) as the measure of agent i’s friends’ mood. It has a straightforward interpretation as the average mood of i’s friends. Hence if the agents learn to herd, their price expectations should depend positively on the peer mood (12).

2.3 Fundamental Solution Benchmark

I define the fundamental solution to the model as the rational expectations (RE) equilibrium. The information provided within network is specified in such a way that it has no effect on the RE solution. In fact, network’s presence or particular structure makes no difference on the behavior of perfectly rational agents. Therefore, the RE framework gives a strong prediction that adding a network into the model will result in the same (long-run) dynamics. See Appendix 1 for a discussion.

2.4 Experimental and Genetic Algorithms Benchmark

The model is based on the experimental market investigated by Hommes et al. (2005), with almost the same parametrization (see later discussion). The authors report that their subjects typically coordinated on price trend extrapolation rules. As a result, realized prices were unlikely to settle on the fundamental value, and often oscillated around the fundamental in an irregular fashion. Robotic agent prevented large bubbles, however. Hommes et al. (2008), who studied an experimental two-period ahead asset pricing model without the robotic trader, found their prices to explode instead of oscillating.

As discussed, AHM15 already investigate the model without the networks. They report that the GA agents learn to use trend following heuristics in a similar fashion to the experimental subjects. Furthermore, long-run simulations of the model revealed that it contains two attractors. The market could switch between periods of stability (prices settling down on the fundamental steady state) and oscillations of varying amplitude. A basic question is whether the introduction of a network will change this outcome, and in particular whether both attractors are robust against the presence of networks.

2.5 Price Expectations and Learning

Agents consider themselves as price-takers and so their task is simply to predict the next price $p_{t+1}$ as accurately as possible, conditional on the market events and friends’ behavior until and including period $t-1$. The GA agents are not perfectly rational and instead rely on a simple rule of thumb, a linear heuristic of the form

$$\begin{aligned} p^e_{i,t+1} = \underbrace{\alpha _{i,t} p_{t-1} + (1-\alpha _{i,t}) p^e_{i,t}}_\text {adaptive expectations} + \underbrace{\beta _{i,t} (p_{t-1} - p_{t-2})}_\text {trend extrapolation} + \underbrace{\gamma _{i,t}\Gamma \text{ Peer }_{i,t-1}}_\text {herding/contrarian}. \end{aligned}$$

(13)

The first two elements of the rule, adaptive and trend extrapolation expectations, come directly from the baseline GA model by AHM15. The new part of the above rule is the last term, the peer effect, which is a weighted sum of the moods of all friends of agent i.⁵

The linear heuristic (13) of agent i depends on the specific parameters chosen at period t: the price weight $\alpha _{i,t}\in [0,1]$, the trend coefficient $\beta _{i,t}\in [-1.3,1.3]$ and finally the trust index $\gamma _{i,t}$. The trust index $\gamma _{i,t}\in [-1,1]$ can be interpreted as the importance agent i attaches to her friends decisions. If $\gamma _{i}>0$, agent i believes it is worth to follow her friends’ past trades, and that the past optimism of her friends is a signal that the price $p_t$ will increase even more than just due to current trend. Conversely, $\gamma _{i}<0$ implies that the agent i behaves in contrast to her friends.⁶ In other words, $\gamma _{i,t}>0$ means herding behavior, while $\gamma _{i,t}<0$ implies contrarian behavior.⁷ The specific value of the trust index $\gamma _{i,t}$ is multiplied by a sensitivity parameter $\Gamma$, which remains constant and homogeneous across agents. The multiplicative form of the herding/contrarian term, with these two factors separated, allows for an easier presentation and interpretation of the results. Future experimental studies can investigate the empirical degree of $\Gamma$.

The agents do not use the same heuristic over time. Depending on the market conditions, the heuristic (13) should be based on different parameters. For instance, in the periods of strong price oscillations, agents should switch from low or negative trend extrapolation to strong trend extrapolation. Furthermore, the goal of the paper is to identify circumstances in which the agents learn herding or contrarian strategies.

We follow AHM15 and model the time evolution of the heuristic (13) by binary Genetic Algorithms. This results in individual learning and heterogeneity of forecasting behavior, similar to the experimental findings. See AHM15 for a technical discussion and parametrization. The intuition of the model is the following.

The agents are endowed with a small set of $H=20$ different parameter triplets $(\alpha _{i,t},\beta _{i,t},\gamma _{it,})$, which correspond to a small list of specific forecasting heuristics (13). At every period t, every agent chooses one particular heuristic $p^e_{i,t+1}$ to predict the next price $p_{t+1}$, according to their relative forecasting performance in the previous period. Next, the price $p_t$ is realized and the agents observe how well their heuristics would forecast $p_t$ in the previous period (conditional on the corresponding information set from period $t-1$). Based on this information, every agent independently updates her heuristics using four evolutionary operators: procreation (better heuristics replace worse), mutation and crossover (experimentation with heuristic specification) and election (screening ineffectual experimentation). Afterward, the next period $t+1$ starts and the procedure is repeated. See AHM15 for technical presentation.

2.6 Coordination Versus Herding

I emphasize the difference between coordination and herding. Herding (contrarian) means that the agents directly follow (contrast) the decisions of their friends, which in this model is embodied by relatively high positive (negative) values of the trust index $\gamma$. On the other hand, coordination is the similarity of agents’ behavior: in this context similarity of the realized individual price forecasts and forecasting rules (similar $(\alpha ,\beta ,\gamma )$ triplets regardless of the particular value of the trust index $\gamma$). I follow Heemeijer et al. (2009) and express this value as the standard deviation of the individual price forecasts, a measure of dis-coordination of the form

$$\begin{aligned} \mathbf {D}_t = \sqrt{\frac{1}{6}\sum _{i=1}^6\left( p^e_{i,t+1} - \frac{1}{6} \sum _{j=1}^6 p^e_{j,t+1} \right) ^2}\quad \in [0,\infty [. \end{aligned}$$

(14)

If $\mathbf {D}_t=0$, then all agents at period t have the same forecast of the next price, while higher values of (14) imply larger dispersion of the contemporary individual price forecasts.

Regardless of the particular network, agents interact indirectly through the market price. Experiments and previous work on the GA model by AHM15 show that such an indirect interaction can be sufficient to impose a large degree of coordination in asset markets, even though the agents cannot observe each other. PGP13 further study dynamics of coordination under local interaction (social learning through networks), but in their model their agents cannot learn actual herding/contrarian strategies (expectations as a function of friends’ behavior). The main goal of this paper is to investigate whether agents will learn herding/contrarian behavior and how does this influence their coordination.

3 Monte Carlo Studies

3.1 Parametrization of the Model

Following the design of the experiment of Hommes et al. (2005), the parameters are set in the following way. Regardless of the network, the gross interest rate is set to $R = 1+r = 1.05$ and the dividend to $y=3$, which gives the fundamental price $p^f = 60$. The standard deviation of the price shocks in (9) is set to $\sigma _{\eta } = 0.1$, which implies that under RE the price should be independently and normally distributed and approximately in the [59.75, 60.25] interval for $99\,\%$ number of periods. It will appear that these small idiosyncratic price shocks play no significant role in the system.⁸

The only difference with Hommes et al. (2005) comes with the parametrization of the robotic trader. Recall the definition of the relative weight of robotic trader (7), which depends on the sensitivity parameter $\phi$. For instance, the robotic trader will take over exactly a quarter of the market ($n_t=0.25$) if the absolute price deviation is

$$\begin{aligned} \bigg |p_{t-1} - p^f\bigg | = \frac{-\ln {0.75}}{\phi }. \end{aligned}$$

(15)

Hommes et al. (2005) set $\phi =1/200$, which means that the robotic traders takes over $25\,\%$ if the price is close to the minimum allowed price $p_t=0$ or the maximum allowed price $p_t=100$.⁹ In this paper I want to study the impact of the networks on market stability and hence I want to scale down possible price oscillations. Hence, I set $\phi = 1/104.281784903$, which implies that the robotic trader will take over a quarter of the market if the price will reach $p_{t-1}=90$ or $p_{t-1}=30$, that is if it deviates from the fundamental by a factor of $50\,\%$ ($100\,\%$ in the setup of Hommes et al. 2005).

The GA model requires parametrization in two respects. First, I take the number of heuristics (chromosomes) and the specification of the evolutionary operators directly from AHM15. In comparison with AHM15, the GA agents in this paper optimize three parameters instead of two. The new parameter, the trust index $\gamma$ is associated with a gene of 20 bits, i.e it has the same length as the genes that represent the two other coefficients of the agent heuristic (13).¹⁰

Second, the GA agents can optimize the heuristic parameters only from a predefined interval (see AHM15, for discussion). The price weight $\alpha \in [0,1]$ has to span a simplex; the trend weight is taken from AHM15 to be constrained by $\beta \in [-1.3,1.3]$. I assume that all agents have their total herding/contrarian effect equal to 6 (in absolute terms), which corresponds to $10\,\%$ of the fundamental price. This implies that the trust sensitivity is set as $\Gamma =6$, given that the trust index has to be chosen from a unit interval $\gamma \in [-1,1]$. Finally, the heuristic (13) is based on the mood index (11), for which I take memory $\tau =5$.¹¹

3.2 Initialization

AHM15 note that the GA model is sensitive to initial conditions. First, the agents require some initial heuristics. Here I follow the authors and sample them at random. Second, the heuristics require past data from at least two periods, including the previous price forecasts itself. In my numerical simulations, the agents in the very first period always predict the fundamental price and only start using their heuristics in the second period, assuming no trend. To be specific,

$$\begin{aligned} p^e_{i,2}&= p^f = 60,\end{aligned}$$

(16)

$$\begin{aligned} p^e_{i,3}&= \alpha _{i,3} p_1 + (1-\alpha _{i,3})p^e_{i,2}\nonumber \\&= 60 + \alpha _{i,3}\eta _1\quad \text{ for } \text{ every } i\in I, \end{aligned}$$

(17)

which implies that the market is initialized at the fundamental value (lest the price shock), $p_1\approx p_2\approx p^f$.

This may seem as a surprising design choice, since ABM’s are often used to study model’s off-equilibrium dynamics and convergence properties. It will turn out that the model in this paper is inherently unstable. Indeed, if initialized in the fundamental, most likely it will diverge at some point!

3.3 Small Networks of Six Agents

In the first part of my study, I will look at networks of six agents, which is is the typical number of subjects in the LtF experiments. Furthermore, it is easy to trace the behavior of only six agents, while this number of nodes is sufficient to have networks with interesting properties, such as regular lattice or asymmetric positioning. I will therefore use these networks to obtain some basic insight into how the network structure and placement affects individual behavior, herding and coordination. The second part of the Monte Carlo study (MC) will shift our attention to large networks.

Six symmetric agents can be arranged on 108 different networks. For the sake of presentation, I focus on six specific: no network, circle, fully connected, two connected clusters, core-periphery and star. See Fig. 1 for a visualization of these networks, and Table 1 for summary statistics.

Fig. 1

Small networks used in Sect. 4. a No network. b Circle. c Fully connected. d Two connected clusters. e Core-periphery. f Star

The model with no network serves as a natural benchmark, a setting which was studied with the LtF experiments and by AHM15. The circle and fully connected networks are important to evaluate the effect of network’s density on price stability, coordination, learning and herding. The three other networks represent asymmetric positioning of the agents, which I will show to have an interesting effect on herding.¹²

Table 1 Properties of the small networks used in Sect. 3, see Appendix 4 for definition

In the later analysis the model turns out to be unstable in terms of the realized prices, but also in terms of individual coordination and strategies. In repeated simulations of the small networks of six agents, a clear median pattern will emerge, but individual simulations will exhibit oscillatory behavior. In order to understand these dynamics, I will focus on three types of evidence.

Every network will be simulated 1000 times, based on the same price shocks $\eta _t$,¹³ but with differently realized learning via different random numbers given to the GA operators. Every market is simulated for 2500 periods, including the initial 100 periods which can be interpreted as a learning phase. This offers two ways to the represent the data.¹⁴

First, for each of the 1000 simulated markets one can look at the realized statistics of that market (for periods 101 till 2500, so excluding the learning phase), which I will refer to as long-run statistics. This gives a distribution of 1000 long-run statistics, and one of particular importance is the distribution of the long-run market price standard deviation. It serves as a direct indicator of market stability.

Second, one can look at realized market variables across the 1000 markets in a particular period. I will focus on the median and $95\,\%$ confidence intervals (CI) and how they evolve over time. The variables of interest are price, dis-coordination measure (14) and the coefficients chosen by the agents to specify the forecasting heuristic (13).

Finally, it will appear that the model does not converge, hence it may be difficult to understand the emergent properties of individual learning based solely on this MC exercise. In order to interpret these results, I will also present some sample time paths of the realized market and learning variables.

3.4 Large Networks

Large networks are empirically more relevant than the ones with six agents only. However, one can identify a myriad of possible and interesting large network topologies. The selection reported in this paper is based on the discussion by PGP13. To be specific, I will focus on networks of size $I\in \{50,100,250,500,1000\}$, with 10 different architectures that range from regular lattice to small-world network. Due to the limits of the study, I will leave large-scale networks for future studies (cf. PGP13).

The non-regular networks are defined through a non-deterministic generating process (see below for details for random and small world networks). In principal one could obtain a distribution of results based on a repeated sampling of these non-regular networks. This in turn would be obtained by a proper MC exercise per every realized network (in line with the MC study for the networks of 6 agents). However, a single sample network of many agents (with 1000 as the maximum market size in this paper) is already numerically involved, and difficult in terms of presentation. Furthermore, we will see that the behavior of the sample large networks is consistent with the behavior observed in the MC study for the small networks. As a result, a full-fledged MC exercise could offer only little additional insight. Instead, for every network size and architecture, I will focus on one sample realized simulation, with a longer time horizon of 25, 000 periods.

I will study four regular networks, with architectures that are based on their 6-agent counterparts:

• No network—every agent has an empty set of friends.

• Fully connected—every agent is befriended with every other agent.

• Regular—every agent has exactly 4 friends. This market can be represented by a circle such that every agent is linked with two agents to the left and two to the right.

• Star—one central (or star) agent, who is connected to all other agents, whereas other edge agents are connected only with the star agent.

Random network with probability $\pi _l$ is typically defined as a random graph, in which every two agents are linked with probability $\pi _l$. Such an architecture can offer a wide distribution of links between the agents. I will focus on two random networks:

• Random(4)—sparse random with $\pi _l$ set in such a way that on average agents have exactly 4 links, which gives the same density as for the regular network defined above.

• Random(16)—dense random with $\pi _l$ such that on average there are exactly 16 links per agent, i.e. with density four times larger than for the regular network defined above.

Empirical social networks often have characteristics of the so-called small world networks (SM): small density (few links between the agents), together with large transitivity (‘cliquishness‘, high probability that a friend of my friend is also a friend of mine), but also small characteristic path (average distance between the agents). In practice such networks look like semi-independent clusters that are connected with each other by infrequent ‘bridge agents’ (see the network in Fig. 1d for a simplest example, in which agents 3 and 4 serve as such a bridge between two clusters). It is impossible to obtain networks with such properties through random graphs. Watts and Strogatz (1998) propose the following algorithm: start with a regular lattice network of K links per node and rewire every link with probability $\pi _r$. Rewired networks based on well chosen parameters K and $\pi _r$ have SM properties, and I will use the following four rewired networks:

• Rewired(4, 0.01)—on average four links per agent and rewiring probability of $\pi _r=1\,\%$. This gives a SM network for the largest market $I=1000$.

• Rewired(4, 0.1)—on average four links per agent and rewiring probability of $\pi _r=10\,\%$. This gives a SM network for the intermediate market $I=100$.

• Rewired(16, 0.01)—on average 16 links per agent and rewiring probability of $\pi _r=1\,\%$.

• Rewired(16, 0.1)—on average 16 links per agent and rewiring probability of $\pi _r=10\,\%$.

The representation of the realized non-regular networks for all five possible network sizes, together with a table of basic characteristics, is available in Appendix 5 (Figs. 18, 19, 20, 21, 22, 23).

4 Networks of Six Agents

This section consists of three parts. First, I will look on the model without a network (or an empty network). This is essentially the same setup as investigated by AHM15, who focused on the model’s fitness to four LtF experiments. I will supplement their investigation by an in-depth analysis of the emergent properties of the GA model for the two-period ahead asset pricing model, specifically what drives the coordination on the oscillatory prices paths and how does this link with the individual learning. Second, I will introduce two regular lattice networks (circle and fully connected; see Fig. 1 for a visualization) in order to study whether the agents learn to herd or rather to contrast the behavior of their friends. Finally, I will study the role of asymmetry by considering three asymmetric networks (two connected clusters, core-periphery and star).

4.1 Benchmark Model Without Network

Observation 1

Without a network, there are two types of attractors in the model: coordination on the fundamental price and oscillations around the fundamental.

In line with the findings of AHM15, I find that there are two possible outcomes in the model if there is no network. First, the GA agents can coordinate on the fundamental price and stay there (see Fig. 2b for a sample market). This is a self confirming steady state, since if the price stays at the fundamental level, the forecasting rule (13) effectively reduces to forecasting the fundamental as well. The trend term $\beta$ is irrelevant and retains wide distribution centered around zero (weak or no trend following). The price shocks $\eta _t$ are too small to push the agents away from this equilibrium.

Fig. 2

Monte Carlo study (1000 markets) of the GA model without network: distribution of long-run price standard deviation; and sample stable and unstable time series of prices, a Price SD over markets. b Stable market. c Unstable market

Since in this scenario the trend coefficient is irrelevant, by chance it may happen that the agents, independently from each other, consider sufficiently strong trend extrapolation (sufficiently large $\beta$). In such a case, they can pick up a sufficiently large shock $\eta _t$ as a sign for future price trend, outweigh the robotic trader and impose a regime of price oscillations (see Fig. 2c for a sample market). This is again a self-confirming regime: if there is significant trend, agents effectively learn to follow it, which amplifies the trend despite the stabilizing effect of the robotic trader. We observe that across 1000 simulations,¹⁵ slightly more than $50\,\%$ of the markets slipped into significant price oscillations. This is visible in the bimodal distribution of the long-run standard deviation of the price, as visible on Fig. 2a. It also corresponds to the results of Hommes et al. (2005), who report that among the seven experimental groups with $p^f=60$, four exhibited oscillations, two monotonic convergence and one an intermediary case.

Observation 2

GA agents, without any direct link, can coordinate well by learning to follow the price trend, which can differ across time and between markets.

Disregarding the initial 100 periods, the predictions of GA agents are sharply correlated with an average correlation coefficient of $99\,\%$ (average from 1000 simulated markets).¹⁶ Across the simulations, the median dis-coordination measure (14) remains low, below 0.1 (see Fig. 3b for the median and $95\,\%$ CI over time). Nevertheless, large outliers are possible and the upper bound of the $95\,\%$ CI exceeds 2. This implies that the agents are typically well coordinated, but occasionally momentary breaks of this coordination occur.

Fig. 3

Monte Carlo study (1000 markets) of the GA model without network: time evolution of important market and individual variables. Median is represented by a red line and $95\,\%$ CI are represented by blue lines. Notice that forecast SE is the squared difference between forecast and realized price, a Price. b Dis-coordination. c Forecast SE. d Price weight $\alpha$. e Forecast weight $1-\alpha$. f Trend coefficient $\beta$. (Color figure online)

The reason that the agents remain well coordinated despite no direct links between them is that they learn similar behavior, and so their predictions react to specific market condition (current price and price trend) in the same manner. This in turn is reinforced by the positive feedback nature of the market. For example, if the GA agents have similar optimistic price forecasts, the realized price will indeed be high and the agents have no incentive to change their behavior. If the prices remain stable, a specific parametrization of the forecasting (13) is in practice irrelevant. On the other hand, the median GA agent converges to the following strong trend rule

$$\begin{aligned} p^e_{i,t+1} \approx 0.9p_{t-1} + 0.1p^e_{t} + 0.5\Delta p_{t-1}, \end{aligned}$$

(18)

as presented at the bottom panel of Fig. 3. Notice that this rule is similar to the median rule reported by AHM15 for the same market. In the unstable markets GA agents learn to coordinate on the price trend. The trend coefficient $\beta$ retains a wide distribution even towards period 2500, including its upper $95\,\%$ CI bound being far away from the median, which suggests that the specific trend is realized differently on different markets. Indeed, the long-run price standard deviation of the unstable markets has a wide distribution, which means that different markets are unstable to a different degree, or the market instability (i.e. the specific price trend) changes over time.

Observation 3

In unstable markets, the robotic trader is responsible for the reversal of price trends (crashes of bubbles and reversals of bursts).

Regardless of whether the market was stable or not, its long-run average price has a degenerate distribution at approximately the fundamental level. Furthermore, the price oscillations are centered around the fundamental and $95\,\%$ of times are approximately contained within the interval [45, 75], that is 75–125 % of the fundamental price (see Fig. 3a). This corresponds to a relative weight of the robotic trader (7) $n_t \approx 13.4\,\%$ at the peak of oscillations.

Fig. 4

Sample market without network, periods 1001 till 1025. Realized market variables in these periods and individual forecasts (including the corresponding heuristic specifications) of price from these periods, a Prices and forecasts. b Dis-coordination. c Robotic trader. d Price trend $(p_{t-1} - p_{t-2})$. e SE of forecasts. f Chosen trend coeff. $\beta$

Consider again the unstable market presented in Fig. 2c. Figure 4 displays a number of variables from that market in periods 1001 till 1025. Within these 25 periods, the market experienced one bubble, a subsequent crash, a period of crisis and then recovery towards a new bubble. The turning points of the bubble and crisis happened in periods 1005 and 1016 respectively (which means that one full cycle took around 20 periods, see Fig. 4a). What caused these market turn-overs?

Throughout periods 1000–1025 the price shocks were not larger than 0.2 (i.e. their two standard deviation) in absolute terms. The cycle of bubbles and crashes arises endogenously, without a need for large exogenous shocks.¹⁷ Before the bubble turning point in period 1006, the GA agents used the strongest possible trend extrapolation (Fig. 4f) and remained well coordinated. Notice that in the period of bubble build-up, the agents undershoot the price, but slowly converge towards it. Indeed, their error approaches zero at the turning point (Fig. 4e). It means that the GA agents are ‘catching up’ with the bubble. This is possible, because they use a linear rule with constant trend coefficient, whereas the actual price trend $(p_{t-1}-p_{t-2})$ looses on its momentum (see Fig. 4d for the price trend observed by the agents). The latter is due to the robotic trader: the more the bubble builds up, the more he becomes active, diminishing the effect of the agents’ trend chasing (Fig. 4c). The maximum price trend happens three periods before the turning point, after which the robotic trader becomes twice as active (with his relative weight increasing from around 5–10 %).

At some moment, the robotic trader becomes influential enough to outweigh the GA agents and to halt the price trend completely.¹⁸ Specifically this happens in period 1006, the last period for the observed price trend to remain positive (albeit already close to zero, see Fig. 4d). However, the GA agents do not realize that the market is about to turn, but rather observe that in the past it paid off to follow the trend (indeed they just ‘caught up’ with the growing price) and so they continue to extrapolate it, despite its relatively meager value.

On the other hand, in period 1007 the robotic trader does not care that the prices have lost momentum. Instead he considers only the absolute deviation of the price from the fundamental and increases his activity on the market even more. The total effect is that the realized price $p_{1007}$ is slightly smaller than the previous price. GA agents momentarily realize that the strong trend following just lost its potency and start to experiment with lower coefficients $\beta$ of the forecasting heuristic (13) for predicting price in the next period $p_{1008}$ (see Fig. 4f). This results in a moment of dis-coordination (Fig. 4b), and also means that the stabilizing effect of the robotic trader becomes even more important and the price starts to drop in a more pronounced way.

The price will not converge to the fundamental, what the robotic trader is trying to achieve. Instead, the GA agents notice the downward trend and immediately follow it (chosen trend coefficients $\beta$ were diverging from their allowed upper bound of 1.3 for only two periods), which reinforces the crash. The market undershoots the fundamental value and a symmetric sequence of events happens around the peak of the burst in period 1015.

Finding 1

Without a network, the market can be both stable and unstable. Instability occurs if GA agents learn to follow the current price trend, which generates a high level of coordination during the build-up of bubbles and bursts. However, a constant price trend cannot be sustained forever because of the robotic trader. When the trend looses enough momentum, the GA agents experiment with their forecasting heuristics. As a result, a tipping point of bubbles and crashes emerges, in which agents are dis-coordinated around a price trend reversal, which renews coordination on extrapolating the reversed price trend.

These findings are not driven by the nature of the robotic trader per se, but by the fact that a stable price trend is unattainable because of the robotic trader. In real markets, a number of factors can have a corresponding effect of breaking up the price trends: liquidity constraints, regulations on prices (such as daily limits on allowed asset price change); and finally ‘common knowledge’ that bubbles cannot grow up forever. Usually this coincides with uncertainty about how exactly the price trend will be broken, because of strategic uncertainty, or because the legal constraints are imprecise. In these cases, market participants find it easy to follow price bubbles and crashes, but are not that skilled at playing out the markets’ tipping points, as was evident during the recent 2007 financial meltdown. The same mechanism emerges in my model as summarized in Finding 1. Just as in real life, the GA agents follow the market, which reinforces its growth, until it reaches its natural limit and, in spite of agents’ optimism, it starts to stagnate. Once the agents realize this, they panic—and the bubble bursts without the optimism it was built upon. A period of crisis thus emerges, when agents’ pessimism reinforces the price drop.

4.2 Contrarian Strategies Induced by Networks

Observation 4

Networks have a destabilizing effect on the market.

Introducing any type of network into the model brings forth additional price instability. MC results for two regular networks, circle and fully connected, are presented in Fig. 5. In comparison with the model without a network, coordination on the fundamental price does not constitute a likely attractor anymore. For the circle network, long-run price’s standard deviation close to zero appears only in about $5\,\%$ of the markets, and virtually never in the case of the denser fully connected network (middle panel of Fig. 5). On the other hand, in almost all markets price oscillations arise. Furthermore, these oscillations are stronger, implying larger market volatility. The prices still fluctuate around the fundamental value, but the $95\,\%$ CI of the realized price across time are approximately twice as wide as without network, specifically they consititute an interval close to [30, 90], i.e. [50, 150 %] of the fundamental price. In addition, price oscillations occur almost immediately (left panel of Fig. 5). In the unstable simulations, typical price long-run standard deviation is also twice as large for both the circle and the fully connected networks than without network. Sample simulations (right panel of Fig. 5) confirm that the price oscillations have a more pronounced amplitude.

Fig. 5

Monte Carlo study (1000 markets) of the GA model without network, circle and fully connected networks: time evolution of prices (median represented by a red line and $95\,\%$ CI represented by blue lines); distribution of long-run price standard deviations; sample realized prices for initial 500 periods. (Color figure online)

Observation 5

Agents learn to use heuristics with strong price trend extrapolation, and also a contrarian attitude towards other agents. Despite the contrarian strategies, they remain well coordinated.

In the remaining of this subsection, I will focus on the fully connected network. Results for the circle network are essentially the same. The first observation is that just as was the case for the model without a network, the GA agents exhibit strong trend following behavior. Figure 6 presents the time distribution of the price weight $\alpha$ and trend coefficient $\beta$ chosen by the agents across 1000 simulated fully connected markets. The median agent quickly converges to a strong trend following rule

$$\begin{aligned} p^e_{i,t+1}\approx p_{t-1} + 1(p_{t-1}-p_{t-2}) - 0.9\Gamma \text{ Peer }_{i,t-1}, \end{aligned}$$

(19)

which is slightly stronger in terms of trend following coefficient $\beta$ than for the case of no network (even though the $95\,\%$ CI have approximately the same width). Notice furthermore that the weight on the previous forecast $1-\alpha$ is close to zero, which is consistent with the findings of AHM15: large price instability induces learning of stronger trend, but also less ‘conservative’ behavior.

Fig. 6

Monte Carlo study (1000 markets) of fully connected network: time evolution of heuristic (13) parameters chosen by the agents to forecast prices. Median is represented by a red line and $95\,\%$ CI are represented by blue lines, a Price weight $\alpha$. b Forecast weight $1-\alpha$. c Trend coefficient $\beta$. (Color figure online)

Fig. 7

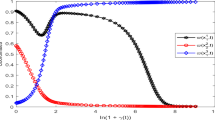
Monte Carlo study (1000 markets) of fully connected network: time evolution of $\gamma _1$ trust index of agent $1; \frac{1}{5}\left( \sum _{i=2}^6\gamma _i\right)$ normalized trust index received by agent 1 from her friends (all other five agents); and standard deviation of the trust indices of all six agents. Median is represented by a red line and $95\,\%$ CI are represented by blue lines, a $\gamma _1$ trust index of agent 1. b Trust received by agent 1. c SD of agents’ trust. (Color figure online)

Interestingly, the agents learn contrarian rules with median $\gamma \approx -0.9$. If the friends of an agent were buying in the past (remained optimistic), she would decrease her price forecast. Figure 7 shows the $95\,\%$ CI of the trust agent 1 puts into her friends and trust she receives herself over time.¹⁹ The median agent quickly learns a strong contrarian heuristic and is furthermore distrusted by her friends. However, the $95\,\%$ CI for both variables remain wide and approach zero from below, which means that the agents are still experimenting with the specific strength of the contrarian strategies. This is further visible in the standard deviation of the realized trust index between the agents (low median, but wide $95\,\%$ CI, see Fig. 7c). Finally, despite the contrarian behavior, GA agents remain well coordinated, as measured by the correlation of their price forecasts equal to $96.8\,\%$. What is the reason for these two facts, and how are they connected with the increased price volatility?

Observation 6

Agents can only look at the past behavior of their friends, but the market is unstable. Therefore, trades that were optimal in the past are inconsistent with contemporary market conditions. As a result, observed mood of friends is ‘sticky’, which induces the agents to learn contrarian strategies.

To study the reason of the contrarian behavior, I will focus on a sample cycle of boom and crisis presented in Fig. 8, for one market with the fully connected network. We observe that this cycle is similar to the one from a sample market without a network, specifically the oscillations have similar period (but a higher amplitude, as discussed in Observation 4) and the timing of the bubble-crisis cycle is symmetric. During a build-up period of the bubble, the agents are ‘chasing’ the bubble with strong trend following rules, until the robotic trader curbs the price trend. Afterwards, there is a small phase when the agents experiment with their rules, what together with the influence of the robotic trader causes a trend reversal, which is quickly picked up by the agents. The evolution of the trust index $\gamma$ is the opposite to that of the trend coefficient: it typically stays close to its lower boundary ($\gamma \approx -1$), but agents experiment with higher trust during the market reversals.

Fig. 8

Sample market with fully connected network, periods 1001 till 1025. Realized market variables in these periods and individual forecasts (including the corresponding heuristic specifications) of price from these periods, a Prices and predictions. b Dis-coordination. c Robotic trader. d SE of forecasts. e Chosen trend coeff. $\beta$. f Chosen trust index $\gamma$. g Agents’ mood index. h Mood observed by agents. i Sign of robotic trades

To interpret these results, the following lemma is useful (see Appendix 2 for the proof):

Lemma 1

Disregarding the price shocks, agent i buys (sells) if her price forecast is higher (lower) than the average market expectation (8), that is if $p^e_{i,t+1}>\hat{p}^e_{t+1}$ ($p^e_{i,t+1}<\hat{p}^e_{t+1}$). Similarly, robotic trader buys (sells) if the average market expectation (8) is below (above) the fundamental price, i.e. robotic trader’s forecast. This implies that the GA agents and the robotic trader can buy (sell) even though they expect negative (positive) price trend.

This lemma follows from the two-period ahead structure of the market and has a simple interpretation. Consider a market at period t with only two agents, no price shocks ($\eta _t=0$) or robotic trader ($n_t=0$). Let both agents expect the price to increase in the next period $t+1$ in comparison with the last observed $p_{t-1}$. Their demand functions (3) however depend not only on their expectations of $p_{t+1}$, but also on the contemporary price $p_t$, which follows the market clearing condition (4). If one agents is more optimistic about the next period (say $p^e_{1,t+1} > p^e_{2,t+1})$, then she will take relatively longer position. Because the market has to clear, she will buy the asset from the other agent, $z_{1,t} = - z_{2,t} > 0$. In a general case of many agents, price shocks and the robotic trader, the market clearing condition implies that a GA agent buys the asset if she is relatively optimistic, not if she is optimistic in absolute terms.

The important consequence of the lemma is that, because of the robotic trader, GA agents are likely to be buying (selling) the asset even after they realize a market reversal. For an illustration consider the sample network of six fully connected agents (Fig. 8). In this market there was a bubble with a peak in period 1010, with a negative price trend afterwards. The agents realized that after observing $p_{1011}$ and their subsequent prediction $p^e_{i,1013}$ for price in period 1013 decreased in comparison with their previous forecast $p^e_{i,1012}$, but was still highly above the fundamental price. Agents noticed that the price gained a negative trend, but did not expect it to fall to or below the fundamental price immediately. On the other hand, the robotic trader is always trading as if the next price will be at the fundamental level. As a result, the GA agents after the reversal of the bubble became pessimistic in absolute terms, but still optimistic relatively to the robotic trader. Figure 8i shows the sign of the robotic trades.²⁰ We observe him to take the short position until period 1014.

The construction of the market is that the agents forecast two-period ahead, and their information set spans until the previous period. This means that they form their forecast of $p_{1010}$, i.e. the peak of the bubble, based on the friends’ behavior until period 1009, which roughly corresponds to the moment when the price (following the previous crisis) surpasses the fundamental level and the GA agents finally become relatively more optimistic than the robotic trader and start to buy the asset. Furthermore, the peer effect is based on an index with a non-trivial memory (of 5 periods). We observe that the agents’ mood indices becomes positive only around the moment of the bubble burst (Fig. 8g), that is the agents acquire reputation of full optimism when the market already crashes or is about to crash. This lag is apparent in Fig. 8h, which shows for every GA agents the mood index averaged between her friends she observes at period t, that is averaged over friends and over periods $t-6$ until $t-1$ , which she uses to predict the next price $t+1$. The GA agents can trade quite efficiently, but their reputation is ‘sticky’ and hence reflects the past, not the contemporary market conditions. A contrarian attitude is therefore natural.

To what extent is this driven by the robotic trader? Because the robotic trader has such a firm belief about the next price, the GA agents are likely to take similar (long or short) positions once the market is far from the fundamental: their individual price forecasts remain heterogeneous, but well coordinated (below or above the fundamental). On the other hand, without the robotic trader the GA agents would be more likely to trade in a more diversified fashion (some would buy, some would sell), and on average their reputation could be less ‘sticky’. Nevertheless, agents who have many friends would still likely observe ‘sticky’ mood [notice the difference between individual mood indices (Fig. 8g) and the observed ones (Fig. 8h)]. Furthermore, even without the robotic trader the lag of the index mood is apparent (especially after the market reversals).²¹ It means that unless the price oscillations can take a relatively long period, the agents will simply never have time to acquire a positive (negative) mood index during the bubble (crisis) build-ups.²² I leave it for future inquiries to study the robustness of this phenomenon in alternative market structures.

Observation 7

Contrarian strategies add momentum to the trend reversal around the tipping points of bubbles and crises. Through interaction with agents’ strong trend following behavior, this causes price oscillations with larger amplitude.

As discussed for the markets without a network, the reason for price trend reversals is that once the price diverges sufficiently away from the fundamental, the robotic trader halts its current trend. This causes dis-coordination and a tipping point: agents start to experiment with their heuristics, while the robotic trader insists on pushing the price back to the fundamental. Therefore, the prices turn around and agents quickly pick the new trend up, causing a new phase of the bubble-crisis cycle.

The contrarian strategies work in the same direction. For example, during a bubble build-up the agents slowly become optimistic. As discussed, this happens not fast enough to make the agents learn herding strategies, since the agents become fully optimistic close to the tipping point of the bubble (in terms of the $Mood_{i,t}$ variable). Thus their heuristics remain strictly contrarian, but the optimism build-up around the tipping point plays a crucial role in the bubble crash.

Once the robotic trader stops the price growth, we see in the price expectation heuristic (13) that the price trend becomes unimportant, while the negative $\gamma$ trust index, together with the newly established optimism among friends, means that the agents are likely to forecast lower price (observed optimism times the contrarian attitude yields an additional negative element in the pricing forecast heuristic). Given the positive feedback between the predictions and price, the initial price drop is therefore more severe relatively to the case without a network, in which no such contrarian attitude can emerge.

One can observe this by comparing the first price increase after the end of the burst: $p_{1019}{-}p_{1018} \approx 7.07$ for the sample fully connected market (Fig. 8a) is much larger than $p_{1016}{-}p_{1015} \approx 1.42$ for the sample no network market (Fig. 4a), which also results with a sharper increase of the corresponding price forecasts. The increased (in absolute terms) initial trend after bubbles burst (or crises finish) makes the agents predict larger price change, which reinforces the size of the trend. This can be mitigated by the robotic trader only once the price deviation is sufficiently larger in comparison with the market without a network, which makes the realized oscillations wider.

Notice that this further confirms the discussed intuition of the contrarian strategies. Agents around the peak of the bubble (crisis) are considered optimistic (pessimistic). They also use contrarian strategies, which reinforces the market reversal (in contrast to the observed mood of the friends), and makes the contrarian attitude self-fulfilling.

The general conclusion about the network effect on the market is therefore only partially in line with the popular belief. The GA agents, if endowed with additional information about friends’ behavior, learn contrarian beliefs. This actually implies larger bubbles and crashes, while not disturbing the high level of forecasting coordination—the two phenomena that some economists would in fact associate with herding (Shiller and Pound 1989).

Finding 2

In markets with a relatively fast bubble-crisis cycle, the history of agents’ trading decisions lags behind the contemporary market conditions. As a result, agents have an incentive to learn contrarian strategies. This has a negative impact on price stability. Because the agents’ reputation catches up with the market conditions just before the tipping point, the contrarian strategies imply that the turning points of the price cycle generates stronger price reversal. This larger initial price trend is in turn reinforced by the agents’ trend extrapolation behavior, which makes it more difficult for the robotic trader to stabilize the market.

4.3 Learning in Asymmetric Networks

Observation 8

An asymmetric position in the network has no direct effect on herding. Instead, agents with fewer friends experiment with relatively weaker contrarian strategies.

Intuition suggests that agents with a unique position in a network—like a center of a star network—should receive more attention and thus play an important role in coordination. However, my model confirms this reasoning only partially. Consider three networks: two connected clusters, core-periphery and star. In all of them, one can distinguish central and non-central agents with interesting asymmetric positions. In the two connected clusters, agents 1 and 3 belong to the same cluster, but agent 3 also links to the second cluster (see Fig. 1d). In the core-periphery network, a reverse case holds: agent 1 lies in the core and links to a periphery agent, while agent 3 is such a periphery agent (see Fig. 1e). The most extreme is the situation of the star network, where agent 1 is the hub of the star, while agent 3 is a typical edge of the star (see Fig. 1f).

Fig. 9

Monte Carlo study (1000 markets) of two connected clusters, core-periphery and star networks: time evolution of trust index $\gamma$ of specified agents. Median is represented by a red line and $95\,\%$ CI are represented by blue lines. (Color figure online)

Figure 9 shows MC results for the trust given by these agents across time. Again the $95\,\%$ CI are wide (demonstrating erratic behavior of these networks), but there is a clear pattern in terms of the median agent across the simulations. Regardless of the network, the central agent is always likely to use strict contrarian strategies, just as was the case of the agents from regular networks. Non-central agents are also contrarian. However, their median trust index can be significantly larger: instead of a low $\gamma \approx -0.9$ for the case of the fully connected network, the median non-central agent 3 in star (core-periphery) uses a weaker contrarian $\gamma \approx -0.6$ ($\gamma \approx -0.75$). This is not the case for the non-central agent 1 in the two connected clusters network, who uses a strong contrarian strategy with $\gamma \approx -0.9$. This indicates that a more central position on its own does not guarantee higher levels of received trust.

What we observe instead is agents experimenting with relatively higher trust levels if they have fewer friends. Specifically, the edge agents in the star network, and the periphery agents in the core-periphery network, have only one friend; and their median trust level is visibly higher (even if still negative) in contrast to other agents.²³ This result will be more apparent in the large networks, and has a natural intuition.

In the setup of my model, the agents cannot distinguish between their friends and look only at the average sign of their friends’ mood. On the other hand, the agents remain heterogeneous (see the previous discussion): even if the agents typically have similar price forecasts, they can have quite different realized moods over time (in particular when the price is close to the fundamental, see Lemma 1). It means that a ‘popular’ agent (with many friends) will have to wait longer to observe ‘sharp’ consensus among her friends, whereas ‘unpopular’ agents are more likely to observe outliers, which can be useful around the tipping points. For instance, consider the sample fully connected network (Fig. 8) and compare the sharply changing individual mood index (Fig. 8g) with much smoother observed friends’ mood index (that is, the average mood index of five friends, Fig. 8h). Therefore the agents with fewer friends are typically contrarian, but are also willing to experiment more when bubbles and crises regimes brake down.

A clear suggestion for future studies follows. First, the above reasoning does not have to hold when the agents can distinguish between their friends.²⁴ Second, this is an important insight when studying models with endogenous network formation. Both issues demand further theoretical and experimental work.

Observation 9

Overall coordination is the same regardless the shape of the network, including whether it is symmetric or not.

Figure 10 presents the MC results for the coordination and stability of the three asymmetric networks: the two connected clusters, the core-periphery and the star, namely the $95\,\%$ CI and median dis-coordination over time (top panel) and SD of the long-run prices over 1000 markets for each network. There is a clear pattern visible. No difference emerges in terms of coordination (which also looks like the coordination in any market with a symmetric network).²⁵ However, across the three networks the star market is likely to experience higher long-run SD of prices, while the two other networks are much more similar to each other. Furthermore, the star network never stays in the stable attractor, which can rarely occur in the case of other asymmetric networks. This indicates that the star network generates unique dynamics in comparison with all the other non-empty networks, which yield more comparable results. We will observe a similar pattern in the large networks.

Fig. 10

Monte Carlo study (1000 markets) of two connected clusters, core-periphery and star networks: time evolution of dis-coordination measure (14) (median represented by a red line and $95\,\%$ CI represented by blue lines); distribution of the long-run standard deviation. (Color figure online)

Finding 3

In asymmetric networks, relatively less contrarian behavior can emerge. This is driven by the fact that agents with fewer links find it easier or more useful to experiment with relatively higher trust. With the exception of the unique dynamics of the star network, this does not influence the overall market stability or coordination.

4.4 Profits and Uutility

Under RE, the expected profits are equal to zero.²⁶ The intuition of this result follows from the arbitrage argument: the fundamental price $p^f$ balances the asset revenue (the dividend y and the resale gain $p_{t+1}$) and the opportunity cost ($Rp_t$). Formally, under RE if $p^e_{i,+1} = \mathbb {E}\{p_{t+1}\} = p^f$ for every period t and disregarding the price shock $\eta _t$, the asset return (1) becomes

$$\begin{aligned} \mathbb {E}\{\rho _{t+1}\} = p^f + y - Rp^f = y - rp^f = 0, \end{aligned}$$

(20)

where the last equality holds because $p^f=y/r$. This further implies that the individual demands (3) are also equal to zero, since $z_{i,t} = \rho ^e_{i,t+1}/(a\sigma _a ^2)$.

Fig. 11

Monte Carlo study (1000 markets) with circle, fully connected and star networks: time evolution of average profit of the GA agents and the robotic trader. Median is represented by a red line and $95\,\%$ CI are represented by blue lines. (Color figure online)

The GA model predicts price oscillations and forecasting heterogeneity. This, in contrast to RE, implies non-trivial trades and asset returns. Notice that furthermore the GA agents are maximizing a trade-off between the asset return and the risk. It is therefore important to understand the distribution of profits and utilities in the model.

Figure 11 shows the MC distribution of average profits for three networks, circle, fully connected and star, for the GA agents (top panel) and the robotic trader (bottom panel). Average profit of agent i is defined as

$$\begin{aligned} \bar{\pi }_{i,t} = \frac{1}{t}\sum _{s=1}^t \rho _{t+1}z_{i,t}. \end{aligned}$$

(21)

Because the robotic trader has a constant price expectation and the market cycle is symmetric, his average profit quickly converges to zero, with narrow $95\,\%$ CI. On the other hand, GA agents seem to be trading quite poorly: regardless of the network, their average profit quickly becomes negative (including the upper bound of $95\,\%$ CI).²⁷

Fig. 12

Monte Carlo study (1000 markets) with circle, fully connected and star networks: time evolution of average utility of the GA agents and the robotic trader. Median is represented by a red line and $95\,\%$ CI are represented by blue lines. (Color figure online)

This does not mean that the GA agents are irrational, however. Their trading is dictated by aversion towards risk, and the pricing equation (9) was defined under the assumption that the agents have myopic mean-variance preferences. Therefore, one can use the same utility, but based on the robotic trader’s decisions, as a reference point for the performance and learning efficiency of the GA agents. Specifically, I focus on the average realized utility

$$\begin{aligned} \bar{U}_{i,t} = \frac{1}{t}\sum _{s=1}^t \rho _{t+1}z_{i,t} - 0.5 z_{i,t}^2. \end{aligned}$$

(22)

Figure 12 shows that the GA agents, regardless of the network, obtain much higher utility than the robotic trader. In fact, after around 1000 period the lower bound of the $95\,\%$ CI of their average utility is higher than the median average utility of the robotic trader.

This observation has a simple interpretation. Because of his constant price expectations, the robotic trader has on average zero profit, but also takes extremely risky positions around the market reversals, i.e. when he also becomes the most active. GA agents forfeit part of the profit and hence increase their utility by avoiding excess risk. This is particularly clear for the case without networks. Figure 13 shows the evolution of average profits and utilities in the sample unstable market with no network, which was presented before in Figs. 2c and 4. We observe that initially the prices are stable, which corresponds to inactive robotic trader and individual trades and profits close to zero. However, once the market switches to the unstable attractor, the robotic trader tries to push the price back to the fundamental, while the GA agents follow price trends. As a result, the relative average profit of the robotic trader increases at the expense of his relative utility.

Finding 4

GA agents, in comparison with the robotic trader, obtain lower economic profits, but also higher utility. The reason is that instead of predicting the fundamental price, they follow the market cycle and thus avoid substantial risk.

Fig. 13

Sample unstable market without network: realized average profit and realized average utility of robotic trader (black line) and GA agents (green lines), a Profit. b Utility

Fig. 14

Standard deviation of price in periods 101–25,000 for different network architecture and size, a Regular networks. b Non-regular networks

5 Large Networks

In this section I present the results for the sample simulations of the large network as a function of their size (with 50–1000 agents). I first show the aggregate dynamics and then discuss individual learning. One of the most important findings of this analysis is that the large networks (even with hundreds of agents) generate similar market dynamics as the small ones, which suggests that the specific network architecture or size is less significant than its existence in the first place.

5.1 Impact of the Network on Price Stability

Observation 10

Network size has a stabilizing effect on the prices only for relatively small networks and past a certain threshold plays no significant role.

Figure 14 shows the long-run price SD of regular and non-regular networks (see Sect. 3 for definition). In comparison with the networks of six agents, large regular networks are marginally more stable (with the markets without a network being the sole exception). For example, the star network of 50 agents has price SD equal to $SD_p = 15.657$ (Fig. 14a), which is below the price SD for the bulk of star networks with 6 agents (see bottom right panel on Fig. 10). Above 100 agents, however, the network size hardly has an effect on price volatility.

Observation 11

Specific network architecture (including its density) plays little role in price volatility, and is important only for extreme cases, namely no network markets and star networks.

Another interesting observation from Fig. 14 is that, with the exception of markets without a network, the long run price SD is similar between the network structures (both regular and non-regular), as it is between networks of the same structure and different size (in fact it is difficult to distinguish individual networks in this Figure, since the relevant lines almost overlap). In all these cases, the long-run price SD falls into a narrow interval $SD_p \in [14.5,15.5]$, despite the networks having different density and other relevant measures. We will see below that the reason for this is that the agents from different networks learn comparable behavior, especially in terms of price trend extrapolation.

As mentioned above, the exception is the no network case. It has long-run price SD $SD_p \approx 8$, half in magnitude of other networks, which is consistent with the findings for the small networks. This shows that the contrarian behavior, absent in the case without a network, increases an initial momentum of the price trends, implying larger oscillations. The GA model without a network is nevertheless unstable in comparison with the RE benchmark, according to which $SD_p = 0.1 \ll 6$.

Finding 5

Specific network size and architecture has a negligible effect on price stability for large enough networks. The exception is the case without a network, which is more stable than markets with any type of a network.

5.2 Impact of the Network on Individual Behavior

Observation 12

Regardless of the network size, agents focus on strong trend extrapolation rules. They continue to experiment with the specific trend coefficient and this learning does not settle down.

In almost all considered networks (both in terms of architecture and size), agents on average use high trend extrapolation coefficients with $\beta \approx 0.85$ (where the specific value does not seem to differ substantially between networks). Figure 15 gives the average $\beta$ for all networks and network sizes. Furthermore, there is no convergence. The SD of $\beta$ is close to 0.55 in all networks, consistent with the small networks outcomes: agents typically use very high $\beta$, but during market reversals they experiment with lower values of the trend extrapolation coefficient. A noticeable exception are agents from the no network markets of small size (up to 100 agents), who do focus on higher $\beta \approx 1$. It means that in the positive feedback type markets, specific network structure has little effect on the emerging trend following behavior.

Fig. 15

Average used trend extrapolation coefficient $\beta$ in periods 101–25,000 for different network architecture and size. a Regular networks. b Non-regular networks

Observation 13

Agents in general use strong contrarian strategies, regardless of the specific network architecture or size. However, the less friends an agent has, the more she is willing to experiment with relatively higher trust levels.

Across all networks, the average trust given by agents is low, with (roughly) $\gamma \in [-0.9,-0.7]$. Nevertheless, there is some variability across time and between agents, as seen in relatively high standard deviations of the relevant trust measures. Furthermore, the number of connected friends has a clear and negative effect on the trust level. The most striking illustration of this effect can be seen in the case of star networks, were the central agent (regardless of the actual network size) on average uses $\gamma \approx -0.8$, but the other agents prefer $\gamma \approx -0.3$, which is close to a neutral strategy (see Fig. 16a).

Fig. 16

Star and non-regular networks with 1000 agents sample simulations: average chosen trust index $\gamma$ of agents with different number of friends, a Star networks. b Non-regular networks (1000 agents)

In all other networks with a diversified number of friends per agent, more popular agents have lower average trust, though this effect becomes negligible once agents have more than a dozen of friends. Figure 17 shows the average trust index $\gamma$ for the sample non-regular networks, as a function of network size and agent’s number of friends. We observe that the effect of network size is small, but the number of friends is important. Furthermore, Fig. 16b shows the average $\gamma$ as a function of the number of friends for the non-regular networks with 1000 agents. The clear pattern is that the more popular agents have lower average trust index, with a decreasing marginal effect of the number of friends. Another interesting observation is that there is little difference between the networks. Indeed, the lines describing this effect for different network architectures almost coincide on one hyperbola, and further MC would be likely to show that the relevant distributions of the trust index are indistinguishable.

Fig. 17

Sample simulations of non-regular networks: average chosen trust index $\gamma$ of agents for different network size and number of friends, a Random (4). b Random (16). c Rewired (4, 0.01). d Rewired (4, 0.1). e Rewired (16, 0.01). f Rewired (16, 0.1)

I argue that the reason for this outcome is in line with Finding 3. Namely, as discussed in the previous section, the more friends an agent has, the smoother over time becomes the average friends mood she observes. As a result, it more closely follows the market cycle with a substantial lag. At any point, the mood index of many agents is more likely to represent the overall market mood in the past, before the latest market reversal. Therefore, the agent with more friends has a higher incentive to remain conservative, unwilling to experiment with strong contrarian attitude.

Finding 6

Agents tend to use strong price trend extrapolation and contrarian heuristics. They experiment with the specific heuristic parametrization after the market reversals. Furthermore, agents with fewer friends are more likely to experiment with trust level, since they are more likely to observe outlier behavior.

To sum up, embedding the agents in a network has a strong effect on the aggregate outcomes: non-empty networks generate stronger price oscillations. However, specific network architecture is less important, because the emerging learning is similar between the networks.

6 Conclusions

In this paper I investigate a financial market, in which agents need to predict the price of an asset two-periods ahead. They are placed in a fixed information network, and use a simple general forecasting heuristic, which contains adaptive and trend extrapolation expectations, and an additional term of (dis-)trust towards friends’ past trading decisions. The agents independently optimize the specification of their heuristics by Genetic Algorithms. This gives a model of endogenous learning of price forecasting and herding/contrarian behavior. My main findings are: (i) networks destabilize the markets; (ii) the Genetic Algorithm agents learn to extrapolate price trends; and (iii) they learn to use contrarian strategies, because the observed pessimism/optimism of their friends lags behind the cyclical market dynamics.

Information networks play a crucial role for real financial investors, but it is not clear how they affect market stability and efficiency. From the perspective of the Rational Expectations framework, information flows can help the agents to converge to the fundamental equilibrium, but if the agents have no private information, networks should play no role in the equilibrium itself. On the other hand, many behavioral economists, in line with the popular opinion, identify networks as one of the reasons for herding and ‘animal spirits’, which enables the agents to coordinate on non-fundamental, self-reinforcing price oscillations. Here herding is understood as following the opinion of friends (or maybe the general market opinion) instead of ones private beliefs or information. Empirical investigations add a twist to the theoretical puzzle: market data gives no clear indication whether herding is a popular strategy, while experiments identify contrarian strategies as a more common behavioral pattern.

In order to shed some light on this puzzle, I design an agent based network model for a simple market of financial asset. Every agent can independently learn whether to follow the observed price trend and in addition, whether to trust the past decisions of her friends (increase or decrease price forecast, if her friends were optimistic). I investigate small networks of six agents to obtain basic understanding of such learning dynamics, and hence I study networks of fifty to one thousand agents with architectures ranging from regular through random to small world properties.

The main outcomes of the model are the following. First, information networks destabilize the market. Without information flows, the model exhibits two types of attractors, the fundamental solution and erratic price oscillations around the fundamental. Once the agents are positioned in an information network of any architecture or size, the stable fundamental steady state attractor disappears and market repeatedly over- and under-prices the asset in a smooth cycle of bubbles and crashes. Second, agents learn to extrapolate the price trend regardless of the network, which makes their price forecasts well coordinated. Third, despite the large degree of coordination in terms of realized price forecasts, agents learn contrarian heuristics. This is because the mood of friends, which the agents observe, is ‘sticky’: it represents past decisions that were made during a different part of the market cycle, and so are different from what is rational in the present. For example, after a bubble crashes, agents should expect the price to decrease, but they remember their friends being optimistic just before the market collapsed. Fourth, the Genetic Algorithms agents (in comparison with the robotic trader) take less risky trading position, which implies lower profit, but higher realized utility. Fifth, the specific network architecture plays little role in market volatility (past network size of mere hundred agents) or emerging learning. The heuristics do not settle, since during market reversals the agents experiment with their specification. These dynamics resemble real markets: during bubbles and crashes financial agents just follow the current trend, but ‘panic’ around bubble/crash tipping points. Finally, agents with fewer links experiment with relatively higher trust during market reversals.

The results of my model offer a good interpretation to many empirical and experimental findings. First, the agents learn contrarian behavior, in line with the findings from experiments. Second, the agents remain well coordinated despite the contrarian attitude, which explains why indirect measures for market data may (mistakenly) point towards herding. It also shows that the popular belief about herding (that it is a driving factor of price oscillations) may be wrong: coordination occurs despite agents’ lack of trust towards each other, since they converge to similar forecasting rules of thumb.

My investigation is based on the selection of two crucial elements: asset market and networks. These choices are independent from the Genetic-Algorithms-based learning itself. In principle, my model can be used for other financial regimes or information networks. Indeed, many of my results should be tested in other economic environments. For example, contrarian behavior emerges because the agents are not able to acquire reputation of optimism (pessimism) before the market bubble crashes (crisis ends). This relies on the fact that the financial market, which I have used, allows for relatively fast price oscillations. Furthermore, the outcomes of my simulations seem to be robust against specification of some key parameters of the model (including the allowed trust), nevertheless further experimental work could fine-tune the model or show its limitations. The model should therefore be thought of as a benchmark for future theoretical and laboratory inquiries.

Appendices

Appendix 1: Rational Solution

Proposition 1

The network $\mathbf {I}$ has no effect on the fundamental RE solution.

Proof

Under RE, at every period t the agents have homogenous price expectations, and by extension homogenous demand schedules (3) and realized demands. The agents know that and so can infer the realized demands (and the mood indices) of all agents in the economy. Since there is no private information, the information set of every agent is the same and publicly known, hence the network cannot provide any additional information.

Proposition 2

Under Rational Expectations, the fundamental price (6) defined as $p^f=y/r$ is the unique stationary steady state such that the predictions are constant over time (in expected terms) and model consistent, namely $p^e_{i,t+1} = E_t\{p_{t+1}\} = E_{t-1}\{p_t\}$ for every period t.

Proof

This result is well known for the baseline version of the model without robotic trader, see e.g. Blanchard and Watson (1982). For the version of the model with robotic trader, the proposition follows trivially from the fact that the robotic trader in practice always predicts the fundamental price (6). $\square$

Appendix 2: Proof of Lemma 1

Proof

Recall that the optimal demand of an agent i is

$$\begin{aligned} z_{i,t} = \frac{p^e_{i,t+1} + y}{a\sigma _a^2} - \frac{R}{a\sigma _a^2}p_t. \end{aligned}$$

(23)

In the same manner, demand of the robotic trader is simply

$$\begin{aligned} z_{ROBO,t} = \frac{p^f+ y}{a\sigma _a^2} - \frac{R}{a\sigma _a^2}p_t. \end{aligned}$$

(24)

Finally, the realized price setting the price shock to zero is

$$\begin{aligned} p_t = \frac{\hat{p}^e_{t+1} + y}{R} = \frac{(1-n_t)\bar{p}^e_{t+1}+n_tp^f + y}{R}. \end{aligned}$$

(25)

Substituting (25) into (23) we obtain

$$\begin{aligned} z_{i,t}&= \frac{p^e_{i,t+1} + y}{a\sigma _a^2} - \frac{R}{a\sigma _a^2}\frac{\hat{p}^e_{t+1} + y}{R}\nonumber \\&= \frac{p^e_{i,t+1} - \hat{p}^e_{t+1}}{a\sigma _a^2}. \end{aligned}$$

(26)

It follows that the demand of agent i at period $t\, z_{i,t}$ is positive only if the price forecast for period $t+1$ of that agent is larger than the average (including the robotic trader) forecast of $p_{t+1}$, namely if $p^e_{i,t+1} > \hat{p}^e_{t+1}$. By extension, the robotic trader will also buy the asset if his prediction (which is the fundamental value) is larger than the average market prediction, that is if the average market prediction is below the fundamental. $\square$

Appendix 3: Equivalence of Forecasting and Trading Peer Bias

In the model, I specified the peer effect and the corresponding herding/contrarian strategies as the bias to the price forecast. In this appendix I will show that this can be reinterpreted as a demand bias. To be specific, following AHM15 the agents in my model forecast the prices with adaptive/trend extrapolation rule (optimized with GA procedure) and hence trade optimally; however, they can also change their price forecast if they observe their friends to be optimistic/pessimistic, which is measured by the trust index $\gamma \in [-1,1]$ in (13). I defined herding (contrarian) behavior as $\gamma >0 (\gamma <0)$.

However, one may think that herding or contrarian behavior has nothing to do with price forecasting itself, but rather reflects an additional (possibly irrational) bias to the demand. In other words, the agent has a price forecast, which in our case is generated by the GA optimized heuristic, but in principle could follow any other model, ranging from fundamental to simple adaptive or naive expectations. The agent hence uses this forecast to compute the optimal demand and only then adds or subtracts an additional quantity to the demand if she follows herding or contrarian strategy.

To see that these two interpretations are equivalent, recall the forecasting heuristic (13). Substituting it into the optimal demand schedule (3) yields

$$\begin{aligned} z_{i,t}&= \frac{p^{e,Peer}_{i,t+1} + y -Rp_t}{a\sigma _a^2}\nonumber \\&= \frac{\alpha p_{t-1} + (1-\alpha ) p^e_{i,t-1} + \beta (p_{t-1} - p_{t-2}) + \gamma \Gamma \text{ Peer }_{i,t-1} + y -Rp_t}{a\sigma _a^2}\nonumber \\&\equiv \frac{p^{e,NoPeer}_{i,t+1} + y -Rp_t}{a\sigma _a^2} + \gamma \tilde{\Gamma } \text{ Peer }_{i,t-1}, \end{aligned}$$

(27)

where $\tilde{\Gamma } = \Gamma /a\sigma _a^2$ is a constant measuring agents’ sensitivity to the peer effect, $\gamma \in [-1,1]$ is the trust index as in the main body of the paper and

$$\begin{aligned} p^{e,NoPeer}_{i,t+1} = \alpha p_{t-1} + (1-\alpha ) p^e_{i,t-1} + \beta (p_{t-1} - p_{t-2}) \end{aligned}$$

(28)

is the original adaptive/trend extrapolation forecasting heuristic from AHM15.

We can see that the demand written as (27) exemplifies the above mentioned interpretation: agents forecast the next price with the typical heuristic, which is agnostic to the friends’ behavior; but then the agents have an additional demand bias depending on the trust index $\gamma$. Consider now a GA model in which the agents use (28) to obtain price forecasts $p^e_{i,t+1}$ and hence use the herding/contrarian biased demand (27). Next, they update $\alpha$ and $\beta$ the parameters of the forecasting heuristic (28) and the bias $\gamma$ with the GA procedure, where the performance of a heuristic specification is measured in terms of logit transformation of the hypothetical utility (2). To be specific,

$$\begin{aligned} V_{i,h,t} = U_{i,h,t+1} + z_{i,t}\left( p^{e,NoPeer}_{i,h,t+1}\right) \left( p_{t+1} + y -Rp_{t} \right) - \frac{a}{2}\sigma _a^2 z_{i,t}\left( p^{e,NoPeer}_{i,h,t+1}\right) ^2. \end{aligned}$$

(29)

Now define the realized return on the asset as

$$\begin{aligned} \rho _{t+1} \equiv p_{t+1} + y - Rp_t. \end{aligned}$$

(30)

The demand function (27) with quantity bias is equivalent to the demand used in the paper (forecasting bias and no quantity bias), and so using (30) we can rewrite

$$\begin{aligned} V_{i,h,t} - U_{i,h,t+1}&= \frac{p^{e,Peer}_{i,h,t+1} + y -Rp_t}{a\sigma _a^2}\left( p_{t+1} + y -Rp_{t} \right) \nonumber \\&\quad - \frac{a\sigma _a^2 }{2}\left( \frac{p^{e,Peer}_{i,h,t+1} + y -Rp_t}{a\sigma _a^2}\right) ^2\nonumber \\&= \frac{(p^{e,Peer}_{i,h,t+1} - p_{t+1} + \rho _{t+1})\rho _{t+1}}{a\sigma _a^2} - \frac{(p^{e,Peer}_{i,h,t+1} - p_{t+1} + \rho _{t+1})^2}{a\sigma _a^2}\nonumber \\&= \frac{(p^{e,Peer}_{i,h,t+1} - p_{t+1})\rho _{t+1} + \rho _{t+1}^2}{a\sigma _a^2}\nonumber \\&\quad - \frac{(p^{e,Peer}_{i,h,t+1} - p_{t+1})^2 + 2(p^{e,Peer}_{i,h,t+1} - p_{t+1})\rho _{t+1} + \rho _{t+1}^2}{2a\sigma _a^2}\nonumber \\&= \frac{\rho _{t+1}^2}{2a\sigma _a^2} - \frac{(p^{e,Peer}_{i,h,t+1} - p_{t+1})^2}{2a\sigma _a^2}. \end{aligned}$$

(31)

It follows that the performance of the quantity-biased demand (27) is equal to a constant term minus MSE of the forecast-biased heuristics (13). Therefore, in practice the two models: in which the peer effect bias appears in the price forecast or directly in the demand, are equivalent, if one properly chooses the sensitivity parametrization of the logit transformation.

Appendix 4: Definition of Network Properties

Consider I agents, who are placed within an unweighted, symmetric and a-transitive network of friends $\mathbf {I}$. First recall that degree between two agents is defined as the shortest path (sequence of linked agents) between them. The following measures are commonly used to describe the architecture of the network $\mathbf {I}$:

• Number of clusters I define cluster as a subset of the network such that (1) all the agents in the cluster are pairwise connected (there exists a path of a finite degree between them) and (2) none of the agent is connected with any agent that does not belong to the cluster. In some of the analyzed networks, the agents form ‘non-trivial’ subsets such that there is no link between them. On the other hand, these agents will still interact indirectly, through the market clearing price. Diameter Also denoted as the characteristic degree or the longest path, simply measures what is the longest path between nodes in the network.²⁸

• Closeness This measure is typically set as the average degree: how far away agents are on average. The drawback of the average path length is that it cannot properly cope with networks of disconnected clusters, and hence I will follow suggestion of Newman (2003) and use the closeness measure instead. First recall that the network is anti-reflexive, or that we disregard whether an agent is linked with herself or not. Instead, we are interested in what is the typical distance between the agent and the remaining $I-1$ agents. Thus define

  $$\begin{aligned} Cl = \frac{1}{0.5I(I-1)} \sum _{i=1}^{I-1} \sum _{j=i+1}^I d^{-1}_{ij}, \end{aligned}$$

  (32)

  where $d_{ij}^{-1}$ is the inverse of the shortest path length (degree) between agents i and j, or 0 if these two agents are not connected. The closeness measure Cl is an index with a straightforward interpretation: if all the agents are connected (disconnected), ${Cl}=1\, ({Cl}=0)$.

• Density Denote the number of links between the agents as E. Density is defined as

  $$\begin{aligned} DE = \frac{E}{0.5I(I-1)}, \end{aligned}$$

  (33)

  which is simply the ratio of realized to potential links: how dense the network is.

• Transitivity Often described as ‘cliquishness’ or clustering, shows whether the nodes in the network form triangles (‘cliques’): friends of my friends are also friends of mine. Among many formal definitions of this measure, I follow Watts and Strogatz (1998) and specify transitivity as computationally efficient index of the form

  $$\begin{aligned} Tr = \frac{1}{I} \sum _{i=1}^I \frac{\text{ number } \text{ of } \text{ triangles } \text{ connected } \text{ to } \text{ vertex } i}{\text{ number } \text{ of } \text{ triples } \text{ centered } \text{ on } \text{ vertex } i}. \end{aligned}$$

  (34)

  If the agents are always (never) connected with the friends of their friends, ${Tr} = 1\, ({Tr} = 0)$.²⁹ Notice that (34) is a local, not a global measure. It shows how close are friends of friends, but not whether the network can be divided into significantly differentiated clusters of ‘sub-networks’. In order to avoid confusion I decided to adopt the name ‘transitivity’ instead of the widely used ‘clustering’.

Appendix 5: Large Networks Characteristics

Fig. 18

Realized random (4) networks, a 50 agents. b 100 agents. c 250 agents. d 500 agents. e 1000 agents. f Network properties

Fig. 19

Realized random (16) networks, a 50 agents. b 100 agents. c 250 agents. d 500 agents. e 1000 agents. f Network properties

Fig. 20

Realized rewired (4, 0.01) networks, a 50 agents. b 100 agents. c 250 agents. d 500 agents. e 1000 agents. f Network properties

Fig. 21

Realized rewired (4, 0.1) networks, a 50 agents. b 100 agents. c 250 agents. d 500 agents. e 1000 agents. f Network properties

Fig. 22

Realized rewired (16, 0.01) networks, a 50 agents. b 100 agents. c 250 agents. d 500 agents. e 1000 agents. f Network properties

Fig. 23

Realized rewired (16, 0.1) networks, a 50 agents. b 100 agents. c 250 agents. d 500 agents. e 1000 agents. f Network properties