The Effect of a Credit Crunch on Equilibrium Market Structure

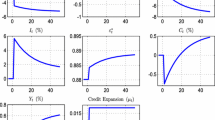
Abstract

This article examines the impact of a credit crunch on market structure. We construct and simulate a dynamic model of a duopolistic industry in which firms’ investments in capacity are constrained by the availability of credit. In such an industry, the dynamic interaction of credit limits and the competitive responses of firms turn out to be a powerful transmission mechanism by which the effects of shocks persist and are amplified. We show that a small, temporary shock to one firm’s capacity can lead to its market exit, even if it is equally productive as the remaining incumbent. Consequently, if a recession is accompanied by a credit crunch, its cleansing effect might lead to monopolization of markets and welfare losses.

Appendices

Appendices

1.1 Appendix 1: Single Period Profit Function

The mode of product market competition is capacity constraint quantity competition as in Besanko and Doraszelski (2004).

The inverse demand function $P(q_{i},q_{j})$ with P as market price and $q_{i}$ as quantity produced by firm i is given by

$$\begin{aligned} P(q_{i}, q_{j}) = \frac{a}{b} - \frac{q_{i}+q_{j}}{b}. \end{aligned}$$

Suppose that firm i and firm j’s capacities are given by $(\bar{q}_{i}, \bar{q}_{j})$ and that they compete in the product market by setting quantities $(q_{i}, q_{j})$.

The profit-maximization problem for firm i with $i,j \in (1,2), i\ne j$ is then given by

$$\begin{aligned} \max _{0<q_{i}<\bar{q}_{i}} P(q_{i}, q_{j})q_{i} \end{aligned}$$

This maximization problem for i and the symmetric problem for j lead to symmetric reaction functions which are known to have a unique Nash equilibrium (Vives 2001). The single period profit function of firm i in the Nash equilibrium of the capacity constrained quantity setting game is therefore

$$\begin{aligned} \pi _{i}(\bar{q}_{i}, \bar{q}_{j}) = P(q_{i}^{*}, q_{j}^{*}) q_{i}^{*}. \end{aligned}$$

The demand parameters used in the simulation are $a=40$ and $b=10$ and are thus the same as in Besanko and Doraszelski (2004). These parameters ensure that a company can have more capacity than the entire market demand (Table 7).

Table 7 Profit for firm 1

1.2 Appendix 2: Welfare Measures

To evaluate the implication of credit rationing on welfare, we calculate the expected consumer surplus and the expected producer surplus of the firms and of the bank.

Expected consumer surplus is calculated by integrating the demand function

$$\begin{aligned} {\textit{CS}}=E\left[ \int _{p_{Market}}^{p_{max}(s)}D(t)dt\right] \end{aligned}$$

where $D(\cdot )$ is the demand function, $p_{max}$ is the choke price and $p_{Market}$ is the prevailing market price. The expectation is taken with respect to the probability of the state in equilibrium.

As marginal costs are normalized to zero, expected producer surplus for every state is calculated as the sum of profits minus the financing costs:

$$\begin{aligned} PS=E\left[ \pi (\bar{q}_{1},\bar{q}_{2})+\pi (\bar{q}_{2},\bar{q}_{1})-d_{1}\cdot r-d_{2}\cdot r\right] . \end{aligned}$$

Expected bank surplus is the interest rate differential multiplied by the sum of debt:

$$\begin{aligned} {\textit{BS}}=E\left[ (r-r_{Bank})\cdot (d_{1}+d_{2})\right] . \end{aligned}$$

1.3 Appendix 3: Transitory Dynamics

Figure 8 shows the distribution after 10, 20, and 50 periods, starting from the initial value of zero capacities for both players. The distribution without credit rationing evolves directly towards symmetry and stays there forever. With credit rationing, first a symmetric configuration with equal capacity for both firms is reached and then the distribution becomes asymmetric. There is a large probability that one firm exits the market on the equilibrium path.

Fig. 8

Transitory Dynamics for $R=5\,\%$ (left) and $R=120\,\%$ (right). Note the capacity states of the two firms are depicted on the x and y axes. The probability of a state is displayed on the z-axis. On the left hand side, the evolution without credit rationing is pictured. On the right hand side, severe credit rationing prevails

1.4 Appendix 4: The Reinforcement Learning Algorithm

In this section, we outline the reinforcement learning algorithm used in this article. It is a variant of the algorithm described in Fershtman and Pakes (2012), to which the reader should refer for an extensive description.

Intuitively, the algorithm employed works as follows: a firm starts in state s and time t. For every potential action a and state s, the firm holds beliefs $W(a_{t}, s_{t})$ about the expected discounted sum of cash flows the action will yield. The firm then chooses the best action $a^{*}$ according to its beliefs and receives an instant payoff of $div(a^{*}_{t}, s_{t})$. The actions together with the law of motions of the state variables prescribe the next state. In the next state, the firm chooses again its best actions according to its belief $W(s_{t+1},a_{t+1})$. At this point, the algorithm can update the belief $W(s_{t},a^{*}_{t})$ because $div(a_{t}, s_{t})$ and $W(a^{*}_{t+1}, s_{t+1})$ are part of the discounted sum of cash flows originating in $s_{t}$ if $a_{t}$ is chosen. This procedure is repeated for ${\textit{Iter}}$ periods. The optimal actions $a_{t}$ in every period are stored in memory for use in the equilibrium testing procedure. To test for an equilibrium, the algorithm simulates a large number of periods with the stored optimal actions and checks whether the resulting beliefs $W^{test}(s,a)$ are the same as the beliefs W(s, a) which justified the actions in the first place.

A Tentative Example Assume that the player is in state s. Assume further that the player is under the impression that storing five more units of cash starting from state s gives—for the sake of illustration—a continuation value of 2000. This is better than the alternative of not doing so as he believes that this gives him a continuation value of 1500. He stores five more units and then finds out during the play that this decision only resulted in a continuation value of 1600. So he adjusts his expectation of storing five units in state s downwards to 1800. He does not adjust it downwards to 1600 as he cannot perfectly distinguish if this was just a matter of bad luck or truly the consequence of his actions. The benefit of this solution algorithm is that it can accommodate larger state spaces than the commonly used Pakes and McGuire (1994) algorithm. This algorithm only calculates policies on the recurrent state space and therefore ignores states which are never played in equilibrium. To give an idea, the state space in our calculation has about $6.25\times 10^{12}$ states. By selecting only those states relevant to the equilibrium, we only have to calculate equilibrium policies for around one million states, which is still large but manageable. The idea of calculating policies in an Ericson–Pakes model only for a sample of states is gaining prominence in numerical analysis, e.g., another algorithm using this method is Farias et al. (2012).

There are also several known problems for this kind of algorithms and numerical simulations of imperfect competition in general:

• 1. It is not guaranteed that an equilibrium exists. Even if one exists, the algorithm does not necessarily converge to it.

• 2. There might be multiple equilibria for reasonable parameter values. Besanko et al. (2009) offer a possible solution, however, we did not explore this issue up to now.

• 3. There might be more than one recurrent class associated with a set of policies.

• 4. It is not clear that the off-equilibrium beliefs are irrelevant for the equilibrium play. This is known as the problem of insufficient exploration.

In line with common practice, we check if the algorithm converges to the same equilibrium for different starting values. Although this appears to be the case, the above mentioned issues should be kept in mind.

Scheme of the Algorithm The algorithm requires the following inputs:

• A set of beliefs about the continuation value for every action in every state W(a, s)

• A counter h(a, s) for every state and action which measures how often the action was taken

• An arbitrary initial state $\breve{s}$ and an arbitrary initial action $\breve{a}$

• An instant return function $div(a_{t}, s_{t})$ for every action and state

• A function assigning the next period’s state $s'$ conditional on today’s state s and action a, $f(\cdot )$.

• Technical parameters: length of iteration (${\textit{Iter}}$), $\epsilon$ precision of the approximation, and the discount factor $\beta$

Algorithm for calculating EBE
1:	$s_{t}=\breve{s}$, $a_{t}=\breve{a}$ {Set initial state and initial actions }
2:	repeat
3:	t:=0 {Set index t for best simulation}
4:	while $\mathbf{t}\varvec{<}\varvec{=}\mathbf{Iter}$ {Begin learning process, last for T periods}
5:	$t=t+1$
6:	$s_{t+1}=f(a_{t}, s_{t})$ {Assign next state in $t+1$ according to the optimal actions and state in t }
7:	Load $W(\cdot , s_{t+1})$ for all $a_{t+1}$ from memory if already visited, otherwise assign initial values.
8:	$a^{*}_{t+1}=arg\max _{a_{t+1}}W(a_{t+1}, s_{t+1})$
	{Calculate the optimal action}
9:	$h(a^{*}_{t+1}, s_{t+1})=h(a, s)+1$
	{Increase the counter of the state $s_{t+1}$ and action $a_{t+1}$ by one. }
10:	$\hat{W}(a^{*}_{t}, s_{t})=div(a^{*}_{t}, s_{t},)+\beta W(a^{*}_{t+1}, s_{t+1})$
	{Calculate the continuation value in t according to the next period’s action and state. $W(a_{t+1}, s_{t+1})$ is a draw of the integral governing the continuation value. }
11:	$W(a^{*}_{t}, s_{t})=W(a^{*}_{t}, s_{t})+\frac{1}{h(a^{*}_{t+1}, s_{t+1})}[W( a^{*}_{t}, s_{t})-\hat{W}(a^{*}_{t}, s_{t})]$
	{save the updated belief $W( a^{*}_{t}, s_{t})$ to memory and store the optimal $a^{*}_{t}$ action}
12:	set $s_{t}=s_{t+1}$ and $a^{*}_{t}=a^{*}_{t+1}$
13:	end
14:	$t=0$
15:	while $\mathbf{t} \varvec{<=}\mathbf{T}${Begin test procedure}
16:	$s_{t+1}=f(a^{*}_{t}, s_{t})$ {Assign new state}
17:	Load $a_{t+1}^{*}$ and $W(a^{*}_{t+1}, s_{t+1},)$ from memory
18:	$h(a^{*}_{t+1}, s_{t+1})=h(a,s)+1$
	{Increase the counter of the state $s_{t+1}$ and action $a_{t+1}$ by one. }
19:	$\hat{W}^{test}(a^{*}_{t}, s_{t})=div(a^{*}_{t}, s_{t})+\beta W(a^{*}_{t+1}, s_{t+1})$
	{Calculate the continuation value in t according to the next period’s action and state. }
20:	$W^{test}( a^{*}_{t}, s_{t})=W^{test}(a^{*}_{t}, s_{t})+\frac{1}{a^{*}_{t+1}, h(s_{t+1})}[W^{test}(a^{*}_{t}, s_{t})-\hat{W}^{test}(a^{*}_{t}, s_{t})]$
	{Update the belief about the continuation value. Also do the procedure for the square of $W^{test}(.)$ to calculate the sampling variance.}
21:	store $W^{test}( a^{*}_{t}, s_{t})$
22:	set $s_{t}=s_{t+1}$ and $a^{*}_{t}=a^{*}_{t+1}$
23:	end
24:	$Bias(s, a)=\frac{W^{test}(a, s)}{W(a, s)}^2-Var(\frac{W^{test}(a, s)}{W(a, s)})$
	{Calculate for every state and action visited on the equilibrium path a bias statistic. The variance term is used to adjust for sampling variance. }
25:	$T=\left\| \sum _{a} \frac{h(a, s)}{\sum _{a} h(a, s)} Bias(a, s)||\right\| _{L^{2}_{P(s)}}$
	{The test statistic is then an $L^2$ norm in the bias term where P(s) is a measure for the fraction of time s is visited on the equilibrium path. The test statistic measures if the stored optimal action can replicate the continuation values. }
26:	until $T<\epsilon$ {The algorithm if T is below the required precision $\epsilon$. }