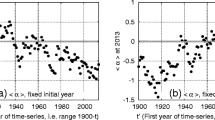
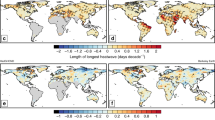
Abstract
The last decade has produced record-breaking heat waves in many parts of the world. At the same time, it was globally the warmest since sufficient measurements started in the 19th century. Here we show that, worldwide, the number of local record-breaking monthly temperature extremes is now on average five times larger than expected in a climate with no long-term warming. This implies that on average there is an 80 % chance that a new monthly heat record is due to climatic change. Large regional differences exist in the number of observed records. Summertime records, which are associated with prolonged heat waves, increased by more than a factor of ten in some continental regions including parts of Europe, Africa, southern Asia and Amazonia. Overall, these high record numbers are quantitatively consistent with those expected for the observed climatic warming trend with added stationary white noise. In addition, we find that the observed records cluster both in space and in time. Strong El Niño years see additional records superimposed on the expected long-term rise. Under a medium global warming scenario, by the 2040s we predict the number of monthly heat records globally to be more than 12 times as high as in a climate with no long-term warming.





Similar content being viewed by others
References
Ballerini R, Resnick SI (1987) Records in the presence of a linear trend. Adv Appl Probab 19:801–828
Barriopedro D, Fischer EM, Luterbacher J, Trigo RM, García-Herrera R (2011) The hot summer of 2010: redrawing the temperature record map of Europe. Science 332:220–224
Benestad RE (2003) How often can we expect a record event? Clim Res 25:3–13
Benestad RE (2004) Record-values, non-stationarity tests and extreme value distributions. Glob Planet Chang 44:11–26
Bunde A, Eichner JF, Kantelhardt JW, Havlin S (2005) Long-term memory: a natural mechanism for the clustering of extreme events and anomalous residual times in climate records. Phys Rev Lett 94(048701):1–4
Coumou D, Rahmstorf S (2012) A decade of weather extremes. Nat Clim Change. doi:10.1038/NCLIMATE1452
Della-Marta PM, Haylock MR, Luterbacher J, Wanner H (2007a) Doubled length of western European summer heat waves since 1880. J Geophys Res 112:1–11
Della-Marta PM, Haylock MR, Luterbacher J, Wanner H (2007b) Doubled length of western European summer heat waves since 1880. J Geoph Res 112:1–11
Diffenbaugh NS, Scherer M (2011) Observational and model evidence of global emergence of permanent, unprecedented heat in the 20th and 21st centuries. Clim Chang. doi:10.1007/s10584-10011-10112-y
Dole R, Hoerling M, Perlwitz J, Eischeid J, Pegion P, Zhang T, Quan X, Xu T, Murray D (2011) Was there a basis for anticipating the 2010 Russian heat wave? Geophys Res Lett 38:L06702
Founda D, Giannakopoulos C (2009) The exceptionally hot summer of 2007 in Athens, Greece—a typical summer in the future climate? Glob Planet Chang 67:227–236
Franke J, Wergen G, Krug J (2010) Records and sequences of records from random variables with a linear trend. J Stat Mech 10(P10013):1–21
Glick N (1978) Breaking records and breaking boards. Am Math Monthly 85:2–26
Hansen JE, Lebedeff S (1987) Global trends of measured surface air temperature. J Geophys Res 92:13345–13372. doi:10.1029/JD092iD11p13345
Hansen J, Ruedy R, Sato M, Lo K (2010) Global surface temperature change. Rev Geophys 48:29
Hansen J, Sato M, Ruedy R (2012) Perception of climate change. Proc Natl Acad Sci 109:14726–14727, E2415–E2423. doi:10.1073/pnas.1205276109
Hoerling M, Eischeid J, Quan X, Xu T (2007) Explaining the record US warmth of 2006. Geoph Res Lett 34:1–4
Hurrel JW, Deser C (2009) North Atlantic climate variability: the role of the North Atlantic oscillation. J Mar Syst 78:28–41
IPCC (2007) In: Solomon S (ed) The physical science basis, contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change, 2007. Cambridge Univ. Press, Cambridge
Kalkstein LS, Smoyer KE (1993) The impact of climate change on human health: some international implications. Experientia 49:969–979
Karoly D (2009) The recent bushfires and extreme heat wave in southeast Australia. Bull Aust Meteorol Oceanogr Soc 22:10–13
Krug J (2007) Records in a changing world. J Stat Mech 07:1–13
Kuglitsch FG, Toreti A, Xoplaki E, Della-Marta PM, Zerefos CS, Turkes M, Luterbacher J (2010) Heat wave changes in the eastern Mediterranean since 1960. Geophys Res Lett 37(L04802):1–5
Kysely J (2010) Recent severe heat waves in central Europe: how to view them in a long-term prospect? Int J Climatol 30:89–109
Levermann A, Born A (2007) Bistability of the Atlantic subpolar gyre in a coarse resolution climate model. Geophys Res Lett 34(L24605):1–6
Lukas R, Hayes SP, Wirtki K (1984) Equatorial sea level response during the 1982–1983 El Niño. J Geoph Res 89:10,425–410,430
Mann ME, Emanuel KA (2006) Atlantic hurricane trends linked to climate change. Eos 87:238–241
McCabe GJ, Wolock DM (2010) Long-term variability in Northern Hemisphere snow cover and associations with warmer winters. Clim Chang 99:141–153
Meehl GA, Tebaldi C (2004) More intense, more frequent, and longer lasting heat waves in the 21st century. Science 305:994–997
Meehl GA, Tebaldi C, Walton G, Easterling D, McDaniel L (2009) Relative increase of record high maximum temperatures compared to record low minimum temperatures in the U.S. Geophys Res Let 36:1–5
Mitchell J, Lowe J, Wood R, Vellinga M (2006) Extreme events due to human-induced climate change. Phil Trans Roy Soc 364:2117–2133
NOAA (2012) National Climatic Data Center (NCDC), state of the climate: global hazards for July 2012, http://www.ncdc.noaa.gov/sotc/national/2012/7
Otto FEL, Massey N, Oldenborgh GJ, Jones RG, Allen MR (2012) Reconciling two approaches to attribution of the 2010 Russian heat wave. Geoph Res Lett 39:1–5
Picaut J, Hackert E, Busalacchi AJ, Murtugudde R, Lagerloef GSE (2002) Mechanisms of the 1997–1998 El Niño–La Niña, as inferred from space-based observations. J Geoph Res 107:1–18
Rahmstorf S, Coumou D (2011) Increase of extreme events in a warming world. Proc Natl Acad Sci USA 108:17905–17909
Redner S, Petersen M (2006) On the role of global warming on the statistics of record-breaking temperatures. Phys Rev E 74:061114
Rybski D, Bunde A, Havlin S, von Storch H (2006) Long-term persistence in climate and the detection problem. Geophys Res Lett 33(L06718):1–4
Schär C, Luigi Vidale P, Lüthi D, Frei C, Häberli C, Liniger M, Appenzeller C (2004) The role of increasing temperature variability in European summer heatwaves. Nature 427:331–336
Smoyer KE (1998) A comparative analysis of heat waves and associated mortality in St. Louis, Missouri—1980 and 1995. Int J Biometeorol 42:44–50
Stott P, Stone D, Allen M (2004) Human contribution to the European heatwave of 2003. Nature 432:610–614
Su H, Neelin JD, Chou C (2001) Tropical teleconnection and local response to SST anomalies during the 1997–1998 El Nino. J Geophys Res 106:20,025–020,043
Tan J, Zheng Y, Song G, Kalkstein LS, Kalkstein AJ, Tang X (2006) Heat wave impacts on mortality in Shanghai, 1998 and 2003. Int J Biometeorol 51:193–200
Trenberth KE, Shea DJ (2006) Atlantic hurricanes and natural variability in 2005. Geophys Res Lett 33(L12704):1–4
Trewin B, Vermont H (2010) Changes in the frequency of record temperatures in Australia, 1957–2009. Aust Meteorol Oceanogr J 60:113–119
UNEP (2004) Impacts of summer 2003 heat wave in Europe. Environ Alert Bull 2:1–4
Wergen G, Krug J (2010) Record-breaking temperatures reveal a warming climate. EPL 92(30008):1–6. doi:10.1209/0295-5075/92/30008
WMO (2011a) Provisional statement on the status of the global climate, http://www.wmo.int/pages/mediacentre/press_releases/gcs_2011_en.html
WMO (2011b) ‘Weather extremes in a changing climate: hindsight on foresight’, World Meteorological Organization, report WMO-No 1075:1–20
Zhu X, Fraedrich K, Liu Z, Blender R (2010) A demonstration of long-term memory and climate predictability. J Clim 23:5021–5029
Zorita E, Stocker TF, Storch H (2008) How unusual is the recent series of warm years? Geoph Res Lett 35:1–6
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
SOM Fig. 1
Global-mean surface temperatures from NASA-GISS2 over the last 131 years for each month. Latitudinal distributions of zonal mean (b) trend and (c) standard deviation for periods 1880–2010, 1911–1940 and 1971–2010. (PDF 196 kb)
SOM Fig. 2
Global maps of serial correlation in non-linearly detrended monthly time-series for boreal summer (top) and austral summer (bottom). Over all continents and almost all ocean regions serial correlation is between −0.2 and 0.2. (PNG 488 kb)
SOM Fig. 3
Results of Monte Carlo experiments showing the deviation of the number of records compared to the iid-solution (1/n) for different levels of autocorrelation. The red dots indicate the mean and the red lines the 5–95 % confidence interval of each Monte Carlo experiment. For autocorrelations from −0.9 to +0.4 the number of records is statistically not significantly different from the iid solution. (PNG 106 kb)
SOM Fig. 4
Number of records in the non-linearly detrended time series, globally averaged (top) and averaged over continents (middle) and oceans (bottom). It shows that the iid-expected 1/n produces accurate results for the number of continental records over a 10 year period. Peaks in the detrended time series for individual years (i.e. 1983 & 1998) are discussed in the main text. (PNG 617 kb)
SOM Fig. 5
Latitudinal distributions of the zonal-mean record ratio X as observed (dashed) and estimated by Eq. 2 (solid), for boreal (a) winter, (b) spring, (c) summer, (d) autumn and (e) annual mean, using the 1971–2010 dataset. (PDF 84 kb)
Rights and permissions
About this article
Cite this article
Coumou, D., Robinson, A. & Rahmstorf, S. Global increase in record-breaking monthly-mean temperatures. Climatic Change 118, 771–782 (2013). https://doi.org/10.1007/s10584-012-0668-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-012-0668-1