Anisotropic Kepler and anisotropic two fixed centres problems

Abstract

In this paper we show that the anisotropic Kepler problem is dynamically equivalent to a system of two point masses which move in perpendicular lines (or planes) and interact according to Newton’s law of universal gravitation. Moreover, we prove that generalised version of anisotropic Kepler problem as well as anisotropic two centres problem are non-integrable. This was achieved thanks to investigation of differential Galois groups of variational equations along certain particular solutions. Properties of these groups yield very strong necessary integrability conditions.

1 Introduction

The anisotropic Kepler system was introduced by Gutzwiller (1973) for description of the motion of an electron in a crystal. The classical Hamiltonian of the system has the form

$$\begin{aligned} H= \frac{1}{2} \left( \mu _1 p_1^2 + \mu _2p_2^2+ \mu _3p_3^2\right) -\frac{1}{\sqrt{q_1^2+q_2^2+q_3^2}}, \end{aligned}$$

(1.1)

where $\mu _1, \mu _2$ and $\mu _3$ are non-zero parameters. Making canonical rescaling

$$\begin{aligned} (q_i,p_i) \longmapsto \left( \sqrt{\mu _i} q_i , \frac{p_i}{\sqrt{\mu _i}} \right) , \qquad i=1,2,3, \end{aligned}$$

(1.2)

we can rewrite (1.1) in the following form

$$\begin{aligned} H = \frac{1}{2} \left( p_1^2 +p_2^2 +p_3^2 \right) - \frac{1}{\sqrt{\mu _1q_1^2 + \mu _2 q_2^2 +\mu _3 q_3^2 }}. \end{aligned}$$

(1.3)

The above Hamiltonian describes a mass point moving in an anisotropic deformation of the gravitational or the electrostatic potential field.

The planar version of the problem is described by the Hamiltonian

$$\begin{aligned} H = \frac{1}{2} \left( p_1^2 +p_2^2 \right) - \frac{1}{\sqrt{\mu _1q_1^2 + \mu _2 q_2^2 }}. \end{aligned}$$

(1.4)

Remark 1.1

In the original formulation the anisotropic Kepler problem was axially symmetric, that is $\mu _i=\mu _j$ for $i\ne j$. If, for example $\mu _2=\mu _3$, then the system has the following first integral

$$\begin{aligned} c_1 = q_2p_3 -q_3p_2. \end{aligned}$$

(1.5)

In the cylindrical coordinates $(q_1, q_2, q_3) = (q, \rho \cos \theta , \rho \sin \theta )$, Hamiltonian (1.3) reads

$$\begin{aligned} H =\frac{1}{2} \left( p_q^2 +p_{\rho }^2 + \frac{p_{\theta }^2}{\rho ^{2}} \right) -\frac{1}{\sqrt{\mu _1 q^2 + \mu _2 \rho ^2}}. \end{aligned}$$

(1.6)

Hence $\theta$ is a cyclic coordinate.

As it was pointed out by Gutzwiller (1989), an anisotropic mass tensor together with gravitational interactions arises fairly often. For example the planar isosceles three body problem that reduces to a natural Hamiltonian system with two degrees of freedom, standard kinetic energy and the anisotropic Kepler potential with an additional radial term (Devaney 1980, 1982). Anisotropic Kepler problem appears also as a subproblem of the rhomboidal charged four body problem (Alfaro and Perez-Chavela 2000). In this paper we propose another realisations of the anisotropic Kepler systems as systems of two point masses whose motion is restricted by two holonomic constraints.

If $\mu _1=\mu _2=\mu _3$ the above systems are just the spatial or planar classical Kepler problems, respectively. Hence, for these values of parameters, the systems are maximally super-integrable and their dynamics is regular. However, if $\mu _{1}\ne \mu _2$ or $\mu _2\ne \mu _3$, the dynamics of the respective systems is very irregular. It was investigated intensively in numerous papers, see e.g. Casasayas and Llibre (1984); Devaney (1982); Gutzwiller (1990). In particular in Gutzwiller (1977) it was shown that there is one-to-one correspondence between a certain set of trajectories of two-dimensional anisotropic Kepler problem and binary Bernoulli sequence. Thus strong chaotic behaviour of the system was proved. Arribas et al. (2003) proved the non-integrability of the planar as well as spatial anisotropic Kepler problems. These proofs were obtained by analysis of properties of differential Galois groups of variational equations around some particular solutions.

In this paper we investigate the integrability problem of a certain generalisation of the anisotropic Kepler problem. Namely, we consider the system given by the following Hamiltonian

$$\begin{aligned} H = \frac{1}{2} \left( p_1^2 +p_2^2 +p_3^2 \right) + V_n(q_1,q_2,q_3), \end{aligned}$$

(1.7)

where

$$\begin{aligned} V_n(q_1,q_2,q_3):= -\left( \mu _1q_1^2 + \mu _2 q_2^2 +\mu _3 q_3^2 \right) ^{-n}, \end{aligned}$$

(1.8)

and $2n \in \mathbb {Z}$. In our further considerations we always assume that none of the parameters $\mu _i$ is equal to zero.

Our motivation to revisit the anisotropic Kepler problem aroused from an analysis of constrained motions of material points. We noticed that the anisotropic Kepler problem is equivalent to a system of two points whose motion is restricted to the coordinates axes, see Sect. 3. This rather unexpected observation justifies other anisotropic models with an arbitrary power law of interactions between material points. Additionally, it also gave us a motivation to revisit the generalised two fixed centres problem.

It is known that the classical two fixed centres problem with each centre attracting according to the inverse square distance law is integrable. In Maciejewski and Przybylska (2004), it was shown that among two fixed centres problems such that each centre is the source of gravity with radial potential $V=-ar^{-2n}$ non-trivially integrable are only two and both of them are separable in elliptic coordinates. It is natural to ask if two fixed centres problem with a certain anisotropic potential is integrable. Here we restrict this general question to the following one: for which values of parameters the system given by Hamiltonian

$$\begin{aligned} H=\dfrac{1}{2}(p_1^2+p_2^2)-[(q_1-1)^2+\mu q_2^2]^{-n}-[(q_1+1)^2+\mu q_2^2]^{-n}, \end{aligned}$$

(1.9)

with $2n\in \mathbb {Z}, \mu \in \mathbb {R}, \mu \ne 0$, is integrable?

In this paper we answer the above posed question. Our results formulated in Sect. 2 have the form of three theorems. Two of them concern the generalised anisotropic Kepler problem and the third gives the necessary and sufficient conditions for the integrability of the generalised anisotropic two fixed centres problem. Proofs of all theorems given in Sects. 4 and 5 are based on the Morales–Ramis theory, see Morales-Ruiz (1999). Basic notions and certain facts from this theory used in this paper are given in Appendix. In Sect. 6 we summarise the obtained results and give final remarks.

2 Results

As it is usually accepted in the context of Hamiltonian mechanics, here by the integrability we always understand the integrability in the Liouville sense. The system is considered as a complex Hamiltonian system. The first integrals required for the integrability are assumed to be complex rational functions. Although later we explain that our results extend to the wider class of meromorphic function, we keep this restriction on the class of first integrals in order to avoid technical difficulties in formulation of theorems. For the Liouville integrability it is required that the first integrals are functionally independent on a certain “large” set. In the case of rational functions the functional dependence is equivalent to the algebraic dependence. So we require that first integrals, necessary for the Liouville integrability, are algebraically independent.

If $n\in \mathbb {Z}$, then the considered Hamiltonians are rational functions of canonical variables $(\varvec{q},\varvec{p})$ and in this case it is natural to ask about integrability in this class of first integrals. A problem appears when $n=\tfrac{1}{2} +l$ for a certain $l\in \mathbb {Z}$. In this case Hamiltonian (1.7) as well as Hamiltonian (1.9) are neither rational nor meromorphic functions of variables $(\varvec{q},\varvec{p})$. However they are algebraic over $\mathbb {C}(\varvec{q},\varvec{p})$. For a study of the integrability of systems with algebraic Hamiltonians with the methods used in this paper, certain mathematical constructions must be used, see paper of Combot (2013). Generally, one can extend the system introducing new variables in such a way that the new system is still Hamiltonian with a rational Hamilton function. We explain this construction in Sect. 3.1.

This is why considering system given by Hamiltonian (1.7) with $n=\tfrac{1}{2} +l$ for a certain $l\in \mathbb {Z}$, we assume that first integrals required for the integrability are rational functions of variables $(\varvec{q},\varvec{p},r)$ where $r^2=\mu _1q_1^2 + \mu _2 q_2^2 +\mu _3 q_3^2$.

Below we formulate two theorems where “integrability” means integrability in the above described sense with obvious modifications for planar version of the system.

We start from an analysis of two degrees of freedom version of (1.7) given by the Hamiltonian

$$\begin{aligned} {{\widetilde{H}}} = \frac{1}{2} \left( p_1^2 +p_2^2 \right) + {{\widetilde{V}}}_{n}(q_1,q_2), \qquad {{\widetilde{V}}}_{n}(q_1,q_2):= -\left( \mu _1q_1^2 + \mu _2 q_2^2 \right) ^{-n}. \end{aligned}$$

(2.1)

Our main result is given in the following theorem.

Theorem 2.1

Hamiltonian system generated by (2.1) with $2n\in \mathbb {Z}$ is integrable if and only if either $\mu _1=\mu _2$, or $n=\pm 1$.

If $\mu _1=\mu _2$, then the additional first integral for the system is $F:=q_1p_2-q_2p_1$. If $n=-1$, then as an additional first integral we can take $F = p_1^2 -2\mu _1q_1^{2}$. In the last integrable case with $n=1$, the additional first integral has the form

$$\begin{aligned} F=(q_1 p_2 - q_2 p_1)^{2}-2(q_1^2+q_2^2)\left( \mu _1q_1^2 + \mu _2 q_2^2 \right) ^{-1}. \end{aligned}$$

(2.2)

Remark 2.2

The form of the first integral given above follows from the following general fact. Hamiltonian system given by

$$\begin{aligned} H(\varvec{q},\varvec{p}) = \frac{1}{2} \varvec{p}^T \varvec{K}\varvec{p}+U(\varvec{q}), \qquad \varvec{q}, \varvec{p}\in \mathbb {C}^n, \end{aligned}$$

(2.3)

where $\varvec{K}=\varvec{K}^T\in \mathbb {M}(n,\mathbb {C})$ is not singular, and $U(\varvec{q})$ is a homogeneous potential of degree $-2$, has a first integral of the form

$$\begin{aligned} F= d(\varvec{q}) H(\varvec{q},\varvec{p}) -\frac{1}{2}\left( \varvec{p}^T\varvec{q}\right) ^2, \quad \text {where}\quad d(\varvec{q})=\varvec{q}^T \varvec{K}^{-1} \varvec{q}. \end{aligned}$$

(2.4)

Theorem 2.1 has a negative character—we did not find a new integrable case. However, the most interesting part of our considerations is hidden in its proof which is relatively simply except one case. Namely, we have to show the following.

Proposition 2.3

Hamiltonian system given by

$$\begin{aligned} {{\widetilde{H}}} = \frac{1}{2} \left( p_1^2 +p_2^2 \right) -a\left( q_1^2 - q_2^2 \right) ^{-3/2},\qquad a\ne 0 \end{aligned}$$

(2.5)

is not integrable.

Let us recall that according to our definition, here non-integrability means that the system does not admit an additional rational first integral $F(\varvec{q},\varvec{p},r)$, where $r^2=q_1^2 - q_2^2$. To prove the above proposition quite involved mathematical tools must be used.

For the the spatial system given by (1.7) result similar to this obtained for the planar is given in the following theorem.

Theorem 2.4

Hamiltonian system generated by (1.7) is integrable if and only if either $\mu _1=\mu _2=\mu _3$, or $n=\pm 1$.

In the case $\mu _1=\mu _2=\mu _3$ the system admits three additional first integrals $\varvec{c}:=\varvec{q}\times \varvec{p}$, so we can take $F_1=H, F_2=\varvec{c}\cdot \varvec{c}$, and $F_3=c_3$ as three functionally independent and commuting first integrals. If $n=-1$, then $F_i=p_i^2- 2\mu _iq_i^2$ with $i=1,2,3$ are such first integrals. For the third integrable case with $n=1$, the corresponding potential

$$\begin{aligned} V_{1}= -\frac{1}{\mu _1q_1^2 +\mu _2q_2^2 +\mu _3q_3^2} \end{aligned}$$

(2.6)

is separable in the sphero-conical coordinates as it was shown by Braden (1982).

Now, we consider the anisotropic two fixed centres problem given by Hamiltonian (1.9). We will keep our definition of the integrability with a modification in a case when 2n is odd integer. In this case we assume that an additional first integral required for integrability is a rational function of $(\varvec{q},\varvec{p},r_1, r_2)$ with

$$\begin{aligned} r_1^2:=(q_1-1)^2+\mu q_2^2, \qquad r_2^2:= (q_1+1)^2+\mu q_2^2. \end{aligned}$$

(2.7)

With the above assumptions and definitions we have the following.

Theorem 2.5

The anisotropic two fixed centres system given by Hamiltonian (1.9) is integrable if and only if either $\mu =1$ and then

• $n=1/2$; this is the classical two centres problem which is separable in elliptic coordinates;

• $n=-2$; this a natural Hamiltonian system with a non-homogeneous potential of degree four separable in elliptic coordinates, see Lakshmanan and Sahadevan (1993).

or $n=-1$ and $\mu \in \mathbb {C}$ is arbitrary. In this last case the system consists of two uncoupled harmonic oscillators.

Fig. 1

Geometry of mechanical planar anisotropic Kepler problem

3 Anisotropic Kepler problems as constrained mechanical systems

3.1 Planar anisotropic Kepler problem

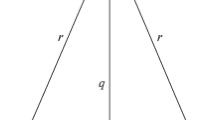
Let us consider two material points with masses $m_1$ and $m_2$, respectively. Motion of the first mass is constrained to the x axis and the second one to the y axis of an orthogonal frame, see Fig. 1. The interaction between masses is radial and inversely proportional to the first power of the distance between masses. The Lagrange function of this system reads

$$\begin{aligned} L=\frac{m_1}{2}\dot{x}^2+\frac{m_2}{2}\dot{y}^2+\frac{a}{\sqrt{x^2+y^2}}. \end{aligned}$$

Hence the Hamiltonian has the form

$$\begin{aligned} H=\frac{p_x^2}{2m_1}+\frac{p_y^2}{2m_2}-\frac{a}{\sqrt{x^2+y^2}}. \end{aligned}$$

(3.1)

After canonical rescaling

$$\begin{aligned} p_x=\sqrt{m_1} p_1,\quad p_y=\sqrt{m_2} p_2,\quad x=\frac{1}{\sqrt{m_1}}q_1,\quad y=\frac{1}{\sqrt{m_2}} q_2, \end{aligned}$$

Hamiltonian (3.1) takes a form of the Hamiltonian for the anisotropic Kepler problem

$$\begin{aligned} {{\widetilde{H}}}=\dfrac{1}{2}( p_1^2+ p_2^2)-\frac{a}{\sqrt{\mu _1 q_1^2 +\mu _2 q_2^2}},\qquad \mu _i=\sqrt{m_i}, \quad i=1,2. \end{aligned}$$

(3.2)

Fig. 2

Poincaré section for two masses moving on perpendicular axes. Parameters: $\mu _1=1,\ \mu _2=1.5,\ a=2.25,\ E=-0.01$, cross-plain $q_1=0,\ p_1>0$

Poincaré cross-section presented in Fig. 2 shows chaotic behaviour of the system.

3.2 Spatial anisotropic Kepler problem

If we constrain the motion of mass $m_1$ to the (x, y) plane and motion of $m_2$ to z axis, see Fig. 3a, then, assuming the same form of interaction as in the previous case, we obtain the following Hamiltonian of the system

$$\begin{aligned} H=\frac{1}{2m_1}(p_1^2+p_2^2)+\frac{1}{2m_2}p_3^2-\frac{a}{\sqrt{x^2+y^2+z^2}}. \end{aligned}$$

(3.3)

Hence after canonical rescaling we obtain Hamiltonian of the axially symmetric anisotropic Kepler problem

$$\begin{aligned} {{\widetilde{H}}}=\dfrac{1}{2}( p_1^2+ p_2^2+ p_3^2)- \frac{a}{\sqrt{ \mu _1(q_1^2+q_2^2)+ \mu _3 q_3^2}}, \end{aligned}$$

(3.4)

where $\mu _1 =\sqrt{m_1}$, and $\mu _{3}=\sqrt{m_2}$. In cylindrical coordinates it takes the form (1.6), thus $\theta$ is a cyclic coordinate and the corresponding momentum $p_{\theta }$ is a first integral. On a level $p_{\theta }=c={\text {const}}$ we obtain a Hamiltonian system with two degrees of freedom for that we are able to make the Poincaré cross section. Figure 4 presents such a section on the surface $q=0$ with $p_q>0$ restricted to the plane $(\rho ,p_\rho )$. As we see, the dynamics is very complex and chaotic.

Fig. 3

Geometry of mechanical models of a symmetric and b general spatial anisotropic Kepler problem

Fig. 4

Poincaré section for the system (1.6). Parameters: $\mu _1=1,\ \mu _2=1.5,\ p_\theta =c=1,\ E=-0.07$, cross-plain $q=0,\ p_q>0$

In order to interpret (1.3) as a Hamiltonian of a certain constrained system we consider two masses and assume that one of them $m_1$ is constrained to move in the plane (x, z) and the second one $m_2$ in the plane (x, y), see Fig. 3. The interactions between points are as in the previous cases. Let $(x_1,z)$ and $(x_2,y)$ denote the respective coordinates of the points, and $({{\widetilde{p}}}_1, p_{z}), ({{\widetilde{p}}}_2, p_{y})$ the corresponding canonical momenta. Then Hamiltonian of the system is

$$\begin{aligned} H=\dfrac{1}{2m_1}(\widetilde{p}_1^2+p_z^2)+\dfrac{1}{2m_2}(\widetilde{p}_2^2+p_y^2)-\frac{a}{\sqrt{(x_1-x_2)^2+y^2+z^2}}. \end{aligned}$$

(3.5)

Its Hamilton’s equations have the first integral $I={{\widetilde{p}}}_1 + {{\widetilde{p}}}_{2}$ which is related to the invariance of the system with respect to translations along the x-axis. This is why it is convenient to introduce the following canonical variables

$$\begin{aligned} q_1= & {} x_1-x_2,\qquad q_2=y, \qquad q_3 = z, \qquad q_4=x_1+x_2,\\ p_1= & {} \dfrac{1}{2}({{\widetilde{p}}}_1-{{\widetilde{p}}}_2),\qquad p_2 =p_y, \qquad p_3=p_z, \qquad p_4=\dfrac{1}{2}({{\widetilde{p}}}_1+\widetilde{p}_2). \end{aligned}$$

Variable $q_4$ is cyclic, so $p_4$ is a first integral. We restrict the considered system to the level $p_{4}=0$. The Hamiltonian restricted to this level reads

$$\begin{aligned} H = \frac{1}{2} \left( \mu _1p_1^2 + \mu _2p_2^2 + \mu _3p_3^2 \right) -\frac{a}{\sqrt{q_1^2+q_2^2+q_3^2}}, \end{aligned}$$

(3.6)

where

$$\begin{aligned} \mu _1:=\frac{1}{m_1}+\frac{1}{m_2}, \qquad \mu _2=\frac{1}{m_2}, \qquad \mu _3 = \frac{1}{m_1}. \end{aligned}$$

(3.7)

Thus, we obtained Hamiltonian of the form (1.1).

4 Proofs of integrability theorems for anisotropic Kepler problems

4.1 Preliminary remarks

If n is an integer, then the considered Hamiltonians are rational functions of $(\varvec{q},\varvec{p})$ and we have to prove that the systems are not integrable in the Liouville sense with rational first integrals.

However, if $n=\tfrac{1}{2}+l$ with $l\in \mathbb {Z}$, then the Hamiltonian (1.7) reads

$$\begin{aligned} H=\frac{1}{2}(p_1^2+p_2^2+p_3^2) -\frac{1}{r^k}, \end{aligned}$$

(4.1)

where $k=2l+1$ and $F(\varvec{q},r):=r^2 -( \mu _1q_1^2+\mu _2q_2^2+\mu _3q_3^2)=0$. With this notation, r is an implicit function of $\varvec{q}$. Hence, using the standard formula for differentiation of implicit functions, we have

$$\begin{aligned} \partial _{\varvec{q}} r= -\frac{1}{\partial _r F(\varvec{q},r)}\partial _{\varvec{q}}F(\varvec{q},r). \end{aligned}$$

(4.2)

Now, H is a rational function of $\varvec{z}:=(\varvec{q},\varvec{p},r)\in \mathbb {C}^{7}$, and we can easily deduce a system of differential equations satisfied by variables $(\varvec{q},\varvec{p},r)$. It reads

(4.3)

Notice that the right hand sides of this system are rational functions of $(\varvec{q},\varvec{p},r)$. Moreover, apart from Hamiltonian H given by (4.1), this system has additional first integral $F(\varvec{q},r)$. On the zero level of integral $F(\varvec{q},r)$ it coincides with the original Hamilton’s equations. As it was shown in Maciejewski and Przybylska (2016), system of the form (4.3) is Hamiltonian with respect to a certain degenerated symplectic structure having constant rank 6, for which $F(\varvec{q},r)$ is a Casimir function. Now, if the original Hamilton’s equations are integrable with the prescribed form of first integrals, then system (4.3) is integrable. For proving non-integrability we take a particular solution which lies on the zero level of Casimir $F(\varvec{q},r)$. More advanced justification of this approach is given in Combot (2013).

Just to simplify the exposition we prove Theorem 2.1 assuming that Proposition 2.3 is valid. The proof of Proposition 2.3 is presented at the end of this section.

4.2 Proof of Theorem 2.1

We have shown already that if $n=\pm 1$, or $\mu _1=\mu _2$, then the system is integrable. Hence we have to prove that if $n\ne \pm 1$ and $\mu _1\ne \mu _2$, then the system is not integrable.

Potential ${{\widetilde{V}}}_{n}(q_1,q_2)$ given in (2.1) is a homogeneous potential of degree $k=-2n$. Hence we can apply to it directly necessary conditions of the integrability in the Liouville sense formulated in Theorem 6.4 given in Appendix. For this potential Darboux points defined by (6.8) take the form

$$\begin{aligned} \varvec{d}_1=\left( 0,(2n)^{\frac{1}{2+2n}}\mu _2^{-\frac{n}{2+2n}}\right) , \qquad \varvec{d}_2=\left( (2n)^{\frac{1}{2+2n}}\mu _1^{-\frac{n}{2+2n}},0\right) . \end{aligned}$$

(4.4)

Hessians of the potential calculated at these points are diagonal matrices

$$\begin{aligned} \widetilde{V}_n''(\varvec{d}_1)={\text {diag}}\left( \dfrac{1}{\mu },-2n-1\right) ,\qquad {{\widetilde{V}}}_n''(\varvec{d}_2)={\text {diag}}\left( -2n-1, \mu \right) , \end{aligned}$$

(4.5)

where $\mu := \mu _2/\mu _1$.

We prove our theorem by a contradiction. Thus, let us assume that the system is integrable with $n\ne \pm 1$ and $\mu \ne 1$. Then, by Theorem 6.4, $\lambda =\mu$ and $\lambda '=1/\mu$ belong to certain items in the Morales–Ramis table (6.16).

Notice that items 3 and 4 of table (6.16) are excluded by assumptions because they correspond to $n=\pm 1$.

We have two possibilities: either $\mu =1/\mu$, or $\mu \ne 1/\mu$. If $\mu =1/\mu$, then either $\mu =1$ or $\mu =-1$. Case $\mu =1$ is excluded by assumptions but case $\mu =-1$ appears only in item 1 for $p=2$ and $n=3/2$. However, for these values of parameters the system is not integrable by Proposition 2.3.

Now we can assume that $\mu \ne 1/\mu$. If $\mu \ne 0$ and $|\mu | <1$, then we find only a finite number of possible choices for $\mu$ and $k=-2n$ in the Morales–Ramis table. They are listed in Table 1. By a direct check we can verify that if a pair $(k,\mu )$ belongs to the above table, then $(k,1/\mu )$ does not belong to an item in the Morales–Ramis table.

If $\mu >1$, we repeat the above reasoning taking $1/\mu$ instead of $\mu$ and this finishes the proof.

Table 1 Admissible values of $(k,\mu )$ with $|\mu |<1$

4.3 Proof of Theorem 2.4

We have to show that if $n\ne -1$ and $\mu _i\ne \mu _j$ for certain $i,j\in \{1,2,3\}$, then Hamiltonian system given by (1.7) is not integrable. Without loss of generality, we assume that $\mu _1\ne \mu _2$.

Potential $V_{n}(q_1,q_2,q_3)$ given in (1.7) is a homogeneous function of degree $k=-2n$. It admits the following Darboux points

$$\begin{aligned} \varvec{d}_{1}=\left( 0,(2n)^{\frac{1}{2+2n}}\mu _2^{-\frac{n}{2+2n}},0\right) , \qquad \varvec{d}_2=\left( (2n)^{\frac{1}{2+2n}}\mu _1^{-\frac{n}{2+2n}},0,0\right) . \end{aligned}$$

(4.6)

Hessians of potential calculated at these points are diagonal matrices

$$\begin{aligned} V_n''(\varvec{d}_1)={\text {diag}}\left( \dfrac{1}{\mu },-2n-1, \mu _{3,2}\right) ,\quad V''(\varvec{d}_2)={\text {diag}}\left( -2n-1, \mu , \mu _{3,1} \right) , \end{aligned}$$

(4.7)

where $\mu := \mu _2/\mu _1$, and $\mu _{3,i}=\mu _3/\mu _i$ for $i=1,2$.

Now, we restrict our attention to eigenvalues $\lambda =\mu$ and $\lambda '=1/\mu$. Repeating the same reasoning as in proof of Theorem 2.1 we show that if $\mu _1\ne \mu _2$ the system is not integrable and this finishes the proof.

4.4 Proof of Proposition 2.3

By assumption, number a in (2.5) is not zero, so we can fix its value as $a=1/3$. The potential

$$\begin{aligned} V = -\frac{1}{3}(q_1^2-q_2^2)^{-3/2} \end{aligned}$$

has Darboux point $\varvec{d}=(1,0)$, and $V''(\varvec{d})={\text {diag}}(-4, -1)$. Hence the first order variational equations (6.9) read

$$\begin{aligned} {\ddot{x}}_i = -\lambda _i \varphi (t)^{k-2} x_{i}, \qquad i=1, 2, \end{aligned}$$

(4.8)

with $k=-3, \lambda _1=- 4$ and $\lambda _2 = -1$. Let us notice that $\lambda _1$ and $\lambda _2$ belong to item 1 in Eq. (6.16). Thus these equations are solvable and its differential Galois group does not give integrability obstructions. This is why we have to extract these obstructions from the analysis of the higher order variational equations as it is discussed in Appendix. The second order variational equations (6.10) have the form

$$\begin{aligned} {\ddot{y}}_{1}= & {} -\lambda _1 \varphi (t)^{k-2} y_1 -\frac{5}{2}\varphi (t)^{k-3} \left( 4x_1^2 +x_2^2 \right) , \nonumber \\ {\ddot{y}}_2= & {} -\lambda _2 \varphi (t)^{k-2} y_2 -5 \varphi (t)^{k-3}x_1x_2. \end{aligned}$$

(4.9)

For further analysis we take the following subsystem of the above equations

$$\begin{aligned} {\ddot{x}}_2= & {} -\lambda _2 \varphi (t)^{k-2} x_2,\nonumber \\ {\ddot{y}}_{1}= & {} -\lambda _1 \varphi (t)^{k-2} y_1 -\frac{5}{2}\varphi (t)^{k-3}x_2^2, \end{aligned}$$

(4.10)

obtained from (4.8) and (4.9) by setting $x_1=\dot{x}_1=0$. After the Yoshida transformation (6.12) this system reads

$$\begin{aligned} x'' = r_2(z) x, \qquad y'' = r_1(z)y +\omega (z) x^2, \end{aligned}$$

(4.11)

where $r_i(z)=r(k,\lambda _i)$ with $r(k,\lambda )$ defined by (6.15), and

$$\begin{aligned} \omega (z) = z^{-\frac{3}{2}-\frac{1}{2k}}(1-z)^{-\frac{5}{4}}. \end{aligned}$$

With the notation used in Appendix we chose $\alpha =2$ and $\gamma =1$. The first equation in (4.11) has the algebraic solution

$$\begin{aligned} x_1 = z^{1/3}(1-z)^{3/4}, \end{aligned}$$

(4.12)

and the algebraic solution of equation $y'' = r_1(z)y$ is

$$\begin{aligned} y_1 = z^{2/3}(1-z)^{3/4}. \end{aligned}$$

(4.13)

Thus, integral $\Phi$ defined by (6.19) takes the form

$$\begin{aligned} \Phi = \int \omega (z) y_1 x_1^2 =\int (1-z)= z -\frac{1}{2}z^2. \end{aligned}$$

(4.14)

Since $\Phi$ is algebraic, as it is explained in Appendix, we have to calculate four integrals $I_{\alpha }, I_{\gamma }, \Psi _{\alpha }$ and $\Psi _{\gamma }$. They are defined in (6.20) and take the following forms

$$\begin{aligned} I_\alpha= & {} \int \frac{1}{x_1^2}=\frac{2z^{1/3}}{\sqrt{1-z}}+\frac{1}{3}B(z,1/3,1/2),\nonumber \\ I_\gamma= & {} \int \frac{1}{y_1^2}=\frac{z^{-1/3}(5z-3)}{\sqrt{1-z}}-\frac{5}{6}B(z,1/3,1/2),\nonumber \\ \Psi _{\alpha }= & {} \int \Phi I'_{\alpha } =\frac{z^{1/3}(3z+2)}{5\sqrt{1-z}}-\frac{2}{15}B(z,1/3,1/2),\nonumber \\ \Psi _{\gamma }= & {} \int \Phi I'_{\gamma }=\frac{z^{2/3}}{\sqrt{1-z}}+\frac{1}{3}B(z,2/3,1/2),\nonumber \end{aligned}$$

(4.15)

where B(z, p, q) denotes the incomplete Euler beta function. Now we apply Theorem 6.5. The first condition of this theorem is fulfilled because for $d_{\alpha }=2/5$ we have

$$\begin{aligned} \Psi _{\alpha } + d_{\alpha }I_{\alpha }=\frac{3}{5}\frac{z^{1/3}(z+2)}{\sqrt{1-z}}\in \mathbb {C}(z)[\omega ]. \end{aligned}$$

The second condition is also satisfied because for $d_{\alpha }=0$ and $d_{\gamma }=2/5$ one obtains

$$\begin{aligned} \Psi _{\gamma } + d_{\alpha }I_{\alpha } + d_{\gamma }I_{\gamma }=\frac{3}{5}\frac{z^{-1/3}(5z-2)}{\sqrt{1-z}}\in \mathbb {C}(z)[\omega ]. \end{aligned}$$

We show that the third condition of Theorem 6.5 is not satisfied. In fact, the second condition is fulfilled with $d_{\alpha }\ne d_{\gamma }$. Moreover, derivatives of integrals are

$$\begin{aligned} I'_{\alpha } = \frac{z^{-2/3}}{(1-z)^{3/2}} \quad \text {and}\quad I'_{\gamma } =\frac{z^{-4/3}}{(1-z)^{3/2}}. \end{aligned}$$

So, taking a small loop around the origin we will find that these expressions change their values when we pass the loop counter-clockwise. Just simple calculations give

$$\begin{aligned} M_0 (I'_{\alpha }) = \chi _{\alpha }I'_{\alpha } \quad \text {and}\quad M_0 (I'_{\gamma })=\chi _{\gamma }I'_{\gamma }, \end{aligned}$$

with

$$\begin{aligned} \chi _{\alpha } = \exp (2\pi \mathrm {i}\,/3) \quad \text {and}\quad \chi _{\gamma }= \exp (-2\pi \mathrm {i}\,/3). \end{aligned}$$

Hence $\chi _{\alpha }-\chi _{\gamma }=\mathrm {i}\,\sqrt{3}\ne 0$, and this why, by Lemma 6.6, for an arbitrary $c\in \mathbb {C}$, expression $I_{\alpha }+cI_{\gamma }$ is not algebraic. This shows that the differential Galois group of the second order variational equations is not virtually Abelian and by Theorem 6.3 the considered system is not integrable.

5 Proof of Theorem 2.5

For $\mu =1$ integrability of generalised two fixed centres problem was investigated in Maciejewski and Przybylska (2004). One would like to obtain a similar result for $\mu \ne 1$, however the additional parameter in the system makes the problem hard. More precisely, one can prove the non-integrability for fixed values of parameter n. However, we do not know how to proceed in general case, even restricting vales of n to half integers. This is why, at first we show the following.

Proposition 5.1

If the anisotropic two fixed centres system given by Hamiltonian (1.9) is integrable, then the corresponding anisotropic Kepler problem is integrable.

Proof

Let us rescale canonical variables and time in our system in the following way

$$\begin{aligned} t = \frac{1}{\varepsilon ^{n+1}} \tau , \qquad \varvec{q}= \frac{1}{\varepsilon }{\widetilde{\varvec{q}}}, \qquad \varvec{p}= \varepsilon ^n{\widetilde{\varvec{p}}}. \end{aligned}$$

After this change of variables, Hamilton’s equations remain Hamiltonian one with the following Hamilton function

$$\begin{aligned} {\tilde{H}} = \frac{1}{\varepsilon ^{n+1}}H = \frac{1}{2}({\widetilde{p}}_1^2+{{{\widetilde{p}}}}_2^2) - {{{\widetilde{r}}}}_1^{-2n} - {\widetilde{r}}_2^{-2n}, \end{aligned}$$

where

$$\begin{aligned} {{{\widetilde{r}}}}_1^2 = ({{\widetilde{q}}}_1 -\varepsilon )^2 +\mu \widetilde{q}_2^2, \qquad {{{\widetilde{r}}}}_2^2 = ({{\widetilde{q}}}_1 +\varepsilon )^2 +\mu {{\widetilde{q}}}_2^2. \end{aligned}$$

Notice that ${{\widetilde{H}}}$ has the following expansions

$$\begin{aligned} {{\widetilde{H}}} = {{\widetilde{H}}}_0 + \varepsilon \widetilde{H}_1 +\cdots , \end{aligned}$$

(5.1)

where dots denote higher order terms with respect to $\varepsilon$, and

$$\begin{aligned} {{\widetilde{H}}}_0 = \frac{1}{2}({\widetilde{p}}_1^2+{{{\widetilde{p}}}}_2^2)- \frac{2}{\left( {{\widetilde{q}}}_1^2 + \mu {{\widetilde{q}}}_2^2\right) ^n}. \end{aligned}$$

(5.2)

Notice that up to rescaling of the potential, this is the Hamiltonian of the generalised anisotropic Kepler problem.

If the generalised two fixed centres problem has a rational first integral $I(\varvec{q},\varvec{p}, r_1, r_2)$, then after rescaling this first integral will have the form

$$\begin{aligned} {{\widetilde{I}}}= \frac{P({\widetilde{\varvec{q}}},{\widetilde{\varvec{p}}}, {{\widetilde{r}}}_1, {{\widetilde{r}}}_2, \varepsilon )}{Q({\widetilde{\varvec{q}}},{\widetilde{\varvec{p}}}, {{\widetilde{r}}}_1, {{\widetilde{r}}}_2, \varepsilon )}, \end{aligned}$$

(5.3)

where P, Q are polynomials of specified variables. It can be expanded in the Laurent series

$$\begin{aligned} {{\widetilde{I}}} = \varepsilon ^k \left( {{\widetilde{I}}}_0 + \varepsilon {{\widetilde{I}}}_1+ \cdots \right) , \qquad k\in \mathbb {Z}, \end{aligned}$$

(5.4)

where coefficients of this expansion ${{\widetilde{I}}}_m$ are rational functions of $({\widetilde{\varvec{q}}},{\widetilde{\varvec{p}}}, {{\widetilde{r}}})$ and ${{\widetilde{r}}}^2= {{\widetilde{q}}}_1^2 + \mu {{\widetilde{q}}}_2^2$. By assumption, $\{{{\widetilde{H}}}, {{\widetilde{I}}}\}=0$ for arbitrary $\varepsilon$ and

$$\begin{aligned} 0= \{{{\widetilde{H}}}, {{\widetilde{I}}}\} = \varepsilon ^k \left( \{ {{\widetilde{H}}}_0, {{\widetilde{I}}}_{0}\} + \varepsilon \cdots \right) . \end{aligned}$$

(5.5)

Thus $\{ {{\widetilde{H}}}_0, {{\widetilde{I}}}_{0}\}=0$, i.e, $\widetilde{I}_{0}$ is an integral of ${{\widetilde{H}}}_{0}$. If ${{\widetilde{I}}}_{0}$ and ${{\widetilde{H}}}_{0}$ are functionally independent, then we finish the proof. If it doesn’t, then by Ziglin Lemma (see Audin 2001; Tosel 2000; Ziglin 1982), there exists a polynomial $W({{\widetilde{H}}}, {{\widetilde{I}}})$, such that W and ${{\widetilde{H}}}$ are functionally independent as well as $W_0$ and ${{\widetilde{H}}}_{0}$ are functionally independent. This ends the proof. $\square$

Now, we can pass to the proof of Theorem 2.5. The case with $\mu =1$ was considered in Maciejewski and Przybylska (2004). This is why, taking into account Theorem 2.1, we have to analyse only case $n=1$. The results of our analysis can be summarized shortly in the following lemma.

Lemma 5.2

Hamiltonian system given by

$$\begin{aligned} H=\dfrac{1}{2}(p_1^2+p_2^2)- \frac{1}{(q_1-1)^2+\mu q_2^2}-\frac{1}{(q_1+1)^2+\mu q_2^2}, \quad \mu \ne 0, \end{aligned}$$

(5.6)

does not admit an additional meromorphic first integral.

Proof

The corresponding Hamilton equations read

$$\begin{aligned} \dot{q}_1= & {} p_1,\quad \dot{p}_1=-\dfrac{2(q_1-1)}{[(q_1-1)^2+\mu q_2^2]^2} -\dfrac{2(q_1+1)}{[(q_1+1)^2+\mu q_2^2]^{2}},\nonumber \\ \dot{q}_2= & {} p_2,\quad \dot{p}_2=-\dfrac{2\mu q_2}{[(q_1-1)^2+\mu q_2^2]^2} -\dfrac{2\mu q_2}{[(q_1+1)^2+\mu q_2^2]^2}. \end{aligned}$$

(5.7)

The above system has two invariant planes

$$\begin{aligned} {{\mathcal {N}}}_1=\left\{ {(q_1,q_2,p_1,p_2) \in \ C^4}\;\vert \;\; {q_1=p_1=0} \,\right\} , \end{aligned}$$

(5.8)

and

$$\begin{aligned} {{\mathcal {N}}}_2=\left\{ {(q_1,q_2,p_1,p_2) \in \ C^4}\;\vert \;\; {q_2=p_2=0} \,\right\} . \end{aligned}$$

(5.9)

System (5.7) restricted to ${{\mathcal {N}}}_1$ reads

$$\begin{aligned} \dot{q}_2=p_2,\qquad \dot{p}_2=-4\mu q_2(1+\mu q_2^2)^{-2}, \end{aligned}$$

(5.10)

and it has first integral $H_{|{{\mathcal {N}}}_1}$. Let $\Gamma _1(e)$ be the phase curve corresponding to the level $H_{|{{\mathcal {N}}}_1}=e$, that is

$$\begin{aligned} \Gamma _1(e):=\left\{ (q_1,q_2,p_1,p_2)\in \mathbb {C}^4\ \Big |\ q_1=p_1=0, \ e=\frac{1}{2} p_2^2-\frac{2}{1+\mu q_2^2}\right\} . \end{aligned}$$

The variational equations along $\Gamma _1(e)$ split into a direct product of two second order equations

$$\begin{aligned} {\ddot{x}}_i = a_{i}x_i, \qquad i=1,2 , \end{aligned}$$

(5.11)

where $a_{i}$ depends on a point on $\Gamma _{1}(e)$. Only the first equation is relevant for further consideration. It describes the variations normal to $\Gamma _{1}(e)$, and explicitly it reads

$$\begin{aligned} {\ddot{x}}_1=\dfrac{4(3-\mu q_2^2)}{(1+\mu q_2^2)^3} x_1. \end{aligned}$$

(5.12)

Similarly, we can take particular solutions lying in ${{\mathcal {N}}}_2$ and defining phase curve

$$\begin{aligned} \Gamma _2(e):=\left\{ (q_1,q_2,p_1,p_2)\in \mathbb {C}^4\ \Big |\ q_2=p_2=0, \ e=\frac{1}{2} p_1^2-\frac{2(q_1^2+1)}{(q_1^2-1)^2}\right\} . \end{aligned}$$

The normal variational equations along this curve have the form

$$\begin{aligned} {\ddot{x}}_2 = -2\mu \left[ \frac{1}{(q_1-1)^4} + \frac{1}{(q_1+1)^4}\right] x_2. \end{aligned}$$

(5.13)

At first we consider variational equations (5.12), and we change independent variable

$$\begin{aligned} z=1+\mu q_2(t)^2. \end{aligned}$$

(5.14)

After this transformation equation (5.12) reads

$$\begin{aligned} x_1''+p(z)x_1'+q(z)x_1=0, \end{aligned}$$

(5.15)

where

$$\begin{aligned} p(z)=\dfrac{{\ddot{z}}}{(\dot{z})^2}=\dfrac{e z^2+2}{2 (z-1) z (2 + e z)},\qquad q(z)=\dfrac{a}{(\dot{z})^2}=\dfrac{z-4}{2\mu z^2(z-1)(ez+2)}. \end{aligned}$$

Next, the following change of dependent variable

$$\begin{aligned} x_1 = w \exp \left[ -\frac{1}{2} \int _{z_0}^z p(s)\, ds \right] , \end{aligned}$$

(5.16)

transforms (5.15) to its reduced form

$$\begin{aligned} w'' = r(z) w, \qquad r(z) = -q(z) + \frac{1}{2}p'(z) + \frac{1}{4}p(z)^2. \end{aligned}$$

(5.17)

Coefficient r(z) has the following form

$$\begin{aligned} r(z)= & {} \dfrac{5\mu -16}{16\mu z^2}-\dfrac{12 - 8 e - 2 \mu + e\mu }{16\mu z} -\dfrac{3}{16(z-1)^2}\nonumber \\&+\,\dfrac{6-\mu }{4\mu (2+e)(z-1)} -\dfrac{3e^2}{16(ez+2)^2} +e^2\dfrac{-4 + e (-8 + \mu )}{16\mu (e+2)(ez+2)}. \end{aligned}$$

(5.18)

For $e\not \in \{\pm 2,0\}$ and $\mu \ne 0$ Eq. (5.17) has four regular singular points $z_1=0, z_2=1, z_3=-2/e$ and $z_4=\infty$. For the reduced Eq. (5.17) we can apply the Kovacic algorithm. Here we apply its original formulation given in Kovacic (1986), see also short formulation in Appendix B of Przybylska and Szumiński (2013).

Differences of characteristic exponents $\Delta _i, i=1,\ldots ,4$ are the following

$$\begin{aligned} \Delta _1=\dfrac{1}{2}\sqrt{9-\dfrac{16}{\mu }},\quad \Delta _2=\Delta _3=\Delta _4=\dfrac{1}{2}. \end{aligned}$$

(5.19)

In the Case I of the algorithm the auxiliary sets $E_k$ take the forms

$$\begin{aligned} E_1=\left\{ \dfrac{1}{4}\left( 2\pm \sqrt{9-\dfrac{16}{\mu }}\right) \right\} , \quad E_2=E_3=E_4=\left\{ \dfrac{1}{4},\dfrac{3}{4}\right\} . \end{aligned}$$

(5.20)

In this case equation has a Liouvillian solution provided that there exists an element $(e_1,e_2,e_3,e_4)$, with $e_i\in E_i$ such that

$$\begin{aligned} m:=e_4-(e_1+e_2+e_3)\in \mathbb {N}_0=\mathbb {N}\cup \{0\}. \end{aligned}$$

(5.21)

This condition is fulfilled if and only if

$$\begin{aligned} \mu \in C_1 :=\left\{ \frac{16}{9-(4m+p)^2}\ \Big |\ m\in \mathbb {N}_0, \text { and }p\in \{1,3,5,7\}\right\} . \end{aligned}$$

(5.22)

In the Case II of the Kovacic algorithm sets $E_i$ have the forms

$$\begin{aligned} E_1= & {} \left\{ 2-\sqrt{9-\dfrac{16}{\mu }},2,2+\sqrt{9-\dfrac{16}{\mu }}\right\} \cap \mathbb {Z},\nonumber \\ E_2= & {} E_3= E_4=\{1,2,3\}. \end{aligned}$$

(5.23)

Condition $E_1\ne \emptyset$ is fulfilled iff

$$\begin{aligned} \mu \in C_2:= \left\{ \dfrac{16}{9-m^2}\ \Big |\ m\in \mathbb {N}_0\right\} . \end{aligned}$$

(5.24)

In the Case III of the algorithm sets $E_k$ are the following

$$\begin{aligned} E_1= & {} \left\{ 6\mp \frac{k}{2}\sqrt{9-\dfrac{16}{\mu }} \ \Big | \ k=0,1,\ldots , 6\right\} \cap \mathbb {Z},\nonumber \\ E_2= & {} E_3=E_4=\{3,4,5,6,7,8,9\}. \end{aligned}$$

(5.25)

Now condition that $E_{1}\ne \emptyset$ is fulfilled iff $\mu$ is a rational number and it takes one of the following forms

$$\begin{aligned} \mu =\dfrac{144}{81-m^2},\quad \mu =\dfrac{400}{225-4m^2},\quad \mu =\dfrac{64}{36-m^2},\quad \mu =\dfrac{16}{9-m^2}, \end{aligned}$$

(5.26)

where $m\in \mathbb {N}_0$. If system is integrable, then by Theorem 6.3, the identity component of differential Galois group of the considered equation is Abelian. This implies that at least one of the conditions deduced from three cases of the Kovacic algorithm is fulfilled. Hence,

$$\begin{aligned} \mu \in C:= C_1 \cup C_2 \cup C_3 \cup C_4 \cup C_5, \end{aligned}$$

(5.27)

where

$$\begin{aligned} C_3= & {} \left\{ \dfrac{144}{81-m^2}\ \Big |\ m\in \mathbb {N}_0\right\} , \nonumber \\ C_4= & {} \left\{ \dfrac{400}{225-4 m^2}\ \Big |\ m\in \mathbb {N}_0\right\} , \\ C_5= & {} \left\{ \dfrac{64}{36-m^2}\ \Big |\ m\in \mathbb {N}_0\right\} .\nonumber \end{aligned}$$

(5.28)

Set C contains infinite number of elements.

However, we can obtain additional conditions analysing the normal variational equation (5.13) along the second particular solution $\Gamma _2(e)$. First we make the following change of the independent variable

$$\begin{aligned} z=q_1(t)^2, \end{aligned}$$

(5.29)

and then we transform the obtained equation into its reduced form

$$\begin{aligned} v''= s(z) v, \end{aligned}$$

(5.30)

where

$$\begin{aligned} s(z)= & {} -\dfrac{3}{16z^2}+\dfrac{3-2\mu }{4(e+2)z}+\dfrac{3-4\mu }{4(z-1)^2}-\dfrac{3-4\mu }{8(z-1)}\nonumber \\&+\dfrac{3 (4e-1)}{4 [e (-1 + z)^2 + 2 (1 + z)]^2} -\dfrac{8 \mu + 4 e (z-2) \mu + e^2 ( z-3) ( 4 \mu -3)}{8 (2 + e) [e (-1 + z)^2 + 2 (1 + z)]}.\nonumber \\ \end{aligned}$$

(5.31)

For $e\not \in \{\pm 2,0\}$ Eq. (5.17) has five regular singular points $z_1=0, z_2=1, z_{3,4}=(e-1\pm \sqrt{1-4e})/e$ and $z_5=\infty$. The differences of exponents $\Delta _i$, at the respective points $i=1,\ldots ,4$ are the following

$$\begin{aligned} \Delta _2=2\sqrt{1-\mu },\quad \Delta _1=\Delta _3=\Delta _4= \Delta _5=\dfrac{1}{2}. \end{aligned}$$

(5.32)

Applying, as for the analysed above variational equations along the first particular solution $\Gamma _1(e)$, the Kovacic algorithm, we obtain necessary conditions for the integrability. Three cases of this algorithm give the following restrictions on $\mu$

$$\begin{aligned} \mu \in B:=\left\{ 1- \left( \dfrac{m}{2p}\right) ^2\ \Big |\ m\in \mathbb {N}_0 \quad \text {and}\quad p\in \{1,2,3,4,5,6\}\right\} . \end{aligned}$$

(5.33)

Now, if the system is integrable, then the necessary integrability conditions deduced from both variational equations must be satisfied. That is if the system is integrable, then $\mu \in C\cap B$. However, the point is that $C\cap B=\emptyset$. In fact, let us assume that $|\mu |\ge 1$ and $\mu \in C\cap B$. So, in particular $\mu \in C$. Clearly there is only a finite number of such values. One can check directly that none of them belongs to set B. On the other hand, if $|\mu |<1$ and $\mu \in C\cap B$, then $\mu \in B$. But set B contains only finitely many elements with absolute value smaller than one. Again, one can directly check that none of these values belongs to set C. This proves our claim and finishes the proof. $\square$

6 Discussion and comments

In a case of integer n Theorems 2.1 and 2.4 remain valid after the change of a class of first integrals required for the integrability, from rational to meromorphic functions of canonical variables $(\varvec{q},\varvec{p})$. This follows from the main Theorem 6.3 of the Morales–Ramis theory. If $n=\tfrac{1}{2} +m$ with a certain $m\in \mathbb {Z}$, then these theorems remain true when we extend the class of first integrals to meromorphic functions of variables $(\varvec{q},\varvec{p},r)$. In fact, if the system given by Hamiltonian (1.9) admits a meromorphic first integral $I(\varvec{q},\varvec{p},r)$, then it is also a first integral of extended system (4.3). To show that the extended system does not admit additional first integral we can invoke the Ayoul–Zung theorem (Ayoul and Zung 2010), and use the same particular solution to show that the differential Galois group of respective variational equations has a non-Abelian identity component. The mentioned paper contains the extension of Theorem 6.3 about differential Galois obstructions for the meromorphic integrability of Hamiltonian systems to the non-Hamiltonian case.

We are not sure if Theorem 2.5 remains valid if we extend the admissible integrals to meromorphic functions of variables $(\varvec{q},\varvec{p},r_1,r_2)$.

Let us remark that for a long time the Ziglin and Morales–Ramis theories were used for study integrability of systems having algebraic, not single valued Hamiltonians. The first who pointed out that this lack of the respect for the basic assumption of the theory can lead to erroneous conclusions was Combot (2013).

In all cases with an algebraic but non-rational potential we can take it as a new variable and proceed as described in Maciejewski and Przybylska (2016) to obtain an extended system. Here we decided to introduce additional variables which are just algebraic expressions occuring in formulae for algebraic potentials. This simply shows other possibility for obtaining the desired result which is a transformation of Hamilton’s equations with algebraic right-hand sides into a system with rational right-hand sides.

Let us notice that the mechanical model given by Hamiltonian (3.5) is not integrable for any positive masses. In fact, according to our Theorem 2.4, the system is integrable only when $\mu _1=\mu _2=\mu _3$, but for positive $m_1$ and $m_2$, it is impossible, see (3.7). We thank to the anonymous referee for this observation.

Appendix: Basic theorems of Ziglin–Morales theory

The general exposition of the Ziglin–Morales–Ramis theory one can find in Morales-Ruiz and Ramis (1999, (2001b, (2001c); Audin (2001). For numerous applications see overview paper of Morales-Ruiz and Ramis (2010) and references therein.

In the Ziglin–Morales–Ramis theory we consider a complex Hamiltonian system defined on complex analytic symplectic manifold $M^{2n}$. However for the purpose of this paper, as well as in many applications, it is enough to assume that $M^{2n}=\mathbb {C}^{2n}$ and that the symplectic form is canonical

$$\begin{aligned} \omega =\sum _{i=1}^n\mathrm {d}q_i\wedge \mathrm {d}p_i. \end{aligned}$$

(6.1)

It is assumed that the considered Hamiltonian system is given by a Hamiltonian which is meromorphic on $M^{2n}$. We say that the system is integrable in the Liouville sense (or simply integrable) if it admits n commuting first integrals which are meromorphic on $M^{2n}$ and functionally independent. Here we refer to the papers of Ziglin (1982) and Baider et al. (Baider et al 1996) where, among other things, the integrability of complex Hamiltonian systems is discussed.

Remark 6.1

Let us recall that a function f is a meromorphic function on a domain $W\subset \mathbb {C}^m$ if locally near each point of W it can be represented as a ratio of two holomorphic functions. More formally, a holomorphic function $f:W\setminus \Sigma (f)\rightarrow \mathbb {C}$, where $\Sigma (f)$ is a codimension one analytic subset of W, is called meromorphic on W, if for each point $\varvec{z}\in W$ there exists a neighbourhood $V\subset W$ of $\varvec{z}$ and two holomorphic functions $g:V\rightarrow \mathbb {C}$, and $h:V\rightarrow \mathbb {C}$, such that

$$\begin{aligned} f(\varvec{x})=\frac{g(\varvec{x})}{h(\varvec{x})}, \quad \text {for}\quad \varvec{x}\in V\setminus \Sigma (f). \end{aligned}$$

(6.2)

Set $\Sigma (f)$ is called the polar set of f. The set ${{\mathscr {M}}}(W)$ of functions meromorphic on W with point wise addition and multiplication forms a field.

Remark 6.2

If functions $f_1(\varvec{x}), \ldots , f_k(\varvec{x})$ are meromorphic on a domain $W\subset \mathbb {C}^m$, and they are functionally independent at a point $\varvec{x}_0\in W, \varvec{x}_{0}\not \in \cup _{i=1}^n\Sigma (f_i)$, then they are functionally independent on a dense subset of W. This fact follows directly from the identity theorem for meromorphic functions, see e.g. Chapter VI in the book of Fischer and Lieb (2012).

Applications of differential Galois theory to study the integrability of Hamiltonian systems are based on the following theorem.

Theorem 6.3

[Morales–Ramis–Simó] If a Hamiltonian system is integrable in the Liouville sense with first integrals which are meromorphic in $M^{2n}$, then the identity component of the differential Galois group of p-th order variational equations along a particular solution is Abelian for all $p\in \mathbb {N}$.

For a proof of the above theorem we refer the reader to Morales-Ruiz et al. (2007) and Casale (2009).

The above theorem has been especially effective for finding necessary integrability conditions of Hamiltonian systems with homogeneous potentials. The Hamiltonian of such systems has the form

$$\begin{aligned} H=\dfrac{1}{2}\left( p_1^2+\cdots +p_n^2\right) +V(\varvec{q}), \end{aligned}$$

(6.3)

where $V(\varvec{q})$ is a homogeneous function of degree k which is a non-zero integer. The equations of motion formulated as Newton’s equations read

$$\begin{aligned} {\ddot{\varvec{q}}} = -V'(\varvec{q}), \quad \text {where}\quad V'(\varvec{q}):={\text {grad}}V(\varvec{q}). \end{aligned}$$

(6.4)

For a given particular solution $\varvec{q}_0(t)$ of this system we put

$$\begin{aligned} \varvec{q}(t) = \varvec{q}_0(t) + \varepsilon \varvec{q}_1(t) + \frac{1}{2}\varepsilon ^2 \varvec{q}_2(t) +\cdots + \frac{1}{p!}\varepsilon ^p \varvec{q}_p(t)+\cdots , \end{aligned}$$

(6.5)

where $\varepsilon$ is a formal small parameter. Inserting the above expansion into equation (6.4) and comparing terms of the same order with respect to $\varepsilon$ we obtain an infinite sequence of differential equations on $\varvec{q}_p, p=0,1,2,\ldots ,$ called p-th order variational equations. The first of them $\ddot{\varvec{q}}_0= -V'(\varvec{q}_0)$, is satisfied by assumptions. For further purposes we need the next two equations which are the following

$$\begin{aligned} {\ddot{\varvec{q}}}_1= & {} -V''(\varvec{q}_0)\varvec{q}_1, \end{aligned}$$

(6.6)

$$\begin{aligned} {\ddot{\varvec{q}}}_2= & {} -V''(\varvec{q}_0)\varvec{q}_2-V'''(\varvec{q}_0)(\varvec{q}_1, \varvec{q}_1). \end{aligned}$$

(6.7)

The first equation is just the first order variational equation along particular solution $\varvec{q}_0(t)$. It is denoted by $\mathrm {VE}_{1}$. The second one, denoted by $\mathrm {VE}_{2}$, is a non-homogeneous linear equation. Its homogeneous part coincides with that of $\mathrm {VE}_{1}$.

Systems with homogeneous potentials have nice property. Namely, they admit particular solutions of the form $\varvec{q}_0(t):=\varphi (t)\varvec{d}$, where $\varvec{d}$, called a Darboux point of V, is a non-zero solution of non-linear equations

$$\begin{aligned} V'(\varvec{d})=\varvec{d}, \end{aligned}$$

(6.8)

and $\varphi (t)$ is a scalar function satisfying differential equation ${\ddot{\varphi }} = -\varphi ^{k-1}$. For this solution $V''(\varvec{q}_0(t))=\varphi (t)^{k-2}V''(\varvec{d})$, and $V'''(\varvec{q}_0(t))=\varphi (t)^{k-3}V'''(\varvec{d})$ thanks to the homogeneity of potential V. Moreover, one can assume that $V''(\varvec{d})={\text {diag}}(\lambda _1, \ldots ,\lambda _n)$. Using this we can rewrite variational equations (6.6) and (6.7) in the following form

$$\begin{aligned} {\ddot{q}}_{i,1}= & {} -\lambda _i \varphi (t)^{k-2} q_{i,1}, \end{aligned}$$

(6.9)

$$\begin{aligned} {\ddot{q}}_{j,2}= & {} -\lambda _j\varphi (t)^{k-2} q_{j,2} - \varphi (t)^{k-3} \sum _{r,s=1}^2 A_{j}^{r,s} q_{r,1} q_{s,1}, \end{aligned}$$

(6.10)

where $i,j =1,\ldots ,n$, and

$$\begin{aligned} \varvec{q}_{m}=(q_{1,m},\ldots , q_{n,m}), \qquad A_{j}^{r,s}= -\frac{\partial ^3V}{\partial q_r \partial q_s \partial q_j}(\varvec{d}). \end{aligned}$$

Let us notice that $\mathrm {VE}_{1}$ splits into a direct product of equations of the form

$$\begin{aligned} {\ddot{q}} = - \lambda \varphi (t)^{k-2} q . \end{aligned}$$

(6.11)

Now, it is clear that on the level of $\mathrm {VE}_{1}$ if a system with a homogeneous potential is integrable, then the differential Galois group of equation (6.11) is virtually Abelian for each $\lambda =\lambda _i, i=1,\ldots ,n$. At this point, all the success of the theory is based on the brilliant idea of H. Yoshida who introduced in Yoshida (1987) transformation

$$\begin{aligned} t\longmapsto z:= \varphi (t)^k, \end{aligned}$$

(6.12)

after that Eq. (6.11) reads

$$\begin{aligned} q'' +a(z)q' +b(z) q =0 , \end{aligned}$$

(6.13)

where

$$\begin{aligned} a(z) = \frac{k-1}{kz} -\frac{z}{2(1-z)}, \qquad b(z)= \frac{\lambda }{z(1-z)}. \end{aligned}$$

This is the Gauss hypergeometric equation. Putting

$$\begin{aligned} q= w\exp \left[ -\frac{1}{2}\int a(z) \right] \end{aligned}$$

(6.14)

we obtain its reduced form

$$\begin{aligned} w''= r(k,\lambda )w, \qquad r(k,\lambda )(z)= \frac{1}{2}a'(z) +\frac{1}{4}a(z)^2 - b(z). \end{aligned}$$

(6.15)

Thanks to the fact that the differential Galois group for Gauss hypergeometric equation is well known by results of Kimura (1969/1970) we have the following theorem due to Morales-Ruiz and Ramis, see Morales-Ruiz (1999); Morales-Ruiz and Ramis (2001a).

Theorem 6.4

Assume that the Hamiltonian system defined by Hamiltonian (6.3) with a homogeneous potential $V\in \mathbb {C}(\varvec{q})$ of degree $k\in \mathbb {Z}\setminus \{0\}$ satisfies the following conditions:

• 1. the potential has a Darboux point $\varvec{d}\in \mathbb {C}^n\setminus \{{{\mathbf {0}}}\}$ satisfying $V'(\varvec{d})=\varvec{d}$;

• 2. matrix $V''(\varvec{d})$ is diagonalisable with eigenvalues $\lambda _1, \ldots , \lambda _n$;

• 3. the system is integrable in the Liouville sense with meromorphic first integrals.

Then each pair $(k,\lambda _i)$ for $i=1,\ldots ,n$ belongs to an item of the following list

$$\begin{aligned} \begin{array}{clcl} 1.&{} \left( k, p + \dfrac{k}{2}p(p-1)\right) ,&{}2.&{} \left( k,\dfrac{1}{2}\left[ \dfrac{k-1}{k}+p(p+1)k\right] \right) , \\ 3.&{} \left( 2, \text {arbitrary}\right) ,&{}4.&{} \left( -2, \text {arbitrary}\right) , \\ 5.&{} \left( 3,-\dfrac{1}{24}+\dfrac{1}{6}\left( 1 +3p\right) ^2\right) , &{} 6.&{} \left( 3,-\dfrac{1}{24}+\dfrac{3}{32}\left( 1 +4p\right) ^2\right) ,\\ 7.&{} \left( 3,-\dfrac{1}{24}+\dfrac{3}{50}\left( 1 +5p\right) ^2\right) ,&{} 8.&{} \left( 3,-\dfrac{1}{24}+\dfrac{3}{50}\left( 2 +5p\right) ^2\right) ,\\ 9.&{} \left( 4,-\dfrac{1}{8} +\dfrac{2}{9} \left( 1+ 3p\right) ^2\right) ,&{} 10.&{} \left( 5,-\dfrac{9}{40}+\dfrac{5}{18}\left( 1+ 3p\right) ^2\right) ,\\ 11.&{} \left( 5,-\dfrac{9}{40}+\dfrac{1}{10}\left( 2+5p\right) ^2\right) ,&{} 12.&{}\left( -3,\dfrac{25}{24}-\dfrac{1}{6}\left( 1+ 3p\right) ^2\right) ,\\ 13.&{}\left( -3,\dfrac{25}{24}-\dfrac{3}{32}\left( 1+4p\right) ^2\right) ,&{} 14.&{}\left( -3,\dfrac{25}{24}-\dfrac{3}{50}\left( 1+5p\right) ^2 \right) ,\\ 15.&{}\left( -3,\dfrac{25}{24}-\dfrac{3}{50}\left( 2+5p\right) ^2\right) ,&{} 16.&{}\left( -4,\dfrac{9}{8}-\dfrac{2}{9}\left( 1+ 3p\right) ^2\right) ,\\ 17.&{}\left( -5,\dfrac{49}{40}-\dfrac{5}{18}\left( 1+3p\right) ^2\right) ,&{} 18.&{}\left( -5,\dfrac{49}{40}-\dfrac{1}{10}(2 +5p)^2\right) ,\\ \end{array} \end{aligned}$$

(6.16)

where p is an integer.

To derive stronger necessary conditions to the integrability one can investigate the second order variational equations (6.10). However, these equations do not have a form of the direct product of separate second order equations. Nevertheless, as it was observed in Duval and Maciejewski (2014, (2015), instead of study the whole system (6.9) and (6.10), it is possible to extract their subsystems. Let us fix $\alpha , \in \{1,\ldots ,n\}$ and put $q_{i,1}=\dot{q}_{i,1}=0$ for $i\ne \alpha$. In this way we obtain $n^2$ subsystems of the form

$$\begin{aligned} {\ddot{q}}_{\alpha ,1}= & {} -\lambda _\alpha \varphi (t)^{k-2} q_{\alpha ,1},\nonumber \\ {\ddot{q}}_{\gamma ,2}= & {} -\lambda _\gamma \varphi (t)^{k-2} q_{\gamma ,2} + \varphi (t)^{k-3}A_{\gamma }^{\alpha ,\alpha } q_{\alpha ,1}^2. \end{aligned}$$

(6.17)

Now, again as in the case of $\mathrm {VE}_{1}$ it is crucial to perform the Yoshida transformation followed by the transformation to the reduced form (6.14). As a result we obtain

$$\begin{aligned} x''= & {} r(k,\lambda _{\alpha }) x, \nonumber \\ y''= & {} r(k,\lambda _{\gamma }) y + \omega x^2, \qquad \omega = z^{-(3k+1)/(2k)}(1-z)^{-5/4}. \end{aligned}$$

(6.18)

The basic assumption for further considerations is that equation $x'' = r(k,\lambda _{\alpha }) x$ has one solution $x_1$ that is algebraic over field $K:=\mathbb {C}(z)[\omega ]$ and the other solution $x_2$ is transcendent. Moreover, equation $y'' = r(k,\lambda _{\gamma }) y$ has the same property, and the respective solutions are denoted by $y_1$ and $y_2$.

According to the theory developed in Duval and Maciejewski (2015), the analysis begins from calculation of the integral

$$\begin{aligned} \Phi := \int \omega y_1 x_1^2. \end{aligned}$$

(6.19)

An ‘easy’ part follows if $\Phi$ is not algebraic. In the case considered in this paper $\Phi$ is algebraic, so we have to pass to more elaborated part of the theory. However here, we just extract a part of final results which are necessary in this paper. All details the interested reader can find in Duval and Maciejewski (2015).

Let us define the following integrals

$$\begin{aligned} I_{\alpha } = \int \frac{1}{x_1^2}, \qquad I_{\gamma }=\int \frac{1}{y_1^2}, \qquad \Psi _{\alpha }=\int \Phi I'_{\alpha },\qquad \Psi _{\gamma }=\int \Phi I'_{\gamma }. \end{aligned}$$

(6.20)

The theorem below is a part of Theorem 5.3 from Duval and Maciejewski (2015).

Theorem 6.5

Assume that $\Phi$ is algebraic and that the differential Galois group of equations (6.18) is virtually Abelian. Then:

• 1. there exists $d_{\alpha }\in \mathbb {C}$ such that $\Psi _{\alpha }+d_{\alpha }I_{\alpha }\in K$;

• 2. there exists $d_{\alpha }, d_{\gamma }\in \mathbb {C}$ such that $\Psi _{\gamma }+d_{\alpha }I_{\alpha } + d_{\gamma } I_{\gamma }\in K$;

• 3. if in the previous relation $d_{\alpha }\ne d_{\gamma }$, then there exist $c_{\alpha }, c_{\gamma }\in \mathbb {C}$ such that $|c_{\alpha } |+|c_{\gamma } |>0$ and $c_{\alpha }I_{\alpha } + c_{\gamma } I_{\gamma }\in K$.

To use the above theorem effectively we have to know how to check relations listed in the successive items of this theorem. Generally it is a difficult task but for the purpose of this paper it is enough to use Lemma 4.3 from Duval and Maciejewski (2015). Here we formulate it in a simplified form.

Let $L\supset \mathbb {C}(z)$ be an algebraic extension of $\mathbb {C}(z)$. We take $f, g \in L$ and put $F=\int f$ and $G=\int g$. For $z_0\in \mathbb {C}$, by $M_{z_0}$ we denote the monodromy operator. For $h\in L$, function $M_{z_0}(h)$ is the continuation of h around a small loop encircling $z_0$. In the case when $h\in \mathbb {C}(z)$, we have $M_{z_0}(h)=h$.

Lemma 6.6

Assume that $G=\int g$ is not algebraic and that for a certain $z_0$

$$\begin{aligned} M_{z_0}(g) = \chi (g) g , \qquad M_{z_0}(f) = \chi (f) f, \end{aligned}$$

where $\chi (g), \chi (f)\in \mathbb {C}$. If $\chi (g)\ne \chi (f)$, then for any $d\in \mathbb {C}$, element $G + d F$ does not belong to L.