Earth–Mars transfers with ballistic capture

Abstract

We construct a new type of transfer from the Earth to Mars, which ends in ballistic capture. This results in substantial savings in capture $\varDelta v$ from that of a classical Hohmann transfer under certain assumptions as well as an alternate way for spacecraft to transfer to Mars. This is accomplished by first becoming captured at Mars, very distant from the planet, and then from there, following a ballistic capture transfer to a desired altitude within a ballistic capture set. This is achieved by using stable sets, which are sets of initial conditions whose orbits satisfy a definition of orbital stability. This transfer type may be of interest for Mars missions because of low capture $\varDelta v$, flexibility of launch period from the Earth, moderate flight time, and the benign nature of the capture process.

Appendices

Appendix 1: Summary of precise definitions of stable sets and weak stability boundary

Trajectories of $P$ satisfying the following conditions are studied (see García and Gómez 2007; Topputo and Belbruno 2009; Hyeraci and Topputo 2010).

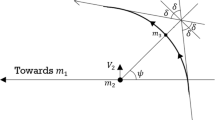
• (i) The initial position of $P$ is on a radial segment $l(\theta )$ departing from $P_2$ and making an angle $\theta$ with the $P_1$–$P_2$ line, relative to the rotating system. The trajectory is assumed to start at the periapsis of an osculating ellipse around $P_2$, whose semi-major axis lies on $l(\theta )$ and whose eccentricity $e$ is held fixed along $l(\theta )$.

• (ii) In the $P_2$-centered inertial frame, the initial velocity of the trajectory is perpendicular to $l(\theta )$, and the Kepler energy, $H_2$, of $P$ relative to $P_2$ is negative; i.e., $H_2<0$ (ellipse periapsis condition). The motion, for fixed values of $e$, $f_0$, $\theta$ depends on the initial distance $r$ only.

• (iii) The motion is said to be $n$-stable if the infinitesimal mass $P$ leaves $l(\theta )$, makes $n$ complete revolutions about $P_2$, $n \ge 1$, and returns to $l(\theta )$ on a point with negative Kepler energy with respect to $P_2$, without making a complete revolution around $P_1$ along this trajectory. The motion is otherwise said to be $n$-unstable (see Fig. 10).

Fig. 10

Stable and unstable motions

The set of $n$-stable points on $l(\theta )$ is a countable union of open intervals

$$\begin{aligned} {\mathcal {W}}_n(\theta , e, f_0) = \bigcup _{k \ge 1}\left( r^*_{2k-1}, r^*_{2k}\right) , \end{aligned}$$

(8)

with $r_1^*=0$. The points of type $r^*$ (the endpoints of the intervals above, except for $r^*_1$) are $n$-unstable. Thus, for fixed pairs $(e, f_0)$, the collection of $n$-stable points is

$$\begin{aligned} {\mathcal {W}}_n(e, f_0) = \!\!\!\!\bigcup _{\theta \in [0,2\pi ]} {\mathcal {W}}_n (\theta , e, f_0). \end{aligned}$$

(9)

The weak stability boundary of order $n$, $\partial {\mathcal {W}}_n$, is the locus of all points $r^*(\theta , e, f_0)$ along the radial segment $l(\theta )$ for which there is a change of stability of the trajectory; i.e., $r^*(\theta , e, f_0)$ is one of the endpoints of an interval $(r^*_{2k-1}, r^*_{2k})$ characterized by the fact that, for all $r \in (r^*_{2k-1}, r^*_{2k})$, the motion is $n$-stable, and there exist $\tilde{r} \not \in (r^*_{2k-1}, r^*_{2k})$, arbitrarily close to either $r^*_{2k-1}$ or $r^*_{2k}$ for which the motion is $n$-unstable. Thus,

$$\begin{aligned} \partial {\mathcal {W}}_n(e, f_0) = \{r^*(\theta , e, f_0)\, |\, \theta \in [0,2\pi ] \}. \end{aligned}$$

Appendix 2: Computation of reference Hohmann transfers

The physical constants used in this work are listed in Table 4. As both the Earth and Mars are assumed as moving on elliptical orbits, there are four cases in which a bitangential transfer is possible, depending on their relative geometry. These are reported in Table 5, where ‘@P’ and ‘@A’ mean ‘at perihelium’ and ‘at aphelium’, respectively. In Table 5, $\varDelta V_1$ is the maneuver needed to leave the Earth orbit, whereas $\varDelta V_{2, \infty }$ is the maneuver needed to acquire the orbit of Mars; these two impulses are calculated by considering the spacecraft already in heliocentric orbit, and therefore $\varDelta V_1$, $\varDelta V_{2,\infty }$ are equivalent to the escape, incoming hyperbolic velocities, respectively. $\varDelta V$ and $\varDelta t$ are the total cost and flight time, respectively. The use of the notation, $\varDelta V_{2,\infty }$ is to distinguish from the use of $\varDelta V_2$ used in Sect. 6 for the actual maneuver cost at $r_p$.

Table 4 Physical constants used in this work

From the figures in Table 5 it can be inferred that although the total cost presents minor variations among the four cases, the costs for the two maneuvers change considerably. That is, by arbitrary picking one of the four bitangential solutions as reference we can have different outcomes on the performance of the ballistic capture orbits devised. Because there is a substantial variation, an averaging does not yield useful results, and therefore, each case is considered.

Table 5 Bitangential transfers and Hohmann transfer