A Simple Method for Simulating Wind Profiles in the Boundary Layer of Tropical Cyclones

Abstract

A method to simulate characteristics of wind speed in the boundary layer of tropical cyclones in an idealized manner is developed and evaluated. The method can be used in a single-column modelling set-up with a planetary boundary-layer parametrization, or within large-eddy simulations (LES). The key step is to include terms in the horizontal velocity equations representing advection and centrifugal acceleration in tropical cyclones that occurs on scales larger than the domain size. Compared to other recently developed methods, which require two input parameters (a reference wind speed, and radius from the centre of a tropical cyclone) this new method also requires a third input parameter: the radial gradient of reference wind speed. With the new method, simulated wind profiles are similar to composite profiles from dropsonde observations; in contrast, a classic Ekman-type method tends to overpredict inflow-layer depth and magnitude, and two recently developed methods for tropical cyclone environments tend to overpredict near-surface wind speed. When used in LES, the new technique produces vertical profiles of total turbulent stress and estimated eddy viscosity that are similar to values determined from low-level aircraft flights in tropical cyclones. Temporal spectra from LES produce an inertial subrange for frequencies $\gtrsim$0.1 Hz, but only when the horizontal grid spacing $\lesssim$20 m.

1 Introduction

Numerical model simulations have been used to help understand tropical cyclones for decades. Standard three-dimensional simulations can, of course, represent many dynamical processes in a tropical cyclone, including the centrifugal acceleration associated with rapidly rotating flow, and the large-scale pressure gradient acceleration that acts to counter centrifugal effects. However, substantial computational resources are often needed for three-dimensional simulations because tropical cyclones span several hundreds of kilometres in the horizontal, and require several days of model integration time. As a relatively inexpensive option, two-dimensional simulations using axisymmetric equations can be used to study many aspects of tropical cyclones. However, even axisymmetric model simulations become expensive to run, especially with continued advances in representation of physical processes such as atmospheric radiation, multi-moment microphysical schemes, and ocean feedback effects, to name but a few. Additionally, axisymmetric models are complex and difficult to modify, and interactions between the various physical parametrizations make it difficult to isolate cause and effect if tropical cyclone structure varies among different simulations.

Moreover, interest is growing in the use of large-eddy simulation (LES) to study the boundary layer of tropical cyclones (roughly, the lowest kilometre above the surface). The primary advantage of LES, of course, is that the statistical properties of turbulent flow can be predicted primarily by the model’s governing equations, with only a small role being played by a subgrid turbulence scheme. Furthermore, coherent structures within the tropical cyclone boundary layer such as quasi-two-dimensional roll vortices (e.g., Foster 2005; Morrison et al. 2005) can only be resolved using grid spacing of $\approx$100 m or less, i.e., typical resolution for LES. However, tropical cyclones extend hundreds of km horizontally, and so LES becomes prohibitively expensive unless the domain size is restricted, thereby making it difficult to account for the dynamical processes in rapidly rotating flow mentioned above (e.g., centrifugal acceleration).

For these reasons, an inexpensive and simple method to study the boundary layer of a tropical cyclone is developed and evaluated herein. This new method can be used in a “single column modelling” framework, in which height z is the only coordinate. In this case, the large-scale inertial and pressure-gradient acceleration terms are included in the governing equations via mesoscale tendency terms (described in the next section) that are similar to those pioneered for boundary-layer modelling by Sommeria (1976). With only minor modifications, these mesoscale tendency terms can also be included within LES, which allows domain sizes to be only a few km in horizontal extent, making high-resolution LES (with grid spacing of O(10) m or less) computationally tractable.

Fig. 1

Conceptual schematic of the modelling framework. A LES domain is shown as a white box. (For single-column model simulations, the model domain is technically infinitesimal in horizontal extent.) The distance from the centre of the tropical cyclone to the centre of the model domain is R. Colour shading illustrates idealized near-surface wind speed U, which is largest ($U = U_{{max}}$) at the radius of maximum winds ($R_{{max}}$). The direction of near-surface flow outside $R_{{max}}$ is illustrated with arrows

With these points in mind, the overall conceptual set-up for this new methodology is that the scale of the LES domain is much smaller than the scale of the entire tropical cyclone, as illustrated schematically in Fig. 1. We envision domain sizes of O(5 km) on a side, which is similar to the horizontal grid spacing for present-day numerical weather prediction systems (e.g., Tallapragada et al. 2014), and is comparable to typical LES domain sizes. The primary circulation of a tropical cyclone, quantified by the tangential velocity (i.e., magnitude of flow around circles centered on the tropical cyclone), is imposed as an initial condition for model simulations and, as discussed below, we consider the radial gradient of tangential velocity to be an important input parameter in our framework because it allows us to include large-scale advection tendencies as in Sommeria (1976); a key difference from Sommeria’s approach, however, is that we utilize model-predicted wind profiles in the mesoscale tendency terms, i.e., advection tendencies are not simply specified and held fixed throughout the simulation. The goal is to allow the model to predict details of the secondary circulation (via the radial velocity profile) after a user essentially specifies the primary circulation (via a few input parameters, namely, a reference wind-speed profile, and its radial gradient). This general concept is very similar to recent studies of tropical cyclones by Kepert and Wang (2001), Foster (2009), and Kepert (2012), although a key difference is that our approach is essentially one-dimensional (in height, z) rather than two-dimensional (radius and height). It is also not clear how several terms from these studies should be included in small-domain, three-dimensional LES (see Fig. 1). Some further comparison to previous studies is provided below (Sect. 2.3).

Compared to other recent studies of the tropical cyclone boundary layer, our method accounts for the advection of momentum by the secondary circulation of the tropical cyclone. Of note, Nakanishi and Niino (2012) and Green and Zhang (2015) considered centrifugal acceleration terms in their model equations, as does our new method, but we show herein that inclusion of radial advection is needed to produce mean wind profiles that are similar to observed profiles in tropical cyclones.

In Sect. 2, we explain the design of the mesoscale tendency terms, using a previously analyzed axisymmetric model simulation for reference. Single-column model simulations are presented and evaluated in Sect. 3, followed by large-eddy simulations in Sect. 4. We summarize this work and provide concluding remarks in Sect. 5.

2 Processes in the Tropical Cyclone Boundary Layer

2.1 Axisymmetric Model Details

To clarify the most important processes in the tropical cyclone boundary layer that must be included for an accurate simulation, we first examine an axisymmetric model simulation of an idealized tropical cyclone. This simulation produces similar flow structures compared with composite observations encompassing many tropical cyclones (e.g., Zhang et al. 2011) such as inflow-layer depth $\approx$1 km, surface inflow angle $\approx$23$^\circ$, and a height of maximum wind speed roughly 500 m above sea level (a.s.l.), as discussed in more detail by Bryan (2012).

Extensive details of this axisymmetric model can be found in Bryan and Rotunno (2009). The simulation analyzed here is nearly the same as the “Setup B” configuration of Bryan (2012) except for a few details of the surface-layer and planetary boundary-layer (PBL) schemes, as explained below. The radial grid spacing is 1 km for radius (r) <250 km, and vertical grid spacing is 20 m at the surface but increases gradually to 250 m at the top of the domain ($z = 25$ km a.s.l.).

Fig. 2

Output from an axisymmetric model simulation of a tropical cyclone: a components of velocity (tangential velocity $u_\phi$ in shading, and radial velocity $u_r$ in black contours), b terms in the $u_\phi$ budget at $r = 40$ km, and c terms in the $u_r$ budget at $r = 40$ km. In a the contour interval for $u_r$ is 4 m s$^{-1}$, negative values are dashed, and the the zero contour is excluded; the blue contour denotes the eyewall (estimated by vertical velocity $w =$ 1 m s$^{-1}$). In b and c, the grey curves show Coriolis acceleration, the red curves show the tendency from the PBL parametrization, and the blue curves show the mesoscale tendency terms. Black curves in b and c denote various components of the mesoscale tendency, as indicated: dotted lines radial advection; dashed lines centrifugal acceleration, dashed dotted lines pressure-gradient acceleration

PBL processes must be parametrized in axisymmetric models, and the PBL scheme for this simulation is a variant of that used by Rotunno and Emanuel (1987), also known as a “Louis PBL scheme” (e.g., Kepert 2012) (after Louis 1979). This scheme determines an eddy viscosity K from the local vertical deformation ($S_v$) and moist Brunt–Vaisala frequency ($N_m$),

$$\begin{aligned} K = {l_v} ^2 ( {S_v}^2 - {N_m}^2 )^{1/2} \end{aligned}$$

(1)

(for formulations of ${S_v}^2$ and ${N_m}^2$, see Bryan and Rotunno 2009, p. 1773). The vertical length scale $l_v (z)$ is determined from the relation $l_v^{-2} = l_\infty ^{-2} + [\kappa ( z + z_0 ) ]^{-2}$ (e.g., Mason and Thompson 1992) where $l_\infty = 75$ m (following Bryan 2012), $\kappa = 0.4$, and $z_0$ is the aerodynamic roughness length. At the surface, a bulk exchange scheme (e.g., Rotunno and Emanuel 1987) is used to determine heat fluxes, with the surface exchange coefficient for both sensible and latent heat a constant, $1.2 \times 10^{-3}$ (based on, Zhang et al. 2008a). The surface stress is based on a simple formulation for the drag coefficient $C_d$ (following, Donelan et al. 2004) where

$$\begin{aligned} C_d = {\left\{ \begin{array}{ll} 1 \times 10^{-3} &{}\text{ for } U_{10} \le 5 \text{ m } \text{ s }^{-1} \\ 1 \times 10^{-3} + c ( U_{10} - 5 ) &{}\text{ for } 5 \text{ m } \text{ s }^{-1}< U_{10} < 25 \text{ m } \text{ s }^{-1} \\ 2.4 \times 10^{-3} &{}\text{ for } U_{10} \ge 25 \text{ m } \text{ s }^{-1} . \end{array}\right. } \end{aligned}$$

(2)

in which $U_{10}$ is wind speed at a height of 10 m a.s.l., and $c = 7 \times 10^{-5}$ s m$^{-1}$. A standard logarithmic-layer relation for neutral conditions, $U (z) = ( u_* / \kappa ) \ln { \left[ ( z+z_0) / z_0 \right] }$, is used to determine both friction velocity $u_*$ and $U_{10}$ using an iterative scheme, given horizontal wind speed at the lowest model level. Roughness length is determined from $C_d$ using the relation $z_0 = 10 / \exp { (\kappa / \sqrt{C_d}})$, and for reference, we note that $z_0$ = 2.8 mm for $U_{10} \ge 25$ m s$^{-1}$.

2.2 Mesoscale Tendency Terms

Figure 2a shows tangential velocity ($u_\phi$, shaded) and radial velocity ($u_r$, contours) averaged over days 8–12 of the simulation, a time period when the simulated tropical cyclone is quasi-steady (i.e., local time-tendency terms in the velocity budgets are negligible). We are here interested in the region outside the eyewall [i.e., for r greater than the radius of maximum wind ($R_{{max}}$)] where the tropical cyclone boundary layer is typically characterized by radial inflow ($u_r < 0$) and vertical advection is typically much smaller than radial advection.

The leading tendency terms of the $u_\phi$ budget at $r = 40$ km are shown in Fig. 2b. (All other terms are at least one order of magnitude smaller.) At this location, the tendency from the PBL parametrization (red curve) is countered by what we refer to as a “mesoscale tendency” term (blue curve), which is the sum of several terms associated with the mesoscale flow patterns in a tropical cyclone. For the $u_\phi$ budget, the mesoscale tendency term is simply 1 / r times the radial advection of absolute angular momentum, or

$$\begin{aligned} - \frac{u_r}{r} \frac{\partial M}{\partial r} = - u_r \frac{ \partial u_\phi }{ \partial r } - \frac{ u_r u_\phi }{ r } - f u_r \, , \end{aligned}$$

(3)

where $M \equiv r u_\phi + 0.5 f r^2,$ and f is the Coriolis parameter (assumed constant herein). The three terms on the right side of (3) are, respectively, radial advection, centrifugal acceleration, and Coriolis acceleration.

As discussed in Sect. 1, in our simple modelling framework (Fig. 1) the primary circulation of the tropical cyclone is essentially specified at the beginning of a simulation by the model user. In this spirit, we choose to specify a reference tangential velocity profile V at a distance R from the tropical cyclone centre, in addition to its radial gradient $\partial V / \partial R$. Considering these as input parameters that do not change during a simulation, and understanding that the model-predicted profiles of wind speed are used to account for the secondary circulation of a tropical cyclone (via model-predicted profile of $u_r$), we consider the following form for the mesoscale tendency for $u_\phi$ ($M_\phi$),

$$\begin{aligned} M_\phi = \underbrace{ - u_r \frac{\partial V}{\partial R} }_{\text {I}} \quad \underbrace{ - u_r \frac{V}{R} }_{\text {II}} , \end{aligned}$$

(4)

where term I is the radial advection and term II is the centrifugal acceleration. We do not account for the Coriolis acceleration in the mesoscale tendency terms, since this term is straightforward to represent in a numerical model of any scale. The variables V and $\partial V / \partial R$ may be functions of height, or could be considered constant with height for shallow domains of a few km depth. Several recent studies (Nakanishi and Niino (2012), hereafter NN12; Green and Zhang (2015), hereafter GZ15) have included centrifugal-like terms in their model equations, similar to the second term of (4). However, inclusion of an advection term (first term) makes this approach clearly different from these recent studies.

Considering now the processes that affect radial velocity $u_r$, we return our attention to the axisymmetric model and note that tendencies from the PBL scheme (red in Fig. 2c) are again countered by a mesoscale tendency (blue in Fig. 2c). For this component of velocity, the mesoscale tendency can be considered the sum of four terms: radial advection, centrifugal acceleration, Coriolis acceleration, and radial pressure-gradient acceleration. Our formulation for the mesoscale tendency to $u_r$ ($M_r$) must account for these terms, although we again consider the Coriolis term to be represented in the model equations in a standard manner, and account for the other three terms for $M_r$, as described below.

For the terms in the mesoscale tendency that represent centrifugal acceleration ($\left. M_\phi \right| _{{cent.}} = -u_r V /R$ from above, and $\left. M_r \right| _{{cent.}}$ to be determined below), energetic consistency requires that

$$\begin{aligned} \frac{ \partial (u_r^2/2) }{ \partial t } + \frac{ \partial (u_\phi ^2/2) }{ \partial t } = \left. u_r M_r \right| _{{cent.}} + \left. u_\phi M_\phi \right| _{{cent.}} =0. \end{aligned}$$

(5)

Consequently, from (4) and (5), the centrifugal term in the radial velocity tendency must be

$$\begin{aligned} \left. M_r \right| _{cent.} = + u_\phi \frac{V}{R} . \end{aligned}$$

(6)

This term has an unusual form in the sense that it contains both model-produced flow $u_\phi$ and the reference velocity V; this form is a consequence of the decision to use the model-predicted $u_r$ to advect the user-specified gradient of angular momentum in $M_\phi$, as discussed above.

For the pressure-gradient term, we assume this is determined from a gradient wind relation,

$$\begin{aligned} - \frac{1}{\rho } \frac{\partial p}{\partial r} = - f V - \frac{V^2}{R} \end{aligned}$$

(7)

where p is pressure and $\rho$ is air density. Here it becomes clear that the reference velocity V is the so-called gradient wind, i.e., the tengential velocity necessary to balance the pressure gradient via Coriolis and centrifugal terms. We note that, although V is assumed to be in gradient-wind balance, the model-predicted tangential velocity $u_\phi$ does not need to obey such a relation.

Finally, for the radial advection term, in order to have a convenient form (in the spirit of the “simple” approach desired herein) we make the approximation

$$\begin{aligned} - u_r \frac{\partial u_r}{\partial r} \approx + \frac{u_r^2}{R}, \end{aligned}$$

(8)

by using the mass-continuity equation for axisymmetric flow,

$$\begin{aligned} \frac{\partial u_r}{\partial r} + \frac{u_r}{r} + \frac{\partial w}{\partial z} = 0 \end{aligned}$$

(9)

and then assuming the last term on the left-hand side is negligible. This assumption, $| \partial w / \partial z |<< | (1/r) \, \partial (r u_r ) / \partial r |$, contrasts with the usual assumption that these two terms are comparable (Smith 1968). However, as shown below, this assumption is reasonably accurate for the axisymmetric simulation outside of the eyewall where radial variations in $u_r$ are greater than vertical variations in w. We also note that the advection of $u_r$ is a fairly small component of the radial velocity budget (Fig. 2), at least for regions outside the eyewall. Finally, as in Foster (2005), NN12, and GZ15, we neglect variations in r, and simply use the constant R, for the right-hand side of (8).

Assembling the three components into one relation, we have

$$\begin{aligned} M_r = \underbrace{ +\frac{u_r^2}{R} }_{\text {I}} \quad \underbrace{ + u_\phi \frac{V}{R} }_{\text {II}} \quad \underbrace{ - f V - \frac{V^2}{R} }_{\text {III}} , \end{aligned}$$

(10)

where term I is the radial advection, term II is the centrifugal acceleration, and term III is the pressure-gradient acceleration. We consider the relations (4) and (10) to be the core of our new modelling method, which is analyzed using numerical simulations in Sects. 3 and 4. We note that, as a consequence of assumptions made in this section, this method is applicable only outside the eyewall of a tropical cyclone (i.e., for $r > R_{{max}}$, see Fig. 1) where $u_r$ and $\partial V / \partial R$ are typically negative, and where vertical advection terms are typically negligible compared to radial advection.

2.3 Comparison to Previous Studies

Some aspects of our mesoscale tendency terms [(4) and (10)] make our study different from other recent numerical studies of the tropical cyclone boundary layer. One major difference is that we intend to utilize these relations at a single point in the flow, in which height z is the only dimension (i.e., single-column modelling). Even for our large-eddy simulations, the horizontal dimensions of the domain are presumed small (e.g., Fig. 1) and so we choose to treat the mesoscale tendencies analogously for LES (details of the LES implementation of these terms are provided in Sect. 4). Consequently, tendency terms that contain radial gradients (e.g., radial advection) must be treated differently as compared to studies that have both r and z as dimensions. In fact, a major motivation for using the approximation (8) is so $\partial u_r / \partial r$ does not need to be specified as an input parameter. For these reasons, the radial advection and centrifugal acceleration terms are subtly different compared to other seemingly similar studies of the tropical cyclone boundary layer (e.g., Kepert and Wang 2001; Foster 2009). We also note that, for radial diffusion and turbulence, we have chosen to neglect these terms because of their complex form, and the lack of a clear method to simplify them for single-column modelling, even though radial turbulence can be important in tropical cyclones (e.g., Rotunno and Bryan 2012), although typically only in the eyewall where the present approach is not valid.

We also clarify that our approximate equations are not derived via linearization of the governing equations, as in Kepert (2001) and Foster (2005). Our underlying approach is essentially a scale analysis in which relatively small terms are neglected. The budgets from a single axisymmetric simulation of an intense tropical cyclone are used here as an example (Fig. 2), but the conclusions are consistent with our previous work (e.g., Rotunno and Bryan 2012). Although we have neglected vertical advection (we reiterate: outside of the eyewall), some studies have found it to be an important contributor, especially in the $u_\phi$ budget (e.g., Kepert and Wang 2001, their Fig. 9). This assumption is not critical to our modelling approach, as vertical advection terms could easily be added to (4) and (10) following the approach of Sommeria (1976). Vertical velocity could also be determined from the simulated flow fields [$u_r(z)$ and $u_\phi (z)$] via the continuity equation, which has been used in several types of analytical and numerical models (e.g., Ooyama 1969; Emanuel 1986; Kepert 2001, 2013). We suspect that vertical advection terms are more important for weaker storms and/or broader storms than the one shown in Fig. 2, and we plan to investigate these issues in the future.

Finally, regarding the assumption that $\partial w / \partial z$ can be neglected in (9) [in contrast to the typical assumption (e.g., Smith 1968)], we provide the following scale analysis. For a point R in the flow with characteristic radial velocity $\overline{U}$, we assume its radial variation is $\delta \overline{U} / \delta R$. Further, assume the vertical variation of w is $\delta \overline{W} / H$, where H is the approximate depth of the inflow layer. Then the $\partial w / \partial z$ term can be neglected in (9) when $\delta \overline{W} / H<< \delta \overline{U} / \delta R$, and if valid, it follows from (9) that $\delta \overline{U} / \delta R \approx - \overline{U} / R$. Using these relations, we find $\delta \overline{W}<< - \overline{U} H / R$, and since $H/R < 0.1$ outside of the eyewall, and $\overline{U} \approx -10$ m s$^{-1}$, the assumption is valid when vertical velocity at the top of the inflow layer is roughly 0.05 m s$^{-1}$ or less. (Clearly, the assumption is not valid in tropical cyclone eyewalls, and the portions of rainbands with strong updrafts.)

The approximation of (9) is only used to estimate the radial advection of radial velocity. Using output from the axisymmetric simulation, we note that the resulting approximation, (8), is reasonable over a large part of the tropical cyclone (Fig. 3). Equation 8 becomes less accurate near the tropical cyclone eyewall where the underlying approximation $\delta \overline{W}<< - \overline{U} H / R$ no longer holds.

Fig. 3

Vertical profiles of the radial advection of radial velocity (solid curves) and estimates of the same field using (8) (dashed curves) at various radii as indicated. The results at $r = 100$ km are multiplied by 10 for clarity

2.4 Neglected Terms

As explained above, the mesoscale tendency terms (4) and (10) are not applicable in the eyewall of tropical cyclones, where vertical advection can be a leading-order process (e.g., Kepert and Wang 2001). They are probably also not applicable in certain parts of rainbands, especially where vertical velocity is large near the surface. Our goal has been to devise a simple set of tendency terms that can be added easily to single-column model simulations and small-domain LES for application over much (but clearly not all) of a tropical cyclone. The results reported in the following two sections demonstrate that our new approach has clear merits, especially when compared with other recently developed approaches.

To be clear about what processes are neglected in our approach, we consider the un-approximated axisymmetric velocity equations (e.g., Hinze 1975)

$$\begin{aligned} \frac{\partial u_r}{\partial t}&= -u_r \frac{\partial u_r}{\partial r} - w \frac{\partial u_r}{\partial z} + u_\phi \left( f + \frac{u_\phi }{r} \right) -\frac{1}{\rho } \frac{\partial p}{\partial r} +\frac{1}{\rho r} \left[ \frac{\partial \left( r \tau _{rr} \right) }{ \partial r } - \tau _{\phi \phi } \right] +\frac{1}{\rho } \frac{\partial \tau _{rz} }{ \partial z } \, , \end{aligned}$$

(11)

$$\begin{aligned} \frac{\partial u_\phi }{\partial t}&= -u_r \frac{\partial u_\phi }{\partial r} - w \frac{\partial u_\phi }{\partial z} - u_r \left( f + \frac{u_\phi }{r} \right) +\frac{1}{\rho r^2} \frac{\partial \left( r^2 \tau _{r \phi } \right) }{ \partial r } +\frac{1}{\rho } \frac{\partial \tau _{\phi z} }{ \partial z } \, , \end{aligned}$$

(12)

where the $\tau$ terms could represent molecular or turbulent stresses. Defining $u_\phi ^\prime (r,z,t) = u_\phi (r,z,t) - V (r,z)$, and making use of the continuity equation [only for the first term on the right-hand side of the $u_r$ equation], we arrive at the following without approximation,

$$\begin{aligned} \frac{\partial u_r}{\partial t}&= \underbrace{+\frac{ u_r^2 }{ r} + u_\phi \frac{V}{r} -\frac{1}{\rho } \frac{\partial p}{\partial r} }_{\text {I}} + f u_\phi +\frac{1}{\rho } \frac{\partial \tau _{rz} }{ \partial z } \, \underbrace{ + u_r \frac{\partial w}{\partial z} + u_\phi \frac{u_\phi ^\prime }{r} +\frac{1}{\rho r} \left[ \frac{\partial \left( r \tau _{rr} \right) }{ \partial r } - \tau _{\phi \phi } \right] }_{\text {II}} \, \underbrace{ - w \frac{\partial u_r}{\partial z} }_{\text {III}}, \end{aligned}$$

(13)

$$\begin{aligned} \frac{\partial u_\phi }{\partial t}&= \underbrace{ -u_r \frac{\partial V}{\partial r} - u_r \frac{V}{r} }_{\text {IV}} -f u_r +\frac{1}{\rho } \frac{\partial \tau _{\phi z} }{ \partial z } \, \underbrace{ -u_r \frac{\partial u_\phi ^\prime }{\partial r} - u_r \frac{u_\phi ^\prime }{r} +\frac{1}{\rho r^2} \frac{\partial \left( r^2 \tau _{r \phi } \right) }{ \partial r } }_{\text {V}} \, \underbrace{ - w \frac{\partial u_\phi }{\partial z} }_{\text {VI}}, \end{aligned}$$

(14)

where term I is $M_r$ and term IV is $M_\phi$, terms II and V are neglected, and terms III and VI are the vertical advection terms. Here, vertical advection is singled out separately because it could be included easily in simulations, and is not a fundamental component of our mesoscale tendency terms. The terms that are not specifically labeled (i.e., Coriolis and vertical stress terms) are typically included in boundary-layer studies, even the classic Ekman-type case (explained below). The only other approximations (aside from neglecting terms II and V) use (7) for the pressure-gradient term, and to replace r by R.

3 Single Column Modelling

3.1 Methodology

For single-column modelling the only dimension is z, and the horizontal velocity equations are simply

$$\begin{aligned} \frac{\partial u_r}{\partial t}&= M_r + f u_\phi + \frac{1}{\rho } \frac{\partial \tau _{rz} }{\partial z} \end{aligned}$$

(15)

$$\begin{aligned} \frac{\partial u_\phi }{\partial t}&= M_\phi - f u_r + \frac{1}{\rho } \frac{\partial \tau _{\phi z} }{\partial z} \, \end{aligned}$$

(16)

where $\tau _{rz}$ and $\tau _{\phi z}$ are parametrized turbulent stresses. The same PBL and surface-layer parametrizations from the axisymmetric model (Sect. 2a) are used, and unless specified otherwise, the M terms are given by (4) and (10). We also integrate a potential temperature ($\theta$) equation,

$$\begin{aligned} \frac{\partial \theta }{\partial t} = - \frac{1}{\rho } \frac{\partial \tau ^\theta _z }{\partial z} \end{aligned}$$

(17)

where $\tau ^\theta _z = - K \partial \theta / \partial z$ is the (parametrized) turbulent heat flux. Potential temperature is not needed for the velocity equations, Eqs. 15–16 but it indirectly affects the solutions through the turbulence parametrization, Eq. 1. Specifically, relatively strong stratification above the boundary layer forces the eddy viscosity K to small values above the PBL, and thus acts to limit growth of the boundary layer. Moisture is neglected herein for simplicity.

We integrate these equations using a third-order Runge–Kutta scheme, with vertical grid spacing of 25 m, and the domain depth of 4 km. To prevent reflection of vertically propagating waves, we apply a Rayleigh damper above 3 km. For initial conditions, we set $u = 0$ and $v (z) = V (z)$, with $\theta = 300$ K at the surface and increasing linearly with height at $5 \times 10^{-3}$ K m$^{-1}$. We use $f = 5 \times 10^{-5}$ s$^{-1}$ for all simulations herein.

Surface heat flux is neglected for these simulations. The implicit assumption here is that boundary-layer turbulence in tropical cyclones is driven primarily by mean vertical wind shear near the surface. Alternatively, we might hypothesize that, in an approximately steady tropical cyclone boundary layer, the net heating via the surface heat flux is exactly canceled by a mesoscale tendency, specifically horizontal advection, that could be added to (17). For convenience, we simply neglect both effects.

3.2 Results

The first example is based on conditions in the axisymmetric model simulation from Sect 2. We choose $R = 40$ km and, from the axisymmetric simulation at this radius, we find that constant values V = 38 m s$^{-1}$ and $\partial V/ \partial R = 8 \times 10^{-4}$ s$^{-1}$ are reasonable matches to the gradient wind for $z < 4$ km in the axisymmetric model [which is determined using (7) and the model-produced pressure field].

Profiles of $u_r$ and $u_\phi$ change rapidly in the first few hours of the simulation as the PBL parametrization modifies the (initially constant) wind profiles, and the mesoscale tendency terms alter with the simulated flow. Approximately steady results emerge after approximately 6 h. Profiles of the mesoscale tendency terms at $t = 12$ h are shown in Fig. 4 (blue curves), along with individual components (black curves) as in Fig. 2. The similarity between Fig. 2 (panels b–c) and Fig. 4 is encouraging. Some subtle quantitative differences are apparent, such as the stronger values of radial advection and centrifugal acceleration near the surface for the single-column model. Nevertheless, the overall shape and approximate magnitude of all terms are replicated reasonably well when using the mesoscale tendency terms (4) and (10).

Fig. 4

Tendency terms, a the $u_\phi$ budget (as in Fig. 2b), and b the $u_r$ budget (as in Fig. 2c), from a single-column model simulation using $R = 40$ km, $V = 38$ m s$^{-1}$, and $\partial V/ \partial R = -8 \times 10^{-4}$ s$^{-1}$

Fig. 5

Profiles of a tangential velocity $u_\phi$ and b radial velocity $u_r$ from single-column model simulations at $t = 12$ h. The dashed-green curve is from a simulation using classic Ekman-type mesoscale tendency terms, (18)–(19), and the red curve is from a simulation using the new method for mesoscale tendency terms, (4) and (10), with the same settings as in Fig. 4. The grey-dashed line is from the axisymmetric model at $r = 40$ km

Fig. 6

As in Fig. 4 but for the simulation using classic Ekman-type mesoscale tendency terms. Note a is the tangential velocity budget, b is the radial velocity budget

The predicted velocity profiles are shown in Fig. 5. The overall qualitative similarity between the single-column model (red curve in Fig. 5) and the axisymmetric model (grey curve) is also quite good, particular in terms of the shapes of both the $u_r$ and $u_\phi$ profiles. [The small-scale fluctuations in the profiles near the top of the boundary layer (at $z = 1.4$ km in this case) are present in all of our single-column simulations, and denote where the simple PBL scheme (Eq. 1) is not used when stratification becomes large; this is a minor cosmetic feature that can be eliminated by requiring that K have a minimum value of O(1 m$^2$ s$^{-1}$) (not shown).] The most noteworthy difference between the axisymmetric model and single-column model results is the magnitude of $u_r$ near the surface, which is $\approx$20 % weaker for the single-column model (Fig. 5b). There are several possible reasons for these differences, such as the assumed constant values for V and $\partial V / \partial R$ in this simulation, or the complete neglect of moisture, for example. It is more likely that the centrifigual acceleration is too large near the surface ($z < 100$ m) compared to the axisymmetric model simulation because we use V instead of $u_\phi$ in (4) and (10). However, we note that our results are reasonably accurate, and clearly improved on other approaches (as shown below).

To place these results into context, we also ran simulations with a classic Ekman-type formulation of the mesoscale tendency terms, which accounts only for large-scale geostrophic pressure gradients. (This approach is common in LES of shear-driven boundary layers.) Assuming $(1/\rho ) \partial p / \partial r = f V$, then mesoscale tendency terms for our set-up are simply

$$\begin{aligned} M_r^{\text {Ekman}} =&- f V \, , \end{aligned}$$

(18)

$$\begin{aligned} M_\phi ^{\text {Ekman}} =&\, 0 \, . \end{aligned}$$

(19)

Fig. 7

As in Fig. 5 but using different values of $\partial V / \partial R$ with the new method for mesocale tendency terms. (The red curve is the same as in Fig. 5)

We hereafter call this a classic “Ekman-type” formulation in the sense that the velocity equations include only large-scale pressure-gradient terms to oppose viscous terms, although unlike the classic analytic solution (see, e.g., Wyngaard 2010, pp. 208–209) the steady assumption is not made and viscosity is not assumed to be constant. Results using (18) and (19) [in place of $M_r$ and $M_\phi$ in (15) and (16)] are shown as green-dashed curves in Fig. 5. This simulation produces smaller $u_\phi$ over all depths, and stronger radial inflow above 200 m a.s.l. that extends over a deeper layer (up to 2 km a.s.l.). The mesoscale tendency terms using the Ekman-type simulation (Fig. 6) are roughly one order of magnitude smaller than using the new method (cf. Fig. 4). A consequence of these weak tendencies is that the PBL scheme reduces $u_\phi$ too much. In comparison, the new method has large-amplitude tendency terms that oppose the PBL tendencies. Results from our new method in comparison to results from the Ekman-type (Fig. 5) show obvious merits.

A possible shortcoming of the new method is a strong sensitivity to the input parameter $\partial V / \partial R$. As an example, wind profiles at $t = 12$ h from five simulations using different values of $\partial V / \partial R$ are shown in Fig. 7; as $\partial V / \partial R$ increases in magnitude, $u_\phi$ decreases and $u_r$ increases in magnitude. In fact, the largest magnitude of $\partial V / \partial R$ produces results similar to the classic Ekman-type solution; the reason is that the $-u_r (\partial V / \partial R)$ term becomes similar in magnitude to the $-u_r ( V / R )$ term in (4), and thus both terms cancel each other, leaving no mechanism to oppose the PBL tendency.

The value of $\partial V / \partial R$ for this first simulation was determined from our axisymmetric model simulation. For actual tropical cyclone cases, the value of $\partial V / \partial R$ may be uncertain, particularly for tropical cyclones far from land with few observations. However, we note that, if tangential velocity $u_\phi$ is a function of r according to a power law¹ that satisfies $u_\phi = V$ at $r = R$, i.e.,

$$\begin{aligned} u_\phi = V \left( \frac{r}{ R } \right) ^{-n} \end{aligned}$$

(20)

then it follows that

$$\begin{aligned} \frac{\partial u_\phi }{\partial r} = -n \frac{V}{R} \left( \frac{r}{R} \right) ^{-n-1} = -n \frac{u_\phi }{R} \left( \frac{r}{R} \right) ^{-1} \, , \end{aligned}$$

(21)

and so

$$\begin{aligned} \frac{ \partial u_\phi }{ \partial r } = -n \frac{u_\phi }{R} \, {\text { at }} \, r = R \, . \end{aligned}$$

(22)

Fig. 8

As in Fig. 5 except using profiles of V and $\partial V / \partial R$ that decrease linearly with height from maximum values at the surface of $V = 40$ m s$^{-1}$ and $\partial V / \partial R = -8 \times 10^{-4}$ s$^{-1}$. In addition, the method of Nakanishi and Niino (2012) (see Eq. 23) is shown by a solid-blue curve, and the method of Green and Zhang (2015) (see Eq. 24) is shown as a dashed-blue curve. The black curve is a composite of dropsonde observations for which mean 500–1000 m a.s.l. wind speed is between 35 and $45\hbox { m s}^{-1}$

Thus, our input parameter $\partial V / \partial R$ can be related to the other two input parameters (V and R) through a decay rate n. We note that the parameters used for the simulation in the first example give $\partial V / \partial R = -0.8 \times (V/R)$; consistently, the simulated vortex in the axisymmetric simulation has $u_\phi \sim r^{-0.8}$ near the surface at $r = 40$ km. Therefore, if $\partial V / \partial R$ is not known from observations, then a guess can be made for the decay rate n, and the relation $\partial V / \partial R = -n (V/R)$ can be used once V and R are specified. Typical values for n for tropical cyclones of various intensity were determined by Mallen et al. (2005, their Table 2). We also note that the largest absolute value of $\partial V / \partial R$ for Fig. 7 corresponds to $n \approx 1$, i.e., $u_\phi \sim r^{-1}$, a potential vortex (Burggraf et al. 1971).

3.3 Comparison to Observations and Other Methods

To further assess the fidelity of these simulations, we compare model results with composite wind-speed profiles from observed tropical cyclones based on dropsonde data from the National Oceanographic and Atmospheric Administration (NOAA). We use the quality controlled dataset of Wang et al. (2015) which contains 17 years of data from 120 tropical cyclones. (We note that dropsondes from the U.S. Air Force, and from field projects that did not use NOAA aircraft, are not included in this dataset.) For this first case, we searched for all dropsonde profiles in which the average wind speed between 500 m and 1000 m a.s.l. was between 35 and 45 m s$^{-1}$. We used only soundings that had at least two data points in this layer and that were separated by at least 250 m, to exclude soundings with a substantial amount of missing data. We also required each sounding to have at least one data point below 100 m a.s.l., and excluded any sounding located more than 300 km from the tropical cyclone centre. From this procedure we obtained 688 soundings that were then averaged to produce composite wind profiles, using 10 m vertical grid spacing, which are shown as black curves in Fig. 8. (Our analysis does not account for observed storm motion, and does not exclude dropsondes from the eyewall of tropical cyclones.) We note that the radial velocity profile (Fig. 8b) suggests very deep inflow up to 2.7 km a.s.l., although the strongest inflow (which is most important dynamically) is confined to the lowest $\approx$1 km a.s.l. The level of strongest inflow is at 100 m a.s.l., and the surface (10 m a.s.l.) inflow angle is 22$^\circ$, both of which are similar to average values from previous studies (e.g., Powell et al. 2009; Zhang et al. 2011; Zhang and Uhlhorn 2012).

The next simulation is based on this composite profile. We assume that V decreases linearly with height from 40 m s$^{-1}$ at the surface to zero at 18 km a.s.l. (to roughly match the composite profile, whereas in the previous subsection we assumed V = constant to roughly match the gradient-wind profile from the axisymmetric model). Similarly, we assume that $\partial V / \partial R$ decreases linearly from its maximum value at the surface to zero at 18 km a.s.l. For lack of any specific data, we retain $\partial V/ \partial R = -8 \times 10^{-4}$ s$^{-1}$ (at the surface), and $R = 40$ km.

Results using the new method for mesoscale tendencies after 12 h of integration (red curves in Fig. 8) are remarkably similar to the observed profiles, especially for $z < 800$ m. In terms of specific quantitative features, the height of maximum inflow is 90 m a.s.l., the inflow-layer depth is 1.1 km, and the surface inflow angle is 23$^\circ$, all of which are comparable with previous observational composites (e.g. Powell et al. 2009; Zhang et al. 2011; Zhang and Uhlhorn 2012). In contrast, a simulation using the Ekman-type method (green-dashed curve in Fig. 8) produces qualitatively similar results as before, i.e., $u_\phi$ is too low and $u_r$ is generally too high.

For comparison, we also show results using two recently developed techniques to simulate the boundary layer of tropical cyclones. NN12 added terms to the governing equations that approximate the centrifugal acceleration in a tropical cyclone, as well as a large-scale pressure-gradient term. Using our nomenclature and set-up (i.e., single-column modelling), their technique can be written,

$$\begin{aligned} M_r^{NN12} =&+ \frac{ u_\phi ^2 }{R} - \left( f V + \frac{V^2}{R} \right) \, , \end{aligned}$$

(23a)

$$\begin{aligned} M_\phi ^{NN12} =&- \frac{u_r u_\phi }{R} \, . \end{aligned}$$

(23b)

GZ15 also considered pressure-gradient and centrifugal acceleration terms, but derived their terms using a different procedure and set of assumptions than NN12. In our nomenclature, their approach can be written,

$$\begin{aligned} M_r^{GZ15} =&+2 \, u_\phi \frac{ V }{R} - \left( f V +2 \frac{V^2}{R} \right) \, , \end{aligned}$$

(24a)

$$\begin{aligned} M_\phi ^{GZ15} =&-2 \, u_r \frac{ V }{R} \, . \end{aligned}$$

(24b)

[The terms with parentheses in (23a) and (24a) are the pressure-gradient terms.] Results using these two methods (using the same profile of V as in the previous paragraph) are shown as blue curves in Fig. 8. Both of these techniques produce shallower inflow layers, by approximately a factor of 2, compared to the new method and the observational composite. Further, the surface inflow angle from these techniques is smaller (by 25–50 %) than the observed average value of 23$^\circ$ (e.g., Powell et al. 2009; Zhang and Uhlhorn 2012). The results have notably greater $u_{\dot{\phi }}$ than the observed profile for $z < 500$ m, and vertical wind shear ($\partial U / \partial z$) is 20 % larger in the surface layer (roughly, lowest 100 m a.s.l.). Very similar mean wind profiles were produced (using LES) by NN12 (their Fig. 3) and GZ15 (their Fig. 4).

Fig. 9

Time series of a inflow-layer depth, $z_{infl}$, b height of minimum radial velocity, $z_{u{{-min}}}$, and c inflow angle at 10 m a.s.l., $\beta _{\text {10-m}}$, for the same simulations shown in Fig. 8

Fig. 10

As in Fig. 8 except for higher wind speed ($V = 60$ m s$^{-1}$ and $\partial V / \partial R = 1.1 \times 10^{-3}$ s$^{-1}$ at the surface). The black curve is a composite of dropsonde observations for which mean 500–1000 m a.s.l. wind speed is between 55 and $65 \hbox { m s}^{-1}$

Time series of some notable flow parameters are shown in Fig. 9, where the inflow-layer depth, $z_{{infl}}$, is defined here as the lowest height at which $u_r$ exceeds $-3$ m s$^{-1}$ (Fig. 9a). The height of strongest inflow, $z_{u{{-min}}}$, is defined as the height at which $u_r$ is a minumum (Fig. 9b), and the surface inflow angle, $\beta _{\text {10-m}}$, is the inflow angle at 10 m a.s.l. (Fig. 9c). In all cases, the variations near the beginning of the simulations are associated with decaying inertial oscillations (e.g., Lewis and Belcher 2004). The Ekman-type method produces oscillations with the longest period, by far (${>}$10 h); for the NN12 and GZ15 methods, the period are very short ($\approx$1 h) and oscillations last for nearly 12 h. For the new method, the period is roughly 2 h, and the signal is practically zero after two oscillations. The primary conclusions from Fig. 9, though, are that the new method produces the most accurate quantitative results ($z_{{infl}} \approx$ 1 km, $z_{u{{-min}}} \approx$ 0.1 km, and $\beta _{\text {10-m}} \approx$ 23$^\circ$) and that these values clearly converge at the analysis time used above ($t = 12$ h).

It could be argued that the techniques of NN12 and GZ15 are preferable to simulations that neglect any inertial terms, i.e., compared to the classic Ekman-type method that only accounts for geostrophic pressure-gradient acceleration (green-dashed curve in Fig. 8). Indeed, the NN12 and GZ15 techniques produce some qualitatively accurate results, such as greatest radial velocity near the surface, and greatest wind shear in the lowest 100 m a.s.l., which is broadly consistent with the observed tropical cyclone boundary layer. Nevertheless, it seems clear that our new formulation (Eqs. 4 and 10) produces better quantitative comparison to observations. The primary reason is the inclusion of radial advection terms, as discussed above.

As one final test of the single-column model, we evaluate simulations at higher wind speeds. In this case, we first calculated a composite of dropsonde observations, using the same methodology as above, but for soundings in which the mean wind speed in the 500-1,000 m layer was between 55 and 65 m s$^{-1}$ (and the same method for excluding soundings with few datapoints); 269 soundings met all criteria. Based on the average results (black curve in Fig. 10) we ran simulations using $V = 60$ m s$^{-1}$ at the surface decreasing to zero at 18 km a.s.l. The average radius of the dropsondes was roughly 40 km, so we set $R = 40$ km. Simulations with the Ekman-type method, the NN12 method, and the GZ15 method exhibit the same qualitative differences from observations as before (Fig. 10).

For the new method, we ran a series of simulations with different values for $\partial V / \partial R$, and show in Fig. 10 the case that best matches the dropsonde composite: $\partial V / \partial R = -1.1 \times 10^{-3}$ s$^{-1}$, corresponding to $n = 0.7$. Results using the new technique (red in Fig. 10) again produce the best match to the observed composite. There are a few subtle differences from the dropsonde composite ($\thickapprox 5$ m s$^{-1}$) that may be attributable to the inclusion of dropsondes from the eyewall of tropical cyclones. (As noted in Sect. 2, our new method is not applicable in the eye and eyewall of tropical cyclones.) Nevertheless, these analyses show that the new method accurately reproduces robust qualitative aspects of the tropical cyclone boundary layer (e.g., depth and magnitude of the inflow layer) that several previous approaches do not.

4 Large-Eddy Simulations

In this section we evaluate the new method when used within LES, which can provide further insight into turbulent processes within the tropical cyclone boundary layer. For example, vertical momentum fluxes (which are notoriously difficult to measure within a tropical cyclone boundary layer due to hazardous conditions) can be estimated using LES results.

Here we use the numerical model “Cloud Model version 1” (CM1) that has been used for several LES studies in recent years (e.g., Kang and Bryan 2011; Kang et al. 2012; Wang 2014; Nowotarski et al. 2014; Markowski and Bryan 2016). Details of the model used here, including a new “two part” subgrid model near the surface, are provided in the Appendix. The parametrization of surface stress uses the same scheme as in Sect. 2, although for LES we use time-averaged values of wind speed at the lowest model level to calculate an average stress, and then calculate instantaneous values following Moeng (1984).

4.1 Mesoscale Tendency Terms

As with NN12 and GZ15, we use a Cartesian grid for our simulations, and for convenience, have chosen to make x and y from our Cartesian grid align with r and $\phi$, respectively, in a cylindrical grid. In other words, we locate the model domain to the east of the tropical cyclone centre, as illustrated schematically in Fig. 1. But our method for the mesoscale tendency terms for the LES model in the two horizontal directions [$M_1^{LES}$ and $M_2^{LES}$] differs from NN12 and GZ15, who derived their terms from the governing equations for flow in cylindrical coordinates. We simply adopt the method developed for single-column modelling (Sect. 2) but replace the variables $u_r$ and $u_\phi$ with domain-average zonal $\left\langle u\right\rangle$ and meridional $\left\langle v\right\rangle$ components of velocity, where angled brackets denote a horizontal average over the domain at each model level. Specifically, we use,

$$\begin{aligned} M_1^{LES} =&\, + \frac{\left\langle u\right\rangle ^2}{R} + \left\langle v\right\rangle \frac{V}{R} - \left( f V + \frac{V^2}{R} \right) \, , \end{aligned}$$

(25)

$$\begin{aligned} M_2^{LES} =&- \left\langle u\right\rangle \frac{\partial V}{\partial R} - \left\langle u\right\rangle \frac{V}{R} \, , \end{aligned}$$

(26)

and note that these mesoscale tendency terms are functions of t and z only. (In contrast, the methods advocated by NN12 and GZ15, discussed below, are calculated independently at each gridpoint.) We intentionally chose this form based on the methodology put forth in Sect. 1 (and discussed, for example, by Sommeria 1976), i.e., that mesoscale tendency terms should account for processes on scales larger than the size of the model domain. In other words, the large-scale gradients in wind speed (which are needed for calculations of large-scale advection) are presumed to not exist on the small domain, and so we assume constant (in x and y) values of large-scale gradient that are specified at the beginning of a simulation; mesoscale horizontal advection terms (first terms on the right side of Eqs. 25 and 26) are then applied uniformly across the entire domain at each timestep. As demonstrated below, this methodology produces realistic wind profiles as compared to observations in the tropical cyclone boundary layer, and also avoids the potential problem of introducing an instability via the vorticity equation (NN12, GZ15). That is, because these tendencies are not functions of x or y, they cannot contribute to the vertical vorticity tendency.

Fig. 11

Horizontal wind speed (m s$^{-1}$) at $t = 4$ h from LES at a 52 m a.s.l. and b 252 m a.s.l. using the same input parameters as in Fig. 8

The three terms on the right-hand side of Eq. 25 represent, respectively: mean radial advection of radial velocity in a tropical cyclone the centrifugal acceleration term associated with the mean flow in a tropical cyclone and the large-scale pressure gradient in a tropical cyclone. For (26), the two terms on the right-hand side represent, respectively: mean radial advection of tangential velocity and centrifugal acceleration. As with the single-column modelling approach, the model user must specify three parameters: R, V, and $\partial V / \partial R$. Finally, we note that, unlike our simple framework for single-column modelling, the potential temperature field plays a direct role in the simulated flow, via the buoyancy term in the velocity equation, Eq. 31a.

4.2 Results

For the first case with LES, we use one of the examples from the previous section: $R = 40$ km; $V = 40$ m s$^{-1}$ at the surface decreasing linearly to zero at 18 km a.s.l.; and $\partial V / \partial R = -8 \times 10^{-4}$ s$^{-1}$ at the surface decreasing linearly to zero at 18 km a.s.l. The LES grid for this case has 512 $\times$ 512 $\times$ 512 grid points spanning 5.12 km $\times$ 5.12 km horizontally. [A few simulations with larger domains in the horizontal were tested and found to produce very similar results (not shown).] The horizontal grid spacing is constant (10 m). In the vertical, the domain is 3 km deep; the vertical grid spacing is 5 m below 2 km, but increases gradually to 12.5 m between 2 and 3 km a.s.l. Rayleigh damping is used above 2 km for u, v, w, and $\theta ^\prime$ (defined in the Appendix) to damp vertically propagating waves. Periodic boundary conditions are used in both horizontal directions.

Fig. 12

Horizontal wind speed U from observations and LES using a classic Ekman-type formulation of mesoscale tendency terms and b the new method for mesoscale tendency terms, using the same input parameters as in Fig. 8. The red curves denote domain-averaged horizontal wind speed $\left\langle U\right\rangle$, averaged between 5 and 6 h, and gray shading encloses the minimum and maximum instantaneous values of U during this time. The black curve is the composite from dropsonde observations as in Fig. 8. Black dots denote flight-level observations from NOAA P3 flights (events listed in Table 1 of Zhang and Drennan (2012)) for which average wind speed was within 4 m s$^{-1}$ of model results at the same level for the simulation in panel (b)

Instantaneous fields of horizontal wind speed U are shown in Fig. 11. Linear “streaks” are apparent in U near the surface (Fig. 11a). Such structures have been observed in hurricane boundary layers (e.g., Wurman and Winslow 1998; Morrison et al. 2005; Zhang et al. 2008b; Kosiba and Wurman 2014) and are thought to be important for strong wind gusts near the surface in tropical cyclone boundary layers. Farther aloft (Fig. 11b), linear features are less obvious, although it is clear that the simulated boundary layer is turbulent.

Vertical profiles of averaged horizontal wind speed $\left\langle U\right\rangle = \left\langle (u^2 + v^2)^{1/2} \right\rangle$ are shown as red curves in Fig. 12, where the simulation for Fig. 12a uses a classic Ekman-type method with only large-scale geostrophic pressure gradient,

$$\begin{aligned} M_1^{\text {LES,Ekman}} =&- f V \, , \end{aligned}$$

(27)

$$\begin{aligned} M_2^{\text {LES,Ekman}} =&\, 0 \, , \end{aligned}$$

(28)

and the simulation for Fig. 12b use the new mesoscale tendency terms, (25)–(26). We also ran simulations using the equation sets advocated by NN12 and GZ15 (not shown). Differences in mean flow fields using these different methods are qualitatively the same as they were for single-column modelling. That is, tangential velocity (not shown) tends to be lowest with the Ekman-type method but greatest with the NN12 and GZ15 methods, and radial inflow (not shown) tends to be be deepest with the Ekman-type method but shallowest with the NN12 and GZ15 methods. The profile of average horizontal wind speed from the composite droposonde profile (see Sect. 3c for details) is shown as a black curve in Fig. 12. Results using the Ekman-type approach are notably weaker than the observed composite (Fig. 12a), whereas results from the new method are in excellent agreement (Fig. 12b). Based on these results, only results using the new method are analyzed for the remainder of this section.

Fig. 13

Total turbulent stress $| \tau | / \rho$ from the LES simulation as in Fig. 12b. The solid-red curve denotes total stress averaged between 5 and 6 h, and grey shading denotes minimum and maximum values from one-minute output during this time. The dashed-red curve denotes the average parametrized part of the stress. Black dots denote observed values of turbulent stress as determined by French et al. (2007) for the same cases used for Fig. 12b

Horizontal wind speed is plotted in Fig. 12 because it gives us an opportunity to compare with in situ low-level data collected in 2003–2004 by NOAA aircraft during the Coupled Boundary Layer Air-Sea Transfer experiment (CBLAST, Black et al. 2007). Specifically, we use data collected in Hurricanes Fabian (2003), Isabel (2003), Frances (2004), and Jeanne (2004) [see Table 1 in Zhang and Drennan (2012)]. A total of 69 “flux runs” below 800 m altitude are analyzed. Quality control and analysis procedures are explained in previous studies (e.g., French et al. 2007; Zhang et al. 2009). For Fig. 12 the black dots are in situ wind-speed measurements, averaged along the length of the flux run. We selected all cases in which this value was within 4 m s$^{-1}$ of the average model value, $\left\langle U \right\rangle$, at the same height in the simulation with the new mesoscale tendency terms (Fig. 12b). This procedure yields 26 observational cases. Additional measurements from these same 26 cases are included in other analyses below.

Figure 13 shows the vertical profile of total turbulent stress $\tau$, calculated as

$$\begin{aligned} \tau / \rho = \left[ \left\langle u^\prime w^\prime \right\rangle + \left\langle v^\prime w^\prime \right\rangle \right] ^{1/2} \end{aligned}$$

(29)

where prime superscripts denote a difference from domain-average values (e.g., $v^\prime = v - \left\langle v \right\rangle$). For the observations, we present averages along each flux run, and for simulations we use horizontal domain averages. The model output (solid-red curve in Fig.13) includes the parametrized value from the subgrid turbulence model (see Appendix), which is shown as a dashed-red curve for reference. The model profiles are averaged over hours 5 and 6 of the simulation, and maximum/minimum instantaneous values are denoted by grey shading. Overall, results (Fig.13) show a substantial positive bias by the model: the mean absolute difference is 0.36 m$^{2}$ s$^{-2}$. The cause of this difference is not clear, but may be related to differences in parametrized and actual surface stress (i.e., drag coefficient). Also, as with the single-column model (Sect. 3), we neglected surface heat flux (except for $t < 50$ min, to spin up turbulence; see Appendix), and we also neglected all moist processes. The averaging methods are also different (i.e., along a flight leg for the observations, as compared to domain-average for the LES). Nevertheless, comparison of LES and turbulence observations in the tropical cyclone boundary layer is quite rare and this first look, without attempts to tune model parametrizations, is encouraging.

Many PBL parametrization schemes for numerical weather prediction models make use of an eddy viscosity $K_m$, including the simple scheme used herein (see Eq. 1). The effective eddy viscosity in a turbulent flow can be estimated using the relation

$$\begin{aligned} K_m = ( \tau / \rho ) \left[ \left( \frac{\partial \left\langle u\right\rangle }{\partial z} \right) ^2 + \left( \frac{\partial \left\langle v\right\rangle }{\partial z} \right) ^2 \right] ^{-1/2} \, . \end{aligned}$$

(30)

We plot estimated eddy viscosity values from in situ turbulence observations (as determined by Zhang and Drennan (2012)) as black dots in Fig. 14. Zhang and Drennan (2012) did not report uncertainty for their estimates, so we provide a rough estimate here. The uncertainty arises from two parts: (1) uncertainty in the calculation of momentum flux; and (2) uncertainty in the calculation of the vertical gradient of wind speed. Drennan et al. (2007) and French et al. (2007) discussed factors that affect turbulent flux calculations using the eddy-correlation method. For momentum flux, the uncertainty is small (<5 %) given the thorough quality control of the CBLAST data. The uncertainty in the calculation of vertical gradient of wind speed is also small, as the uncertainty in the wind observations is only $\approx$1 % (Hock and Franklin 1999). (Of note, dropsonde data were collocated with the flux runs for CBLAST.) Overall, we estimate an uncertainty of <10 % in the observational values of vertical eddy viscosity.

Fig. 14

Effective eddy viscosity $K_m$ from the same LES as in Fig. 12b. The solid-red curve is the total, and the dashed-red curve is the subgrid component, averaged between 5 and 6 h. Grey shading denotes minimum and maximum values from 1-min output during this time. Black dots are observed estimates from NOAA P3 flux runs (Zhang and Drennan 2012) for the same cases used for Fig. 12b

Fig. 15

Power spectral density for along-wind velocity component at approximately 200 m a.s.l. from LES (for three different grid resolutions, as indicated by the legend) and for flight-level observations (solid-black)

Fig. 16

As in Fig. 15 but for vertical velocity

The LES results (red in Fig. 14) again have a mean positive bias compared with the observational estimates. In this case, the mean absolute difference is 22.0 m$^2$ s$^{-1}$. Nevertheless, we are encouraged to see comparable magnitudes in the lower half of the boundary layer (below roughly 500 m a.s.l.). An over-prediction of boundary-layer depth by our LES seems apparent when comparing the observations at $z \approx 0.75$ km to model results. We find this over-prediction can be ameliorated by inclusion of subsidence terms to (25)–(26) (not shown).

4.3 Spectral Analysis

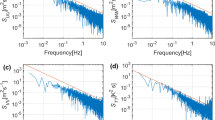
As another method to evaluate the LES, we examine temporal spectra of wind components near the surface. The observational data for this analysis were collected on 12 September 2003 in Hurricane Isabel, at an average radius of 130 km from the tropical cyclone centre, and at an average altitude of 194 m a.s.l. Mean flight-level wind speed was 33 m s$^{-1}$. The flight leg was $\approx$54 km in length ($\approx$6 min in time), which was one of the longest flux runs during CBLAST. Power spectral density is calculated using fast Fourier transform of in situ 40-Hz data. Results are shown as black curves for the along-wind component of velocity in Fig. 15 and for vertical velocity in Fig 16. The power spectral density of both velocity components have roughly $f^{-5/3}$ structure, indicative of a turbulent inertial subrange, for $f > 0.1$ Hz, similar to a recent analysis (of a different dataset) by Nolan et al. (2014).

For LES, the input parameters are chosen to match data from this case. We estimate V using dropsonde data (Fig. 2 from Zhang and Drennan 2012); based on values near the top of the boundary layer, we choose $V = 37$ m s$^{-1}$. For $\partial V / \partial R$, we use the radial gradient of wind speed from flight-level data, which is approximately $-1.6 \times 10^{-4}$ s$^{-1}$. Finally, the mean radius of the flight gives $R = 130$ km.

For this simulation, the model domain extends 6 km $\times$ 6 km horizontally, and is 4 km deep with a Rayleigh damper above 3 km. As a test of sensitivity to resolution, we use three different grid spacings: $\Delta x =$ 31.25, 15.625, and 7.8125 m. In all cases, $\Delta z = \Delta x / 2$. For the analysis of temporal spectra, we have wind speed every timestep from a location in the middle of the domain. To compare model results to the CBLAST observations, we use an ensemble average of power spectral density calculated using 50 %-overlapping, 6-min segments of the model time series at $z \approx 190$ m. A 6-min segment was chosen to match the duration of the CBLAST data, resulting in 39 segments for the ensemble average.

For all three model resolutions, the power spectral densities of the along-wind component of wind speed (Fig. 15) are similar to each other in the low-frequency portion of the spectrum, from the lowest frequency ($2.7 \times 10^{-3}$ Hz) to a critical frequency $f_c$ above which the spectra decrease rapidly. As expected, $f_c$ is larger for simulations with smaller grid spacing. The magnitude of $f_c$ is apparently related to the mean advective velocity $U_a$ divided by the smallest resolvable scale in the simulated flow, i.e., $f_c \approx U_a / (6 \Delta )$, where $\Delta$ is horizontal grid spacing, and $6 \Delta$ is approximately the smallest scale that is unaffected by numerical filtering in CM1 (see, e.g., Appendix of Bryan et al. 2003).

There is a notable difference between model spectra and the observational spectrum at low frequencies ($f < 0.1$ Hz) which is likely related to the different measuring techniques (i.e., at a single point for the model results, and along a flight path for the observations). The difference is especially pronounced for the w spectra.

Most important, though, the LES spectra have $f^{-5/3}$ structure, similar to the observational spectrum, for a certain range of frequencies (specifically, between about 0.08 Hz and the cut-off frequency $f_c$). This behaviour is most apparent for the two highest resolution simulations, and suggests that $\Delta < 20$ m is needed to produce an inertial subrange in the tropical cyclone boundary layer for this model; we note that this conclusion is technically only valid for this level (190 m a.s.l.), and that higher resolution may be needed near the surface. As further evidence for the existence of an inertial subrange in our simulations, we note that the cross-stream and vertical velocity spectra have amplitude roughly four-thirds of the along-stream spectra (as expected by theory (e.g., Wyngaard 2010)) for frequencies of $\approx$0.08–0.5 Hz (not shown).

5 Summary and Conclusions

An inexpensive method to simulate wind profiles in the boundary layer of tropical cyclones is developed and evaluated. The method is intended for single-column modelling and for three-dimensional modelling with small domains (of order 5 km in extent), and can be used with a PBL parametrization or within large-eddy simulations. The key step is to account for processes that occur on scales larger than the proposed model domain.

The core of the new procedure is to add “mesoscale tendency” terms to the horizontal velocity equations to account for large-scale radial advection, centrifugal acceleration, and pressure-gradient acceleration within a tropical cyclone. The method utilizes three simple input parameters: R, the distance from the centre of the tropical cyclone, V, a reference wind profile, and $\partial V / \partial R$, the radial gradient of V. Ideally, these three parameters can be determined by observations from within a tropical cyclone, or from a reference simulation (such as the axisymmetric simulation used in Sects. 2–3). The value for $\partial V / \partial R$ is particularly difficult to estimate from observed storms, and model output can be quite sensitive to its value. But as shown in Sect. 3.2, if the tangential velocity varies as a power law, i.e., $u_\phi \sim r^{-n}$, then the relation $\partial V / \partial R = - n (V / R)$ can be used to estimate $\partial V / \partial R$ once V and R are chosen, and assuming a reasonable guess can be made for n.

Two slightly different formulations for the mesoscale tendency terms are presented: one intended for single-column modelling, given by (4) and (10); and one formulation to be used with LES, (25)–(26). Previous methods for simulating the boundary layer of tropical cyclones were evaluated alongside the new method, including a classic Ekman-type method that adds only a large-scale (geostrophic) pressure gradient acceleration to the horizontal velocity equations, and two recently developed methods that also account for centrifugal-acceleration-like terms (Nakanishi and Niino 2012; Green and Zhang 2015). The new method, which also accounts for large-scale radial (i.e., horizontal) advection, has clear advantages: it produces realistic mean wind-speed profiles compared with composites of dropsonde observations in tropical cyclones. Also, comparison of LES results with low-level data from NOAA flights during CBLAST shows reasonable results, including an effective eddy viscosity of O(50 m$^2$ s$^{-1}$) and temporal spectra with frequency dependence of $f^{-5/3}$ for frequencies $\gtrsim 0.1$ Hz.

Before concluding, we note again that simulations discussed herein neglected surface heat flux and all moist processes, for simplicity. We also do not include any mesoscale tendency term for $\theta$, which would tend to cool the boundary layer. Consequently, $\theta$ profiles tend to be nearly well mixed in our simulations (not shown), whereas observed $\theta$ profiles tend to be stratified (for $z > 100$ m) in observed tropical cyclones (e.g., Kepert et al. 2016). Despite these approximations, the modelled wind profiles compare well with observations from the tropical cyclone boundary layer. Our results suggest that effects from stratification and moisture play a relatively minor role, compared to shear-driven turbulence mechanisms, in the boundary layer of tropical cyclones. Nevertheless, stratification and moisture should be considered in future work, which would necessitate inclusion of mesoscale tendency terms (i.e., radial advection) in equations for potential temperature and water vapour, and perhaps also the evaporation of water, which Kepert et al. (2016) found to be a major contributor to the $\theta$ profile in tropical cyclones.

Appendix: Details of the Large-Eddy Simulations

This study utilizes “Cloud Model version 1” (CM1) (e.g., Bryan and Fritsch 2002; Bryan and Rotunno 2009), which uses a three-step Runge–Kutta method for the time integration scheme, and a fifth-order scheme for advection terms, following Wicker and Skamarock (2002). CM1 integrates a variety of equation sets including compressible, anelastic, or incompressible equations. This study uses the solver for compressible equations using the split-explicit technique (e.g., Skamarock and Klemp 1994), primarily because it is the most efficient of the CM1 solvers for distributed-memory supercomputers.

Using tensor notation (subscript i or $j = 1,2,3$) the governing equations are,

$$\begin{aligned} \frac{\partial u_i}{\partial t}&= - u_j \frac{\partial u_i}{\partial x_j} - c_p \theta \frac{\partial \pi ^\prime }{\partial x_i} + \delta _{i3 } g \frac{\theta ^\prime }{\theta _0} + \varepsilon _{ij3} u_j f + \frac{1}{\rho } \frac{\partial \tau ^t_{ij} }{\partial x_j} + \delta _{i1} M_1^{LES} + \delta _{i2} M_2^{LES} \, , \end{aligned}$$

(31a)

$$\begin{aligned} \frac{\partial \theta ^\prime }{\partial t}&= - u_j \frac{\partial \theta }{\partial x_j} - \frac{1}{\rho } \frac{\partial \tau ^{\theta }_{j} }{\partial x_j} \, , \end{aligned}$$

(31b)

$$\begin{aligned} \frac{\partial \pi ^\prime }{\partial t}&= - u_j \frac{\partial \pi }{\partial x_j} - \frac{R_a}{c_v} \pi \frac{\partial u_j}{\partial x_j} \, , \end{aligned}$$

(31c)

$$\begin{aligned} \frac{\partial e}{\partial t}&= - u_j \frac{\partial e}{\partial x_j} + \frac{1}{\rho } \left[ \left( \tau ^t_{ij} + \tau ^d_{ij} \right) \frac{\partial u_i}{\partial x_j} + \frac{g}{\theta _0} \tau ^\theta _{3} + \frac{\partial \tau ^e_j}{\partial x_j} \right] + \epsilon \end{aligned}$$

(31d)

where $u_i$ is the model-predicted (i.e., resolved) velocity in Cartesian coordinates ($u_1 = u$, $u_2 = v$, $u_3 =w$), $\theta$ is potential temperature, $\pi = (p/p_r)^{R_a/c_p}$ is non-dimensional pressure, and e is subgrid TKE. Other symbols are defined as follows: g is the acceleration due to gravity, $c_p$ and $c_v$ are specific heats of air at constant pressure and volume respectively, $R_a$ is the gas constant, $p_r = 1000$ hPa is a reference pressure, $\tau ^t_{ij}$ is stress from the subgrid turbulence model, $\tau ^d_{ij}$ represents stress from the diffusive component of the advection scheme (explained below), $\tau ^\theta _j$ is subgrid diffusivity for $\theta$, $\tau ^e_j$ is diffusivity for e, and $\epsilon$ is dissipation. The equation of state $\pi = ( \rho R_a \theta / p_r)^{R_a/c_v}$ is used to determine $\rho$. Prime superscripts in (31) denote perturbations from a one-dimensional, time-independent, hydrostatic base state that is denoted by subscript 0; for example, $\pi ^\prime (x,y,z,t) = \pi (x,y,z,t) - \pi _0(z)$. The $\pi _0$ profile obeys the hydrostatic equation, $d \pi _0 / d z = - g / (c_p \theta _0)$. Herein, $\theta _0$ is assumed to vary linearly with height at a rate of 5 K km$^{-1}$; we use surface values of $\theta _0 (z=0) = 300$ K and $\pi _0 (z=0) = 1$. At the initial time, $v = V$ and $u = w = \theta ^\prime = \pi ^\prime = e = 0$, except random small-amplitude (±0.1 K) perturbations are used for $\theta ^\prime$ in the lowest 100 m a.s.l. As in Moeng and Sullivan (1994) we apply a surface heat flux for the first 50 min of the simulation to facilitate development of turbulence. Moist processes are neglected herein for simplicity.

The LES subgrid model is a “two part” scheme following Sullivan et al. (1994), which is an extension of the frequently used TKE-based scheme for LES (e.g., Deardorff 1980; Moeng 1984). The subgrid stress terms are parametrized as follows,

$$\begin{aligned} \tau ^t_{11} = 2 \rho K_m \gamma \frac{\partial u}{\partial x} , \qquad&\tau ^t_{22} = 2 \rho K_m \gamma \frac{\partial v}{\partial y} , \nonumber \\ \nonumber \tau ^t_{33} = 2 \rho K_m \gamma \frac{\partial w}{\partial z} , \qquad&\tau ^t_{12} = \rho K_m \gamma \left( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \right) ,\nonumber \\ \tau ^t_{13} = \rho K_m \gamma \left( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \right) + \rho K_w \frac{\partial \widetilde{u}}{\partial z} , \qquad&\tau ^t_{23} = \rho K_m \gamma \left( \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y} \right) + \rho K_w \frac{\partial \widetilde{v}}{\partial z} \, , \end{aligned}$$

(32)

where $K_m = c_m l e^{1/2}$ is a standard subgrid eddy viscosity, $K_w$ is a supplemental near-surface eddy viscosity used to address the common problem of excessive mean vertical wind shear near the surface in LES (following Sullivan et al. 1994, their Eq. 23), and $\gamma$ is a non-dimensional parameter used to blend these two eddy viscosities. We set the constant $c_m = 0.1$ and use the same formulation for length scale l as Stevens et al. (1999). The variables $\widetilde{u}$ and $\widetilde{v}$ in (32) are average values: although Sullivan et al. (1994) used domain averages, we use 2-min time averages for these variables, and also to compute $K_w$. For our applications, we find that these two types of averaging procedures produce very similar results for simulations of horizontally homogeneous shear-driven boundary layers, but that time averaging is more clearly applicable for the horizontally heterogeneous hurricane boundary layers that were are studying with a different application of CM1 (to be reported elsewhere).

Similar to other LES models, we use $\tau _j^\theta = - \rho K_h ( \partial \theta / \partial x_j)$, $\tau _j^e = 2 \rho K_m ( \partial e / \partial x_j )$, and $\epsilon = c_\epsilon e^{3/2} / l$, where $K_h = c_h K_m$, and the parameters $c_h$ and $c_\epsilon$ are formulated as in Stevens et al. (1999). One notable difference from other LES modes used in the atmospheric sciences is that our subgrid TKE equation, Eq. 31d, includes a second scale transfer term, $\tau ^d_{ij} ( \partial u_i / \partial x_j )$. This term is associated with the fifth-order advection scheme in CM1, which contains flow-dependent diffusion (see, e.g., Wicker and Skamarock 2002). The specific formulation for $\tau ^d_{ij}$ for CM1 was documented by Bryan and Rotunno (2014, pg. 1130). We note that this term is not needed in (31d) for numerical purposes, but is included primarily for completeness; also, this term is necessary for precise calculations of TKE budgets for CM1 (not shown).