1 Introduction

The second generation of performance-based earthquake engineering (PBEE) methodologies (FEMA P-58-1 2012; FEMA P-695 2009) considers the inherent uncertainties in response prediction within a probabilistic framework. The variance on the seismic structural response depends on several factors such as the selected set of earthquake ground motions, the type of structure (e.g., mass and stiffness regularity), the considered response quantity, and the choice of the intensity measure (IM). In this paper, efficient IMs are evaluated to reduce the collapse capacity dispersion, due to record-to-record (RTR) variability, of highly inelastic non-deteriorating single-degree-of-freedom (SDOF) systems vulnerable to second-order effects.

Fundamental studies of the P-delta effect on inelastic SDOF systems subjected to earthquakes have been presented, for instance, by Husid (1967), Bernal (1987), and MacRae (1994). More recently, in the research group of the authors (Adam and Jäger 2012a; Jäger and Adam 2013) collapse capacity of P-delta sensitive SDOF systems has been assessed for a set of characteristic structural parameters. In Adam and Jäger (2012a) and Tsantaki et al. (2015) the presentation of the collapse capacity and its dispersion has been referred to as collapse capacity spectra, providing a compact and easily applicable tool for the practicing engineer.

The ground motion uncertainty is represented by one parameter or a vector of a few parameters related to a set of appropriately selected earthquake records, referred to as IM (Jalayer et al. 2012). The IM is the interface between seismology and earthquake engineering (Baker 2007). It quantifies the severity of a seismic event, and it serves as a scale factor for non-linear dynamic analysis. Since there is no unique definition of intensity of an earthquake record, several IMs have been proposed. They can be classified into (a) elastic ground motion based scalar IMs (Adam and Jäger 2012b), such as peak ground acceleration (PGA), peak ground velocity (PGV) and peak ground displacement (PGD); (b) elastic and inelastic spectral based IMs such as spectral acceleration and spectral displacement at the fundamental period of the structure, as well as spectral values related to higher modes effect or period elongation (Cordova et al. 2001; Haselton and Baker 2006; Luco and Cornell 2007; Bianchini et al. 2009; Kadas et al. 2011; Cantagallo et al. 2012; Vamvatsikos and Cornell 2005; Bojorquez and Iervolino 2011); and (c) vector valued IMs (e.g., Baker and Cornell 2005; Vamvatsikos and Cornell 2005). Currently, the most widely accepted IM is the 5 % damped pseudo-spectral acceleration at the (fundamental) period of the structure, which serves in the present study as the benchmark IM.

Although many advanced IMs have been proposed, there are still a few limitations, such as the derivation of attenuation relations, the selection of the spectral values in case of higher modes and period elongation incorporation, their validation for several structural systems, etc. Based on information theory concepts, Jalayer et al. (2012) quantified the suitability of commonly used IMs against some others. The importance of the spectral shape consideration has been clearly demonstrated by Baker and Cornell (2006). Haselton (2009) evaluated several ground motion selection and modification methods utilizing a point of comparison methodology, and O’Donnell et al. (2013) investigated both experimental and analytical scaling methods for elastic systems. However, most of these studies did not address the collapse limit state, and were mainly focused on the efficiency of the considered IMs. The properties of sufficiency, scaling robustness and hazard computability have been studied by Shome and Cornell (1999), Luco and Cornell (2007), Bianchini et al. (2009), and Bojorquez and Iervolino (2011), among others.

In the present study, a slightly modified version of an IM proposed by Bianchini et al. (2009) is employed, based on the geometric mean of the pseudo-spectral acceleration over a certain period interval that yields the smallest dispersion of the collapse capacities. A preliminary study of Tsantaki and Adam (2013) showed that for the considered P-delta vulnerable SDOF systems this IM satisfies better the property of efficiency, compared with outcomes of benchmark studies (Adam and Jäger 2012a; Jäger and Adam 2013), where the 5 % damped spectral pseudo-acceleration at the structural period has been used as IM. Eads et al. (2015) evaluated the efficiency and sufficiency of a similar IM for collapse prediction using almost 700 moment-resisting frame and shear wall structures. Also, Kazantzi and Vamvatsikos (2015) compared the effectiveness of several IMs based on the geometric mean concept superposing the spectral acceleration read at different logarithmically and linearly equally spaced periods. Lin et al. (2013a, b) demonstrated the importance of the conditioning period for the conditional spectrum in an intensity-based assessment, in contrast to a risk-based assessment.

The averaged period intervals depend on certain structural parameters, and system’s level of inelasticity. Several codes and standards provide recommendations for the elongated period and higher mode effect intervals. For example, spectral matching period intervals of 0.2 to 2.0 T (Eurocode 8 2004), 0.4 to 1.5 T (NZSEE 2006) and 0.2 to 1.5 T (ASCE/SEI 41-13 2014) are proposed, with T denoting the fundamental period of vibration. Recently, Katsanos et al. (2012) suggested to reduce the period interval specified in Eurocode 8 (i.e., 0.2T < T < 1.5 T), at least for new buildings designed for low or moderate levels of ductility and low-to-medium stiffness degradation. Moreover, period elongation has been investigated numerically (Katsanos et al. 2012), as well as experimentally by testing full-scale models (Pinho and Elnashai 2000; Zembaty et al. 2006) and conducting response measurements of instrumented buildings (Mucciarelli et al. 2004; Clinton et al. 2006; Mucciarelli et al. 2012). However, most of the proposed code-bounds of the period intervals are based on expert elicitation, without referring to specific research studies. Thus, Sect. 3 presents a parametric study aimed to derive an “optimal” upper period bound that leads to the smallest collapse capacity dispersion of P-delta vulnerable SDOF systems. Subsequently, in Sect. 4 a single target IM is introduced for the collapse capacity assessment of P-delta vulnerable non-deteriorating SDOF systems. This IM is the 5 % damped pseudo-acceleration at the period of vibration in the presence of gravity loads, \(T_{SDOF}^{P\Delta }\) and referred to as “P-delta” IM, \(S_{a} (T_{SDOF}^{P\Delta } )\). A comparison of the efficiency property of the utilized IMs is provided in Sect. 5, followed by a comparison of the sufficiency and scaling robustness property in Sect. 6.

2 Definitions and framework

2.1 P-delta effect on an inelastic SDOF system

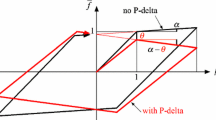
In an inelastic SDOF system the gravity load generates a shear deformation of its hysteretic force–displacement relationship. Characteristic displacements (such as the yield displacement x y ) of this relationship remain unchanged, whereas the characteristic forces (such as the strength f y ) are reduced. As a result, the slope of elastic and post-elastic branch of deformation is decreased. The magnitude of this reduction can be expressed by means of the stability coefficient θ (MacRae 1994). The parameter θ is a function of the gravity load P, geometry, and stiffness. Based on an inverted mechanical pendulum of length h and rotational base spring stiffness k r (Fig. 1a), the stability coefficient is (Adam and Jäger 2012a)

$$\theta = \frac{Ph}{{k_{r} }},\,\,\,\,\,\,\,P = \vartheta W$$
(1)

where W is the effective seismic weight, and ϑ = (live load + dead load)/dead load. Figure 1 shows the P-delta effect on the non-dimensional hysteretic behavior of a SDOF system with non-deteriorating bilinear characteristics. In this example, the post-yield stiffness is negative, because the stability coefficient θ is larger than the hardening ratio α.

Fig. 1
figure 1

a P-delta vulnerable SDOF system. b Normalized bilinear cyclic behavior with and without destabilizing effect of gravity loads (modified from Adam and Jäger 2012a)

Full size image

A negative slope of the post-yield stiffness; i.e., θ − α > 0, is a necessary condition for structural collapse under severe earthquakes. Adam and Jäger (2012a) showed that collapse of inelastic SDOF systems vulnerable to P-delta is mainly governed by the following parameters:

  • the negative slope of the post-yield stiffness expressed by θ − α,

  • the elastic structural period of vibration T SDOF,

  • the viscous damping coefficient ζ (usually 5 %), and

  • the shape of the hysteretic loop.

In this paper SDOF systems with bilinear hysteretic behavior (Fig. 1b) are studied, considering a wide range of system configurations for various values of T SDOF , θ − α, and ζ.

2.2 Collapse capacity variability

Collapse capacity is defined as the maximum ground motion intensity at which the structure still maintains dynamic stability (Krawinkler et al. 2009). An Incremental Dynamic Analysis (IDA) is commonly used to predict collapse capacity, and consists of a series of time history analyses in which the intensity of the ground motion record is monotonically increased (Vamvatsikos and Cornell 2002). In IDA curves, the IM is plotted against an engineering demand parameter (e.g., roof drift), until this parameter grows unbounded, indicating structural failure. The corresponding IM is referred to as collapse capacity of the considered structure.

When the IM is an acceleration quantity such as the PGA, or the 5 % spectral pseudo-acceleration at a target period of the structure, it is beneficial to relate the IM at collapse to the product of the base shear coefficient at onset of yield, γ, and acceleration gravity, g,

$$\left. {CC_{i} } \right|_{IM} = \frac{{\left. {IM_{i} } \right|_{collapse} }}{g\gamma },\;\gamma = \frac{{f_{y} }}{mg}$$
(2)

In this equation, f y is the yield strength, and m the mass of the SDOF system. \(\left. {CC_{i} } \right|_{IM}\) is the relative collapse capacity of the considered SDOF system subjected to the ith ground motion record.

Since RTR variability leads to different collapse capacities for different ground motion records, the collapse capacities are determined for all records of the considered ground motion set, and evaluated statistically. Shome and Cornell (1999) and Ibarra and Krawinkler (2005, 2011) provide good arguments for representing a set of collapse capacities by a log-normal distribution. The log-normal distribution of the individual collapse capacities, CC j , can be characterized by the median, the 16th, and 84th percentiles of the collapse capacities denoted as CC, CC P16, and CC P84, respectively. In the following, the dispersion quantity \(s^{*}\) (Adam and Jäger 2012a)

$$s^{*} = \ln \sqrt {s_{u} s_{l} } ,\;s_{u} = \frac{{CC_{P84} }}{CC},\;s_{l} = \frac{CC}{{CC_{P16} }}$$
(3)

is utilized as a representative measure of the variability of the individual collapse capacities. In the log-domain \(s^{*}\) is related to the standard deviation: σ ≈ \(s^{*}\) (Limpert et al. 2001).

In this study, ground motion induced uncertainties are computed employing the 44 far-field ground motions of the FEMA P-695 far-field record set (FEMA P-695 2009), referred to as FEMA P-695-FF, and also known as PEER-NGA-FF and ATC63-FF. The records of the PEER- FEMA P-695-FF set originate from severe seismic events of magnitude between 6.5 and 7.6, and closest distance to the fault rupture larger than 10 km. Only strike-slip and reverse sources are considered. The 44 records were recorded on NEHRP site classes C (soft rock) and D (stiff soil).

Exemplarily, Fig. 2 shows record dependent collapse capacity spectra based on the conventional IM \(S_{a} (T_{SDOF} )\) for an SDOF system subjected to the FEMA P-695-FF record set. The SDOF system consists of a bilinear hysteretic loop, θ − α = 0.20 and ζ = 0.05. Black lines with circle markers represent the corresponding 16th, 50th, and 84th percentile spectra.

Fig. 2
figure 2

FEMA P-695-FF 44 record dependent collapse capacity spectra (grey lines) based on the conventional IM S a (T SDOF ), corresponding statistical spectra (black lines with circle markers), and smooth empirical approximations (red lines)

Full size image

2.3 Evaluated intensity measures

In Sects. 3, 4, and 5 of this paper the efficiency of the following three IMs is evaluated with respect to the collapse capacity dispersion attributed to RTR variability:

  • the benchmark IM, \(S_{a} (T_{SDOF}^{{}} )\); i.e., the 5 % damped pseudo-acceleration at the period of vibration T SDOF ,

  • a set of “averaged” IMs, abbreviated by S a,gm , where the 5 % damped pseudo-acceleration is averaged in a certain period interval, taking into account the period elongation due to the presence of gravity loads and inelastic deformations, and

  • a single target IM, referred to as “P-delta” IM, \(S_{a} (T_{SDOF}^{P\Delta } )\); i.e., the 5 % damped pseudo-acceleration at the period of vibration in the presence of gravity loads, \(T_{SDOF}^{P\Delta }\). This IM is introduced, because in the presence of gravity loads the initial period of vibration of an SDOF system, T SDOF , is elongated by the factor \(\sqrt {{1 \mathord{\left/ {\vphantom {1 {(1 - \theta }}} \right. \kern-0pt} {(1 - \theta }})}\): \(T_{SDOF}^{P\Delta } =\) \(T_{SDOF}^{{}} \sqrt {{1 \mathord{\left/ {\vphantom {1 {(1 - \theta }}} \right. \kern-0pt} {(1 - \theta }})}\).

According to Bianchini et al. (2009) an appropriate IM should comply with three additional characteristics:

  • Hazard computability; i.e., the IM quantifies appropriately the ground motion hazard at the site. The single target spectral pseudo-acceleration based IMs, \(S_{a} (T_{SDOF} )\) and \(S_{a} (T_{SDOF}^{P\Delta } )\), fulfill this property since attenuation relationships that describe the probability distribution of spectral pseudo-accelerations at single target periods are widely available. Seismic hazard analysis for the averaged IMs S a,gm can also be applied based on correlation equations between spectral accelerations at multiple periods derived by Baker and Jayaram (2008).

  • Sufficiency; i.e., the IM is conditionally statistically independent of ground motion characteristics such as magnitude, distance, and epsilon, among others.

  • Scaling robustness; i.e., the independence of IMs from scaling factors.

The sufficiency and the scaling robustness property of the utilized IMs is further discussed in Sect. 6.

3 Averaged intensity measure

3.1 Definition

In the present study, a slightly modified form of an averaged IM as defined in Bianchini et al. (2009) is implemented. This averaged IM is based on the geometric mean of the 5 % damped spectral pseudo-accelerations S a over the period interval ΔT,

$$\Delta T = T_{n} - T_{1} \,,\,\,\,\,\,T_{n} > T_{1}$$
(4)

between a lower bound period T 1 and an elongated upper bound period T n larger than T 1. In contrast to Bianchini et al. (2009), where S a is discretized at 10 log-spaced periods within ΔT, in the present study S a is discretized at equally spaced periods T i within ΔT,

$$T_{i} = T_{1} + \left( {i - 1} \right)\delta T\,\,,\,\,\,\,\,\,i = 1, \ldots ,n,\;\delta T = \frac{\Delta T}{n - 1} = \frac{{T_{n} - T_{1} }}{n - 1}$$
(5)

The discrete values of S a (T i ) (i = 1, …, n) are combined as proposed in Bianchini et al. (2009):

$$S_{a,gm} (T_{1} ,T_{n} ) = \left( {\prod\limits_{i = 1}^{n} {S_{a} (T_{i} )} } \right)^{1/n}$$
(6)

T i is the ith period in the set of n periods T 1, …, T i , …, T n , and in general, it does not coincide with a system period.

3.2 Sets of averaged intensity measures

The effect of various spectral-averaged IMs S a,gm such as \(S_{a,gm} (T_{1} = T_{SDOF} ,\,T_{n} > T_{SDOF} )\), \(S_{a,gm} (T_{1} < T_{SDOF} ,\,T_{n} = T_{SDOF} )\) and \(S_{a,gm} (T_{1} < T_{SDOF} ,\,T_{n} > T_{SDOF} )\) on the collapse capacity dispersion \(s^{*}\) is evaluated, and compared with the benchmark IM \(S_{a} (T_{SDOF} )\). Note that all S a,gm based IMs are equivalent to the conventional IM \(S_{a} (T_{SDOF} )\) for ΔT equal to 0. For the analyses presented in this section, the SDOF systems have a bilinear cyclic behavior and viscous damping ζ of 5 %, unless otherwise indicated.

The first set of averaged IMs \(S_{a,gm} (T_{1} = T_{SDOF} ,\,T_{n} > T_{1} ) \equiv S_{a,gm} (T_{SDOF} ,\,T_{n} )\) has a lower bound period \(T_{1} = T_{SDOF}\), and an upper bound period \(T_{n} = T_{SDOF} + \Delta T\), which varies with the selected intervals ΔT of 0.4 s, 0.6 s, 0.8 s, 1.0 s, 1.2 s, and 1.4 s. The considered SDOF systems exhibit a negative post-yield stiffness ratio of θ − α = 0.20, and system periods in the range \(0 < T_{SDOF} \le 5.0\,{\text{s}}\), equally spaced at increments of 0.1 s. The collapse capacity is calculated at each discrete period T SDOF for all FEMA P-695-FF ground motions using an IDA approach, and the dispersion measure \(s^{*}\) is evaluated using Eq. 3. This dispersion \(s^{*}\) is plotted in Fig. 3 as a function of T SDOF . The red solid line corresponds to \(s^{*}\) for the original base case study using the conventional IM S a (T SDOF ), as presented in Adam and Jäger (2012a). Black lines represent outcomes utilizing the averaged IM S a,gm (T SDOF , T n ) for various period intervals ΔT. As observed, the conventional IM renders the smallest dispersion for very stiff systems, up to a period T SDOF  = 0.22 s. As discussed in Jäger and Adam (2013), collapse capacity of a rigid system (T SDOF  = 0) does not exhibit aleatory uncertainty; i.e. \(s^{*}\) = 0, when using the spectral acceleration at T SDOF as IM. However, the conventional IM leads to the largest dispersion for flexible systems with T SDOF  > 0.8 s. For larger T SDOF the S a,gm (T SDOF , T n ) IM is more efficient, and leads to smaller \(s^{*}\) values. For systems with periods \(0.22\,{\text{s}} \le T_{SDOF} \le 0.9\,{\text{s}}\) the IM based on interval ΔT = 0.4 s leads to the smallest dispersion. For more flexible systems with T SDOF  > 1.58 s, the parameter \(s^{*}\) is smallest for the IM with ΔT = 1.4 s., although the difference between the outcomes based on ΔT = 1.2 s and ΔT = 1.4 s is negligible. Note that for the considered SDOF systems the largest efficiency of the spectral averaged IM is for systems with periods \(2.6\,{\text{s}} \le T_{SDOF} \le 2.9\,{\text{s}}\), where the reduction of \(s^{*}\) is more than 55 %, compared to the outcome using the conventional IM.

Fig. 3
figure 3

Dispersion measure \(s^{*}\) of the collapse capacity. IM: \(S_{a,gm} (T_{SDOF} ,T_{n} )\) with various intervals ΔT ≥ 0. Negative post-yield stiffness ratios θ − α = 0.20

Full size image

The study is extended considering a series of negative post-yield stiffness ratios θ − α and additional intervals ΔT to find a general trend for the effect of the S a,gm (T SDOF , T n ) averaged IM on \(s^{*}\). The following values of θ − α and ΔT values are assigned to the SDOF systems: θ − α = 0.04, 0.06, 0.08, 0.10, 0.20, 0.30, 0.40, 0.50, 0.60, 0.80; and ΔT = 1.8 s, 2.4 s, 3.0 s, and 4.0 s. The mean \({\text{E}}_{\theta - \alpha } [s^{*} ]\) of \(s^{*}\) for each negative post-yield stiffness ratio θ − α at a certain period T SDOF is determined as

$${\text{E}}_{\theta - \alpha } [s^{*} ] = \frac{1}{10}\sum\limits_{k = 1}^{10} {s^{*} \left( {(\theta - \alpha )_{k} } \right)}$$

In Fig. 4, \({\text{E}}_{\theta - \alpha } [s^{*} ]\) is plotted against T SDOF for each IM (with different ΔT) separately. The solid line in red corresponds to \({\text{E}}_{\theta - \alpha } [s^{*} ]\) based on the conventional IM S a (T SDOF ), whereas lines in black and blue represent the mean dispersion for different intervals ΔT of the IM \(S_{a,gm} (T_{SDOF} ,\,T_{n} )\). These results confirm the findings of Fig. 3. Except for very stiff structures, the conventional IM leads to a mean dispersion \({\text{E}}_{\theta - \alpha } [s^{*} ]\) of the collapse capacity of about 0.37, while \({\text{E}}_{\theta - \alpha } [s^{*} ]\) based on S a,gm exhibits an average minimum of about 0.23, when considering only the most efficient period intervals ΔT at different periods T SDOF . Therefore, an averaged IM \(S_{a,gm} (T_{SDOF} ,\,T_{n} )\) can reduce the collapse capacity dispersion caused by RTR variability.

Fig. 4
figure 4

Mean values of the dispersion measure \(s^{*}\) with respect to the considered post-yield stiffness ratios θ − α. IM: \(S_{a,gm} (T_{SDOF} ,T_{n} )\) with various intervals ΔT ≥ 0

Full size image

Additionally, for IMs \(S_{a,gm} (T_{SDOF} ,\,T_{n} )\) (\(0 \le \Delta T \le 1.4\,{\text{s}}\)) the mean of dispersion \(s^{*}\), read at 53 discrete periods \(T_{SDOF,j}\) (\(j = 1,2, \ldots ,53\)) in the range \(0.001\,\text{s} \le T_{SDOF,j} \le 5\,\text{s}\)),

$${\text{E}}_{{T_{SDOF} }} [s^{*} ] = \frac{1}{53}\sum\limits_{j = 1}^{53} {s_{{}}^{*} (T_{SDOF,j} )}$$

is determined at each discrete negative post-yield stiffness ratio θ − α. Figure 5 displays \({\text{E}}_{{T_{SDOF} }} [s^{*} ]\) as a function of θ − α. In this representation, the conventional IM (i.e., ΔT = 0) leads to the poorest performance in the entire range of θ − α. For small θ − α (\(\theta - \alpha < 0.10\)) the reduction of \({\text{E}}_{{T_{SDOF} }} [s^{*} ]\) based on \(S_{a,gm} (T_{SDOF} ,\,T_{n} )\) is small compared to that obtained for larger \(\theta - \alpha\) (\(\theta - \alpha > 0.10\)). These trends, as well as the increase of \({\text{E}}_{{T_{SDOF} }} [s^{*} ]\) as θ − α becomes larger than 0.40, will be discussed further in Sect. 6.

Fig. 5
figure 5

Mean values of the dispersion measure \(s^{*}\) with respect to the considered structural periods T SDOF  as a function of the post-yield stiffness ratio θ − α. IM: \(S_{a,gm} (T_{SDOF} ,T_{n} )\) with various intervals ΔT ≥ 0

Full size image

For SDOF systems the collapse capacity dispersion cannot be reduced by averaging the pseudo-acceleration for periods smaller than T SDOF because of the lack of higher mode effects. For the sake of completeness, however, s * is quantified assuming that the lower bound period T 1 of interval ΔT is smaller than the system period; i.e., T 1 < T SDOF , and the upper bound period T n  = T SDOF . The corresponding set of IMs is \(S_{a,gm} (T_{1} < T_{SDOF} ,\,T_{n} = T_{SDOF} )\) referred to as \(S_{a,gm} (T_{1} ,\,T_{SDOF} )\). As shown in Fig. 6, the use of averaged IM S a,gm in which T 1 < T SDOF leads to a larger collapse capacity variability compared to that obtained from the conventional IM S a (T SDOF ).

Fig. 6
figure 6

Dispersion measure s * of the collapse capacity. IMs: \(S_{a} (T_{SDOF} ),\,S_{a,gm} (T_{1} ,T_{SDOF} )\). Negative post-yield stiffness ratio a \(\theta - \alpha = 0.20\), b θ − α = 0.40

Full size image

As expected, the use of sets of IMs \(S_{a,gm} (T_{1} < T_{SDOF} ,\,T_{n} > T_{SDOF} )\) \(\equiv S_{a,gm} (T_{1} ,\,T_{n} )\), such as \(S_{a,gm} (0.2T_{SDOF} ,\,1.6T_{SDOF} )\), leads to larger collapse capacity dispersions compared to those based on IM \(S_{a,gm} (T_{SDOF} ,\,1.6T_{SDOF} )\), as shown in Fig. 7. The use of IM \(S_{a,gm} (T_{SDOF} ,\,1.6T_{SDOF} )\,\) leads to the smallest s * for most periods. Also, the use of an IM with the period interval ΔT below the system period (T 1 = 0.2T SDOF and T n  = T SDOF ) performs poor with respect to s *, except for very stiff systems.

Fig. 7
figure 7

Dispersion measure s * of the collapse capacity. Various intensity measures. Negative post-yield stiffness ratio a θ − α = 0.20, b θ − α = 0.40

Full size image

3.3 “Optimal” averaged intensity measure

Based on the above results, an extensive parametric IDA study has been carried out to identify the upper bound period limit \(T_{n} = T_{SDOF} + \Delta T > T_{SDOF}\) that leads to the “optimal” (i.e., the minimum) dispersion \(s^{*}\) of collapse capacities.

According to Fig. 4, there is no “optimal” IM with constant ΔT for the entire range of system periods, because the “optimal” interval ΔT is a function of T SDOF . That is, the larger the elastic period T SDOF becomes, the larger the elongated inelastic period, and consequently, the larger is the required ΔT to render the minimum achievable dispersion measure s *. To obtain a relation between T SDOF and the “optimal” interval ΔT opt (\(\hbox{min} s^{*} \rightarrow \Delta T_{opt}\)), the dispersion measure s * is determined as a function of ΔT for discrete system periods. Figure 8 shows the mean dispersion \({\text{E}}_{\theta - \alpha } [s^{*} ]\) for nine system periods (T SDOF  = 0.2, 0.5, 0.7, 1.0, 1.5, 2.1, 3.0, 4.0, and 5.0 s) plotted against interval ΔT of the averaged IM \(S_{a,gm} (T_{1} = T_{SDOF} ,T_{n} > T_{SDOF} )\) and the conventional IM S a (T SDOF ) (i.e., ΔT = 0). \({\text{E}}_{\theta - \alpha } [s^{*} ]\) is determined comprising the complete set of considered post-yield stiffness ratios θ − α (i.e., 0.04, 0.06, 0.08, 0.10, 0.20, 0.30, 0.40, 0.50, 0.60, 0.80). Alternatively, only the collapse capacities for θ − α in the range of \(0.08 \le \theta - \alpha \le 0.40\) (referred to as “most common” θ − α) are used to calculate the mean dispersion measure \({\text{E}}_{\theta - \alpha } [s^{*} ]\). In the latter set of θ − α, extreme (unlikely) values, which might distort the general trend of the response behavior, are excluded. Exemplarily for a system with T SDOF  = 1.5 s, Fig. 9 shows both the dispersion s * for each discrete θ − α value and the corresponding \({\text{E}}_{\theta - \alpha } [s^{*} ]\) values. It can be observed that the trend of the dispersion for systems with an extremely large negative post-yield stiffness ratio of θ − α = 0.80 is very different from the other depicted cases. The results of Fig. 8 confirm that the “optimal” interval \(\Delta T_{opt}\) strongly depends on the system period T SDOF , and that the optimal interval ΔT opt becomes larger with increasing T SDOF . In all the plots of Fig. 8, the interval ΔT opt that leads to the minimum mean dispersion is specified. For example, for T SDOF  = 1.0 s the minimum mean dispersion is 0.21 (all θ − α), compared to 0.38 for the benchmark IM (i.e., ΔT = 0). For the minimum mean \({\text{E}}_{\theta - \alpha } [s^{*} ]\) the corresponding ΔT opt is about 0.8 s. The ratio ɛ opt between the “optimal” upper bound period \(T_{n,opt} = T_{SDOF} + \Delta T_{opt}\) and period \(T_{1} = T_{SDOF}\) is

$$\varepsilon_{opt} = \frac{{T_{n,opt} }}{{T_{SDOF} }}$$
(7)
Fig. 8
figure 8

Mean values of dispersion s * with respect to the negative post-yield stiffness ratios θ − α as a function of period interval ΔT for nine discrete structural periods T SDOF . Black curves: mean from all considered discrete values of θ − α. Blue curves: mean from discrete values of θ − α in the range of 0.08 ≤ θ − α ≤ 0.40. Intensity measure S a,gm (T SDOF , T n ) with various intervals ΔT ≥ 0

Full size image
Fig. 9
figure 9

Dispersion measure s * for various negative post-yield stiffness ratios θ − α as a function of period interval ΔT. Black graph: mean from all considered discrete values of θ − α. Blue graph: mean from discrete values of θ − α in the range of 0.08 ≤ θ − α ≤ 0.40. Intensity measure S a,gm (T SDOF , T n ) with various intervals ΔT ≥ 0

Full size image

This ratio ɛ opt lies between 1.4 and 2.0 for all the evaluated periods.

Figure 10 shows ratio \(\varepsilon_{opt}\) as a function of T SDOF for three stiffness ratios θ − α of 0.10, 0.20 and 0.40, and for the mean of s * with respect to these θ − α values. As observed, for rigid SDOF systems ɛ opt is 1, because the dispersion is 0 when using the benchmark IM S a (T SDOF ) (Jäger and Adam 2013). Then follows a sharp rise of ɛ opt for stiff systems with T SDOF  < 0.5 s. In this period range ɛ opt can be larger than 2. For periods T SDOF  > 0.8 s, ɛ opt fluctuates around 1.6. For smaller values of θ − α the fluctuation of ɛ opt around 1.6 is larger. The mean of s *with respect to outcomes for different θ − α values exhibits the same global behavior. Figure 10 reveals that the impact of θ − α on ɛ opt is insignificant. In addition to the evaluation of 5 % damped SDOF systems, Fig. 10d also presents results for undamped and 2 % damped systems. As can be seen, the fluctuation around 1.6 is preserved.

Fig. 10
figure 10

Ratio ɛ opt of the “optimal” elongated period T n,opt and the system period T SDOF leading to the minimum dispersion s *. Viscous damping ζ = 0, 2, and 5 %. a–c Ratios for individual negative post-yield stiffness ratios as specified, d ratios based on \({\text{E}}_{\theta - \alpha } [s^{*} ]\)

Full size image

Figure 11 compares the dispersion measure s * that corresponds to the optimal period interval ΔT opt (and thus to T n,opt and to ɛ opt ) to the dispersion obtained from the benchmark IM S a (T SDOF ) for the same systems. According to Fig. 11d the mean \({\text{E}}_{\theta - \alpha } [s^{*} ]\) is on average about 0.23 for the entire period interval T SDOF . This value remains the same considering the complete set of θ − α and, alternatively, the set including the “most common” θ − α. The mean dispersion of collapse capacities based on the benchmark IM S a (T SDOF ); i.e., \({\text{E}}_{\theta - \alpha } [s^{*} ]\), is on average about 0.37, which is about 60 % larger than the dispersion based on ΔT opt , proving the superiority of the averaged IM S a,gm in reducing the effect of RTR variability on the collapse capacity dispersion. Furthermore, the results of Fig. 11 show that, not only the ratio ɛ opt , but also the dispersion measure s * is globally unaffected from viscous damping for all utilized IMs. The outcomes for individual negative stiffness ratios θ − α confirm these findings. It is also shown that dispersion measure s * is practically independent from θ − α.

Fig. 11
figure 11

Smallest dispersion measure \(s^{*}\). Intensity measures: S a,gm (T SDOF , T n,opt ), S a (T SDOF ). Viscous damping ζ = 0, 2, and 5 %. a–c s * for individual negative post-yield stiffness ratios as specified; d mean \({\text{E}}_{\theta - \alpha } [s^{*} ]\)

Full size image

Based on the above observations, the following analytical approximation for ɛ opt , denoted as ɛ α , is proposed:

$$\varepsilon_{\alpha } (T_{SDOF} ) = \left\{ {\begin{array}{*{20}l} {1 + 4T_{SDOF} } \hfill & {0 \le T_{SDOF} \le 0.15\;{\text{s}}} \hfill \\ {1.6} \hfill & {T_{SDOF} \ge 0.15\;{\text{s}}} \hfill \\ \end{array} } \right.$$
(8)

The expression is independent of θ − α, viscous damping in the range 0 ≤ ζ ≤ 0.05, and \(T_{SDOF} \ge 0.15\;{\text{s}}\). Additionally, the averaged IM based on the selected ɛ α also leads to an efficient IM when using the peak-oriented hysteretic model instead of the bilinear model (Tsantaki 2014). Subsequently, for \(T_{SDOF} \ge 0.15\;{\text{s}}\) the corresponding averaged IM \(S_{a,gm} (T_{1} ,T_{n,\alpha } )\), with the elongated period

$$T_{n,\alpha } = \varepsilon_{\alpha } T_{SDOF}$$
(9)

is denoted as \(S_{a,gm}^{\alpha } (T_{SDOF} ,\,1.6T_{SDOF} )\,\), or briefly \(S_{a,gm}^{\alpha }\).

4 “P-delta” intensity measure

In this section, the dispersion of the 5 % damped pseudo-acceleration response spectra S (i) a , i = 1, …, 44, of the 44 ground motions of the FEMA P-695-FF is studied when scaled to the “P-delta” IM \(S_{a} (T_{SDOF}^{P\Delta } )\) and to the conventional IM \(S_{a}^{{}} (T_{SDOF} )\). Figure 12a shows the 5 % damped pseudo-acceleration response spectra \(S_{a}^{(i)} (T_{SDOF} )\) scaled at the period (without P-delta) T SDOF  = 3.0 s. Assuming a large stability coefficient of θ = 0.40, \(T_{SDOF}^{P\Delta } =\) \(T_{SDOF}^{{}} \sqrt {{1 \mathord{\left/ {\vphantom {1 {(1 - \theta }}} \right. \kern-0pt} {(1 - \theta }})}\) becomes 3.87 s. At \(T_{SDOF}^{P\Delta }\) the dispersion of the response spectra, \(\sigma_{\ln Sa}\), scaled to \(T_{SDOF}\) is already 0.35, see Fig. 11a. Thus, even in the elastic range a distinct dispersion of the system response can be observed. To correct this additional variability in the records, Fig. 12b shows the corresponding scaled spectra based on \(S_{a}^{(i)} (T_{SDOF}^{P\Delta } )\). The same reference spectral acceleration equal to 0.1 g was used for both IMs.

Fig. 12
figure 12

Scaled individual record dependent elastic pseudo-acceleration response spectra and their corresponding 50th, 16th and 84th percentiles for a \(S_{a} (T_{SDOF}^{{}} )\), b \(S_{a} (T_{SDOF}^{P\Delta } )\)

Full size image

Figure 13 shows RTR dispersion spectra s * based on the “P-delta” IM \(S_{a} (T_{SDOF}^{P\Delta } )\) for negative post-yield stiffness ratios θ − α of 0.04, 010, 0.20, 0.30, 0.40, 0.60 and 0.80. With increasing θ − α the system becomes more prone to collapse due to the steep negative post-yielding slope, and less dependent on RTR variability. It is observed that IM \(S_{a} (T_{SDOF}^{P\Delta } )\) reflects appropriately this physical behavior.

Fig. 13
figure 13

RTR dispersion spectra \(s^{*}\) for different negative post-yield stiffness ratios θ − α based on IM \(S_{a} (T_{SDOF}^{P\Delta } )\)

Full size image

5 A comparison of the efficiency of different intensity measures

In this section, the effect of the RTR variability on the collapse capacity variability of P-delta vulnerable SDOF systems is compared for the “optimal” averaged IM \(S_{a,gm}^{\alpha }\) and two single target pseudo-spectral acceleration IMs: the “P-delta” IM \(S_{a} (T_{SDOF}^{P\Delta } )\) and the benchmark IM \(S_{a} (T_{SDOF}^{{}} )\). System configurations for 50 values of \(T_{SDOF}\) = 0.1, 0.2, 0.3,…, 5 s., and 13 cases of θ − α = 0.04, 0.06, 0.08, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.60 and 0.80 are considered, using a damping value ζ = 0.05.

Figure 14 presents the dispersion s * spectra for the three studied IMs and nine θ − α values. For small negative post-yield stiffness ratios; i.e., \(\theta - \alpha \, \le \,0.10\), the two single target IMs yield similar RTR dispersion spectra that are larger than those based on the averaged IM \(S_{a,gm}^{\alpha }\). The reduction of RTR variability based on IM \(S_{a,gm}^{\alpha }\) becomes more evident when the post-yield stiffness increases up to 0.20. Also, the efficiency of IM \(S_{a} (T_{SDOF}^{P\Delta } )\) starts to increase noticeably for \(\theta - \alpha\) > 0.45. For \(0.30\, \le \,\theta - \alpha \le \,0.45\) the collapse capacity dispersion based on IM \(S_{a} (T_{SDOF}^{P\Delta } )\) is shifted to smaller RTR values leading to similar spectra based on the IM \(S_{a,gm}^{\alpha }\). For \(\theta - \alpha \, = \,0.60\) and 0.80, the IM \(S_{a} (T_{SDOF}^{P\Delta } )\) is the most efficient IM.

Fig. 14
figure 14

RTR dispersion s *spectra. IMs and negative post-yield stiffness ratios θ − α as specified

Full size image

These trends are verified in Fig. 15, which summarizes the mean dispersions \({\text{E}}_{{T_{SDOF} }} [s^{*} ]\) and \({\text{E}}_{\theta - \alpha } [s^{*} ]\) for the three studied IMs. As observed, \({\text{E}}_{{T_{SDOF} }} [s^{*} ]\) and \({\text{E}}_{\theta - \alpha } [s^{*} ]\) are significantly larger for the benchmark IM \(S_{a} (T_{SDOF} )\). Figures 15a shows the mean dispersion \({\text{E}}_{{T_{SDOF} }} [s^{*} ]\) of s *, as a function of θ − α, with respect to 50 values of periods T SDOF . For \(\theta - \alpha \, \le \,0.10\) the period elongation is mainly due to the potential of large inelastic deformations. Hence, the only IM that reduces the collapse capacity dispersion is \(S_{a,gm}^{\alpha }\).

Fig. 15
figure 15

Mean dispersion measures a \(E_{{T_{SDOF} }} [s^{*} ]\) and b \(E_{\theta - \alpha } [s^{*} ]\). IMs, negative post-yield stiffness ratios θ − α and system periods T SDOF as specified

Full size image

As θ − α increases, the systems become more prone to failure, and less dependent on the frequency content of the ground motions. Therefore, for very steep negative post-yield stiffness, collapse capacity dispersion is less affected by RTR variability. The expected behavior of increasing efficiency with increasing θ − α is only observed for outcomes based on the IM \(S_{a} (T_{SDOF}^{P\Delta } )\).

A contradicting trend is observed for IM \(S_{a} (T_{SDOF} )\) if \(\theta - \alpha \, \ge \,0.30\), and for the IM \(S_{a,gm}^{\alpha }\) if \(\theta - \alpha \, \ge \,0.45\). As θ − α increases, the difference between the periods T SDOF and \(T_{SDOF}^{P\Delta }\) becomes so large that the dispersion starts to increase. At θ = 0.41 period \(T_{SDOF}^{P\Delta }\) is about 1.3 times T SDOF , and thus, it is in the center of averaging period interval ΔT. Consequently, at \(\theta - \alpha \, \approx \,0.45\) the efficiency of IM \(S_{a,gm}^{\alpha }\) and IM \(S_{a} (T_{SDOF}^{P\Delta } )\) is about the same because “higher mode effects” and effect of period elongation cancel out. Further increase of θ − α (> 0.45) impairs the efficiency of IM \(S_{a,gm}^{\alpha }\).

It can be concluded that IM \(S_{a,gm}^{\alpha }\) is the most efficient IM for \(\theta - \alpha \, \le \,0.45\). However, for larger θ − α values, IM \(S_{a} (T_{SDOF}^{P\Delta } )\) leads to the smallest collapse capacity dispersion. Figure 15b shows the mean with respect to 13 values of θ − α as a function of T SDOF . A fluctuation of the mean collapse capacity variability \({\text{E}}_{\theta - \alpha } [s^{*} ]\) around 0.23 is observed for relative IMs \(S_{a,gm}^{\alpha }\) and \(S_{a} (T_{SDOF}^{P\Delta } )\), as opposed to 0.37 for the IM \(S_{a} (T_{SDOF} )\).

Note that an averaged IM, where the lower bound period corresponds to P-delta affected period; i.e. \(T_{1} = T_{SDOF}^{P\Delta }\), is not more efficient than IM \(S_{a,gm}^{\alpha } (T_{SDOF} ,1.6T_{SDOF} )\) proposed in Sect. 3.3. Additionally, for such IM the ratio between the upper bound and lower bound period is not constant, but depends strongly on the negative post-yield stiffness ratio and actual system period. Consequently, the definition of a simple “global” IM with \(T_{1} = T_{SDOF}^{P\Delta }\) valid for a wide range of system parameters is not possible (Tsantaki 2014).

6 Sufficiency and scaling robustness of the utilized intensity measures

The sufficiency and scaling robustness properties of the utilized IMs with respect to the natural logarithm of the 44 collapse capacities of the FEMA P-695-FF record set are examined for 500 structural configurations with system periods \(T_{SDOF}\)  = 0.1, 0.2, 0.3, …, 4.8, 4.9, 5.0 s, and post-yield stiffness ratios θ − α = 0.04, 0.06, 0.08, 0.10, 0.20, 0.30, 0.40, 0.50, 0.60, 0.80. The sufficiency property is studied for two ground motion characteristics: the earthquake magnitude (M), and the natural logarithm of the source-to-site distance (Bozorgnia and Campbell 2004; Bommer and Akkar 2012). The selected measures of source-to-site distance are the epicentral distance R epi as a point-source distance metric, and the Joyner-Boore distance R JB as an extended-source distance metric. The present evaluation on the linear or logarithmic dependencies of the natural logarithm of the collapse capacities is consistent with the studies of Cornell et al. (1979), Abrahamson and Silva (1997), Bianchini et al. (2009), and Bojórquez and Iervolino (2011) on the considered ground motion characteristics, such as the magnitude, the natural logarithm of the source-to-site distance, and the natural logarithm of the scaling factors.

Initially, scatter plots have been used to explore by visual inspection the possible linear or non-linear relationship between paired sets consisting of the natural logarithm of the collapse capacities and the considered parameter. For instance, Fig. 16 shows the scatter plots of the natural logarithm of the 44 collapse capacities of the FEMA P-695-FF record set for two system configurations, T SDOF  = 1.0 s, θ − α = 0.10, and T SDOF  = 3.0 s, θ − α = 0.20, for all the utilized IMs as a function of the magnitude M. Figure 17 shows similar scatter plots as a function of the scaling factors SF. Note that these figures show the non-logarithmic values plotted in logarithmic scaled axes (for logarithmic quantities). The scatter plots of all the considered structural configurations have not revealed any apparent non-linear relationship. Therefore, only a linear relationship is further examined. Firstly, linear regression analyses were conducted, and the linear regression slope coefficients β estimated, where a β value close to 0 indicates negligible correlation of the two paired sets. For each parameter set and IM of Figs. 16 and 17, the corresponding linear regression fit and estimate of the linear regression coefficient β are specified.

Fig. 16
figure 16

Scatter plots and linear regression fits about the sufficiency property with respect to the earthquake magnitude M for IM a, d \(S_{a} (T_{SDOF} )\), b, e \(S_{a,gm}^{a}\) c, f \(S_{a} (T_{SDOF}^{P\Delta } )\) and the 44 collapse capacities of the FEMA P-695-FF record set for two system configurations (a–c) \(T_{SDOF} = 1.0\,\text {s},\,\theta - \alpha = 0.10\) and (d–f) \(T_{SDOF} = 3.0\,\text {s},\,\theta - \alpha = 0.20\)

Full size image
Fig. 17
figure 17

Scatter plots and linear regression fits about the scaling robustness property for IM a, d \(S_{a} (T_{SDOF} )\), b, e \(S_{a,gm}^{a}\), c, f \(S_{a} (T_{SDOF}^{P\Delta } )\) with respect to the scaling factors and the 44 collapse capacities of the FEMA P-695-FF record set for two system configurations a–c \(T_{SDOF} = 1.0\,\text {s},\,\theta - \alpha = 0.10\) and d–f \(T_{SDOF} = 3.0\,\text {s},\,\theta - \alpha = 0.20\)

Full size image

In a further step the potential correlation between the evaluated parameters for all the considered structural configurations is quantified in terms of the linear correlation coefficient r and the p value function. The linear correlation coefficient r measures the strength and direction of a linear regression between two variables, and it is computed from the covariance of the two variables divided by the product of their standard deviations. Correlation coefficient r varies from −1 to 1 (Fenton and Neil 2012), where values close to 0 indicate a negligible correlation, values smaller than 0.5 a weak correlation, and values larger than 0.8 a strong correlation (Roberts and Roberts 2015). The p value determines the “statistical significance” of the correlation coefficients r, representing the probability of obtaining a correlation as large as the observed linear correlation coefficient by random chance when the true correlation is zero (MATLAB and Statistics Toolbox Release 2015a, 2015). Since a p value is a probability quantity, it ranges from 0 to 1 (GraphPad Statistics Guide 2015). A threshold p value equal to 0.05 was predefined before conducting the statistical test. A p value smaller than this threshold indicates the “statistical significance” of the observed values and the rejection of the null hypothesis of non-correlation. This means that the computed r-values would rarely occur (i.e., with a probability equal to 0.05) due to random sampling if the two paired sets were correlated from identical populations. For the considered system configurations, IMs, and paired sets in Figs. 16 and 17 also the corresponding correlation coefficient r and the p value are specified.

Figures 18, 19, 20 and 21 show the correlation coefficients r and p values as a function of T SDOF for the negative post-yield stiffness ratios θ − α = 0.04, 0.10, 0.20, 0.30, 0.40 and 0.80. Figures 18, 19 and 20 reveal that the correlation coefficients r with respect to the sufficiency property ranges in general from −0.25 to 0.25 for all considered ground motion parameters, IMs, and θ − α values. Exceptions are larger r values for the extremely large negative post-yield stiffness ratio θ − α = 0.80, and a few structural parameter configurations with steep post-yield negative slopes, such as θ − α = 0.30 and 0.40, in particular for the benchmark IM S a (T SDOF ). In the period range 0 < T SDOF  < 2 s, the r-value fluctuates around 0, in contrast to longer system periods where larger r-values are observed. Correspondingly, the p values are in general above the threshold 0.05 for the majority of configurations, except for θ − α = 0.80 and a few additional θ − α cases in system period domains with values larger than 2.0 s. As observed, the system period regions with r-values larger than 0.25 correspond, in general, to the system period domains with a p value smaller than 0.05. These system period domains depend on the ground motion characteristics and the underlying IM. For example, the period domain is \(T_{SDOF} > 3.0\,{\text{s}}\) for magnitude M and IM \(S_{a} (T_{SDOF} )\), \(T_{SDOF} > 4.0\,{\text{s}}\) for M and IM \(S_{a,gm}^{\alpha }\), \(T_{SDOF} \, > 2\,.5\,{\text{s}}\) for point-source distance metric R epi and \(S_{a} (T_{SDOF} )\), \(T_{SDOF} \, > 4\,.0\,{\text{s}}\) for R epi and IM \(S_{a,gm}^{\alpha }\), \(2.0\,{\text{s}} < T_{SDOF} < 3.5\,{\text{s}}\) for the extended-source distance metric R JB and IM \(S_{a} (T_{SDOF} )\), and \(2.0\,{\text{s}} < T_{SDOF} < 2.8\,{\text{s}}\) for R JB and \(S_{a} (T_{SDOF}^{P\Delta } )\). In all other combinations just a few narrow banded and scattered period domains are observed.

Fig. 18
figure 18

a–c Correlation coefficient and d–f p value plots as a function of system period \(T_{SDOF}\) about the sufficiency property of a, d \(S_{a} (T_{SDOF} )\), b, e \(S_{a,gm}^{a}\), c, f \(S_{a} (T_{SDOF}^{P\Delta } )\) IM with respect to the earthquake magnitude (M). Negative post-yield stiffness ratios \(\theta - \alpha\) as specified

Full size image
Fig. 19
figure 19

a–c Correlation coefficient and d–f p value plots as a function of system period \(T_{SDOF}\) about the sufficiency property of a, d \(S_{a} (T_{SDOF} )\), b, e \(S_{a,gm}^{a}\), c, f \(S_{a} (T_{SDOF}^{P\Delta } )\) IM with respect to the epicentral distance (R epi ). Negative post-yield stiffness ratios θ − α as specified

Full size image
Fig. 20
figure 20

a–c Correlation coefficient and d–f p value plots as a function of system period T SDOF about the sufficiency property of a, d \(S_{a} (T_{SDOF} )\), b, e \(S_{a,gm}^{a}\), c, f \(S_{a} (T_{SDOF}^{P\Delta } )\) IM with respect to the Joyner-Boore distance (R JB ). Negative post-yield stiffness ratios θ − α as specified

Full size image
Fig. 21
figure 21

a–c Correlation coefficient and d–f p value plots as a function of system period T SDOF about the scaling robustness property of a, d \(S_{a} (T_{SDOF} )\) b, e \(S_{a,gm}^{a}\) c, f \(S_{a} (T_{SDOF}^{P\Delta } )\) IM. Post-yield stiffness ratios θ − α as specified

Full size image

The correlation coefficients \(r\) with respect to scaling robustness property is expressed by the relation between the natural logarithm of the collapse capacities and the natural logarithm of the scaling factors. In general, this coefficient ranges between −0.50 and 0.0 for all considered IMs and system configurations, except for systems with θ − α = 0.80 (Fig. 21). For both single-target IMs, r is around 0.35 if T SDOF  < 3 s. In contrast, in this period range for the averaged IM S α a,gm the r-value is only about 0.20. For system periods T SDOF  > 3 s the collapse capacities based on the benchmark IM exhibit smaller correlation coefficients r varying from 0 to −0.25, while for the “P-delta” and the averaged IM r is in general about 0.25, except for a few cases of θ − α values. Also, p values less than 0.05 are observed for all IMs, however, in case of the single target IMs the corresponding period regions are more extended and include larger numbers of the considered θ − α values.

The p values in Figs. 18, 19, 20 and 21 below the selected threshold of 0.05 indicate that the computed r values are “statistical significant”. For such cases, the selected IM is conditionally linearly dependent with respect to the natural logarithm of collapse capacities on the considered parameters, such as ground motion characteristics and scaling factors. Therefore, these period domains do not strictly meet the properties of sufficiency and scaling robustness. However, the period intervals in which p values are below the predefined threshold of 0.05 are very limited, except for the scaling robustness property (Fig. 21). More important, in all cases the correlation coefficient is smaller than r < 0.5, indicating a weak correlation between the selected IM and the ground motion characteristics or scaling factors.

For instance, the natural logarithm of scaling factors is weakly correlated (r < 0.5) with the natural logarithm of the 44 collapse capacities of the FEMA P-695-FF record set, and for some scenarios it is statistically significant (p value < 0.05). This correlation is negative (Figs. 17 and 21), revealing a decrease of the natural logarithm of collapse capacities as the natural logarithm of scaling factors increases. This finding is consistent with results of Bianchini et al. (2009). In all other cases with p values larger than the selected threshold, the correlation is considered as “statistical insignificant”.

7 Conclusions

Two alternative elastic pseudo-spectral acceleration based IMs were compared with the widely accepted IM, S a (T SDOF ); i.e., the 5 % damped pseudo-spectral acceleration at the system period T SDOF of the structure without P-delta. The efficiency of the two alternative IMs to reduce collapse capacity dispersion caused by record-to-record (RTR) variability was presented. Initially, three different sets of averaged IMs were studied with different lower and upper bounds of the period interval to obtain the “optimal” averaged IM that leads to the smallest collapse capacity dispersion due to RTR variability. From the results of this parametric study in a wide range of structural configurations, the following conclusions can be drawn for the considered type of P-delta vulnerable and non-deteriorating simple systems:

  • The lower bound of the period interval corresponds to the SDOF period of vibration because no higher modes effects do exist. This result cannot be transferred to multi-degree-of-freedom (MDOF) structures.

  • The “optimal” upper bound of the period interval for the averaging IM is on average about 1.6 times the system period. The period elongation is either a result of large inelastic deformations in the case of small negative post-yield stiffness slopes, or the results of the presence of gravity loads in systems with steeper negative slopes.

  • An “optimal” averaged IM \(S_{a,gm}^{\alpha } (T_{SDOF} ,\,1.6T_{SDOF} )\,\), or briefly \(S_{a,gm}^{\alpha }\) is introduced for system periods larger than 0.15 s, which is composed of the geometric mean of the 5 % damped spectral acceleration in the range between the system period and 1.6 times this period. Note that the upper limit of this period range is similar to values proposed in several guidelines, without being clearly verified by or/and related to previous research studies.

Subsequently, an alternative single target IM is introduced, \(S_{a} (T_{SDOF}^{P\Delta } )\), which corresponds to the 5 % damped pseudo-spectral acceleration at the system period considering gravity load effects. This “P-delta” IM leads to smaller collapse capacity dispersion as the negative post-yield stiffness ratio becomes larger than 0.45.

The most efficient IM, leading to the smallest RTR dispersion, for systems with negative post-yield stiffness ratios \(\theta - \alpha \le 0.45\) is \(S_{a,gm}^{\alpha }\); for systems with θ − α > 0.45 the most efficient IM is \(S_{a} (T_{SDOF}^{P\Delta } )\).

For IMs \(S_{a,gm}^{\alpha }\) and \(S_{a} (T_{SDOF}^{P\Delta } )\), the mean RTR variability is on average 0.23, with respect to the considered post-yield stiffness ratios. In contrast, for \(S_{a} (T_{SDOF}^{{}} )\), this mean is 0.37; i.e., about 60 % larger.

The sufficiency and scaling robustness property of the utilized IMs with respect to the natural logarithm of the 44 collapse capacities of the FEMA P-695-FF record set were examined for the considered structural configurations. The sufficiency property was studied for two ground motion characteristics; i.e., the earthquake magnitude and the natural logarithm of the source-to-site distance. Two measures of source-to-site distance were selected: the epicentral distance as a point-source distance metric, and the Joyner-Boore distance as an extended-source distance metric. The scatter plots revealed that there is no apparent non-linear relationship between the natural logarithm of the collapse capacities and the corresponding ground motion characteristics. Therefore, only the potential of linear relationship was further examined, quantifying the linear correlation coefficients r and their corresponding p values. The outcomes can be summarized as follows.

  • For the selected structural configurations the period domains and negative post-yield stiffness ratios θ − α with r > 0.25 and p value < 0.05 were identified for all the considered paired sets and IMs. Note that p values below the selected threshold of 0.05 indicate that the computed r values are “statistically significant”. For such cases, the selected IM is conditionally linearly dependent on the considered ground motion parameters or scaling factors (with respect to the natural logarithm of collapse capacities), and may not meet the properties of sufficiency and scaling robustness. These domains are more extended for the conventional IM S a (T SDOF ).

  • The natural logarithm of scaling factors exhibits a weak correlation with the natural logarithm of the collapse capacities. This correlation is negative, revealing a decrease of the natural logarithm of collapse capacities as the natural logarithm of scaling factors increases.

The presented results are only valid for single-degree-of-freedom systems and should not be extrapolated to multi-degree-of-freedom structures.