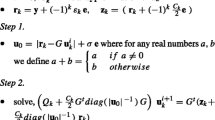A ν-twin support vector machine based regression with automatic accuracy control

Abstract

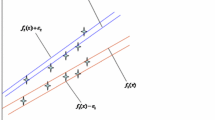
This paper presents an efficient ν-Twin Support Vector Machine Based Regression Model with Automatic Accuracy Control (ν-TWSVR). This ν-TWSVR model is motivated by the celebrated ν-SVR model (Schlkoff et al. 1998) and recently introduced 𝜖-TSVR model (Shao et al., Neural Comput Applic 23(1):175–185, 2013). The ν-TSVR model can automatically optimize the parameters 𝜖 ₁ and 𝜖 ₂ according to the structure of the data such that at most certain specified fraction ν ₁(respectively ν ₂) of data points contribute to the errors in up (respectively down) bound regressor. The ν-TWSVR formulation constructs a pair of optimization problems which are mathematically derived from a related ν-TWSVM formulation (Peng, Neural Netw 23(3):365–372, 2010) and making use of an important result of Bi and Bennett (Neurocomputing 55(1):79–108, 2003). The experimental results on artificial and UCI benchmark datasets show the efficacy of the proposed model in practice.

Appendices

Appendix A

Proposition 1

Suppose ν-TWSVR is applied on a dataset which results 𝜖 ₁ (respectively 𝜖 ₂ ) > 0, then following statements hold.

• (a) v ₁ (respectively v ₂ ) is an upper bound on fraction of error ξ(respectively η).

• (b) v ₁ (respectively v ₂ ) is a lower bound on fraction of support vectors for up bound (respectively down bound) regressor.

Proof

• (a) Using the KKT conditions (21) and (25) for up bound regressor, we can find that for ξ _i > 0, β _i = 0 and $\alpha _{i} = \frac {c_{2}}{l}$. Since from (22) and (26), e ^T α≤c ₂ v ₁, so there may exist at most l v ₁ points for which ξ _i ≠0. In the similar way using the K.K.T. optimality conditions for down bound regressor we can prove that there are at most l v ₂ points for which η _i ≠0.

• (b) Using the KKT conditions (22) and (25) for 𝜖 ₁≠0 we find that γ = 0. This implies that e ^T α = c ₂ v ₁.

  Since $0 \leq \alpha _{i} \leq \frac {c_{2}}{l}$ so there must be at least l v ₁ points for which α _i ≠0. In similar way using the K.K.T conditions for down bound regressor we can prove that there are at least l v ₂ points for which λ _i ≠0 .

□

Appendix B: ν-TWSVR via ν-TWSVM

Bi and Bennett [5] have shown the equivalence between a given regression problem and an appropriately constructed classification problem. They have shown that for a given regression training set (A,Y), a regressor y = w ^T x + b is an 𝜖-insensitive regressor if and only if the set D ⁺ and D ⁻ locate on different sides of n+1 dimensional hyperplane w ^T x−y + b = 0 respectively where

$$\begin{array}{@{}rcl@{}} D^{+} = \{(A_{i},y_{i}+\epsilon),i=1,2,...,l\}\\ D^{-} = \{(A_{i},y_{i}-\epsilon),i=1,2,...,l\}. \end{array} $$

In veiw of this result of Bi and Bennett [5], the regression problem is equivalent to the classification problem of sets D ⁺ and D ⁻ in R ⁿ⁺¹. If we use the TWSVM methodology [6] for the classification of these two sets D ⁺ and D ⁻ then we can find TWSVM based Regression [8]. It is relevant to mention here that the classification of set D ⁺ and D ⁻ is a special case of classification where we have following privilege informations.

• (a) D ⁺ and D ⁻ classes are symmetric in nature and have equal number of sample points.

• (b) Points in the class D ⁺ and D ⁻ are separated by the distance 2𝜖.

These privileged informations must be exploited for the better classification as better classification of the set D ⁺ and D ⁻ will eventually lead to better regressor. The classification of the set D ⁺ and D ⁻ in R ⁿ⁺¹ using ν-TWSVM results into following QPPs

$$\begin{array}{@{}rcl@{}} \underset{(w_{1},\eta_{1},b_{1},\rho_{+})}{Min} & \frac{c_{1}}{2}\left( ||w_{1}||^{2}\,+\, {\eta_{1}^{2}} + {b_{1}^{2}}\right) \,+\,\frac{1}{2}||Aw_{1}\,+\,\eta_{1}(Y+\epsilon e)\,+\,eb_{1}||^{2} \\ & - c_{2}v_{1}\rho_{+} \ \\ \text{subject to,} & \\ &(Aw_{1}+\eta_{1}(Y-\epsilon e)+eb_{1})+\rho_{+}e \leq 0,\\ ~&\rho_{+} \geq 0, \end{array} $$

(40)

and

$$\begin{array}{@{}rcl@{}} &&{}\underset{(w_{2},\eta_{2},b_{2},\rho_{-})} { Min} \frac{c_{3}}{2}\left( ||w_{2}||^{2}+ {\eta_{2}^{2}}+{b_{2}^{2}} \right) +\frac{1}{2}||Aw_{2}\\ & &+\eta_{2}(Y-\epsilon e)+eb_{2}||^{2} -c_{4}v_{2} \rho_{-} \\ &\text{subject to,} & \\ && (Aw_{2}+\eta_{2}(Y+\epsilon e)+eb_{2})-\rho_{-}e \geq 0, \\ &&\qquad\qquad\rho_{-} \geq 0 . \\ \end{array} $$

(41)

Let us first consider the problem (40). Here we note that η ₁≠0 and therefore, without loss of generality, we can assume that η ₁ > 0. The constraint of (40) can be rewriteen as

$$\left[-A\!\left( \frac{-w_{1}}{\eta_{1}}\right) \,+\, (Y\!-\epsilon e) \!-e\left( \frac{-b}{\eta_{1}}\right)\right] + \frac{\rho_{+}e}{\eta_{1}} \leq 0 ,\,\, \rho_{+} \geq 0$$

On replacing w ₁:=−w ₁/η ₁, b ₁:=−b ₁/η ₁ and noting that η ₁≥0, (40) reduces to

$$\begin{array}{@{}rcl@{}} \underset{(w_{1},b_{1},\rho_{+})}{Min} \frac{1}{2}||w_{1}||^{2}+{b_{1}^{2}} +||(Y+\epsilon e) \,-\,(Aw_{1}+eb_{1})||^{2} - c_{2}v_{1}\rho_{+} \\ &\text{subject to,} \\ & Aw_{1} + eb_{1} +\epsilon e \geq Y + \frac{\rho_{+}e}{\eta_{1}}, \\ & \rho_{+} \geq 0 . \end{array} $$

(42)

Next, if we replace e b ₁: = e b ₁−𝜖 e in (42) then it reduces to

$$\begin{array}{@{}rcl@{}} \underset{(w_{1},b_{1},\rho_{+})}{Min} \frac{1}{2}||w_{1}||^{2}+{b_{1}^{2}} +||Y \!-(Aw_{1}+eb_{1})||^{2} \,-\, c_{2}v_{1}\rho_{+} \\ &\text{subject to,} \\ & Aw_{1} + eb_{1} \geq Y -\left( 2\epsilon e-\frac{\rho_{+}e}{\eta_{1}}\right) \\ & \rho_{+} \geq 0 . \end{array} $$

(43)

Let $\left (2e\epsilon -\frac {\rho _{+}}{\eta _{1}}\right ):=e\epsilon _{1}$ then it will reduce to

$$\begin{array}{@{}rcl@{}} \underset{w_{1} ,b_{1},\epsilon_{1}}{Min } & \frac{1}{2}||w_{1}||^{2}+{b_{1}^{2}} +\frac{1}{2}||(Y-(Aw_{1}+eb_{1})||^{2} \\& +c_{2}v_{1}\epsilon_{1} \\ \text{subject to,} & (Aw_{1}+eb_{1}) -Y\geq -\epsilon_{1} e. \end{array} $$

(44)

In the similar manner, assuming η ₂ > 0 and using the replacement w ₂:=−w ₂/η ₂, b ₂:=−b ₂/η ₂, problem (41) can be written as

$$\begin{array}{@{}rcl@{}} \underset {(w_{2},b_{2},\rho_{-})}{Min} \frac{1}{2}||w_{2}||^{2}+{b_{2}^{2}} +\frac{1}{2}||(Y-\epsilon e) \,-\,(Aw_{2}+eb_{2})||^{2} -c_{4}v_{2}\rho_{-} \\ & \text{~~ subject to,}, \\ & (Aw_{2}+eb_{2})-\epsilon e \leq Y -\frac{\rho_{-}}{\eta_{2}}e, \\ &\rho_{-} \geq 0 . \end{array} $$

If we replace e b ₂: = e b ₂ + 𝜖 e and $(2e\epsilon -\frac {\rho _{-}}{\eta _{2}}):=e\epsilon _{2}$ then problems reduces to

$$\begin{array}{@{}rcl@{}} \underset{w_{2} ,b_{2},\epsilon_{2}}{Min } & \frac{1}{2}||w_{2}||^{2}+{b_{2}^{2}} +\frac{1}{2}||(Y-(Aw_{2}+eb_{2})||^{2} \\&& +c_{4}v_{1}\epsilon_{2} \\ \text{subject to,} & Y-(Aw_{2}+eb_{2})\geq -\epsilon_{2}e. \end{array} $$

(45)

Looking at problems (44) and (45 ) we observe that our approach is valid provided we can show that $\epsilon _{1}=(2\epsilon -\frac {2\rho _{+}}{\eta _{1}}) \geq 0$ and $\epsilon _{2} = (2\epsilon -\frac {2\rho _{-}}{\eta _{2}}) \geq 0$. We can prove this assertion as follow.

As the first hyperplane w ^T x + η ₁ y + b ₁ = 0 is the least square fit for the class D ⁺ so there certainly exists an index j such that

$$\begin{array}{@{}rcl@{}} \eta_{1}(y_{j}+\epsilon) +{w_{1}^{T}}x_{j}+b_{1} \geq 0. \end{array} $$

(46)

Also from (40),

$$\begin{array}{@{}rcl@{}} \eta_{1}(y_{i}-\epsilon) +{w_{1}^{T}}x_{j}+b_{1}+\rho_{+} \leq 0,~~\text{for all \textit{i}} \end{array} $$

(47)

In particular, taking (47) for j we get

$$\begin{array}{@{}rcl@{}} \eta_{1}(y_{j}-\epsilon) +{w_{1}^{T}}x_{j}+b_{1} + \rho_{+} \leq 0, \\ \text{i.e.~~} -\eta_{1}(y_{j}-\epsilon) -{w_{1}^{T}}x_{j}-b_{1}-\rho_{+} \geq 0 \end{array} $$

(48)

Adding (47) and (48) we get $\epsilon _{1} = \left (2\epsilon -\frac {\rho _{+}}{\eta _{1}}\right ) \geq 0$. Similarly we can prove that $\epsilon _{2} = \left (2\epsilon -\frac {\rho _{-}}{\eta _{2}}\right ) \geq 0$.

Remark 2

The above proof can be appropriately modified to show that 𝜖-TSVR formulation of Shao et al. [9] also follows from Bi and Bennett [5] results and TWSVM methodology.