Skip to main content
SpringerLink
Log in

High order schemes for the tempered fractional diffusion equations

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

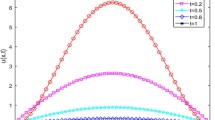
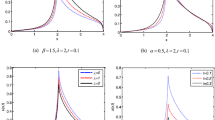
Abstract

Lévy flight models whose jumps have infinite moments are mathematically used to describe the superdiffusion in complex systems. Exponentially tempering Lévy measure of Lévy flights leads to the tempered stable Lévy processes which combine both the α-stable and Gaussian trends; and the very large jumps are unlikely and all their moments exist. The probability density functions of the tempered stable Lévy processes solve the tempered fractional diffusion equation. This paper focuses on designing the high order difference schemes for the tempered fractional diffusion equation on bounded domain. The high order difference approximations, called the tempered and weighted and shifted Grünwald difference (tempered-WSGD) operators, in space are obtained by using the properties of the tempered fractional calculus and weighting and shifting their first order Grünwald type difference approximations. And the Crank-Nicolson discretization is used in the time direction. The stability and convergence of the presented numerical schemes are established; and the numerical experiments are performed to confirm the theoretical results and testify the effectiveness of the schemes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Baeumera, B., Meerschaert, M.M.: Tempered stable Lévy motion and transient super-diffusion. J. Comput. Appl. Math. 233(10), 2438–2448 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  2. Buschman, R.G.: Decomposition of an integral operator by use of Mikusinski calculus. SIAM J. Math. Anal. 3(1), 83–85 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  3. Carmi, S., Turgeman, L., Barkai, E.: On distributions of functionals of anomalous diffusion paths. J. Stat. Phys. 141(6), 1071–1092 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  4. Cartea, Á., del-Castillo-Negrete, D.: Fractional diffusion models of option prices in markets with jumps. Phys. A 374(2), 749–763 (2007)

    Article  Google Scholar 

  5. Cartea, Á., del-Castillo-Negrete, D.: Fluid limit of the continuous-time random walk with general Lévy jump distribution functions. Phys. Rev. E 76, 041105 (2007)

    Article  Google Scholar 

  6. del-Castillo-Negrete, D.: Truncation effects in superdiffusive front propagation with Lévy flights. Phys. Rev. E 79, 031120 (2009)

    Article  Google Scholar 

  7. Çelik, C., Duman, M.: Crank-Nicolson method for the fractional diffusion equation with the Riesz fractional derivative. J. Comput. Phys. 231(4), 1743–1750 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  8. Chechkin, A.V., Gonchar, V.Yu., Klafter, J., Metzler, R.: Natural cutoff in Lévy flights caused by dissipative nonlinearity. Phys. Rev. E 72, 010101 (2005)

    Article  MathSciNet  Google Scholar 

  9. Deng, W.H., Chen, M.H., Barkai, E.: Numerical algorithms for the forward and backward fractional Feynman-Kac equations. J. Sci. Comput. 62(3), 718–746 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  10. Fornberg, B.: Calculation of weights in finite difference formulas. SIAM Rev. 40(3), 685–691 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  11. Golub, G.H., Van Loan, C.F.: Matrix Computations, 3rd edn. The Johns Hopkins University Press, Baltimore (1996)

    MATH  Google Scholar 

  12. Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic, New York (1974)

    MATH  Google Scholar 

  13. Podlubny, I.: Fractional Differential Equations. Academic, San Diego (1999)

    MATH  Google Scholar 

  14. Samko, S., Kilbas, A., Marichev, O.: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, London (1993)

    MATH  Google Scholar 

  15. Srivastava, H.M., Buschman, R.G.: Convolution Integral Equations with Special Function Kernels. Wiley, New York (1977)

    MATH  Google Scholar 

  16. Lynch, V.E., Carreras, B.A., del-Castillo-Negrete, D., Ferreira-Mejias, K.M., Hicks, H.R.: Numerical methods for the solution of partial differential equations of fractional order. J. Comput. Phys. 192, 406–421 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  17. Liu, F., Ahn, V., Turner, I.: Numerical solution of the space fractional Fokker-Planck equation. J. Comput. Appl. Math. 166(2), 209–219 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  18. Marom, O., Momoniat, E.: A comparison of numerical solutions of fractional diffusion models in finance. Nonl. Anal.: R.W.A. 10(6), 3435–3442 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  19. Metzler, R., Klafter, J.: The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A 37(31), R161–R208 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  20. Mantegna, R.N., Stanley, H.E.: Stochastic process with ultraslow convergence to a Gaussian: the truncated Lévy flight. Phys. Rev. Lett. 73(22), 2946–2949 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  21. Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for fractional advection-dispersion flow equations. J. Comput. Appl. Math. 172(1), 65–77 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  22. Meerschaert, M.M., Zhang, Y., Baeumer, B.: Tempered anomalous diffusion in heterogeneous systems. Geophys. Res. Lett. 35, L17403 (2009)

    Article  Google Scholar 

  23. Meerschaert, M.M., Sikorskii, A.: Stochastic Models for Fractional Calculus. De Gruyter Studies in Mathematics, vol. 43. Walter de Gruyter, Berlin/Boston (2012)

  24. Nasir, H.M., Gunawardana, B.L.K., Abeyrathna, H.M.N.P.: A second order finite difference approximation for the fractional siffusion equation. Inter. J. Appl. Phys. Math. 3, 237–243 (2013)

    Article  Google Scholar 

  25. Ortigueira, M.D.: Riesz potential operators and inverses via fractional centred derivatives. Int. J. Math. Math. Sci. 2006, 1–12 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  26. Pang, H.-K., Sun, H.W.: Multigrid method for fractional diffusion equations. J. Comput. Phys. 231(2), 693–703 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  27. Podlubny, I.: Fractional Differential Equations. Academic, San Diego (1999)

    MATH  Google Scholar 

  28. Quarteroni, A., Sacco, R., Saleri, F.: Numerical Mathematics, 2nd edn. Springer, Berlin (2007)

    Book  MATH  Google Scholar 

  29. Sokolov, I.M., Chechkin, A.V., Klafter, J.: Fractional diffusion equation for a power-law-truncated Lévy process. Phys. A 336(3), 245–251 (2004)

    Article  Google Scholar 

  30. Sousa, E., Li, C.: A weighted finite difference method for the fractional diffusion equation based on the Riemann-Liouville derivative. Appl. Numer. Math. 90, 22–37 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  31. Tian, W.Y., Zhou, H., Deng, W.H.: A class of second order difference approximations for solving space fractional diffusion equations. Math. Comp. 84, 1703–1727 (2015)

  32. Varga, R.S.: Matrix Iterative Analysis. Springer, Berlin (2000)

    Book  MATH  Google Scholar 

  33. Wang, H., Wang, K., Sircar, T.: A direct N l o g 2 N finite difference method for fractional diffusion equations. J. Comput. Phys. 229(21), 8095–8104 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  34. Zhao, L.J., Deng, W.H.: A series of high order quasi-compact schemes for space fractional diffusion equations based on the superconvergent approximations for fractional derivatives. Numer. Methods Partial Differential Equations 31, 1345–1381 (2015)

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, School of Sciences, Xi’an University of Technology, Xi’an, Shaanxi, 710054, People’s Republic of China

    Can Li

  2. Beijing Computational Science Research Center, Beijing, 100084, People’s Republic of China

    Can Li

  3. School of Mathematics and Statistics, Gansu Key Laboratory of Applied Mathematics and Complex Systems, Lanzhou University, Lanzhou, 730000, People’s Republic of China

    Weihua Deng

Authors
  1. Can Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weihua Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weihua Deng.

Additional information

Communicated by: Jan Hesthaven

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, C., Deng, W. High order schemes for the tempered fractional diffusion equations. Adv Comput Math 42, 543–572 (2016). https://doi.org/10.1007/s10444-015-9434-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10444-015-9434-z

Keywords

Mathematics Subject Classifications (2010)

Search

Navigation