Abstract
Human Papillomavirus (HPV) types are sexually transmitted infections that cause a number of human cancers. According to the competitive exclusion principle in ecology, HPV types that have lower transmission probabilities and shorter durations of infection should be outcompeted by more virulent types. This, however, is not the case, as numerous HPV types co-exist, some which are less transmissible and more easily cleared than others. This paper examines whether this exception to the competitive exclusion principle can be explained by the aggregation of infection with HPV types, which results in patchy spatial distributions of infection, and what implications this has for the effect of vaccination on multiple HPV types. A deterministic transmission model is presented that models the patchy distribution of infected individuals using Lloyd’s mean crowding. It is first shown that higher aggregation can result in a reduced capacity for onward transmission and reduce the required efficacy of vaccination. It is shown that greater patchiness in the distribution of lower prevalence HPV types permits co-existence. This affirms the hypothesis that the aggregation of HPV types provides an explanation for the violation of the competitive exclusion principle. Greater aggregation of lower prevalence types has important implications where type-specific HPV vaccines also offer cross-protection against non-target types. It is demonstrated that the degree of cross-protection can be less than the degree of vaccine protection conferred against directly targeted types and still result in the elimination of non-target types when these non-target types are patchily distributed.



Similar content being viewed by others
References
Anderson RM, May RM (1991) Infectious diseases of humans: dynamics and control. Oxford University Press, Oxford
Arima Y, Winer RL, Feng Q, Hughes JP, Lee SK, Stern ME, O’Reilly SF, Koutsky LA (2010) Development of genital warts after incident detection of human Papillomavirus infection in young men. J Inf Dis 202(8):1181–1184
Barlow ND (1991) A spatially aggregated disease/host model for bovine Tb in New Zealand possum populations. J Appl Ecol 28(3):777–793
Bliss CI, Owen ARG (1958) Negative binomial distributions with a common k. Biometrika 45(1/2):37–58
Bogaards J, Berkhof J, Coupe V, Xiridou M, Meijer C, Wallinga J, Berkhof J (2011) Long-term impact of human Papillomavirus vaccination on infection rates, cervical abnormalities, and cancer incidence. Epidemiol Bull 22(4):505–515
Bremermann HJ, Thieme HR (1989) A competitive exclusion principle for pathogen virulence. J Math Biol 27(2):179–190
Brown DR, Kjaer SK, Sigurdsson K, Iversen O-E, Hernandez-Avila M et al (2009) The impact of quadrivalent human Papillomavirus (HPV; types 6, 11, 16, and 18) L1 virus-like particle vaccine on infection and disease due to oncogenic nonvaccine HPV types in generally HPV-naive women aged 16–26 years. J Inf Dis 199(7):926–935
Canfell K, Barnabas R, Patnick J, Beral V (2004) The predicted effect of changes in cervical screening practice in the UK: results from a modelling study. Br J Cancer 91(3):530–536
Carter JJ, Koutsky LA, Hughes JP, Lee SK, Kuypers J, Kiviat N, Galloway DA (2000) Comparison of human Papillomavirus types 16, 18, and 6 capsid antibody responses following incident infection. J Inf Dis 181(6):1911–1919
Castillo-Chavez C, Huang W, Li J (1996) Competitive exclusion in Gonorrhea models and other sexually transmitted diseases. SIAM J Appl Math 56(2):494
Castillo-Chavez C, Huang W, Li J (1999) Competitive exclusion and coexistence of multiple strains in an SIS STD model. SIAM J Appl Math 59(5):1790–1811
Chaturvedi AK, Katki HA, Hildesheim A, Rodríguez AC, Quint W, Schiffman M, Van Doorn LJ, Porras C, Wacholder S, Gonzalez P, Sherman ME, Herrero R (2011) Human Papillomavirus infection with multiple types: pattern of coinfection and risk of cervical disease. J Inf Dis 203(7):910–920
Clifford GM, Smith JS, Plummer M, Munoz N, Franceschi S (2003) Human Papillomavirus types in invasive cervical cancer worldwide: a meta-analysis. Br J Cancer 88:63–73
Clifford GM, Gallus S, Herrero R, Munoz N, Snijders PJF, Vaccarella S, Anh PTH et al (2005) Worldwide distribution of human Papillomavirus types in cytologically normal women in the international agency for research on cancer HPV prevalence surveys: a pooled analysis. Lancet 366(9490):991–998
de Visser RO, Smith AMA, Rissel CE, Richters J, Grulich AE (2003) Sex in Australia: Heterosexual experience and recent heterosexual encounters among a representative sample of adults. Aust NZ J Pub Health 27(2):146–154
De Vuyst H, Clifford G, Li N, S F (2009) HPV infection in Europe. Eur J Cancer 45(15):2632–2639
Donovan B, Franklin N, Guy R, Grulich AE, Regan DG, Ali H, Wand H, Fairley CK (2011) Quadrivalent human Papillomavirus vaccination and trends in genital warts in Australia: analysis of national sentinel surveillance data. Lancet Inf Dis 11(1):39–44
Du P, Lemkin A, Kluhsman B, Chen J, Roth R, MacEachren A, Meyers C, Zurlo J, Lengerich E (2010) The roles of social domains, behavioral risk, health care resources, and chlamydia in spatial clusters of US cervical cancer mortality: not all the clusters are the same. Cancer Cause Control 21(10):1669–1683
Dunne EF, Unger ER, Sternberg M, McQuillan G, Swan DC, Patel SS, Markowitz LE (2007) Prevalence of HPV infection among females in the United States. J Am Med Assoc 297(8):813–819
Elbasha EH, Galvani AP (2005) Vaccination against multiple HPV types. Math Biosci 197(1):88–117
Fisher R (1941) The negative binomial distribution. Ann Eugenics 11:182–187
Gertig DM, Brotherton JML, Saville AM (2011) Measuring human Papillomavirus (HPV) vaccination coverage and the role of the national HPV vaccination program register, Australia. Sex Health 8(2):171–178
Giuliano A, Lee JH, Fulp W, Villa L, Lazcano E, Papenfuss M, Abrahamsen M, Salmeron J, Anic G, Rollison D, Smith D (2011) Incidence and clearance of genital human Papillomavirus infection in men (HIM): a cohort study. Lancet 377(9769):932–940
Giuliano AR, Harris R, Sedjo RL, Baldwin S, Roe D, Papenfuss MR, Abrahamsen M, Inserra P, Olvera S, Hatch K (2002) Incidence, prevalence, and clearance of type-specific human Papillomavirus infections: the young wome’s health study. J Inf Dis 186(4):462
Giuliano AR, Lu B, Nielson CM, Flores R, Papenfuss MR, Lee JH, Abrahamsen M, Harris RB (2008) Age specific prevalence, incidence, and duration of human Papillomavirus infections in a cohort of 290 US men. J Inf Dis 198(6):827–835
Goldie S, Kohli M, Grima D, Franco EL, Weinstein MC, Bosch FX (2004) Projected clinical benefits and cost-effectiveness of a human Papillomavirus 16/18 vaccine. J Natl Cancer Inst 96(8):604–615
Goldie SJ, Grima D, Kohli M, Wright TC, Weinstein M, Franco E (2003) A comprehensive natural history model of HPV infection and cervical cancer to estimate the clinical impact of a prophylactic HPV-16/18 vaccine. Int J Cancer 106(6):896–904
Hardin G (1960) The competitive exclusion principle. Sci Agric 131(3409):1292–1297
Hartley S, Shorrocks B (2002) A general framework for the aggregation model of coexistence. J Anim Ecol 71(4):651–662
Herrero R (2009) Human Papillomavirus (HPV) vaccines: limited cross-protection against additional HPV types. J Inf Dis 199(7):919–922
Hilker FM, Langlais M, Petrovskii SV, Malchow H (2007) A diffusive SI model with Allee effect and application to FIV. Math Biosci 206(1):61–80
Ho GYF, Studentsov Y, Hall CB, Bierman R, Beardsley L, Lempa M, Burk RD (2002) Risk factors for subsequent cervicovaginal human Papillomavirus (HPV) infection and the protective role of antibodies to HPV-16 virus-like particles. J Inf Dis 186(6):737–742
Hyman JM, Li J (1997) Behavior changes in SIS STD models with selective mixing. SIAM J Appl Math 57:1082–1094
Insinga R, Dasbach E, Elbasha E, Liaw KL, Barr E (2007) Progression and regression of incident cervical HPV 6, 11, 16 and 18 infections in young women. Infect Agent Cancer 2(1):15
Insinga RP, Dasbach EJ, Elbasha EH, Liaw KL, Barr E (2007) Incidence and duration of cervical human Papillomavirus 6, 11, 16, and 18 infections in young women: an evaluation from multiple analytic perspectives. Cancer Epidem Biomar 16(4):709–715
Iwao S (1968) A new regression method for analyzing the aggregation pattern of animal populations. Res Pop Ecol 10(1):1–20
Iwao S (1976) A note on the related concepts mean crowding and mean concentration. Res Pop Ecol 17(2):240–242
Iwao S, Kuno E (1968) Use of the regression of mean crowding on mean density for estimating sample size and the transformation of data for the analysis of variance. Res Pop Ecol 10(2):210–214
Keeling MJ (2000) Simple stochastic models and their power-law type behaviour. Theor Pop Biol 58(1):21–31
Keeling MJ, Rohani P (2008) Modelling infectious diseases in humans and animals. Princeton University Press, Princeton
Kulasingam S, Connelly L, Conway E, Hocking JS, Myers E, Regan DG, Roder D, Ross J, Wain G (2007) A cost-effectiveness analysis of adding a human Papillomavirus vaccine to the Australian National Cervical Cancer Screening Program. Sex Health 4(3):165–175
Kuno E (1988) Aggregation pattern of individuals and the outcomes of competition within and between species: differential equation models. Res Pop Ecol 30(1):69–82
Lefevere E, Hens N, De Smet F, Van Damme P (2011) Dynamics of HPV vaccination initiation in Flanders (Belgium) 2007–2009: a Cox regression model. BMC Pub Health 11:470
Liaw KL, Hildesheim A, Burk RD, Gravitt P, Wacholder S, Manos MM, Scott DR, Sherman ME, Kurman RJ, Glass AG, Anderson SM, Schiffman M (2001) A prospective study of human Papillomavirus (HPV) type 16 DNA detection by polymerase chain reaction and its association with acquisition and persistence of other HPV types. J Inf Dis 183(1):8–15
Lloyd M (1967) Mean crowding. J Anim Ecol 36(1):1–30
Lloyd-Smith JO (2007) Maximum likelihood estimation of the negative binomial dispersion parameter for highly overdispersed data, with applications to infectious diseases. PLoS ONE 2(2):e180
Lu B, Hagensee ME, Lee JH et al (2010) Epidemiologic factors associated with seropositivity to human Papillomavirus type 16 and 18 virus? Like particles and risk of subsequent infection in men. Cancer Epidem Biomar 19(2):511–516
Lu B, Viscidi RP, Lee JH, Wu Y, Villa LL, Lazcano-Ponce E, da Silva C, J R, Baggio ML, Quiterio M, Salmerón J, Smith DC, Abrahamsen, Martha, Papenfuss M, Stockwell HG, Giuliano AR (2011) Human Papillomavirus (HPV) 6, 11, 16, and 18 seroprevalence is associated with sexual practice and age: results from the multinational HPV infection in men study (HIM study). Cancer Epidem Biomar 20(5):990–1002
MacArthur R, Wilson E (1967) The theory of island biogeography. Princeton University Press, Princeton, NJ, USA
Malik ZA, Hailpern SM, Burk RD (2009) Persistent antibodies to HPV virus-like particles following natural infection are protective against subsequent cervicovaginal infection with related and unrelated HPV. Vir Immunol 22(6):445–449
Mao C, Koutsky LA, Ault KA, Wheeler CM, Brown DR, Wiley DJ, Alvarez FB, Bautista OM, Jansen KU, Barr E, Investigators ftPoPS (2006) Efficacy of human Papillomavirus-16 vaccine to prevent cervical intraepithelial neoplasia: a randomized controlled trial. Obstet Gynecol 107(1):18–27
May RM, Anderson RM (1987) Transmission dynamics of HIV infection. Nat Biotechnol 326(6109):137–142
Molano M, den Brule A, Plummer M, Weiderpass E, Posso H, Arslan A, Meijer CJ, Munoz N, Franceschi S (2003) Determinants of clearance of human Papillomavirus infections in Colombian women with normal cytology: a population-based, 5-year follow-up study. Am J Epidemiol 158(5):486–494
Orozco-Colin A, Carrillo-Garcia A, Mendez-Tenorio A et al (2010) Geographical variation in human Papillomavirus prevalence in Mexican women with normal cytology. Int J Inf Dis 14(12):e1082–e1087
Paaso AE, Louvanto K, Syrjänen KJ, Waterboer T, Grénman SE, Pawlita M, Syrjänen SM (2011) Lack of type-specific concordance between human Papillomavirus (HPV) serology and HPV DNA detection in the uterine cervix and oral mucosa. J Gen Virol 92(9):2034–2046
Pielou E (1969) An introduction to mathematical ecology. Wiley Interscience, New York, NY, USA
Plummer M, Vaccarella S, Franceschi S (2011) Multiple human Papillomavirus infections: the exception or the rule?. J Inf Dis 203(7):891–893
Regan D, Philp D, Waters E (2010) Unresolved questions concerning human Papillomavirus infection and transmission: a modelling perspective. Sex Health 7(3):368–375
Richardson H, Kelsall G, Tellier P, Voyer H, Abrahamowicz M, Ferenczy A, Coutlee F, Franco EL (2003) The natural history of type-specific human Papillomavirus infections in female university students. Cancer Epidemiol Biomar 12(6):485–490
Sanders G, Taira A (2003) Cost effectiveness of a potential vaccine for Human Papillomavirus. Emerg Infect Dis 9(1):37–48
Schiffman M, Clifford G, Buonaguro F (2009) Classification of weakly carcinogenic human Papillomavirus types: addressing the limits of epidemiology at the borderline. Infect Agent Cancer 4(1). doi:10.1186/1750-9378-4-8
Shih-Yen C, Delius H, Halpern A, Bernard H (1995) Analysis of genomic sequences of 95 Papillomavirus types: uniting typing, phyolgeny and taxonomy. J Virol 69(5):3074–3083
Skjeldestad FE, Mehta V, Sings HL et al (2008) Seroprevalence and genital DNA prevalence of HPV types 6, 11, 16 and 18 in a cohort of young Norwegian women: study design and cohort characteristics. Acta Obstet Gyn Scan 87(1):81–88
Solomon D, Davey D, Kurman R, Moriarty A, O’Connor D, Prey M, Raab S, Sherman M, Wilbur D, Wright T, Young N et al (2002) The 2001 Bethesda system. J Am Med Assoc 287(16):2114–2119
Southwood TRE (1978) Ecological methods. 2nd edn. Chapman&Hall, London
Swinton J, Garnett GP, Brunham RC, Anderson RM (1992) Gonococcal infection, infertility, and population growth: I. Endemic states in behaviourally homogeneous growing populations. Math Med Biol 9(2):107–126
Sycuro LK, Xi F Long, Hughes JP, Feng Q, Winer RL, Lee SK, O’Reilly S, Kiviat NB, Koutsky LA (2008) Persistence of genital human Papillomavirus infection in a long-term follow-up study of female university students. J Inf Dis 198(7):971–978
Taira A, Neukermans C, Sanders G (2004) Evaluating human Papillomavirus vaccination programs. Emerg Infect Dis 10(11):1915–1923
The FUTURE II Study Group: (2007) Quadrivalent Vaccine against human Papillomavirus to prevent high-grade cervical lesions. N Engl J Med 356(19):1915–1927
The FUTURE I/II Study Group (2010) Four year efficacy of prophylactic human Papillomavirus quadrivalent vaccine against low grade cervical, vulvar, and vaginal intraepithelial neoplasia and anogenital warts: randomised controlled trial. Br Med J 341(jul20_1):c3493–
Trottier H, Mahmud S, Prado JCM, Sobrinho JS, Costa MC, Rohan TE, Villa LL, Franco EL (2008) Type-specific duration of human Papillomavirus infection: implications for human Papillomavirus screening and vaccination. J Infect Dis 197(10):1436–1447
Trottier H, Ferreira S, Thomann P, Costa MC, Sobrinho JS, Prado JCM, Rohan TE, Villa LL, Franco EL (2010) Human Papillomavirus infection and reinfection in adult women: the role of sexual activity and natural immunity. Cancer Res 70(21):8569–8577
Vandepapeliere P, Barrasso R, Meijer CJLM, Walboomers JMM, Wettendorff M, Stanherry LR, Lacey CJN (2005) Randomized controlled trial of an adjuvanted human Papillomavirus (HPV) type 6 L2E7 vaccine: infection of external anogenital warts with multiple HPV types and failure of therapeutic vaccination. J Inf Dis 192(12):2099–2107
Viscidi RP, Schiffman M, Hildesheim A (2004) Seroreactivity to human Papillomavirus (HPV) types 16, 18, or 31 and risk of subsequent HPV infection: results from a population-based study in Costa Rica. Cancer Epidem Biomar 13:324–327
Wang Z (2009) Backward bifurcation in simple SIS model. Acta Math Sin 25(1):127–136
Winer RL, Kiviat NB, Hughes JP, Adam DE, Lee SK, Kuypers JM, Koutsky LA (2005) Development and duration of human Papillomavirus lesions, after initial infection. J Inf Dis 191(5):731–738
Winer RL, Hughes JP, Feng Q, Xi LF, Cherne S, O’Reilly S, Kiviat NB, Koutsky LA (2011) Early natural history of incident, type-specific human Papillomavirus infections in newly sexually active young women. Cancer Epidem Biomar 20(4):699–707
Yamamura K (1989) Effect of aggregation on the reproductive rate of populations. Res Pop Ecol 31(2):161–168
Acknowledgments
Mr Edward K Waters would like to thank Drs David G Regan, David J Philp and Andrew J Hamilton for their helpful advice and support in bringing this work to publication. He would also like to thank Dr Lia Hemerik, associate editor for Acta Biotheoretica for her helpful comments. This paper was funded from the following sources: the Australian Government Department of Health and Ageing; Australian Research Council (ARC) Linkage Project (LP0883831) which included contributions from CSL Ltd and Victorian Cytology Service Inc. The views expressed in this publication do not necessarily represent the position of the Australian Government.
Author information
Authors and Affiliations
Corresponding author
Additional information
E. K. Waters—formerly at Kirby Institute, the University of New South Wales.
An erratum to this article is available at http://dx.doi.org/10.1007/s10441-016-9279-y.
Appendix
Appendix
Here the local stability conditions for Eq. (10) and given in Table 4 are derived. The Jacobian is
The eigenvalues of the Jacobian at (0,0) are α X N − γ X − α X c X − α X and α Y N − γ Y − α Y c Y − α Y . Only if both \(\frac{\alpha_{i}{N}}{\gamma_i} \geq 1+alpha_{i}{c_{i}} -\alpha_i\) the equilibrium is locally stable; otherwise it is unstable.
Using the notation \(\acute{I}_i\) to represent the exclusion equilibrium density, at (0,\(\acute{I}_Y\)) HPV X is extinct and the number of individuals infected with HPV Y is at \(N-\frac{\alpha_Y}{\gamma_Y}\). According to the competitive exclusion principle this implies that \(\acute{I}_X < \acute{I}_Y, \frac{\alpha_X N}{\gamma_X} < \frac{\alpha_Y N}{\gamma_Y}\) and therefore also rα X N − γ X < α Y N − γ Y . The equilibrium may be stable if \(\frac{\alpha_X N}{\gamma_X} < 1+\alpha_X c_X +\alpha_X,\) that is, it converges to the single disease model. The exclusion equilibrium where HPV Y is extinct and the number of individuals infected with HPV X is at endemic equilibrium will be stable under similar conditions.
When both HPV X and HPV Y are present at equilibrium (competitive coexistence) their equilibrium densities must be below their exclusion equilibrium levels, which reflects the extent to which their level of aggregation limits their reach into the susceptible population. The determinant of the Jacobian at this point is \(\alpha_{X}\alpha_{Y}\acute{I}_{X} \acute{I}_{Y}\left(m_{X}m_{Y}-1\right)\). The determinant is >0 when m X m Y > 1, so if m X and m Y > 1 the equilibrium is stable. This suppoerts Kuno’s (1988) conclusion that aggregation, as expressed by values the slope of Iwao’s linear relation >1, can facilitate coexistence.
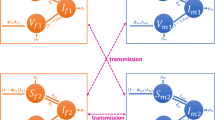
The partial derivatives and the eigenvalues of the Jacobian also become extremely complicated. It is also instructive to substitute \(\acute{I}_i=\frac{N-\frac{\gamma_i}{\alpha_i}-c_i -1}{m_i}\) for all \(\acute{I}_i\). These substitutions make it clear that for competitive coexistence to occur, whichever group of HPV is less prevalent must be able to infect individuals who are less uniformly dispersed throughout the susceptible population. For example, if \(\acute{I}_X > \acute{I}_Y,m_Y > \frac{\acute{I}_X}{\acute{I}_Y}\). A few other conditions are obvious; α i N ≤ γ i + α i c i + α i for all i, or else one of the equilibria involving extinction would have been achieved. Under these conditions, provided that all c i > − 1 and all m ≥1, the coexistence equilibrium may be stable. When an equilibrium is stable the point of intersection of the nullclines of the competitive equations lies above the K′ connector - a line connecting the two competitive exclusion equilibria (\(I_i=\frac{N-\frac{\gamma_i}{\alpha_i}- c_i-1}{m_i},I_j=0\)) (see Table 4, lines 2–3). The K′ connector is so called because K′ is traditional notation for carrying capacity. A consequence of this is that the sum of I X and I Y at stable competitive coexistence is greater than the number of infecteds of a single type present at a competitive exclusion equilibria. These results are shown graphically in Fig. 2.
Rights and permissions
About this article
Cite this article
Waters, E.K. Aggregation and Competitive Exclusion: Explaining the Coexistence of Human Papillomavirus Types and the Effectiveness of Limited Vaccine Conferred Cross-Immunity. Acta Biotheor 60, 333–356 (2012). https://doi.org/10.1007/s10441-012-9161-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10441-012-9161-5