Introduction

Context of Stroke Volume Estimation

Stroke volume (SV) and instantaneous stroke volume variations (SVV) are of a crucial interest, particularly for hemodynamic monitoring of critical care patients. As this cardiovascular parameter stands at a cardiac level, a reliable estimation still remains difficult, based on compromises between proximal cardiac/peripheral arterial, continuous/discontinuous, more or less easy, and more or less invasive methods. Unlike the continuous beat-to-beat SVV, the real SV basal level estimation requires calibration by proximal measures such as cardiovascular bolus dilution or esophageal echo-doppler. Among the various methods for the estimation of SVV, methods based on the analysis of arterial blood pressure (ABP) waveform are easily applicable, minimally invasive, accurate, and affordable.

Semi-Classical Signal Analysis and Arterial Pulse Contour Methods

ABP analysis methods, called pulse contour methods, aim at finding a relation between one or several parameters characterizing the shape of the pressure and SV or cardiac output (CO).6,14,20,21 These methods have been widely compared.3,25,26,30 The simplest model supposes a proportionality between CO and the mean arterial pressure. Other approaches, based on Windkessel models, link SV to different lumped parameters such as the pulse pressure, systolic, and diastolic pressures.6 These approaches, considering the arterial system as a lumped system, appear not sufficiently accurate. Approaches that consider the nonlinear aspects of the arterial system have also been proposed, as Modelflow,29 but the latter is not very efficient in a number of cases.22 Other methods, resulting from distributed arterial models, have been developed. They use the pressure area so that SV is supposed to be proportional to the area under the systolic part of the pressure curve (see Fig. 5).28 Corrected versions of this relation have also been proposed.14 However, this approach requires the detection of the end systole, which is nontrivial, particularly in peripheral ABP waveforms.

In this study, we propose a new method for SVV estimation using ABP measurements based on a semi-classical signal analysis (SCSA). This method is connected to the latest class of pulse contour approaches presented above. Indeed, when the SCSA is applied to ABP signals, it provides a parameter called the first systolic invariant (INVS1) which is mathematically related in a linear way to SV. It appears that INVS1 is nothing else than the area under the systolic part of the pressure curve. However, the main difference between the two approaches concerns the detection of the end of the systole which seems simpler and more reliable with the SCSA and especially for peripheral pressures.

This study aims at validating the hypothesis of linearity between SVV measured with a well-known pulse contour method and INVS1, over 20 mechanically ventilated patients in intensive care units during a 15-min of ABP recording. We have used the PiCCO technology,4 considered as reliable and widely used in intensive care units.4 The calibration of SV is done by transpulmonary thermodilution, with a cold isotonic sodium chloride bolus. This calibration technique is considered as a “gold standard” in many studies and was validated through its comparison to reference methods. For instance, in Elkayam et al.,10 the thermodilution technique was compared to the dye dilution technique for critically ill patients. The difference between values obtained with the two methods was not statistically significant when CO was reported as the average value of either the first three, all five or three middlemost determinations (the error was about 3.9% for five determinations).

SCSA Background

The SCSA method has been recently proposed in Laleg.15 The ABP signal is reconstructed enabling the computation of some spectral parameters, the eigenvalues, and the invariants. These parameters are different from the usual spectral parameters computed with a standard Fourier transform. Indeed, instead of analyzing the spectrum of the signal computed with the Fourier transform, the signal is interpreted as a multiplication operator so that the spectrum of a regularized version of this operator is considered. The SCSA eigenvalues and invariants have already given promising results in some physiological applications. On the one hand, in Laleg et al.,19 we showed the ability of the SCSA parameters to discriminate between two different situations unlike classical cardiovascular parameters: first heart failure subjects vs. control subjects and secondly highly fit triathlets subjects before and after training. On the other hand, in Laleg15 we showed the ability of the invariants to represent physiological parameters, particularly the SV variations, in two well-known conditions: the head-up 60 degrees tilt-test and the handgrip-test.

Materials and Methods

This prospective study was conducted in the 16-bed medical-surgical intensive care unit (ICU) of the Sud-Francilien General Hospital (Evry, France). The study protocol was approved by the ethics committee of the Francophone Society for Critical Care (No.  08−280), who waived the need for written informed consent, because of the noninterventional nature of the study.

Patients

  • Inclusion criterion: all mechanically ventilated patients whose CO was continuously monitored with a transpulmonary thermodilution catheter (PiCCO, Pulsion Medical Systems, Munich, Germany) were included, except those satisfying the following excluding criteria. PiCCO is routinely used in this unit to monitor hemodynamically compromised patients.

  • Exclusion criteria: patients presenting cardiac arrhythmias or breathing spontaneously were excluded. SVV estimation is not relevant for such patients because the induced changes in intra-thoracic and intra-abdominal pressures modify the preload response to volume expansion.12

  • Protocol: all patients were sedated with midazolam and fentanyl in dosages that were titrated to achieve full adaptation to the ventilator. Ventilator settings were as follows: volume assist-control mode; tidal volume (Vt), 6 mL/kg ideal body weight; breathing rate, 20 cycles/min; inspiratory/expiratory ratio, ½; and FiO2 adjusted to maintain transcutaneous oxygen saturation in blood 94%. Positive end-expiratory pressure (PEEP) was set at 5 cm H2O but some hypoxemic patients required an increase in PEEP to 10 cm H2O during the data acquisition, to improve arterial oxygenation. The increase in PEEP was left to the discretion of the attending physician, as well as the adaptation of vasoactive drug dosages, adjusted to maintain an adequate circulatory status during the protocol.

Data Acquisition

Arterial pressure, measured from a femoral catheter, and respiratory flow signals were recorded during a 15-min period using a Biopac 100 system (Biopac systems, Goleta, CA, USA). Data were sampled at 1000 Hz and stored on a hard disk. CO was calibrated just before the data acquisition as follows: successive calibrations with cold isotonic sodium chloride boluses of 20 mL were performed to ensure at least five comparable values of CO. Inconsistent values were discarded and the mean value of the five remaining calibrations was selected as calibration value. As our PiCCO version did not include a module for SV computation, SV was computed by dividing CO by heart rate (HR). CO estimations were delivered every 30 s during the 15-min period.

Signal Analysis

Signal processing was performed using the Scilab and Matlab environments at the French National institute for Research in Computer Science and Control (INRIA-Sisyphe team).

An SCSA method

In this section, we introduce the SCSA technique and some results of its application to ABP analysis. We also show the relation between INVS1 and SV.

The SCSA principle: Let \(y: t\,\longmapsto \,y(t) \) be a real valued function representing the signal to be analyzed such that

$$ y \in L_{1}^{1}({\mathbb{R}}), y(t)\geq 0, \quad \forall t\in {\mathbb{R}},\qquad \frac{\partial^{m} y}{\partial x^{m}}\in L^1({\mathbb{R}}), \quad m=1,2, $$
(1)

with,

$$ L_1^1({\mathbb{R}})= \left\{V | \int\limits_{-\infty}^{+\infty}{|V(t)|(1+|t|) dt}<\infty\right\}.$$
(2)

The main idea in the SCSA consists in interpreting the signal y as a multiplication operator, ϕ → y · ϕ, on some function space. Then, instead of the standard Fourier transform, we use the spectrum of a regularized version of this operator, known as the Schrödinger operator in \(L^2({\mathbb{R}}),\) for the analysis of y

$$ H(h; y) = -h^2\frac{d^2}{dt^2} - y, $$
(3)

for a small h > 0.

By using this approach, the signal is a potential of the Schrödinger operator H(h; y). We are interested in the spectral problem of this operator which is given by

$$ -h^2\frac{d^2 \psi}{dt^2} - y \psi = \lambda \psi,\quad t\in{\mathbb{R}}, $$
(4)

where \(\lambda, \lambda \in {\mathbb{R}},\) and \(\psi, \psi\in H^2({\mathbb{R}})\) (\(H^2({\mathbb{R}})\) denote the Sobolev space of order 2) are respectively the eigenvalues of H(h; y) and the associated eigenfunctions. Under Eq. (1), the spectrum of H(h; y) consists of

  • a continuous spectrum λ ≥ 0,

  • a discrete spectrum composed of negative eigenvalues. There is a nonzero, finite number N h of negative eigenvalues of the operator H(h; y). We put λ = −κ 2 nh with κ nh  > 0 and κ1h > κ2h > ··· > κ nh , n = 1,…, N h . Let ψ nh , n = 1,…, N h be the associated L 2-normalized eigenfunctions.15

The main idea in the SCSA technique is to reconstruct the signal y with the discrete spectrum of H(h;y) using the following formula

$$ y_h(t)= 4 h \sum_{n=1}^{N_h}{\kappa_{nh }\psi_{nh}^2(t)}, \quad t\in {\mathbb{R}}. $$
(5)

The SCSA method seems to be better suited for the analysis of some pulse-shaped signals than the Fourier transform.15 This is because the elementary functions κ nh ψ 2 nh are localized in time unlike the Fourier transform basis functions which are given by sines and cosines.

The parameter h in the SCSA plays an important role. As h decreases, the approximation of the signal improves. However, as h decreases, the number of negative eigenvalues N h increases and hence the time required to perform the computation increases. So, in practice, what we are looking for is a value of h that provides a sufficiently small estimation error with a reduced number of negative eigenvalues. We summarize the main steps for reconstructing a signal with the SCSA as follows:

  1. 1.

    Interpret the signal to be analyzed y as a potential of the Schrödinger operator H(h;y) (Eq. 3);

  2. 2.

    compute the negative eigenvalues and the associate L 2-normalized eigenfunctions of H(h;y)15;

  3. 3.

    compute y h according to Eq. (5);

  4. 4.

    look for a value of h to obtain a good approximation with a small number of negative eigenvalues.

ABP analysis with the SCSA: Now, we will introduce some results on the application of the SCSA to ABP analysis. We denote by P the ABP signal and \(\hat{P}\) its estimation with the SCSA such that

$$ \hat{P}(t)=4h\sum_{n=1}^{N_h}{\kappa_{nh}\psi_{nh}^2(t)}, $$
(6)

where \(-\kappa_{nh}^2, n=1,\ldots,N_h\) are the N h negative eigenvalues of the Schrödinger operator H(h;P) and ψ nh the associated L2-normalized eigenfunctions.

The ABP signal was estimated for several values of the parameter h and hence N h . Figures 1 and 2 illustrate measured and estimated pressures for one beat of an ABP signal for N h  = 3, 5, 7, and 9. Signals measured at the aorta (invasively) and at the finger (non invasively), respectively, were considered. We point out that 5 to 9 negative eigenvalues are in general sufficient for a good estimation of an ABP beat16,18 against 10 to 15 harmonics with a Fourier analysis method.23

FIGURE 1
figure 1

Reconstruction of the pressure at the aorta level with different numbers of negative eigenvalues N h : (a) N h  = 3, (b) N h  = 5, (c) N h  = 7, (d) N h  = 9

Full size image
FIGURE 2
figure 2

Reconstruction of the pressure at the finger with different numbers of negative eigenvalues N h : (a) N h  = 3, (b) N h  = 5, (c) N h  = 7, (d) N h  = 9

Full size image

One application of the SCSA to ABP signals consists in decomposing the signal into its systolic and diastolic parts. This application was inspired by a reduced model of ABP based on solitons (solitons are solutions of some nonlinear partial derivative equations like the Korteweg-de Vries (KdV) equation) proposed in Crépeau and co-workers.8,17 This model suggests the decomposition of the ABP into a sum of two terms. The first term is given by an N-soliton (N = 1, 2, 3 in general), solution of a KdV equation which describes fast phenomena that are dominant during the systole. The second term is given by a two-elements Windkessel model describing slow phenomena predominating during the diastole. Considering the relation between solitons and the discrete spectrum of a Schrödinger operator with a potential given by the solution of a KdV equation, each negative eigenvalue is associated to one soliton.11 Moreover we know that these eigenvalues characterize solitons velocities.11 So the largest eigenvalues describe fast solitons. From these remarks, we proposed in Laleg et al. 15,16 the decomposition of (6) into two partial sums: the first one, composed of the N s (N s  = 1, 2, 3 in general) largest κ nh and the second composed of the remaining components. Then, the first partial sum represents rapid phenomena of the systolic phase and the second one describes slow phenomena of the diastolic phase. We denote by \(\hat{P}_{\text{s}}\) and \(\hat{P}_{\text{d}}\) the systolic pressure and the diastolic pressure, respectively, estimated with the SCSA. Then we have

$$ \hat{P}_{\text{s}}(t) = 4 h\sum_{n=1}^{N_{s}}{\kappa_{nh}\psi_{nh}^2(t)}, $$
(7)
$$ \hat{P}_{\text{d}}(t) =4 h \sum_{n=N_{s}+1}^{N_h}{\kappa_{nh}\psi_{nh}^2(t)}. $$
(8)

Figures 3 and 4 show measured pressure and estimated systolic and diastolic pressures, respectively. We notice that \(\hat{P}_{\text{s}}\) and \(\hat{P}_{\text{d}}\) are, respectively, localized during the systole and the diastole.

It is worth noting that our decomposition of the ABP into an N-soliton and a Windkessel model, and so its decomposition into the systolic and diastolic pressures \((\hat{P}_{\text{s}} + \hat{P}_{\text{d}})\) can be related to a decomposition proposed by Wang et al. 27 The latter showed that the aortic pressure can be separated into a reservoir pressure generated by a Windkessel effect and a wave pressure generated by the arterial waves. In our case the wave pressure is given by the N-soliton or the systolic pressure \(\hat{P}_{\text{s}}.\) The study of Wang et al. has been extended to the pressure at arbitrary locations in arteries by Aguado-Sierra et al. 1,2 It has been shown that this separation of the ABP into a reservoir pressure and a wave pressure is also valid at different locations for example at the brachial artery, the abdominal artery, and the femoral artery. Moreover, it has been shown that the highest contribution of the wave pressure to the total waveform occurs during systole while the reservoir pressure is dominant during the diastole. The approach of Aguado-Sierra et al. is based on the extension of the observation made by Wang et al. 27: the wave pressure in the ascending aorta is linearly related to the measured flow (see Fig.2 of Wang et al.27). So, in Aguado-Sierra et al.,1 they started from the assumption that the wave pressure at an arterial location is approximately proportional to the CO and showed the consistency of this assumption. We will need this relation in our analysis, therefore we will write it using our notations. If we denote Q the CO, then we have

$$ Q=\alpha \hat{P}_{\text{s}} + \gamma $$
(9)

where α and γ depend upon a number of factors such as the local wave speed and the cross-sectional area of the artery.1

FIGURE 3
figure 3

Estimated systolic pressure

Full size image
FIGURE 4
figure 4

Estimated diastolic pressure

Full size image

SCSA parameters: As seen previously, the SCSA technique provides a new description of the ABP signal with some spectral parameters which are the negative eigenvalues and the so-called invariants (these parameters are called invariants because they are related to the KdV invariants in time). The latter consist in some momentums of the κ nh , n = 1,…, N h . So, we define the first two global invariants by

$$ {\text{INV}}_1=4h \sum_{n=1}^{N_h}{\kappa_{nh}}, \quad {\text{INV}}_2=\frac{16}{3}h\sum_{n=1}^{N_h}{\kappa_{nh}^3}.$$
(10)

Systolic (INVS1,2) and diastolic (INVD1,2) invariants are deduced from the decomposition of the pressure into its systolic and diastolic parts and are then given by

$$ {\text{INVS}}_1=4h \sum_{n=1}^{N_s}{\kappa_{nh}}, $$
(11)
$$ {\text{INVS}}_2=\frac{16}{3}h\sum_{n=1}^{N_s}{\kappa_{nh}^3}, $$
(12)
$$ {\text{INVD}}_1=4h \sum_{n=N_s+1}^{N_h}{\kappa_{nh}}, $$
(13)
$$ {\text{INVD}}_2=\frac{16}{3}h\sum_{n=N_s+1}^{N_h}{\kappa_{nh}^3}. $$
(14)

INVS1for SV estimation: We will see here how INVS1 is related to SV. For this purpose, we will recall the relation between SV and the cardiac outflow Q,

$$ {\text{SV}} = \int\limits_{T_{1}}^{T_{2}}{Q dt}, $$
(15)

where T1 and T2 are, respectively, the times of the beginning and the end of the systole for one beat. Then, considering the relation (9) to a first approximation (we recall that in this study we consider ABP measured at the femoral artery), we have

$$ {\text{SV}}= \alpha \int\limits_{T_1}^{T_2}{\hat{P}_{\text{s}} dt} + \beta,$$
(16)

where β depends on T2, T1, and γ. Referring to (7) and (11), and remembering that ψ nh are L2-normalized, we have

$$ {\text{INVS}}_1= \int\limits_{-\infty}^{+\infty} {\hat{P}_{\text{s}}(t)dt} \simeq \int\limits_{T_1}^{T_2} {\hat{P}_{\text{s}}(t)dt}. $$
(17)

We recall that \(\hat{P}_{\text{s}}\) is an estimation of the systolic pressure. Then,

$$ {\text{SV}} \simeq \alpha {\text{INVS}}_1 + \beta,$$
(18)

which shows the linear relation between SV and INVS1.

One can notice the existence of a relation between INVS1 and the pulse contour method that supposes proportionality between SV and the area under the systolic part of the pressure curve as described in the “Introduction” section. We have,

$$ {\text{SV}}_{\text{PC}} = k P_{\text{sa}}, $$
(19)

where P sa denotes this area (see Fig. 5), k is a positive constant, and SVPC is the SV estimated with the pulse contour method. Indeed, (17) shows that INVS1 refers to the area under the systolic curve \(\hat{P}_{\text{s}}.\) Thus, one can remark that both P sa and INVS1 describe the area under the systolic pressure but they may not be equal because the detection of the end systole in the two cases is not the same (see Figs. 3 and 5). Indeed, while P sa is computed by detecting the dichrotic notch which is not trivial in peripheral ABP waves, INVS1 results from a nonlinear model of ABP based on solitons that consider the propagation of the pulse wave8,17 as was described in the section “ABP Analysis with the SCSA”. The relation (18) can be rewritten as follows

$$ {\text{INVS}}_1= a {\text{SV}}_{\text{PC}} + b,$$
(20)

where a and b depend upon α and β and we recall that these parameters depend on a number of factors related to the considered artery and its characteristics.

FIGURE 5
figure 5

Area under the systolic part of the pressure curve used to estimate SV

Full size image

Resulting Time Series Used to Compare INVS1 to PiCCO SV

The HR was computed from the pulse interval, which is the distance between two systolic occurrences of ABP. HR and INVS1 were resampled at 4 Hz, by interpolation of a third-order spline function to obtain equidistant data and to guarantee their synchronization. They were then averaged over 12 s and delivered every 30 s, like the PiCCO protocol. COPiCCO was divided by HR to give the SV (SVPiCCO).

Statistical Analysis

Linear Regression

Remembering that the PiCCO technique is based on the pulse contour method and according to the previous section, SVPiCCO and INVS1 are linearly related (Eq. 20). A linear regression analysis was applied, using SigmaStat. This analysis provides the Pearson R coefficient, which measures the degree of linear correlation between the two estimates, and the parameters of the linear Eq. (20), a and b.

Cross-Correlation Analysis

Moreover, the cross-correlation analyzes the temporal similarity between two time series by estimating the correlation between one time series at time t and the other at time t ± x lags (in samples).24 It was used to comfort linear regression results and also to verify wether delays were generated by filters between the two signal processing algorithms or not. PiCCO algorithms being not available, it is only known that time series are averaged every 12 s and that estimations are delivered every 30 s, without more precision about windowing. The cross correlation was performed between averaged SVPiCCO and INVS1 estimations. Coefficients were computed using the Matlab xcorr function (The MathWorks Inc.) after subtracting the means from the time series. Cross-correlation coefficients were computed for all lags (−30; +30), each lag corresponding to a 30-s interval. The correlation coefficients of the unlagged data stand at the midpoint (lag 0). A 5% level of probability for the correlation coefficients was considered significant (Bravais-Pearson table). An average estimate of the correlation over all the subjects was allowed after homogeneity tests (nonsignificant z-test and Jarque–Bera test).13 The individual correlation coefficients were averaged for each lag.

Results

Patients

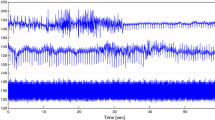
The 20 patients recordings were analyzed over 900 s, representing about 30 averaged values, except 2 recordings, analyzable for only 16 and 21 averaged values. The SVPiCCO and INVS1 time series of the 20 subjects are shown in Fig. 6. Some of them were submitted to variations of vaso active drug dosage (such as the seventh patient of column four) or ventilatory condition (such as the first patient of column two), or without any change in ventilatory parameter nor in drugs (such as the first patient of column one).

FIGURE 6
figure 6

SVPiCCO and INVS1 from SCSA time series for the 20 subjects. Each mark stands for a 30-s averaged value. Except for two subjects, only analyzable for 480 and 630 s, about 30 mean values are available for the others. For each subject, SCSA time series (top panel) represent the linear regression of INVS1 (Eq. 20) and PiCCO time series (bottom panel) represent SVPiCCO, expressed in liter. Their dynamics are very similar, even if filtering processes could not be exactly the same; some local differences over few values could be due to differences in artifact treatment

Full size image

Linear Relation Between SVPiCCO and INVS1

The mean R coefficient of linear regression and the mean coefficient of cross correlation at lag 0 are both equal to 0.90 ± 0.01 SEM, meaning a great degree of linearity between the PiCCO and the SCSA methods, for all the subjects. The R coefficient is between 0.78 and 0.98 (Fig. 7) and the cross-correlation coefficient is between 0.77 and 0.99. Figure 8 represents the cross-correlation coefficients for the 20 subjects (dashed lines). As homogeneity was verified, averaged values were also plotted (−•−). The vertical axis depicts the correlation coefficients. The horizontal axis depicts the lag, in number of 30-s averaged values of one time series on another. The correlation coefficients of the unlagged data are plotted at horizontal midpoint (lag 0). The two symmetrical continuous lines represent critical r values for a level 5 of probability (Bravais-Pearson table). The greatest correlation stands at lag 0 for all the remaining subjects (mean correlation = 0.90; SEM = 0.01; p = 0.00001). This result shows an excellent temporal similarity between the successive measures, indicating that they change in the same way over time, as shown in Fig. 6, even if filtering processes could not be exactly the same. Some local differences over few values could be due to differences in artifact treatment.

FIGURE 7
figure 7

Linear regression plots for the 20 subjects. They all show a strong linear relation with R between 0.78 and 0.98 and a mean coefficient equal to 0.9 ± 0.01 SEM. Slopes are different because the a and b parameters of linear regression depend upon various factors such as local wave speed and cross-sectional area of the artery

Full size image
FIGURE 8
figure 8

Cross correlation between the 30-s averaged SVPiCCO and INVS1 values in 20 subjects. Each line (dashed) stands for a subject; the strong line (−•−) represents the average of the 20 subjects; continuous lines represent critical r values for a 5% level of probability (Bravais-Pearson table). The vertical axis depicts the correlation coefficients. The horizontal axis depicts the lag, in number of 30-s measures, of one time series on another. The correlation coefficients of the unlagged data are shown at horizontal midpoint (lag 0). All time series are exactly synchronized, with a mean correlation coefficient equal to 0.9 at lag 0 (p = 0.00001)

Full size image

Discussion

Similarity Between SCSA and Arterial Pulse Contour Methods

SV is a fundamental parameter for hemodynamic monitoring. Historically, its measurement was done using invasive methods and therefore was limited to critically ill patients. Because the ABP can be measured continuously with minimal invasiveness, many studies have been devoted to the estimation of SV from ABP waveform leading to pulse contour methods. These methods which are based on some systemic models relate SV to ABP waveform characteristics. Therefore, a dozen estimators have already been proposed like the mean pressure, the pulse pressure, and the area under the systolic part of the pressure curve. Although they may not be very efficient for the estimation of SV, they are performant for detecting significant changes in SV. A comparison between the efficiency of these estimators can be found for example in Sun et al. 26 and Yu et al. 30

We have used an ABP waveform analysis as a basis of a new method for assessing SV variations. The SCSA method considers the signal as a multiplication operator and uses the discrete spectrum of a regularized version of this operator which is given by a Schrödinger operator to analyze the pressure waveform. Because the elementary functions of our decomposition formula are given by the squared eigenfunctions associated to the negative eigenvalues of the Schrödinger operator (see Eq. 5) and because these functions are localized, the SCSA is well suited to the analysis of pulse-shaped signals such as the ABP signals. In particular, we know that the first eigenfunction is localized in the minimum of the potential (we recall that the potential here is given by the inverse of the ABP signal). Then using these properties and the relation of the SCSA to a soliton-based model of ABP, the SCSA is well adapted to the decomposition of the ABP into its systolic and diastolic components. This decomposition can be related to the results of Wang et al. 27 and Aguado-Sierra et al. 1,2 The latter showed that the pressure can be separated into a reservoir pressure generated by a Windkessel effect and a wave pressure generated by the arterial waves. The reservoir pressure describes the diastolic part and the wave pressure describes the systolic pressure. Then combining this decomposition to basic relations among SV, CO, and the systolic pressure, we showed that INVS1, a parameter computed when the SCSA is applied to the ABP, is linearly related to SV.

Moreover, we have seen that INVS1 is nothing else than the area under the estimated systolic pressure curve. The results have been validated using PiCCO SV measurements. The PiCCO is based on a pulse contour method with a venous catheter calibration. We have especially compared the pulse contour used by the PiCCO with the SCSA which is used for computing the instantaneous beat-to-beat variations of a proportional SV. The results show a very strong linear relation between the parameters of the two approches. The tiny differences observed could be due to differences in the pre or post-processing of the two time series. Indeed, PiCCO algorithms are not available, it is only known that time series are averaged every 12 s and that estimations are delivered every 30 s without more precisions about windowing. So, filtering processes could not be exactly the same. Moreover, some local differences over few values could be due to differences in artifact treatment. Thus, we can conclude that INVS1 is similar to the pulse contour estimator.

Difference Between SCSA and Arterial Pulse Contour Methods

However, the detection of the end systole with the SCSA differs from the pulse contour approach. On the one hand, the pulse contour approach uses an algorithm to detect the dicrotic notch which is not always trivial because this notch does not always clearly appear in a pressure signal. In addition, the detection of the dicrotic notch in peripheral pressures is not evident because the pressure waveform changes during its propagation along the arterial tree. On the other hand, the SCSA uses an ABP model based on solitons that take into account the propagation phenomena as described in the section “ABP Analysis with the SCSA.” Indeed, the decomposition of the pressure into its systolic and diastolic parts is simply obtained by decomposing the sum in Eq. (5) into two partial sums, one of them describing the systolic part and the other the diastolic part. Hence, we feel that the detection of the end systole with the SCSA could be more efficient and particularly when the dicrotic notch does not appear clearly and for peripheral pressure waves. This hypothesis will be assessed in a future work.

Limitations

The limitations of this study are mostly related to physio–pathological conditions. For instance, the analyzed population is relatively small, but similar sample sizes have previously been used in other studies in order to assess newly developed hemodynamic monitoring devices (see for example De Castro et al. 9 and Linton and Linton20). The reason is principally ethical, because PiCCO devices are inserted only in patients with severe circulatory failure, a condition rather unusual; so collecting a large data bank requires a long time. However, this study will be extended to a larger population for improving the evaluation.

A general first limitation of the SCSA as well as most of the pulse contour methods is that they estimate continuous beat-to-beat SVV but not real SV basal level, which requires an invasive calibration by thermodilution technique4 or lithium dilution for LiDCO method.7 In fact, the estimation of SVV may be sufficient for clinical purposes even if the exact value of SV is not directly measured. Respiratory SV variations are particularly useful in critical care or anesthesia to predict the fluid responsiveness of unstable patients, and therefore to improve their hemodynamic status, avoiding inappropriate fluid administration, which can be harmful.5 SV variations could also give precious information in a lot of physiological and pathological conditions such as functional explorations (autonomic tests (orthostatic tilt test, isometric handgrip test), training of athletes, assessment of the rehabilitation, and/or treatment in several diseases (chronic heart failure, obstructive sleep apnea, obesity), monitoring purposes in hemodynamically stable patients, for example during anesthesia.

A second general limitation is related to the quality of pressure measurements, mostly depending upon physio–pathological conditions and the site of the sensors. Indeed, the measurements can be invasive when ABP is recorded from arterial catheter (radial or femoral) already in place in intensive care patients, or totally noninvasive when ABP is recorded from a distal sensor from the finger, as the FINOMETER device. For instance, in this study, finger blood pressure was not rather analyzable in all subjects. For most critically ill patients with acute circulatory failure and/or receiving vasoconstrictive drugs, the distal waveform was of very poor quality. However, in other settings, as previously described, finger measurements are of a good quality. This latter point should be a new perspective for a simple noninvasive SVV estimation. In addition, thanks to the SCSA approach for detecting the end systole, this method seems less dependant on the ABP measurements site than the other pulse contour methods.

Conclusion

A new method for SV variation assessment has been presented in this study: the ABP signal is reconstructed with an SCSA which enables the decomposition of the signal into its systolic and diastolic parts. Some spectral parameters, that give relevant physiological information, are then computed, especially the INVS1, given by the area under the estimated systolic pressure curve. The hypothesis of linearity between SV measured with a PiCCO and INVS1 has been validated, through very strong coefficients of correlation, over 20 mechanically ventilated patients during 15 min of ABP recording.

This study is a first step in the validation of the SCSA for the estimation of changes in SV. The study must be orientated at a second step to the comparison between the performance of the SCSA and the performance of other pulse contour methods at different physiological and pathological conditions and also to the estimation of SV variations from noninvasive measurements for example at the finger level.