A probabilistic model for rainfall—induced shallow landslide prediction at the regional scale

Abstract

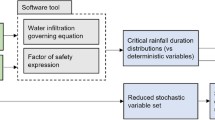
This paper presents a new probabilistic physically-based computational model (called PG_TRIGRS) for the probabilistic analysis of rainfall-induced landslide hazard at a regional scale. The model is based on the deterministic approach implemented in the original TRIGRS code, developed by Baum et al. (USGS Open File Report 02–424, 2002) and Baum et al. (USGS Open File Report 08–1159, 2008). Its key innovative features are: (a) the application of Ordinary Kriging for the estimation of the spatial distributions of the first two statistical moments of the probability density functions of the relevant soil properties over the entire area, based on limited available information gathered from available information from limited site investigation campaigns, and (b) the use of Rosenblueth’s Point Estimate method as a more efficient alternative to the classical Monte Carlo method for the reliability analysis performed at the single-cell level to obtain the probability of failure associated to a given rainfall event. The application of the PG_TRIGRS code to a selected study area located in the Umbria Region for different idealized but realistic rainfall scenarios has demonstrated the computational efficiency and the accuracy of the proposed methodology, assessed by comparing predicted landslide densities with available field observations reported by the IFFI project. In particular, while the model might fail to identify all individual landslide events, its predictions are remarkably good in identifying the areas of higher landslide density.

Appendices

Closed-form solution of the saturated infiltration problem

The closed-form solution of the saturated infiltration problem governed by Eq. (5), provided by Baum et al. (2002), is based on Iverson’s (2000) solution, extended to account for variable infiltration rate and impermeable basal boundary placed at finite depth d _b .

In order to account for variable infiltration rate, a suitable discretization of the time interval of interest t ∈ [0, t _fin] into N time steps Δt _n + 1 = t _n + 1 − t _n (with n = 0 ,  …  , N − 1, t ₀ = 0, and t _N  = t _fin) is introduced so that the infiltration rate can be considered as constant during each time step:

$$ I( t)={I}_{n+1}=\mathrm{const}.\kern2.5em \mathrm{for}\kern0.5em t\in \left[{t}_n,{t}_{n+1}\right]\kern2.5em \left( n=1,\dots, N-1\right) $$

Under such conditions, the pore pressure head is given by

$$ \begin{array}{l}\psi \left( Z, t\right)=\left( Z-{d}_w\right)\beta +2\sum_{n=0}^{N-1}\Big({I}_n/{k}_s\Big)\kern0.1em \mathcal{H}\left( t-{t}_n\right)\left\{{S}_1\right( Z, t-{t}_n\left)+{S}_2\right( Z, t-{t}_n\left)\right\}\kern1em \\ {}-2\kern0.2em \sum_{n=0}^{N-1}\left({I}_n/{k}_s\right)\kern0.1em \mathcal{H}\left( t-{t}_{n+1}\right)\left\{{S}_1\right( Z, t-{t}_{n+1}\left)+{S}_2\right( Z, t-{t}_{n+1}\left)\right\}\kern1em \end{array} $$

(26)

In Eq. (26), $\beta ={ \cos}^2\kern0.2em \alpha -\left({I}_{LT}/{k}_s\right)$ is a coefficient function of the slope angle and the steady-state surface flux I _LT ; d _w is the steady-state depth of the phreatic surface, measured along the vertical direction; the functions S ₁(Z, τ) and S ₂(Z, τ) are given by:

$$ {S}_1\left( Z,\tau \right):=\sqrt{D_{\alpha}\tau}\ \sum_{m=1}^{\infty}\mathrm{ierfc}\ \left\{\frac{\left(2 m-1\right){d}_b-\left({d}_b- Z\right)}{2\sqrt{D_{\alpha}\tau}}\right\} $$

(27)

$$ {S}_2\left( Z,\tau \right):=\sqrt{D_{\alpha}\tau}\ \sum_{m=1}^{\infty}\mathrm{ierfc}\ \left\{\frac{\left(2 m-1\right){d}_b+\left({d}_b- Z\right)}{2\sqrt{D_{\alpha}\tau}}\right\} $$

(28)

in which the function ierfc (x) is given by

$$ \mathrm{ierfc}\ (x):=\frac{1}{\sqrt{\pi}} \exp \left(-{x}^2\right)- x\ \mathrm{erfc}\ (x) $$

(29)

and erfc (x) is the complementary error function; finally, $\mathcal{H}(x)$ is the Heaviside step function. Eq. (26) specializes easily to the case of constant infiltration rate and basal boundary at infinite depth.

Following Iverson (2000), the pressure head provided by Eq. (26) is subject to the physical limitation that, under downward gravity-driven flow, it cannot exceed the pressure head which would result from the phreatic surface being at the ground surface:

$$ \psi \le \beta Z $$

(30)

Setting I _LT  = 0 results in a steady-state pore pressure distribution corresponding to uniform water flow parallel to the ground surface.

Closed-form solution of the unsaturated infiltration problem

The closed form solution of the unsaturated infiltration problem governed by Eqs. (3) and (4) is provided by (Baum et al. 2002). The soil cover is treated as a two-layer system: the saturated zone and the capillary fringe constitute the lower layer; the unsaturated zone extending to the ground surface the upper layer.

To account for variable infiltration rate, we considered the same discretization of the time interval of interest t ∈ [0, t _fin] into N time steps Δt _n + 1 = t _n + 1 − t _n as done in the previous section devoted to saturated conditions. 1 is adopted.

Pressure head in the unsaturated zone

The pressure head in the unsaturated zone is obtained from the integration of Eq. (3) in the unsaturated zone, which yields

$$ \psi \left( Z, t\right)={\psi}_0+\frac{ \cos \alpha}{a_{\alpha}} \ln \left\{\frac{\kappa \left( Z, t\right)}{k_s}\right\}\kern2em \mathrm{with}:\kern2em {\psi}_0=\frac{1}{a_{\alpha}} $$

(31)

and

$$ \kappa \left( Z, t\right)=\sum_{n=0}^{N-1}\mathcal{H}\left( t-{t}_n\right)\left\{{Q}_1(Z)-{Q}_2(Z){S}_3\left( Z, t-{t}_n\right)\right\}-\sum_{n=0}^{N-1}\mathcal{H}\left( t-{t}_{n+1}\right)\left\{{Q}_1(Z)-{Q}_2(Z){S}_3\left( Z, t-{t}_{n+1}\right)\right\} $$

(32)

where

$$ {Q}_1(Z):={I}_n-\left\{{I}_n-{k}_s \exp \left({a}_{\alpha}{\psi}_0\right)\right\} \exp \left\{-{a}_{\alpha}\left({d}_u- Z\right)\right\} $$

(33)

$$ {Q}_2(Z):=-4\left({I}_n-{I}_{LT}\right) \exp \left(\frac{a_{\alpha} Z}{2}\right) $$

(34)

$$ {S}_3\left( Z,\tau \right):= \exp \left\{\frac{D_{\psi}\tau}{4}\right\}\ \sum_{m=1}^{\infty}\frac{\mathit{\sin}\left[{\Lambda}_m{a}_{\alpha}\left({d}_u- Z\right)\right]\mathit{\sin}\left({\Lambda}_m{a}_{\alpha}{d}_u\right)}{1+{a}_{\alpha}{d}_u/2+2{\Lambda}_m^2{a}_{\alpha}{d}_u} \exp \left\{-{\Lambda}_m^2{D}_{\psi}\tau \right\} $$

(35)

In the above equations, d _u  = d _w  − 1/a is the vertical depth of the top of the capillary fringe; D _ψ  :  = a _α k _s /(θ _s  − θ _r ), and the quantities Λ _m are the positive roots of the pseudo-periodic characteristic equation

$$ \tan \left(\Lambda {a}_{\alpha}{d}_u\right)+2\Lambda =0 $$

(36)

which, in TRIGRS implementation, are found numerically by a combination of bracketing, bisection, and Newton–Raphson methods.

Water table rise

Water table rise occurs as a consequence of vertical infiltration, when the amount of water flow exceeds the maximum water flow that can be drained by gravity.

The simplified numerical strategy provided by Baum et al. (2008) for the computation of the water table rise during the infiltration process, based on a spatial discretization of the vertical axis into M uniform elements of thickness ΔZ _k + 1 = Z _k + 1 − Z _k (with k = 0 ,  …  , M − 1, Z ₀ = 0 and Z _M  = d _b ), is detailed in the following.

The volume of water V _A (per plan-view unit area) accumulating at the top of the capillary fringe is computed by numerically integrating the excess flow at Z = d _u :

$$ {V}_A(t)=\underset{0}{\overset{t}{\int }}{q}_{\mathrm{ex}}\left({d}_u,\tau \right) d\tau $$

(37)

where:

$$ {q}_{\mathrm{ex}}=\left\{\begin{array}{ll}0\hfill & \mathrm{if}\kern0.5em q\left({d}_u, t\right)\le {c}_d\left({q}_{\max }-{I}_{LT}\right)\hfill \\ {} q\left({d}_u, t\right)-{c}_d\left({q}_{\max }-{I}_{LT}\right)\hfill & \mathrm{otherwise}\hfill \end{array}\right. $$

(38)

$$ q\left({d}_u, t\right)=\sum_{n=0}^{N-1}\mathcal{H}( x)\left( t-{t}_n\right)\left\{{I}_n-{Q}_2\left({d}_u\right){S}_4\left({d}_u, t-{t}_n\right)\right\}-\sum_{n=0}^{N-1}\mathcal{H}( x)\left( t-{t}_{n+1}\right)\left\{{I}_n-{Q}_2\left({d}_u\right){S}_4\left({d}_u, t-{t}_{n+1}\right)\right\} $$

(39)

and

$$ {S}_4\left( Z,\tau \right):= \exp \left\{\frac{D_{\psi}\tau}{4}\right\}\ \sum_{m=1}^{\infty}\frac{\Lambda_m\mathit{\sin}\left({\Lambda}_m{a}_{\alpha}{d}_u\right)}{1+{a}_{\alpha}{d}_u/2+2{\Lambda}_m^2{a}_{\alpha}{d}_u} \exp \left\{-{\Lambda}_m^2{D}_{\psi}\tau \right\} $$

(40)

In Eq. (38), the constant c _d is set to 1 when the basal impervious boundary is at infinite depth, and to a small number (0.1) otherwise.

The volume V _A is then compared to the available pore space above the water table, V _f (Z, t), given by:

$$ {V}_f\left( Z, t\right)=\left({\theta}_s-{\theta}_r\right)\left\{{d}_u- Z+ T\left( Z, t\right)\right\} $$

(41)

with:

$$ T\left( Z, t\right):=\frac{1}{k_s}\underset{d_u}{\overset{Z}{\int }}\kappa \left(\zeta, t\right) d\zeta $$

(42)

and κ(ζ, t) given by Eq. (32). An explicit expression for the integral in Eq. (42) is provided by Baum et al. (2008) and is not reported here for brevity. In order to find the new position of the water table, the element k for which:

$$ {V}_f\left({Z}_k, t\right)\le {V}_A(t)\le {V}_f\left({Z}_{k+1}, t\right) $$

is searched first. Then, the new value of d _u is obtained by linear interpolation between Z _k and Z _k + 1.

Pressure head in the saturated zone

The pressure head variation below the water table due to a decrease h _n of water table depth is computed solving the saturated infiltration problem governed by Eq. (5), with a pressure boundary condition Δψ _hn  = βh _n applied at the initial water table position for the nth time step. Setting:

$$ {Z}^{\prime }:= Z-{d}_u\kern3em {d}_b^{\prime }:={d}_b-{d}_u, $$

the pore pressure head variation at early and intermediate times, for the case of finite depth basal impervious boundary, is given by:

$$ \begin{array}{l}\Delta \psi \left({Z}^{\prime }, t\right)=\sum_{n=0}^{N-1}\Delta {\psi}_{hn}\mathcal{H}\left( t-{t}_n\right)\left\{{S}_5\right({Z}^{\prime }, t-{t}_n\left)+{S}_6\right({Z}^{\prime }, t-{t}_n\left)\right\}\kern1em \\ {}-\sum_{n=0}^{N-1}\Delta {\psi}_{hn}\mathcal{H}\left( t-{t}_{n+1}\right)\left\{{S}_5\right({Z}^{\prime }, t-{t}_{n+1}\left)+{S}_6\right({Z}^{\prime }, t-{t}_{n+1}\left)\right\}\kern1em \end{array} $$

(43)

where:

$$ {S}_5\left( Z^{\prime },\tau \right):=\sum_{m=1}^{\infty }{\left(-1\right)}^{m+1}\mathrm{erfc}\kern0.2em \left\{\frac{\left(2 m-1\right){d}_b^{\prime }-{Z}^{\prime }}{2\sqrt{D_{\alpha}\tau}}\right\} $$

(44)

$$ {S}_5\left({Z}^{\prime },\tau \right):=\sum_{m=1}^{\infty }{\left(-1\right)}^{m+1}\mathrm{erfc}\kern0.2em \left\{\frac{\left(2 m-1\right){d}_b^{\prime }+{Z}^{\prime }}{2\sqrt{D_{\alpha}\tau}}\right\} $$

(45)

An alternative expression based on a Fourier series solution, valid for later times during the transient process, is provided by Baum et al. (2008) and is not reported here for brevity.