Forecasting rock slope failure: how reliable and effective are warning systems?

Abstract

Warning systems are increasingly applied to reduce damage caused by different magnitudes of rockslides and rockfalls. In an integrated risk-management approach, the optimal risk mitigation strategy is identified by comparing the achieved effectiveness and cost; estimating the reliability of the warning system is the basis for such considerations. Here, we calculate the reliability and effectiveness of the warning system installed in Preonzo prior to a major rockfall in May 2012. “Reliability” is defined as the ability of the warning system to forecast the hazard event and to prevent damage. To be cost-effective, the warning system should forecast an event with a limited number of false alarms to avoid unnecessary costs for intervention measures. The analysis shows that to be reliable, warning systems should be designed as fail-safe constructions. They should incorporate components with low failure probabilities, high redundancy, have low warning thresholds, and additional control systems. In addition, the experts operating the warning system should have limited risk tolerance. In an additional hypothetical probabilistic analysis, we investigate the effect of the risk attitude of the decision makers and of the number of sensors on the probability of detecting the event and initiating a timely evacuation, as well as on the related intervention cost. The analysis demonstrates that quantitative assessments can support the identification of optimal warning system designs and decision criteria.

Introduction

Mountain regions are prone to gravitationally driven natural hazard processes. Mid- (>10⁴ m³) and high-magnitude (>10⁶ m³) rockfalls and rockslides can cause much damage due to on-site and off-site effects such as inundation, dam failure, and subsequent debris flow activity in released debris (Hewitt et al. 2008). In some areas, especially those affected by melting permafrost and rapid deglaciation, there is increasing evidence for rising frequencies of rock slope failure (Ravanel and Deline 2011; Huggel et al. 2012; Krautblatter et al. 2013). Out of 38 recorded landslide disasters (1000–1999 AD) that have each caused more than 1000 casualties worldwide, 75 % were due to massive high-magnitude rock slope failure (Evans 2006). But also, mid-magnitude rockfalls pose a great risk to densely populated alpine areas. This is because of their sudden release, fast propagation, long and (often unpredictable) runout, and impact energy far beyond the retention capacity of most rockfall nets or other protection measures (Zimmer et al. 2012). They often result in total destruction of buildings and infrastructure as has recently been demonstrated by a 3000-m³ rockfall on the major Gotthard Railway (Switzerland) on June 5, 2012, which caused one casualty and closed the railway line for more than a month.

To protect individuals and mobile objects close to potential release areas, warning systems are increasingly applied as a risk mitigation measure. They can generate timely information and allow at-risk people to act and to reduce their impacts (UNISDR 2007). Warning systems are especially useful when the capacity of structural rockfall protection measures is likely to be exceeded; they are typically associated with low life cycle cost, a high flexibility, and with minimal impact on the environment (Hattenberger and Wöllik 2008). Modern warning systems for forecasting mid- and high-magnitude rockfall events consist of technical components, models, and human decision making (Ganerød et al. 2008; Sturny and Bründl 2014). They make use of typical velocity patterns of rockfall processes for detecting events.

To this end, displacements are monitored, often with total stations and extensometers. In the operation of rockfall warning systems (RWS), two phases can be distinguished, which are related to the progress of a rockfall failure. In the first phase, to which we refer to as “detachment phase,” warning systems constantly monitor movement patterns of the unstable rock mass to send warning information instantaneously when a predefined threshold is exceeded. Higher-magnitude rock slope failures characteristically evolve slowly, typically weeks to several years, until a critical level of detachment is developed. Failing slopes show early signs of deformations such as tension cracks, movement, and increasing rockfall activity (Hungr and Evans 2004). This progressive failure includes daily fluctuations and depends on temperature, rain, snow melt, and long-term stress–strain behavior of slopes which control fracture propagation. Rainfall, earthquakes and snow melting, weathering, and aging can be important triggers or driving factors that weaken the rock mass during the first phase (Lacasse et al. 2008). Rainfall and snow melt directly influence the pore water pressure, which can be a major driver for rock displacement and the final failure (Loew et al. 2012). To include these contributing factors in decision procedures associated with warning systems, they are often equipped with rain gauges and sensor measuring pore water pressures.

In the second phase, which we refer to as the “acceleration phase", the final failure occurs after an acceleration in which rock bridges are destroyed, often preceded by subcritical fracture propagation and stress corrosion, especially in a brittle rock mass (Petley et al. 2005a, b; Petley and Petley 2006). In this acceleration phase, experts should analyze sensor data and apply models to forecast the event time and execute appropriate intervention measures. The time of failure can be forecasted using measured velocity (Fukuzono 1990). Figure 1 illustrates how the inverse velocity (1/v) is plotted against time in a linear 1/v model to obtain an event forecast (Saito 1969; Hashimoto et al. 1982).

Fig. 1

Sketch of a 1/v model to predict the event date of brittle rock slope failure based on a measured kinematic time series

Many authors emphasize the applicability of the linear 1/v model, especially for brittle rock slope failures, i.e., forming of a rupture surface and first time failure in cohesive materials whereas asymptotic trends can be often observed in pre-existing shear surfaces or ductile deformations in the basal region (Petley and Petley 2006). Successful forecasts of a mid-magnitude icefall (1*10⁵ m³) and a hazardous rockfall (3000–5000 m³) in the early 1990s are described by Wegmann et al. (2003). Krähenbühl (2006) presents an application of the 1/v model to forecast two successive rockfall events (40,000 and 200,000 m³) in the alpine region of Switzerland. Accurate forecasts could also be made for three major rockfall events (1, 2, and 18 million m³), which occurred in two open pit gold mines in northeastern Nevada (Rose and Hungr 2007); the largest event was even forecasted 3 months prior to the event.

In contrast to these successful forecasts, a number of catastrophic events have occurred where prediction has failed. An infamous example is the Vajont landslide (270 million m³) in 1963, which triggered a 245-m-high flood wave in a water reservoir that consequently overtopped the dam and killed almost 2000 people in villages downstream (Kilburn and Petley 2003). Event analyses demonstrated the difficulty in forecasting the Vajont landslide with the 1/v model and confirmed that the final failure depends on the characteristics of the rock slope failure (brittle, ductile) and on the type of movement. Although clear accelerations were monitored over years at Vajont, they were misinterpreted, and the failure occurred more rapid than expected in a period of 45 s. Experts assumed that velocities would slow down following a nonlinear trend as two previous, smaller events did (Kilburn and Petley 2003; Petley and Petley 2006). Even 50 years after the events, there is still uncertainty as to why the velocity patterns changed during the multiple deformation phases from 1960 to 1963 (Barla and Paronuzzi 2013).

Accurate event forecasts are still a major challenge. Finding the balance between an early and safe evacuation and cost caused by unnecessary intervention measures remains a critical task for decision makers, who can be landslide experts, politicians, or a combination of both. To support decision makers in selecting an optimal risk mitigation strategy, the effectiveness and cost of alternative measures should be quantified and compared. However, existing frameworks for evaluating the effectiveness of mitigation measures focus on structural measures such as dams, rockfall nets, and galleries (Fell et al. 2005; Penning-Rowsell et al. 2005; Romang et al. 2011; SafeLand 2012). The effectiveness of rockfall warning systems and warning systems for other types of natural hazard has so far not been considered systematically or quantitatively. This study aims to address this by quantitatively analyzing the reliability and effectiveness of a rockfall warning system installed for slowly evolving mid- and high-magnitude rockfalls. First, we assess the reliability of the warning system installed in Preonzo, Switzerland, to detect a past rockfall event on May 15, 2012. The reliability is expressed as the probability that an evacuation is set up timely before the event, and the analysis is conducted for both the detachment and the acceleration phase. Second, we investigate the influence of human decision-making and the number of sensors on the system effectiveness and the intervention cost using hypothetical predictive analysis.

Evaluation criteria for warning systems

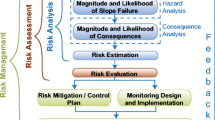
Warning systems are part of an integrated risk management aimed at increasing the preparedness for potential risks created by natural hazards and improving the capability to respond to and recover from an event. To compare preventive warning systems with alternative risk mitigation measures and to identify an optimal risk mitigation strategy, the effect on risk reduction and related cost should ultimately be considered in cost-benefit analyses (Penning-Rowsell et al. 2005; Safe Land 2012; Špačková and Straub 2015). For warning systems, these evaluation criteria should address specific needs. Where the cost associated with the hazard consequence is explicitly quantified, a cost-effectiveness analysis can be carried out in which the cost of mitigation measures is compared against their effectiveness.

The effectiveness of a warning system is a function of the reduction in risk it achieves. The effectiveness E_S can be defined through the relative risk reduction achieved with the warning system (Sättele et al. 2015). With R being the overall risk without the warning system and R^(S) the risk with the warning system installed, the effectiveness is as follows:

$$ {E}_S=1-\frac{R^{(S)}}{R} $$

(1)

The risk R_ij associated with an exposed object i and a hazard scenario j can be calculated as follows (e.g., (Fuchs 2006; Bründl et al. 2009)):

$$ {R}_{ij}={p}_j\times p{e}_{ij}\times {v}_{ij} \times {A}_i $$

(2)

Here, p_j is the probability of occurrence of a scenario j, pe_ij is the exposure probability of object i in scenario j, v_ij is the vulnerability of object i in scenario j and A_i is the value of object i. The overall risk R is calculated by summing over all exposed objects i and hazard scenarios j:

$$ R={\displaystyle \sum_{j=1}^{n_{scen}}}{\displaystyle \sum_{i=1}^{n_{obj}}}{R}_{ij} $$

(3)

Warning systems reduce the risk primarily by decreasing the exposure probability pe_ij of persons and mobile objects i in a hazard scenario j. Therefore, this paper addresses two questions: (i) How can the reduced exposure probability achieved with a rockfall warning system be quantified? (ii) And how can a rockfall warning system be optimized to minimize pe_ij with minimal cost?

Reliability analysis has been identified as an accurate basis for a comprehensive system evaluation of structural risk mitigation measures (Margreth and Romang 2010; Balbi et al. 2014) and can be applied to determine the exposure probability pe_ij of warning systems (Sättele et al. 2015). The reliability of a system is defined as its ability to fulfill the designated performance over a certain time (IEEE 2010). RWS for high- and mid-magnitude rockfalls are reliable if they detect dangerous events in time and lead to measures that reduce the exposure probability pe_ij. The reliability of a rockfall warning system can be quantified through the probability of detection, i.e., the probability that a warning system detects a hazardous event and adequate measures are taken and the probability of false alarms, i.e., the probability that measures are taken when they were unnecessary. A large number of false alarms can reduce the effectiveness, because frequent false alarms reduce the probability that people comply to an issued warning (Breznitz 1989; Sättele et al. 2015). In addition, the available lead time and the consequences of missed events must be taken into account as it contributes to the effectiveness (Paté-Cornell 1986; Schröter et al. 2008; Busslinger 2009; UNEP 2012). A missed event means that an alarm is not given in time, as it happened in Vajont in 1963, when the destructive rockfall occurred before persons at risk were evacuated.

A reliability analysis for warning systems must address both the technical reliability and the inherent reliability of the system (Sättele et al. 2015). The technical reliability accounts for failures of technical system components due to aging and external causes such as lightning and destruction. It considers the configuration of components within the system and addresses redundancies as well as dependencies of the system components. It results in the probability of technical system failure. The inherent reliability of a warning system describes the general ability of the system to detect an event. It is primarily a function of the warning thresholds, the model forecast accuracy of models, and human decision-making.

The technical and inherent reliability of a rockfall warning system should be analyzed separately for the detachment and acceleration phase of rockfall processes. During the detachment phase, the technical reliability remains constant and can be modeled using classical methods such as fault, event or decision tree analysis, and failure mode and effect analysis (Stewart and Melchers 1997). Here, we model this technical reliability of warning systems with Bayesian networks (BN), which are increasingly applied to probabilistically model probabilities of systems failures (Bensi et al. 2012) and natural risks (Aguilera et al. 2011) such as rockfall hazard rating (Straub 2005). The Bayesian network is a probabilistic graphical modeling tool, in which nodes represent random variables and arcs describe the stochastic dependencies among the nodes (Jensen and Nielsen 2007). The inherent reliability during the detachment phase depends initially on the warning thresholds, the measured sensor data, and their positioning in the field. All these aspects can also be modeled in the Bayesian network (see “Inherent reliability” section).

In the acceleration phase, the technical reliability of the system is no longer constant, but decreases over time, because sensors reach their mechanical limits or are likely to be destroyed by the failure. Additionally, power support and communication lines may be interrupted on purpose to prevent additional consequences in case of a direct hit. Thus, the power supply of the rockfall warning system becomes less reliable close to the event. We propose to address these increasing failure probabilities of technical failures through inhomogeneous Poisson processes (see “Technical reliability” section). The inherent reliability during the acceleration phase addresses the ability of the warning system and the decision makers to implement an evacuation before the event. The forecast ability depends on the ability of the 1/v model to forecast the event time and on the risk tolerance of the decision maker. To assess the inherent reliability achieved with the rockfall warning system, event forecasts are calculated and summarized graphically (see “Inherent reliability” section).

The Preonzo rock slide warning system

Description of the event in May 2012

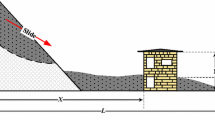
An unstable rock mass which threatens the community of Preonzo (Switzerland) has been recognized for decades. Slope failures occurred in the 18th century followed by temporary stabilization. A new tension crack was discovered by residents in 1989. Since 1991, the movement has been increasing significantly, and in May 2002, about 150,000 m³ of the rock mass failed in the southern area of the Alpe di Rioscioro. This event, together with a minor event in May 2010, did not cause loss or damage to the downslope factories and roads (Willenberg et al. 2009; Loew et al. 2012).

Here, we investigate the latest event, which took place on May 15, 2012. The entire spring period of 2012 was characterized by unusually high displacement rates. At the beginning of May, local authorities were informed about critical displacements from the geologist operating the warning system. Immediately, a crisis team was established comprising local authorities, safety officers, and geologists operating the rockfall warning system. After several days of heavy rainfall, the velocity of the rock mass increased significantly, and on May 6, the crisis team evacuated people from the underlying factories and closed the nearest road. On May 8, the rain stopped, the velocity decreased, and intervention measures were discontinued to avoid losses from business interruption. On May 12, the velocity increased again, and a second evacuation was initiated. In the early morning of May 15, approximately 300,000 m³ detached from the rock face. Fortunately, the rock mass stopped on the slope and did not damage any infrastructure or injure any person.

Components of the Preonzo rockfall warning system

Between 1999 and May 2012, a rockfall warning system was installed at the Preonzo site. The system was operated and maintained by the local geologists responsible for natural hazard management in the Canton Ticino. From 1999 onward, five extensometers continuously measured the rock movements to detect accelerations and to automatically generate warning information. To increase the system reliability, an automated total station with 14 reflectors was set up in summer 2010 (Loew et al. 2012). The configuration of the Preonzo warning system has three units for monitoring, data interpretation, and information dissemination (Sättele et al. 2012).

The monitoring unit incorporated two main sensor technologies. In the tension crack of the northern section, five extensometers monitored the displacement (Fig. 2a). The extensometer measurements (every 15–60 min) were controlled by a remote data logger. Sensors and the logger communicated via protected cable connections. The power supply was provided by a battery and was recharged by a solar panel. In addition to the extensometers, an automated total station measured the distances to 14 reflectors on the front face of the slope (Fig. 2b). The total station in the valley was connected to a computer that initiated measurements every 20 min. Power was provided by the power network, and the system was located in a heated cabin, built on a concrete foundation to minimize movement. In addition, a rain gauge was installed close to the tension cracks.

Fig. 2

a Positioning of the five extensometers in the tension cracks and b 14 reflectors in the front face which were regularly monitored by an automated total station

The data interpretation unit included two main decision levels: one in the detachment and one in the acceleration phase. During the detachment phase, warnings were automatically generated when predefined warning thresholds were exceeded; in the acceleration phase, the crisis team analyzed the data to decide on intervention measures. To generate automated warning information, three threshold levels were defined for each extensometer in the tension crack (3 mm/day, 5 mm/day, and 5 mm/h) and one threshold for the total station (50 mm/day). The threshold for the total station was higher, because measured displacements were generally higher at the front face. Whenever a threshold for an extensometer was exceeded, the remote data logger issued warning information via the mobile network to the geologists. Independently, the computer connected to the total station in the valley issued a warning if the threshold was exceeded. While data from the remote data logger was transmitted via mobile network, data from the total station was sent via cable connection. Whenever the system operators received automated warning information, they analyzed sensor data to decide on further responses. The rain gauge serves as additional information source and decision add but is not associated with a threshold. All data were collected, processed, and visualized on a central server, and the event date was forecasted by the application of the 1/v model. The final decision about an evacuation was made by the crisis team and was based on the calculated forecasts. The warning system included a control system, which observed the availability of individual sensors, the status of the remote batteries, and the availability of the mobile network at regular intervals. Consequently, system failures could be detected intermediately to implement alternative temporary risk mitigation measures.

The information dissemination unit of the Preonzo warning system consisted of intervention plans, which summarized mitigation measures and responsibilities. The intervention was planned and coordinated by the crisis team to protect the underlying factories and roads. The evacuation of the factories could be initiated through activation of acoustic signals and was organizationally led by the police, who were also responsible for closing the roads below.

Quantifying the reliability of the Preonzo warning system

This section describes the reliability analysis of the warning system installed before and during the event in 2012, considering both the technical and the inherent reliability. The reliability analysis is presented separately for the detachment and acceleration phase. In each phase, factors that determine the system reliability are described, selected methods used to assess the reliability are presented, and main results are summarized.

System reliability during the detachment phase

During the detachment phase, the warning system monitored the displacement to alert local geologists about relevant accelerations. Whether or not the geologists received timely information depended on the reliability of the technical system configuration and on the predefined warning thresholds.

Technical reliability

Accurate automated warning information can be generated only when technical system components work properly. In Preonzo, the warning system is equipped with a control system that sends information when system components fail. In this situation, experts are alerted to assess the situation on-site. Due to this fail-safe system configuration, technical failure of the system will not lead to events being missed. Nevertheless, to avoid high cost due to unnecessary interventions because of frequent alarms, the technical reliability is relevant and should be maximized.

The Bayesian network (BN) to model the technical reliability of the Preonzo warning system consists of two different types of nodes (Fig. 3). Grey nodes describe the causal chain from measured sensor data to the warning provided to system operators. The conditional probability tables of the gray nodes define the logical relations between the different nodes and are here modeled deterministically. As an example, the node “warning issued” incorporates both serial connections (“AND”) and parallel connections (“OR”). Figure 4a exemplarily depicts an OR connection and the associated conditional probability table. Here, only one single sensor has to indicate an event (state 1) to issue a warning. Figure 4b represents an exemplarily AND connection with the associated conditional probability table. Here, both the logger and the battery have to work to issue a warning.

Fig. 3

Bayesian network to model the technical reliability in the detachment phase. The monitoring unit incorporates 5 extensometers and 14 reflectors and the data interpretation components to initiate and transfer warnings

Fig. 4

Illustrative example to represent the relations between the nodes of a Bayesian network: a “OR” connection and associated conditional probability table; b “AND” connection and associated conditional probability table

White nodes in the Bayesian network specify the failure probabilities of system components. These depend on internal failure causes and external factors. Most components are installed in rough alpine terrain, and they are exposed to external failure sources such as lightning, animals, and extreme weather. Assuming that failures occur randomly through time, failure probabilities of individual technical system components at time t (the unavailability) can be calculated as follows (Straub 2012):

$$ \Pr \left(F(t)\right) \approx \lambda \times \mathrm{E}\left[{T}_r\right] $$

(4)

where λ is the failure rate of the system component and E[T _r ] is the expected time it takes to detect and repair a failure. This approximation is valid for small values of λ, i.e., for $\lambda \ll \frac{1}{\mathrm{E}\left[{T}_r\ \right]\ }$. The failure rate λ of a system component includes both the internal failure rate λ _IF and the rate of failures caused by external influences λ _EF :

$$ \lambda = {\lambda}_{IF} + {\lambda}_{EF} $$

(5)

The failure probabilities for components of the Preonzo system were adapted from results of a similar case study (Sättele et al. 2015) and are estimated for individual components as Pr(F(t)) ∼ 5 × 10^− 4. Only the failure probability of the mobile network is significantly higher at 1.2 × 10^− 2 according to a study conducted by the Swiss Federal Office for Civil Protection (FOCP 2013).

The analysis shows that the technical reliability achieved with the Preonzo system is high, due to multiple and redundant sensor units. The system is equipped with two sensor technologies that both incorporate redundant sensors. The limiting factor for the technical reliability is the availability of the mobile network, which has no redundancy. This results in an unavailability of the technical system of Pr(F _s (t) = 1.2 × 10^− 2. Despite this relatively high probability of system failure, this is not critical due to the fail-safe configuration, in which decision makers are alerted if the alarm system has a technical malfunction.

Inherent reliability

The inherent reliability of a warning system is its ability to interpret the measured sensor data, to distinguish between noise and real displacement, and to inform system operators before the event occurs. During the detachment phase, the relationship between the probability of detection and the probability of false alarms is determined by the predefined warning thresholds. To achieve a large probability of detection, thresholds for the Preonzo warning system are intentionally set low (see “Components of the Preonzo rockfall warning system” section). However, the warning thresholds are high enough to avoid perpetual false alarms due to displacement noise that arises from daily fluctuations, e.g., due to temperature changes.

Existing movement records summarize the displacement rates measured by the extensometers and the total station between August 2010 and May 2012. Dilatations measured by extensometers positioned in the northern section are higher (extensometers 3–5) than those measured by similar sensors in the southern section (Fig. 5). A few hours before the event, extensometers 4 and 5 reached their technical limits and failed. The reflectors show similar displacement characteristics to the extensometers (Fig. 6). Reflectors 1–6 and 8, 9 were mounted in the northern sector and showed large displacement rates. The remaining reflectors (7, 11–14) were installed in the southern section and did not indicate any discernable acceleration. Reflector 10 had already failed in the summer of 2011.

Fig. 5

Displacements measured by the extensometers 1–5 in the tension cracks between August 2010 and May 2012. Extensometers positioned in the northern section (3–5) indicate higher acceleration before the event

Fig. 6

Displacements measured by the reflectors 1–14 installed at the front face of the slope between August 2010 and May 2012. Reflectors positioned in the northern section (1–7, 9) indicate higher acceleration before the event

In Fig. 7, the sensor data measured by extensometer 5 from January to May 2012 is compared to the lowest warning level. The lowest warning threshold (1 mm/day) was regularly exceeded by those sensors installed in the northern section from the beginning of March onward. Starting in early April, the warning threshold was constantly exceeded, and system operators started to analyze the sensor data at more frequent intervals independent of the automated warning information. The two upper thresholds (3 and 5 mm/h) were reached several days before the event. Other extensometers in the northern section showed similar results. The only warning level defined for the reflectors (50 mm/day) was also exceeded before the event by those reflectors installed in the northern section.

Fig. 7

Velocities measured by extensometer 5. The velocities temporarily exceeded the lowest warning threshold in March and then constantly from beginning of April

The influence of warning thresholds on the system reliability can be modeled within the Bayesian network, by making the conditional probability of the nodes “event indicated” dependent on the threshold. Such an approach was followed in Sättele et al. (2015). However, during the detachment phase, a low threshold can generally be chosen, which leads to a probability of detection of one. This is because the effect of false alarms is less relevant in this phase, as the warning information is sent to system operators and not directly to endangered people. System operators should be interested in receiving information from every unexceptional displacement. In combination with the fail-safe configuration of the technical system components, the overall probability of identifying an event in the detachment phase is very close to one. The high reliability of the Preonzo warning system also leads to a reasonably small number of false alarms to system operators.

System reliability during the acceleration phase

During the acceleration phase, specialists analyze the sensor data to forecast the failure time and support the crisis team in planning appropriate response. The system reliability in this phase is a function of increasing failure probabilities of technical system components, the forecast accuracy of the 1/v model, and human decision-making.

Technical reliability

The technical reliability in the acceleration phase influences the warning system’s ability to support the crisis team in reaching an accurate event forecast. The forecast of the event time depends directly on the availability and quality of the measured sensor data. Power interruptions due to safety reasons or sensor failures due to large movements in the surrounding area occur more frequently close to the event. The effect of increasing system failure probabilities on the forecast accuracy should therefore be considered in warning system technical reliability analyses. In the northern section of the Preonzo rock face, the majority of sensors failed in the hours before the event (Fig. 8). Three out of five extensometers and all reflectors positioned in the fast moving slope were destroyed.

Fig. 8

Failures of sensors before the event on May 15, 2012. Many sensors are destroyed shortly before the event due to the fast moving slope

To quantify the accelerating destruction of sensors in Preonzo before the event 2012, a function describing the probability of failure was fitted to the observed number of sensors that failed in the northern section (extensometer 1–5; reflectors 1–6 and 8, 9, 10). The failure probability P _f for the Δt  days to the event in Preonzo is modeled as follows:

$$ {P}_f\left(\varDelta t\right)={p}_{basic}+{p}_{end}\times \exp \left(-b\times \varDelta t\right) $$

(6)

where the basic failure probability of technical system components p _basic is 5.0 × 10^− 4 (section “Technical reliability”). To obtain values for p _end and b, a likelihood function describing the observed number of failures is established. The probability of n _F failures out of n sensors on a given day is described through the binomial distribution as follows:

$$ \Pr \left({N}_F={n}_F\right) = \left(\begin{array}{c}\hfill n\hfill \\ {}\hfill {n}_F\hfill \end{array}\right)\left\{{P}_f{\left(\varDelta t\right)}^{n_F}\times {\left[1-{P}_f\left(\varDelta t\right)\right]}^{n-{n}_F}\right\} $$

(7)

The parameters b and p _end are found by maximizing the log-likelihood function, which is defined as follows:

$$ \ln L\left({p}_{end},b\right) = {\displaystyle \sum_{t=1}^{44}} \ln \Pr \left({N}_F={n}_F(t)\Big|{p}_{end},b\right) $$

(8)

where n _F (t) are the observed failures on days 1–44 before the event. By maximizing Eq. 7, maximum likelihood estimates for p _end and b are calculated as p _end  = 0.689 and b = 0.510. In Fig. 9, the percentage of sensors that failed in the northern section and the calculated failure probabilities using Eq. 6 for days 1–44 before the event are summarized.

Fig. 9

During the acceleration phase, an increasing number of sensors fail just before the event. The bars (left axis) show the observed percentage of sensors that fail; the line (right axis) depicts the failure probabilities according to Eq. 6

Inherent reliability

The inherent reliability in the acceleration phase is a function of the available sensor data, the accuracy of the 1/v model, and the expert’s ability to forecast the event based on these data. The decision to evacuate depends on the risk tolerance of the crises team. Due to the dependence on the available sensor data, the inherent reliability is related to the technical reliability of the rockfall warning system. An increasing number of sensor failures reduces the forecast ability.

To assess the inherent reliability of the Preonzo system, we apply a linear 1/v model using measured sensor data to obtain event forecasts. The inverse velocity at time t is calculated as follows:

$$ \frac{1}{v(t)}=a + b \times t $$

(9)

a and b are the modeled parameters and t is the time (in days). To avoid a large scatter generated by small velocity values deteriorating the accuracy of the forecast, the parameters are fitted to the measured velocity rather than to its inverse. Specifically, a least-squares fit of a and b to measured values of v(t) is carried out through the following relationship:

$$ v(t)=\frac{1}{a + b \times t} $$

(10)

Figure 10a exemplarily illustrates the velocities measured by extensometer 1 in the 10 days before May 14 and the model fit. To obtain a forecast of the event time, the inverse velocities 1/v are calculated according to Eq. 8 for dates t in the future. The event date forecasted with the 1/v model is the day where the inverse velocity (1/v) cuts the x-axis. In Fig. 10b, the inverse velocity corresponding to Fig. 10a is shown. On May 14, the forecast of the event with extensometer 1 is made for May 16, 1 day later than the event actually happened.

Fig. 10

a Velocity recorded by extensometer 1 from May 4 to May 14 and fitted function; b 1/v versus time using data from extensometer 1. On May 14, the 1/v model forecasts the event to occur on May 16, which is 1 day later than the observed event

Following the approach illustrated above for extensometer 1 and data available before May 15, event forecasts were made for every sensor and each day between April 1 and May 14. Figure 11a displays the forecasted event dates using data from different sensors installed in the northern section as a function of the date on which the prediction is made. In April, the forecasts made by different sensors vary significantly, but they become more aligned by the end of April. In this final phase, the predictions based on extensometer data show larger scatter than those based on reflector data. On May 14, the majority of sensors provided velocity data that indicated a hazardous event for the next day. Extensometers 1 and 2 are located further south, where the measured displacements were less significant. They forecast the event with a delay of 1 day. Nevertheless, 10 out of 12 sensors lead to an accurate event forecast.

Fig. 11

a Daily forecasted event date calculated with the 1/v model for the sensors in the northern section between April 1 and May 14; b forecasted number of days to the event calculated with the 1/v model for sensors in the northern section on every day between April 1 and May 14

The inherent reliability in the phase of acceleration depends on the decision of the crises team, who analyze the displacement rates with respect to quantities of rain that has fallen and is expected to fall. To understand the human impact on the inherent reliability, the forecasted number of days to the event is plotted for days between April 1 and May 14 (Fig. 11b) for all five extensometers and reflectors showing large displacement rates in the northern section (reflectors 1–5 and 8, 9). There are several days in April on which extensometers 3–5 and all those northern reflectors forecast the event for the following day. Here, different experts may reach different decisions. In May, the forecasts vary less, and the influence of human decision-making becomes less important. It can be assumed that even decision makers with different risk tolerances would come to the same decision in this period (which is the one that was actually taken by the crisis team in Preonzo).

Hypothetical analysis: optimizing warning systems

To compare the effectiveness and the cost for varying designs of the Preonzo system, the probability of detection achieved with the system and the expected cost arising from the intervention measures are estimated in a hypothetical analysis. Since the actual decision on intervention measures is based on expert assessments, which can include more information than only sensor data, e.g., rain measurements, the analysis is simplified and likely to underestimate the true capacities of the warning system.

To assess the effect of sensor numbers on the reliability, we vary their amount between 5 and 50 in the hypothetical analysis. To investigate the effect of human decision-making, we specify two decision makers with different risk types. A risk averse and a risk tolerant decision maker are associated with different evacuation criteria (Table 1). A technical evacuation criterion determines the minimum numbers of sensors that must be available for a forecast. Whenever fewer sensors are functioning, the crisis team initiates an evacuation and the closure of the road. The inherent evacuation criterion defines the minimum proportion of sensors that must forecast a failure for the next day in order to initiate an evacuation and road closure.

Table 1 Definition of risk types based on different evacuation criteria

Using a Monte Carlo analysis, we estimate the probability of detection and intervention cost for the specified risk averse and tolerant decision maker and modified numbers of sensors. In the Monte Carlo analysis, the investigated Preonzo rockfall event is randomized, as is the response of the individual sensors. We use n_S = 10, 000 random realizations (run) of the process. For each run, it is checked if and when evacuations would be initiated, based on technical and inherent evacuation criteria. In each run, the number of functioning sensors for all days between April 1 and May 14 is simulated and compared to the minimal required number to investigate whether the technical evaluation criterion is fulfilled. The number of functioning sensors on each day is simulated based on the binomial distribution (Eq. 5) with parameters determined following section “Technical reliability.”

To assess whether the inherent evacuation criteria is fulfilled, the percentage of simulated positive event forecasts for the next day is compared to the specified percentage. The number of available event forecasts on each day depends on the remaining number of sensors. The forecasts for the group of sensors are modeled by a probability distribution, in which no distinction is made between individual sensors (i.e., they are considered as statistically identical and independent). To obtain probability distributions for daily forecasts between April 1 and May 14, Lognormal distributions are fitted to sensor forecasts calculated for extensometers 1–5 and reflectors 1–5, 8, and 9 (Fig. 11b). Figure 12 illustrates the empirical and the fitted cumulative distribution functions of the forecasted days to event calculated on April 18 and May 14. The fitted distributions are applied in the Monte Carlo analysis to randomly generate forecasts for each day. The percentage of sensors that forecast an event for the next day is calculated and compared to the percentage defined by the inherent evacuation criterion.

Fig. 12

The empirical (observed) and the fitted cumulative probability distribution function of the forecasted days to the event for the group of sensors. The observed sensor forecasts are those shown in Fig. 11b. a On April 18, the probability of an event on the next day is estimated as 0.034 and for an event in 5 days as 0.43; b on May 14, the probability of an event to occur within the next day is estimated as 0.65 and for the second day 0.99

Intervention costs arise whenever an evacuation is initiated. This cost is primarily estimated from interruptions of business processes in the subjacent factories at 100,000 CHF/ day based on the information of local experts. If the technical evacuation criterion is fulfilled, a 5-day evacuation is necessary to install a replacement system. In this time, a temporary monitoring system (e.g., interferometric radar) must be installed to decide if the access for installation to the area is safe. Total intervention costs are estimated at 800,000 CHF, with 500,000 CHF at this due to the 5 days of evacuation, and the remaining 300,000 CHF are the investment cost for the replacement system, including cost for temporarily monitoring measures. Separate costs occurring to different stakeholders are not considered. If the inherent evacuation criterion is fulfilled, a 2-day evacuation is initiated, and the corresponding cost is 200,000 CHF.

In this analysis, the probability of detection is the probability that the evacuation and road closure are in place on May 15, the day of the actual event.

Figure 13a displays the probability of detection calculated for the different risk types as a function of the number of initially installed sensors. For the more risk-averse decision maker, the probability of detection is close to one, only slightly depending on the number of sensors. More risk-tolerant decision makers achieve a probability of detection between 0.65 and 0.85 which reaches its minimum at 11 sensors. Figure 13b displays the expected intervention cost calculated for both risk types as a function of the sensors. As expected, the risk-averse decision maker creates higher expected intervention cost, especially with a small number of sensors. In this case, large costs for evacuation and replacement systems are generated. With a highly redundant sensor unit (around 30 sensors), the expected cost for the risk-averse decision maker reaches their minimum at 400,000 CHF. The expected cost for intervention incurred by the risk-tolerant decision maker reaches minimal costs (215,000 CHF) at 20. For larger number of sensors, the expected cost increases slightly up to a maximum of 236,000 CHF. This sum does not include the cost for installing the initial sensors. A comprehensive cost analysis should also consider the acquisition cost of the warning system, which increases with a rising number of sensors, to determine the optimal number of sensors.

Fig. 13

a The probability of detection as a function of the decision maker’s risk-taking profile and the number of initially installed sensors. The probability of detection is the probability of an evacuation being in place on the day of the event; b the expected cost for intervention (evacuation, road closure) as a function of the decision maker and the number of initially installed sensors

The intervention on the day of the event, May 15, can be because the event was correctly forecasted (inherent reliability) or because the failure of multiple sensors triggered an intervention (technical failures). In Figs. 14 and 15, the probabilities of detection and expected intervention costs obtained with the inherent evacuation criterion and the technical evacuation criterion are shown individually for both risk tolerance profiles. To this end, both evacuation criteria are checked daily, independent of whether or not the other criterion has been fulfilled and an evacuation may already be in place. For this reason, the sum of the two individual probabilities of detection may be greater than one. The quality of the inherent forecasts during the time of reinstalling the system after technical failures may be poor, since only few sensors are left during that period. If no more sensors are available 1 day before the event occurred, zero forecasts can be made and the probability of detection associated with the inherent evacuation criteria becomes zero.

Fig. 14

The probabilities of detection achieved with the inherent and technical evacuation criteria are individually shown for both risk-averse and risk-tolerant decision makers

Fig. 15

Expected intervention cost achieved with the inherent and technical evacuation criteria are individually shown for both risk-averse and risk-tolerant decision makers

The probability of detection achieved due to technical failures decreases with the increase of sensors (Fig. 14). Evacuations due to an insufficient number of sensors are less likely to occur when the decision maker has a high-risk tolerance. For the risk-averse decision maker, an interesting peak is formed around 7 sensors. For minimal numbers of sensors (5–6), an evacuation because of technical failures is low, because the warning system got already substituted before the event. For 7–9 sensors, the probability that the system fails during the event is maximal and so is the probability of detection achieved with the technical evacuation criterion. The probability of detection because of an accurate event forecast increases with increasing number of sensors and is close to 1 for systems with at least 20 sensors for the risk-averse decision maker. The probability of detection achieved by the more risk tolerant person never exceeds the probability of detection reached by the risk-averse decision maker and never exceeds 0.84.

In Fig 15, the expected intervention cost created through the evacuation criteria are separately illustrated for both risk tolerance profiles. The expected cost due to the technical evacuation criterion decreases, when the number of initial sensors increases, because system failures become less likely. The risk-averse type generates immense cost from fewer sensors. The expected intervention cost generated by event forecasts becomes constant for more than 10 sensors and are higher for the risk-averse decision maker.

To understand how the intervention costs arise, the probability of an evacuation being mandated due to sensor forecasts (inherent evacuation criterion) is illustrated in Fig. 16 for the last 44 days before the event, with 10 sensors (a) and 30 sensors (b). The risk-tolerant person would evacuate on 3 days with a significant probability, namely on days 8, 9, and 1 before the event. When comparing Fig. 16a with Fig. 16b, it is clear that the forecast accuracy increases with more sensors. The probability of the risk-tolerant person proposing an evacuation due to sensor signals on the day of the event is 0.59 with 10 sensors and 0.76 with 30 sensors. The probability of wrongly initiating an evacuation on days 8 and 9 stays between 0.37 and 0.35 when increasing the number of sensors from 10 to 30. The same tendencies are observed for the risk-averse decision makers, whose evacuation probabilities are significantly higher. With 30 sensors instead of 10, the probability of detection increases from 0.91 to 0.99.

Fig. 16

Probability of evacuation due to sensor forecasts (inherent evacuation criteria) calculated for 10 (a) and 30 (b) initial sensors and different risk-taking profile types for 44 days before the event

Discussion

The effectiveness of warning systems was quantified as a function of the achieved risk reduction. Rockfall warning systems for mid- and high-magnitude events reduce the exposure probability of people to a hazardous event if the event is detected in time for intervention measures to be implemented. This effect can be calculated directly from the system reliability, which can be quantified by the probability of detection and the probability of false alarms. For the quantification of warning systems, the effect of false alarms can be neglected, because the events are rare and the warning information is sent to system operators. In other cases, especially when the information is issued directly to endangered people, the effect of false alarms can decrease the compliance to the alarm (Sättele et al. 2015).

Within the Preonzo case study, we conducted a comprehensive reliability analysis, which demonstrated the importance of assessing the technical and the inherent reliability for the displacement and the acceleration phase individually. During the detachment phase, the technical reliability depends on failure probabilities of components and their configuration in the system. In a similar case study, the failure probabilities of individual technical system components of a debris flow alarm system were analyzed in detail (Sättele et al. 2015). In that study, internal failure rates λ _IF were derived from specified mean time to failure and for repairable parts for mean time between failure values, with λ _IF  ∼ 5.0 × 10^− 5/day. The rates of external failure λ _IE were obtained from repair records and expert estimates as λ _EF  ∼ 4.5 × 10^− 4/day. The mean repair time to detect and to repair was estimated as E[T _r ] = 1 day for systems equipped with a control system. For the current study, we adopted these values to simplify the reliability analysis. We could show that a high reliability can be achieved with redundancies and is limited through dependencies, e.g., data transmission is not redundant. To obtain more accurate reliabilities, failure probabilities should be determined for each component and field-site individually. The inherent reliability depends on the position of the sensors in the field and warning thresholds. Sensors located in the southern section showed lower displacements (extensometers 1–2) or no movement (reflectors 10–14) and did not exceed the thresholds.

The reliability analysis in the acceleration phase is more complex, because failure probabilities of components increase significantly before the event, and because of the data quality, the forecast accuracy of the model and the risk tolerance of decision makers influence the reliability. For Preonzo, forecasts could be made with an increasing accuracy toward the actual event. Nevertheless, some sensors (Ext. 4 and 5) underestimated the acceleration and forecasted the event with a delay. As in the detachment phase, the positioning of the sensors was a crucial factor for the forecast accuracy. The reliability was high because of the multiple and redundant sensor unit. In our simulation, the days with high probability of evacuation coincide with days on which evacuations were actually initiated by the crisis team in Preonzo.

A rockfall warning system can be designed as a fail-safe system. This implies that even if the technical system fails, damage is prevented because an evacuation is initiated. But, such a fail-safe design can create a large intervention cost. We modeled the effect of the initial number of sensors and human decision-making on the effectiveness and cost in the hypothetical analysis. The behavior of the experts was replicated through simple rule-driven decisions, specified in evacuation criteria. Such an approach is novel and facilitates the quantitative assessment of warning systems that are expert-driven systems. The hypothetical analysis demonstrated that the forecast accuracy increases with the number of initial sensors and becomes maximal for risk-averse decision makers. These less risk-tolerant decision makers will create larger cost for intervention with a small number of sensors but achieve acceptable cost with a highly redundant sensor configuration.

Findings from the case study and the hypothetical analysis can be used to develop a method for quantifying the effectiveness of warning systems and will support practitioners in designing and operating cost-efficient systems. The technical and the inherent probability during the detachment phase can be modeled with Bayesian networks, similarly to the reliability of warning systems installed for processes that are triggered rapidly such as debris flows. A cost-effective warning system includes redundant sensor units with multiple measuring techniques. Sensors have a maximal coverage to ensure that precursors are detected early. They should be redundant to maintain high forecast accuracy when the number of failure increases close to the event. To detect system failures, an independently operated control system is in place. The warning thresholds in the detachment phase are low to detect significant changes, but high enough to avoid constant false alarms due to daily fluctuations, etc.

The quantification of rockfall warning systems in the detachment phase remains a major challenge. We showed an approach to model human decision-making by simple evacuation rules, but predictive models describing the forecast accuracy of the 1/v model or similar models are not available. We used the Preonzo event data from May 15 to model the forecast accuracy retrospectively. To assist decision makers in identifying an optimal risk mitigation strategy, the forecast accuracy of 1/v model must be investigated in the future. Such investigations should quantify the model accuracy with respect to the movement patterns, material characteristics, and the positioning of the sensors in the field.

Conclusion

The reliability of rockfall warning systems is quantifiable and capable of distinguishing between the detachment and acceleration phase of the rockfall process. The reliability analysis confirmed that the Preonzo rockfall warning system as installed detected the rockfall event in May 2012 and was highly reliable. We showed that with Bayesian networks, one can assess the system’s ability to generate automated warning during the detachment phase. A highly reliable system includes redundant and multiple sensor technologies, an area-wide sensor positioning, low warning thresholds in combination with a control system. During the acceleration phase, a maximal probability of evacuation on the day of the event is achieved with a sufficient number of sensors and conservative decision makers. Both factors have a considerable effect on the system effectiveness and on the related intervention cost. The effect of human decision-making could be modeled with rule-driven decision criteria. Those and other findings will be used to develop a generic framework approach that allows the quantification of the reliability and the effectiveness achieved with early warning system for natural hazards.