An alternative direct method towards mean dynamic topography computations

Abstract

An alternative “direct method” to “mean dynamic topography” (MDT) computations using satellite altimetry-derived “mean sea surface” (MSS) and “global geopotential model” (GGM), without direct application of the geoid, is devised. The developed approach, which is based on derivation of an equipotential surface of the gravity field of the Earth that fits to global MSS in least squares sense, is formulated via a constrained optimization problem. The validity of our method is numerically tested by computing a global MDT model based on DNSC08 MSS model and EGM2008 GGM as input data.

Appendices

Appendix 1

1.1 (Ellipsoidal harmonic expansion of gravity potential field of the Earth in terms of Jacobi ellipsoidal coordinates {β, λ, η})

Gravity potential field of the Earth as the additive summation of the gravitational potential U(β, λ, η) and the centrifugal potential V(β, η) can be written as follows:

$$ W\left( {\beta, \lambda, \eta } \right) = U\left( {\beta, \lambda, \eta } \right) + V\left( {\beta, \eta } \right) $$

(19)

Where the ellipsoidal harmonic expansion of the gravitational field of the Earth U(β, λ, η) as the solution of ellipsoidal Dirichlet boundary value problem in terms of Jacobi ellipsoidal coordinates {β, λ, η} reads as follows (see Ardalan 2000 for details):

$$ U\left( {\beta, \lambda, \eta } \right) = \sum\limits_{n = 0}^{{n_{\max }}} {\sum\limits_{m = - n}^n {{u_{nm}}\frac{{Q_{n\left| m \right|}^*\left( {\sinh \eta } \right)}}{{Q_{n\left| m \right|}^*\left( {\sinh {\eta_0}} \right)}}{e_{nm}}\left( {\beta, \lambda } \right)} } $$

(20)

The Jacobi ellipsoidal coordinates {β, λ, η} are related to the Cartesian coordinates {x, y, z} as follows (see Ardalan 2000 for more details):

$$ \left\{ \begin{gathered} x = \varepsilon \cosh \eta \cos \beta \cos \lambda \hfill \\y = \varepsilon \cosh \eta \cos \beta \sin \lambda \hfill \\z = \varepsilon \sinh \eta \sin \beta \hfill \\\end{gathered} \right. $$

(A21)

In Eq. 20, u _nm are the normalized ellipsoidal harmonic coefficients, and ${\eta_0} = {\cosh^{ - 1}}\left( {{a \mathord{\left/{\vphantom {a {\sqrt {{{a^2} - {b^2}}} }}} \right.} {\sqrt {{{a^2} - {b^2}}} }}} \right)$ specifies the surface of the reference ellipsoid. In Eq. 20 $Q_{n\left| m \right|}^*\left( {\sinh \eta } \right)$ are fully normalized associated Legendre functions of the second kind and e _nm (β, λ) are surface ellipsoidal harmonics with the following definition.

$$ {e_{nm}}\left( {\beta, \lambda } \right) = \left\{ \begin{gathered} P_{n\left| m \right|}^*\left( {\sin \beta } \right)\cos m\lambda \,\,\,\,\,\,\,\,\,\,m \geqslant 0 \hfill \\P_{n\left| m \right|}^*\left( {\sin \beta } \right)\sin \left| m \right|\lambda \,\,\,\,\,\,\,\,\,\,m < 0 \hfill \\\end{gathered} \right. $$

(22)

where the fully normalized $P_{n\left| m \right|}^*$ associated Legendre functions of the first kind appearing in Eq. 22 are related to associated Legendre functions of first kind ${P_{n\left| m \right|}}$ as follows:

$$ \left\{ \begin{gathered} P_{n\left| m \right|}^*\left( {\sin \beta } \right) = \sqrt {{2n + 1}} {P_{n\left| m \right|}}\left( {\sin \beta } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,m = 0 \hfill \\P_{n\left| m \right|}^*\left( {\sin \beta } \right) = \sqrt {{2\left( {2n + 1} \right)\frac{{\left( {n - m} \right)!}}{{\left( {n + m} \right)!}}}} {P_{n\left| m \right|}}\left( {\sin \beta } \right)\,\,\,\,\,\,\,\,\,\,m \ne 0 \hfill \\\end{gathered} \right. $$

(23)

The centrifugal potential in terms of Jacobi ellipsoidal coordinates can be presented as:

$$ V\left( {\beta, \eta } \right) = \frac{1}{2}{\omega^2}{\varepsilon^2}{\hbox{co}}{{\hbox{s}}^2}\beta { \cos }{{\hbox{h}}^2}\eta $$

(24)

where ω is the angular velocity of the Earth and $\varepsilon = \sqrt {{{a^2} - {b^2}}}$ is the linear eccentricity.

Appendix 2

2.1 (Computation of the coefficient matrix A defined by Eq. 9)

For calculation of ∂W/∂H we have:

$$ \frac{{\partial W}}{{\partial H}} = \frac{{\partial W}}{{\partial \beta }}\frac{{\partial \beta }}{{\partial H}} + \frac{{\partial W}}{{\partial \lambda }}\frac{{\partial \lambda }}{{\partial H}} + \frac{{\partial W}}{{\partial \eta }}\frac{{\partial \eta }}{{\partial H}} $$

(25)

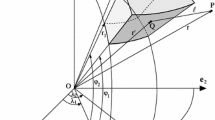
Since P and $P\prime$ in Fig. 1 are along normal to surface of reference ellipsoid, therefore (see Ardalan 2000 for details):

$$ \frac{{\partial \lambda }}{{\partial H}} = 0,\,\,\,\frac{{\partial \beta }}{{\partial H}} \doteq 0 $$

(26)

Therefore, Eq. 25 can be written as follows:

$$ \frac{{\partial W}}{{\partial H}} \doteq \frac{{\partial W}}{{\partial \eta }}\frac{{\partial \eta }}{{\partial H}} $$

(27)

where

$$ \frac{{\partial \eta }}{{\partial H}} = \frac{{\partial \eta }}{{\partial x}}\frac{{\partial x}}{{\partial H}} + \frac{{\partial \eta }}{{\partial y}}\frac{{\partial y}}{{\partial H}} + \frac{{\partial \eta }}{{\partial z}}\frac{{\partial z}}{{\partial H}} $$

(28)

where η is the Jacobi ellipsoidal coordinate which is related to the Cartesian coordinates {x, y, z} as follows (see Ardalan 2000 for more details):

$$ \eta = {\hbox{arccosh}}{\left[ {\frac{1}{{2{\varepsilon^2}}}\left( {{x^2} + {y^2} + {z^2} + {\varepsilon^2} + \sqrt {{{{\left( {{x^2} + {y^2} + {z^2} + {\varepsilon^2}} \right)}^2} - 4{\varepsilon^2}\left( {{x^2} + {y^2}} \right)}} } \right)} \right]^{\frac{1}{2}}} $$

(29)

and

$$ \begin{gathered} x = \left( {N + h - H} \right)\cos \varphi \cos \lambda \Rightarrow \frac{{\partial x}}{{\partial H}} = - \cos \varphi \cos \lambda \hfill \\y = \left( {N + h - H} \right)\cos \varphi \sin \lambda \Rightarrow \frac{{\partial y}}{{\partial H}} = - \cos \varphi \sin \lambda \hfill \\z = \left( {N\left( {1 - {e^2}} \right) + h - H} \right)\sin \varphi \Rightarrow \frac{{\partial z}}{{\partial H}} = - \sin \varphi \hfill \\\end{gathered} $$

(30)

where

$$ {e^2} = \frac{{{a^2} - {b^2}}}{{{a^2}}},\,\,\,N = \frac{a}{{\sqrt {{1 - {e^2}{{\sin }^2}\varphi }} }} $$

(31)

In Eq. 31, a is semi-major and b is semi-minor axis of the reference ellipsoid. The derivatives ∂η/∂x, ∂η/∂y, and ∂η/∂z can be readily derived by symbolic operation within, for example, “MATLAB”, “MAPLE”, or “MATHEMATICA” software. For the computation of ∂W/∂η, we refer to Ardalan (2000).