Abstract
The technique of hierarchical matrices is used to construct a solution operator for a discrete elliptic boundary value problem. The solution operator can be determined once for all from a recursive domain decomposition structure. Then, given boundary values and a source term, the solution can be evaluated by applying the solution operator. The complete procedure yields all components of the solution vector. The data size and computational cost is \(O(n\hbox {log}^{*}n),\) where \(n\) is the number of unknowns. Once the data of the solution operator are constructed, components related to small subdomains can be truncated. This reduces the storage amount and still enables a partial evaluation of the solution (restricted to the skeletons of the remaining subdomains). The latter approach is in particular suited for problems with oscillatory coefficients, where one is not interested in all details of the solution.





Similar content being viewed by others
Notes
In multi-grid methods, the restriction is applied to the right-hand side; here it is applied to the nodal points of the finite element solution.
The type of boundary condition is not really essential for the method. For other types, the arising boundary conditions in the later subdomains \(\omega \) will be of Dirichlet type for \(\partial \omega \cap \Omega \) and of the given type on \(\partial \omega \cap \Gamma \).
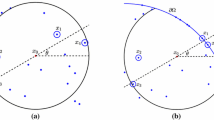
This illustration shows a regular decomposition. Of course, any kind of decomposition is possible.
Note that ‘T’ in \(T(\Omega )\) means ‘triangulation’, not ‘tree’.
The finite elements are called ‘triangles’, since this corresponds to the 2D figures. The method, however, can be used for any spatial dimension.
The notation \(a_{\omega }\) and \(f_{\omega }\) with the index \(\omega \) emphasises the integration domain which is variable.
\(\bar{V}_{h}\) is the direct sum of \(V_{h}\) and \(V_{h}(\partial \omega ),\) where the latter space is spanned by the basis functions with boundary nodal points in \(\partial \omega .\) The variation over \(w_{h}\in \bar{V}_{h}\) can be replaced by the variation over \(w_{h}\in V_{h}(\partial \omega )\), since both sides of the equation vanish for \(w_{h}\in V_{h}\).
This holds only for finite element nodes lying on the boundary of the element. If there are inner nodes (so-called bubble functions), one has still to solve for these degrees of freedom in all triangles. Since one can eliminate these degrees of freedom from the beginning, one may assume without loss of generality that only boundary nodes are present.
The three subsets are disjoint and correspond to two subdomains and one separating line. It is essential that the two subdomains are not neighboured, i.e., two indices from different the subdomains do not belong to the matrix graph. For standard FE discretisations using triangles or tetrahedra as elements this means that those points do not belong to a common element.
If no geometric data are available, a black box version can be applied which uses the graph distance and graph diameter (cf. [6]),
For isoparametric finite elements compare [9, §8.5.3].
Complete_evaluation \((\omega ,r,x)\) is equivalent to partial_evaluation \( (\omega ,G_{\Omega },r,x).\)
For all \(x\in \Omega \) the closed ball centred at \(x\) with radius \(H/2\) contains at least one point of \(\partial G_{\Omega ,H}^{\mathrm {coarse} }\,\).
When we proceed to larger subdomains or even to \(\Omega ,\) the storage requirement may increase.
References
Bebendorf, M., Hackbusch, W.: Existence of \({\cal H}\)-matrix approximants to the inverse FE-matrix of elliptic operators with \(L^{\infty }\)-coefficients. Numer. Math. 95, 1–28 (2003)
Börm, S., Grasedyck, L., Hackbusch, W.: Introduction to hierarchical matrices with applications. Eng. Anal. Bound. Elem. 27, 405–422 (2003)
Drechsler, F.: Über die Lösung von elliptischen Randwertproblemen mittels Gebietszerlegungstechniken, Doctoral thesis. Universität Leipzig, Hierarchischer Matrizen und der Methode der finiten Elemente (2011)
Grasedyck, L., Hackbusch, W.: Construction and arithmetics of \({\cal H} \)-matrices. Computing 70, 295–334 (2003)
Grasedyck, L., Kriemann, R., Le Borne, S.: Domain decomposition based \({\cal H}-LU\) preconditioners. In: Widlund, O.B., Keyes, D.E. (eds.) Domain Decomposition Methods in Science and Engineering XVI. Lectures Notes in Computational Science and Engineering, vol. 55, pp. 661–668. Springer, Berlin (2006)
Grasedyck, L., Kriemann, R.: Borne, Sabine: Parallel black box \({\cal H}-LU\) preconditioning for elliptic boundary value problems. Comput. Vis. Sci. 11, 273–291 (2008)
Hackbusch, W.: Elliptic Differential Equations, 2nd edn. Theory and numerical treatment, Springer, Berlin: (Third Germany edition: Lecture Notes 28/2005, 2005. Max-Planck-Institut für Mathematik, Leipzig (2003)
Hackbusch, W.: Multi-grid Methods and Applications, 2nd edn. Springer, Berlin (2003)
Hackbusch, W.: Elliptic Differential Equations. Theory and Numerical Treatment, SCM., Vol. 18, 2nd edn. Springer, Berlin (2003)
Hackbusch, W.: A sparse matrix arithmetic based on \({\cal H}\)-matrices. Part I: introduction to\({\cal H}\)-matrices. Computing 62, 89–108 (1999)
Hackbusch, W.: Direct domain decomposition using the hierarchical matrix technique. In: Herrera, I., Keyes, D.E., Widlund, O.B., Yates, R. (eds.) Domain decomposition methods in science and engineering. Fourteenth international conference on domain decomposition methods, pp. 39–50. National Autonomous University of Mexico, Mexico, City (2003)
Hackbusch, W.: Hierarchische Matrizen—Algorithmen und Analysis. Spinger, Heidelberg (2009)
Hackbusch, W., Khoromskij, B.N., Kriemann, R.: Direct Schur complement method by domain decomposition based on \({\cal H}\)-matrix approximation. Comput. Vis. Sci. 8, 179–188 (2005)
Hou, T.Y., Wu, X.-H.: A multiscale finite element method for elliptic problems in composite materials and porous media. J. Comput. Phys. 134, 169–189 (1997)
Hou, T.Y., Wu, X.-H., Cai, Z.: Convergence of a multiscale finite element method for elliptic problems with rapidly oscillating coefficients. Math. Comput. 68, 913–943 (1999)
Litvinenko, A.G.: Application of hierarchical matrices for solving multiscale problems, Doctoral thesis. Universität Leipzig (2007)
www.dealii.org A Finite Element Differential Equations Analysis Library
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Gabriel Wittum.
Rights and permissions
About this article
Cite this article
Hackbusch, W., Drechsler, F. Partial evaluation of the discrete solution of elliptic boundary value problems. Comput. Visual Sci. 15, 227–245 (2012). https://doi.org/10.1007/s00791-013-0211-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00791-013-0211-6