An attorney fee as a signal in pretrial negotiation

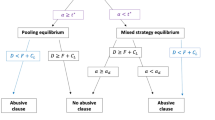
Abstract

We consider the signaling role of attorney fees which have been usually assumed as exogenous in literature. We show that there exists an equilibrium in which the informed plaintiff uses both the attorney fee and the settlement demand as signals for his damage amount. If attorney service is not productive, this equilibrium yields higher social welfare than the equilibrium involving solely the settlement demand as a signal. If attorney service is productive, however, social welfare is lower in the former equilibrium. This has a policy implication that regulating attorney fees is socially desirable if the attorney service is productive.

Appendix

Proof of Lemma 1: If $D\$rejects $s>s_H$, his loss is at most $qH+C_d \equiv s_H$, which is strictly better than accepting $s>s_H$. On the other hand, if $D\$rejects $s<s_L$, his loss at court is at least $qL+C_d \equiv s_L$, which is strictly worse than accepting $s<s_L$.

Proof of Lemma 2: First, it is not possible that $s^{*}(L)<s_{L}$ because any $s$ such that $s^{*}(L)<s< s_{L}$ would be better, since it is also accepted with probability one by Lemma 1. If $s^*(L)>s_{L}$, his equilibrium demand is rejected and he gets $qL-c_p <s_{L}$. Consider a deviation to $s_L$. Under the most pessimistic belief, $\hat{\lambda }(s_L )=0$. $D\$is indifferent between accepting $s_{L}$ and not. Thus, the payoff that the low-type $P\$is expected to get by deviating to $s_L$ is $rs_L (1-r)(qL-c_p )\ge qL-c_p$ for all $r\in [0, 1]$ with equality if and only if $r=0$. So, the deviation to $s_{L}\$is profitable. Contradiction. Now, suppose $c^* (L)>0$. A deviation to zero always saves the cost at least without affecting the posterior belief. Therefore, it must be that $c^* (L)=0$. It remains to show that $s^* (L)=s_L$ is supported by $r=1$. If $r(s_L )<1$, it is always better for a low type to demand $s_L -\epsilon$, which will be accepted with probability 1, since $s_L -\epsilon >rs_L +(1-r)(qL-c_p )$ for some small $\epsilon (>0)$. This completes the proof.

Proof of Lemma 3: Suppose that $r(s_1 )\le r(s_2 )$. Then, the type of $P\$who demands $s_1$ in equilibrium would have an incentive to deviate to $s_2$.

Proof of Lemma 4: (i) If $r(s_L )<1$, it is always better for $P\$to demand $s<s_L$ by Lemma 1. (ii) In a separating equilibrium, it must be that $s^* (H) >s_L$. If $r^* (s^* (H) )=1$, it violates Lemma 3 due to Lemma 4(i).

Proof of Lemma 5: Since $0<r^* (s^* (H))<1$ in the first case, $D\$is indifferent between accepting $s^* (H)$ and rejecting it, implying that $s^* (H) =qH+C_d \equiv s_H$. Suppose $s^* (H)<s_H$ when $r^* (s^* (H))=0$. If $D\$rejects it, his loss at court is $qH+C_d =s_H$. Therefore, $D\$strictly prefers $s^* (H)$ being accepted to his demand being rejected since $s^* (H)< s_H$. This is a contradiction to $r^* (s^* (H))=0$.

Proof of Proposition 1: First, we will find the range of equilibrium values for $r(s_H )$. If the low-type $P\$prefers demanding $s_L$ to $s_H$, the following must be satisfied. Inequality (1) implies that $r^* (s_H )\le \frac{c_{p}+C_{d}}{s_{H}-qL+c_{p}}=\frac{T}{q\Delta w +T}<1$. Also, inequality (2) implies that $r^{**}(s_H )\ge \frac{T-q\Delta w}{T}$. The two incentive compatibility conditions imply that

$$\begin{aligned} \frac{T-q\Delta w}{T}\le r^* (s_H )\le \frac{T}{q\Delta w +T}. \end{aligned}$$

We have $I\ne \emptyset$, since $\frac{T-q\Delta w}{T}<\frac{T}{q\Delta w +T}$ and $0<\frac{T}{q\Delta w +T}<1$. Hence, the proof is completed.

Proof of Lemma 6: We will show that if $r(c^* (H), s^* (H))=1$, the incentive compatibility conditions for the low type ($IC_{L}$) and the high type ($IC_{H}$) are contradictory to each other except when $s^{*}(H)-s_{L}=c^{*}(H)$. When $r(c^* (H), s^* (H))=1$, the two incentive compatibility conditions are given by

$$\begin{aligned}&s_{L}\ge s^{*}(H)-c^{*}(H), \qquad \qquad \qquad \qquad \qquad \qquad \qquad [IC1_{L}]\\&s^{*}(H)-c^{*}(H)\ge s_{L}.\qquad \qquad \qquad \qquad \qquad \qquad \qquad [IC1_{H}] \end{aligned}$$

Since both equilibrium demands are accepted with probability one, equilibrium payoffs do not depend on the true type at all in this case. Therefore, both ($IC1_{L}$) and ($IC1_{H}$) can be satisfied only when $s_{L}=s^{*}(H)-c^{*}(H)$, i.e., $s^{*}(H)-s_{L}=s^{*}(H)$. This corresponds to the trivial equilibrium. However, ($IC2_L$) and ($IC2_H$) at the demand stage require that $s_L \ge s^* (H)$ and that $s^* (H)\ge s_L$ simultaneously, which means that $s^* (H)=s_L$. This is a contradiction to $c^* (H)>0$. Therefore, $r^* (c^{*}(H), s^{*}(H))<1$.

Proof of Lemma 7: Since $D$’s decision is not affected by $c^* (H)$, the proof of Lemma 5 is exactly carried over to Lemma 7.

Proof of Proposition 2: For $I'\ne \emptyset$, $\frac{T+c^* (H) }{q\Delta w +T}>0$ or $\frac{T-q\Delta w +c^* (H) }{T}\le 1$. Also, Lemma 6 implies that $r^* =\frac{T+c^* (H) }{q\Delta w +T}<1$. Therefore, $c^{*}(H)< q\Delta w$.

Proof of Proposition 3: Let $r^*$ and $r^{**}$ be $D$’s equilibrium acceptance probability in SDE and in SFDE respectively. The difference in the equilibrium payoffs of a high-type $P\$is

$$\begin{aligned} \psi&= \left[ r^{**}(qH+C_d )+(1-r^{**})(q H-c_p )-c^* \right] \nonumber \\&-\left[ r^* (qH+C_d )+(1-r^* )(qH-c_p ) \right] \\&= (r^{**}-r^* )T-\Delta c^* . \end{aligned}$$

Since $I$ and $I'$ are not single-valued, let us evaluate the sign of difference at the corresponding $r^*$ and $r^{**}$. Then, we have

$$\begin{aligned} r^{**}(t)-r^* (t)&= (1-t) \left[ \frac{T-q\Delta w+\Delta c^{*}}{T}-\frac{T-q\Delta w}{T}\right] \nonumber \\&+t\left[ \frac{T+\Delta c^{*}}{q\Delta w+T}-\frac{T}{q\Delta w+T}\right] \\&= (1-t)\frac{\Delta c^{*}}{T}+ t\frac{\Delta c^{*}}{q\Delta w+T} \\&< \frac{\Delta c^{*}}{T}. \end{aligned}$$

Therefore, $\psi (t) =(r^{**}(t)-r^* (t))T-\Delta c^{*}\le \Delta c^{*}-\Delta c^{*} =0$ for all $t\in [0, 1]$.

Finally, the difference in social welfare is $\Delta W (t)= \psi (t) +\Delta c^{*} = (r^{**}(t)-r^* (t))T> 0$.

Proof of Proposition 4: To apply D1 criterion, define the following two sets for an off-the-equilibrium message $(c, s)$;

$$\begin{aligned} D(w, c, s)&= \left\{ r\in [0,1]\mid U_{P}^{*}(w)< U_P (c, s, r, w)\right\} ,\\ D_0 (w,c, s)&= \left\{ r\in [0,1]\mid U_{P}^{*}(w)= U_P (c, s, r, w)\right\} . \end{aligned}$$

$D(w, c, s )$ is the set of $D$’s strategies that make $w$-type $P\$it profitable to demand $s$, and $D_0 (w, c, s )$ is the set of $D$’s strategies that make $w$-type $P\$indifferent between the equilibrium combination of fee and demand $(c^* , s^* )$ and the off-the-equilibrium combination $(c, s)$. If there exists a type $w'\ne w$ such that $D(w, c, s )\cup D_0 (w, c, s )\subset D(w', c, s )$, type $w'$ is more likely to deviate to $(c, s)$ than type $w$ and assign the posterior belief zero to type $w$.

Now, we will apply D1 criterion to separating equilibria.

Claim 1

Vacuous SDE do not satisfy D1 criterion.

Proof of Claim 1. Consider vacuous demand equilibria. For a deviant demand $s=s_H -\epsilon$, define $r_0 (H, s)$ by the value of $r$ satisfying

$$\begin{aligned} rs+(1-r)(qH-c_p )=qH-c_p . \end{aligned}$$

(17)

This holds for $r=0$ and for all other values of $r$, the left-hand side is greater than the right-hand side. Thus, $r_0 (H, s)=0$. On the other hand, $r_0 (L, s)$ is determined by

$$\begin{aligned} rs+(1-r)(qL-c_p )=qL+C_d . \end{aligned}$$

(18)

It is easy to see that $r_0 (L, s) \in (0, 1)$. Therefore, it directly follows that $D(L, c, s)\cup D_0 (L, c, s)\subset D(H, c, s)$, implying that $s$ comes from a high type. This subverts the equilibrium. This completes the proof.

Claim 2

No SFDE satisfy D1 criterion.

Proof of Claim 2: Consider an out-of-equilibrium message $\mathbf {m'}=(s_H , 0)$. Similarly, $r_0 (H, \mathbf {m'})$ and $r_0 (L, \mathbf {m'})$ can be found from

$$\begin{aligned} r s_H +(1-r)( q H-c_p ) =r^* s_H +(1-r^* )(qH -c_p ) -c^* (H) , \end{aligned}$$

(19)

$$\begin{aligned} rs_H +(1-r)(qL-c_p ) = s_L , \end{aligned}$$

(20)

respectively. If $r^* =\frac{T+c^{*}(H)}{q\Delta w+T}$ is the upper bound of $I'$ so that the low-type $P\$is indifferent between the two equilibrium strategies, we have

$$\begin{aligned} r^* s_H +(1-r^* )(qL -c_p ) -c^* (H)=s_L . \end{aligned}$$

(21)

By using Eqs. (21), (20) can be rewritten as

$$\begin{aligned} rs_H +(1-r)(qL-c_p ) = r^* s_H +(1-r^* )(qL -c_p ) -c^* (H) . \end{aligned}$$

(22)

Comparing Eqs. (19) and (22) yields $r_0 (L, \mathbf {m'})>r_0 (H, \mathbf {m'})$. Thus, D1 criterion requires that $\hat{\lambda }(\mathbf {m'})=1$. This implies that a high-type $P\$has an incentive to deviate from the equilibrium by cutting the attorney fee to $0$. Therefore, the equilibria do not satisfy D1 criterion. If $r^* =\frac{T-q\Delta w +c^{*}(H)}{T}$ is the lower bound of $I'$ so that the high-type $P\$is indifferent between two equilibrium strategies, we can easily check that $r_0 (L, \mathbf {m'})>r_0 (H, \mathbf {m'})$ in a similar way. Since Eqs. (19) and (20) are linear in $r$ and $r^*$, this inequality holds for all $r^* \in I$.

It remains to show that only the meaningful demand equilibrium with $r^* =\frac{T}{q\Delta w +T}$ survives D1 criterion. Consider an off-the-equilibrium demand $s\in (s_L , s_H )$. Similarly defined $r_0 (H, s)$ and $r_0 (L, s)$ can be found by

$$\begin{aligned} rs+(1-r)(qH-c_p )=r^* s_H +(1-r^* )(qH-c_p ), \end{aligned}$$

(23)

$$\begin{aligned} rs+(1-r)(qL-c_p )=s_L , \end{aligned}$$

(24)

respectively, yielding $r_0 (H, s)=\frac{r^{*}T}{s-qH+c_{p}}$ and $r_0 (L, s)=\frac{T}{s-qL+c_{p}}$. Now, to support the equilibrium, the belief must be that $s$ comes from a low type and, accordingly rejected. Thus, according to D1 criterion, this requires $r_0 (H, s)>r_0 (L, s)$, i.e., $r^* \ge \frac{s-qH+c_{p}}{s-qL+c_{p}}\equiv h(s)$ for all $s\in (s_L , s_H )$. Since $h'(s)>0$, $r^* \ge h(s_H )=\frac{T}{q\Delta w+C_{d}}$. This means that $r^* = h(s_H )=\frac{T}{q\Delta w+C_{d}}$ is the only equilibrium acceptance probability that survives D1 criterion.

Proof of Lemma 8: Comparing the maximum payoff of a high-type $P\$and a low-type $P$, we have

$$\begin{aligned} q(c_{H}^{f})H+C_d -c_{H}^{f} >q(c_{L}^{f})L+C_d -c_{L}^{f}, \end{aligned}$$

implying that $q(c_{H}^{f})H-q(c_{L}^{f})L>c_{H}^{f}-c_{L}^{f}$.

Proof of Proposition 5: It suffices to show that a high-type $P\$has no incentive to deviate from $c_L$. The most profitable deviation given his demand is accepted is to maximize $q(c)L+C_d -c$ which is to choose $c^* (L)=c_L$. This is a contradiction to $c^* (L)\ne c_L$. Thus, his demand must be rejected and the most profitable deviation is to maximize $q(c)H-c_p -c$ as to choose $c_H$ and then demand, say, $q_H H+C_d$ that will be rejected. Then, he gets $q_H H-c_p - c_H$. Since he gets $q_L H+C_d -c_L$ in equilibrium, he does not deviate if $q_L H+C_d -c_L \ge q_H H-c_p -c_H$, i.e., $T\ge q_H H-q_L H -\Delta c >0$.

Proof of Proposition 6: A high-type $P\$can deviate to $c_H$ most profitably and is perceived to be a low-type. Then, the incentive compatibility conditions require

$$\begin{aligned} r^* (q_{H}^{*} H+C_d )+(1-r^* )(q_{H}^{*} H-c_p )-c^* (H)\ge \max \{ q_L L +C_d , q_H H -c_p \}-c_H , \end{aligned}$$

(25)

$$\begin{aligned} r^* (q_{H}^{*} H+C_d )+(1-r^* ) (q_{H}^{*} L-c_p )-c^* (H)\le q_L L+C_d -c^* (L). \end{aligned}$$

(26)

The right hand side of inequality (25) is $q_L L +C_d$ if $q_L L +C_d \ge q_H H -c_p$, i.e., $q_H H -q_L L \ge T$, and $q_H H -c_p$ otherwise. In the former case, a high-type $P\$asks $s^* (L)=q_L L +C_d$ which is accepted with probability one, and in the latter case, he asks any $s>s^* (L)$ which is rejected with probability one. In the former case, these imply that

$$\begin{aligned} \frac{T-(q_{H}^* H-q_{L}L)+c^{*}(H)-c^{*} (L) }{T}\le r^* \le \frac{T-(q_{H}^* -q_{L})L+c^{*}(H)-c^{*} (L) }{q_{H}^* (H-L)+T}. \end{aligned}$$

(27)

Then, due to Lemma 8, $0<r^* <1$ in any equilibrium. Non-emptyness of $J'$ requires that $\frac{T-(q_{H}^* H-q_{L}L)+c^{*}(H)-c^{*} (L) }{T}<1$, i.e., $q_{H}^* H-c^{*}(H)>q_L L-c^* (L)$. This implies that $c^* (H)<\hat{c}$. Therefore, it must be $c^* (H)\in (c_L , \hat{c})$ in a SFDE. In the latter case, we obtain

$$\begin{aligned} \frac{q_{H}H -c_{H}-(q_{H}^* H-c^{*}(H))}{T}\le r^* \le \frac{T-(q_{H}^* -q_{L})L+c^{*}(H)-c^{*} (L) }{q_{H}^* (H-L)+T}.\nonumber \\ \end{aligned}$$

(28)

Since $\lim _{T\rightarrow 0}\hbox {LHS}=0$ and $\lim _{T\rightarrow 0}\hbox {RHS}=\frac{ q_{L}L-c^{*} (L) -(q_{H}^{*}L -c^{*}(H))}{q_{H}^* (H-L)} >0$, there exists $\underline{T}>0$ such that $\hbox {LHS}<\hbox {RHS}$ so that $J'\ne \emptyset$, and thus $J''\ne \emptyset$ for all $T\ge \underline{T}$.

Proof of Proposition 7: (i) First, we compare the upper bound of the equilibrium acceptance probability. The difference is

$$\begin{aligned} \Xi&= r^{**}-r^* \nonumber \\&= \frac{T-(\Delta q)L+\Delta c^{*}}{q_{H}^* y+T}-\frac{T}{q_{L}y+T}\nonumber \\&= \frac{T-\phi (L)}{q_{H}^{*}y+T}-\frac{T}{q_{L}y+T}\nonumber \\&= \left( \frac{T}{q_{H}^{*}y+T}-\frac{T}{q_{L}y+T}\right) -\frac{\phi (L)}{q_{H}^{*}y+T}<0 \end{aligned}$$

(29)

where $y=H-L$, $\phi (w)=(\Delta q)w-\Delta c^{*}$ and $\Delta q=q_{H}^{*}-q_L$.

(ii) Let $P$’s payoff in SFDE and in SDE be $\pi ^{**}$ and $\pi ^*$. Then, we have

$$\begin{aligned} \pi ^{**}-\pi ^*&= \phi (H)+(r^{**}-r^* )T\\&= \phi (H)-\frac{T}{q_{H}^{*}y+T}\phi (L)+\left( \frac{1}{q_{H}^{*}y+T}-\frac{1}{q_{L}y+T}\right) T^2 \\&= \frac{q_{H}^{*}y\phi (H)+\Delta q yT}{q_{H}^{*}y+T}-\frac{\Delta q y T^{2}}{(q_{H}^{*}y+T)(q_{L}y+T)}\\&> \frac{q_{H}^{*}y\phi (H)}{q_{H}^{*}y+T}>0 \end{aligned}$$

since $\frac{T}{q_{L}y+T}<1$. Comparison of $D$’s payoffs can be similarly made.

(iv) The social welfare can be defined by $W=U_P +U_D +U_A$ where $U_A$ is the attorney’s payoff. Considering that the attorney fee and the settlement demand are of zero-sum nature, the result is immediate from (i).

Proof of Proposition 8: (i) First, we will show that no SDE satisfies D1 criterion. Consider a deviation to $\mathbf {m}= ( c_H , q_H H+C_d )$. Similarly, $r_0 (H, \mathbf {m})$ and $r_0 (L, \mathbf {m})$ can be defined from

$$\begin{aligned} r (q_H H+C_d ) +(1-r)( q_H H-c_p )- c_H =r^* (q_L H +C_d ) +(1-r^* )(q_L H -c_p ) -c_L , \end{aligned}$$

(30)

$$\begin{aligned} r(q_H H+C_d )+(1-r)(q_H L-c_p )- c_H = q_L L+C_d -c_L , \end{aligned}$$

(31)

respectively. Since the low-type $P\$is indifferent between $\mathbf {m_H} = (c_L , q_L H+C_d )$ and $\mathbf {m_L} =(c_L , q_L L+C_d )$ in the equilibrium with the highest equilibrium $r^*$, Eq. (31) can be rewritten as

$$\begin{aligned} r(q_H H+C_d )+(1-r)(q_H L-c_p )-c_H&= r^* (q_L H+C_d ) \nonumber \\&+(1-r^* )(q_L L -c_p ) -c_L.\qquad \end{aligned}$$

(32)

To compare $r_{0} (H, \mathbf {m})$ and $r_0 (L, \mathbf {m})$, Eqs. (30) and (32) can be rewritten as

$$\begin{aligned} r (q_H H+C_d ) + (1-r)( q_H w-c_p )&= r^* (q_L H + C_d \nonumber \\&+\Delta c) + (1-r^* )(q_L w -c_p + \Delta c),\qquad \end{aligned}$$

(33)

where $w=H, L$. To compare $r_{0} (H, \mathbf {m})$ and $r_0 (L, \mathbf {m})$, first note that $r<r^*$ for $w=H$ because $q_H H-c_H >q_L H -c_L$ i.e., $q_H H >q_L H +\Delta c$. If $r\ge r^*$ for $w=L$, clearly $r_{0}(H, \mathbf {m})<r_0 (L, \mathbf {m})$. If $r<r^*$, differentiating (33) yields $\frac{dr}{dw}=\frac{(1-r^{*})q_{L}-(1-r)q_{w}}{T}<0$, implying that $r_{0}(H, \mathbf {m})<r_0 (L, \mathbf {m})$. Thus, D1 criterion requires that $\hat{\lambda }(\mathbf {m})=1$. This implies that a high-type $P\$has an incentive to deviate from the equilibrium by increasing the attorney fee to $c^f (H)$. Therefore, the equilibria do not satisfy D1 criterion.

(ii) We will show that any fee-demand equilibrium cannot satisfy D1 criterion unless $c^* (H)=c_H$. Consider an off-the-equilibrium message $\mathbf {m}=(c_H , q_H H+C_d )$. The borderlines $r$ of each type, $r_0 (H, \mathbf {m})$ and $r_0 (L, \mathbf {m})$ are defined by

$$\begin{aligned}&r (q_H H+C_d ) +(1-r)( q_H H-c_p )- c_H =r^* (q(c) H +C_d )\nonumber \\&\quad +\,\,(1-r^* )(q(c )) H -c_p ) -c , \end{aligned}$$

(34)

$$\begin{aligned}&r(q_H H+C_d )+(1-r)(q_H L-c_p )- c_H = q_L L+C_d -c_L \end{aligned}$$

(35)

respectively, where we abuse the notation of $c=c^* (H)$. Similarly, by using the indifference condition of the low-type $P$, Eq. (35) can be rewritten as

$$\begin{aligned} r(q_H H+C_d )+(1-r)(q_H L-c_p )- c_H&= r^* (q(c) H+C_d )\nonumber \\&+\,\,(1-r^*)(q(c) L -c_p ) -c.\qquad \end{aligned}$$

(36)

Equations (34) and (36) can be rewritten as

$$\begin{aligned} r(q_H H +C_d )+(1-r)( q_H w-c_p )&= r^* (q(c) w +C_d +c_H -c ) \nonumber \\&+\,\, (1-r^* )(q(c) w -c_p +c_H -c ),\qquad \end{aligned}$$

(37)

where $w=H, L$. Since $q_H H>q(c)H +c_H - c$ for any $c\ne c_H$, $r<r^*$ for $w=H$. If $r\ge r^*$ for $w=L$, it directly follows that $r_{0}(H, \mathbf {m})<r_0 (L, \mathbf {m})$. If $r< r^*$ for $w=L$, differentiation of (37) yields

$$\begin{aligned} \frac{dr}{dw}=\frac{(1-r^{*})q(c)-q_{H}(1-r)}{q_{H}H -q_{H}w+T}. \end{aligned}$$

This implies that $r_{0}(H, \mathbf {m})<r_0 (L, \mathbf {m})$. Thus, D1 criterion requires that $\hat{\lambda }(\mathbf {m})=1$. Therefore, the equilibria do not satisfy D1 criterion unless $c^* (H)=c_H$.

Proof of Proposition 9: It is sufficient to focus on the case of productive legal services. Two incentive compatibility conditions are given by

$$\begin{aligned} s^* (L)-c^* (L)&\ge r^* (s^* (H) )(s^* (H)-c^* (H)) \nonumber \\&+(1-r^* (s^* (H) ))\left[ q_{H}^{*}L-(1-q_{H}^{*})(c^* (H)+T)\right] , \end{aligned}$$

(38)

$$\begin{aligned} s^* (L)-c^* (L)&\le r^* (s^* (H) )(s^* (H)-c^* (H)) \nonumber \\&+(1-r^* (s^* (H) ))\left[ q_{H}^{*}H-(1-q_{H}^{*})(c^* (H)+T)\right] . \end{aligned}$$

(39)

Simplifying (12) and (13) by using $s^* (L)=q_L (L+c^* (L)+T)$ and $s^* (H)=q_{H}^{*} (H+c^* (H) +T)$, we have

$$\begin{aligned}&\frac{T-c^{*}(H)-c^{*}(L)- (q_{H}^{*}H-q_{L}L)-\nabla }{T}\nonumber \\&\qquad \le r^* (s^* (H))\le \frac{T-c^{*}(H)-c^{*}(L)- (q_{H}^{*}-q_{L})L-\nabla }{q_{H}^{*}(H-L)+T}, \end{aligned}$$

(40)

where $\nabla =q_{H}^{*}(C^{*}(H)+T)-q_{L}(c^{*}(L)+T)$. Since $\nabla >0$, we can conclude that $r^* (s^* (H))$ is lower under the British fee system by comparing (40) with (29).