Reeb Graphs: Approximation and Persistence

Abstract

Given a continuous function f:X→ℝ on a topological space X, its level set f ⁻¹(a) changes continuously as the real value a changes. Consequently, the connected components in the level sets appear, disappear, split and merge. The Reeb graph of f summarizes this information into a graph structure. Previous work on Reeb graph mainly focused on its efficient computation. In this paper, we initiate the study of two important aspects of the Reeb graph, which can facilitate its broader applications in shape and data analysis.

The first one is the approximation of the Reeb graph of a function on a smooth compact manifold M without boundary. The approximation is computed from a set of points P sampled from M. By leveraging a relation between the Reeb graph and the so-called vertical homology group, as well as between cycles in M and in a Rips complex constructed from P, we compute the H ₁-homology of the Reeb graph from P. It takes O(nlogn) expected time, where n is the size of the 2-skeleton of the Rips complex. As a by-product, when M is an orientable 2-manifold, we also obtain an efficient near-linear time (expected) algorithm for computing the rank of H ₁(M) from point data. The best-known previous algorithm for this problem takes O(n ³) time for point data.

The second aspect concerns the definition and computation of the persistent Reeb graph homology for a sequence of Reeb graphs defined on a filtered space. For a piecewise-linear function defined on a filtration of a simplicial complex K, our algorithm computes all persistent H ₁-homology for the Reeb graphs in $O(n n_{e}^{3})$ time, where n is the size of the 2-skeleton and n _e is the number of edges in K.

1 Introduction

Given a topological space X and a continuous scalar function f:X→ℝ, the set {x∈X:f(x)=a} is a level set of f for some value a∈ℝ. The level sets of f may have multiple connected components. The Reeb graph of f is obtained by continuously collapsing each connected component in the level set into a single point. Intuitively, as a changes continuously, the connected components in the level sets appear, disappear, split and merge; and the Reeb graph of f tracks such changes. Hence, the Reeb graph provides a simple yet meaningful abstraction of the input scalar field. It has been used in a range of applications in computer graphics and visualization; see, for example, the survey [3] and references therein on applications of Reeb graph.

Our Results

Most of the previous work on the Reeb graph focused on its efficient computation. In this paper, we initiate the study of two questions related to Reeb graphs both of which are important in shape and data analysis applications.

The first question is concerned with the approximation of the Reeb graph from a set of points sampled from a hidden manifold. It turns out that the Reeb graph homology is also related to the so-called vertical homology groups. These relations enable us to develop an efficient algorithm to approximate the Reeb graph of the manifold from its point samples.

As a by-product of our approximation result, we also obtain a near-linear time algorithm that computes the first Betti number β ₁(M) of an orientable smooth compact 2-manifold M without boundary from its point samples. This result may be of independent interest even though the correctness of our algorithm needs a slightly stronger condition than the previous best-known approach for computing β ₁(M) from point data. In particular, it is shown in [1] that β ₁(M) can be computed as the first Betti number of a certain Rips complex constructed out of the input data.¹ A straightforward computation of Betti numbers of the Rips complex using Smith normal form [23] takes cubic time whereas our algorithm runs in near-linear expected time.

The second question we study concerns with the definition and computation of loops in Reeb graphs which remain “persistent” as its defining domain “grows”. We propose a definition of the persistent Reeb graph homology for a sequence of Reeb graphs. They are computed for a function defined on a filtered space in the same spirit as the standard persistent homology [19]. Interestingly, this problem does not seem to be easier than computing the standard persistent homology, potentially due to the fact that the domains in question (the sequence of Reeb graphs) do not have an inclusion between them, as was the case for standard persistence homology.

Related Work

As mentioned already, most previous work on the Reeb graph focused on its efficient computation. Shinagawa and Kunii [26] presented the first provably correct algorithm to compute Reeb Graphs for a triangulation of a 2-manifold in Θ(m ²) time where m is the number of vertices in the triangulation. Cole-McLaughlin et al. [11] improved the running time to O(mlogm). Tierny et al. [27] proposed an algorithm that computes the Reeb graph for a 3-manifold with boundary embedded in ℝ³ in time O(nlogn+hn), where h is number of independent loops in the Reeb graph. For a piecewise-linear function defined on an arbitrary simplicial complex, a simple algorithm is proposed in [15] that runs in time O(nlogn+L), where L=Θ(nm) is the total complexity of all level sets passing through critical points. Doraiswamy and Natarajan [16] extended the sweeping idea to compute the Reeb graph in O(nlogn(loglogn)³) time from an arbitrary simplicial complex, where n is the size of the 2-skeleton of this simplicial complex. A streaming algorithm was presented in [25] to compute the Reeb graph for an arbitrary simplicial complex in an incremental manner in Θ(nm) time. Recently, Harvey et al. [20] presented an efficient randomized algorithm to compute the Reeb graph for an arbitrary simplicial complex in O(nlogm) expected running time. The Reeb graph for a time-varying function defined on a 3-dimensional space was studied in [18].

Recently a flurry of research has been initiated on estimating topological information from point data, such as computing ranks of homology groups [8], cut locus [13], and the shortest set of homology loops [14]. In [6], Chazal et al. initiated the study of approximating topological attributes of scalar functions from point data, and showed that the standard persistent diagram induced by a function can be approximated from input points. This result was later used in [7] to produce a clustering algorithm with theoretical guarantees. The results from [6, 7] can be used to approximate loop-free Reeb graphs (also called contour trees) from point data, thus providing a partial solution to our first question. However, it is unclear how to approximate loops in the Reeb graph which correspond to a subset of essential loops in the input domain which represent a subgroup of H ₁-homology.

2 Background and Notations

Homology

A homology group of a topological space X encodes its topological connectivity. We consider the simplicial homology group if X is a simplicial complex, and consider the singular homology group otherwise, both denoted with H _p (X) for the pth homology group. The definitions of these two homology groups can be obtained from any standard book on algebraic topology. Here we single out the concepts of p-chains and p-cycles in singular homology whose definitions are not as widely known in computational geometry as their simplicial counterparts. See [21, 23] for detailed discussions on this topic.

A singular p-simplex for a topological space X is a continuous map σ from the standard p-simplex Δ^p⊂ℝ^p to X. For example, a 1-simplex σ is a continuous map σ:[0,1]→X. A p-chain is a formal sum of singular p-simplices. A singular p-cycle in X is a p-chain whose boundary is a zero (p−1)-chain. Therefore, technically speaking, a p-chain or a p-cycle for X is a formal sum of maps. In this paper we will only deal with 1-chains and 2-chains. Let a loop refer to a continuous map $\mathbb{S}^{1} \rightarrow\mathsf{X}$ or a finite union of such maps. For any 1-cycle α=σ ₁+⋯+σ _k , there is a corresponding loop ϕ whose image in X coincides with the disjoint union of images σ _i ([0,1]), for i∈[1,k] (see pp. 108–109 in [21]). We call this loop the carrier of α, and that α is carried by loop ϕ. All singular 1-cycles carried by the same loop are homologous. Hence, in the remainder of the paper, we sometimes abuse the notations slightly and talk about a loop as if it is a 1-cycle. For example, we will say that two loops are homologous which means that cycles carried by these two loops are homologous.

We assume that X is compact and triangulable. Its simplicial homology defined by a triangulation identifies to its singular homology. We also assume that the homology groups are defined over $\mathrm{\mathbb{Z}}_{2}$ coefficients. Since $\mathrm{\mathbb {Z}}_{2}$ is a field, H _p (X) is a vector space of dimension p. It will be clear from the context whether we are talking about simplicial or singular homology of X. Unless specified, we assume singular homology for X. Let Z _p (X) denote the pth cycle group in X. A continuous map Φ:X ₁→X ₂ between two topological spaces induces a map among its chain groups which we denote as Φ _#. Clearly, Φ _# provides a map from the cycle group Z _p (X ₁) to the cycle group Z _p (X ₂) which in turn induces a homomorphism Φ _∗:H _p (X ₁)→H _p (X ₂).

Horizontal and Vertical Homology

Following [9], we now extend the standard homology to the so-called horizontal and vertical homology with respect to a function f:X→ℝ. Given a continuous function f, its level sets and interval sets are defined by X _a :=f ⁻¹(a) and X _I :=f ⁻¹(I) for a∈ℝ and for an open or closed interval I⊆ℝ, respectively. From now on we sometimes omit the use of f when its choice is clear from the context.

A homology class ω∈H _p (X) is horizontal if there exists a discrete set of iso-values {a _i } such that ω has a pre-image under the map $\mathsf{H}_{p}( \bigcup_{i} \mathsf{X}_{a_{i}}) \rightarrow\mathsf{ H}_{p}(\mathsf{ X})$ induced by inclusion. The set of horizontal homology classes form a subgroup $\overline{\mathsf{H}}_{p}(\mathsf{X})$ of H _p (X) since the trivial homology class is horizontal, and the addition of any two horizontal homology class is still horizontal. We call this subgroup $\overline{\mathsf{ H}}_{p}(\mathsf{ X})$ the horizontal homology group of X with respect to f. The vertical homology group of X with respect to f is defined as:

$$\breve{\mathsf{ H}}_p(\mathsf{ X}):= \mathsf{ H}_p( \mathsf{ X})/\overline{\mathsf{ H}}_p(\mathsf{ X}),\quad \mbox{the quotient of $\mathsf{ H}_{p}(\mathsf{ X})$ with $\overline{\mathsf{ H}}_{p}(\mathsf{ X})$}. $$

The coset $\omega+\overline{\mathsf{ H}}_{p}(\mathsf{ X})$ for every class ω∈H _p (X) provides an equivalence class in $\breve{\mathsf{ H}}_{p}(\mathsf{ X})$. We call ω a vertical homology class if $\omega+\overline{\mathsf{ H}}_{p}(\mathsf{ X})$ is not identity in $\breve {\mathsf{ H}}_{p}(\mathsf{ X})$. In other words, $\omega\not\in\overline{\mathsf{ H}}_{p}(\mathsf{ X})$. Two homology classes ω ₁ and ω ₂ are vertically homologous if $\omega_{1} + \omega_{2}\in\overline{\mathsf{ H}}_{p}(\mathsf{ X})$.

We percolate the definitions from the homology classes to cycles. A cycle α is horizontal if [α], the standard homology class represented by α, is a horizontal class. Two cycles α ₁ and α ₂ are vertically homologous if [α ₁] and [α ₂] are vertically homologous. Obviously, two p-cycles α ₁ and α ₂ are vertically homologous if and only if there is a (p+1)-chain B such that ∂B+α ₁+α ₂ is a horizontal cycle. See the torus in the below figure for an example, where α ₂ is a horizontal cycle as it is homologous to α ₃ carried by a loop contained in a connected component of a level set; while α ₁ is a vertical cycle, i.e., [α ₁] is a vertical homology class. We say that {α ₁,…,α _k } is a set of base cycles for H _p (X) if {[α ₁],…,[α _k ]} form a basis for H _p (X). A set of base cycles for $\overline{\mathsf{ H}}_{p}(\mathsf{ X})$ and $\breve {\mathsf{ H}}_{p}(\mathsf{ X})$ are defined analogously.

Finally, the range of a loop γ⊆X, denoted by range(γ), is the interval [min _x∈γ f(x),max _x∈γ f(x)]. The height of this loop, height(γ), is simply the length of range(γ). We extend the definitions of range and height to cycles by saying that range(α)=range(γ) and height(α)=height(γ) where the cycle α∈Z ₁(X) is carried by the loop γ. The height of a homology class ω, denoted by height(ω), is the minimal height of any cycle in this class. Notice that the height of a horizontal class ω is not necessarily zero since ω may be the addition of multiple height-0 horizontal classes.

Reeb Graph

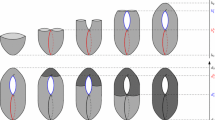
Given a triangulable topological space X and a continuous function f:X→ℝ, we say that two points x,y∈X are equivalent, denoted by x∼y, if and only if x and y belong to the same connected component of X _a for some a∈ℝ. Consider the quotient space X _∼ which is the set of equivalence classes equipped with the quotient topology induced by this equivalence relation; X _∼ is also called the Reeb graph of X with respect to f, denoted by Rb _f (X). See Fig. 1 (a) and (b) for an example.

Fig. 1

(a) X is a solid torus and its Reeb graph w.r.t. the height function f is shown in (b). (c) f is a level-set-tame function w.r.t. discrete values {c ₁,…,c ₆}. There is a continuous map $\mu: \mathsf{ X}_{\mathrm{c}}\times\allowbreak[0,1] \rightarrow\mathsf{ X}_{[\mathrm{c}_{3}, \mathrm{c}_{4}]}$ whose restriction to the open set X _c×(0,1) is a homeomorphism. In the top row, there are three disjoint interval-components in $\mathsf{ X}_{(c_{3},c_{4})}$ whose closures may intersect in level sets $\mathsf{ X}_{\mathrm{c}_{3}}$ and $\mathsf{ X}_{\mathrm{c}_{4}}$

An alternative way to view the Reeb graph is that there is a natural continuous surjection Φ:X→X _∼ where Φ(x)=Φ(y) if and only if x and y come from the same connected component of a level set of f. In this sense, Rb _f (X) is obtained by continuously identifying each connected component. The map Φ induces a scalar function $\tilde{f}:\mathsf{ Rb}_{f}(\mathsf{ X}) \rightarrow\mathbb{R}$ where $\tilde{f}(p) = f(x)$ if p=Φ(x). Since f(x)=f(y) whenever Φ(x)=Φ(y), the function $\tilde{f}$ is well-defined. Since f is continuous, so is $\tilde{f}$. The range or height of a loop in Rb _f (X) is measured with respect to this function $\tilde{f}$. In this paper, we also use f to refer to $\tilde{f}$ for simplicity.

3 Reeb Graphs and Vertical Homology

In this section, we show that H ₁(Rb _f (X)) and the first vertical homology group $\breve{\mathsf{ H}}_{1}(\mathsf{ X})$ of X are isomorphic. This relation is observed for 2-manifolds in [9], but, to the best of our knowledge, it has not been formally introduced and proved anywhere yet for general topological spaces. We include it here for completion.

The surjection Φ:X→Rb _f (X) induces a chain map Φ _# from the 1-chains of X to the 1-chains of Rb _f (X) which eventually induces a homomorphism Φ _∗:H ₁(X)→H ₁(Rb _f (X)). For the horizontal subgroup $\overline{\mathsf{ H}}_{1}(\mathsf{ X})$, we have $\varPhi_{*}(\overline{\mathsf{ H}}_{1}(\mathsf{ X})) = \{ 0 \} \subseteq \overline{\mathsf{ H}}_{1}(\mathsf{ Rb}_{f}(\mathsf{ X}))$. Hence Φ _∗ induces a well-defined homomorphism between the quotient groups

$$\check{\varPhi}: \breve{\mathsf{ H}}_1(\mathsf{ X}) = \frac{\mathsf{ H}_1(\mathsf{ X})}{\overline{\mathsf{ H}}_1(\mathsf{ X})} \rightarrow\frac{\mathsf{ H}_1(\mathsf{ Rb}_f(\mathsf{ X}))}{\overline{\mathsf{ H}}_1(\mathsf{ Rb}_f(\mathsf{ X}))} = \mathsf{ H}_1\bigl( \mathsf{ Rb}_f(\mathsf{ X})\bigr). $$

The right equality above follows from that $\overline{\mathsf{ H}}_{1}(\mathsf{ Rb}_{f}(\mathsf{ X})) = \{ 0\}$, which holds because every level set of Rb _f (X) consists only of a set of disjoint points. In what follows, we show that $\check{\varPhi}$ is an isomorphism under some mild conditions. Intuitively, this is not surprising as Φ maps each contour in the level set to a single point, which in turn also collapses every horizontal cycle.

For technical reasons, we consider functions that behave nicely. Specifically, we call a continuous function f:X→ℝ level-set-tame if there exist finite number of discrete values {c ₁,…,c _k } so that the following holds: for any two consecutive c _i and c _i+1, (i) there is a homeomorphism $\mu_{i}: \mathsf{ X}_{c} \times(0,1) \rightarrow\mathsf{ X}_{(c_{i}, c_{i+1})}$ for an arbitrary c∈(c _i ,c _i+1); and (ii) the homeomorphism μ _i can be extended to a continuous map $\mu_{i}: \mathsf{ X}_{c} \times[0,1] \rightarrow X_{[c_{i}, c_{i+1}]}$. In this case, we also say that f is level-set-tame w.r.t. the set of discrete values {c ₁,…,c _k }; note that the choice of c _i s and μ _i s are not unique. See Fig. 1(c) for an example. It can be shown that Morse functions on a compact smooth manifold and piecewise-linear functions on a finite simplicial complex are both level-set-tame functions.

First, we prove the following result, which implies that the map $\check{\varPhi}: \breve{\mathsf{ H}}_{1}(\mathsf{ X}) \rightarrow\mathsf{ H}_{1}(\mathsf{ Rb}_{f}(\mathsf{ X}))$ as introduced above is injective.

Lemma 3.1

Let f:X→ℝ be a level-set-tame function, and Φ,Φ _∗ as defined before. Then we have $\operatorname{ker}(\varPhi_{*}) = \overline{\mathsf{ H}}_{1}(\mathsf{ X})$ where $\operatorname{ker}(\varPhi_{*})$ denotes the kernel of Φ _∗.

Proof

Since Φ maps all points in the same connected component in a level set of f into a single point, we have $\overline{\mathsf{ H}}_{1}(\mathsf{ X}) \subseteq\operatorname{ker}(\varPhi_{*})$. Hence we now focus on proving the opposite direction $\operatorname{ker}(\varPhi_{*}) \subseteq\overline{\mathsf{ H}}_{1}(\mathsf{ X})$. That is, for any homology class h∈H ₁(X), if Φ _∗(h)=0, then $h \in\overline{\mathsf{ H}}_{1}(\mathsf{ X})$. Specifically, take a loop γ⊆X carrying a cycle from the class h. We will show that there exists a loop ${\widehat {\gamma}}$ which is contained in the union of a discrete set of level sets and which is homologous to γ. This will then imply that h is horizontal.

Assume without loss of generality that γ is the image of a map $\mathbb{S}^{1} \rightarrow\mathsf{ X}$; the case when γ is a finite union of such images can be handled by applying the following proof to each image of $\mathbb{S}^{1}$.

Let {c ₁,…,c _k } be a set of discrete values with respect to which f is level-set-tame. Fix an arbitrary interval [c _z,c _z+1] and any c∈(c _z,c _z+1). By definition of a level-set-tame function, there exists a continuous map $\mu: \mathsf{ X}_{\mathrm{c}} \times[0,1] \rightarrow\mathsf{ X}_{[\mathrm {c}_{\mathrm{z}}, \mathrm{c}_{{\mathrm{z}}+1}]}$ whose restriction to the open set X _c×(0,1) is a homeomorphism onto $\mathsf{ X}_{(\mathrm{c}_{\mathrm{z}},\mathrm{c}_{{\mathrm{z}}+1})}$. The product space X _c ×[0,1] has several connected components each of which, called a cylinder, corresponds to the product between a connected component in the level set X _c and [0,1]. The images of all such cylinders under μ can touch each other only in $\mathsf{ X}_{\mathrm{c}_{\mathrm{z}}}$ or in $\mathsf{ X}_{\mathrm{c}_{{\mathrm{z}}+1}}$ when μ is no longer a homeomorphism. See Fig. 1(c) for an illustration, where in this example, X _c×[0,1] has three cylinders. Let us consider a single cylinder $\mathcal{C}= S \times[0,1]$, where S is the corresponding connected component in X _c. Denote by ${\mathcal{C}}^{o}$ the open cylinder S×(0,1). We call the image $\mu({\mathcal{C}}^{o}) (\subseteq\mathsf{ X})$ of every open cylinder ${\mathcal{C}}^{o}$ an interval-component of  X. Note that all interval-components of X are disjoint, and so are their images under the map Φ in the Reeb graph Rb _f (X).

Next, consider $\gamma_{{\mathcal{C}}^{o}} = \gamma\cap\mu({\mathcal {C}}^{o})$ and $\gamma_{\mathcal{C}}= \gamma\cap\mu(\mathcal{C})$, which are the intersections of γ with the interval-component $\mu({\mathcal{C}}^{o})$ and with the closure of $\mu({\mathcal {C}}^{o})$, respectively. Each connected component in $\gamma_{{\mathcal{C}}^{o}}$ is a path of the following two types: a through-path π where the two endpoints of its closure lie in $\mathsf{ X}_{\mathrm {c}_{\mathrm{z}}}$ and $\mathsf{ X}_{\mathrm{c}_{{\mathrm{z}}+1}}$, respectively; and a turning-path π where the endpoints of its closure either lie both in $\mathsf{ X}_{\mathrm {c}_{\mathrm{z}}}$ or both in $\mathsf{ X}_{\mathrm{c}_{{\mathrm{z}}+1}}$. The closure of a through-path or a turning-path in $\mu({\mathcal{C}}^{o})$ is called a through-path or a turning-path in $\mu(\mathcal{C})$. It can be verified that any turning-path π with endpoints p and q can be continuously deformed to a path connecting p and q within the same contour of a level set, using an argument similar to what we invoke below. Therefore we can transform γ to another homologous loop that contains only through-paths in $\gamma_{\mathcal{C}}$. See Fig. 2(a) for an illustration. As such, from now on, we assume that $\gamma_{\mathcal{C}}$ contains only through-paths.

Fig. 2

(a) Left: the interval-component $\mu(\mathcal{C})$ contains three through-paths and one turning-path. Middle: the turning-path can be deformed to a path contained in the level set $\mathsf{ X}_{\mathrm{c}_{\mathrm{z}}}$. Right: $\gamma_{\mathcal{C}}$ is modified so that at most one through-path is left. (b) The image of the singular simplex σ _i is the through-path in this interval-component. Its image is a singular simplex $\tilde{\sigma}_{i}: [0,1] \rightarrow|e_{i}|$ which we draw with the thin curve slightly off |e _i | for illustration purpose

Our arguments consist of two steps. In Step 1, we modify γ into another homologous loop γ′ which contains at most one through-path within any interval-component of X. In Step 2, we show that if Φ(γ′) is null-homologous in Rb _f (X), then γ′ must have no through-path in any interval-component of X, implying that γ′ is contained only in the level sets $\bigcup_{i} \mathsf{ X}_{\mathrm{c}_{i}}$. Hence γ′ carries a horizontal cycle and h is a horizontal homology class.

Step 1. In this step, we modify $\gamma_{\mathcal{C}}$ so that it contains only portions lying in the two level sets $\mathsf{ X}_{\mathrm{c}_{\mathrm {z}}} \cup\mathsf{ X}_{\mathrm{c}_{{\mathrm{z}}+1}}$, together with at most one through-path in $\mu(\mathcal{C})$. See Fig. 2(a). Specifically, suppose there are more than one through-paths in $\gamma_{\mathcal{C}}$. Then, for any pair of through-paths π ₁ and π ₂, we show that there exists a 2-chain B such that ∂B+π ₁+π ₂ is contained in the two level sets $\mathsf{ X}_{\mathrm{c}_{\mathrm{z}}}$ and $\mathsf{ X}_{\mathrm {c}_{{\mathrm{z}}+1}}$. Hence, we can convert γ to γ′=γ+(∂B+π ₁+π ₂) and the intersection $\gamma_{\mathcal{C}}' = \gamma' \cap\mu(\mathcal{C})$ has two fewer through-paths than $\gamma_{\mathcal{C}}$. Obviously, γ is homologous to γ′. By continuing this process, we cancel out all pairs of through-paths in $\gamma_{\mathcal{C}}$ till at most one through-path is left, and the resulting loop γ′ is homologous to γ.

We now show how to construct a 2-chain B for a pair of through-paths π ₁ and π ₂ from $\gamma_{\mathcal{C}}$. Let $\pi_{1}^{o}$ and $\pi_{2}^{o}$ denote the interiors of π ₁ and π ₂, respectively. Note that $\pi_{1}^{o}$ and $\pi_{2}^{o}$ are contained in the image $\mu ({\mathcal{C}}^{o} ) \subseteq\mathsf{ X}_{(\mathrm{c}_{\mathrm{z}}, \mathrm{c}_{{\mathrm{z}}+1})}$ of the open cylinder ${\mathcal{C}}^{o} = S \times(0,1)$. Since the restriction of μ to the open set ${\mathcal{C}}^{o}$ is a homeomorphism, $\pi_{1}^{o}$ and $\pi_{2}^{o}$ have unique pre-images $s_{1}^{o}$ and $s_{2}^{o}$ in ${\mathcal{C}}^{o}$ under μ. Let s ₁ (resp. s ₂) denote the closure of $s_{1}^{o}$ (resp. $s_{2}^{o}$) in $\mathcal{C}$, with p ₁ and p ₂ (resp. q ₁ and q ₂) being its endpoints. See Fig. 3(a) for an illustration. Notice that μ(s ₁)=π ₁ and μ(s ₂)=π ₂ due to the continuity of μ.

Fig. 3

(a) An illustration of the cylinder $\mathcal{C}= S \times[0,1]$, where each horizontal slice of this cylinder is a copy of S. (b) $\hat{s}$ is the projection of s=s ₁∘s ₃∘s ₂ from the product space onto the slice $\mathcal{C}[1]$. (c) The boundary of the surface B′ is $s+\hat{s}$

Since the cylinder $\mathcal{C}$ is the product space S×[0,1], every point $\mathbf{x}\in\mathcal{C}$ can be represented as x=(x,t), where x∈S is called its horizontal coordinate and t∈[0,1] is its vertical coordinate (or height). We use a slice $\mathcal{C}[t]$ to refer to one copy of S at height t.

Since each slice $\mathcal{C}[t]$ of the cylinder $\mathcal{C}$ is path-connected, there is a path, say s ₃, that connects p ₁ and q ₁ in $\mathcal{C}[0]$. Let s denote the concatenated curve s ₁∘s ₃∘s ₂; see Fig. 3(b). Now for every point x=(x,t _x )∈s, consider the “vertical line” l _x ={(x,t)∣t∈[t _x ,1]}. That is, l _x contains the images of x in each slice $\mathcal{C}[t]$ with t≥t _x . The union of l _x s for all x∈s traces out a 2-dimensional surface B′. The boundary of B′ is $\partial B' = s \circ\hat{s}$ where $\hat {s}$ is the image of s in $\mathcal{C}[1]$. See Fig. 3 (b) and (c). Through the continuous map μ, we obtain a 2-chain B whose carrier is $\mu(B') \subseteq\mathsf{ X}_{[\mathrm{c}_{\mathrm {z}},\mathrm{c}_{{\mathrm{z}}+1}]}$ and $\partial\mu(B') = \pi_{1} \circ\mu(s_{3}) \circ\pi_{2} \circ\mu (\hat{s})$. Furthermore, μ(s ₃) and $\mu(\hat{s})$ lie in the level sets $\mathsf{ X}_{\mathrm{c}_{\mathrm{z}}} \cup\mathsf{ X}_{\mathrm{c}_{{\mathrm{z}}+1}}$. Hence by taking γ′=γ+∂μ(B′), we have reduced a pair of through-paths.

Now we group through-paths in $\gamma_{\mathcal{C}}$ into pairs, with at most one left unpaired. We construct a 2-chain for every pair, and let $\mathcal{B}$ denote the union of all these 2-chains. Obviously, $\gamma' = \gamma+ \partial\mathcal{B}$ is homologous to γ and its intersection $\gamma' \cap\mu(\mathcal{C})$ has at most one through-path. By performing this procedure for all cylinders and for all intervals [c_z,c_z+1], z=1,…,k−1, we obtain a loop ${\widehat{\gamma}}$ which is homologous to γ, and has at most one through-path within each interval-component in X.

Step 2. We now choose a specific 1-cycle $\alpha= \sum_{i=1}^{r} \sigma_{i} + \sum_{j=1}^{t} \rho_{j}$ carried by ${\widehat{\gamma}}$ that is of the following form: there are two types of singular simplex in α: a simplex σ _i whose image in X is a through-path and a simplex ρ _j whose image is completely contained within a level set $\mathsf{ X}_{\mathrm{c}_{\mathrm{z}}}$ for some z∈[1,k]. Consider the image of α in Z ₁(Rb _f (X)), ${\tilde{\alpha}}:= \varPhi_{\#}(\alpha) = \sum_{i=1}^{r} \tilde {\sigma}_{i} + \sum_{j=1}^{t} \tilde{\rho}_{j}$, with $\tilde{\sigma}_{i} = \varPhi_{\#}(\sigma_{i})$ and $\tilde{\rho}_{j} = \varPhi_{\#}(\rho_{j})$. Since the map Φ collapses each connected component in a level set to a single point, each $\tilde{\rho}_{j}$ is a constant map, and hence ${\tilde{\alpha}}$ is homologous to $\sum_{i=1}^{r} \tilde{\sigma }_{i}$, which we still denote as ${\tilde{\alpha}}$ for simplicity.

Now insert a set of vertices V to Rb _f (X), which is the set of points with function value f(c _i ) for i∈[1,k]. The removal of these vertices from Rb _f (X) leaves a set of connected components. Since the function f:X→ℝ is level-set-tame w.r.t. {c₁,…,c _k }, each such connected component is necessarily the image of some continuous bijection g:(0,1)→Rb _f (X), and we call each connected component an arc of Rb _f (X). Indeed, each such connected component is the image of some interval-component of X under the map Φ. Since an interval-component T of X is the evolution of a connected component in a level set without changing its topology, Φ(T) is necessarily a piece of curve monotone in the function values. Also observe that by the definition of interval-components all such arcs are disjoint. Hence we obtain a triangulation K of Rb _f (X) whose vertices are V and edges are the closures of those arcs defined above.

By the construction of ${\widehat{\gamma}}$, the image of each singular simplex σ _i is contained in a different interval-component. Hence $\tilde{\sigma}_{i}([0,1])$ is contained within the underlying space of a single edge e in K. The boundary of $\tilde{\sigma}_{i}$ coincides with endpoints of e which are vertices in V. See Fig. 2(b) for an illustration. Given an edge e∈K, let |e|⊆|K|=Rb _f (X) denote the underlying space of e. Let e _i ∈K denote the edge such that $\tilde{\sigma}_{i}$ is a map $\tilde{\sigma}_{i}: [0,1] \rightarrow|e_{i}|$. Observe that each $\tilde{\sigma}_{i}$ is mapped to a unique edge e _i .

Finally, consider the singular cycle $\tilde{\alpha}=\sum_{i=1}^{r} \tilde{\sigma}_{i}$. The carrier for this cycle is homotopic to the carrier of the cycle $h=\sum_{i=1}^{r} (h_{i}: [0,1]\rightarrow|e_{i}|)$ where h _i is a homeomorphism. Thus the two cycles h and $\tilde{\alpha}$ are homologous. Consider the simplicial cycle $g = \sum_{i=1}^{r} e_{i}$, and let $[g] \in\overline{\mathsf{ H}}_{1}(K)$ denote the simplicial homology class it belongs to. The class [g] identifies to [h] via the standard isomorphism between simplicial homology groups H ₁(K) and the singular homology group H ₁(|K|) (see e.g., p. 194 of [23]). Therefore, this standard isomorphism also identifies [g] to $[\tilde{\alpha}]$. On the other hand, in simplicial homology, as there are no 2-simplices in K, g is null-homologous if and only if g=∅, which means that the number r of singular simplices in ${\tilde {\alpha}}$ is necessarily zero if ${\tilde{\alpha}}$ is null-homologous. This implies that the loop ${\widehat{\gamma}}\subset\mathsf{ X}$ does not contain any through-path, and is completely contained within the union of level sets $\bigcup_{\mathrm{z}}\mathsf{ X}_{\mathrm{c}_{\mathrm{z}}}$. Hence ${\widehat{\gamma}}$ (and thus γ) carries a horizontal cycle and its corresponding homology class h is horizontal. In other words, if Φ _∗(h)=0 then $h \in\overline{\mathsf{ H}}_{1}(\mathsf{ X})$, implying $\operatorname{ker}(\varPhi_{*}) \subseteq\overline{\mathsf{ H}}_{1}(\mathsf{ X})$. Combining this with that $\overline{\mathsf{ H}}_{1}(\mathsf{ X}) \subseteq \operatorname{ker}(\varPhi_{*})$ completes our proof. □

Theorem 3.2

Given a level-set-tame function f:X→ℝ, let $\check{\varPhi}: \breve{\mathsf{ H}}_{1}(\mathsf{ X}) \rightarrow \mathsf{ H}_{1}(\mathsf{ Rb}_{f}(\mathsf{ X}))$ be the homomorphism induced by the surjection Φ:X→Rb _f (X) as defined before. The map $\check{\varPhi}$ is an isomorphism. Furthermore, for any vertical homology class $\omega\in \breve{\mathsf{ H}}_{1}(\mathsf{ X})$, we have $\mathrm{height}(\omega) = \mathrm{height}(\check{\varPhi}(\omega))$.

Proof

First, for any loop γ in Rb _f (X), it is easy to show that there exists a loop (pre-image) $\hat{\gamma}$ in X such that $\varPhi(\hat{\gamma}) = \gamma$ (see Claim 3.1 in the conference version of this paper). Hence Φ _∗:H ₁(X)→H ₁(Rb _f (X)) is also surjective. It then follows that the induced quotient map $\check{\varPhi}$ is also surjective. The injectivity of $\check{\varPhi}$ follows from Lemma 3.1. Hence $\check{\varPhi}$ is an isomorphism.

For the second part of the theorem, suppose α is a vertical cycle such that [α]=ω and height(α)=height(ω), i.e., α is a thinnest cycle in the vertical homology class ω. Let γ be the loop in Rb _f (X) that carries a thinnest cycle in the homology class $\check{\varPhi}(\omega) \in\mathsf{ H}_{1}(\mathsf{ Rb}_{f}(\mathsf{ X}))$. We have

(1)

On the other hand, there is a loop $\widehat{\gamma}$ in X (which is a pre-image of γ under Φ) such that $\varPhi(\widehat{\gamma}) = \gamma$ and $\mathrm{height}(\widehat{\gamma}) = \mathrm{height}(\gamma)$. Let $\hat{\alpha}$ be any 1-cycle carried by $\widehat{\gamma}$. By Lemma 3.1, we have $[\hat{\alpha}] = \omega$, as the cycle $\alpha+ \hat{\alpha}$ is mapped to a null-homologous cycle in Rb _f (X). Hence $\mathrm{height}(\gamma) = \mathrm{height}(\widehat{\gamma}) \ge\mathrm{height}(\alpha)$. Combining this with (1) proves that $\mathrm {height}(\check{\varPhi}(\omega)) = \mathrm{height}(\omega)$. □

4 Approximating Reeb Graphs

Let M be a compact and smooth m-manifold without boundary embedded in ℝ^d. The reach ρ(M) of M is the minimal distance from any point x∈M to the so-called medial axis of M. Given a point p∈M, let B _M (p,r) denote the open geodesic ball centered at p with radius r. Let r _p be the maximal radius so that B _M (p,r _p ) is convex in the sense that the minimizing geodesics between any two points in B _M (p,r _p ) is contained in B _M (p,r _p ). The convexity radius of M is simply ρ _c (M)=inf _p∈M r _p .

A set of points P is an ε-sample ² of M if P⊂M and for any point x∈M, there is a point p∈P within ε geodesic distance from x. Given P and a real r>0, the Čech complex $\mathcal{C}^{r}(P)$ is a simplicial complex where a simplex $\sigma\in\mathcal{C}^{r}(P)$ if and only if the vertices of σ are the centers of d-balls of radius r/2 with a non-empty common intersection. Instead of common intersection, if we only require pairwise intersection among the set of d-balls, we obtain the so-called Vietoris–Rips complex (Rips complex for short) $\mathcal{R}^{r}(P)$.

Overview

Consider an ε-sample P⊂M and a function f:M→ℝ with its value only available at sample points in P. In what follows, we show that for an appropriate r, the Reeb graph of the Rips complex $\mathcal{R}^{r}(P)$ approximates Rb _f (M) both in terms of the rank of the first homology group, and in terms of the range and the height of cycles and homology classes. Our precise definition of approximation will be given later. Once the Rips complex is constructed, computing its Reeb graph takes only O(nlogn) expected time [20], where n is the size of the 2-skeleton of $\mathcal{R}^{r}(P)$. Since f is only available at sample points in P, the approximation quality naturally depends on how well the function f:M→ℝ behaves. We assume that f is Lipschitz with Lipschitz constant Lip _f .

In Sect. 4.1 we first introduce some relations between cycles of M and those of the geometric realization $|\mathcal{R}^{r}(P)|$ of the Rips complex $\mathcal{R}^{r}(P)$. Using these relations, in Sect. 4.2, we show that there are maps between H ₁(M) and $\mathsf{ H}_{1}(|\mathcal{R}^{r}(P)|)$ that are not only isomorphic, but also preserve the height / range of a homology class. This, combined with Theorem 3.2, eventually leads to our approximation of Rb _f (M). This approximation result can be used to estimate the first Betti number of an orientable 2-manifold from its point samples in near-linear expected time.

4.1 Relation Between Cycles in M and $|\mathcal{R}^{r}(P)|$

The simplicial complex $\mathcal{R}^{r}(P)$ as defined is not necessarily embedded in ℝ^d. Consider the embedding ${\mathrm{e}}\colon\mathcal {R}^{r}(P)\rightarrow\Delta^{|P|}$ of $\mathcal{R}^{r}(P)$ into the standard simplex in ℝ^|P|. Let $|\mathcal{R}^{r}(P)|$ denote the underlying space of the geometric realization ${\mathrm {e}}(\mathcal{R}^{r}(P))$. A piecewise-linear function f on $\mathcal{R}^{r}(P)$ defines naturally a piecewise-linear function on its geometric realization $|\mathcal{R}^{r}(P)|$ which we also denote as f. The Reeb graph of a PL-function f on $\mathcal{R}^{r}(P)$ is in fact the Reeb graph of f on its geometric realization $|\mathcal{R}^{r}(P)|$. Hence $\mathsf{ Rb}_{f}(\mathcal{R}^{r}(P)):= \mathsf{ Rb}_{f}(|\mathcal{R}^{r}(P)|)$. Analogously, the vertical/horizontal homology groups of $\mathcal{R}^{r}(P)$ with respect to a PL-function f are also defined using $|\mathcal{R}^{r}(P)|$. In this section, we relate cycles from M and those from $|\mathcal{R}^{r}(P)|$ via (simplicial) cycles of $\mathcal{R}^{r}(P)$. We will show how to construct the maps as indicated in Fig. 4 below, such that these maps not only induce isomorphisms in the corresponding homology groups, but also preserve height and range of cycles.

Fig. 4

Maps between cycle groups

A general version of the next claim which establishes an isomorphism between the homology groups of M and those of Čech and Rips complexes is well known (see, e.g. [24] for Čech-complexes and [22] for Rips complexes; a variant for compact spaces was also observed by Steve Oudot (personal communications) and a much stronger result showing that Rips complexes capturing topology of sampled shapes is given in [1]). We include a proof of it for completeness. First, we quote a result from [14], the map of which will be used later as well.

Proposition 4.1

(Proposition 3.3 of [14])

Let P⊂M be an ε-sample and r a parameter such that $2{\varepsilon}\le r \le\sqrt{\frac{3}{5}} \rho(\mathsf{ M})$. There is a homotopy equivalence $\theta: \mathcal{C}^{2r}(P) \rightarrow \mathsf{ M}$ such that θ(p)=p for any p∈P and θ(σ)⊂M∩(⋃ _p∈Vert(σ) B _M (p,r)).

Lemma 4.2

Let P⊂M be an ε-sample and r a parameter such that $4{\varepsilon}\le r \le\frac{1}{2} \sqrt{\frac{3}{5}} \rho(\mathsf{ M})$. Then,

$$\mathsf{ H}_1\bigl(\mathcal{C}^{r}(P)\bigr) \simeq \mathsf{ H}_1 \bigl(\mathcal{R}^r(P)\bigr) \simeq\mathsf{ H}_1\bigl(\mathcal{C}^{2r}(P)\bigr) \simeq\mathsf{ H}_1(\mathsf{ M}). $$

The first two isomorphisms are induced by the natural inclusion from $\mathcal{C}^{r}(P)$ to $\mathcal{R}^{r}(P)$ and then to $\mathcal {C}^{2r} (P)$. The last isomorphism is induced by the homotopy equivalence θ from Proposition 4.1.

Proof

Consider the following sequence of inclusions:

$$\mathcal{C}^r(P) \stackrel{i_1}{\hookrightarrow}\mathcal{R}^r(P) \stackrel{i_2}{\hookrightarrow}\mathcal{C}^{2r}(P). $$

By Proposition 3.4 [14], we know that the inclusion i=i ₂∘i ₁ induces an isomorphism $\mathsf{ H}_{1}(\mathcal{C}^{r}(P)) \simeq\mathsf{ H}_{1}(\mathcal{C}^{2r}(P))$. On the other hand, note that $\mathcal{C}^{r}(P)$ and $\mathcal{R}^{r}(P)$ share the same edge set, and $\mathcal{R}^{r}(P)$ only has more triangles than $\mathcal{C}^{r}(P)$. Hence the inclusion i ₁ induces a surjective homomorphism from $\mathsf{ H}_{1}(\mathcal{C}^{r}(P))$ to $\mathsf{ H}_{1}(\mathcal{R}^{r}(P))$. It then follows that both i ₁ and i ₂ must induce isomorphisms in the corresponding first homology groups. □

Maps d and h_#

We now define maps as indicated in Fig. 4. First, given a cycle α∈Z ₁(M), we map it to a cycle $\mathrm{d}(\alpha) \in\mathbf{Z}_{1}(\mathcal{R}^{r}(P))$ using the same Decomposition method [2] as applied in [14]. In particular, use an arbitrary, but fixed, way to break the carrier of α into pieces where each piece has length at most r−2ε. For each piece with endpoints x _i and x _i+1, find the closest sample points p _i and p _i+1 from P to x _i and x _i+1, respectively, and connect p _i and p _i+1 (which is necessarily an edge in $\mathcal{R}^{r}(P)$ by triangle inequality). The resulting simplicial 1-cycle in $\mathcal{R}^{r}(P)$ is d(α). Later in Lemma 4.3, we will show that this map d indeed takes homologous cycles to homologous cycles, and as such induces a well-defined homomorphism d_∗ at the homology level.

We define the map $\mathrm{h}: \mathcal{R}^{r}(P) \rightarrow\mathsf{ M}$ as the inclusion map $\mathcal{R}^{r}(P) \hookrightarrow\mathcal {C}^{2r}(P)$ composed with the homotopy equivalence $\theta: \mathcal{C}^{2r}(P) \rightarrow \mathsf{ M}$ introduced in Proposition 4.1. The corresponding chain map h_# induces a homomorphism $\mathrm{h}_{*}: \mathsf{ H}_{p}(\mathcal{R}^{r}(P)) \rightarrow\mathsf{ H}_{p}(\mathsf{ M})$. We restrict h_∗ only to the first homology group $\mathrm{h}_{*}: \mathsf{ H}_{1}(\mathcal{R}^{r}(P)) \rightarrow \mathsf{ H}_{1}(\mathsf{ M})$. By Lemma 4.2, h_∗ is an isomorphism.

The following lemma states that $\mathrm{d}\colon\mathbf{Z}_{1}(\mathsf{ M})\rightarrow\mathbf {Z}_{1}(\mathcal{R}^{r}(P))$ is in fact the homology-inverse of h_#. The ranges of mapped cycles are also related. We put the proof of the following lemma in Appendix A to maintain the flow of the presentation. Given two intervals I ₁=[a,b] and I ₂=[c,d], we say that I ₁ is oneside-δ-close to I ₂ if [a,b]⊆[c−δ,d+δ]. and I ₁ and I ₂ are δ-Hausdorff-close if the two intervals are oneside-δ-close to each other. In the Lemma below, assume that f is a (Lip _f )-Lipschitz function on M and its values for the vertices P⊂M define a piecewise-linear function on $\mathcal{R}^{r}(P)$ which we also denote as f.

Lemma 4.3

• (i) $\mathrm{h}_{*}: \mathsf{ H}_{1}(\mathcal{R}^{r}(P)) \rightarrow \mathsf{ H}_{1}(\mathsf{ M})$ is an isomorphism. The map d induces an isomorphism $\mathrm{d}_{*}\colon\mathsf{ H}_{1}(\mathsf{ M})\rightarrow\mathsf{ H}_{1}(\mathcal{R}^{r}(P))$ such that h_∗=(d_∗)⁻¹.

• (ii) The range of the cycle $\mathrm{d}(\alpha) \in\mathbf{Z}_{1}(\mathcal {R}^{r}(P))$ is oneside-(r⋅Lip _f )-close to the range of α∈Z ₁(M). Similarly, the range of the cycle $\mathrm{h}_{\#}(\hat{\alpha}) \in \mathbf{Z}_{1}(\mathsf{ M})$ is oneside-(r⋅Lip _f )-close to $\hat{\alpha} \in\mathbf{Z}_{1}(\mathcal{R}^{r}(P))$.

• (iii) The ranges of any homology class ω∈H ₁(M) (resp. $\hat{\omega} \in\mathsf{ H}_{1}(\mathcal {R}^{r}(P))$) and its image $\mathrm{d}_{*}(\omega) \in\mathsf{ H}_{1}(\mathcal{R}^{r}(P))$ (resp. $\mathrm{h}_{*}(\hat{\omega}) \in\mathsf{ H}_{1}(\mathsf{ M})$), are (r⋅Lip _f )-Hausdorff-close.

Maps u and g

The map u is taken as the standard map between the simplicial chain groups of a simplicial complex and the singular chain groups of its underlying space; see e.g., the map μ defined on p. 194 of [23].

We now define the map $\mathrm{g}: \mathbf{Z}_{1}(|\mathcal{R}^{r}(P)|) \rightarrow\mathbf {Z}_{1}(\mathcal{R}^{r}(P))$. Recall we have embedded $\mathcal{R}^{r}(P)$ in the standard simplex Δ^|P|⊂ℝ^|P|, and $|\mathcal{R}^{r}(P)|$ is the underlying space of this geometric realization ${\mathrm{e}}(\mathcal{R}^{r}(P))$ of $\mathcal{R}^{r}(P)$. In particular, Each vertex p _i ∈P is mapped to the point v _i =(0,…,0,1,0,…,0)∈ℝ^|P| with the ith position 1; and a simplex in $\mathcal{R}^{r}(P)$ with vertices $\{p_{i_{0}}, \ldots, p_{i_{l}} \}$ is mapped to the simplex in ℝ^|P| with vertices $\{v_{i_{0}}, \ldots, v_{i_{l}} \}$. Consider a cycle α in $|\mathcal{R}^{r}(P)|$. The carrier of α passes through a sequence of simplices S of ${\mathrm{e}}(\mathcal{R}^{r}(P))$; if a point in the carrier is contained in multiple simplices, then keep the one with the minimum dimension. Let S={σ ₁,…,σ _m }. Now choose an arbitrary but fixed vertex u _i for each σ _i , and let $p_{u_{i}} \in P$ denote the unique pre-image of u _i in $\mathcal{R}^{r}(P)$ under the embedding map u. Notice that for any two consecutive simplices σ _i and σ _i+1 that the carrier of α passes through, it is necessary that either σ _i is face of σ _i+1 or σ _i+1 is a face of σ _i . Hence either $p_{u_{i}}=p_{u_{i+1}}$ or $p_{u_{i}} p_{u_{i+1}}$ is an edge in $\mathcal{R}^{r}(P)$. Therefore, we map α simply to the cycle g(α) given by the sequence of vertices $(p_{u_{1}}, \ldots, p_{u_{m}}, p_{u_{1}})$ and edges between them. We have the following result about maps u and g.

Lemma 4.4

• (i) Every cycle α in $\mathcal{R}^{r}(P)$ is mapped to a cycle u(α) with the same range in $|\mathcal{R}^{r}(P)|$ under $\mathrm{u}: \mathbf{Z}_{1}(\mathcal {R}^{r}(P)) \to \mathbf{Z}_{1}(|\mathcal{R}^{r}(P)|)$. The map $\mathrm{u}_{*}: \mathsf{ H}_{1}(\mathcal{R}^{r}(P)) \rightarrow\mathsf{ H}_{1}(|\mathcal{R}^{r}(P)|)$ is an isomorphism, and the ranges of any homology class $\omega\in \mathsf{ H}_{1}(\mathcal{R}^{r}(P))$ and its image $\mathrm{u}_{*}(\omega) \in \mathsf{ H}_{1}(|\mathcal{R}^{r}(P)|)$ are also the same.

• (ii) Every cycle α in $|\mathcal{R}^{r}(P)|$ is mapped to a cycle g(α) in $\mathcal{R}^{r}(P)$ whose range is oneside-(r⋅Lip _f )-close to that of α. The map $\mathrm{g}:\mathbf{Z}_{1}(|\mathcal{R}^{r}(P)|) \rightarrow \mathbf{Z}_{1}(\mathcal{R}^{r}(P))$ induces an isomorphism $\mathrm{g}_{*}: \mathsf{ H}_{1}(|\mathcal{R}^{r}(P)|) \rightarrow\mathsf{ H}_{1}(\mathcal{R}^{r}(P))$, and g_∗=(u_∗)⁻¹. The ranges of any homology class $\hat{\omega} \in\mathsf{ H}_{1}(|\mathcal{R}^{r}(P)|)$ and its image $\mathrm{g}_{*}(\hat{\omega}) \in\mathsf{ H}_{1}(\mathcal{R}^{r}(P))$ are (r⋅Lip _f )-Hausdorff-close.

Proof

For part (i) of the lemma, note that it is well known that u induces an isomorphism between the respective simplicial and singular homology groups (see e.g., Theorem 34.3 of [23]). Furthermore, since u maps each simplex to a map whose range is its underlying space, u preserves the range of a cycle.

For part (ii) of the lemma, first observe that for any cycle α from $|\mathcal{R}^{r}(P)|$, we have [u∘g(α)]=[α]. Indeed, by the construction of g, it is easy to verify that u∘g(α) and α are homotopic. Since u induces an isomorphism from $\mathcal{R}^{r}(P)$ to $|\mathcal{R}^{r}(P)|$, it follows that g maps homologous cycles in $|\mathcal {R}^{r}(P)|$ to homologous cycles in $\mathcal{R}^{r}(P)$. Hence g induces a well-defined homomorphism $\mathrm{g}_{*}: \mathsf{ H}_{1}(|\mathcal{R}^{r}|) \rightarrow\mathsf{ H}_{1}(\mathcal{R}^{r})$. Furthermore, g∘u(α′)=α′ for any cycle $\alpha' \in\mathcal{R}^{r}(P)$. It follows that g_∗ is the inverse of u_∗ and hence is an isomorphism.

Finally, note that for each simplex $\sigma\in \mathrm{e}(\mathcal{R}^{r}(P))$, the function value difference between any two points x,y∈σ is bounded by r⋅Lip _f . Let γ be the carrier of a cycle α in $|\mathcal{R}^{r}(P)|$. By the construction of g, for each piece γ∩σ _i of γ within the simplex σ _i ∈S, we have |f(x)−f(u _i )|≤r⋅Lip _f for any point x∈γ∩σ _i . Since $f(u_{i}) = f(p_{u_{i}})$, we have

On the other hand, we have $\mathrm{range}(\mathrm{g}(\alpha)) \subseteq[\min_{i \in[1,m]} f(p_{u_{i}}), \max_{i \in[1,m]} f(p_{u_{i}})]$. Hence range(g(α)) is oneside-(r⋅Lip _f )-close to range(α). By a similar argument as in the proof of Lemma 4.3 (iv), the closeness between the corresponding homology classes follows. □

Combining Lemma 4.3 and 4.4, we obtain a similar result for maps between Z ₁(M) and $\mathbf{Z}_{1}(|\mathcal{R}^{r}(P)|)$.

Theorem 4.5

Let P⊂M be an ε-sample and r a parameter such that $4{\varepsilon}\le r \le\frac{1}{2} \sqrt{\frac{3}{5}} \rho(\mathsf{ M})$.

• (i) There is a map ρ:=u_#∘d from Z ₁(M) to $\mathbf{Z}_{1}(|\mathcal{R}^{r}(P)|)$ that induces an isomorphism $\rho_{*}: \mathsf{ H}_{1}(\mathsf{ M})\rightarrow\mathsf{ H}_{1}(|\mathcal{R}^{r}(P)|)$. The range of cycle ρ(α) is oneside-(r⋅Lip _f )-close to the range of α.

• (ii) There is a map ξ:=h_#∘g from $\mathbf{Z}_{1}(|\mathcal{R}^{r}(P)|)$ to Z ₁(M) that induces an isomorphism $\xi_{*}: \mathsf{ H}_{1}(|\mathcal{R}^{r}(P)|) \rightarrow\mathsf{ H}_{1}(\mathsf{ M})$. The range of cycle $\xi(\hat{\alpha})$ is oneside-(2r⋅Lip _f )-close to the range of cycle $\hat{\alpha}$.

• (iii) Furthermore, ρ _∗ is the inverse of ξ _∗. The ranges of any homology class ω∈H ₁(M) (resp. $\hat{\omega} \in\mathsf{ H}_{1}(|\mathcal{R}^{r}(P)|)$) and its image $\rho_{*}(\omega) \in\mathsf{ H}_{1}(|\mathcal{R}^{r}(P)|)$ (resp. $\xi_{*}(\hat{\omega}) \in\mathsf{ H}_{1}(\mathsf{ M})$) are (2r⋅Lip _f )-Hausdorff-close.

4.2 Rb _f (M) and $\mathsf{ Rb}_{f}(\mathcal{R}^{r}(P))$

We now show that under mild conditions on M, the induced isomorphisms ρ _∗ and ξ _∗ as defined above in fact map horizontal classes to horizontal classes, and vertical classes to vertical classes.

Set $s = \mathrm{rank}(\overline{\mathsf{ H}}_{1}(\mathsf{ M}))$. It turns out that we can find a basis {[α ₁],…,[α _s ]} for the horizontal subgroup $\overline{\mathsf{ H}}_{1}(\mathsf{ M})$ such that each class [α _i ], i∈[1,s], has height 0; as well as a set of base cycles {α ₁,…,α _s } corresponding to this basis with height(α _i )=0 for any i∈[1,s]. Such a 0-height basis for $\overline{\mathsf{ H}}_{1}(\mathsf{ M})$ can be constructed by a simple greedy approach, where at each iteration we take a homology class with smallest height that is independent of all the previous elements in the basis. The details can be found in Appendix B. The corresponding set of base cycles {α ₁,…,α _s } with height(α _i )=0 is called a set of 0-height base cycles for $\overline{\mathsf{ H}}_{1}(\mathsf{ M})$. For a horizontal homology class ω with height 0, the span of ω is the length of the maximal interval I such that ω has a pre-image in the level set X _a for any a∈I. Intuitively, this is the interval in function values in which this homology class survives in the level sets.

Let s ^∗(M) denote the smallest span of any 0-height horizontal class of the input manifold M, and t ^∗(M) the minimal height of any vertical class of M. We assume that both s ^∗(M) and t ^∗(M) are positive for our input level-set-tame function on M.

Theorem 4.6

Given a level-set-tame function f on a manifold M, let r>0 be such that s ^∗(M),t ^∗(M)>2r⋅Lip _f . Let ρ _∗ and ξ _∗ be as defined in Theorem 4.5. Then we have $\rho_{*}(\overline{\mathsf{ H}}_{1}(\mathsf{ M})) = \overline{\mathsf{ H}}_{1}(|\mathcal{R}^{r}(P)|)$, $\xi_{*}(\overline{\mathsf{ H}}_{1}(|\mathcal{R}^{r}(P)|)) = \overline{\mathsf{ H}}_{1}(\mathsf{ M})$ and $\breve{\mathsf{ H}}_{1}(\mathsf{ M}) \simeq\breve{\mathsf{ H}}_{1}(|\mathcal {R}^{r}(P)|)$.

Proof

For simplicity, in this proof let R denote $|\mathcal{R}^{r}(P)|$. Below we first show that $\rho_{*}(\overline{\mathsf{ H}}_{1}(\mathsf{ M})) = \overline{\mathsf{ H}}_{1}(\mathrm{R})$. Consider a set of 0-height base cycles {α ₁,…,α _s } for $\overline{\mathsf{ H}}_{1}(\mathsf{ M})$ with $s = \mathrm {rank}(\overline{\mathsf{ H}}_{1}(\mathsf{ M}))$.

Take an arbitrary α _i for i∈[1,s], and let [a,b] denote the maximal interval³ such that [α _i ] has a preimage in the level set M _c for any c∈[a,b]. The span of [α _i ] is b−a and is at least s ^∗(M)>2r⋅Lip _f . Take a representative cycle γ _a from M _a and γ _b from M _b of the homology class [α _i ]. Set I _a :=[a−r⋅Lip _f ,a+r⋅Lip _f ] and I _b :=[b−r⋅Lip _f ,b+r⋅Lip _f ]. It follows from Theorem 4.5 that the carrier of ρ(γ _a ) is contained in the interval level set $\mathrm{R}_{I_{a}}$ while the carrier of ρ(γ _b ) is contained in $\mathrm{R}_{I_{b}}$. (Note that [ρ(α _i )]=[ρ(γ _a )]=[ρ(γ _b )] is a non-trivial homology class in H ₁(R).) Since b−a>2r⋅Lip _f , we have I _a ∩I _b =∅. A simple application of the Mayer–Vietoris sequence provides that the homology class [ρ(α _i )] has a preimage in the level set R _c for any c∈[a+r⋅Lip _f ,b−r⋅Lip _f ], which in turn implies that [ρ(α _i )] is horizontal. (A similar argument is used in [9].) Since [ρ(α _i )] is horizontal for any i∈[1,s], $\rho_{*}(\overline{\mathsf{ H}}_{1}(\mathsf{ M}))$ is a subgroup of $\overline {\mathsf{ H}}_{1}(\mathrm{R})$.

We now show that the opposite direction $\overline{\mathsf{ H}}_{1}(\mathrm{R}) \subseteq\rho_{*}(\overline{\mathsf{ H}}_{1}(\mathsf{ M}))$ is also true, which would imply that $\rho_{*}(\overline{\mathsf{ H}}_{1}(\mathsf{ M})) = \overline{\mathsf{ H}}_{1}(\mathrm{R})$. Specifically, take a set of 0-height base cycles {β ₁,…,β _t } for $\overline{\mathsf{ H}}_{1}(\mathrm{R})$. By Theorem 4.5, their images {ξ(β ₁),…,ξ(β _t )} in M is a set of independent cycles such that height(ξ(β _i ))≤2r⋅Lip _f . Since the minimal height of any vertical cycle in M is t ^∗(M)>2r⋅Lip _f , each ξ(β _i ) has to be a horizontal homology cycle. As such, $\xi_{*}(\overline{\mathsf{ H}}_{1}(R)) \subseteq\overline{\mathsf{ H}}_{1}(\mathsf{ M})$, which means that $\overline{\mathsf{ H}}_{1}(R) = \rho_{*} (\xi_{*} (\overline{\mathsf{ H}}_{1}(R))) \subseteq\rho_{*}(\overline{\mathsf{ H}}_{1}(\mathsf{ M}))$. It then follows that $\rho_{*}(\overline{\mathsf{ H}}_{1}(\mathsf{ M})) = \overline {\mathsf{ H}}_{1}(R)$. Since the isomorphism ρ _∗ sends $\overline{\mathsf{ H}}_{1}(\mathsf{ M})$ to $\overline{\mathsf{ H}}_{1}(R)$, the induced homomorphism at the quotient level is also an isomorphism; that is, $\breve{\mathsf{ H}}_{1}(\mathsf{ M}) \simeq\breve{\mathsf{ H}}_{1}(R)$. □

4.3 Putting Everything Together

We say that a Reeb graph Rb _f (A) δ-approximates another Reeb graph Rb _g (B) if there is an isomorphism between H ₁(Rb _f (A)) and H ₁(Rb _g (B)) such that the ranges of corresponding pairs of homology classes are δ-Hausdorff-close.⁴ Combining Theorems 3.2, 4.5 and 4.6, we have our first main result.

Theorem 4.7

Let f:M→ℝ be a level-set-tame function defined on M with Lipschitz constant Lip _f . Given an ε-sample P of M, let r be a parameter such that $4{\varepsilon}\le r < \min\{ \frac {1}{4} \rho(\mathsf{ M}), \frac{1}{4}\rho_{c}(\mathsf{ M}), \frac{\mathbf {t}^{*}}{2 \mathrm{Lip}_{f}}, \frac{\mathbf{s}^{*}}{2\mathrm{Lip}_{f}} \}$, and $\mathcal{R}^{r}(P)$ the Rips complex constructed from P using radius r/2. Then $\mathsf{ Rb}_{f}(\mathcal{R}^{r}(P))$ is a (2r⋅Lip _f )-approximation of Rb _f (M), and $\mathsf{ Rb}_{f}(\mathcal{R}^{r}(P))$ can be computed in O(nlogn) expected time [20], where n is the size of the 2-skeleton of $\mathcal{R}^{r}(P)$.

Remark 1

Here we provide a brief discussion of why we focus only on the first homology information of the Reeb graph, as well as the intuition behind our definition of a δ-approximate Reeb graph.

The Reeb graph is an abstract graph and contains only the 0- and 1-dimensional topological information. Given a Reeb graph Rb _f (M), its zeroth homology simply encodes the connected components information of M, and can be approximated from point data easily by returning the number of connected components in an appropriately constructed Rips complex in linear time.

At the same time, compared to general abstract graphs, the Reeb graph has the extra information of the natural function f defined on it. Hence one may also ask what the 0th persistent homology of Rb _f (X) induced by f is. This turns out to be the same as approximating the 0th persistent homology for X and can be solved using results from [6, 7].

Therefore, the only remaining issue is to approximate the first homology of a Reeb graph. Similar to the case for the zeroth homology, there are two aspects: (i) computing H ₁(Rb _f (M)) itself; and (ii) computing the first persistent homology of Rb _f (M) induced by the function f. For (i), our result shows that $\mathsf{ H}_{1}(\mathsf{ Rb}_{f}(\mathcal{R}^{r}(P)))$ for a certain Rips complex $\mathcal{R}^{r}(P)$ constructed from the point samples P is isomorphic to H ₁(Rb _f (M)). For (ii), since every 1-cycle in a Reeb graph is essential, the standard persistence is not able to describe them, and one has to use the extended persistence as introduced in [9], which is determined by the range of essential cycles. Hence our definition of the approximation also requires that ranges of corresponding homology classes (and even cycles) are also close.

Remark 2

One can strengthen Theorem 4.7 slightly to show that if the parameter r does not satisfy the conditions that $r < \frac {\mathbf{t}^{*}}{2 \mathrm{Lip}_{f}}$ or $r < \frac{\mathbf {s}^{*}}{2\mathrm{Lip}_{f}}$, then all homology classes of H ₁(Rb _f (M)) with height at least 2r⋅Lip _f are preserved in $\mathsf{ H}_{1}(\mathsf{ Rb}_{f}(\mathcal{R}^{r}(P)))$ (and vice versa).

Computing β ₁(M) for Orientable 2-Manifolds

It was shown in [11] that for a Morse function f:M→ℝ defined on a compact orientable surface M without boundary, one has rank(H ₁(M))=2⋅rank(H ₁(Rb _f (M))). Hence intuitively, using Theorem 4.7, we can compute β ₁(M)=rank(H ₁(M)) by $2 \cdot\mathrm{rank}(\mathsf{ H}_{1}(\mathsf{ Rb}_{f}(\mathcal{R}^{r}(P))))$ from an appropriate f and a Rips Complex $\mathcal{R}^{r}(P)$ constructed from a point sample P of M. Specifically, choose a function f:M→ℝ so that we can evaluate it at points in P. For example, pick a base point v∈P and define a function f _v (x) to be the Euclidean distance from x∈M to the base point v. Observe that the Lipschitz constant of this function f _v is at most 1. Our algorithm simply computes the Reeb graph $\mathsf{ Rb}_{f_{\mathbf{v}}}(\mathcal{R}^{r}(P))$ and returns $2\cdot\mathrm{rank}(\mathsf{ H}_{1}(\mathsf{ Rb}_{f_{\mathbf{v}}}(\mathcal{R}^{r}(P))))$.

Corollary 4.8

Let M be an orientable smooth compact 2-manifold M without boundary and P an ε-sample of M. The above algorithm computes β ₁(M) in O(nlogn) expected time if t ^∗(M) and s ^∗(M) are positive for the chosen function f, and the parameters satisfy $4{\varepsilon}\le r < \min\{ \frac{1}{4} \rho(\mathsf{ M}), \frac {1}{4}\rho_{c}(\mathsf{ M}), \frac{\mathbf{t}^{*}}{2 \mathrm{Lip}_{f}}, \frac {\mathbf{s}^{*}}{2\mathrm{Lip}_{f}} \}$.

Observe that a Morse function on an orientable 2-manifold provides positive t ^∗ and s ^∗. We remark that our algorithm produces a correct answer only under good choices of f and r; while previously, the best algorithm to estimate β ₁(M) only depends on choosing r small enough. The advantage of our algorithm is its efficiency, as the previous algorithm needs to compute the first-Betti number of the simplicial complex $\mathcal{R}^{r}(P)$ for certain r, which takes O(n ³) time no matter what the intrinsic dimension of M is, where n is the size of the 2-skeleton of $\mathcal{R}^{r}(P)$.

5 Persistent Reeb Graph

Imagine that we have a set of points P sampled from a hidden space X, and f:X→ℝ a function whose values at points in P are available. We wish to study this function f through its Reeb graph. A natural approach to approximate X from P is to construct a Rips complex $\mathcal{R}^{r}(P)$ from P. Since it is often unclear what the right value of r should be, it is desirable to compute a series of Reeb graphs from Rips complexes constructed with various r, and then find out which cycles in the Reeb graph persist. This calls for computing persistent homology groups for the sequence of Reeb graphs.

Let K ₁⊆K ₂⊆⋯⊆K _n be a filtration of a simplicial complex K _n . A piecewise-linear function f:|K _n |→ℝ provides a PL-function for every K _i , i∈[1,n]. Let R _i :=Rb _f (K _i ) denote the Reeb graph of f defined on the geometric realization |K _i | of K _i . Below we first show that there is a sequence of homomorphisms H ₁(R _i )→H ₁(R _i+1) induced by the inclusions K _i ⊂K _i+1. We then present an algorithm to compute the persistent homologies induced by these homomorphisms.

5.1 Persistent Reeb Graph Homology

Let Φ _i denote the associated quotient map from |K _i |→R _i , for any i∈[1,n]. Since the canonical inclusion |K _i |↪|K _j | respects the equivalence relation that defines the quotient space R _i , the maps Φ _i s, along with inclusions between K _j s, induce a well-defined continuous map between the quotient spaces ξ:R _i →R _j , for any i<j. Let ι _i denote the inclusion map from |K _i | to |K _i+1|, and ξ _i the induced map from R _i to R _i+1. We have the following diagram that commutes.

The sequence of continuous maps ξ _i induces the following sequence of homomorphisms:

Following [17], we can now define the persistent homology groups as the images of maps $\xi^{i,j}_{*}= \xi_{j*} \circ\cdots\circ\xi_{i*}: \mathsf{ H}_{1}(\mathbf{R}_{i}) \rightarrow\mathsf{ H}_{1}(\mathbf{R}_{j})$. In other words, the image consists of homology classes from H ₁(R _j ) that also have pre-images in H ₁(R _i ) (i.e., persist from H ₁(R _i ) to H ₁(R _j )). The persistent Betti number β ^i,j is defined as the rank of the persistent homology group . Set

$$\mu^{i,j} := \beta^{i-1,j} - \beta^{i,j} + \beta^{i,j-1} - \beta^{i-1,j-1}. $$

Intuitively, μ ^i,j is the number of independent loops created upon entering R _i and destroyed upon leaving R _j . A persistence pair (i,j) is recorded if μ ^i,j>0, and the value μ ^i,j indicates the multiplicity of this pairing.

We focus on persistent H ₁-homology for R _i s in this paper. The persistent H ₀-homology for R _i s is the same as persistent H ₀-homology for K _i s, and thus can be easily computed by a union-find data structure in near-linear time. We also remark that by Theorem 3.2, persistent H ₁-homology for R _i is isomorphic to persistent vertical homology $\breve{\mathsf{ H}}_{1}(|K_{i}|)$.⁵

5.2 Computation

We now present an algorithm to compute the persistent Betti number β ^i,j. The numbers μ ^i,j and the persistence pairs can be computed easily once we have these persistence Betti numbers.

Given a filtration K ₁⊆⋯⊆K _n , assume K _i+1∖K _i is one simplex. Since the Reeb graph is completely decided by the 2-skeleton of a simplicial complex, we assume that K _i s are 2-complexes. Let n _v , n _e and n _t denote the number of vertices, edges and triangles in K _n , and n=n _v +n _e +n _t . Observe that the complexity of each Reeb graph R _i , for i∈[1,n], is bounded by O(n _e ). The set of Reeb graphs R _i s can be computed in O(nn _v ) time using the incremental algorithm from [25]. We use this algorithm as it can also maintain the image of each edge from K _i in R _i in O(n _v ) time at each incremental step, thus providing Φ _i , for i∈[1,n].

Recall that a set of base cycles for H _p (⋅) is a set of cycles whose classes form a basis of H _p (⋅). For the sake of exposition in this section, we abuse the notation slightly and use a cycle to also refer to its carrier in the Reeb graph. Specifically, we will see later that our algorithm in fact maintains the carriers of a set of base cycles for H ₁(R _i ), which we also call a cycle-basis. We say that a set of cycles are independent if the set of homology classes these cycles represent are independent.

To compute β ^i,j, one can construct a set of base cycles {α ₁,…,α _r } for H ₁(R _i ) with r=rank(H ₁(R _i )), and check how many of their images in R _j remain independent. A straightforward implementation of this approach takes $O(n^{2} n_{e}^{3})$ time. Indeed, r=O(n _e ) and the complexity of each cycle α _i is bounded by O(n _v ) (by representing them as a sequence of vertices). Computing the images of all α _i s takes $O(r n_{v}^{2}) = O(n_{e} n_{v}^{2})$ time using the incremental algorithm from [25], and the independence test for these r cycles takes $O(r n_{e}^{2}) = O(n_{e}^{3})$ time.Finally, there are n ² pairs of i and j that we need to test, giving rise to $O(n^{2} n_{e}^{3})$ total time complexity. To improve the time complexity, we follow the idea of the standard persistence algorithm [19] and perform only one scan of the sequence of Reeb graphs, while maintaining a set of base cycles at any moment during the course.

Notice that the standard persistence algorithm cannot be directly applied to the sequence of Reeb graphs as there are no inclusions among them. In fact, the underlying spaces of two consecutive Reeb graphs can change dramatically. See Fig. 5 for such an example. We also remark that there may not be an inclusion relation between R _i and R _i+1 in either direction, that is, R _i ⊈R _i+1 and R _i ⊉R _i+1: see Case 3 discussed later. Hence while it is possible to model the persistent Reeb graph homology via zigzag persistence theory [4], the efficient algorithm to compute zigzag persistence as developed in [5] cannot yet be applied here.

Fig. 5

(a) shows a genus-g torus with the two caps missing; g=3 in this case. Darker color regions indicate the two holes (missing caps) on this torus. Its Reeb graph w.r.t. the height function is shown in (b). Now if we fill the left triangle, as shown in (c), then Θ(g) number of independent vertical homological classes become horizontal, thus killing Θ(g) number of loops in the Reeb graph, which is shown in (d). In other words, by adding just one simplex (a triangle), the first Betti number decreases by Θ(g)

Consistent Base Cycles

From now on, let G ⁽ⁱ⁾ denote the cycle-basis of H ₁(R _i ) that we maintain at the ith step. For each cycle γ∈G ⁽ⁱ⁾, we associate with it a birth-time t(γ), which is the earliest time (index) k≤i such that some pre-image of the homology class [γ] under the map $\xi^{k,i}_{*}: \mathsf{ H}_{1}(\mathbf{R}_{k}) \rightarrow\mathsf{ H}_{1}(\mathbf {R}_{i})$ exists. In order to extract β ^i,j, we wish to maintain the following consistency condition between G ⁽ⁱ⁾ and G ^(j): let ${\mathbf{G}^{({i})}} = \{ \alpha_{1}^{(i)}, \alpha_{2}^{(i)}, \ldots, \alpha_{r}^{(i)} \}$ and ${\mathbf{G}^{({j})}} = \{ \alpha_{1}^{(j)}, \ldots, \alpha_{s}^{(j)} \}$. Consider the set $\widehat{G}$ of images of cycles $\{\alpha_{l}^{(i)}\}$ in R _j . G ⁽ⁱ⁾ and G ^(j) are consistent if the cardinality of $\widehat{G} \cap{\mathbf{G}^{({j})}}$ is exactly β ^i,j. Notice that there are always β ^i,j number of independent cycles in $\widehat{G}$. However, its intersection with G ^(j) may have much smaller cardinality. A sequence of cycle-bases {G ⁽ⁱ⁾∣i∈[1,n]} is consistent if the consistency condition holds for any pair G ⁽ⁱ⁾ and G ^(j), 0≤i<j≤n. The following claim implies that we can read off β ^i,j easily from a consistent sequence of cycle-bases.

Lemma 5.1

If a sequence of cycle-bases {G ⁽ⁱ⁾∣i∈[1,n]} is consistent, then for any 1≤i<j≤n, β ^i,j equals the number of cycles in G ^(j) whose birth-time is smaller than or equal to i.

Proof

Consider a pair of indices i<j and the corresponding cycle-basis G ⁽ⁱ⁾ for H ₁(R _i ) and G ^(j) for H ₁(R _j ). Assume that there are k cycles in G ^(j) with birth-time smaller than or equal to i. Since all these cycles are independent in R _j (and thus in ξ ^i,j(R _i )), we have k≤β ^i,j. On the other hand, since G ⁽ⁱ⁾ and G ^(j) are consistent, we have k≥β ^i,j, implying that k=β ^i,j. □

Algorithm Description

In light of Lemma 5.1, our goal is to maintain consistent cycle-bases at any moment. We now describe how we update the set of base cycles as we move from K _k to K _k+1=K _k∪{σ}; σ can be a 0-, 1-, or 2-simplex. Set g _i :=rank(H ₁(R _i )) for any i∈[1,n]. Assume at kth step we already have consistent {G ⁽ⁱ⁾∣i∈[1,k]}. For each cycle-basis G ⁽ⁱ⁾, we also maintain the birth-time of each cycle in it. Assume cycles in ${\mathbf{G}^{({{\mathrm{k}}})}} = \{ \mathrm{\gamma}_{1}, \ldots, \mathrm{\gamma}_{\mathrm{g}_{\mathrm{k}}} \}$ are sorted by their birth-times. At the beginning of the kth step, we first use the incremental algorithm from [25] to compute the Reeb graph R _k+1 from R _k. We next need to update G ^(k) to G ^(k+1) for R _k+1 so that G ^(k+1) is consistent with each G ⁽ⁱ⁾ for i∈[1,k]. There are three cases.

Case 1: σ is a vertex.

A new connected component is created in K _k+1, consisting of only σ. Similarly, a new node is created in R _k+1. The set of base 1-cycles are not affected, and G ^(k+1)=G ^(k).

Case 2: σ=pq is an edge.

Let $\widehat{p} = \varPhi_{\mathrm{k}}(p)$ and $\widehat{q} = \varPhi_{\mathrm{k}}(q)$ be the images of endpoints p and q of σ in the Reeb graph R _k. Adding σ to K _k creates a new edge $e = \widehat{p}\,\widehat{q}$ in R _k+1. If $\widehat{p}$ and $\widehat{q}$ are not in the same connected component in R _k, then adding e will only reduce the rank of H ₀(R _k) by 1 and does not affect H ₁(R _k). In that case G ^(k+1)=G ^(k). Otherwise, $\widehat{p}$ and $\widehat{q}$ are already connected in R _k. Adding e results in rank(H ₁(R _k+1))=rank(H ₁(R _k))+1. Let γ be any cycle in R _k+1 that contains e (which can be computed easily in linear time). All previous base cycles in G ^(k) will remain independent in R _k+1, and we simply set G ^(k+1)=G ^(k)∪{γ}. The birth-time for γ is k+1.

Case 3: σ is a triangle.

The first two cases are simple and similar to the cases of standard persistence algorithm. Case 3 is much more complicated. In particular, unlike the standard persistence algorithm wherein adding a triangle may reduce β ₁ by at most 1, the rank of H ₁(R _k) may decrease by Θ(g_k). What happens is that even though β ₁(K _k) is reduced by at most 1, arbitrary number of vertical homology classes can be converted into horizontal homology classes. An example is given in Fig. 5.

Let σ=△pqr, and let $\widehat{p} = \varPhi_{\mathrm {k}}(p)$, $\widehat{q} = \varPhi_{\mathrm{k}}(q)$ and $\widehat{r} = \varPhi_{\mathrm{k}}(r)$ be the images of the three endpoints of σ in R _k, respectively. Assume without loss of generality that f(p)≤f(q)≤f(r), and set e ₁=pq, e ₂=qr and e ₃=pr. First, we compute the image of each e _i in R _k, which is necessarily a monotone path (i.e., monotonic in function values) denoted by π _i =Φ _k(e _i ). These images can be computed in O(n _v ) time using the incremental algorithm and the data structure of [25]. By our assumption of f(p)≤f(q)≤f(r), π ₁ and π ₂ are disjoint in their interiors, while π ₃ may share subcurves with π ₁ and π ₂. Set π _1,2:=π ₁∘π ₂ to be the concatenation of π ₁ and π ₂, which is still a monotone path, and note π _1,2 and π ₃ share the same two endpoints.

Now if π _1,2 and π ₃ coincide in R _k, the addition of triangle σ does not ensue any change, that is, R _k+1=R _k and G ^(k+1)=G ^(k). In this case, the vertical homology of K _k remains the same; either σ destroys a horizontal homology class in H ₁(K _k), or it creates a 2-cycle.

Otherwise, the H ₁-homology of the Reeb graph changes. Assume the two monotone paths π _1,2 and π ₃ form s simple loops between them (see the figure below where s=3). Then, with the addition of σ, each point in π ₃ is mapped to the corresponding point in π _1,2 with the same function value. Hence this process collapses all these s independent loops and we have g_k+1=g_k−s.

We now describe how to compute G ^(k+1) for this case. First, we need to compute the image $\widehat{G}:=\xi_{\mathrm {k}}({\mathbf{G}^{({{\mathrm{k}}})}})$ of the set of base cycles G ^(k) in R _k+1. To do this, we need the map ξ _k. Observe that ξ _k maps each edge in R _k either to the same edge in R _k+1, or to a monotone path in R _k+1. The latter case can potentially happen only for edges in the paths π _1,2 and π ₃—in particular, for those edges in subcurves from π _1,2 and π ₃ that are merged together. Since both π _1,2 and π ₃ are monotone, images of edges from π _1,2 and π ₃ can be computed in O(|π _1,2|+|π ₃|)=O(n _v ) time by merging the sorted lists of vertices in π _1,2 and π ₃. Hence we can compute the map ξ _k in O(n _v ) time.

Once ξ _k is computed, given a simple cycle γ from R _k, we can compute its image in R _k+1 in O(n _v ) time. This is because (i) there are O(n _v ) number of edges in γ; and (ii) the total size of the images of edges from γ in R _k+1 has an upper bound |γ|+|ξ _k(π _1,2)|+|ξ _k(π ₃)|=O(n _v ). The set of cycles $\widehat{G}:=\xi_{\mathrm{k}}({\mathbf {G}^{({{\mathrm{k}}})}})$ in R _k+1 can then be computed in O(n _v g_k) time. Let $\widehat{G} = \{ \widehat{\mathrm{\gamma}}_{1}, \ldots, \widehat{\mathrm{\gamma}}_{\mathrm{g}_{\mathrm{k}}} \}$.

The remaining task is to construct G ^(k+1) that is consistent with G ⁽ⁱ⁾ for any i≤k. One needs $\mathrm{g}_{{\mathrm{k}}+1}= \mathrm{rank}(\xi^{{\mathrm {k}},{\mathrm{k}}+1}_{*})$ independent cycles from $\widehat{G}$ to make G ^(k+1) consistent with G ^(k). To this end, we perform the following two steps.

• (S1) We represent each cycle in $\widehat{G}$ as a linear combination of cycles in a basis for the graph R _k+1.

• (S2) We check the dependency of cycles in $\widehat{G}$ in order of their birth-times, and remove redundant cycles to obtain G ^(k+1).

Step (S1) Since R _k+1 is a graph, we compute a canonical basis of cycles, $B = \{\alpha_{1}, \ldots, \alpha_{\mathrm{g}_{{\mathrm{k}}+1}}\}$, in the following standard way. Construct an arbitrary spanning tree T of R _k+1. Let $E = \{e_{1}, \ldots, e_{\mathrm{g}_{{\mathrm{k}}+1}} \}$ denote the set of non-tree edges in R _k+1. Each edge e _i =pq∈E creates a canonical cycle that concatenates edge e _i with the two unique paths in T from p and q to their common ancestor. We set α _i to be this canonical cycle created by e _i . Obviously, each e _i appears exactly once among all cycles in B. Given a cycle $\gamma\in\widehat{G}$, we need to find coefficients c _i s such that $\gamma= \sum_{i = 1}^{\mathrm{g}_{{\mathrm{k}}+1}} c_{i}\alpha_{i}$, where each c _i is either 0 or 1. Since e _i appears only in α _i , we have c _i equal the number of times e _i appears in γ modulo 2. Since γ is a simple curve, c _i is 1 if e _i ∈γ and 0 otherwise. Hence all c _i s for i∈[1,g_k+1] can be computed in O(n _v ) time for one curve γ. Computing the coefficients of all cycles in $\widehat{G}$ takes O(n _v g_k) time.

Step (S2) Recall that cycles in ${\mathbf{G}^{({k})}} = \{\mathrm{\gamma}_{1}, \ldots, \mathrm{\gamma}_{\mathrm{g}_{\mathrm{k}}} \}$ are sorted by increasing order of their birth-times. Note that the birth-time of the cycle $\widehat{\mathrm{\gamma}}_{i} \in\widehat{G}$, which is the image of the cycle $\mathrm{\gamma}_{i} \in{\mathbf{G}^{({{\mathrm{k}}})}}$ in R _k+1, may be smaller than the birth-time of $\mathrm{\gamma}_{i}$. Now represent cycles in $\widehat{G}$ with respect to the canonical basis $B = \{\alpha_{1}, \ldots, \alpha_{\mathrm{g}_{{\mathrm{k}}+1}} \}$ in a matrix M, where the ith column of M, denoted by col _M [i], contains the coordinates of $\widehat{\mathrm{\gamma}}_{i}$ under basis B; that is, $\widehat{\mathrm{\gamma}}_{i} = \sum_{j=1}^{g_{{\mathrm{k}}+1}} \mathrm{col}_{M}[i][j] \alpha_{j}$. Obviously, the matrix M has size g_k×g_k+1.

Next, we perform a left-to-right reduction of matrix M, which is the same as the reduction of the adjacency matrix used in the standard persistence algorithm [10, 19]. In particular, the only operation that one can use is to add a column to another one on its right. For a column col _M [i], let its low-row index denote the largest index j such that col _M [i][j]=1. At the end of the reduction, each column is either empty or has a unique low-row index; that is, no other column can have the same low-row index as this one. We set G ^(k+1) as the subset of $\widehat{G}$ whose corresponding columns in the reduced matrix M′ is not all zeros. The reduction takes time $O(\mathrm{g}_{{\mathrm{k}}+1} \mathrm {g}_{\mathrm{k}}^{2})$. Intuitively, the consistency of G ^(k+1) with each G ⁽ⁱ⁾ for i∈[1,k] follows from the left-to-right reduction. It guarantees that if a set of cycles in $\widehat{G}$ are dependent, then only those created earlier (i.e., with smaller birth-time) will be kept.

Lemma 5.2

G ^(k+1) as constructed above provides a basis of H ₁(R _k+1). Furthermore, if {G ⁽¹⁾,…,G ^(k)} is consistent, so is {G ⁽¹⁾,…,G ^(k+1)}.

Proof

Let M′ denote the reduced matrix of M. Recall that $\widehat{G} = \{\widehat{\mathrm{\gamma}}_{1}, \ldots, \widehat{\mathrm{\gamma}}_{\mathrm{g}_{\mathrm{k}}} \}$ contains the images of cycles from G ^(k) in R _k+1. Set $\widehat{G}_{i} = \{ \widehat{\mathrm{\gamma}}_{1}, \ldots, \widehat{\mathrm{\gamma}}_{i} \}$, and let $G'_{i}$ be the set of cycles from $\widehat{G}_{i}$ whose corresponding column in the reduced matrix M′ is non-empty (i.e., not all zeros). In other words, $G'_{i} = \widehat{G}_{i} \cap{\mathbf{G}^{({{\mathrm {k}}+1})}}$ is the intersection between $\widehat{G}_{i}$ and the set G ^(k+1) constructed by our algorithm. By induction on i, it is easy to show that for any i∈[1,g_k], cycles in $G_{i}'$ generate the same subgroup of H ₁(R _k+1) as $\widehat{G}_{i}$. It then follows that, in the end, cycles in ${\mathbf{G}^{({{\mathrm{k}}+1})}} = G'_{\mathrm{g}_{\mathrm{k}}}$ are all independent in R _k+1 and |G ^(k+1)| equals the rank of the homology group generated by cycles in $\widehat{G}$, which is β ^k,k+1=g_k+1. This proves the first part of the claim.

For the second part of the claim, first note that G ^(k+1) is consistent with G ^(k) as $\widehat{G} \cap{\mathbf{G}^{({{\mathrm{k}}+1})}} = {\mathbf {G}^{({{\mathrm{k}}+1})}}$ and has cardinality g_k+1. Now consider an arbitrary G ⁽ⁱ⁾ with i<k. Since {G ⁽¹⁾,…,G ^(k)} are consistent,and cycles $\{ \mathrm{\gamma}_{1}, \ldots, \mathrm{\gamma}_{\mathrm {g}_{\mathrm{k}}} \}$ in G ^(k) are sorted by their birth-times, it follows from Lemma 5.1 that the first s=β ^i,k number of cycles $G_{s} = \{ \mathrm{\gamma}_{1}, \ldots, \mathrm{\gamma}_{s} \}$ from G ^(k) are images of cycles from G ⁽ⁱ⁾. Hence the image of cycles from G ⁽ⁱ⁾ in R _k+1 are exactly the cycles in $\widehat{G}_{s}$, and classes of cycles in $\widehat{G}_{s}$ generate the persistent homology group $\xi^{i,{\mathrm{k}}+1}_{*}(\mathsf{ H}_{1}(\mathsf{ Rb}_{f}(K_{i})))$. On the other hand, as mentioned above, classes of cycles in $G'_{s} = \widehat{G}_{s} \cap{\mathbf {G}^{({{\mathrm{k}}+1})}}$ generate the same subgroup of H ₁(R _k+1) as $\widehat{G}_{s}$. Since cycles in $G'_{s}$ are independent, $G'_{s}$ has rank β ^i,k+1, implying that G ^(k+1) is consistent with G ⁽ⁱ⁾, for any i∈[1,k]. The second part of the claim then follows. □

Finally, for our algorithm to continue into the next iteration, we also need to maintain the birth-times for each cycle in G ^(k+1). This is achieved by the following claim.

Claim 5.3

Let ${\mathbf{G}^{({{\mathrm{k}}+1})}} = \{ \widehat{\mathrm{\gamma }}_{I_{1}}, \ldots, \widehat{\mathrm{\gamma}}_{I_{\mathrm {g}_{{\mathrm{k}}+1}}} \}$, where I _i s are the set of indices of non-zero columns in the reduced matrix M′. Then the birth-time of $\widehat{\mathrm{\gamma}}_{I_{i}}$ equals the birth-time of $\mathrm{\gamma}_{I_{i}}$ for any i∈[1,g_k+1].

Proof

Recall that G ^(k+1) contains the set of cycles $\widehat{\mathrm{\gamma}}_{I_{i}}$ where {I _i } is the set of indices of non-zero columns from the reduced matrix M′. Given a cycle α∈G ⁽ⁱ⁾, let birthtime(α) denote the birth-time of α. Assume that one of the cycles, say $\widehat{\mathrm{\gamma}}_{m} \in {\mathbf{G}^{({{\mathrm{k}}+1})}}$, has a birth-time that is different from that of $\mathrm{\gamma}_{m} \in{\mathbf{G}^{({{\mathrm{k}}})}}$. Set $t:=\mathit{birthtime}(\widehat{\mathrm{\gamma}}_{m})$. Since $\widehat{\mathrm{\gamma}}_{m} = \xi^{\mathrm{k}}(\mathrm {\gamma}_{m})$, we have $t \le\mathit{birthtime}(\mathrm{\gamma}_{m})$. Since the two birth-times are different, t must be strictly smaller than the birth-time of $\mathrm{\gamma}_{m}$.

Furthermore, there exists a cycle α∈R _t such that its image α ₁:=ξ ^t,k(α) in R _k is not homologous to $\mathrm{\gamma}_{m}$, while its image α ₂:=ξ ^t,k+1(α) in R _k+1 is $\widehat{\mathrm{\gamma}}_{m}$. On the other hand, α ₁ can be uniquely written as a linear combination of a subset of cycles from G ^(k), say $\alpha_{1} = \mathrm{\gamma}_{J_{1}} + \cdots+ \mathrm{\gamma}_{J_{r}}$. It is easy to verify that the birth-time of each $\mathrm{\gamma}_{J_{i}}$ is at most t. Since $t < \mathit{birthtime}(\mathrm{\gamma}_{m})$, it follows that all indices J _i s are strictly smaller than m (as cycles in G ^(k) are sorted by their birth-times). However, this is not possible since the resulting mth column will be all zero at the time when we reduce the mth column to construct G ^(k+1) as $\widehat{\mathrm{\gamma}}_{m} = \sum_{i} \widehat{\mathrm {\gamma}}_{J_{i}}$. Hence the cycle $\widehat{\mathrm{\gamma}}_{m}$ cannot be chosen as a base cycle in G ^(k+1) reaching a contradiction. It follows that $t = \mathit{birthtime}(\mathrm{\gamma}_{m})$, or more generally, $\mathit{birthtime}(\widehat{\mathrm{\gamma}}_{I_{i}}) = \mathit{birthtime}(\mathrm{\gamma}_{I_{i}})$ for every index I _i of non-zero column in the reduced matrix M′. □

Putting everything together, we conclude with the following main result.

Theorem 5.4

Given a filtration K ₁⊂⋯⊂K _n of a simplicial complex K _n with a piecewise-linear function f:K _n →ℝ, we can compute all persistent first Betti numbers for the induced sequence of Reeb graphs Rb _f (K _i )s in $O(\sum_{i=1}^{n} (n_{v}\mathrm{g}_{i} + \mathrm{g}_{i}^{3})) =O(nn_{e}^{3})$ time, where n _v and n _e are the number of vertices and edges in K _n , respectively, n is the size of 2-skeleton of K _n , and g _i is the first Betti number of the Reeb graph Rb _f (K _i ).

6 Conclusions and Discussions

In this paper, we present a simple and efficient algorithm to approximate the Reeb graph Rb _f (M) of a map f:M→ℝ from point data sampled from a smooth and compact manifold M. Given that Reeb graph is an abstract graph with a function defined on it, we only approximate its topology together with the range information for each loop in it. It will be interesting to see whether the Reeb graph we compute from the point data is also geometrically close to some specific embedding of the Reeb graph Rb _f (M) in the hidden domain M. To this end, our results in Sect. 4.1 on mappings between cycles can be useful.

We also study how to compute the “persistence” of loops in a Reeb graph by measuring their life time as the defining domain grows. An immediate question is to see whether the time complexity can be further improved to match that of the standard persistence algorithm in the worst case.

Finally, it will be interesting to explore whether one can leverage the simple structure and efficient computation of the Reeb graph to retrieve topological information for various spaces efficiently. For example, given a 3-manifold with a function f defined on it, its vertical H ₁-homology is already encoded in the Reeb graph and can thus be computed in near-linear time. Can we retrieve the horizontal H ₁-homology efficiently by tracking the level sets of f, or by defining another function that is somewhat “orthogonal” to f?

Appendices

Appendix A: Proof for Lemma 4.3

Proof of Claim (i)

Lemma 4.2 implies that h_# induces an isomorphism $\mathrm{h}_{*}: \mathsf{ H}_{1}(\mathcal{R}^{r}(P)) \rightarrow \mathsf{ H}_{1}(\mathsf{ M})$. We now prove the second part of claim (i).

First, we show the following two results: (C-1) given a cycle α from Z ₁(M), [α]=[h_#(d(α))]; and (C-2) given a cycle $\hat{\alpha}\in\mathbf{Z}_{1}(\mathcal {R}^{r}(P))$, we have $[\hat{\alpha}] = [\mathrm{d}(\mathrm{h}_{\# }(\hat{\alpha}))]$. Note that cycles in $\mathbf{Z}_{1}(\mathcal{R}^{r}(P))$ are simplicial cycles, while cycles in Z ₁(M) are singular cycles.

These two results (C-1) and (C-2) imply that d maps homologous cycles from Z ₁(M) to homologous cycles in $\mathbf{Z}_{1}(\mathcal{R}^{r}(P))$. Hence it indeed induces a homomorphism $\mathrm{d}_{*}: \mathsf{ H}_{1}(\mathsf{ M}) \rightarrow\mathsf{ H}_{1}(\mathcal{R}^{r}(P))$. Furthermore, these two results mean that d_∗ is the inverse of the map h_∗. Since h_∗ is an isomorphism, so is d_∗. This proves Claim (i) of the lemma.

Proof of (C-1)

We show that given a cycle α from Z ₁(M), [α]=[h_#(d(α))]. Let γ⊆M be the carrier of α. To map α to d(α), suppose that its carrier γ is broken into k pieces as described earlier using the Decomposition method. For the ith piece with endpoints x _i and x _i+1, let p _i and p _i+1 be their closest point in P, respectively; recall that d(α) is the concatenation of all edges p _i p _i+1 for i∈[1,k].

Now consider the cycle h_#(d(α)) in M: its carrier γ′ is the concatenation of h(p _i p _i+1)⊂M for all i∈[1,k]. By Proposition 3.3 of [14], each curve h(p _i p _i+1) has endpoints p _i and p _i+1, and it is contained in the union of the two Euclidean balls of radius r centered at p _i and at p _i+1. Since p _i and p _i+1 are within r Euclidean distance, h(p _i p _i+1) is contained in the Euclidean balls of radius 2r centered at p _i and at p _i+1. Notice that the geodesic distance and the Euclidean distance between two points x,y∈M approximate each other when x and y are close enough (see e.g., Proposition 1.2 from [14]). It follows that when r is smaller than ρ(M)/4, h(p _i p _i+1) is contained in both geodesic balls of radius 3r centered at p _i ∈M and p _i+1∈M.

Let γ[x _i ,x _i+1] denote the subcurve of γ from x _i to x _i+1. Since the length of γ[x _i ,x _i+1] is less than r by construction, the curve γ[x _i ,x _i+1] is contained in the geodesic balls of radius r centered at x _i and x _i+1. This implies that the curve γ[x _i ,x _i+1] is contained in the geodesic tubular neighborhood

$$\mathrm{Tub}_r\bigl(\pi_g(x_i, x_{i+1})\bigr) := \bigl\{ y \in\mathsf{ M}\mid d\bigl(y, \pi_g(x_i, x_{i+1}) \bigr) \le r \bigr\} $$

where π _g (x,y) denote a minimizing geodesic between two points x,y∈M. By Proposition 3.7 of [14], Tub _r (π _g (x _i ,x _i+1)) is contractible and hence γ[x _i ,x _i+1] is homotopy equivalent to π _g (x _i ,x _i+1).

On the other hand, due to the sampling condition, the geodesic distances between x _i and p _i , and between x _i+1 and p _i+1, are both bounded by r. Combining this with the fact that h(p _i p _i+1) lies within the geodesic balls of radius 3r centered at both p _i and p _i+1, we see that any point in h(p _i p _i+1) is within geodesic distance 4r to both x _i and to x _i+1. Hence h(p _i p _i+1) lies within the geodesic tubular neighborhood Tub_4r (π _g (x _i ,x _i+1)). Again by Proposition 3.7 of [14], when r≤ρ _c (M)/4, the curve π _g (x _i ,p _i )∘h(p _i p _i+1)∘π _g (p _i+1,x _i+1) is homotopy equivalent to π _g (x _i ,x _i+1) and thus homotopy equivalent to γ[x _i ,x _i+1]. In fact, one can find a homotopy h _i that keeps p _i and p _i+1 on the geodesics π _g (x _i ,p _i ) and π _g (x _i+1,p _i+1), respectively, so that two maps h _i and h _i+1, for i∈[1,k−1], are consistent in mapping the common endpoints x _i+1. Therefore, we can combine all such h _i ’s to obtain a homotopy between γ′ (which is the carrier of h_#(d(α))) and γ (which is the carrier of α). It follows that [h_#∘d(α)]=[α]. □

Proof of (C-2)

We now show that given any (simplicial) cycle $\hat{\alpha}\in \mathbf{Z}_{1}(\mathcal{R}^{r}(P))$, we have $[\hat{\alpha}] = [\mathrm {d}\circ\mathrm{h}_{\#}(\hat{\alpha})]$. First, consider the image $\gamma= \mathrm{h}(\hat{\alpha})$ of $\hat{\alpha}$ in M; γ is the carrier of the cycle $\mathrm{h}_{\#}(\hat{\alpha}) \in\mathbf{Z}_{1}(\mathsf{ M})$. By construction, γ is the concatenation of h(e)s for every edge e=pq in the simplicial cycle $\hat{\alpha}$. By Proposition 3.3 in [14], each curve h(e) is contained inside M∩(B _r (p)∪B _r (q)). Hence, for any point x∈h(e), its geodesic distance to p and to q is bounded by 3r.

Now consider mapping the cycle $\mathrm{h}_{\#}(\hat{\alpha})$ carried by γ back to $\mathcal{R}^{r}(P)$ using the decomposition method described earlier. Consider the set of breaking points x _i ’s in the subcurve h(e)⊂γ—assume for simplicity that the endpoints of h(e), that is, p and q, are also break points. Each break point x _i in h(e) will be mapped to its nearest point p _i ∈P and the geodesic distance between x _i and p _i is at most r. Hence p _i is within 3r+r=4r geodesic distance to both endpoints p and q of the edge $e \subset\hat{\alpha}$. This means that both p _i p and p _i q are edges in the Rips complex $\mathcal{R}^{4r}(P)$. Hence the concatenation of arcs p _i p _i+1 is homotopy equivalent to the edge e in the simplicial complex $\mathcal{R}^{4r}(P)$. Combining this homotopy equivalent map for every edge $e \in\hat{\alpha}$, we find that $\mathrm{d}(\mathrm{h}_{\#}(\hat{\alpha}))$ is homotopy equivalent, and thus homologous, to $\hat{\alpha}$ in $\mathcal{R}^{4r}(P)$. Finally, since the inclusion map from $\mathcal{R}^{r}(P)$ to $\mathcal {R}^{4r}(P)$ induces an isomorphism in the first homology groups when r is small, we see that $\mathrm{d}(\mathrm{h}_{\#}(\hat{\alpha}))$ is homologous to $\hat{\alpha}$ in $\mathcal{R}^{r}(P)$ as well. Thus $[\hat{\alpha}] = [\mathrm{d}(\mathrm{h}_{\#}(\hat{\alpha}))]$. □

Proof of Claim (ii)

Claim (ii) follows easily from the constructions of d and h. In particular, consider a cycle α∈Z ₁(M) and $\mathrm{d}(\alpha) \in\mathbf{Z}_{1}(\mathcal {R}^{r}(P))$. (The case for $\hat{\alpha}$ from $\mathbf{Z}_{1}(\mathcal {R}^{r}(P))$ and $\mathrm{h}_{\#}(\hat{\alpha})$ from Z ₁(M) can be similarly argued.) Let γ⊂M be the carrier of α. The Decomposition method breaks γ into k pieces γ(x _i ,x _i+1)s, for i∈[0,k]. Each piece γ(x _i ,x _i+1) is mapped to the edge p _i p _i+1 where p _i is the closest point of x _i in P. Since P is an ε-sample of M, and since the length of γ(x _i ,x _i+1) is at most r−2ε, any point x in γ(x _i ,x _i+1) is within r geodesic distance to the point p _i ∈M. Hence by the Lipschitz condition of f, we have |f(x _i )−f(p _i )|≤r⋅Lip _f . It follows that

On the other hand, note that under $\mathrm{\mathbb{Z}}_{2}$ coefficient, range(d(α))⊆[min _i∈[0,k] f(p _i ),max _i∈[0,k] f(p _i )] (and it can be much smaller than this interval). It then follows that range(d(α)) is oneside-(r⋅Lip _f )-close to range(α). □

Proof of Claim (iii)

Consider any homology class ω∈H ₁(M). By Claim (ii) we see that the range of d_∗(ω) is oneside-(r⋅Lip _f )-close to the range of ω: indeed, choose the thinnest cycle α of ω, we have range(d(α)) is oneside-(r⋅Lip _f )-close to range(α)=range(ω). Since range(d_∗(ω))⊆range(d(α)), range(d_∗(ω)) is also oneside-(r⋅Lip _f )-close to range(ω).

Now map d_∗(ω) back to H ₁(M), we find that the range of h_∗(d_∗(ω)) is also oneside-(r⋅Lip _f )-close to the range of d_∗(ω) by Claim (ii). Since h_∗(d_∗(ω))=ω, the ranges of ω and d_∗(ω) are (r⋅Lip _f )-Hausdorff-close.

The statement for $\hat{\omega}$ and $\mathrm{h}_{*}(\hat{\omega})$ can be argued similarly. □

Appendix B: Existence of a Set of 0-Height Basis for $\overline{\mathsf{ H}}_{1}(\mathsf{ M})$

Recall that $s = \mathrm{rank}(\overline{\mathsf{ H}}_{1}(\mathsf{ M}))$. We now show how to construct a basis {h ₁,…,h _s } for the horizontal subgroup $\overline{\mathsf{ H}}_{1}(\mathsf{ M}) \subset\mathsf{ H}_{1}(\mathsf{ M})$ such that height(h _i )=0 for any i∈[1,s].

Suppose we have already constructed a partial basis H _k−1:={h ₁,…,h _k−1}, each of which has 0-height. Our goal is to find a 0-height class h _k that is independent of elements in H _k−1. In particular, let h be any horizontal homology class that is independent of H _k−1. By definition, we can find a representative cycle $\gamma= \sum_{i=1}^{r} \gamma_{i}$ of h such that each γ _i is contained in a distinct level set of M. Take γ ₁: if [γ ₁] is independent of H _k−1, then simply set h _k =[γ ₁]. Otherwise, consider the cycle $\gamma' = \sum_{i=2}^{r}$ and obviously [γ′] is necessarily independent of classes in H _k−1. Now set h to be γ′ and repeat the above process. Either we terminate when some γ _i which is independent of classes in H _k−1, in which case we set h _k =[γ _i ] which is of height zero. Or the process ends when h can be represented by a cycle γ which itself is contained in a level set. In this case, set h _k =h, which is again of height 0.

Perform the above procedure for s rounds. In the end, H _s gives the desired 0-height basis for $\overline{ \mathsf{ H}}_{1}(\mathsf{ M})$. Note that by this construction, we also obtain a corresponding set of 0-height base cycles for $\overline{\mathsf{ H}}_{1}(\mathsf{ M})$.