Abstract
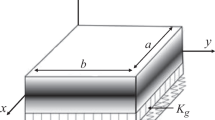
The subject of the study is an orthotropic thin-walled sandwich band plate with trapezoidal main core and three-layer facings. The external sheets of the faces are flat, whereas the core of the faces is trapezoidal corrugated. The directions of the corrugations of both cores are perpendicular to each other. The band plate considered in this paper has the crosswise corrugated main core and the lengthwise corrugated core of the faces. The main goal of the study is to solve the problem of buckling and vibrations of the band plates. The mathematical and physical model of this band plate has been formulated, in particular the field of displacement and rigidities of corrugated layers which are both original elements of the work. The system of equations of motion is analytically derived using the energy method. The obtained solutions are verified numerically. The finite element analysis of stability of the sandwich band plate is performed with the use of the ABAQUS and ANSYS systems.
Similar content being viewed by others
1 Introduction
A sandwich structure is the answer for the need of a light and rigid construction. Depending on the application sandwich structures may take many different forms. A classical solution is the composition of two thin and rigid faces with a light, relatively thick, core closed between them. The core can be made of the foam, polyurethane or metal one, wood or corrugated sheet. Since the total thickness of a sandwich beam or plate is high and the properties of particular layers are distinctly different, a proper theoretical description of the behaviour of such structures is needed.
The theoretical bases for sandwich beams are described in the literature [1, 2]. Computational models for sandwich plates and shells, predictor-corrector procedures, and the sensitivity of the response of a sandwich structure to variations in geometric and material parameters have been studied by Noor et al. [3]. Carlsson et al. [4] derived tension, shear, bending and twisting rigidities for sandwich structures with a corrugated core. Analytical description of the shear stiffness of a corrugated core can be found in [5–7]. Carrera [9] formulated the zigzag hypotheses for multilayered plates. The paper by Buannic et al. [10] is devoted to the computation of the effective properties of sandwich panels with a corrugated core. Porous plates with mechanical properties which vary through the thickness are analysed by Magnucki et al. [11]. Zenkour [8] applied the simple and mixed first-order shear deformable plate theories to develop analytical solutions for deflections and stresses of rectangular plates. Talbi et al. [12] presented an analytical homogenization model for corrugated cardboard and its numerical implementation in the FE method with the use of shell elements. In the work by Cheng et al. [13] authors employed the finite element method (FEM) to derive equivalent stiffness properties of sandwich structures with various types of cores. Similar results can be found in [14, 15]. Magnucki et al. [16] presented analytical and numerical (FEM) calculations as well as experimental verification of the obtained results devoted to a sandwich beam with a crosswise or lengthwise corrugated core. The considered beam was made of an aluminium alloy. The plane faces (outer layers) and the corrugated core were glued together. Global buckling of sandwich beam-rectangular plates and columns with metal foam core has been analysed by Jasion et al. [17] and Jasion and Magnucki [18]. Local phenomena in beams and columns have been described by Hadi [19] and Jasion and Magnucki [20], to mention a few.
The current work was inspired by the results obtained in the following papers [21–26]. The subject of the study is an orthotropic sandwich band plate. The plate is composed of seven layers as shown in Fig. 1—the main core and two three-layer faces. The main core is a crosswise corrugated sheet with the corrugation in the form of trapezoid. The core of the faces, closed between two flat sheets—internal and external—is also a corrugated sheet with the same type of corrugation, yet the direction of corrugation is perpendicular to the direction of the corrugation of the main core. The material of all seven layers is an isotropic one.
The goal of the present paper is to formulate the mathematical and physical model of the band plate. The field of displacements has been defined in the way to take into account the shear effect which appear in the core of the faces. This hypothesis makes a basis for formulation of displacements, strains, stresses and equilibrium equations. Moreover the finite element model (FE model) of the band plate has been prepared, and the results from the FE analyses were compared to the results of the analytical solution. Two types of analyses have been performed. First, the buckling analysis is to determine the buckling modes and buckling load for a family of band plates. Second, the modal analysis is to investigate the influence of the length of the band plate on the natural frequencies as well as on the modes of vibrations.
2 Analytical studies
The field of displacements of the cross section of the band plate has been assumed as it is presented in Fig. 2. The following symbols have been introduced: the thickness of the main core \(t_{\mathrm{c}1}\), the thickness of the core of the faces \(t_{\mathrm{c}2}\), and the thickness of the flat sheets of the faces \(t_\mathrm{s}\).
In this section the following field of displacements is introduced:
-
the outer sheets:
-
the upper sheet—\(\left( \frac{1}{2}t_{\mathrm{c}1}+2t_\mathrm{s}+t_\mathrm{c2} \right) \le z \le -\left( \frac{1}{2}t_{\mathrm{c}1}+t_\mathrm{s}+t_{\mathrm{c}2} \right) \)
$$\begin{aligned} v(y,z)=-z\frac{\mathrm{d}w}{\mathrm{d}y}-v_1(y), \end{aligned}$$(1) -
the lower sheet \(\frac{1}{2}t_\mathrm{c1}+t_\mathrm{s}+t_\mathrm{c2}\le z \le \frac{1}{2}t_\mathrm{c1}+2t_\mathrm{s}+t_\mathrm{c2}\)
$$\begin{aligned} v(y,z)=-z\frac{\hbox {d}w}{\mathrm{d}y}+v_1(y), \end{aligned}$$(2)
-
-
the lengthwise corrugated cores of facings:
-
the upper core \(-\left( \frac{1}{2}t_\mathrm{c1}+t_\mathrm{s}+t_\mathrm{c2} \right) \le z \le -\left( \frac{1}{2}t_\mathrm{c1}+t_\mathrm{s}\right) \)
$$\begin{aligned} v(y,z)=-z\frac{\mathrm{d}w}{\mathrm{d}y}+\left[ z+t_\mathrm{c1}\left( \frac{1}{2}+x_1\right) \right] \phi (y), \end{aligned}$$(3) -
the lower core \(\frac{1}{2}t_\mathrm{c1}+t_\mathrm{s} \le z \le \frac{1}{2}t_\mathrm{c1}+t_\mathrm{s}+t_\mathrm{c2}\)
$$\begin{aligned} v(y,z)=-z\frac{\mathrm{d}w}{\mathrm{d}y}+\left[ z-t_\mathrm{c1}\left( \frac{1}{2}+x_1\right) \right] \phi (y), \end{aligned}$$(4)
-
-
the inner sheets:
-
the upper—\(\left( \frac{1}{2}t_\mathrm{c1}+t_\mathrm{s} \right) \le z \le -\frac{1}{2}t_\mathrm{c1}\),
$$\begin{aligned} v(y,z)=-z\frac{\mathrm{d}w}{\mathrm{d}y}, \end{aligned}$$(5) -
the lower \(\frac{1}{2}t_\mathrm{c1} \le z \le \frac{1}{2}t_\mathrm{c1}+t_\mathrm{s}\)
$$\begin{aligned} v(y,z)=-z\frac{\mathrm{d}w}{\mathrm{d}y}, \end{aligned}$$(6)
-
-
the crosswise corrugated main core \(-\frac{1}{2}t_\mathrm{c1} \le z \le \frac{1}{2}t_\mathrm{c1}\)
$$\begin{aligned} v(y,z)=-z\frac{\mathrm{d}w}{\mathrm{d}y}, \end{aligned}$$(7)
where \(x_1=t_\mathrm{s}/t_\mathrm{c1}\)—dimensionless parameter, \(\phi (y)=v_1(y)/t_{\mathrm{c2}}\)—dimensionless function determines the field of displacement. Strains in all layers of the band plate are as follows
-
the flat sheets and the crosswise corrugated main core
$$\begin{aligned} \varepsilon _{y}^{(\mathrm{s})}=\frac{\partial v}{\partial y}, \quad \gamma _{yz}^{(\mathrm{s})}=0,\quad \varepsilon _{y}^{(\mathrm c1)}=\frac{\partial v}{\partial y},\quad \gamma _{yz}^{(\mathrm c1)}=0, \end{aligned}$$(8) -
the lengthwise corrugated cores of facings
$$\begin{aligned} \varepsilon _{y}^{(\mathrm{c2})}=\frac{\partial v}{\partial y}, \quad \gamma _{yz}^{(\mathrm{c2})}=\frac{\partial v}{\partial z}+\frac{\mathrm{d}w}{\mathrm{d}y}=\phi (y). \end{aligned}$$(9)
The physical relations, according to Hooke’s law, are
-
the flat sheets and the crosswise corrugated main core
$$\begin{aligned} \sigma _y^{(\mathrm{s})}=E\varepsilon _y^{(\mathrm{s})}, \quad \tau _{yz}^{(\mathrm{s})}=0,\quad \sigma _y^{(\mathrm c1)}=E_{y}^{(\mathrm c1)}\varepsilon _y^{(\mathrm c1)}, \quad \tau _{yz}^{(\mathrm c1)}=0, \end{aligned}$$(10) -
the lengthwise corrugated cores of facings
$$\begin{aligned} \tau _{yz}^{(\mathrm{c2})}=G_{yz}^{(\mathrm{c2})}\gamma _{yz}^{(\mathrm{c2})},\quad \sigma _y^{(\mathrm{c2})}=E_{y}^{(\mathrm{c2})} \varepsilon _y^{(\mathrm{c2})}, \end{aligned}$$(11)
where
and E—the Young’s modulus of metal sheets, \(\widetilde{G}_{yz}^{(\mathrm{c2})}\)—the shear modulus introduced in [7], denotations—indexes \(\mathrm c1\), 01—main core, \(\mathrm{c2}\), 02—inner corrugated layer of facings, s—sheets.
On the basis of Hamilton’s principle
where
the equations of motion are analytically derived
where
\(\rho _s\)—the mass density of the sheet, b—the width of the band plate.
The system of Eq. (13) will serve as the basis in the following analytical investigation of buckling and vibrations of the band plate.
2.1 Buckling
The detailed calculations have been carried out for the simply supported band plate compressed by the axial force \(F_0\) (Fig. 3). To solve the buckling problem the following equalities (for a shear force Q and a bending moment \(M_\mathrm{b}\)) have been used
Taking into account the above and basing on the system (13), the governing equations for the buckling problem were obtained, assuming that the buckling phenomenon is time independent
The form of two unknown function in the system of equations of statics (15) has been assumed as follows
where \(w_\mathrm{a}\)—the amplitude of deflection, \(\phi _\mathrm{a}\)—the amplitude of dimensionless function. The functions (16) identically satisfy the following boundary conditions
After substituting functions (16) to the system (15) the following expression for the critical load has been derived
where
The results of exemplary calculations of buckling load for a family of band plates are provided in Sect. 3.2. The results obtained with the use of Eq. (18) and these given by the FE analysis are compared.
2.2 Vibrations
In the equations of motion (13) the following formulas have been assumed:
-
of two unknown functions
$$\begin{aligned} w(y,t)=w_a(t)\sin \frac{\pi y}{L}, \quad \phi (y,t)=\phi _a(t)\cos \frac{\pi y}{L}, \end{aligned}$$(20) -
of the pulsating load
$$\begin{aligned} F_0(t)=F_c+F_a\cos (\varTheta t), \end{aligned}$$(21)where \(F_\mathrm{c}\)—an average value of the load, \(F_\mathrm{a}\)—an amplitude of the load, and \(\varTheta \)—a frequency of the load.
Then the system (13) could be reduced to the Mathieu equation
where
and the angular frequency of the band plate is as follows
The natural frequency in Hertz [Hz] is given by the formula
The two unstable regions can be determined according to the monograph [27]
-
the first unstable region
$$\begin{aligned} 2\varOmega \sqrt{1-\mu }<\varTheta <2\varOmega \sqrt{1+\mu }, \end{aligned}$$(26) -
the second unstable region
$$\begin{aligned} \varOmega \sqrt{1-2\mu ^2}<\varTheta <\varOmega \sqrt{1+\frac{1}{3}\mu ^2}. \end{aligned}$$(27)
The results of exemplary calculations of natural frequencies for a family of band plates are provided in Sect. 3.3. The results obtained with the use of the Eq. (24) and these given by the FE analysis are compared.
3 Results of numerical studies
Numerical studies have been conducted on a family of band plates of the width \(b=230\) mm and the length L which takes the following values: 1000, 1200, 1400, 1600, 1800, 2000, 2200, 2400 mm. The thickness of the plate \(t=67\) mm. All layers are made of a sheet of the thickness \(t_\mathrm{s}=0.8\) mm. Other dimensions are given in Fig. 4. In the following subsections the results obtained from FE analyses are compared with these given by analytical formulae.
3.1 FE model of the band plate
Due to the symmetry of the problem only half of the band plate has been modelled. All seven layers have been treated as thin plates—only a mid-surface of each layer has been modelled (see Fig. 5c). A first-order shell element (shell181 in ANSYS and S4R in ABAQUS) has been used with four nodes and six degrees of freedom in each node. The distance between particular layers equals the thicknesses of the sheet metal. The ’face-to-face’ type of contact with tie constraints for ABAQUS and bonded constraints for ANSYS have been applied between particular layers as shown in Fig. 5d. Such constraints prevent from separation and mutual movements of the connected parts. The plate is simply supported at the end—the longitudinal displacement v is free, whereas the lateral u and vertical w displacements are blocked. The support is applied to all edges as shown in Fig. 5b. Since the stiffness of the main core in the plane of buckling is far more higher then the stiffness of the core of the faces the compression force has been applied to the inner sheets of the faces only (Fig. 5a). Such approach may reduce the possibility of the local buckling to appear.
To determine a proper size of the finite element a mesh convergence analysis has been performed. The results showing the relation between the buckling load and the number of finite elements are shown in Fig. 6. It is seen that the use of two finite elements on the base of the trapezoid is enough to obtain a convergent result. Finally, the size of the element has been set at 5 mm (the last point on the plot in Fig. 6).
The model of the linear elastic material has been used with mechanical properties corresponding to steel: Young’s modulus \(E=2\times 10^5\) MPa and Poisson’s ratio \(\nu =0.3\). The density \(\rho =7800\) kg/m\(^3\). For both types of analyses geometrically perfect model has been used.
3.2 Buckling analysis
Stability analysis has been performed using linear buckling analysis procedure. The value of the first buckling load is looked for as well as the buckling shape corresponding to it. For the boundary conditions considered here the buckling mode should take the shape of one longitudinal half-wave. Such shape function has been assumed in the analytical solution [Eq. (16)]. However due to complex geometry of the band plate local buckling may also appear.
The results of analyses are shown in Fig. 7. On the plot the comparison of the results obtained numerically and with the use of analytical formula is shown. The horizontal axis corresponds to the length of the plate, whereas the vertical axis to the value of the critical load. For the global modes the analytical results are consistent with the numerical ones. For shorter plates, \(L<1600\) mm, a local buckling appears in the form of short waves located on the outer sheets of the plate as shown in Fig. 7b. For the plate of the length \(L=1400\) mm a combined mode appeared—global-local—what can be seen in Fig. 7c.
3.3 Vibrations
The modal analysis has been performed to determine the natural frequencies as well as the modes of vibrations of the band plates. The boundary conditions applied to the model forces the first mode of vibrations to has the shape of one longitudinal half-wave. Having this in mind a half-model of the plate with the symmetry boundary conditions in the mid-length has been used. The results of both analytical and numerical calculations are shown in Fig. 8. On the plot the relation between the length L of the band plate (horizontal axis) and the natural frequencies f corresponding to the first mode of vibration (vertical axis) is shown. A good agreement between all solutions can be seen. The first mode, bending in yz-plane, is presented in Fig. 8b.
4 Discussion of the results
The results of the analyses presented in the previous section concern only one family of band plates. Nevertheless they show clearly the behaviour of this kind of structures. First of all the deformation of the cross section assumed in the analytical solution seams to be correct since it follows the deformation observed in the FE analyses as shown in Fig. 9a. The main core does not deform, whereas a considerable deformation of the core of the faces can be seen.
Second feature that characterize the analysed structures is the susceptibility to the local phenomena. The local deformation, as shown in Fig. 9b, appears on the narrow thin stripes of sheets which are not connected to other elements of the band plate. The local deformation is observed during the loss of stability of the band plate (Fig. 7b).
Analysing the selected results of the analytical and numerical investigation presented in Tables 1 and 2 a good agreement can be observed between the obtained values. The relative errors describe the discrepancy between the analytical and both numerical solution. As for the buckling load the relative error is in the range between 2.0 and 4.5 % for the ANSYS and between 1.6 and 5.0 % for the ABAQUS, taking into account only global modes of buckling. Even better consistency is observed for the modal analysis: the relative error for the ANSYS is up to 3.0 % and for the ABAQUS up to 3.5 %.
It should be noted that for plates of the length smaller than \(L=1600\) mm the buckling load obtained analytically—global mode, is higher than this obtained from ANSYS and ABAQUS—local mode. The difference is higher for shorter beams. It comes from the fact that for a global mode of buckling the band plate behaves as an Euler column—the buckling load increases with the decrease of the length; the whole structure undergoes bending. The local mode, however, has similar shape for all shorter beams; only some of narrow stripes of sheet between trapezoids buckles. This suggest that the local phenomena may decrease the buckling resistance of this kind of band plate considerably. The numerical analysis of local phenomena will probably need a finer mesh.
5 Conclusions
The proposed seven-layer band plate is a light and very stiff structure. The stiffness can be easily modified by changing the hight of the corrugation of the main core and the core of the faces. The stiffness can be increased by using thicker external sheets in which, according to the foregoing results, deformations are the highest and which are subjected to the highest stresses. The band plate can be made of easily available materials like steel and assembled with the use of laser welding or an adhesive. The band plates can be used to design of many different plated structures like containers, floor in railway carriages. The high stiffness and the susceptibility to local buckling make the global loss of stability unlikely to appear.
The presented analyses were limited to linear ones, and a perfect geometry of the plate has been assumed. However, due to a complex shape of the plate there is a high possibility to introduce many geometrical imperfections during manufacturing process. These may significantly influence the buckling behaviour of the plate. Then the nonlinear study should be carried out to validate the results. The experiments are also planned as a further step of the project.
References
Allen, H.G.: Analysis and Design of Structural Sandwich Panels. Pergamon Press, Oxford, London, Edinburgh, New York, Sydney, Paris, Braunschweig (1969)
Ventsel, E., Krauthammer, T.: Thin Plates and Shells. Theory, Analysis and Applications. Marcel Dekker Inc, New York, Basel (2001)
Noor, A.K., Burton, W.S., Bert, C.W.: Computational models for sandwich panels and shells. Appl. Mech. Rev. ASME 49(3), 155–199 (1996)
Carlsson, L.A., Nordstrand, T., Westerlind, B.: On the elastic stiffnesses of corrugated core sandwich. J. Sandw. Struct. Mater. 3, 253–267 (2001)
Libove, C., Hubka, R.E.: Elastic Constants for Corrugated-Core Sandwich Plates, Technical Note 2289. NACA, Washington (1951)
Magnucka-Blandzi, E., Magnucki, K.: Transverse shear modulus of elasticity for thin-walled corrugated cores of sandwich beams. Theoretical study. J. Theor. Appl. Mech. 52(4), 971–980 (2014)
Lewinski, J., Magnucka-Blandzi, E., Szyc, W.: Shear modulus of elasticity for thin-walled trapezoidal corrugated cores of seven-layer sandwich plates. Eng. Trans. 63(4), 421–438 (2015)
Zenkour, A.M.: A state of stress and displacement of elastic plates using simple and mixed shear deformation theories. J. Eng. Math. 44(1), 1–20 (2002)
Carrera, E.: Historical review of Zig-Zag theories for multi-layered plates and shells. Appl. Mech. Rev. 56(3), 287–308 (2003)
Buannic, N., Cartraud, P., Quesnel, T.: Homogenization of corrugated core sandwich panels. Compos. Struct. 59, 299–312 (2003)
Magnucki, K., Malinowski, M., Kasprzak, J.: Bending and buckling of a rectangular porous plate. Steel Compos. Struct. 6(4), 319–333 (2006)
Talbi, N., Batt, A., Ayad, R., Guo, Y.Q.: An analytical homogenization model for finite element modelling of corrugated cardboard. Compos. Struct. 88, 280–289 (2009)
Cheng, Q.H., Lee, H.P., Lu, C.: A numerical analysis approach for evaluating elastic constants of sandwich structures with various core. Compos. Struct. 74, 226–236 (2006)
Biancolini, M.E.: Evaluation of equivalent stiffness properties of corrugated board. Compos. Struct. 69, 322–328 (2005)
Seong, D.Y., Jung, C.G., Yand, D.Y., Moon, K.J., Ahn, D.G.: Quasi-isotropic bending responses of metallic sandwich plates with bi-directionally corrugated cores. Mater. Des. 31, 2804–2812 (2010)
Magnucki, K., Jasion, P., Krus, M., et al.: Strength and buckling of sandwich beams with corrugated core. J. Theor. Appl. Mech. 51, 15–24 (2013)
Jasion, P., Magnucka-Blandzi, E., Szyc, W., Magnucki, K.: Global and local buckling of sandwich circular and beam-rectangular plates with metal foam core. Thin-Walled Struct. 61, 154–161 (2012)
Jasion, P., Magnucki, K.: Global buckling of a sandwich column with metal foam core. J. Sandw. Struct. Mater. 15(6), 718–732 (2013)
Hadi, B.K.: Wrinkling of sandwich column: comparison between finite element analysis and analytical solutions. Compos. Struct. 53, 477–482 (2001)
Jasion, P., Magnucki, K.: Face wrinkling of sandwich beams under pure bending. J. Theor. Appl. Mech. 50(4), 933–941 (2012)
Magnucki, K., Krus, M., Kuligowski, P., Wittenbeck, L.: Strength sandwich beams with corrugated core under pure bending. In: The 2011 World Congress on Advances in Structural Engineering and Mechanics, ASEM’11, Seoul Korea, CD, pp. 321–330 (2011)
Magnucki, K., Kuligowski, P., Krus, M., Magnucka-Blandzi, E.: Bending and buckling of orthotropic sandwich beams with three-layer faces, coupled instabilities in metal structures. In: Proceedings of the 6th International Conference on Coupled Instabilities in Metal Structures held in Glasgow, Scotland, pp. 587–594 (2012)
Grygorowicz, M., Paczos, P., Wittenbeck, L., Wasilewicz, P.: Experimental three-point bending of sandwich beam with corrugated core. In: AIP Conference Proceedings, vol. 1648, pp. 800002-1–800002-4 (2015)
Magnucka-Blandzi, E., Walczak, Z.: Bending of five-layer beams with lengthwise corrugated main core. In: AIP Conference Proceedings, vol. 1648, pp. 800003-1–800003-4 (2015)
Magnucka-Blandzi, E., Walczak, Z.: Bending of five-layer beams with crosswise corrugated main core. In: AIP Conference Proceedings, vol. 1648, pp. 800004-1–800004-4 (2015)
Wittenbeck, L., Grygorowicz, M., Paczos, P.: Numerical analysis of sandwich beam with corrugated core under three-point bending. In: AIP Conference Proceedings, vol. 1648, pp. 800007-1–800007-3 (2015)
Zyczkowski, M. (eds.).: Mechanika techniczna. Wytrzymałość elementów konstrukcyjnych. Tom IX. Warszawa: Państwowe Wydawn. Nauk. (1988) (in polish)
Acknowledgments
The project was funded by the National Science Centre allocated on the basis of the decision number DEC-2013/09/B/ST8/00170.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Magnucka-Blandzi, E., Walczak, Z., Jasion, P. et al. Modelling of multi-layered band plates with trapezoidal corrugated cores: stability analysis. Arch Appl Mech 87, 219–229 (2017). https://doi.org/10.1007/s00419-016-1188-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-016-1188-7