Introduction

Yield-stress liquids are broadly defined as materials that are solid below a critical applied stress and flow like mobile liquids at higher stresses. They are typically composed of colloidal or nanoscale constituents, and they are prevalent in consumer products, coatings and paints, industrial fluids, foods, mineral wastes, etc. Understanding bubble motion in yield-stress liquids is sometimes important, as exemplified by the need to remove air bubbles from cement and the emission of flammable gas bubbles from tanks of radioactive colloidal sludge at the US Department of Energy’s Hanford, Washington site.

The prototypical yield-stress liquid is the Bingham fluid, for which the shear stress in a viscometric flow with positive shear rate \(\dot{\gamma}\) is written

$$ \label{eq1a} \tau =\tau _{\rm y} +\eta _{\rm p} \dot{\gamma},\,\tau \ge \tau _{\rm y} , $$
(1a)
$$ \label{eq1b} \dot{\gamma} =0, \,\tau <\tau _{\rm y} . $$
(1b)

τ y is the yield stress and η p is commonly known as the plastic viscosity. The Bingham equation is linear in the shear rate following the onset of flow, but the fluid is in fact highly shear thinning; the viscosity, which is defined as the ratio of the shear stress to the shear rate, is

$$ \label{eq2} \eta =\tau /\dot{\gamma} =\eta _{\rm p} +\tau _{\rm y} /\dot{\gamma}. $$
(2)

Hence, the “plastic viscosity” is a measure of the true viscosity only in the limit of an infinite shear rate, and the choice of the name is unfortunate. Common generalizations of the Bingham fluid in shear flow are the Herschel–Bulkley and Casson equations, given respectively as

$$ \label{eq3} \mbox{Herschel-Bulkley}:\quad \tau =\tau _{\rm y} +{\rm K} \dot{\gamma}^m,\,\tau \ge \tau _{\rm y} ; $$
(3)
$$ \label{eq4} \mbox{Casson}:\quad \tau ^{1/2}=\tau _{\rm y} ^{1/2}+\eta _{\rm p}^{1/2} \dot{\gamma}^{1/2},\,\tau \ge \tau _{\rm y}. $$
(4)

Pressure-driven flow in a plane channel of infinite length is the typical textbook example of the flow of yield-stress fluids. The shear stress varies linearly over the channel cross-section, passing through zero at the centerplane. Hence, there must be a finite region around the centerplane where the stress is below the yield stress; here, the fluid cannot be deformed and must flow with a constant velocity. The boundary of this plug flow is defined by the distance y 0 from the centerplane at which the stress equals the yield stress. If we perform a macroscopic force balance on a segment of the plug of length L, where the pressure drop is Δp, it readily follows that y 0 = τ y L/Δp. As long as y 0 is smaller than the channel half-width, we must have shear banding, in which there is a plug of undeformed material adjacent to the centerplane and a sheared layer between the center plug and the wall, with a discontinuity in the velocity gradient at the interface. We then easily obtain the full velocity and stress distribution by integrating the equation of motion with the appropriate stress constitutive equation (Bingham, Herschel–Bulkley, Casson) between y 0 and the wall, requiring continuity of the velocity and shear stress at y = y 0. The requirement of continuity of the tangential velocity is a very strong statement about the material, to which we will return subsequently; classical plasticity permits tangential velocity discontinuities at interior slip planes, whereas slip planes are forbidden in the classical treatment of yield stress liquids. The analysis of channel flow is straightforward because it is possible to carry out an a priori computation of the location of the boundary between yielded and unyielded material.

Non-viscometric flows

Properly invariant three-dimensional constitutive equations for the Bingham fluid were introduced by Oldroyd (1947) and Prager (1961). Oldroyd’s formulation assumes that the material is a linearly elastic solid at stresses below the yield criterion, where the yield surface is defined by a von Mises criterion. The full constitutive equation is then as follows:

$$ \label{eq5a} \boldsymbol{\tau} = \left[{\eta _{\rm p} + \frac{\tau_{\rm y}}{\sqrt {\frac{1}{2}\mbox{II}_\Delta}}}\right] \boldsymbol{\Delta},\quad \frac{1}{2}\mbox{II}_{\boldsymbol{\tau}} \ge \tau _{\rm y}^2 , $$
(5a)
$$\label{eq5b} \boldsymbol{\tau} = G \boldsymbol{\gamma},\quad \frac{1}{2}\mbox{II}_{\boldsymbol{\tau}} <\tau _{\rm y}^2 . $$
(5b)

Here, \(\mbox{II}_{\bf A} \equiv \bf{A:A}\) is the second invariant of the tensor A, \(\boldsymbol{\Delta} \equiv \nabla {\bf v} + \nabla {\bf v}^{\rm T}\) is the rate of deformation tensor, and \(\boldsymbol{\gamma}\) is the strain tensor. Equation 5b is rarely employed in applications; it is conventional to assume that the modulus G is infinite, in which case there can be no deformation; the condition in the unyielded region is then

$$ \label{eq5c} G\to \infty :\boldsymbol{\Delta} =\boldsymbol{0}, \quad \frac{1}{2}\mbox{II}_{\boldsymbol{\tau}} <\tau _{\rm y}^2 . $$
(5c)

The equivalent three-dimensional generalizations of the Herschel–Bulkley and Casson equations are straightforward; for simplicity, we will restrict ourselves in the discussion to the Bingham fluid, but the important observations made in this paper generalize immediately to these constitutive equations. Some yield-stress liquids appear to be viscoelastic following yielding, and a properly invariant generalization of the Bingham model to account for viscoelasticity was first introduced by White (1979).

Flows of Bingham fluids are frequently characterized by the dimensionless Bingham number, \(\mbox{Bn}=\tau _{\rm y} R/\eta _{\rm p} V\), where R and V are a characteristic length and velocity, respectively. τ y is a characteristic stress at low deformation rates, while η p V/R characterizes the viscous stress at very high rates, where the yield stress is irrelevant; hence, this dimensionless group has obvious applicability only in the limits of zero or infinity. The true viscosity scales as \(\eta \sim \eta _{\rm p} (1+\mbox{Bn})\), so a comparison of τ y to ηV/R meaningfully reflects the relative importance of the yield stress and the stress from viscous deformation; this comparison suggests that the relevant group for scaling is \(\mbox{Bn}/(1 + \mbox{Bn})\) rather than Bn. It is also important to keep in mind that this type of scaling is the sole determinant of the flow only when there is a single characteristic length scale.

The location of the yield surface is unknown in general flows. It is straightforward to demonstrate from strictly kinematical arguments that continuity of the velocity and stress at the yield surface cannot be satisfied within the context of conventional lubrication theory, and asymptotic methods must be used with delicacy (Lipscomb and Denn 1984); the issues are addressed in recent work by Putz et al. (2009). Variational methods can be used, but these are best for bounding macroscopic quantities (the drag coefficient, for example) and less satisfactory for establishing the details of velocity and stress fields. The most common approach is to remove the discontinuity by regularization, which transforms the computational problem into a conventional one for a purely viscous liquid, and then to vary the regularization parameter to try to obtain convergence to the solution of the discontinuous problem. Three regularizations are in common use:

Bercovier and Engelman (1980):

$$ \label{eq6a} \boldsymbol{\tau} =\left[ {\eta _{\rm p} +\frac{\tau _{\rm y}}{\sqrt {\frac{1}{2}\mbox{II}_{\boldsymbol{\Delta}} +\varepsilon ^2}}} \right]\boldsymbol{\Delta} $$
(6a)

Two viscosity (Lipscomb and Denn 1984; Gartling and Phan-Thien 1984):

$$ \begin{array}{rll} \label{eq6b} \boldsymbol{\tau} &=&\frac{\eta _{\rm p}}{\varepsilon}\boldsymbol{\Delta}, \quad {\sqrt {\frac{1}{2}{\rm II}_{\boldsymbol{\Delta}}} <\varepsilon \tau_{\rm y} /\eta _{\rm p}} \\ \boldsymbol{\tau} &=& \left[{\eta _{\rm p} +\frac{(1-\varepsilon )\tau _{\rm y} }{\sqrt {\frac{1}{2}\mbox{II}_{\boldsymbol{\Delta}}}}} \right]\boldsymbol{\Delta},\quad {\sqrt {\frac{1}{2}\mbox{II}_{\boldsymbol{\Delta}}} \ge \varepsilon \tau _{\rm y} /\eta _{\rm p}} \end{array} $$
(6b)

Papanastasiou (1987):

$$ \label{eq6c} \boldsymbol{\tau}=\left[ {\eta _{\rm p} +\frac{\tau _{\rm y} \left\{{1-\exp \left( {-\frac{1}{2}\mbox{II}_{\boldsymbol {\Delta}} /\varepsilon} \right)} \right\}}{\sqrt {\frac{1}{2}\mbox{II}_{\boldsymbol{\Delta}}}}} \right]\boldsymbol{\Delta} $$
(6c)

The Bingham model should be approached in all three formulations in the limit as ε→0. There are no universal convergence proofs, and numerical issues usually become important in numerical solutions before ε can become sufficiently small to establish convergence of the stress field. Thus, whenever regularization is employed there must be a small amount of flow (apparent creep) in what is interpreted as the unyielded region, since ε must always be non-zero. A large number of solutions can be found in Mitsoulis (2008). Convergence of the smooth regularizations is discussed in Frigaard and Nouar (2005). A detailed treatment of convergence for creeping flow around a sphere that is not discussed by Frigaard and Nouar can be found in Liu et al. (2002). The “gold standard” for checking the validity of calculations of flow around a sphere in a Bingham fluid is that of Beris et al. (1985). Some new results demonstrating convergence problems when the yield surface is discontinuous are described in Putz et al. (2009). Overall, the regularization methodology appears to be satisfactory in most instances and is incorporated into commercial CFD codes, although some authors (e.g., Putz and Frigaard 2010) have recently employed an augmented Lagrangian approach that allows more accurate determination of the unyielded regions. The two illustrative calculations shown subsequently in this paper employ the Bercovier–Engelman regularization.

One of the consequences of the structure of the Bingham model and its generalizations is that, in the creeping flow limit, a flow in a geometry with fore-aft symmetry must exhibit fore-aft symmetry in the streamlines. Figure 1 shows the computed flow at zero Reynolds number for a Bingham fluid in a plane channel with a cylinder that is offset from the centerplane; this geometry is often used to test computational algorithms and constitutive equations for polymer melts. The flow is from left to right, and Bn based on the channel width equals 125. The shaded regions are unyielded. The upstream and downstream flows approach the flow expected in an infinite channel for such a large Bingham number, namely an unyielded plug across most of the channel cross-section and small sheared regions near the walls. There is no flow in the narrow gap between the cylinder and the near wall. The shaded “island” between the cylinder and the far wall is a consequence of the no-slip condition at the solid surfaces, which requires that there be a velocity maximum at an interior point in the channel where the derivative goes to zero; as long as the tensile stresses are sufficiently small, which is expected in this gradual contraction and expansion, the stress invariant will be below the critical value. This is therefore a region in space where the velocity is a constant and the von Mises criterion is satisfied everywhere on the surface, but the plug itself does not move; rather, fluid enters and leaves at a fixed velocity everywhere on the surface. We might think of this as analogous to a freezing/melting transition.

Fig. 1
figure 1

Creeping flow of a Bingham liquid in a channel with an offset cylinder, Bn = 125, Re = 0 (calculation by John Singh; reprinted from Denn 2008)

Full size image

Figure 2 shows a calculation of a rising two-dimensional bubble with zero surface tension at zero Reynolds number and Bn = 1.38 (Singh and Denn 2008), where the free surface was determined using the method of level sets. Because of the unyielded (shaded) region far from the bubble, where the stress invariant falls below the critical value, continuity of mass requires that there be a recirculating flow within the yielded shell, which induces a rotation. The unyielded “ears” on the equatorial plane are expected, and, since they must move with the bubble, they rotate and precess along the free surface in order to maintain a fixed position relative to the bubble, with something akin to “melting” along the forward portion and “freezing” on the aft. The size of the ears increases with increasing Bn, while the outer unyielded region approaches closer to the bubble; the two regions connect and the rise velocity goes to zero \((\mbox{Bn} \to \infty)\) when τ y ≥ (Δρ)gR/6, where Δρ is the density difference and g is the gravitational acceleration. (The 6 in the denominator is replaced by 8.33 for a falling drop at zero Reynolds number.) Other computational results for bubbles and drops in Bingham liquids using regularization methods may be found in Potapov et al. (2006) and Tsamopoulos et al. (2008).

Fig. 2
figure 2

Rising bubble with zero surface tension at Re = 0 and Bn = 1.38 (Singh and Denn 2008)

Full size image

Measurement issues

Direct measurement of the rheological functions of a yield-stress liquid is fraught with difficulty. Extrapolation of measured shear stress data to zero shear rate in order to obtain the yield stress is unreliable. Furthermore, wall slip often occurs; slip may be evident from the shape of the measured rheological functions (e.g., Nguyen and Boger 1983), and it has been observed directly by painting markers on the free surface in a rotational viscometer (e.g., Kalyon 2005) and through magnetic resonance imaging (e.g., Bertola et al. 2003; Wassenius and Callaghan 2004). In contrast to the behavior of polymer melts, where slip may occur at high deformation rates (Denn 2001, 2008), slip in yield-stress liquids is most likely to occur at low rates. Roughened surfaces are routinely employed to minimize slip, but a common means to avoid slip while measuring the shear stress is to use a rotating vane. The vane does not provide a direct measurement of the shear stress and requires a theoretical treatment to extract the shear stress–shear rate relation.

Nguyen et al. (2006) reported the results of a study of the yield stress of 50% and 60% TiO2 suspensions carried out at six laboratories using a variety of measurement techniques, as well as flow curve fitting and extrapolation. The reported yield stresses differed by a factor of two, both from laboratory to laboratory and within laboratories that used multiple methods. The overall standard deviation was 49% of the mean for the 50% suspension and 40% of the mean for the 60% suspension. The laboratory-to-laboratory variability is easily explained by the fact that samples were prepared on site, and the preparation methods differed substantially, pointing to the significance of the microstructure in determining the yield stress. The very large deviations with different techniques within several laboratories point to the unreliability of some methods. Three laboratories used the vane method, and the reported standard deviation was approximately 10% of the mean for both concentrations.

There has been little attention given to the material properties prior to yielding. Nguyen and Boger’s (1983) vane measurements on “red mud”, a colloidal waste suspension from aluminum processing, provide some interesting insight. For a 66% suspension they found that the vane gave a consistent value of the yield stress (154 to 169 Pa, with a mean of 162) as long as the rotational speed of the vane was below 8 RPM. At higher speeds the measured yield stress increased with speed, reaching a value of 351 Pa at 256 RPM. This behavior is inconsistent with Oldroyd’s notion of a linearly elastic solid prior to yielding (Eq. 5b), but it is suggestive of linearly viscoelastic behavior, as mentioned by White (1979) and discussed by Saramito (2007). Suppose we presume, for example, that the rheology of the unyielded material is described by a Kelvin–Voigt solid, for which the shear stress satisfies \(\tau =G\gamma +\eta \dot{\gamma}\), where γ is the shear strain. If failure occurs at a critical yield strain, γ y, then the static value of the yield stress τ y is G γ y. In an experiment at constant shear rate we would then have a dynamic apparent yield stress τ app,y such that \(\tau _{\rm app,y} -\tau _{\rm y} =\eta \dot{\gamma}\). Nguyen and Boger’s data for the 66% red mud suspension are shown in Fig. 3, where it appears that the behavior expected for the Kelvin–Voigt material is roughly followed. What appears to be Kelvin–Voigt behavior in ketchup prior to yielding was recently reported by Benmouffok-Benbelkacem et al. (2010).

Fig. 3
figure 3

Apparent yield stress less equilibrium yield stress as determined by vane measurement as a function of RPM for a 66% red mud suspension. Calculated from data of Nguyen and Boger (1983)

Full size image

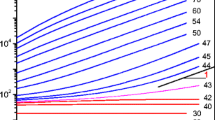
In a provocative paper entitled “The yield stress myth,” Barnes and Walters (1985) questioned the very existence of the yield stress, and, in a subsequent review, Barnes (1999) showed data for a number of materials that suggest that there is no yield stress, but rather a very large Newtonian viscosity at stresses below the apparent yield stress. Møller et al. (2009a) recently repeated these experiments and reached a different conclusion; their data on a 0.2% Carbopol, which is one of the materials cited by Barnes, are shown in Fig. 4. What appears to be a Newtonian viscosity is observed below the apparent yield stress, but the magnitude scales with a 0.6 power of waiting time (the exponent varies, depending on the material), indicating that the apparent viscosity below the apparent yield stress will become infinite as the waiting time goes to infinity. This is a remarkable result, since the 0.2% Carbopol used by Møller and coworkers does not exhibit thixotropy in a typical cyclic shearing experiment; as discussed by Bonn and Denn (2009) and Møller et al. (2009b), this Carbopol appears to be an unusual “ideal” yield-stress liquid. (Note that this is not true of all Carbopols; see Divoux et al. (2010) for an example of complex time-dependent behavior during startup of shear in a Carbopol system.) One conclusion appears to be that the yield stress is a material property that separates the mobile liquid from the solid at equilibrium. Several questions also immediately arise: First, what is the meaning of an infinite viscosity? A fluid with an infinite viscosity is not a solid; a fluid requires velocity continuity in the bulk, while a solid can accommodate slip planes, as in classical plasticity. Second, what is the physical origin of the plateau in the apparent viscosity below τ y, and what is the origin of its time dependence?

Fig. 4
figure 4

Apparent viscosity of 0.2% Carbopol for different waiting times (Møller et al. 2009a)

Full size image

Shear-dependent structure

The inclined plane method is one of the techniques employed to measure a yield stress. In this method the material is placed on a horizontal plane that is then slowly inclined until the gravitational stress overcomes the yield stress at a critical angle of inclination and the material flows. As the film thins, the gravitational stress drops below the yield value and the flow stops. Figure 5 shows the results of an inclined plane experiment of a 4% suspension of bentonite clay in water (Coussot et al. 2002a). The dashed line in Fig. 5b is the expected length of the material sample on the plane as a function of time for a liquid satisfying a constitutive equation like Eq. 5, whereas the actual data show the length increasing steadily with time, as demonstrated in the accompanying photos (Fig. 5a). This runaway behavior is characteristic of an avalanche, as often seen with snow or mud. The likely explanation is straightforward: bentonite suspensions are known to be thixotropic; i.e., ascending and descending stress curves with a cyclic shear rate are different. There must therefore be a stress-dependent microstructure. The equilibrium structure determines an equilibrium yield stress. As the flow begins, the structure breaks down; the new structure will have a smaller yield stress and more mobility. This is a positive feedback system, and it may run away. In fact, in a creep experiment carried out below a critical stress the structure of 4% bentonite builds up and flow stops (aging); above the critical stress the structure equilibrates at a new value and steady flow occurs (shear rejuvenation) (Coussot et al. 2002b).

Fig. 5
figure 5

a Avalanche flow of a 4% bentonite suspension in water over an inclined plane covered with sandpaper. The pictures are taken at the critical angle for which the suspension just starts to flow. b Distance traveled as a function of time (symbols) compared to the prediction for an ideal yield-stress fluid (dashed line) (Coussot et al. 2002a)

Full size image

Figure 6 shows a direct observation of the effect of stress-dependent structure in a colloidal gel. Here, the gel is made up of 1.3 \(\mu\)m fluorescent PMMA particles and 3 ×107 Mw polystyrene in a mixture of decalin and cyclohexyl bromide. At rest (A), the gel exhibits a percolated structure and exhibits a yield stress of about 5 Pa. Just after flow (B), the gel has broken up into individual flocs and there is no measurable yield stress.

Fig. 6
figure 6

A colloidal gel a at rest, with a percolated structure and a yield stress of ∼5 Pa, and b just after flow, with individual flocs and no measurable yield stress (Bonn group; from Bonn and Denn 2009)

Full size image

Predictive ability of classical models

There is a dearth of quantitative comparisons between the predictions of classical models like Eq. 5 and experiments on yield-stress liquids in non-trivial geometries, but two recent publications using particle imaging velocimetry to obtain detailed velocity data for yield-stress fluids moving past single spheres at very low Reynolds numbers are instructive. Both groups found fore-aft symmetry for Newtonian fluids, as expected, but both observed large deviations from fore-aft symmetry with the yield-stress liquids. Gueslin et al. (2006) studied a Laponite clay suspension, which is a thixotropic material (Abou et al. 2003); the settling velocity depended on the aging time, which in turn depended on the stress. (Aluminum and brass spheres, with buoyant forces differing by a factor of four, were used.) Putz et al. (2008) used a 0.08% Carbopol solution, which, unlike most observations on Carbopol, appeared to exhibit a degree of shear hysteresis. A constitutive description in the form of Eq. 5, or any generalization without a time dependence resulting from structural change, cannot describe these observations even qualitatively. (Topkavi et al. (2009) reported velocity profiles for the flow of a Carbopol gel past a stationary cylinder in which they, too, observed a deviation from fore-aft symmetry, but they provided no data with a Newtonian fluid for comparison.)

There are two other important experimental observations that are inconsistent with the classical rheological models. Shear banding is required for Bingham-like fluids when there is a stress gradient and the stress falls below the critical value in some region of the flow field; shear banding cannot occur in a uniform stress field, however. Magnetic resonance imaging studies of a bentonite clay suspension in a cone-and-plate instrument, where the shear stress should be uniform, do show shear bands above a critical shear rate (Møller et al. 2008). Finally, visual observation of the free surface of a 0.48% Laponite clay suspension in a parallel plate rheometer during transient stress development at a constant rate shows the onset of shear localization at the midplane, reminiscent of a slip plane in a solid, apparently indicating that the material yielded only locally (Pignon et al. 1996).

Requirements for simulation

Any model intended to simulate the behavior of yield-stress fluids like those discussed here must be able to describe the following phenomena:

  • Thixotropy

  • Avalanche behavior

  • Loss of fore-aft symmetry in flow

  • Shear banding without a stress gradient

  • Shear localization

Clearly, microstructure must be incorporated into the rheological description. If we wish to pursue a continuum approach then we need to introduce a variable that characterizes the microstructure. The simplest way to do this is to introduce a scalar structural parameter that is a measure of the connectivity of the structure, in much the same way that transient network models have been used for entangled polymers (e.g., Mewis and Denn 1983). Typically, the parameter, which we will denote λ, varies between zero and unity, where unity corresponds to the equilibrium structure and zero to complete structural breakdown. (Some investigators prefer to permit 0 ≤ λ ≤ ∞.) If the structure is anisotropic then we would require a structural tensor.

The kinetic equation for the structural variable requires expressions for the rates of buildup and breakdown. The rate of breakdown in models of structured fluids is typically taken to depend on the magnitude of the deformation rate in the form \(\lambda \dot{\gamma}^a\); the buildup rate is typically taken to depend on the distance from equilibrium and, in some cases, on the rate of deformation, in the form \((1-\lambda)\dot{\gamma}^b\). The parameters a and b are typically taken to have integer values. If the rate of buildup is driven only by the distance from equilibrium then b would be expected to be zero, as is usually done in polymer network theories. For a simple shear flow we would then have a kinetic equation of the form

$$ \label{eq7} \frac{d\lambda}{dt}=k_1 (1-\lambda)\dot{\gamma}^b-k_2 \lambda \dot{\gamma}^a. $$
(7)

For a general flow we would replace the time derivative d/ dt by the substantial derivative D/ Dt and the shear rate \(\dot{\gamma}\) by \(\sqrt {\frac{1}{2}\mbox{II}}_{\boldsymbol{\Delta}}\). There is a steady-state structure in a steady shear flow:

$$ \label{eq8} \lambda _{\rm ss} =\left[ {1+\frac{k_2}{k_1}\dot{\gamma}^{a-b}}\right]^{-1}. $$
(8)

Clearly, a > b to ensure the correct limits λ→1, 0 as \(\dot{\gamma}\to 0\), ∞. (Equations of this type for the structural variable do not appear to admit the possibility of avalanches.) Many such models of structured liquids have been proposed, and they are reviewed in papers by Mujumdar et al. (2002) and Mewis and Wagner (2009); interestingly, the condition a > b is violated by some of these models. Some models include two mechanisms for structure buildup, a Brownian term that depends only on (1 − λ) and a shear-dependent term. Pinder (1964) and Coussot et al. (2002b) assume a constant rate of buildup, which permits λ to become infinite; the latter formulation does admit avalanches.

In a conventional network model, like rubber elasticity, the modulus is proportional to the connectivity, so we would have G = λG o, where G o is the equilibrium modulus. For a fractal structure the form would be \(G = \lambda^{n}G_{\rm o}\), n > 1. It is likely that the yield stress would have the same dependence on λ as the modulus. The dependence of the dissipative parameters on λ would more than likely be taken initially to be a power law; in fact, most of the models reviewed by Mewis and Wagner take the plastic viscosity to be proportional to λ. A minimal generalization of Eq. 5 would then be of the form

$$ \label{eq9a} \boldsymbol{\tau}=\left[ {\eta _{\rm p} +\frac{\tau _{\rm y} }{\sqrt {\frac{1}{2}\mbox{II}_\Delta}}} \right]\boldsymbol{\Delta},\quad \frac{1}{2}\mbox{II}_{\boldsymbol{\tau}} \ge \tau _{\rm y}^2 , $$
(9a)
$$ \label{eq9d} \boldsymbol{\tau} =G\boldsymbol{\gamma},\quad \frac{1}{2}\mbox{II}_{\boldsymbol{\tau}} <\tau _{\rm y}^2 . $$
(9b)
$$ \label{eq16} \frac{\partial \lambda }{\partial t}+{\rm {\bf v.}}\nabla \lambda =k_1 (1-\lambda )\left({\frac{1}{2}\mbox{II}_\Delta} \right)^{b/2}-k_2\lambda \left( {\frac{1}{2}\mbox{II}_\Delta} \right)^{a/2} $$
(9c)
$$ G=\lambda ^nGo,\;\tau _{\rm y} =\lambda ^n\tau _{\rm yo} ,\;\eta _{\rm p} =\lambda ^{\rm k}\;\eta _{\rm po} . $$
(9d, e, f)

Perhaps, based on Fig. 4, the yield criterion should be strain-based:

$$ \label{eq10a} 1/2\;\mbox{II}_{\gamma} <\mbox{or}> \gamma_{\rm y}^2 , $$
(10a)

and the constitutive equation of the unyielded material should be

$$ \label{eq10b} \boldsymbol{\tau}=G\boldsymbol{\gamma}+\eta \boldsymbol{\Delta}, \quad 1/2\;\mbox{II}_{\gamma} < \gamma_{\rm y}^2 . $$
(10b)

Incorporation of the structural variable into the conventional Bingham formulation, with G → ∞, does not introduce new conceptual issues, whereas any attempt to include the viscoelastic deformation of the unyielded region appears to be incompatible with conventional regularization approaches. Viscoelasticity after yielding can be accommodated by extending the structural parameter format or using a memory functional approach like that of White (1979), who proposed incorporating thixotropy through a memory-dependent yield stress (see also Suetsugu and White 1984). Separately, the issue of continuity of the velocity under all circumstances is a major unresolved conceptual issue.

Concluding remarks

Many yield-stress liquids do not correspond to the classical description, which fails to take stress-dependent structure into account. Modification of the classical regularized continuum description to incorporate a structural variable is conceptually straightforward as long as one does not seek to include the deformation of the unyielded material, but it appears that new solution techniques would be required if one wished to incorporate a strain-based yield criterion and possible viscoelastic behavior of the unyielded solid. The elementary structure formulation described here does not appear to be able to describe avalanche behavior, and one of the most challenging unresolved issues is whether tangential velocity continuity is always appropriate in a yield-stress liquid.