The reliability of single precision computations in the simulation of deep soil heat diffusion in a land surface model

Abstract

Climate models need discretized numerical algorithms and finite precision arithmetic to solve their differential equations. Most efforts to date have focused on reducing truncation errors due to discretization effects, whereas rounding errors due to the use of floating-point arithmetic have received little attention. However, there are increasing concerns about more frequent occurrences of rounding errors in larger parallel computing platforms (due to the conflicting needs of stability and accuracy vs. performance), and while this has not been the norm in climate and forecast models using double precision, this could change with some models that are now compiled with single precision, which raises questions about the validity of using such low precision in climate applications. For example, processes occurring over large time scales such as permafrost thawing are potentially more vulnerable to this issue. In this study we analyze the theoretical and experimental effects of using single and double precision on simulated deep soil temperature from the Canadian LAnd Surface Scheme (CLASS), a state-of-the-art land surface model. We found that reliable single precision temperatures are limited to depths of less than about 20–25 m while double precision shows no loss of accuracy to depths of at least several hundred meters. We also found that, for a given precision level, model accuracy deteriorates when using smaller time steps, further reducing the usefulness of single precision. There is thus a clear danger of using single precision in some climate model applications, in particular any scientifically meaningful study of deep soil permafrost must at least use double precision. In addition, climate modelling teams might well benefit from paying more attention to numerical precision and roundoff issues to offset the potentially more frequent numerical anomalies in future large-scale parallel climate applications.

1 Introduction

Climate models use sophisticated numerical algorithms to solve the complex primitive equations of atmospheric and oceanic motions. These algorithms contain two well-known and unavoidable sources of errors: truncation errors (because computations must be completed in a finite time), which are caused by replacing the continuous time and space differentials of the original field equations with finite increments, and rounding errors (because computer memory is not infinite), which are caused by replacing real numbers of infinite precision with finite-sized computer words. The fundamental goal in algorithmic design is to make sure that the combined effect of those errors will remain “small” in the sense that the computed solution will always stay “close” to, and highly correlated with, the real solution. Decades of research in numerical weather prediction (NWP) and climate modelling have largely focused on minimizing truncation errors through improved numerical techniques and higher spatial and temporal resolutions (see for example Haltiner and Williams 1980; Durran 1999 or Kalnay 2003 for in-depth treatments). However, the necessary use of floating-point arithmetic and the inevitable effects of rounding errors in NWP and climate models seem to have received far less attention. Still there are many ways in which floating-point operations can cause degradation in accuracy. This includes summation operations involving numbers that differ by several orders of magnitude (e.g. 1.234 × 10¹⁰ + 1.234 × 10⁶ + 123.4)—because large bit-shifting operations are then required—and subtraction of two nearly identical numbers that differ only in the last few bits of their significand (or mantissa) (e.g., 1.234567 × 10⁻³–1.234562 × 10⁻³). The result is the inevitable loss of several bits of significance. For that reason floating-point operations have a peculiar property: they best preserve accuracy when dealing with numbers that are on average neither too different nor too similar. In contrast, operations involving very different or very similar numbers will be much more vulnerable to such occurrences.

One of the few studies found that treated the issue of rounding errors in climate models is that of He and Ding (2001) who addresses the issue of reproducibility and stability in climate models. They showed how a crucial part of their code involving global summation operations gave completely different answers depending on the order of the summation and the number of processors used. The reason was that, in this particular part of their code, double precision arithmetic turned out to give insufficient accuracy despite its relatively high precision because of the extreme dynamic range of some of the variables involved. By using either a higher precision or a modified summation method which took into account rounding errors explicitly, they were able to dramatically improve the model accuracy, and hence its stability and reproducibility. Another study led by Goel and Dash (2007) described a method to reduce the accumulation of rounding errors in their weather forecast model by modifying the internal representation of the model’s initial data. Rosinsky and Williamson (1997) documented the initial growth of rounding errors in the National Center for Atmospheric Research (NCAR) Community Climate Model 2 (CCM2) and used it as a basis for validating the porting of model code across different computing platforms. However, the present authors found citations of the above-mentioned works coming mostly in papers not related to NWP or climate modeling fields, but rather to mathematics or computer science. The comprehensive survey of Einarsson (2005) on the topics of accuracy and reliability in scientific computing mentions the keyword “climate” only twice. The main reason for this discrepancy is probably due to the fact that 64-bit precision has traditionally been viewed by the NWP and climate communities as providing more than adequate accuracy. In addition it could be that, as was pointed out by Bailey (2005), few scientists—including NWP or climate modelers—have a formal background in numerical analysis.

Yet, it is generally recognized in the wider communities of numerical analysis and high performance computing that increasing the level of parallel processors and the number of floating-point operations increase the probability that numerical anomalies will happen—including excessive accumulation of rounding errors—irrespective of human programming errors (e.g., see Gropp 2005). For instance, if rounding errors in a computer-implemented algorithm are not perfectly random, their accumulation could become significant if the problem’s dimensions become large enough and the peculiarities of the algorithm allow it (Demmel 1993). This is especially true with summations of global arrays, a very common operation in NWP and climate codes (e.g., spectral transforms in many atmospheric models and the solving of elliptic equations in implicit time integration schemes) due to the previously mentioned danger of adding terms differing by several orders of magnitude. Extending such operations to parallel platforms introduces additional difficulties in that the enforcement of a strict order of summation in parallel codes typically comes at the cost of added communication and data synchronization steps (Gropp 2005). When adding more and more processors, the accumulation of such additional costs becomes prohibitive and can severely restrict the scaling of the algorithm, thus defeating the purpose of using a large number of processors in the first place (Gropp 2005).

On the more general topic of scientific computing, Bailey (2005) mentions how some users of numerical codes running on massively parallel systems often found their results to be of questionable accuracy even when using 64-bit precision. In fact, high-precision floating-point arithmetic has become more and more prevalent in general scientific computing circles over the past 10–15 years as some applications as diverse as quantum theory, supernova simulations and experimental mathematics were found to require 128-bit or 256-bit arithmetic or even higher (Smith 2003; Bailey 2005). This led Bailey (2005) to suggest that the topic of “numeric precision in scientific computations could be as important to program design as algorithms and data structures”.

Of course, when dealing with NWP or climate model codes, the aforementioned issues should also apply since the vast majority of them now run on parallel systems of various scales. But while most climate models in the scientific community have been designed to use the current 64-bit (or double precision) standard, other climate models, rather surprisingly, have started to use 32-bit (or single precision) code. One such model is the latest Canadian Regional Climate Model version 5 (CRCM5; Zadra et al. 2008; Martynov et al. 2013), a single precision regional climate model designed to run on highly parallel computing architectures using hundreds of processor cores, and therefore moving in the opposite direction of the trend of scientific computing at precisions beyond 64-bit. CRCM5 is based on a limited-area version of the global environmental multiscale (GEM) model used for NWP forecasts in Canada (Côté et al. 1998a, b; Yeh et al. 2002). Despite the apparent disadvantages of this choice, operational forecasting constraints have always dictated the design of Canadian NWP models toward the use of single precision because doing so allows for considerable savings in memory, CPU usage and energy costs. Now that CRCM5 has inherited single precision from its parent model, the need arises to investigate its consequences in a climate mode setting.

The choice of using single precision in a climate model could have several important ramifications, but the scope of this paper will be limited to processes occurring over long time scales, i.e. decades to centuries. In particular, we would like climate models to be able to capture deep soil temperature trends that are consistent with current climate change projections, i.e. of order 1–10 K century⁻¹, meaning instantaneous rates of change at least accurate to order 10⁻⁹ to 10⁻¹⁰ K s⁻¹. This is turn demands that temperatures be accurate to within 10⁻⁶ to 10⁻⁷ K when using typical time steps of order 10³ s. We will show that such accuracies are minimally required for resolving the vanishingly small temperature gradients typically encountered in deep soil.

Our concern for deep soil temperatures comes from the rather large body of literature on permafrost degradation related to the rise of Arctic air temperatures, a reflection of the considerable attention that has been given to this topic over the past 10–15 years (Osterkamp and Romanovsky 1999; Romanovsky et al. 2002; Payette et al. 2004; Jorgenson et al. 2006). This is due in large part to the complex positive feedbacks associated with permafrost degradation such as the release of carbon dioxide and methane to the atmosphere (Zimov et al. 2006) and the replacement of high albedo tundra by low albedo shrubs (Sturm et al. 2005). A number of permafrost model studies have notably shown that soil depths of several tens of meters are required to capture deep permafrost dynamics (Alexeev et al. 2007; Nicolsky et al. 2007; Lawrence et al. 2008). Other model studies have quantified present and future Arctic permafrost extent and active layer thickness (ALT) (Sushama et al. 2006, 2007; Paquin and Sushama 2015). In particular the Paquin and Sushama (2015) study singularly used the single precision CRCM5 to investigate its sensitivity to soil depth, organic matter and snow conductivity formulations for simulating contemporary near-surface permafrost, using column depths of 3.5 and 65 m.

In this paper we propose to shed some light on the impact of using single precision in numerical simulations of deep soil temperature. We will first present a simple formalism of finite arithmetic borrowed from the field of numerical analysis which will be used to define metrics of machine accuracy as applied to the problem of heat diffusion in deep soil. We will then use those concepts to analyze a set of numerical simulations of deep soil temperature using an offline version of the Canadian LAnd Surface Scheme (CLASS version 3.6; Verseghy 1991; Verseghy et al. 1993). CLASS is a state-of-the-art land surface model that simulates the energy and water fluxes and balances of vegetation, snow and soil, and is able to handle soil columns of arbitrary depths. Since the mid-1990s several key atmospheric global models and regional climate models in Canada have used CLASS as their operational land-surface component, for example the Canadian Fourth Generation Atmospheric Global Climate Model (CanAM4, von Salzen et al. 2013), the Canadian Regional Climate Model version 4 (CRCM4, de Elía and Côté 2010; Music and Caya 2007), and CRCM5.

The CLASS experiments of the present study will address the following three aspects of model sensitivity to rounding errors:

• 1. Initial spin-up behavior

• 2. Monotonically increasing surface radiative forcing

• 3. Different temporal resolutions

Item (1) is routinely a matter of concern in climate model runs. Spin-up errors can be caused by out-of-balance initial data due to missing or erroneous observations, or by disagreement between the equilibrium states in models and the real world. For soil depths beyond several tens of meters, spin-up times can reach well over a century. Item (2) will relate to the manner in which the model responds to a state of non-equilibrium when a positive thermal trend continuously propagates downward into the soil, approximating a “global warming” scenario. Finally, item (3) will show how rounding errors actually increase when using shorter time steps, despite a decrease in truncation errors.

The paper is organized as follows: Sect. 2 will present some theoretical background including formal definitions related to floating-point arithmetic and their application to machine accuracy metrics. This will be followed in Sect. 3 by a short description of CLASS and the methodology used in the experiments. In Sect. 4 experimental results will be described after checking the validity of assuming the double-precision solutions as the “true” solutions when comparing them with single-precision simulations. In Sect. 5 a discussion will be presented further analyzing the previous results and Sect. 6 will complete the paper with a summary and some conclusions.

2 Theoretical analysis

2.1 Floating point arithmetic

The theoretical aspects of floating point arithmetic have been treated in several standard texts and for this paper we will follow Higham’s (2002) formalism with some notation changes. Formally, a floating point number is a real number x represented as $\hat{x} \in {\text{F}}$ belonging to a subset ${\text{F}} \subset {\mathbb{R}}$ of the set of all real numbers and whose definition requires four integer parameters arranged such that:

$$\hat{x} = \pm m \cdot b^{e - p}$$

(1)

where m is the mantissa (or the significand), b is the base (or radix) of the number, e is the exponent with range $e_{min} \le e \le e_{max}$ and p is the precision, i.e., the number of digits included in the significand. The “hat” operator “$\hat{\,}$” indicates the floating point representation of the real number x, seen as an implicit mapping from the set of real numbers to the subset ${\text{F}}$ of floating point numbers: $x \in {\mathbb{R}} \to x \in {\text{F}}$. The mapping operation is called rounding and causes the familiar rounding errors of numerical computations. To avoid ambiguity in representation, floating point numbers are always normalized, thus the mantissa must satisfy $m \ge b^{p - 1}$, i.e., it must be filled with significant digits.

Because we use finite precision, the set of floating point numbers contains “gaps” and we need to know their sizes if we want to assess their effect on calculations. However those gaps vary in width depending on the power of b, therefore, to again avoid ambiguity, a standard floating point spacing metric is defined, called the machine epsilon $\epsilon_{M}$, which uses a power of 0 and is defined as the distance from the floating point number 1.0 to the next larger floating point number that is different from 1.0, thus: $\epsilon_{M} = b^{{ - \left( {p - 1} \right)}}$. For instance, a 32-bit floating point binary number (b = 2) has 24 bits in its significand, hence $\epsilon_{{M\left( {32 - bit} \right)}} = 2^{{ - \left( {24 - 1} \right)}} = 1.2 \times 10^{ - 7}$.

An important theorem of numerical analysis states that rounding causes a relative rounding error δ such that:

$$\hat{x} = x\left( {1 + \delta } \right),\quad \left| \delta \right| \le u$$

(2)

where $u = \frac{1}{2}\epsilon_{M}$ is called the unit roundoff (see Higham 2002, p. 38, for a formal proof). The relative error made when replacing a real number of infinite precision with a finite floating point approximation is never larger than this unit roundoff. An equivalent form for Eq. (2) is $x\delta = \hat{x} - x$, and this defines the accuracy of the floating point number. It is important in passing to keep in mind that accuracy and precision are two different concepts: precision reflects the number of significant digits used in the significand and this number will always produce the same relative error, while accuracy is the linear difference between a real number and its floating point representation, which is also the absolute error. For example the three real numbers 27316123.456789123456…, 273.16123456789123456… and 0.000027316123456789123456… can be represented with the same 8-digit precision (27316123, 273.16123 and 0.000027316123, respectively, with identical relative errors of ∼10⁻⁸) but they have entirely different accuracies (10⁰, 10⁻⁵, and 10⁻¹², respectively).

Most computers today follow the IEEE standard for binary floating-point arithmetic (IEEE 2008). The standard guarantees that the result of any single floating point calculation is made to be as good as if one would calculate with infinite precision, then would round the result to the nearest floating point number. Thus if ${ \circledast }$ is a generic arithmetic operator, and $x, y \in {\text{F}}$ are two real numbers belonging to ${\text{F}}$:

$$\widehat{{x{ \circledast }y}} = \left( {x{ \circledast }y} \right)\left( {1 + \delta } \right), \left| \delta \right| \le u$$

(3)

Equation (3) is true for a single operation, but of course the standard cannot prevent rounding errors from accumulating beyond unit roundoff when a sequence of operations is performed.

While the current IEEE 754-2008 standard applies to both binary and decimal numbers, in this paper we will only deal with binary numbers, therefore base b = 2 from now on, and three degrees of precision will be used: single precision, corresponding to 32-bit words, double precision, corresponding to 64-bit words, and quadruple precision, corresponding to 128-bit words (details are listed in Table 1). Figure 1 shows an example of the internal machine representation of single precision as an IEEE 32-bit word which in this case has 24 bits of precision in the significand. Similarly, 64-bit words have 53 bits of precision and 128-bit words have 113 bits of precision (see Table 1).

Table 1 IEEE-754 binary formats used in the paper, with the same notation as in the equations

Fig. 1

An IEEE-754 32-bit word representation of the decimal number 273.16

2.2 Heat diffusion in soils: theoretical rounding errors

Let us now estimate the smallest theoretical machine rounding errors that can occur when using floating-point arithmetic in simulating heat diffusion in soils. To this end we will compute the minimum level of accuracy achievable (i.e. when we are left with only 1 bit of significance) for a given level of precision in the discretized form of the one-dimensional heat diffusion equation (similar to the one used in CLASS):

$$\frac{\partial T}{\partial t} = D\frac{{\partial^{2} T}}{{\partial z^{2} }}$$

(4)

where T is soil temperature in Kelvin, z is depth in meters and D is soil thermal diffusivity in units of m² s⁻¹ defined as the ratio of thermal conductivity λ (units of W m⁻¹ K⁻¹) and volumetric heat capacity C (units of J m⁻³ K⁻¹), i.e., D ≡ λ/C.

If we discretize Eq. (4) using, as in CLASS, an explicit forward finite-difference on the left-hand side and a second-order central difference on the right-hand side applied to a vertical domain composed of i grid points with non-uniform spatial resolution ${\Delta}z_{i}$ integrated over j time steps ${\Delta}t$, we get:

$$\frac{{T_{i,j + 1} - T_{i,j} }}{{{\Delta}t}} + O\left( {{\Delta}t} \right) = D\frac{{T_{i + 1,j} - 2T_{i,j} + T_{i - 1,j} }}{{{\Delta}z_{i}^{2} }} + O\left( {{\Delta}z_{i}^{2} } \right)$$

(5)

This discretization step causes truncation errors in Eq. (5) of order $O\left( {{\Delta}t} \right)$ on the left-hand side and of order $O\left( {{\Delta}z_{i}^{2} } \right)$ on the right-hand side and this would be the only source of error if we used a computer with infinite precision. The use of a floating-point representation introduces an additional relative rounding error $\delta_{{T_{i,j} }}$ on temperature, so that Eq. (5) becomes:

$$\frac{{\hat{T}_{i,j + 1} - \hat{T}_{i,j} }}{{{\Delta}t}} + O\left( {{\Delta}t} \right) = D\frac{{\hat{T}_{i + 1,j} - 2\hat{T}_{i,j} + \hat{T}_{i - 1,j} }}{{{\Delta}z_{i}^{2} }} + O\left( {{\Delta}z_{i}^{2} } \right)$$

(6)

where $\hat{T}_{i,j}$ is the floating point representation of T _i,j as discussed in Eq. (2) and can be represented as

$$\hat{T}_{i,j} = T_{i,j} \left( {1 + \delta_{{T_{i,j} }} } \right) ;\, \left| {\delta_{{T_{i,j} }} } \right| \le u_{p}$$

(7)

with u _p being unit roundoff for precision p (as defined in Table 1). The relative error can have any value up to unit roundoff, but to remain conservative in our analysis, we will assume the worst possible case and will simply define the relative error as identically equal to the unit roundoff: $\delta_{{T_{i,j} }} \equiv u_{p}$ so that Eq. (7) can be rewritten as:

$$\hat{T}_{i,j} = T_{i,j} + \in_{T,p}$$

(8)

where

$$\epsilon_{T,p} = u_{p} T_{i,j}$$

(9)

will be called the machine temperature rounding error for precision p. For example, typical soil temperatures (~280 K, say) show a minimum rounding error of $2^{ - 24} \cdot 280 K =\, \sim2 \times 10^{ - 5} K$ when represented in single precision, $2^{ - 53} \cdot 280 K =\, \sim3 \times 10^{ - 14} K$ when represented in double precision, and $2^{ - 113} \cdot 280 K =\, \sim1 \times 10^{ - 32} K$ when represented in quadruple precision.

Let us now apply the machine temperature rounding error to compute the time rate of change term (which will hereinafter be called the time tendency term) in Eq. (6) using temperatures differing at most by this rounding error without vanishing. This is the smallest tendency resolvable by the current level of precision (equivalent to computing a time derivative having at most 1 bit of significance) and will be called the machine tendency rounding error τ _p for temperature:

$$\mathop {\hbox{min} }\limits_{ p} \left( { \left| {\frac{{T_{i,j + 1} - T_{i,j} }}{{{\Delta}t}}} \right| > 0 } \right) = \frac{{\epsilon_{T,p} }}{{{\Delta}t}} \equiv \tau_{p}$$

(10)

Similarly, the smallest non-vanishing spatial gradient achievable with precision p on the right-hand-side of Eq. (6) is:

$$\mathop {\hbox{min} }\limits_{ p} \left( { \left| {\frac{{T_{i + 1,j} - T_{i,j} }}{{{\Delta}z}}} \right| > 0 } \right) = \frac{{\epsilon_{T,p} }}{{{\Delta}z}} \equiv \gamma_{p}$$

(11)

where γ _p will be called the machine gradient rounding error for temperature.

In other words, τ _p and γ _p are minimum roundoff—or accuracy—metrics that define thresholds below which any non-zero tendency or gradient will never be detected in computations involving p digits or less of precision.

We can use Eq. (10) to give us an idea of the minimal tendency rounding errors that are possible in practice. If we apply Eqs. (9) and (10) by taking a time step Δt = 1800 s (which is a typical value for a state of the art global climate model), a characteristic soil temperature $T_{0} = 280 K$ and p = 24, we get for the single precision machine tendency rounding error:

$$\tau_{single} = \frac{{\epsilon_{T,p} }}{{{\Delta}t}} = \frac{{u_{p} T_{i,j} }}{{{\Delta}t}} = \frac{{2^{ - 24} \cdot 280 K}}{1800 s} \approx 9.3 \times 10^{ - 9} K \cdot s^{ - 1}$$

which is equivalent to ~$30 {\text{K}} \cdot {\text{century}}^{ - 1}$. For double precision, p = 53 and therefore:

$$\tau_{double} = \frac{{2^{ - 53} \cdot 280 K}}{1800 s} \approx 1.7 \times 10^{ - 17} K \cdot s^{ - 1}$$

or ~$3 \times 10^{ - 8} {\text{K}} \cdot {\text{century}}^{ - 1}$. In the same manner, substituting say ${\Delta}z = 5 {\text{m}}$ in Eq. (11) for single precision (see Fig. 2):

$$\gamma_{single} \approx 3.3 \times 10^{ - 6} K \cdot m^{ - 1}$$

and for double precision:

$$\gamma_{double} \approx 6.2 \times 10^{ - 15} K \cdot m^{ - 1}$$

Importantly, those roundoff metrics depend on the size of the time and space increments found in Eq. (5). For instance, the machine tendency rounding error is really the temperature rounding error scaled by the time step. Since by nature the machine temperature rounding error must have a limited range due to the limited range of soil temperature itself, all variations of the tendency rounding error will be almost exclusively attributed to time step variations. In particular smaller time steps will cause rounding errors to actually increase, even though this formally results in a smaller truncation error (the same conclusion can be reached with the machine gradient rounding error). This is in fact a well-known problem encountered when computing derivatives in numerical analysis, for which the difference expressed in the numerator is forced to approach zero as the denominator Δt → 0 (assuming of course a continuously twice differentiable function), yet the same numerator cannot go below machine roundoff imposed by the level of precision. This implies inevitable trade-offs between the aim to achieve small truncation errors (from using a small enough Δt) and that of achieving small rounding errors (from using a “not-too-small” Δt).

Fig. 2

Configuration of soil levels for the maximum total depth of this study, i.e., 60 m, for a total of 26 layers

3 Experimental setup

As mentioned previously, CLASS is a state-of-the-art land surface model that simulates the energy and water budgets at the land surface. Vegetation, soil and snow cover are modelled separately (Verseghy 1991; Verseghy et al.1993). Extensive testing and improvement of the model algorithms have been carried out over the years, involving the participation of numerous university and government colleagues (e.g. see Verseghy 2000). In its original operational configuration, CLASS incorporates three modelled soil layers, 0.10, 0.25 and 3.75 m thick. Liquid and frozen soil moisture are modelled explicitly. The current version of the model, version 3.6 (Verseghy 2012) offers the added flexibility of allowing user-specified numbers and thicknesses of soil layers, and also the option of modelling multiple mosaic tiles. Two parallel developmental versions of CLASS are available, one incorporating carbon fluxes (Arora et al. 2009), and the other transfers of moisture between mosaic tiles via processes such as streamflow and blowing snow redistribution (Pietroniro et al. 2007).

Table 2 outlines five experiments of 100-year duration each which were performed with CLASS 3.6 in single-column mode, each one consisting of two identical runs except that one was compiled at single precision while the other was compiled at double precision (the SPIN_60M_1800S experiment was also run at quadruple precision for validation of the double precision run). The model was run on a 64-bit architecture Dell Optiplex 9020 computer with an Intel^® Core™ i5 CPU running a 64-bit Ubuntu operating system (Linux Mint “Petra” distribution) as a VMWare virtual machine inside a Windows 7 host, and compiled with the GNU Fortran compiler (gfortran, version 4.8.1).

Table 2 Set of runs used in this study

All runs were forced at the surface with half-hourly meteorological data measured at the Southern Old Aspen Site (Prince Albert, Saskatchewan), archived by Fluxnet-Canada and publicly available from the Fluxnet-Canada Research Network Data Information System (FCRN-DIS; http://fluxnet.ccrp.ec.gc.ca). Data included incoming shortwave and longwave radiation, precipitation, air temperature, atmospheric pressure, wind speed and specific humidity. This dataset is available for the period 1997–2010, but to allow the model to be run for 100 years, data for the year 1997 were arbitrarily chosen and repeated every year for 100 years. This setup had the extra benefit of removing inter-annual effects and leaving only intra-seasonal variations, except for any imposed artificial trend such as in the “global warming” experiments. The lower boundary condition was defined as a zero heat flux. The model time step for four experiments was set to 30 min (1800 s), the same interval as the input data. Two other experiments (“SPIN_60M_300S” and “GW_60M_300S”) used a 300 s time step to assess its impact on numerical accuracy, using input values linearly interpolated in time. The soil texture profile was determined from information gleaned from the observation station’s website, and was set as a fibric organic soil in the first layer (10 cm thickness), then as a sandy clay loam mineral soil composed of 49 % sand and 24 % clay for depths down to 1.1 m, then followed by solid bedrock. Data for the depth to bedrock were missing, but the chosen value of 1.1 m was assumed to be representative of average conditions in boreal forests. In any case most soils at mid-latitudes do not attain depths much beyond 2–3 m before reaching bedrock. Note that we assume an idealized non-fractured bedrock and therefore all hydrological processes were restricted to within 1.1 m of the surface. Bedrock thermal conductivity was set to the default CLASS value of 2.5 W m⁻¹ K⁻¹, a value typical of plutonic rocks such as granite (Clauser and Huenges 1995). The vegetation canopy consisted mostly of trembling aspen (Populus tremuloides Michx.) with some balsam poplar (Populus balsamifera L.). Vegetation fraction in CLASS was therefore set to 100 % “broadleaf trees” (one of the four vegetation types defined in CLASS) with roots reaching down to 0.6 m. Finally, all water phases were allowed to exist in the soil column, except below bedrock depth where water content was set to zero. Note that the aforementioned experimental design is intended to represent a realistic sample of actual land-surface calculations in climate models; this was judged to be more suitable for the goals of this study than a more canonical experiment where soil water, snow and vegetation would be absent and where soil levels would have uniform thickness.

In Table 2, experiments “SPIN_60M_1800S” and “SPIN_20M_1800S” are the spin-up experiments for two different total soil depths (60 m and 20 m respectively) initialized with an isothermal profile of 0 °C. “SPIN_60M_300S” is a repeat of “SPIN_60M_1800S” but with a 5-min or 300-s time step. “GW_60M_1800S” (with time step 1800 s) and “GW_60M_300S” (with time step of 300 s) refer to the “global warming” runs which were initialized with an isothermal profile of 3.5 °C. This latter initial temperature was chosen because it represented the approximate equilibrium value reached by deep soil in the spin-up experiments, thereby allowing the overall temperature trend to come only from the warming signal at the surface. The thicknesses for the 26 levels of the 60 m runs were set as illustrated in Fig. 2. For the 20 m run (“SPIN_20M_1800S”) only the top 18 levels were used.

4 Experimental results

4.1 Validation of double precision calculations

We have assumed up until now that the double precision runs are the “true” solutions in that their rounding errors are considered negligible compared to those in the single precision runs. We decided to test this assumption by running a spin-up experiment identical to “SPIN_60M_1800S” but using quadruple (or “quad”) precision (128 bits, see Table 1 for the parameters) and using it to evaluate the relative errors in double precision soil temperature. The results, shown in Fig. 3, indicate that relative errors in double precision temperatures generally remain under 10⁻⁵, but with frequent excursions up to 10⁻³, meaning that at least 3–5 decimal digits remain consistently correct throughout the simulation. Yet this is more than ten orders of magnitude larger than what one would expect from unit roundoff for double precision (~10⁻¹⁶), suggesting that the propagation of rounding errors is quite extensive relative to the accuracy potential inherent in double precision calculations. Subsequent tests done by the authors showed that a non-negligible portion of those errors turned out to be due to the type of iteration algorithm used in solving the surface energy balance of CLASS (not shown). However, the source of the vast majority of rounding errors was identified from one additional test in which all input precipitation and soil water content were artificially set to zero. The result, shown in Fig. 4, shows that the rounding errors for this test remained much closer to unit roundoff (within four orders of magnitude), suggesting that most of the errors seen in Fig. 3 were likely caused by various code branches associated with soil water processes, perhaps ill-conditioned branching tests associated with abrupt phase transitions (examples of ill-conditioned branching tests include checking for exact equality between two real numbers or checking for a real number strictly greater than “0.0”—such as for the presence of precipitation—instead of using a finite interval of order machine precision as a comparison basis; such practices are not actual coding errors but are nonetheless frowned upon in numerical analysis circles, even if they remain common in climate and NWP work). For example Fig. 3 shows a series of rather large roundoff events during which relative errors climbed to values slightly above ~10⁻³ at the surface, but then recessed back to more tame values afterwards. Although the ultimate causes for those large rounding errors are still under investigation, the figure tends nonetheless to confirm that rounding error propagation is fundamentally random despite the regularly forced annual cycle at the surface and that the triggering of one roundoff event does not necessarily follow one at the same date the following year (if at all). The above results therefore suggest that code branching effects in soil water processes dominate rounding errors over those due to pure arithmetic operations.

Fig. 3

Absolute magnitudes of the relative errors in soil temperatures of the SPIN_60M_1800S double precision run as compared with an otherwise identical run but compiled at quadruple (128-bit) precision. All CLASS processes were included (moist + dry)

Fig. 4

Same as in Fig. 3 but with CLASS dry processes only, i.e., no surface precipitation and all water removed from the soil, for both double and quadruple precision runs

Despite these considerations, absolute temperature errors in double precision were found to be well below 0.01 °C compared to quadruple precision (not shown) and it is therefore reasonable to assume that the double precision solution is an overall very good approximation of the quadruple precision (i.e., “true”) solution. This is a fortunate result as it circumvents the requirement to use quadruple precision arithmetic for our study—a much more costly alternative.

4.2 Impact of machine roundoff on model spin-up

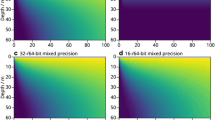
We start our analysis by examining the SPIN_60M_1800S experiment (pair of spin-up runs with a 60 m total depth and initial isothermal conditions of 0 °C). The evolution of soil temperatures over the 100-year period is clearly different between the two levels of precision, as shown in Fig. 5. In the single precision run, the annual cycle signal is well captured and penetrates down to a depth of about 20 m. Also present is a short spin-up signal toward equilibrium during the first 10 years. This penetrating depth of 20 m for the annual cycle is confirmed in Figs. 6 and 7, both in how the amplitude of the annual cycle reaches a threshold of about 0.1 °C at 20 m (chosen to correspond to the accuracy of the soil thermistor probes used in our dataset [Louis Duchesne 2013, personal communication]), and in how the spectral peak of the signal disappears at 20 m in the associated amplitude spectra. We will call this depth the Annual Cycle Penetrating Depth (ACPD) and the depth of 20 m found here is consistent with a detectable annual cycle penetration in permafrost of 15–20 m reported by Yershov (1998). Below the ACPD the single precision simulation is at a standstill with constant temperatures identical to the initial conditions. On the other hand, the double precision run shows a long term spin-up trend clearly superimposed on top of the annual cycle, which extends throughout the entire depth of the profile, and equilibrium has not even quite been reached after 100 years.

Fig. 5

Time evolution of daily soil temperatures for spin-up simulation with soil column depth of 60 m and initial isothermal profile set to 0 °C (SPIN_60M_1800S experiment)

Fig. 6

a Soil temperature time series for the SPIN_60M_1800S experiment at the 15 m depth. Horizontal axis represents time in units of model time steps for the 100-year period of the simulation. b Associated amplitude spectrum, with units in cycles year⁻¹. Red: single precision run; green: double precision run

Fig. 7

Same as in Fig. 6, but for soil level at 20 m depth

This difference in numerical response is more clearly seen when looking at the time rate of change of temperature (i.e., the temperature tendency as defined above), as illustrated in Figs. 8 and 9 where only the first 20 years are shown for clarity. Above the ACPD both precision levels show similar tendency amplitudes associated with the annual cycle of up to ~10⁻⁴ K s⁻¹, or ~10 K day⁻¹, albeit with a slightly smoother appearance in double precision. Below the ACPD tendencies of ~10⁻⁹ K s⁻¹ are present in the double precision run and allow it to capture the long term trend throughout the simulated period. In the single precision run tendencies below 20 m randomly oscillate between zero and ~10⁻⁹–10⁻⁸ K s⁻¹. This is evidently not sufficient to drive the single precision temperatures beyond their initial conditions below the ACPD. The reasons for this are apparent in Fig. 10 in which we see the 100-year averaged annual cycles of temperature tendencies for selected depths. Grey regions represent the width of machine tendency roundoff for single precision, i.e. a width equal to 2τ _single . The figure clearly shows how single precision tendencies deteriorate as they approach their machine precision, until they break down and reach meaningless numerical noise at 20 m. At this point temperatures remain close to their initial values to within machine precision. The double precision tendencies, on the other hand, remain smooth and allow the capture of a true physical signal, as they remain well above their own machine precision of ~10⁻¹⁷ K s⁻¹ right down to the bottom of the profile.

Fig. 8

Absolute magnitudes of daily averaged total soil temperature tendencies for the single precision run of the SPIN_60M_1800S experiment, using a color log scale. The values should be compared with the machine tendency roundoff for single precision $\tau_{single} = 0.9 \times 10^{ - 8} \,{\text{K}}/{\text{s}}$ for a time step of 1800 s. White areas represent tendency magnitudes <$10^{ - 15} {\text{K}}/{\text{s}}$

Fig. 9

Same as in Fig. 8, except for the double precision run of the SPIN_60M_1800S experiment, and values should be compared with the machine tendency roundoff for double precision $\tau_{double} = 1.7 \times 10^{ - 17} {\text{K}}/{\text{s}}$ for a time step of 1800 s. White areas represent tendency magnitudes <$10^{ - 15} {\text{K}}/{\text{s}}$

Fig. 10

Mean annual cycles of soil temperature tendencies for selected depths for experiment SPIN_60M_1800S. The X-axis is labeled with the Day of Year number but data are plotted to show each 30-min time step. Grey shaded rectangles illustrate regions of tendencies that are below machine tendency roundoff for single precision, i.e., where $\left| {\partial T/\partial t} \right| \le \tau_{single}$ for the current time step (invisible at this scale for double precision)

Fig. 11

Temperature time series at the 10 m level for simulations initialized at 0 °C and total column depth of 60 m (SPIN_60M_1800S runs). Red: single precision run; blue: double precision run

Given that single precision calculations were only useful above a depth of 20 m in the experiment, an experiment was performed with the lower boundary set to 20 m (SPIN_20M_1800S, see Fig. 12 showing temperatures at the 10 m depth). The single and double precision runs were found to be much more similar than with the run with a 60 m depth (SPIN_60M_1800S, Fig. 11) although they both achieve a quick spin-up equilibrium after a mere 10–15 years and at a warmer temperature than in the SPIN_60M_1800S runs. This is likely caused by the bottom boundary condition of zero heat flux assumed in CLASS, limiting the effective heat capacity of the soil column. The experiment highlights the fact that double precision cannot be exploited to the fullest with a shallow soil column, nor should single precision be used for deep columns, as this results in both cases in a waste of computer resources.

Fig. 12

Temperature time series at the 10 m level for simulations initialized at 0 °C and total column depth of 20 m (SPIN_20M_1800S runs). Red: single precision run; blue: double precision run

4.3 Impact of machine roundoff in a “global warming” scenario

We next investigate the effect of numerical precision upon the propagation characteristics of a generic surface temperature signal used as a rough proxy for a secular “global warming” signal (GW_60M_1800S experiment). To emulate such a signal, a small positive trend was imposed on the prescribed surface air temperature and downwelling longwave flux data. The added energy is roughly equivalent to a total greenhouse gas forcing of 8 W m⁻² century⁻¹. To avoid contamination of our results by spin-up effects, an isothermal profile of 3.5 °C was set as the initial condition for the soil profile, which was the value found to be the equilibrium temperature of the soil column. Results are shown in Fig. 13. We see that the double precision run can capture a warming trend through the entire 60 m depth of the soil column, whereas the warming in the single precision run barely reaches half this depth by the end of the simulation. Even within its well-resolved region the single precision run slightly underestimates the warming trend compared to the double precision run.

Fig. 13

Time evolution of daily soil temperatures when initialized with an isothermal profile of 3.5 °C with the additional forcing imposed on air temperature and downwelling terrestrial radiation as a small positive trend to emulate a “global warming signal” whose total radiative forcing is roughly equal to 8 W m⁻² century⁻¹ (GW_60M_1800S experiment)

4.4 Impact of time step on machine roundoff

It has already been remarked in Sect. 2 how the length of the time step should influence both machine tendency rounding errors and truncation errors, although these effects should work in opposite directions.

To assess whether this statement holds true, we redid the 60-m deep spin-up and “global warming” experiments but with a time step decreased from 1800 s to 300 s (“SPIN_60M_300S” and “GW_60M_300S”, respectively). The effect on temperature is seen in Fig. 14 where the single precision SPIN_60M_300S run has a distinctly shallower spin-up depth than the SPIN_60M_1800S run in Fig. 5.

Fig. 14

Same as in Fig. 5 but for a time step of 5 min (300 s), and machine roundoffs $\tau_{single} = 5.5 \times 10^{ - 8} {\text{K}}/{\text{s}}$ and $\tau_{double} = 10 \times 10^{ - 17} {\text{K}}/{\text{s}}$ (SPIN_60M_300S experiment)

The same effect can also be seen in the GW_60M_300S experiment. Figure 15 shows that the thermal signal in the single precision run is slower than the GW_60M_1800S experiment in propagating downward, confirming that single precision suffers more readily from a reduction in time step because its basic unit roundoff is already very large.

Fig. 15

Same as in Fig. 13 but with a time step of 5 min (300 s), and machine roundoffs $\tau_{single} = 5.5 \times 10^{ - 8} {\text{K}}/{\text{s}}$ and $\tau_{double} = 10 \times 10^{ - 17} {\text{K}}/{\text{s}}$ (GW_60M_300S experiment)

5 Discussion

To better understand some of the results shown in the last section, we present a simple analytical model in which we assume all surface temperature forcings of our experiments can be approximated by the sum of some periodic functions. We follow Carslaw and Jaeger’s (1959) classic treatment of heat conduction in solids and solve analytically (using notation from Alexeev et al. 2007) the heat equation shown in Eq. (4) over a semi-infinite domain subject to the boundary condition T(z, 0) = A ₀ e ^iωt, giving:

$$T\left( {z,t} \right) = A_{0} e^{ - z/h} e^{{i\left( {\omega t - z/h} \right)}}$$

(12)

Here A ₀ is the amplitude of the forced surface temperature signal, ω is its frequency, z is depth, and $h = \sqrt {2D/\omega }$ is an e-folding damping depth with a dependence on both surface signal frequency and soil thermal diffusivity D. To simplify the analysis the diffusivity D will be held constant. In essence Eq. (12) states that the forced surface temperature signal will both be damped with depth and phase-shifted at a rate $e^{ - z/h}$. Therefore the damping depth is a measure of the rate of decay of the solution with depth and as such has an influence on the region of numerically resolved calculations.

Taking the derivative of Eq. (12) we get:

$$\frac{\partial T}{\partial t} = A_{0} \omega i e^{ - z/h} e^{{i\left( {\omega t - z/h} \right)}}$$

(13)

where the periodic function has now phase-shifted by π/2 due to the imaginary factor ωi appearing through differentiation. The actual amplitude of the tendency signal is the original surface amplitude A ₀ modulated by the signal frequency to give a new tendency amplitude B(z):

$$B\left( z \right) = A_{0} \omega e^{ - z/h} = B_{0} e^{ - z/h}$$

(14)

where B ₀ = 2πA ₀/P is the initial surface tendency amplitude and P is the signal period for frequency ω. Clearly, tendencies will be numerically resolved as long as B(z) remain larger than our machine tendency roundoff metric, i.e., B(z) > τ _p . Equation (14) says that the surface signal tendency B ₀ not only depends on the signal’s initial amplitude A ₀ but also on its period. In particular: (1) signals with short periods (e.g., <~10⁷ s or ~1 year) will tend to have large surface tendencies but will quickly damp with depth (due to the e ^−z/h factor), and (2) signals with long periods (e.g., ≫ 1 year) will tend to have small surface tendencies but will damp slowly with depth. Therefore, even though they suffer less from damping with depth, it is the relatively large time scales that are more vulnerable to lower numerical precision. For extremely long periods, even the forcing signal at the surface will eventually fall below machine precision (assuming constant amplitude). Equation (14) further shows that the only way to compensate for the small tendencies of a long period signal is to increase its signal amplitude A ₀, but this has minimal effect in general because amplitude values are usually orders of magnitude smaller than the typical values of long periods (~10⁸–10⁹ s or ~10–100 years). Therefore Eq. (14) tells us that signals with large time scales will be best resolved by using high precision and a deep enough domain to correctly capture their (weakly damped) downward propagation. For small time scales, normally associated with large tendencies, more modest precision and a shallow domain are sufficient, and there is no strict need to use a deep domain (since they tend to damp quickly with depth anyway).

Our analytical model also elucidates why only the single precision diurnal (~10⁵ s period) and annual (~10⁷ s period) cycles could comfortably be resolved within the ACPD since they correspond to surface tendencies B ₀ of ~10⁻⁴ and 10⁻⁶ K s⁻¹, respectively, equivalent to only 2–4 significant decimal digits. Further, the much shorter spin-up times of single precision (as was observed in Fig. 5) can be explained by the fact that, as the initial, crudely resolved single precision tendencies are only slightly larger than τ _single , they quickly level off into unresolved territory near τ _single . In fact a rough estimate of the theoretical upper limit of the spin-up time for single precision would give a value of about 21 years (solving for P _max  = 2πA ₀/4τ _p with B ₀ = τ _p , or machine roundoff, and $A_{0} = 4 K$), slightly larger than our estimated 10–15 years in Fig. 11. In contrast, the same P _max applied to double precision would give a value of about 80 billion years, while the maximum possible depth z in Eq. (14) would reach beyond 1000 m.

Regarding the “global warming” runs (GW_60M_1800S and GW_60M_300S), temperature gradients (due to the continuous input of energy at the surface) must build up to much higher values when using single precision before triggering a non-zero heat flux, resulting in a much slower downward propagation of the thermal signal. Therefore single precision would not be sufficient to capture important processes such as the thawing of deep permafrost in future climate scenarios, and the thawing of shallow permafrost would likely be underestimated.

Finally, the peculiar sensitivity of rounding errors to the time step used in time derivatives could have a negative impact on regional climate models whose horizontal resolutions now routinely go below 20 km, and which, for reasons of computational stability, impose an upper limit of a few 100 s on their time steps (e.g. 300 s for CRCM5 run at 10 km resolution). In the case of experimental numerical weather prediction (NWP) models, now often running at sub-kilometer resolutions, this constraint is even more severe, with time steps that can reach values well under 30 s, forcing values of τ _single to be no better than ~10⁻⁶ K s⁻¹. In other words if such a model would happen to be used in a climate mode setting it would not be able to capture deep soil temperature tendencies smaller than the equivalent of about 3000 K century⁻¹ (this of course assumes that both land surface and atmosphere run with the same time step length—which is not mandatory in principle—however, as far as we are aware, most climate models use the same time step operationally for the land and atmosphere). This strongly suggests that, in the not-so-distant future, the use of single precision models for simulating deep soil temperatures will become more difficult to justify with the expected high resolution levels mentioned earlier, whereas the same models used at double precision will still be able to resolve tendencies of at least ~10⁻¹⁵ K s⁻¹, or about ~10⁻⁶ K century⁻¹.

6 Summary and conclusions

The arrival of large-scale distributed-memory parallel platforms in scientific computing has been associated with the potential occurrence of more frequent numerical anomalies such as potentially more frequent rounding errors. This is because achieving the highest performance in parallel platforms almost always requires making compromises on stability and reproducibility due to the need to minimize data coordination and transfer between processors and maximizing scaling toward large-scale platforms. While the occurrence of rounding errors seem to have been quite rare in the narrower fields of numerical weather prediction and climate modelling, this could change if single precision models begin to be used in long-term climate simulations (e.g. the near-surface permafrost study of Paquin and Sushama 2015).

This paper has investigated the impact of using different levels of numerical precision on offline simulations of deep soil temperatures using the Canadian Land Surface Scheme CLASS. We have shown that single precision offers very limited levels of accuracy, with time tendencies restricted to no better than about 10⁻⁸ K s⁻¹, meaning that deep soil tendencies less than the equivalent of about 30 K century⁻¹ simply cannot be computed. This is at least three times too large compared to the expected secular increase in soil temperatures over the next several decades, and it prevents useful single precision calculations from reaching much beyond depths of 20–25 m. Even within these depths, our results indicated that time scales larger than a few years were poorly captured at best, a fact confirmed by an analytical model of deep soil diffusion. Therefore soil temperature spin-up times from arbitrary initial conditions were found to be much shorter than in double precision runs by a factor of at least 10 due to the single precision tendencies quickly reaching their minimal accuracies after only 10–15 years. In fact, double precision calculations showed no sign of deterioration through the entire 60-m deep columns, and they could theoretically be used over soil depths of at least several 100 m. Simulations imposing a constant “global warming” heat input at the surface also showed similar depth restrictions due to the use of single precision, with the warming signals being systematically underestimated compared to double precision. Finally, we have shown that using smaller time steps caused rounding errors to actually increase, even though this also caused an equivalent reduction in time truncation errors, further reducing the global usefulness of single precision calculations. We conclude that there is an overall clear danger in using single precision in some applications of climate models. In particular all deep soil climate studies, including those related to permafrost, must at least use double precision.

With the scale of parallel computers continuing to grow in the foreseeable future (rendering software users more vulnerable to rounding errors and other numerical anomalies), it would undoubtedly be beneficial for climate modelling circles (and even NWP) to make a paradigm shift in their model development toward new practices of software verification that go beyond the standard (but still essential) validation against observed data. First, our results clearly show that climate and NWP development circles both should plan on limiting precision of future model versions to double precision as a bare minimum. Even if many such models already run at double precision at the present time, large discrepancies still exist between modelled and observed data (although this does not necessarily invalidate the model’s usefulness), and the contribution of rounding errors to these differences is largely unknown. However before implementing complex and costly plans for such endeavors, simple solutions can already be tried out. For example, at some stage in the development of a new parameterization scheme, the code could be run cheaply offline at say quadruple precision and compared with a double precision run to identify potentially excessive rounding errors, or even help diagnose other programming issues related to parallel code implementations that would otherwise be hard to detect. Our own quadratic precision runs showed that double precision errors could be much larger than what one would naively expect by simply looking at the magnitude of unit roundoff. Our proposed paradigm shift could become even more relevant at a time when NWP and climate models (especially regional climate models) will eventually move toward spatial resolutions below 10 km; this will reveal new smaller-scale and more rapid motions (unresolved until now) and their steep gradients will likely be resolved with adequate accuracies (albeit with large truncation errors), but the scales that used to be resolved with coarser grids and longer time steps will now involve smaller differences in time and space. It is conceivable that the resultant loss of accuracy (due to smaller time steps and space increments) could force the adoption of larger word sizes when computing the same derivatives so as to maintain a reasonably high level of accuracy. It remains to be seen whether this, coupled with the fact that those models will be run on parallel computers of ever increasing scale, will require the use of precision levels even larger than double precision. Is this paper only the tip of the iceberg for unforeseen numerical problems in large-scale parallel simulations of the climate system? Only time will tell.