Path Coverings with Prescribed Ends in Faulty Hypercubes

Abstract

We discuss the existence of vertex disjoint path coverings with prescribed ends for the $n$-dimensional hypercube with or without deleted vertices. Depending on the type of the set of deleted vertices and desired properties of the path coverings we establish the minimal integer $m$ such that for every $n \ge m$ such path coverings exist. Using some of these results, for $k \le 4$, we prove Locke’s conjecture that a hypercube with $k$ deleted vertices of each parity is Hamiltonian if $n \ge k +2.$ Some of our lemmas substantially generalize known results of I. Havel and T. Dvořák. At the end of the paper we formulate some conjectures supported by our results.

Appendices

Appendix A: 2-Path Coverings of ${\mathcal {Q}}_4$

When a neutral pair is deleted from ${\mathcal {Q}}_4$ one can still freely prescribe the ends for a 2-path covering of the resulting graph. In spite the fact that the dimension is so low we find it difficult to verify this statement by inspection. Therefore, we provide a proof below for the benefit of the reader.

Lemma 7.1

Let ${\mathcal {F}}=\{r,g\}$ be a neutral fault in ${\mathcal {Q}}_4,$ and $r_1,r_2,g_1,g_2$ be two red and two green vertices in ${\mathcal {Q}}_4-{\mathcal {F}}.$ Then there exists a 2-path covering of ${\mathcal {Q}}_4 -{\mathcal {F}}$ with one path connecting $r_1$ to $g_1$ and the other connecting $r_2$ to $g_2.$

Proof

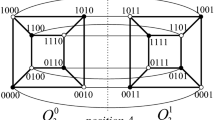
The deleted vertices $r$ and $g$ have opposite parity and belong to ${\mathcal {Q}}_4$. Therefore we can split ${\mathcal {Q}}_4$ in such way that both vertices belong to the same plate, say ${\mathcal {Q}}_4^{top}$. We consider all essentially different cases that depend on the distribution of the vertices $r_1,r_2,g_1,g_2$ between the plates.

Case 1. $r_1,r_2,g_1,g_2 \in {\mathcal {Q}}_4^{top}$.

Subcase 1(a). Let $\{r_1,g_1\}, \{r_2,g_2\} \in \mathcal {B}_{\{r,g\}}.$ Then there exists a one-letter word $x$ such that $(r_1,x), (g_1,x)$ is a 2-path covering of ${\mathcal {Q}}_4^{top} -\{r,g,r_2,g_2\}.$ Let $(r_1 x v, \mu ), (r_2 v, \nu )$ be a 2-path covering of ${\mathcal {Q}}_4^{bot}$ that connects $r_1 xv$ to $g_1 x v,$ and $r_2 v$ to $g_2v.$ Such path covering exists since $[0,0,2,0]=2.$ The desired 2-path covering of ${\mathcal {Q}}_4 -\{r,g\}$ is $(r_1, x v \mu v x),$ $(r_2, v \nu v ).$

Subcase 1(b). If either $\{r_1,g_1\}$ or $\{r_2,g_2\}$ is not in $\mathcal {B}_{\{r,g\}}$ we can assume without loss of generality that $\{r_1,g_1\} \not \in \mathcal {B}_{\{r,g\}}.$ Then, according to Lemma 3.5(1), there exists a Hamiltonian path $(r_1, \xi )$ of ${\mathcal {Q}}_4^{top}-\{r,g\}$ that connects $r_1$ to $g_1$. Let $\xi = \eta \theta \zeta$ with $(r_1 \eta , r_1 \eta \theta )$ equals $(r_2, g_2)$ or $(g_2,r_2).$ Let also $(r_1 \eta ' v, \mu )$ be a Hamiltonian path of ${\mathcal {Q}}_4^{bot}$ that connects $r_1 \eta ' v$ to $g_1 (\zeta ^R)'v.$ The desired 2-path covering of ${\mathcal {Q}}_4 - \{r,g\}$ is $(r_1, \eta ' v \mu v \zeta ^*), (r_1\eta , \theta ).$ Case 2. $r_1,r_2,g_1$ are on the top plate and $g_2$ is on the bottom plate.

Subcase 2(a). If $\{g_1,r_2\} \not \in \mathcal {B}_{\{r,g\}}$ then, according to Lemma 3.5(1), there exists a Hamiltonian path $(g_1, \omega )$ of ${\mathcal {Q}}_4^{top}- {\mathcal {F}}$ that connects $g_1$ to $r_2.$ Let $\omega = \xi \eta$ with $g_1 \xi = r_1$ and let $( r_1 \varphi (\eta )v, \theta )$ be a Hamiltonian path of $Q_4^{bot}$ that connects $r_1 \varphi (\eta )v$ to $g_2.$ The desired 2-path covering of ${\mathcal {Q}}_4 - \{r,g\}$ is $(g_1, \xi ), (g_2,\theta ^R v \eta ^*).$

Subcase 2(b). If $\{g_1,r_2\} \in \mathcal {B}_{\{r,g\}}$ then $\{g_1,r_1\} \not \in \mathcal {B}_{\{r,g\}}$ and there exists a Hamiltonian path $(g_1, \omega )$ of ${\mathcal {Q}}_4 - {\mathcal {F}}$ that connects $g_1$ to $r_1.$ Let $\omega =\xi \eta$ with $g_1 \xi = r_2.$ We have to consider two sub-subcases:

• (i) $g_2v = r_1$ or $g_2v = r_2.$ We observe that the lengths of $\xi$ and $\eta$ are $1$ and $4$ or $3$ and $2.$ If $\xi$ is the longer word, then we use $[0,0,2,0]=2$ to produce a 2-path covering $(g_1 \xi 'v, \mu ), (g_1 \xi ''v, \nu )$ of ${\mathcal {Q}}_4^{bot}$ that connects $g_1 \xi ' v$ to $g_2$ and $g_1 \xi ''v$ to $r_2 \varphi (\eta )v.$ The desired 2-path covering of ${\mathcal {Q}}_4 - \{r,g\}$ is $(g_1, \xi ''v\nu v \eta ^*), (g_2,\mu ^R v \varphi (\xi ^R)).$ If $\eta$ is the longer word, then we use $[0,0,2,0]=2$ to produce a 2-path covering $(g_1 \xi 'v, \mu ), (r_2 \varphi (\eta )v , \nu )$ of ${\mathcal {Q}}_4^{bot}$ that connects $g_1 \xi ' v$ to $r_1 (\eta ^R)''v$ and $r_2 \varphi (\eta )v$ to $g_2.$ The desired 2-path covering of ${\mathcal {Q}}_4 - \{r,g\}$ is $(g_1, \xi 'v\mu v \eta ^{**}), (r_2, \varphi (\eta )v\nu ).$

• (ii) $g_2v$ is an interior vertex of the path $(g_1, \omega ).$ If $\xi = \theta \zeta$ with $g_1 \theta = g_2 v$ then we use $[1,1,0,1]=2$ to produce a Hamiltonian path $(g_1 \theta ' v , \mu )$ of ${\mathcal {Q}}_4^{top} - \{g_2\}$ that connects $g_1\theta ' v$ to $r_2 \varphi (\eta )v.$ The desired 2-path covering of ${\mathcal {Q}}_4 - \{r,g\}$ is $(g_1, \theta ' v \mu v \eta ^* ), (r_2, \zeta ^R v ).$ If $\eta = \theta \zeta$ with $r_2 \theta = g_2 v$ then we use $[1,1,0,1]=2$ to produce a Hamiltonian path $(g_1 \xi ' v , \mu )$ of ${\mathcal {Q}}_4^{top} - \{g_2\}$ that connects $g_1\xi ' v$ to $r_1 (\zeta ^R)'v.$ The desired 2-path covering of ${\mathcal {Q}}_4 - \{r,g\}$ is $(g_1, \xi ' v \mu v \zeta ^* ), (r_2, \theta v).$

Case 3. $r_1,r_2 \in {\mathcal {Q}}_4^{top}$ and $g_1,g_2 \in {\mathcal {Q}}_4^{bot}$.

Find a Hamiltonian path of ${\mathcal {Q}}_4^{top}-\{g\}$ that connects $r_1$ to $r_2$. The vertex $r$ belongs to that path. Cut that path just before $r$ and right after $r$ and connect these two vertices with bridges to the bottom plate. Let $r_3$ and $r_4$ be the ends of these bridges that belong to the bottom plate. Then use $[0,0,2,0]=2$ to find a 2-path covering of the bottom plate that connects $r_3$ and $r_4$ to the appropriate vertices $g_1$ and $g_2$.

Case 4. $r_1,g_1 \in {\mathcal {Q}}_4^{top}$ and $r_2,g_2 \in {\mathcal {Q}}_4^{bot}$.

Consider ${\mathcal {Q}}_4^{top}$. It is not difficult to verify that either there is a Hamiltonian path for ${\mathcal {Q}}_4^{top}-\{r,g\}$ that connects $r_1$ to $g_1$ or there is a path with length $3$ connecting $r_1$ to $g_1$ such that exactly one edge remains not covered. In the first case use $[0,0,1,0]=1$ to find a Hamiltonian path for ${\mathcal {Q}}_4^{bot}$ connecting $r_2$ to $g_2$. In the second case denote by $r_3$ and $g_3$ the vertices in the bottom plate that are neighbors of the vertices in ${\mathcal {Q}}_4^{top}$ that are not covered. Use Corollary 3.2 to find a Hamiltonian path for ${\mathcal {Q}}_4^{bot}$ that connects $r_2$ to $g_2$ and passes trough the edge $\{r_3,g_3\}$. Cut that path at that edge and using two bridges connect both pieces to the non-covered edge from the top plate.

Case 5. $r_1,g_2 \in {\mathcal {Q}}_4^{top}$ and $r_2,g_1 \in {\mathcal {Q}}_4^{bot}$.

We consider two subcases:

Subcase 5(a). Assume that $\{r_1,g_2\} \not \in \mathcal {B}_{\{r,g\}}.$ Then there is a Hamiltonian path $(r_1, \xi )$ of ${\mathcal {Q}}_4^{top}- \{r,g\}$ that connects $r_1$ to $g_2.$ There are three sub-subcases that depend on whether or not $r_2$ or $g_1$ are adjacent to vertices inside of the path $(r_1, \xi ).$

• (i) Assume that $\xi = \eta \theta$ with $r_1 \eta v= g_1.$ Let $(r_1 \eta \varphi (\theta )v, \mu )$ be a Hamiltonian path of ${\mathcal {Q}}_4^{bot}- \{g_1\}$ that connects $r_1 \eta \varphi (\theta )v$ to $r_2.$ The desired 2-path covering of ${\mathcal {Q}}_4 - {\mathcal {F}}$ for this case is $(r_1, \eta v), (r_2, \mu ^R v \theta ^*).$

• (ii) Assume that $\xi = \eta \theta$ with $g_2 \theta ^R v= r_2.$ Let $(r_1 \eta 'v, \mu )$ be a Hamiltonian path of ${\mathcal {Q}}_4^{bot}- \{r_2\}$ that connects $r_1 \eta ' v$ to $g_1.$ The desired 2-path covering of ${\mathcal {Q}}_4 - {\mathcal {F}}$ for this case is $(r_1, \eta ' v \mu ), (r_2, v \theta ).$

• (iii) Finally, let neither $r_2$ nor $g_1$ be adjacent to a vertex in the path $(r_1,\xi ).$ Let $\xi = x y \eta$ for some letters $x,y,$ and a word $\eta .$ Then there is a 2-path covering $(r_1xv, \mu ), (r_1 xyv,\nu )$ of ${\mathcal {Q}}_4^{bot}$ that connects $r_1xv$ to $g_1$ and $r_1 xy v$ to $r_2.$ The desired 2-path covering of ${\mathcal {Q}}_4 - {\mathcal {F}}$ for this case is $(r_1,xv \mu ), (r_2, \nu ^R v\eta ).$

Subcase 5(b). Let $\{r_1,g_2\} \in \mathcal {B}_{\{r,g\}}.$ Then, according to Lemma 3.5, there exist two distinct 2-path coverings of ${\mathcal {Q}}_4^{top}-\{r,g\}$ with paths of length $2,$ one starting at $r_1$ and the other starting at $g_2.$ We can choose a 2-path covering of ${\mathcal {Q}}_4^{top}-\{r,g\}$ to be $(r_1, \xi ), (g_2,\eta ),$ with $r_1 \xi v \ne g_1$ or $g_2 \eta v \ne r_2.$ There are three sub-subcases:

• (i) Let $r_1 \xi v \ne g_1$ and $g_2 \eta v \ne r_2.$ Let $(r_1 \xi v, \mu ), (g_2 \eta v, \nu )$ be a 2-path covering of ${\mathcal {Q}}_4^{bot}$ that connects $r_1 \xi v$ to $g_1$ and $g_2 \eta v$ to $r_2.$ The desired 2-path covering of ${\mathcal {Q}}_4 - {\mathcal {F}}$ for this case is $(r_1,\xi v \mu ), (g_2, \eta v \nu ).$

• (ii) Let $r_1 \xi v \ne g_1$ and $g_2 \eta v = r_2.$ Let $(r_1 \xi v, \mu )$ be a Hamiltonian path of ${\mathcal {Q}}_4^{bot}- \{r_2\}$ that connects $r_1 \xi v$ to $g_1.$ The desired 2-path covering of ${\mathcal {Q}}_4 - {\mathcal {F}}$ for this case is $(r_1,\xi v \mu ), (g_2, \eta v ).$

• (iii) Let $r_1 \xi v = g_1$ and $g_2 \eta v \ne r_2.$ This case is completely symmetrical to case (ii).

Case 6. $r_1 \in {\mathcal {Q}}_4^{top}$ and $r_2,g_1,g_2 \in {\mathcal {Q}}_4^{bot}$.

Use Lemma 3.4 to find a Hamiltonian path of ${\mathcal {Q}}_4^{top}-\{g\}$ that connects $r$ to $r_1$ and such that the vertex $g_3$ which is next to $r$ in this path is not adjacent to $r_2$. Let the second end of the bridge that begins at $g_3$ be $r_3$. Use $[0,0,2,0]=2$ to find a 2-path covering of the bottom plate that connects $r_3$ to $g_1$ and $r_2$ to $g_2$.

Case 7. $r_1,r_2,g_1,g_2 \in {\mathcal {Q}}_4^{bot}$.

Use [0,0,2,0]=2 to find a 2-path covering of $Q_4^{bot}$ that connects $r_1$ to $g_1$ and $r_2$ to $g_2$. Then find an edge that belongs to one of the two paths whose neighbors $r_3$ and $g_3$ in $Q_4^{top}$ are not deleted vertices and also $\{r_3,g_3\} \not \in \mathcal {B}_{\{r,g\}}.$ Cut that path at that edge and use Lemma 3.5 to find a Hamiltonian path for $Q_4^{top}-\{r,g\}$ that connects $r_3$ to $g_3$. $\square$

Appendix B: Summary of Results

The following table summarizes some of the results obtained in this paper. The rows represent admissible combinations of $M$ and $C$ and the columns contain all the values of $N$ and $O$ such that $N+O \le 3$. Each star in the table represents an impossible case. The missing entries in the table correspond to values of $[M,C,N,O]$ that we do not know yet. The inequalities in the table represent an upper or lower bound of the corresponding entry. Finally, the entries with an asterisk are results that were obtained after this paper was submitted for publication and therefore their proofs are not contained in this paper.

$MC \backslash NO$	01	10	20	11	02	30	21	12	03
00	$\star$	1	2	$\star$	4	5	$\star$	$4^*$	$\star$
11	2	$\star$	$\star$	4	$\star$	$\star$	$5^*$	$\star$	$5^*$
20	$\star$	4	4	$\star$	5		$\star$		$\star$
22	$\star$	$\star$	$\star$	$\star$	4	$\star$	$\star$	$\le 6$	$\star$
31	4	$\star$	$\star$	5	$\star$	$\star$		$\star$
33	$\star$	$\star$	$\star$	$\star$	$\star$	$\star$	$\star$	$\star$	$\le 6$
40	$\star$	5	$5^*$	$\star$			$\star$		$\star$
42	$\star$	$\star$	$\star$	$\star$	5	$\star$	$\star$		$\star$
44	$\star$	$\star$	$\star$	$\star$	$\star$	$\star$	$\star$	$\star$	$\star$
51	5	$\star$	$\star$	$\ge 5$	$\star$	$\star$		$\star$